 , 李柏纬, 陈文
, 李柏纬, 陈文河海大学力学与材料学院工程与科学数值模拟软件中心, 南京 211100
GENERALIZED FINITE DIFFERENCE METHOD FOR BIOHEAT TRANSFER ANALYSIS ON SKIN TISSUE WITH TUMORS1)
LiAilun, FuZhuojia , LiPowei, ChenWen
, LiPowei, ChenWen中图分类号:O302
文献标识码:A
通讯作者:
收稿日期:2018-05-9
网络出版日期:2018-09-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
展开
摘要
关键词:
Abstract
Keywords:
-->0
PDF (3985KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
生物传热分析在低温外科手术、肿瘤热疗法、病热诊断技术等临床医学的治疗与诊断中有着广泛的应用. 生物传热分析检测肿瘤的基本原理是由于肿瘤与健康皮肤组织的代谢热和血液灌注率存在较大差异, 导致健康皮肤组织内的温度在肿瘤附近区域有明显升高, 以此通过比较正常组织和感染组织的温谱图来检测皮肤组织内的肿瘤生长.目前主要的生物传热数值方法包括有限差分法(finite difference method)[1-2]、有限元法(finite element method)[3-4]、边界元法(boundary element method)[5-6]等网格类离散方法. 其中, 邓中山等[7] 将双重互易边界元法应用至低温外科手术中的多维相变问题; 刘朝霞等[8]利用特解边界元法模拟热疗温度场; Dehghan等[9] 利用谱元法模拟含肿瘤皮肤组织的温度分布.
另一方面, 近年来一些****将无需网格划分且编程简单的配点技术引入到各类传热问题中[10-12], 并进一步应用至生物传热问题数值计算中, 如: Chebyshev谱配点法[13]、 径向基函数配点法[14-15]、近似特解法[16]等. 无网格法按采用的加权余量法分类可以分为伽辽金型方法[17]、配点型方法[18]、局部弱形式方法等[19-20]. 伽辽金型方法与局部弱形式方法仍需布置背景网格并进行积分计算, 而配点型方法在计算时借助离散点来构造近似函数, 并通过插值得到数值解, 无需划分网格, 前后处理简便. 然而大多数配点技术离散得到的插值矩阵通常高度病态, 大大限制了此类算法的大规模工程应用.
为了克服配点型方法的这一算法缺陷, 一些处理矩阵病态性的技术相继被提出, 如: 局部支撑基函数技术[21]、局部化无网格配点技术
[22]、 扩展精度技术等[23]. 其中, 广义有限差分法(generalized finite difference method)首先由Benito等[24] 于2001年提出. 该方法属于一类局部化无网格配点技术, 其主要思想是将计算区域内每个离散点在其邻近点进行泰勒展开, 并基于最小二乘法的原理将离散点上的物理量导数表示成邻近点物理量及权重系数的线性累加, 进而构建得到仅含各离散点未知物理量的线性方程组. 该方法不仅保留了无网格配点法本身的优点, 同时得到类似于有限元法的稀疏矩阵, 避免产生大多数配点技术的病态矩阵问题. 鉴于这些特点, 近年来广义有限差分法被广泛应用于诸如三维瞬变电磁问题[25]、求解浅水波方程[26]等各类问题的求解.
本文将广义有限差分法应用于含肿瘤皮肤组织的传热数值模拟. 首先给出模拟含肿瘤皮肤组织传热过程的广义有限差分法离散模型. 随后通过不含肿瘤与含规则形状肿瘤的基准算例, 检验广义有限差分法的计算精度与收敛性; 在此基础上, 数值研究不同肿瘤形状及肿瘤位置分布对皮肤组织内温度分布的影响.
1 数学模型
1.1 控制方程
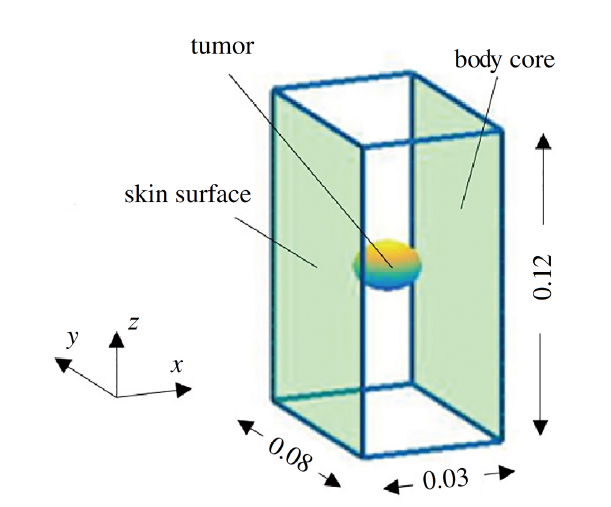
Pennes生物传热方程[27]是目前应用最广泛的描述生物传热过程及特性的数学模型. 本文以含肿瘤的皮肤组织作为研究对象, 选取一个经典模型[15-16,28]进行计算分析. 如图1所示, 该模型考虑一个长方体型的皮肤组织区域, 其计算域范围为$[0,0.03]\times[-0.04,0.04]\times[-0.06,0.06]$, 即计算域的大小为$0.03~\text m\times0.08~\text m\times0.12~\text m$. 该模型假定皮肤组织全部为真皮组织, 肿瘤则嵌在真皮组织内. 其中, $\varOmega_\textrm{τ}$与$\varOmega_\text s$ 分别表示肿瘤组织及健康皮肤组织; $\varGamma_1$为面向人体内部的边界, $\varGamma_2$为人体皮肤外表面, $\varGamma_\text I$为肿瘤组织与皮肤组织交界面, 其他绝热边界为$\varGamma_3$
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图1计算域示意图
-->Fig.1Schematic diagram of computational domain
-->
在计算域内温度分布满足Pennes方程
\begin{equation*}\begin{split}&\rho c\dfrac{\partial}{\partial t}u(x,y,z,t)=k\nabla^2 u(x,y,z,t)+\\&\quad\quad\quad\omega_\text b\rho_\text b c_\text b(u_\text a-u(x,y,z,t))+Q\end{split}\tag*{(1)}\end{equation*}
式中, $k$, $\rho$, $c$分别表示皮肤组织的恒定热传导率、密度以及比热; $\omega_\text b$, $\rho_\text b$, $c_\text b$, $Q$分别表示求解区域的血液的灌注率、密度、比热及代谢产热率. $u_\text a$表示皮肤组织正常温度, 即$u_\text a=37^\circ \text C$. 表1 给出了肿瘤与健康皮肤组织的各参数取值[9,29].
Table 1
表1
表1Pennes方程的各参数取值
Table 1Parameters of Pennes equation
| Parameters | Skin tissue | Tumor tissue |
|---|---|---|
| P(Pb) | 1000 kg/m3 | 1000 kg/m3 |
| C(Cb) | 4000 J/(kg ·°C) | 4000 J/(kg ·°C) |
| k | 0.5 W/(m ·°C) | 0.55 W/(m ·°C) |
| Q | 420 W/m3 | 4200 W/m3 |
| Wb | 0.000 5 m3/s | 0.002 m3/s |
新窗口打开
1.2 边界条件及初始条件
由于边界$\varGamma_1$面向人体内部组织, 认为该边界上有第一类热边界条件\begin{equation*}u(x,t)=37^\circ\text C,x\in\varGamma_1\tag*{(2)}\end{equation*}
边界$\varGamma_2$与外界环境接触, 假设皮肤被衣物覆盖, 热量不向外扩散, 有边界条件
\begin{equation*}\dfrac{\partial u(x,t)}{\partial n}= 0,x\in\varGamma_2\tag*{(3)}\end{equation*}
其他边界记为$\varGamma_3$, 由于距离肿瘤较远区域不受肿瘤影响, 因此有边界条件
\begin{equation*}\dfrac{\partial u(x,t)}{\partial n}= 0,x\in\varGamma_3\tag*{(4)}\end{equation*}
在人体组织与肿瘤组织的分界面$\varGamma_\text I$上, 温度与热通量均保持连续, 则有界面连续性条件
\begin{equation*}\left.\begin{split}&u_\text T(x,t)=u_\text s(x,t) &\dfrac{\partial}{\partial n}u_\text T(x,t)+\dfrac{\partial}{\partial n}u_\text s(x,t)= 0,x\in\varGamma_\text I\\\end{split}\right\}\tag*{(5)}\end{equation*}
初始条件为
\begin{equation*}u(x,0)=37^\circ\text C,x\in\varOmega\tag*{(6)}\end{equation*}
2 数值方法
2.1 时间离散
本文采用了无条件稳定的隐式差分格式对Pennes方程(1)中的时间项进行离散, 得到以下形式\begin{equation*}\begin{split}&\Bigg(1+\Delta t\cdot\dfrac{\omega_\text b\rho_\text b c_\text b}{\rho c}-\Delta t\cdot\dfrac{k}{\rho c}\nabla^2\Bigg)u^{j+1}=\\&\quad u^j+\Delta t\cdot\dfrac{\omega_\text b\rho_\text b c_\text b}{\rho c}\cdot u_\text a+\Delta t\cdot\dfrac{Q}{\rho c}\end{split}\tag*{(7)}\end{equation*}
式中, $u^j$与$u^{j+1}$分别为$j$时刻与$j+1$时刻的温度, $\Delta t$为时间步长.
2.2 广义有限差分法
将计算域进行空间离散, 针对计算域中的某个离散点$f_k(x_k,y_k,z_k)$, 其在点$f_j(x_j,y_j,z_j)$ 的二阶泰勒展开形式为\begin{equation*}f_k=f_j+\nabla f_j{ H_j}+\dfrac{1}{2}{ H_j}\nabla^2f_j{ H_j}+o(\rho^2)\tag*{(8)}\end{equation*}
式中$ H_j=(x_j-x_k,y_j-y_k,z_j-z_k)$, 表示两点间的欧式距离, $o(\rho^2)$表示2阶余项.
令点$f_k$在邻近的$ns$个离散点进行泰勒展开, 并据此定义一个残差函数$B$
\begin{equation*}B=\sum\limits^{ns}_{j=1}\Bigg[\Bigg(f_j-f_k+\nabla f_j H_j+\dfrac{1}{2} H_j\nabla^2f_j H_j\Bigg)\omega_j\Big( H_j\Big)\Bigg]^2\tag*{(9)}\end{equation*}
式中, $\omega_j$为与欧式距离有关的权重函数[30]
\begin{equation*}\omega_j={d_{jk}}^{-3}\tag*{(10)}\end{equation*}
权重函数表征邻近点对离散点的影响程度, 与离散点距离越近影响越大, 反之越小.
令$ D_k$表示点$f_k$的物理量导数向量
\begin{equation*}\begin{split}& D_k=\Bigg\lgroup\dfrac{\partial f_k}{\partial x},\dfrac{\partial f_k}{\partial y},\dfrac{\partial f_k}{\partial z},\dfrac{\partial^2 f_k}{\partial x^2},\dfrac{\partial^2 f_k}{\partial y^2},\dfrac{\partial^2 f_k}{\partial z^2},\\&\quad\quad\quad\dfrac{\partial^2 f_k}{\partial x\partial y},\dfrac{\partial^2 f_k}{\partial x\partial z},\dfrac{\partial^2 f_k}{\partial y\partial z}\Bigg\rgroup^\text T\end{split}\tag*{(11)}\end{equation*}
根据最小二乘法的思想, 令残差函数$B$取极小值
\begin{equation*}\dfrac {\partial B}{\partial D_k}= 0\tag*{(12)}\end{equation*}
由式(12)可以推导得到包含9个未知量$( D_k)$的线性方程组. 该方程组可以表示成如下的矩阵形式
\begin{equation*} A_k D_k= b_k\tag*{(13)}\end{equation*}
式中
\begin{equation*} A_k=\sum\limits^{ns}_{j=1}\text{diag}( E_{jk}) L\text{diag}( E_{jk})\tag*{(14)}\end{equation*}
$ A_k$为对称矩阵, $ L$为9×9矩阵, 元素全部为1, $\text{diag}( E_{jk})$ 代表对角元素为$ E_{jk}$的对角矩阵. 其中
\begin{equation*} E_{jk}=\omega_j( H_j)\begin{bmatrix}x_j-x_k\\y_j-y_k\\z_j-z_k\\(x_j-x_k)^2/2\\(y_j-y_k)^2/2\\(z_j-z_k)^2/2\\(x_j-x_k)(y_j-y_k)(x_j-x_k)(z_j-z_k) (y_j-y_k)(z_j-z_k)\end{bmatrix}\tag*{(15)}\end{equation*}
$ b_k$为$9\times 1$的向量, 可以分解为如下形式
\begin{equation*} b_k= M_k F_k=\Bigg(-\sum\limits^{ns}_{j=1} E_{jk}, E_{1k},\cdots, E_{jk}\Bigg)\begin{bmatrix}f_k\\f_1\\f_2\\\vdots\\f_{ns}\end{bmatrix}\tag*{(16)}\end{equation*}
则由式(13) $\sim$式(16)可得
\begin{equation*} D_k=\begin{bmatrix}\dfrac{\partial f_k}{\partial x}\\\dfrac{\partial f_k}{\partial y}\\\dfrac{\partial f_k}{\partial z}\\\vdots\\\dfrac{\partial^2 f_k}{\partial y\partial z}\end{bmatrix}= A_k^{-1} M_k\begin{bmatrix}f_k\\f_1\\f_2\\\vdots\\f_{ns}\end{bmatrix}= K\begin{bmatrix}f_k\\f_1\\f_2\\\vdots\\f_{ns}\end{bmatrix}\tag*{(17)}\end{equation*}
即离散点的物理量导数项可以由已知矩阵$K$与离散点的物理量值表示. 令计算域内的点满足控制方程(7), 同时强迫边界点满足边界条件(2) $\sim$ (5), 即可得到仅含离散点未知物理量的线性方程组, 求解此线性方程组即可得到各离散点上的数值解.
3 数值结果与讨论
本节首先通过求解文献中的经典算例来验证本文算法的有效性, 并在此基础上数值研究不同肿瘤形状及肿瘤位置分布对皮肤组织内温度分布的影响. 其中数值解达到稳态的判定依据如下\begin{equation*}|u^{j+1}-u^j|\leqslant\varepsilon\tag*{(18)}\end{equation*}
3.1 算例1$~$不含肿瘤皮肤组织热传导问题
首先考虑不包含肿瘤的情况, 即$\varOmega_\text T=\varnothing$. 文献中给出了达到稳态情况时的温度分布[29]\begin{equation*}u_\text s(x,y,z,\infty)=37+\dfrac{Q}{\omega_\text b\rho_\text bc_\text b}\Bigg(1-\dfrac{\text e^{Px}+\text e^{-Px}}{\text e^{0.03x}+\text e^{-0.03x}}\Bigg)\tag*{(19)}\end{equation*}
式中, $P=\sqrt{\dfrac{\omega_\text b\rho_\text bc_\text b}{k}}$.
表2比较了广义有限差分法和有限元法(COMSOL软件)的计算结果, 其中广义有限差分法采用均匀布点, 时间步长设为250 s, 达到稳态的判定为$\varepsilon=10^{-3}$. 同时由于广义有限差分法中每个离散节点仅包含一个自由度(degree of freedom), 因此其自由度即等价于离散点数. 有限元法的计算网格按照COMSOL软件自带网格生成技术产生, 广义有限差分法选取与有限元法所需自由度相近的离散点数进行计算. 由表2可知, 广义有限差分法与有限元法(COMSOL 软件)的计算精度相当, 且具有较好的计算稳定性.
Table 2
表2
表2算例1计算结果比较
Table 2Numerical comparisons in Example 1
 |
新窗口打开
接着研究时间步长对计算结果的影响, 采用20 657自由度的均匀布点进行计算, 得到趋于稳态$(t=5000~\text s)$ 的计算结果, 如表3. 由表3可知, 最大相对误差随时间步长的减小而减小. 然而时间步长的减小势必增加迭代次数进而影响计算效率. 经过综合考虑, 本文后续算例将时间步长设为250 s.
Table 3
表3
表3时间步长对计算结果的影响
Table 3Effect of time steps on numerical results
| Time step/s | ε | Maximum relative error |
|---|---|---|
| 50 | 1.04 × 10-4 | 6.77 × 10-5 |
| 100 | 2.16 × 10-4 | 7.05 × 10-5 |
| 250 | 6.04 × 10-4 | 7.87 × 10-5 |
| 500 | 1.40 × 10-3 | 9.09 × 10-5 |
| 1000 | 3.42 × 10-3 | 1.11 × 10-4 |
新窗口打开
随后研究散乱布点对广义有限差分法计算结果的影响. 图2给出同为20 657自由度的均匀布点与散乱布点图. 相应的相对误差结果见表4.
Table 4
表4
表4均匀布点与散乱布点的相对误差比较
Table 4Comparisons of relative error by using uniform and scattered nodes
| DOFs | Maximum relative error | |
|---|---|---|
| uniform nodes | scattered nodes | |
| 380 | 1.05 × 10-4 | 3.34 × 10-4 |
| 1250 | 1.14 × 10-4 | 5.77 × 10-4 |
| 7889 | 1.23 × 10-4 | 7.45 × 10-4 |
| 20 657 | 1.18 × 10-4 | 2.49 × 10-4 |
新窗口打开
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图2均匀布点与散乱布点对比图
-->Fig.2Comparison of uniform and scattered nodes
-->
由表4可以看出, 散乱布点时, 广义有限差分法的计算精度虽稍有降低, 但仍然可以得到令人满意的结果. 另外, 有限元法的网格质量对计算结果影响较大, 且在两种介质交界面附近需要适当加密网格才能确保得到正确的计算结果. 而广义有限差分法无需划分网格, 仅需散乱的节点信息即可计算三维含肿瘤皮肤组织的热传导问题.
3.2 算例2$~$含规则形状肿瘤的皮肤组织热传导问题
本算例考虑含规则形状肿瘤的皮肤组织热传导问题, 分别假定计算域中心存在长方体与球体两种规则形状的肿瘤, 其中长方体肿瘤的尺寸为$0.01~\text m\times 0.02~\text m\times 0.02~\text m$, 球体肿瘤半径为0.008 m.由于此算例的解析解较难通过推导得到, 这里将广义有限差分法采用极度稠密离散点(长方体肿瘤: 157 607; 球体肿瘤: 157 257)计算所得的结果作为参考解, 并分析不同点数对计算精度的影响, 结果见表5. 由表5可知, 广义有限差分法随着离散点数增加, 相对误差逐渐减小. 这说明该方法在计算含规则形状肿瘤的皮肤组织热传导问题时具有较好的计算稳定性.
Table 5
表5
表5算例2中的数值稳定性
Table 5Numerical stability in Example 2
| Cube | Sphere | ||
|---|---|---|---|
| DOFs | maximum relative error | DOFs | maximum relative error |
| 2789 | 1.22 × 10-3 | 3159 | 2.61 × 10-3 |
| 9012 | 5.68 × 10-4 | 9342 | 3.33 × 10-4 |
| 20 763 | 4.24 × 10-4 | 21 021 | 2.01 × 10-4 |
| 67 761 | 1.36 × 10-4 | 67 779 | 5.86 × 10-5 |
新窗口打开
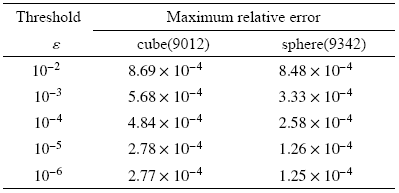
在此基础上, 以算例2为例研究迭代阈值对计算结果的影响, 结果见表6. 由表6可知, 当迭代阈值$\varepsilon\leqslant 10^{-3}$后计算结果精度变化不大. 因此下文中未作特殊说明的算例均以$10^{-3}$为迭代阈值, 即$\varepsilon=10^{-3}$.
Table 6
表6
表6迭代阈值对计算结果的影响
Table 6Effect of $\varepsilon$ on numerical results
 |
新窗口打开
3.3 算例3$~$肿瘤形状对皮肤组织温度分布的影响
由于肿瘤形状一般都是不规则的, 本算例以3类体积相同形状不同的肿瘤为例, 研究肿瘤形状对皮肤组织温度分布的影响. 其中, 椭球形状肿瘤参数方程为\begin{equation*}(x-0.015)^2+y^2+\dfrac{z^2}{16}\leqslant r^2,r=0.005~636~258~259\tag*{(20)}\end{equation*}
红细胞形状肿瘤参数方程为
\begin{equation*}\begin{split}&z=10\sqrt{\Bigg(1-\dfrac{x^2+y^2}{r^2}\Bigg)}\Bigg[\text c_0+\text c_1\dfrac{x^2+y^2}{r^2}+\text c_2\Bigg(\dfrac{x^2+y^2}{r^2}\Bigg)^2\Bigg],\\&\quad r=0.006~876~135~848,~c_0=0.207~1,\\&\quad c_1=2.002~6,c_2=-1.122~8\end{split}\tag*{(21)}\end{equation*}
豌豆形状肿瘤参数方程为
\begin{equation*}\begin{split}&\dfrac{(x-0.015)^2}{0.64\Big[1-0.1\text{cos}\Big(\tfrac{\textrm{π} z}{r}\Big)\Big]^2}+\dfrac{\Big[y+0.003\text{cos}\Big(\tfrac{\textrm{π} z}{r}\Big)\Big]^2}{0.64 \Big[1-0.4\text{cos}\Big(\tfrac{\textrm{π} z}{r}\Big)\Big]^2}+\\& z^2\leqslant r^2,~r=0.010~683~125~409\end{split}\tag*{(22)}\end{equation*}
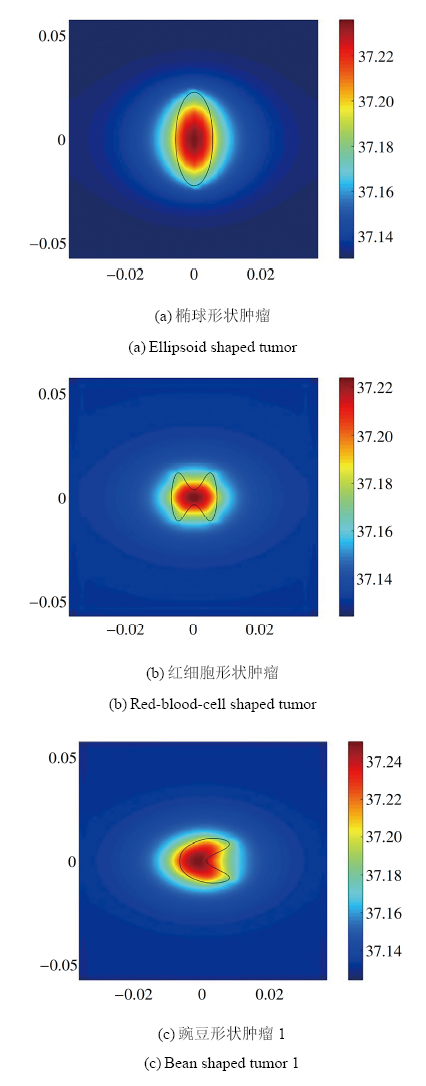
图3给出不同形状肿瘤情况下截面$x=0.015$上的温度分布结果. 由图3可知, 肿瘤形状对远离肿瘤区域的皮肤组织的温度分布影响较小, 而肿瘤附近区域皮肤组织的温度分布与肿瘤形状密切相关, 且温度分布具有明显的指向性.
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图3肿瘤形状对皮肤组织温度分布的影响 $(x=0.015)$
-->Fig.3Effect of tumor geometries on temperature distribution in skin tissue $(x=0.015)$
-->
3.4 算例4$~$肿瘤位置对皮肤组织温度分布的影响
本算例研究肿瘤位置对皮肤组织外表面温度分布的影响. 在肿瘤体积相同的情况下, 考虑以下3种情况:(a)~花生形状肿瘤, 其参数方程为
\begin{equation*}\begin{split}&(x-0.015)^2+y^2+(|z|-0.75r)^2\leqslant r^2,\\& r=0.006~443~237~57\end{split}\tag*{(23)}\end{equation*}
(b)~2个球形肿瘤, 球心位于$(0.015,0,\pm0.01)$;
(c)~2个球形肿瘤, 球心位于$(0.015,0,\pm0.015)$.
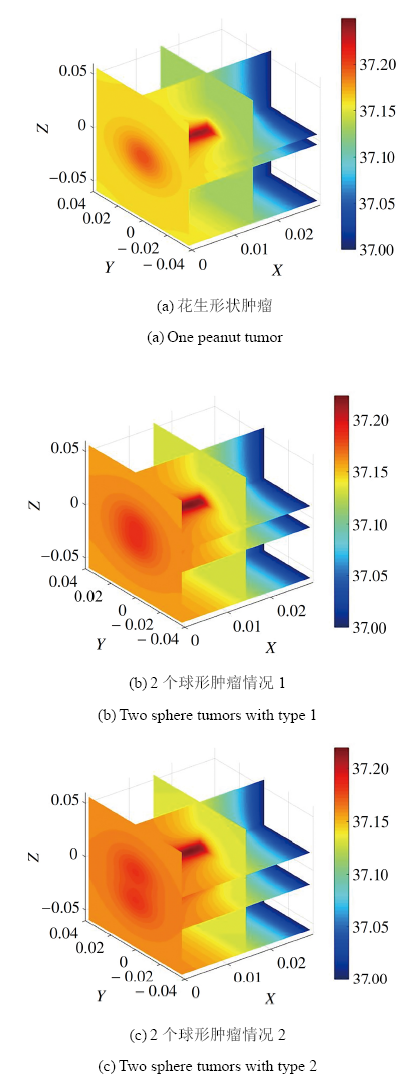
图4给出上述3种情况下皮肤表面及肿瘤中心所在平面的温度分布结果. 由图4可以看出, 距离较近或未完全分开的两个肿瘤难以通过皮肤组织的温度分布图进行区分.
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图4肿瘤位置对皮肤组织温度分布的影响
-->Fig.4Effect of tumor location on temperature distribution of skin tissue
-->
4 结论
本文采用广义有限差分法结合隐式差分格式模拟含肿瘤皮肤组织的传热过程. 通过计算无肿瘤及含肿瘤皮肤组织的温度分布验证了该方法的精确性和高效性, 并在此基础上进一步研究肿瘤的形状及位置对皮肤组织温度分布的影响. 研究发现: (a) 相较于有限元法, 广义有限差分法无需划分网格, 前后处理简便, 同时避免产生大多数配点技术普遍存在的病态矩阵问题, 是一类非常有发展潜力的局部型无网格配点技术; (b) 肿瘤形状对远离肿瘤区域的皮肤组织温度分布影响较小, 而肿瘤附近区域的温度分布与肿瘤形状密切相关, 且具有明显的指向性; (c) 距离较近或未完全分开的两个肿瘤难以通过皮肤组织的表面温度分布图进行区分, 这在临床医学诊断时需要特别关注. 最后需要指出的是, 本文主要侧重于验证广义有限差分法在计算含肿瘤皮肤组织传热过程时的有效性, 所采用的模型及其相关参数均作了不同程度的简化. 因此, 后续的研究工作中将引入更为贴近真实情况的模型及相关参数并采用广义有限差分法进行数值计算.The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . . |
| [2] | . . |
| [3] | . . |
| [4] | . . |
| [5] | . . |
| [6] | . |
| [7] | . |
| [8] | . . |
| [9] | . |
| [10] | . . |
| [11] | . . |
| [12] | . . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . . |
| [18] | . . |
| [19] | . . |
| [20] | . . |
| [21] | . |
| [22] | . . |
| [23] | . . |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | |
| [29] | // |
| [30] | . |
