丁洲祥
* , 北京交通大学土木建筑工程学院,北京 100044
ONE-DIMENSIONAL QUASI-STATIC CONSOLIDATION MODEL CONSIDERING INERTIA OF FLUID PHASE DingZhouxiang
* , School of Civil Engineering, Beijing Jiaotong University, Beijing 100044,China 中图分类号: TU431
文献标识码: A
通讯作者: * 丁洲祥,副教授,主要研究方向:固结理论与工程应用. E-mail:dingzhouxiang@163.com * 丁洲祥,副教授,主要研究方向:固结理论与工程应用. E-mail:dingzhouxiang@163.com 收稿日期: 2018-03-5
接受日期: 2018-03-5
网络出版日期: 2018-07-18
版权声明: 2018力学学报期刊社力学学报期刊社 所有
基金资助: 国家自然科学基金资助项目(51278028, 41172221, 50708077). 展开
摘要
经典Terzaghi一维固结理论不考虑孔隙流体惯性影响,且该理论在不同时期模型推导和表述结果差别较大,导致当前仍存在诸多困惑甚至认识混乱的现象. 在笔者前期研究大变形动力固结理论框架内,忽略固相惯性而重点考虑液相惯性影响,经过合理简化建立反映孔隙流体惯性的一维小变形固结波动模型. 该固结波模型具有频散和耗散特性. 采用分离变量法,可得到单面排水和瞬时加载条件下无量纲形式固结波解析解答. 算例分析结果表明:固结波发展规律受无量纲数D c D c D c 关键词: 固结波 ;
孔隙流体惯性 ;
固结 ;
Terzaghi一维固结理论 ;
Mandel-Cryer效应 ;
阶跃现象 Abstract
Terzaghi’s one-dimensional classic consolidation theory ignores inertia of pore water in saturated soils, and has outstanding differences in its derivation and formulation during various publication periods. This leads to a strange phenomenon that considerable misunderstandings and confusion of it still prevail in the current literature. Within the previous framework of large strain dynamic consolidation theory, a one-dimensional infinitesimal strain consolidation wave model is obtained to consider the effect of inertia of pore water with necessary simplification and hypotheses. The present consolidation wave model is characterized by velocity dispersion and dissipative attenuation. The method of separation of variables is used to obtain an analytical solution for a consolidation wave model under the condition of one-way drainage and instantaneous loading. A numerical case study shows that behaviors of consolidation wave are actually controlled by the value of a dimensionless number D c D c D c D c Keywords: consolidation wave ;
inertia of pore water ;
consolidation ;
Terzaghi’s one-dimensional consolidation theory; ;
Mandel-Cryer effect ;
jump phenomenon -->
0
PDF (7943KB) 元数据 多维度评价 相关文章 收藏文章 本文引用格式导出
EndNote Ris Bibtex 收藏本文 -->
丁洲祥 . 一种考虑液相惯性的一维准静力固结模型[J].
力学学报 , 2018, 50(4): 908-928
https://doi.org/10.6052/0459-1879-18-053 Ding Zhouxiang . ONE-DIMENSIONAL QUASI-STATIC CONSOLIDATION MODEL CONSIDERING INERTIA OF FLUID PHASE[J].
Acta Mechanica Sinica , 2018, 50(4): 908-928
https://doi.org/10.6052/0459-1879-18-053 引言 西方****
[ 1 - 2 ] 通常将土力学诞生的标志归于Terzaghi著作
[ 3 ] ——其中提出了经典(一维)固结理论. 但固结理论的发展经历并不平凡,以至于当前仍存在一些困惑,这主要表现为2个方面:(1)经典固结模型是否具有大变形 属性;(2)模型是否需要考虑液相惯性.
首先,对经典固结理论变形属性的研究进行概述. Terzaghi
[ 3 ] 于1925年提出的固结方程为
c ? 2 w ? z 2 = ? w ? t ( 1 ) 式中,
c = k / a ,
k 表示渗透系数,
a 是所谓压缩系数(“
a sei die verdichtungsziffer genannt.”),
w 是超静孔压,
z 是竖向坐标,
t 是时间. Poskitt
[ 4 ] 认为Terzaghi在早期论文中使用厘米
? 克
? 秒单位制,并令水重度
γ w = 1 ;de Boer等
[ 5 ] 还将Terzaghi固结理论追溯到1923和1924年的2篇德语文章. 这些研究
[ 4 - 5 ] 还认为,Terzaghi在早期表述固结理论时,使用了简化Lagrangian坐标系统和简化水力传导系数
k x ,并假定
k x 与真实水力传导系数
k 都是常数,由此得到小应变线性固结理论,但隐含孔隙比
e 不变即没有固结发生的矛盾. 这一矛盾贯穿在传统小应变理论范畴内,只能通过考虑几何非线性的大变形固结理论,如Gibson等理论
[ 6 ] ,才能解决
[ 4 ] .
令人惊讶的是,Znidarcic和Schiffman
[ 7 ] 提出:Terzaghi(1923)以德语发表的固结理论
k r a v ? 2 u ? z 2 = ? u ? t ( 2 ) 其实是线性有限应变(大变形)固结理论,而非普遍认为的小变形理论. 式(2)中,
u 是超静孔压,
z 是物质坐标系统,
a v 是压缩系数,
k r 是物质坐标系统简化渗透系数,且
k r = k / 1 + e ,
k 是常用渗透系数,
e 是孔隙比. 在忽略材料自重,假定
k r ,
a v 和总应力增量
Δ σ 为常数的条件下,Gibson等
[ 6 ] 大变形固结理论就退化为
k r γ w a v ? 2 u ? z 2 = ? u ? t ( 3 ) 于是,当忽略水重度
γ w 时,式(3)精准地等价于Terzaghi(1923)模型
[ 7 ] ,由此表明式(2)是线性有限应变模型. Znidarcic和Schiffman
[ 7 ] 调研结果还表明:(1) Terzaghi于1931年及之前关于固结理论的所有文章,都使用方程式(3)的阐述;(2) Terzaghi和Frohlich (1936)将之前坐标系统改变为Lagrangian系统,这就导致Terzaghi原始有限应变理论简化为无限小应变(即小变形)理论,即
[ 7 ] k 1 + e γ w a v ? 2 u ? a 2 = ? u ? t ( 4 ) 式中,
a 是物质点的Lagrangian (初始)构形
[ 8 ] . 式(4)是Terzaghi固结理论的惯用表达式
[ 6 - 7 ] .
Znidarcic和Schiffman在针对文献[
7 ]讨论稿
[ 8 ] 答复中,补充了控制方程
[ 8 ] ? ? z k γ w 1 + e ? u ? z + ? e ? t = 0 ( 5 ) 认为式(5)就是Terzaghi(1923)原始表述结果,并且也是Gibson等大应变理论
[ 6 ] 的3种表述方法之一,其中
z 定义为表示土 体中固相高度的物质坐标. Lee和Szalwinski
[ 8 ] 对文献[
7 ]这一观点表示质疑——鉴于实践上人们用的是Terzaghi自1936年以来的小应变固结方程, 该观点说明理论土力学尚未从倒退中得到恢复,另外Terzaghi原始方程可写为
? ? k r ? u / γ w ? z = a v ? u ? t ( 6 ) 式中,
u 是超静孔压,
γ w 是孔隙流体密度,
a v 是瞬时压缩系数,
k r 是简化渗透系数,
k r = k / 1 + e ,而
k 是土样渗透系数. Lee等
[ 8 ] 则认为,由于Terzaghi利用初始空间坐标在固定空间域中求解其方程,由此导致其理论局限于小应变情况.
抛开上述国际上对
Terzaghi(1925) 模型是否是大变形模型的争议,但就对模型小变形属性分歧较少的1943年至今3篇Terzaghi著作
[ 9 - 11 ] 而言,经典固结理论数学表述结果仍存在较大差异.
具体而言,
Terzaghi(1943) 固结方程为
[ 9 ] ? u ? t = c v c ? 2 u ? z 2 ( 7 ) 式中,
u 是超静孔压,
z 是竖向普通坐标,
c v c 是固结系数,定义为
c v c = k / γ w m v c = k 1 + e 0 / γ w a v c ( 8 ) 其中,
k 是常用渗透系数,
m v c 是体积减小系数,
a v c 是压缩系数,
e 0 是孔隙比初始值. 值得注意的是,
Terzaghi(1943) 强调——式(7)就是Terzaghi(1923)水平黏土层固结过程微分方程. Terzaghi等
[ 10 ] 后来又使用体积应变
s 替换文献[
9 ]中孔隙率
n 来推导控制方程,其结果与式(7)一样. 但是,最近Terzaghi等
[ 11 ] 又将固结方程表述为
c v ? 2 u ' ? z 2 = ? u ' ? t ( 9 ) 式中,
u ' 是不同于以往的超静孔压,固结系数
c v = k v / γ w m v = k v 1 + e / γ w a v ( 10 ) 其中,
e 是固结过程中当前孔隙比. 可见,除了超静孔压内涵发生变化,固结系数定义也不同.
这种不统一的固结系数表述结果,对土力学研究造成很大影响乃至歧义:在介绍Terzaghi固结理论的著作中,文献[
12 ,
13 ,
14 ,
15 ,
16 ,
17 ,
18 ,
19 ]等使 用了式(8),而文献[
20 ,
21 ,
22 ]等则采用式(10). 袁大军等
[ 23 ] 尽管从连续介质力学角度,解释了式(8)和式(10)之间的联系,但尚未深入研究其根源,即模型的变形属性.
其次,经典固结理论一直存在的另一个关键问题是:忽视孔隙流体惯性. Terzaghi
[ 9 ] 援引他人工作,间接否认孔隙流体惯性对固结的实质影响,却没有给出具体控制方程并阐明可以忽略惯性的条件. 根据de Boer等
[ 5 ] ,Terzaghi这一论断可能源于前期学术争议,但其影响无疑是深远的. 迄今为止,除了Biot动力固结理论
[ 24 - 26 ] 外,无论Biot静力固结理论
[ 27 ] 还是Terzaghi理论
[ 11 ] ,均不考虑孔隙流体惯性. 调研结果还表明,尚未发现经多方验证的充分理由,可以科学地否定流体惯性对固结研究的意义.
综上所述,本文将结合作者近20年来在固结领域的学习体会,主要按数学方程形式,首先讨论
Terzaghi(1943) 固结理论的内涵和严格表述,并以考虑孔隙流体惯性为主要任务,发展提出准静力(不计固相惯性)固结范畴内一维固结波动模型,并研究其解析解答. 然后将结合算例,分析固结波与经典固结理论的联系与区别,探讨固结波模型揭示的阶跃效应、Mandel-Cryer效应等现象的规律. 最后,将探讨经典理论早期历史和矛盾,并在此背景下展望固结波模型在土力学发展和学科交叉中的意义.
1 Terzaghi (1943)固结理论模型 1.1 基本假定 Terzaghi采用的基本假定如下
[ 9 ] :(1)土体孔隙完全充满水;(2)土体中水和固相成分均不可压缩;(3)达西定律严格成立;(4)渗透系数
k 是常数;(5)固结时滞完全出于土体低渗透性. 补充假定有:(1)黏土侧向受限;(2)对固结过程每个阶段,任意水平剖面内各点总正应力和有效正应力相等;(3)有效应力从初始值
p ? 0 增加到最终值
p ? 将使黏土孔隙比由初始值
e 0 减小到最终值
e ;(4)压缩系数
a v c 在有效应力增大范围内是常数.
1.2 固结过程微分方程 1.2.1 有效应力方程
对施加超载之前的静力平衡关系,Terzaghi
[ 9 ] 准确使用了有效应力方程,即初始有效应力
p ? 0 等于初始 总应力
p 0 减去初始孔隙水压力
u w p ? 0 = p 0 - u w ( 11 ) 但在超载施加后,Terzaghi
[ 9 ] 却使用了超静孔压
u (初始超静孔压默认为0)与有效应力增量
p ? - p ? 0 之和等于总应力增量
p 1 (即超载)的关系
2cm
u + p ? - p ? 0 = p 1 ( 12 ) 这与有效应力原理并非严格相符,而隐含着忽略地下水位变化和土体沉降影响的假设.
对式(12)中超静孔压
u ,求关于时间的偏导数
? u ? t = - ? p ? ? t ( 13 ) 其中隐含
? p 1 + p ? 0 / ? t = 0 ,即外载不随时间变化.
1.2.2 土体骨架本构关系
有效应力
p ? 与孔隙率
n 之间服从
n 0 - n = m v c p ? - p ? 0 ( 14 ) 式中,
m v c 具有相对初应力状态的起始割线模量含义,但孔隙率
n 令人费解,可能是
n 01 的笔误.
在式(14)基础上,得到有效应力
p ? 关于时间的偏导数(率型骨架本构方程)
? p ? ? t = - 1 m v c ? n ? t ( 15 ) 式中,隐含
? m v c / ? t = 0 假定,或
m v c = m v c z .
结合方程(15)和(13),有
? n ? t = m v c ? u ? t ( 16 ) Terzaghi将式(16)应用于厚度
d z 的薄层土体
- ? n ? t d z = - m v c ? u ? t d z ( 17 ) 并赋予
- ? n / ? t 一种物理意义——考察点处单位时间和单位体积的黏土中挤出的水量,因而,式(17)就表示厚度
d z 的薄层土体在单位时间和单位薄层面积上挤出的水量.
1.2.3 连续性方程
为将式(16)或式(17)中
n 反映的变形场和
u 反映的渗流场联系起来,Terzaghi认为,孔隙水溢出速度
v 在向上方向上经过
d z 距离的增量应满足
? v ? z d z = - ? n ? t d z ( 18 ) 其物理意义是:式(18)等号左端项表示的单位时间内流出和进入单元土体的水量差,必须等于该式等号右端项表示的单位时间内挤出单元体的水量.
1.2.4 土体液相本构方程:Darcy渗流定律
Terzaghi使用Darcy定律,将考察点在时刻
t 的
溢出速度
v 与水力梯度
i 和渗透系数
k 联系起来
v = ik ( 19 ) 式中
13mm
i = - ? h / ? z = - 1 / γ w ? u / ? z ( 20 ) 1.2.5 固结控制方程的导出
基于上述基本方程,式(17)左端变形场有关项就可以采用渗流场相关项,即式(18)等号左端项,进行等价替换,最终得到以超静孔压
u 为场变量的固结控制方程式(7)及其固结系数定义式(8).
1.3 对Terzaghi(1943)模型的再认识 从推导过程来看,
Terzaghi (1943) 建模关键方程为连续性方程式(18),由此实现渗流场与骨架变形场耦合. 由于固结问题针对瞬态平衡,连续性方程的本质是率型的. 不难发现,Terzaghi(1943)使用了苛刻的假设:(1)由式(14)到式(15),只需要满足
? m v c / ? t = 0 ,即
m v c = m v c z 即可,而不必要求
m v c 为常数; (2)隐含
? k / ? z = 0 假定,即
k = k t ,而不必要求
k 为常数. 所以,
Terzaghi (1943) 模型其实一定程度上可以考虑材料非线性,即式(8)为
c v c z , t = k t / γ w m v c z ( 21 ) 式中,
c v c z , t 是关于时间和空间变量的固结系数.
换言之,Terzaghi推导模型之前的某些假定,其实不是推导模型的必需条件,而仅是为了简化数学求解. 这一简化的结果是,人们通常认为Terzaghi理论中土体特性都是常数,而试验研究却表明:在现场条件对应的应力范围内固 结系数会有相当大的变化
[ 28 ] . 因此,式(21)能够在Terzaghi理论框架内,部分反映土体变化的影响. 修正Terzaghi模型
[ 9 ] 的进展还包括:Yin和Graham
[ 29 ] 将弹黏塑性本构引入固结理论,并采用差分法进行求解;Liu和Griffiths
[ 30 ] 考虑总应力随时间和埋深变化,采用Laplace变换得到解析解;Verruijt
[ 31 ] 考虑可含气泡液相压缩性,据此改进连续性方程;Chai和Zhou
[ 32 ] 基于固结过程中土体渗透性和体积压缩性空间和时间变化,提出一种折减固结系数及固结度算法,但没讨论这种折减 方法与Terzaghi模型之间的相容性. 可见,
探明Terzaghi (1943) 理论
[ 9 ] 存在的不足,对于理论发展具有重要意义,在后文将另行分析.
2 一维小变形固结波模型的建立 2.1 力学基础 丁洲祥等
[ 33 ] 提出欧拉描述的大变形固结理论 框架,其中连续性方程和动力平衡方程可作为发展固结波模型的主要依据. 该理论不同于混合物理论和小变形Biot理论思想,而是着眼于具有普遍性的大变形欧拉描述方法,将饱和土体连续介质构形定义 为固相(或骨架)在空间占据的区域,并以固相随时间变化来考察饱和土运动变形,在此基础上考虑液相与控制体外界质量交换, 同时运用散度定理、传运公式和局部化假设,得到了饱和土质量守恒方程,并给出固液两相不可压缩条件下的特殊形式
[ 33 ] v s i , i = - q i , i ( 22 ) 式中,
v s i 是固相速度;
q i 是渗流速度,服从某种渗流定律(如Darcy定律).
一般情况下,饱和土欧拉运动方程
[ 33 ] 为
τ ji , j + ρ f i = ρ v ? s i - v s i ρ f q j , j + ρ f v s j , j q i + 2 mm ] D ρ f q i / D t ( 23 ) 式中,
τ ji 是欧拉应力张量,
ρ 是
t 时刻空间点
x i 处土体密度,
f i 是单位质量体力,
ρ f 是液相密度.
考虑到钱学森
[ 34 ] 物理力学研究方法之一——“
? ? 制造出一个简单的模型,使模型里只包括机理里面最重要的因素. 唯有这样,分析运算才能进行”,可以证明:在一维和固、液两相不可压缩简化条件下,式(23)等号右端第2项与第3项之和为零;如果进一步忽略固相惯性,即
v ? s i = 0 ,最终得到两相不可压缩一维大变形饱和土体准静力平衡方程
? τ / ? x + ρ f = ρ f q ? ( 24 ) 式中,为简化表述而省略若干下标. 式(22)退化为
? v s / ? x = - ? q / ? x ( 25 ) 式(24)和式(25)构成本文进行固结波研究的基础.
2.2 一维小变形固结波的基础方程 在小变形条件下,式(24)和式(25)退化为
2cm
? σ / ? z + ρ f = ρ f ? q / ? t ( 26 ) 2cm
? v s / ? z = - ? q / ? z ( 27 ) 上式中,
z 是普通或物质坐标,
σ 是Cauchy应力,
q 的物质时间导数退化为普通时间导数.
2.3 固相速度场散度及其转换所需基本方程 2.3.1 固相速度场散度的等价变换
设固相位移为
u s z , t ,当二阶混合偏导数
? 2 u s / ? t ? z 与
? 2 u s / ? z ? t 在问题求解域内某点
z 都 存在且连续,则
? 2 u s / ? t ? z = ? 2 u s / ? z ? t . 于是
? v s ? z = ? ? z ? u s ? t = ? ? t ? u s ? z = ? ε s ? t ( 28 ) 式中,
ε s 是一维工程应变或小应变,
ε s = ? u s / ? z .
2.3.2 土体小应变时间变化率及骨架本构的引入
土体小应变(按连续介质力学符号约定)
ε s = e - e 0 / 1 + e 0 ( 29 ) 当忽略土体变形次压缩效应,孔隙比
e 仅是有效应力的函数,即
e = e σ ' ,小应变时间变化率为
? ε s ? t = 11 + e 0 ? e ? t = 11 + e 0 d e d σ ' ? σ ' ? t = 2 mm ] - a v 1 + e 0 ? σ ' ? t ( 30 ) 式中,
a v = - d e / d σ ' ,表示切线压缩系数.
2.3.3 有效应力时间变化率及有效应力方程的引入
根据Terzaghi有效应力方程
σ ' = σ - u w ( 31 ) 式中,
σ 是土中某点的总应力,
u w 是孔隙水压力. 因此
? σ ' / ? t = ? σ / ? t - ? u w / ? t ( 32 ) 2.3.4 总应力时间变化率及准静力平衡方程、土水势方程和Darcy定律的引入
根据式(26)进行坐标积分,并忽略自重影响,得到总应力在时刻
t 的空间分布
σ = ∫ z G S z ? ρ f ? q / ? t d z + p G S t ( 33 ) 式中,
z G S 表示地表坐标;
p G S t 是地表
z = z G S 处的总应力或总面力载荷,可以随时间变化.
对式(33)两端求关于时间的偏导数
? σ ? t = ? ? t ∫ z G S z ? ρ f ? q / ? t d z + ? p G S t ? t ( 34 ) 式中,等号右端第1项是难点. 根据积分号下求导定理
[ 35 ] ,在满足有关连续、收敛和一致收敛条件下
? ? t ∫ z G S z ? ρ f ? q / ? t d z = ∫ z G S z ? ? ? t ρ f ? q / ? t d z ( 35 ) 饱和土土水势方程为
ψ = γ f z - z d p + u w = γ f z - z d p + γ f z w t - z + u e ( 36 ) 式中,
γ f z - z d p 表示位置势能,
γ f z w t - z 表示静水压力有关的势能,
u e 表示超静孔压有关的势能,
z d p 是零势能参考面位置,
z w t 是水位位置.
式(36)等价于
ψ = γ f z w t - z d p + u e ( 37 ) 假设Darcy定律成立,则有
q = - k γ f ? ψ ? z = - k γ f ? u e ? z ( 38 ) 再设
k 与
z 和
t 无关,则式(35)右端项
∫ z G S z ? ? ? t ρ f ? q / ? t d z = - ρ f k γ f ∫ z G S z ? ? 2 ? t 2 ? u e ? z d z ( 39 ) 设三阶混合偏导数
? 3 u e / ? z ? t 2 和
? 3 u e / ? t 2 ? z 在问题求解域内存在且连续,则
∫ z G S z ? ? 2 ? t 2 ? u e ? z d z = ? 2 u e ? t 2 z - ? 2 u e ? t 2 z G S ( 40 ) 对实际工程和常规固结试验而言,土层或地表通常为排水边界,此时
u e = 0 ,且恒满足
? 2 u e / ? t 2 z G S = 0 ( 41 ) 式(34)最终简化为
? σ ? t = - kg ? 2 u e ? t 2 + ? p G S t ? t ( 42 ) 式中,
g 是重力加速度,
g = γ f / ρ f .
2.3.5 孔压变化率及孔压方程的引入
根据式(36),容易得到孔压方程
u w = γ f z w t - z + u e ( 43 ) 在
? z w t - z / ? t = 0 条件下,孔压和超静孔压的时间变化率满足
? u w / ? t = ? u e / ? t ( 44 ) 联立式(28),式(30),式(32),式(42)和式(44),得到土体固相速度的散度为
? v s ? z = a v 1 + e 0 kg ? 2 u e ? t 2 - ? p G S t ? t + ? u e ? t ( 45 ) 2.4 液相速度场散度及其转换所需的基本方程 根据Darcy渗流方程式(38)
- ? q ? z = - ? ? z - k γ f ? u e ? z = k γ f ? 2 u e ? z 2 ( 46 ) 2.5 一维小变形固结波的控制方程 联立式(27),式(45)和式(46),得到一维小变形固结波控制方程
c a ? 2 u e ? t 2 - ? p G S t ? t + ? u e ? t = c v ? 2 u e ? z 2 ( 47 ) 其中
12mm
c a = k / g ( 48 ) 12mm
c v = k 1 + e 0 / γ f a v ( 49 ) 可以证明,当
u e 和
p G S 采用土力学符号约定时,方程式(47)的形式不变. 故后面分析中,仍以
u e 和
p G S 表示土力学意义的相应量.
当边界上外载荷瞬时施加并维持不变,即
? p G S t / ? t = 0 时,式(47)简化为
c a ? 2 u e ? t 2 + ? u e ? t = c v ? 2 u e ? z 2 ( 50 ) 这是一种近乎极简的一维固结波方程,属于双曲型方程,区别于经典固结理论
[ 9 ] 的抛物型方程.
3 一维小变形固结波基本特征 3.1 固结波的频散关系 考虑如下形式的平面波解
[ 36 ] u e z , t = e i k z z - ω t ( 51 ) 设
0 < k z < ∞ ,将式(51)代入 式(50),得
c a ω 2 + i ω - c v k z 2 = 0 ( 52 ) 当
ω = - i ± 4 c a c v k z 2 - 1 2 c a = ± 4 c a c v k z 2 - 1 2 c a - i 12 c a ( 53 ) 时,式(52)的解答为
k z < 1 / 2 c a c v 而当
ω = i - 1 ± 1 - 4 c a c v k z 2 2 c a ( 54 ) 时,式(52)的解答为
I m ω ? 0 对式(53)和式(54)两种情况,都有
[ 36 ] ,所以方程式(50)的解稳定
k z < 1 / 2 c a c v . 对
v p = Re ω k z = ± 4 c a c v k z 2 - 1 2 c a k z ( 55 ) 和
v p = 0 ( 56 ) 两种情况,相位速度分别为
k z < 1 / 2 c a c v I m ω 这表明,当
? 2 u e ? t 2 + γ ? u e ? t = c t 2 ? 2 u e ? z 2 ( 57 ) 时,固结波有频散;当
γ 时,固结波无频散. 又因为
γ = 1 / c a 不恒等于0,所以固结波方程(50)是耗散的.
3.2 固结波的波动方程形式 按一维波动方程的一般形式,将式(50)改写为
c t 式中,
c t 2 = c v / c a = E s / ρ f ( 58 ) 表示阻尼,
E s ;
E s = 1 + e 0 / a v 表示一种波速
v p 2 = c t 2 - γ 2 4 k z 2 < c t 2 ( 59 ) 其中,
lim k z → ∞ v p 2 = c t 2 ( 60 ) 是土体压缩模量,
v p 2 ∈ 0 , c t 2 .
根据式(55)
15mm
? u e z , t ? z = 0 , z = 0 ( 61 ) 15mm
u e z , t = 0 , z = H ( 62 ) 因此,固结波相位速度变化范围为
t = 0 ,具有显著的频散特征. 此外,大部分细颗粒土渗透系数很小,所以固结波阻尼值通常会较大。
4 固结波一般定解问题及解析解 4.1 一维小变形固结波定解问题 结合泛定方程式(50),拟研究如下初边值问题. 设求解域下边界不透水、上边界透水,即边界条件
10mm
f z 10mm
g z 而初始时刻
u e z , t = f z , 0 ? z < H , t = 0 ( 63 ) 域内超静孔压及其时间变化率分别假设为函数
? u e z , t ? t = g z , 0 ? z < H , t = 0 ( 64 ) 和
~ ,即相应的初始条件
D c 2 ? 2 Φ ? T v 2 + ? Φ ? T v = ? 2 Φ ? ξ 2 ( 65 ) Φ = u e / p , p = max f z ( 66 ) 4.2 固结波定解问题的无量纲化 定解问题式(50)及式(61)
ξ = z / H ( 67 ) 式(64)对应的无量纲泛定方程与求解条件分别为
T v = c v t / H 2 ( 68 ) 式中
15mm
D c 2 = c a c v / H 2 ( 69 ) 15mm
? Φ / ? ξ = 0 , ξ = 0 ( 70 ) 15mm
Φ ξ , T v = 0 , ξ = 1 ( 71 ) 15mm
Φ ξ , T v = f ξ , 0 ? ξ < 1 , T v = 0 ( 72 ) 无量纲化边值条件为
15mm
? Φ ξ , T v / ? T v = g ξ , 0 ? ξ < 1 , T v = 0 ( 73 ) 15mm
Φ ξ , T v = Ξ ξ T T v ( 74 ) 初始条件为
Ξ '' ξ T T v = D c 2 Ξ ξ T '' T v + Ξ ξ T ' T v ( 75 ) Ξ ξ T T v 4.3 固结波定解问题的分离变量法解答 4.3.1 分离变量
设目标特解具有分离变量形式,即
- λ 将式(74)代入式(65),即得
Ξ '' ξ Ξ ξ = D c 2 T '' T v T T v + T ' T v T T v = - λ ( 76 ) 上式两端除以
Ξ '' ξ + λ Ξ ξ = 0 ( 77 ) ,并令结果为
D c 2 T '' T v + T ' T v + λ T T v = 0 ( 78 ) ,即
φ ξ , T v 其中蕴含两个常微分方程
Ξ ' ξ = 0 , ξ = 0 , T v = T v ( 79 ) Ξ ξ = 0 , ξ = 1 , T v = T v ( 80 ) 将
Ξ ξ T 0 = f ξ , 0 ? ξ < 1 ( 81 ) 代入边界条件式(70)和式(71),得
Ξ ξ T ' 0 = g ξ , 0 ? ξ < 1 ( 82 ) λ ? 0 相应的初始条件(72)和(73)为
Ξ ξ λ > 0 4.3.2 求解本征值问题
容易证明:当
Ξ ξ = C 1 cos λ ξ + C 2 sin λ ξ ( 83 ) 时,式(77)的
cos λ = 0 仅有平
凡解;只有当
λ n = 2 n + 1 2 2 / 4 , n = 0,1 , 2 , ? ( 84 ) ,解答才有意义,此时的通解为
Ξ n ξ = cos 2 n + 1 ξ / 2 , n = 0,1 , 2 , ? ( 85 ) 再根据边界条件(79)和(80),要得到非平凡解,只能是
Δ = 1 - D c 2 2 n + 1 2 2 ,由此得到本征值
n = 0,1 , 2 , ? 相应的本征函数为
α = 1 / 2 D c 2 ( 86 ) 4.3.3 一般解
记
β n = Δ / 2 D c 2 , n = 0,1 , 2 , ? ( 87 ) ,
r 1,2 = - α ± Δ / 2 D c 2 ( 88 ) ,以及
D c 2 Δ ≠ 0 则时间域常微分方程式(78)特征方程的特征根为
Δ > 0 讨论:(1) 对于实际问题,
n < 1 / D c - 1 / 2 , n = 0,1 , 2 , ? ( 89 ) 一般不会是无理数,所以
T n T v = e - α T v A n cosh β n T v + B n sinh β n T v , 2 mm ] n = 0,1 , 2 , ? ( 90 ) . (2)当
Δ < 0 ,即
n > 1 / D c - 1 / 2 , n = 0,1 , 2 , ? ( 91 ) 时,式(78)的解答为
T n t = e - α T v A n cos β n T v + B n sin β n T v ( 92 ) (3)
F D c = [ 1 / ( D c ) - 1 ] / 2 ,即
F D c ≠ 0 时,式(78)的解答为
N 为表述简洁,另设
N ,同理
N = i nt F D c , F D c > 02 mm ] - 1 , F D c < 0 ( 93 ) . 引入整数
Φ ξ , T v = ∑ n = 0 ∞ ? Ξ n ξ T n T v = ,
∑ n = 0 N ? e - α T v A n cosh β n T v + B n sinh β n T v ? 定义为
cos 2 n + 1 2 ξ + 于是,得到分离变量法的一般解答为
∑ n = N + 1 ∞ ? e - α T v A n cos β n T v + B n sin β n T v ? cos 2 n + 1 2 ξ ( 94 ) 1.797 7 × 1 0 + 308 e - α T v A n cosh β n T v + B n sinh β n T v = 2 mm ] 12 A n e - α + β n T v + e - α - β n T v + 2 mm ] 12 B n e - α + β n T v - e - α - β n T v ( 95 ) A n 在实际计算中,式(94)右端项很可能遇到很大的实数,如超过Matlab最大正浮点数
B n ,此时将导致计算失败. 这里提出一种对策,即将式(94)中部分函数进行如下等效转换
A n , B n 4.3.4 初始条件的引入及系数
n = 0,1 , 2 , ? ,
∑ n = 0 ∞ ? A n cos [ ( 2 n + 1 ) ξ / 2 ] = f ( ξ ) ( 96 ) 确定
根据初始条件式(81)和式(82)确定式(94)中的系数
∑ n = 0 ∞ ? ( - α A n + β n B n ) cos [ ( 2 n + 1 ) ξ / 2 ] = g ( ξ ) ( 97 ) ,
f ξ ,两者应满足
g ξ ( - 1,0 ] 对式(96)和式(97)中的
cos [ ( 2 n + 1 ) ξ / 2 ] 和
A n = 2 ∫ 0 1 ? f ξ cos [ ( 2 n + 1 ) ξ / 2 ] d ξ ( 98 ) 分别在
- α A n + B n β n = 2 ∫ 0 1 ? g ξ cos [ ( 2 n + 1 ) ξ / 2 ] d ξ ( 99 ) 上进行偶延拓,展开为周期为2且以
B n = 2 α β n ∫ 0 1 ? f ξ cos [ ( 2 n + 1 ) ξ / 2 ] d ξ + 2 mm ] 2 β n ∫ 0 1 ? g ξ cos [ ( 2 n + 1 ) ξ / 2 ] d ξ ( 100 ) 为基本函数族的Fourier余弦级数,同时考虑本征函数正交性质,最后得到
f z = p 1 [ 9 ] (98)和式(99),得到
u ( z , t ) = 4 p 1 ∑ k = 0,1 , ? ∞ ? - 1 k 2 k + 1 e - 2 k + 1 2 2 c v t 4 H 2 ? 2 mm ] cos 2 k + 1 z 2 H ( 101 ) 5 经典算例的Terzaghi解和固结波解 针对上边界排水和下边界不排水、面力载荷瞬时施加且维持不变的一维经典固结算例,这里给出无量纲化的
Terzaghi(1943) 理论解析解以及相应条件下本文固结波精确理论解,为后面分析提供依据.
5.1 Terzaghi固结解答及其无量纲化 在边界条件式(61)和式(62)以及初始条件(63)
z ' = H - z 情况下,Terzaghi原著
u ( z ' , t ) = 4 p 1 ∑ k = 0 ∞ ? 12 k + 1 e - 2 k + 1 2 2 c v t 4 H 2 sin 2 k + 1 z ' 2 H ( 102 ) 固结解答是错误的,因为混淆了本征函数,正确的表达式可写为
[ 9 ] 如果采用坐标变换,
z ' = 0 ,则式(101)等价于
z ' = H 此结果与
Terzaghi(1943) 解答
~ 在形式上一致,但边界条件将变为
f ξ = 1 , 0 ? ξ < 1 ( 103 ) 处排水而
[ 9 ] 处不排水.
采用同上的无量纲化方法式(66)
? Φ T ? T v = ? 2 Φ T ? ξ 2 ( 104 ) 式(68)、边界条件式(70)和式(71)以及初始条件式(72)且其中
Φ T ξ , T v = 4 ∑ k = 0,1 , ? ∞ ? - 1 k 2 k + 1 e - 2 k + 1 2 2 T v 4 cos 2 k + 1 ξ 2 ( 105 ) 那么容易得到
Terzaghi(1943) 模型定解问题
f ξ = 1 , 0 ? ξ < 1 ( 106 ) 的无量纲泛定方程
g ξ = 0 , 0 ? ξ < 1 ( 107 ) 及其无量纲超静孔压解答(按式(101)进行修正)
A n = 4 / π - 1 n / 2 n + 1 , n = 0,1 , 2 , ? ( 108 ) 5.2 经典算例固结波理论解 为便于对比,固结波算例的单面排水边界条件同式(70)和式(71),而初始条件式(72)和式(73)则分别为
12mm
B n = 4 α / π - 1 n / 2 n + 1 / β n , n = 0,1 , 2 , ? ( 109 ) 12mm
Φ ξ , T v 根据式(98)和式(100),得待定系数
D c 2 [ 37 ] 将式(108)和式(109)代入式(94),就得到给定问题的固结波解析解
k = 1 × 1 0 - 7 .
6 算例参数研究与对比分析 6.1 参数变化范围和计算条件 固结波方程式(65)中除自变量和因变量之外的唯一参数是
E s = 2 . 参考经验,对黏性土
H = 1 ,取
g = 9.81 cm/s,
2 MPa;
D c 2 = 2.078 × 1 0 - 17 m;
k = 1 × 1 0 - 1 m/s
E s = 40 ;由式(69)得到
D c 2 = 4.154 × 1 0 - 4 . 若以
H = 1 cm/s和
D c 2 MPa表征粗颗粒土,则在相同厚度条件下,
[ 1 0 - 18 , 1 0 - 3 ] . 可见,在
D c 2 m条件下,
∑ n = 0 N ? ≈ ∑ n = 0 N o d ? , ∑ n = N + 1 ∞ ? ≈ ∑ n = N + 1 N + N u d ? ( 110 ) 变化范围大致为
N o d ;对于更薄的土体,
N 会增大.
在保证计算精度条件下,固结波级数解式(94)等号右端的两项级数之和,按下式进行实际计算
N 其中,
N > 1 0 7 仅在第1项级数和中作为
N u d 的替代值,适用于
D c 很大(如
N )的情况;
Φ ξ , T v 用于截断第2项无穷级数和的求和项数.
实际计算的硬件条件和软件环境为:Intel Core i7-7700 CPU,金士顿16GB DDR4内存,Win10 64位专业版操作系统和MATLAB R2017a数学软件.
D c 数值或对应的
N = 1 值对固结波函数
D c 的变化规律有重要影响. 以下将重点针对
D c = 0.1 值较大和较小两种典型情况,探讨固结波模型蕴含的阶跃效应和Mandel-Cryer效应,
并与Terzaghi(1943) 固结模型加以对比.
6.2 阶跃现象与波动效应 6.2.1
N = 1 与一级阶跃
对
N u d = 3 × 1 0 5 较大的情况,首先不妨以
ξ = 0 为例:在固结波级数解答式(94)的数学结构中,
ξ = 0.5 . 这意味着固结波解中仅有2项涉及过阻尼机理贡献,其余则为欠阻尼机理贡献. 兼顾精度和效率起见,欠阻尼级数和中,取
ξ = 0.9 . 考察不透水边界点
Φ 、中点
D c = 0.1 和距离排水边界为0.1的点
Φ 等3个代表点,其时程曲线如
图1 所示.
显示原图 |
下载原图ZIP |
生成PPT 图1固结波D c = 0.1 ) ξ = 0.9 -->
Fig. 1Consolidation wave Φ ( 0.9 , 0.009 98 ) ≈ 1.00 Φ 0.9 , 0.010 05 ≈ 0.39 -->
由
图1 ,可观察到给定初边值条件下固结波阶跃现象. 对点
ξ = 0.5 ,发生阶跃的相邻时间计算点和函数值分别为
ξ = 0.0 和
Φ 0.5,0.049 93 ≈ 1.00 ;对中心点
Φ 0.5,0.050 27 ≈ 0.92 和不透水边界点
Φ 0.0,0.099 66 ≈ 1.00 ,发生阶跃的相邻点和函数值分别为
Φ 0.0,0.100 35 ≈ 0.99 ,
ξ ,
ξ = 1 - , 以及
Φ . 随着
N u d = 1 × 1 0 6 ? N ? u d 数值的减小即远离排水边界,阶跃的幅值越来越小. 而对紧邻排水边界点
N u d = 3 × 1 0 5 ? N ? u d , 波函数
ξ = 1.0 理论值将由初始时刻1.0阶跃为边界值0,这是最大阶跃幅值.
关于上述阶跃现象的计算精度,相对于
ξ = 0.9 的结果而言,
Φ N ? u d - Φ N ? u d 对应的计算误差随着与排水边界
[ - 1.668 7 × 1 0 - 4 距离的增大而在总体上逐渐减小. 其中,对于考察点
1.139 4 × 1 0 - 3 ] 而言,
ξ < 0.9 的范围即误差限是
Φ ,
c ? T ,其余
c ? T = 1 / D c 的各点误差范围均包含于此界限并逐渐收缩.
如前所述且易证,固结波
v ? T 相速度上限值
D c = 0.1 存在理论关系
c ? T = 10 .
ξ = 0.9 , 0.5 , 0 也是波前速度. 上述阶跃现象本质是波前达到. 这里
T v = 0.01 , 0.05 , 0.10 ,故
ξ . 对点
Φ ,波前理论到达时间分别为
N = 0 ,各自准确落在上述阶跃对应的相邻时域计算点区间,与理论相符.
由
图1 还可看到,在波前达到前,各
D c = 0.3 点
N = 0 值均保持为初值1.0,只有当波前到达之后,超静孔压才开始下降. 通常视为超静孔压消散过程的固结现象,实质是波的传播. 后续分析也将不断验证这点.
6.2.2
γ Φ = 1 / D c 2 与多级阶跃
不妨再以
D c 为例,此时
γ Φ ,式(94)最后1个等号右端第1个求和级数的项数仅有1项,即此时固结波解中仅有1项反映过阻尼机理影响. 式(65)蕴含波动方程阻尼项为
Φ . 显然,
D c = 0.3 的提高将降低阻尼系数
Φ ,导致欠阻尼波动特征更突出,这是
图2 出现多级阶跃的根本原因.
显示原图 |
下载原图ZIP |
生成PPT 图2固结波D c = 0.3 ) N = - 1 -->
Fig. 2Consolidation wave D c > 1 / N = - 1 -->
6.2.3
Φ 与波动中的负压
当
D c = 0.5 时,恒有
10.0 ,此时固结波函数
Φ 将不受过阻尼项任何影响,而呈现完全欠阻尼波 动特点. 不妨以
D c = 0.5 和
Φ 为例继续计算,结果分别如
图3 和
图4 所示.
显示原图 |
下载原图ZIP |
生成PPT 图3固结波D c = 0.5 ) Φ -->
Fig. 3Consolidation wave D c = 10.0 Φ -->
显示原图 |
下载原图ZIP |
生成PPT 图4固结波D c = 10.0 ) D c = 0.5 -->
Fig. 4Consolidation wave D c T v -->
图3 结果表明,
γ Φ = 1 / D c 2 的固结波不仅存在多级阶跃,而且随时间发展还出现负孔压. 当
D c 增大到10.0时,
图4 中负孔压现象更显著,体现欠阻尼波动规律. 随着
γ Φ 增大,固结波幅值呈衰减趋势,这是阻尼作用的效果.
如前所述式(65)蕴含系统阻尼系数
1 / 400 . 当
[ 38 ] 由0.5增加到10.0时,阻尼系数
[ 39 ] 减小到原来的
D c ,由此造成
图3 和
图4 结果差异.
至于负压现象,在考虑流体惯性的流体力学研究中较常见,如输水管道在阀门关闭时水锤效应将引起管道流体压力或冲击力波动
[ 40 - 42 ] (阀门打开将产生负水锤),流固界面上液体压强时程
T v = 0.049 9 也有液压正负波动现象. 对土体而言,在微观上孔隙水在骨架形成的特殊通道中渗流,具有流固耦合特征. 当土体单面排水路径极短,相应
D c = 0.1 值可能引起不同程度的负孔压波动或孔压振荡. 这有待未来试验证实. 另外,对于同时考虑土体固相加速度的动力固结过程,孔压正负波动现象
[ 9 ] 则较为常见.
6.3 固结波与Terzaghi(1943)固结理论对比 区分固结波时空分布特征与Terzaghi(1943) 固结理论结果的相应差别是很有意义的. 不妨选择
D c 和0.200 3两个时刻,考察
Φ , 0.2, 0.3等3种情况下固结波的空间分布,分别如
图5 和
图6 所示,其中给出了Terzaghi理论
T v = 0.049 9 ) 解答.
显示原图 |
下载原图ZIP |
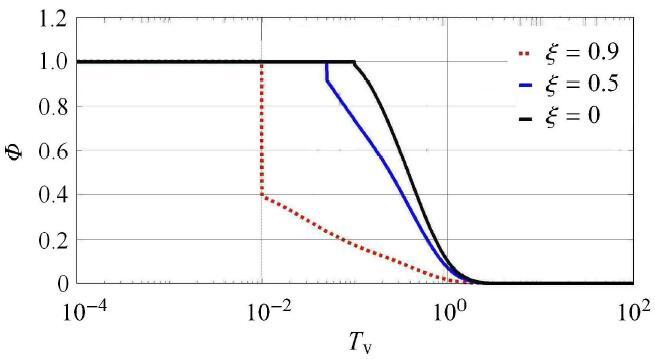
生成PPT 图5不同Φ D c T v = 0.049 9 -->
Fig. 5Spatial distribution of consolidation wave D c Φ T v = 0.200 3 ) -->
显示原图 |
下载原图ZIP |
生成PPT 图6不同Φ D c T v = 0.200 3 -->
Fig. 6Spatial distribution of consolidation wave T v = 0.049 9 ξ Φ -->
图5 显示
ξ 时刻3种不同固结波的波前位置. 在波前到达之前,各
Φ 点的
D c = 0.1 值始终为初值1.0,而波前过后各
ξ = 1.0 点的
D c = 0.5 值则有不同程度的下降. 此外,
ξ = 1.0 对应的波前距离排水边界
c ? T 最远,而
D c 对应的波前则距离
ξ 最近,这是由于波前速度
Φ 与
[ 43 ] 成反比的缘故. 还可看到:Terzaghi理论结果的分布曲线较光滑,各
T v = 0.049 9 点
D c = 0.1 值都有所下降——该模型默认边界扰动传播速度无穷大;固结波在波前附近变化剧烈——其较大梯度值意味着渗流冲击力产生,Terzaghi理论显然无法预测此现象. 这种渗流冲击效应对于深化渗透力概念
ξ = 0 研究可能具有重要意义.
由
ξ = 0 发展到0.203 3时,在
图6 中
Φ 的固结波波前早已通过不透水边界
Φ ,故
D c 处
ξ = 0 值有明显下降,并且各点
ξ = 0.5 值总体上 与Terzaghi理论曲线相符. 其他2种
D c 值对应的波前已更靠近但仍未达到不排水面,所以仍存在阶跃.
固结波时域发展规律可通过
[ 9 ] 和
D c 两个点的时程分析来考察,其中考虑上述3种
Φ 值,并以Terzaghi理论
ξ = 0.0 ) 作对比,结果见
图7 和
图8 .
图7 和
图8 同样体现固结波的波动特征——波前到达前固结波函数值不变,或边界扰动传播速度有限, 而Terzaghi理论则不能反映这一规律.
显示原图 |
下载原图ZIP |
生成PPT 图7不同Φ D c ξ = 0.0 -->
Fig. 7Consolidation wave D c Φ ξ = 0.5 ) -->
显示原图 |
下载原图ZIP |
生成PPT 图8不同Φ D c ξ = 0.5 -->
Fig. 8Consolidation wave Φ D c = 0.1 ) Φ -->
也可以采用三维瀑布图,
进一步展示固结波模型与Terzaghi(1943) 模型分别预测的无量纲超静孔压在时空中的发展规律,结果依 此如
图9 和
图10 所示. 对比可见:Terzaghi(1943)模型无法反映波动效应;本文固结波能够较好地预测超静孔压的阶跃现象及其时空发展过程.
显示原图 |
下载原图ZIP |
生成PPT 图9固结波模型预测的超静孔压D c = 0.1 Φ -->
Fig. 9Spatial and time distribution of excess pore water pressure Φ [ 37 ] -->
显示原图 |
下载原图ZIP |
生成PPT 图10Terzaghi(1943) 模型预测的超静孔压[ 44 ] -->
Fig. 10Spatial and time distribution of excess pore water pressure t 1 (1943) -->
6.4 Mandel-Cryer效应的新机理 6.4.1 Mandel-Cryer效应机理经典诠释
Mandel-Cryer效应是指在一定条件下,固结初期部分土体中孔隙水压力不仅不消散而且呈上升的现象
r B . 钱家欢和殷宗泽
r B 对均布压力作用的土球径向向外排水固结问题,提出Mandel-Cryer效应的一种机理解释:设在固结初期某一时间
r B ,排水边界周边处孔压下降仅波及到半径
r B 之外,
[ 37 ] 以内孔隙水尚未排出;此时
[ 44 ] 以外土体固结过程将产生收缩,由此引起内部总应力随时间而提高;在
? p G S t / ? t = 0 以内土体不固结前提下,这种外壳收缩引起的总应力增大只能通过内部孔压提高来承担. 龚晓南
? σ / ? t = - [ k t / g ] ? 2 u e / ? t 2 ( 111 ) 也提出一种精辟解释:排水边界土体收缩变形对内部土体产生压缩力,由此引起超静孔压的提高量大于排水固结引起的下降量时,就产生Mandel-Cryer效应. 传统观点还认为,该效应仅是二维和三维固结中的现象,一维固结并不存在——因为没有总应力变化
k t ≠ 0 .
6.4.2 固结波模型对总应力时间变化率的考虑
按固结波理论,Mandel-Cryer效应并不受问题维数限制. 固结波模型中总应力随时间的变化率,即式(42)表明:在模型推导各前提下,进一步忽略边界外载荷变化率,即
? σ / ? t ,将有
u e 对
? 2 u e / ? t 2 的固结过程,显然总应力时间变化率
R = 15 受超静孔压
p = 10 二阶时间变化率
E = 10 控制,而不再恒为零. 因此,一维固结同样具备Mandel-Cryer效应产生条件:总应力随时间变化.
6.4.3 Mandel-Cryer效应算例及其对称性和一维化
为说明一维固结可以发生Mandel-Cryer效应,对文献[
44 ] 算例进行分析. 该算例针对假想半径
ν = 0.3 m的土柱,在周边受径向均布压力
K = 1.16 × 1 0 - 6 kPa作用下,按Biot固结理论有限元法分析径向向外排水固结过程. 土体弹性模量
E s = 13.461 5 MPa,泊松比
g = 9.81 ,渗透系数
2 cm/s. 文献[
44 ]给出某些时刻孔压沿半径分布及圆心处孔压随时间变化图,显示初期孔压升高现象.
上述算例缺乏土柱高度,故暂按长圆柱体处理,再考虑到周边外荷载和排水边界对称性,于是孔压分布将只与径向位置和 时间有关,这在数学上等效于一维情况(土球径向固结也等效于一维数学问题). 再按弹性力学换算关系,得到压缩模量
D c = 9.146 3 × 1 0 - 9 MPa;重力加速度
ξ = 0 m/s
ξ = 0.5 ;最终得到固结波无量纲量
ξ = 0.9 .
6.4.4 算例的固结波分析及Mandel-Cryer效应
算例[44]等效一维固结问题的固结波结果分别如
图11 和
图12 所示. 其中,
图11 给出
Φ ,
T v 和
ξ = 0 等3个位置处超静孔压
Φ 随
T v = 0.053 1 的变化规律,可见:(1)在固结初期阶段,
ξ = 0.5 处同样出现超静孔压随时间发展先增大而后减小的现象,
ξ = 0.9 的极大值1.022 2在
ξ = 0 时刻出现. (2)对
ξ = 0 和
D c = 9.146 3 × 1 0 - 9 ) 两点,由于更靠近排水边界,其Mandel效应并没有
D c = 9.146 3 × 1 0 - 9 ) 处明显. (3)在
D c = 9.146 3 × 1 0 - 9 处的Terzaghi理论结果没有Mandel-Cryer效应,这与传统观点一致,同时也说明Terzaghi理论中忽略流体惯性的局限性.
显示原图 |
下载原图ZIP |
生成PPT 图11存在Mandel Cryer效应的算例(D c = 9.146 3 × 1 0 - 9 -->
Fig. 11Case study of Mandel-Cryer effect (ξ -->
显示原图 |
下载原图ZIP |
生成PPT 图12Mandel Cryer效应中固结波空间分布([ 44 ] -->
Fig. 12Spatial distribution of consolidation wave for Mandel-Cryer effect (r B -->
图12 给出典型时刻沿
T v ? 1.412 8 × 1 0 - 4 (径向)的超静孔压空间分布. 钱家欢和殷宗泽
ξ = 0 Mandel-Cryer效应机理解释的出发点是排水和不排水分界半径
Φ = 1 这个假想概念,但此概念尚未见有明确的理论支持.
图11 和
图12 结果表明,在
t 1 阶段,
r B 处的超静孔压满足
t 1 ,意味着确实存在这样的某个时刻“
r B ”和对应半径
T v = 0.020 3 (对不同考察点,
ξ = 0 和
Φ = 1.010 0 不同). 因此,固结波模型可为诠释Mandel-Cryer效应机理的上述假设提供理论依据.
图12 中,
T v = 0.167 3 时刻的
ξ = 0 处超静孔压达到
Φ = 0.900 4 ;
[ 9 ] 时刻的
T v = 0.053 1 处超静孔压
0.167 3 . 作为对比,给出Terzaghi理论
ξ = 0 预测的超静孔压在
0.995 7 和
0.832 2 两时刻的空间分布规律:(1) Terzaghi理论超静孔压结果均偏小于固结波对应值;(2) 在
[ 37 ] 处,Terzaghi结果分别为
T v = 0.05 和
u / P ,两种理论的结果差异随固结而变化,这表明固结波模型具有研究意义.
6.4.5 算例结果简要对比
龚晓南
T v = 0.053 1 在圆形土柱径向排水固结Biot理论数值分析中,给出圆柱体中心处超静孔压在
Φ ≈ 1.022 2 时刻达到较高无量纲值
[ 45 ] ,该结果介于1.1和1.2,明显高于本文前述
[ 46 ] 时刻达到的极大值
C s c .
Mandel-Cryer效应中最大孔压的固结波预测值相对偏小的原因主要有:(1)不同分析中物理力学和几何参数的差异;(2)问题 维度差异;(3)土体体力的影响——固结波模型与Terzaghi理论都没考虑土体体力影响,但丁洲祥等
ε - ε 0 = - ε 0 p 2 p = - ap ( 112 ) 认为土体体力具有 非保守属性,当变形较大时对结果影响显著;(4)材料和几何双线性化的影响;(5)黏性或次固结效应. 仇玉良和丁洲祥
d ε = - a d p ( 113 ) 在一维小变形主、次固结耦合研究中发现,随着无量纲主、次固结耦合系数
d q = - a d p ( 114 ) 变化,单面排水不透水边界上无量纲超静孔压会在不同程度上超过外载荷,即出现类似Mandel效应现象——这与殷建 华等EVP模型预测的早期超静孔压异常升高的黏性本质是一致的. 但黏性效应造成初期超静孔压升高的同时降低了有效应力,固结过程中总应力不变,因此区别于本文固结波孔隙流体惯性机理. 在固结波模型中,如果进一步考虑黏性,那么固结初期超静孔压理论值会有所提高.
7 深入讨论和展望 上述固结波的理论对比采用了
Terzaghi(1943) 模型,该模型通常被视为小变形模型. 然而,Terzaghi固结理论的变形属性和表述结果在不同时期存在较大差异甚至争议,从历史发展角度剖析其根源仍然有益, 这也为固结波模型的发展和完善提供学术背景. 下面将通过讨论不同阶段Terzaghi理论模型的内在矛盾及改进轨迹,得到Terzaghi固结理论复杂的2种坐标背景和4种固结系数, 由此拓展本文固结波的相应表述、对比与 Tsytovich理论和Fillunger理论的异同,以及展望固结波潜在的学术意义.
7.1 Terzaghi固结理论的内在矛盾及改进历史 7.1.1
Terzaghi(1925) 固结理论的基本方程
Terzaghi(1925) 在推导其固结模型时,先后使用了如下方程. 固相本构方程
ω = p 1 - p ( 115 ) 针对该方程,另有两个附注公式
i = Qk = - d ω d z ( 116 ) d Q d z = a d p d t = - a d ω d t ( 117 ) 超静孔压方程(或有效应力方程)
c ? 2 p ? z 2 = ? p ? t ( 118 ) 液相本构方程(Darcy定律)
c = k / a 连续性方程(质量守恒方程)
[ 3 ] 最终得到固结方程即式(1),以及等效的固结方程
[ 3 ] 式中,
[ 7,8 ] . 其余各式符号意义见文献[
3 ].
文献[
47 ]汇编了Terzaghi(1923)首次发表的固结理论德语论文,其推导方法和结果与
Terzaghi(1925) 上述方程
z 基本一致.
7.1.2
Terzaghi(1925) 模型的内在矛盾
Terzaghi(1925) 模型
a 是否是一种线性化大应变模型
z ?笔者认为,问题核心在于连续性方程式(117)的解读方式. 当坐标
a 为普通坐标且系数
a 为压缩系数含义时,式(117)在力学意义上不成立. 如果在坐标
~ 为普通坐标条件下保证式(117)的正确性,则系数
m v c 的含义应当是体积压缩系数. 但是,系数
[ 9 ] 已经在方程式(112)
[ 10 ] 式(114)中被赋予压缩系数的含义,这样就产生了内在矛盾.
7.1.3
Terzaghi(1943) 模型中的努力:
[ 9 ] 的引入
Terzaghi
[ 3 ] 和Terzaghi和Jelinek
~ 先后不断努力解决上述矛盾. 首先,在固相本构关系的表征方面,Terzaghi
~ 在与Terzaghi
m v c 基本一致的孔隙比--有效应力关系方程(文献[
9 ]式(1)
[ 9 ] 式(3))后面,没有说明原因情况下,以应变--有效应力关系形式,补充了表示相同固相本构规律 的方程(文献[
9 ]式(4)
m v c 式(6)),其中涉及新的体积减小系数
[ 3 ] (文献[
9 ]式(5)). Terzaghi
a 在连续性条件中以
z 替代Terzaghi
n 模型式(117)中的系数
[ 9 ] . 于是,上述逻辑矛盾暂时得到解决:坐标
[ 9 ] 是普通坐标,且连续性方程正确.
7.1.4
Terzaghi(1943) 模型中的努力:新矛盾即
e 0 歧义
然而,Terzaghi修补工作
n 0 = e 0 / 1 + e 0 在体积变化度量方面却产生新矛盾. 这是因为,Terzaghi
e 将初始孔隙比
n 01 = e / 1 + e 0 对应于每单位土体体积的孔隙体积
Δ n ,最终孔隙比
Δ n = n 0 - n 01 = ? = m v c p ? - p ? 0 = m v c Δ p ? ( 119 ) 对应于
Δ n ,所以每单位初始土体体积的孔隙体积减小量
n 0 - n = m v c p ? - p ? 0 ( 120 ) (即文献[
9 ]式(4))
n 于是,
n 被赋予小应变含义,表示土体在固结完成后相对于固结前初始状态的体积应变. Terzaghi随后又将式(119)写为(文献[
9 ])
n 01 Terzaghi把
n 理解为黏土的孔隙体积. 显然,如果要保持前后一致,式(120)中
Δ s 应当为
n ——概念
[ 10 ] 的内涵产生歧义.
7.1.5
Terzaghi(1954) 模型的努力:
Δ s 的引入
为了解决
ε = n 0 - Δ s / 1 - n 0 ( 121 ) 的上述歧义,Terzaghi和Jelinek
ε - ε 0 = n 0 1 - n 0 - n 0 - Δ s 1 - n 0 = Δ s 1 - n 0 = 1 + ε 0 Δ s ( 122 ) 引入
[ 9 ] 表示应变,即(文献[
10 ] 式(3a))
Δ s = ε - ε 0 1 + ε 0 = ? = m v c p ? - p ? 0 = m v c Δ p ? ( 123 ) 和本应完全等价的关系(文献[
10 ]式(3c))
ε - ε 0 以改进Terzaghi
ε 0 - ε 中(即文献[
9 ]中式(4))式(119)的符号歧义问题,而有(即文献[
10 ]式(4))
[ 48 ] 但仍有遗憾的是,式(122)和式(123)中
? ε s ? t = 11 + e ? e ? t ( 124 ) 应更正为
c v ,否则等式不成立.
Terzaghi理论的自我完善在力学上局限于本文连续性条件式(27)的范畴.
7.2 Terzaghi固结理论2种小变形固结系数的起源 Taylor
1 + e 认为土体微元体积在固结过程中固相体积不变,据此求出单位土体微元体积时间变化率,相当于式(30)第1个等号右端变为
1 + e 0 由此导致固结系数
[ 48 ] 变为式(10)所示包含
[ 3,9 - 10 ] 项的形式,从而区别于式(8)涉及
[ 48 ] 的结果.
Taylor
[ 11 ] 使用的坐标是欧拉坐标,而非普通坐标,这区别于Terzaghi
d x d y d z / 1 + e 0 作法. 很多文献沿用Taylor上述推导思路
1 + e . 例如,Terzaghi等
1 + e 0 引入
[ 48 ] 为常数的假定,却又前后不一致地采用
c v 替换
[ 20 ] ,得到式(10)所示与Taylor结果
c v 相同的固结系数
[ 49 ] . 再以同济大学土力学教材为例,其第2版
[ 50 ] 中
c v 是式(10),而第3版
[ 6 ] 和第5版
[ 6 ] 中
? ? z k e γ w 1 + e d σ ' d e ? e ? z + ? e ? t = 0 ( 125 ) 则为式(8),但没有见到深入讨论.
7.3 Gibson理论框架内Terzaghi理论的变形属性 下面基于Gibson
γ w 大变形固结理论,探讨Terzaghi理论的变形(几何)属性. 忽略自重影响时,Gibson模型
σ z , t 退化为
k e / 1 + e 式中,
z 表示液相重度. 当总应力
k e γ w 1 + e - d e / d σ ' ? 2 u w ? z 2 = ? u w ? t ( 126 ) 为常数且
- d e / d σ ' 是关于坐标
[ 7 ] 的常数时,由式(125)得到
k = k e / γ w 1 + e 由式(125)至式(126),并不需要假定
a = - d e / d σ ' 为常数,这不同于Znidarcic 和 Schiffman
u w = w 的认识. 如果记
c = k / a 和
[ 3 ] ,并假设地下水位不随时间变化、忽略固相运动速度、
[ 3 ] ,以及
z ,此时式(126)等同于Terzaghi方程
[ 3,9 - 10,47 ] 即式(1). 这似乎表明,Terzaghi固结理论
[ 51 ] 是一种大应变固结理论. 然而,式(126)中坐标
c ? 2 p z ? z 2 = ? p z ? t ( 127 ) 的属性是固相体积坐标或简化Lagrangian坐标,而不是普通坐标. Terzaghi
p z 并没有对超越普通意义的坐标含义多样性予以明确阐述.
7.4 Tsytovich理论与Terzaghi理论的联系 7.4.1 Tsytovich (崔托维奇) (1951)的固结控制方程
Tsytovich
t 提出一种固结模型
c 式中,
c = k / [ a ( 1 + ε 1 ) Δ 0 ] ( 128 ) 是“传递于土固体颗粒上的压力”,
k 是时间,
a 是“土的固结系数”
ε 1 其中,
Δ 0 是透水系数或渗透系数,
p w 是土的压缩(压密)系数,
p z 是相应于天然产状条件的土孔隙比,
p w 是水的容重(水的重度). 式(127)也可以改写为以
p z + p w = p 取代
p 的形式,其中
z 表示传递于水上的压力,且有
h 0 = h / ( 1 + ε 1 ) ( 129 ) ,
h 0 表示外部压力.
7.4.2 Tsytovich (1951)理论的坐标属性和关键概念
文献[
51 ]并没有明确式(127)中坐标
[ 51 ] 的性质,但却阐明“引用高度”的概念,“这个高度在土的整个压缩过程中都不变”,它等于
z 此外,在解方程式(127)时,“必须考虑到土层的引用厚度
z ”
[ 51 ] . 由此推论,式(127)中的坐标
k 0 应当具有土体固相体积坐标的含义,即与式(126)中坐标
k 的含义相同. 因此,崔托维奇
k 0 = k / ( 1 + ε 1 ) ( 130 ) 模型式(127)与式(126)是一致的.
Tsytovich (1951)还给出3点:(1)“土的引用渗透系数”
q = - k 0 ? H / ? z ( 131 ) 概念,以区别于渗透系数
H ,即
? q / ? z = - ? ε / ? t ( 132 ) (2) Darcy定律的表述形式
ε 其中,
~ 是水头. (3)关键原理——“对于任何一个时间间隔,在饱水土体基本分层中,水流量增大值将等于土湿度(相对孔隙度)减小值”,即
ζ 式中,
q = - k 0 ? H ? ζ ? ζ ? z = - k 1 + ε 1 ? H ? ζ 1 + ε 1 1 = - k ? H ? ζ ( 133 ) 是孔隙比.
式(129)
[ 51 ] 式(132)是 Tsytovich (1951)固结理论的重要依据. 其中,式(131)和式(132)并不容易理解和验证. 这里尝试加以探讨. 设土体Lagrangian坐标为
ζ ,则式(131)可写为
[ 33 ] 因此,崔托维奇
[ 52 ] 默认Darcy定律基于普通坐标
[ 51 ] . 再根据丁洲祥等
h ( r ed ) 连续性方程式(22)以及丁洲祥等
[ 47 ] 大变形固结连续性条件严格表述方法,可以证明, Tsytovich
h ( r ed ) = h / ( 1 + ε 0 ) ( 134 ) 连续性方程式(132)是严谨成立的.
7.4.3 Tsytovich理论与Terzaghi理论的关系
Terzaghi用过特殊土体厚度
c 概念
[ 3 ] ,即
k 这与土体固相体积坐标本质相符. 在计算固结系数
k = k d / ( 1 + ε ) ( 135 ) 算例
k d 中,Terzaghi使用渗透系数
ε 计算式
[ 3 ] 式中,
a 是Darcy渗透系数,
c = k / a 是孔隙比(不是常数). 同时,Terzaghi
c 在算例中将
γ w 按压缩系数使用,最终以
[ 3 ] 得到
c = ka γ w = k d a ( 1 + ε ) γ w ( 136 ) 的具体数值. 因此,根据量纲原理,引入水重度
[ 53 ] ,则Terzaghi
[ 48 ] 固结系数可以展开为
[ 7 ] ASCE
[ 47 ] 报道过固结系数定义由式(136)到式(10)的奇怪变化,但没有原因说明. Taylor
[ 3 ] 与Znidarcic和Schiffman
z 等也先后注意到这个问题. Terzaghi
[ 9 ] 认为,Terzaghi
z 理论中坐标
[ 9 ] 具有固相体积坐标属性,不同于后期Terzaghi
[ 9 ] 理论中
[ 3,47 ] 的普通坐标属性,这种差异导致不同的控制方程及固结系数. 然而,Terzaghi
[ 9,47 ] 较早时却阐明:Terzaghi
[ 51,54 ] 模型与早期Terzaghi
[ 3,47 ] 模型是一样的. 显然Terzaghi
[ 6 ] 论述之间充满自相矛盾.
注意到这些历史事实后可以发现,不同时期的 Tsytovich理论模型明显受到Terzaghi理论表述变化的影响. 在某种意义上,早期 Tsytovich
[ 55 - 56 ] 理论与早期Terzaghi理论
[ 51,54 ] 都可以理解为一定条件下线性化的一维大变形固结理论即Gibson理论
[ 9 ] 的特例. 但后期 Tsytovich模型
[ 51,54 ] 不再与 Tsytovich
c 相同,而与Terzaghi后期模型
ε 1 一样,即可理解为小变形模型.
然而,这两种理论固结系数定义之间仍存在细微差异,即 Tsytovich
e 1 固结系数
[ 3,47 ] 中孔隙比
c (或
ε )是常数,而Terzaghi
e 固结系数
[ 3,47 ] 中孔隙比
k d (或
[ 51,54 ] )并非常数. 笔者认为,其根本原因在于:Terzaghi
k 潜在使用了Eulerian描述的Darcy定律,其中渗透系数为
[ 51,54 ] ; Tsytovich
k 0 则使用了Lagrangian描述的Darcy定律,其对应渗透系数是
k ? 0 = k / ( 1 + ε ) ( 137 ) . 换言之,在 Tsytovich
[ 51,54 ] 框架内,如果采用Eulerian描述的Darcy定律,那么“土的引用渗透系数”
[ 3,47 ] 即式(130)就相应地更新为
z 于是,在其他条件不变情况下, Tsytovich
z 与Terzaghi
c ζ ? 2 u w ? ζ 2 = ? u w ? t ( 138 ) 两种固结理论完全等价.
7.5 2种坐标背景及4种固结系数 通过前述分析,对于传统一维固结理论:当坐标
c ζ 为普通土体坐标或Lagrangian坐标含义时,后期Terzaghi模型有式(8)和式(10)所示的2种小变形固结系数;当坐标
ζ 为固相体积坐标含义时,早期Terzaghi固结理论则具有2种大变形固结系数,即式(136)和式(128).
为便于比较,传统一维固结模型写为统一形式
c ζ = c G EH = k e 1 + e 0 2 γ w 1 + e - d e / d σ ' ( 139 ) 式中,
[ 3,47 ] 是基于Lagrangian坐标
c ζ T , 1925 的形式上统一的固结系数.
对简化Gibson大变形固结模型式(126)
c ζ T , 1925 = c G EH ( 140 ) 可以证明,早期Terzaghi
[ 51,54 ] 大变形固结模型对应的固结系数
c ζ Ts , 1940 为
c ζ Ts , 1940 = 1 + e / 1 + e 0 c G EH ( 141 ) 而 Tsytovich
[ 9 ] 大变形固结模型的固结系数
c ζ T , 1943 为
[ 48 ] 小变形的Terzaghi
[ 11 ] 模型固结系数
c ζ T aylor , 1948 和Taylor
c ζ T , 1943 = 1 + e / 1 + e 0 c G EH ( 142 ) 或Terzaghi等
c ζ T aylor , 1948 = 1 + e 2 / 1 + e 0 2 c G EH ( 143 ) 模型固结系数
c ζ ? 2 u e ? ζ 2 = c a ? 2 u e ? t 2 + ? u e ? t ( 144 ) 分别为
c ζ = c ζ T , 1943 c ζ 7.6 固结波模型拓展与历史背景 7.6.1 固结波模型拓展
固结波模型式(50)也可以写为统一形式
c ζ T , 1925 当
c ζ ( Ts , 1940 ) 时,式(144)等价于式(50). 当式(144)中
c ζ T aylor , 1948 分别取
[ 5,57 ] ,
[ 58 ] 和
[ 5 ] 时,则在形式上得到固结波模型其他3种表述形式.
7.6.2
Fillunger(1936) 固结理论
援引de Boer等和de Boer论述
? v w ? t + v w ? v w ? z = gn γ w - Z - ? n σ ? z ( 145 ) ,对Fillunger
? v s ? t + v s ? v s ? z = g 1 - n γ s Z - ? 1 - n σ ? z ( 146 ) 固结理论加以对比讨论. Fillunger固结基本方程(组)
? n ? t + ? n v w ? z = 0 ( 147 ) 为
- ? n ? t + ? 1 - n v s ? z = 0 ( 148 ) Z = - v w - v s n 0 k ' γ w ( 149 ) ~ n 0 k ' 式(145)
[ 5 ] 式(149)中各符号定义见文献[5,58]. Fillunger理论领先孔隙介质力学约30年,但缺乏一般和具体的初边值条件,并认为不可能通过试验获得
? v s / ? z + ? q / ? z = 0 ( 150 ) 和
q = n v w - v s 合理值
? v w / ? t + v w ? v w / ? z = v ? w .
7.6.3 Fillunger理论分析及与固结波模型对比
对Fillunger(1936) 理论尝试作如下分析和对比.
将式(147)和式(148)左右两端相加,得到
? v s / ? t + v s ? v s / ? z = v ? s 式中,
g / n γ w = 1 / ρ w . 式(150)与 式(27)等价.
根据物质导数概念,式(145)和式(146)等号左端项分别有
g / [ ( 1 - n ) γ s ] = 1 / ρ s 和
ρ w v ? w + ρ s v ? s = - ? σ / ? z ( 151 ) . 再按混合物理论记法
v ? ? ,
v ? ? = ρ w v ? w + ρ s v ? s / ρ ,所以将式(145)和(146)在等号两端对应相加,整理后有
ρ v ? ? = - ? σ / ? z ( 152 ) 式(151)等号左端有3种等价处理方法. 第1种方法:按混合物思想,引入平均化加速度概念
[ 33 ] ) ,即
ρ w v ? w + ρ s v ? s = ρ v ? s + ρ w n v ? w - v ? s ( 153 ) ,从而式(151)等价表述为
ρ = ρ w + ρ s 显然,这与单相连续介质力学对应方程形式一致.
第2种方法:不引入新变量,而按固相控制土体构形思想(丁洲祥等
ρ w = ρ w / n = γ w / g ,式(151)等号左端项
q 0 = v w - v s 式中,
q 0 ,
q = n q 0 ,并特别地记
ρ v ? s + ρ w n q ? 0 = - ? σ / ? z ( 154 ) ,
q 的意义是液相相对于固相的真实流速,而非Darcy速度;
ρ v ? s + ρ w q ? - ρ w q 0 n ? = - ? σ / ? z ( 155 ) . 因此,式(151)等价于以下形式
n q ? 0 = q ? 若采用Darcy速度
ρ w q 0 n ? ,则得式(151)第3种表示
[ 58 ] 可见,当
ρ v ? s 或忽略
ρ w q 0 n ? 项时,Fillunger理论
ρ w n q ? 0 推论式(155)与本文固结波模型式(23)在固液两相不可压缩、忽略土体自重和一维条件下的对应方程本质上完全一致. 如果考虑自重但忽略
d ρ f q i / d t 和
ρ w q ? ,那么Fillunger理论推论式(155)与本文固结波基本方程式(26)也相互等价.
目前不清楚造成Fillunger理论推论式(154)等号左端第2项
ρ ? f = 0 区别于本文式(23)中
w = f 即
[ 59 ] (流体不可压缩
v ? w 、一维和下标符号
n )的根本原因,这有赖于更深入的基础研究. 有关进展是,Tani
ρ w q 0 n ? 发现Fillunger理论隐含Darcy定律的新形式——其中含有
[ 24 - 25 ] 并且与孔隙率
[ 58 ] 和孔隙率梯度均相关,这不同于传统模型中Darcy定律与孔隙率无关的情况,但尚没发现解决这一分歧的毋庸置疑的方案.
综合而言,以基本方程式(150)和式(155)为 基础,再联合其他条件和假设,可以得到Fillunger理论框架内相应的一维动力固结控制方程和忽略固相加速度的一维准静力固结控制方程(固结波),但其中
[ 60 ] 特有项的存在,将导致其求解比本文固结波模型更加困难.
7.6.4 Biot动力固结理论与固结波模型对比
Biot动力固结理论
[ 40 ] 比Fillunger
[ 61 ] 理论滞后约20年,但前者逐渐发展成为主流并仍是研究热点,如宋佳等
[ 24 - 27 ] 和Xu等
[ 62 - 63 ] 在体积波传播特征等方面取得新认识. 然而,Voyiadjis和Song
[ 64 ] 认为:Biot模型不是从力学和热力学基本公理和原理发展得出,所以复杂难懂. 在Biot
u - p 成果基础上, Zienkiewicz等
D c 和Zienkiewicz
D c 2 = c a c v / H 2 = k 2 E s / ( g 2 ρ w H 2 ) 提出一种简化的
[ 65 ] 模型,其中仅考虑固相加速度而忽略液相加速度,不同于本文固结波仅考虑液相惯性的情况.
7.7 固结波的土力学意义及学科交叉 7.7.1 缩尺固结试验的不确定性原则
固结波模型表明,土体固结响应特征主要取决于
D c 值. 由
D c 可见,标准固结试验
D c 试样
D c 值(厚度常取20 mm)与现场实际土层
D c 值(厚度可达数十米)可能出现较大差别. 按相似理论,只有当试样与现场土样
[ 66 - 67 ] 值相等时,才能通过室内试验准确模拟现场土体固结响应规律. 这就引出缩尺固结试验不确定性原则——即使能够获得未受扰动的最理想原状土样及其传统物理力学参数准确值,缩尺固结试验在理论上也无法准确模拟 足尺现场条件下土体的固结波响应;在
H 等价条件下,扰动土样的缩尺固结试验反而更接近于真实固结波响应. 缩尺试验可以加快试验,却因改变
D c 值而违反相似定律. 传统Terzaghi一维固结模型无法反映这一规律.
需要注意的是:确定土体最终沉降量仍需原状土样;应重视并尽量准确获得现场土体真实排水状况和排水路径. 旧金山Bay Farm 岛和Kansai国际机场工程实践
[ 68 ] 经验之一就是——准确的沉降速率预测需要对黏性土中嵌入砂层所提供的内部排水评估方法进行改进,尽管该建议尚未注意到固结波效应,但结论与本文相符.
7.7.2 尺度效应与微观土力学
固结波模型基于连续介质力学基本概念而提出,当土样
[ 68 ] 值减小到适用范围极限——表征体元REV (RVE或unit cell)对应特征长度值时,
[ 68 ] 值较大,而相应试验结果可能表现为显著的波动过程.
这种尺度效应对微观土力学研究将具有实际意义:在一定观测精度条件下,土体材料尺度的巨大差异可能导致微观上和宏观上根本不同的固结响应. 如何评价和应用基于微观土力学的相应结果值得深入思考.
7.7.3 固结波与学科交叉
赵亚溥
[ 69 ] 在纳米和介观力学问题研究中,提到Yakobson和Smalley为代表的一种观点——“连续介质理论在纳米尺度依然适用”. 但固结波模型能否应用于纳米尺度,仍有待探索.
从数学方程来看,固结波方程与若干反映其他物理现象的模型方程基本一致:(1)描述分子扩散过程的考虑弛豫时间 的non-Fick第二定律
[ 70 ] ;(2)描述传热传质现象的包含弛豫时间的non-Fourier导热方程
[ 71 ] 、非傅里叶CV导热方程
[ 72 ] 或称为热波的方程
[ 72 - 73 ] ;(3)描述运动规律的Maxwell黏弹性介质一维波动方程
c v = E s / ρ w c a 和阻尼弦振动方程
τ 1 ;(4)描述传输线上电压和电流关系的电报方程或传输线方程
D .
固结波方程两个系数之间存在相关性,即
[ 68 ] . 这与其他物理现象有所不同,例如扩散运动中弛豫时间
c a = 0 与扩散系数
k = 0 相互独立
c v = 0 等. 当
? u e / ? t = 0 即
[ 74 ] 时,
[ 75 ] ,此时固结波方程退化为
[ 76 ] ,即超静孔压是定常的. 固结波这些特征导致其应用范围与其他物理现象存在差别,如过增元和曹炳阳
[ 77 ] “只有在超快加速加热或极低温的情况下, 才必需考虑热量以波动方式传递的非傅里叶导热现象”. 未来研究应加强精密仪器、测试技术开发和跨学科合作,进一步结合精细化室内试验和现场观测来验证和发展固结波理论,正如赵 成刚等
[ 78 ] 指出“如果总是停留在简单的土力学理论上,不再前进,土力学理论就难有实质性进展,这不符合科学发展规律”. 也可以结合热固结
[ 79 ] 、非饱和地基
[ 33 ] 、垃圾土
n ∈ 0 , N 甚至混凝土
n ∈ N + 1 , ∞ 等方向新近成果,探讨固结波理 论的应用.
8 结 语 在一维固结范畴内,研究了忽略固相惯性但考虑液相惯性的准静力固结模型,主要成果和结论为:
(1)基于丁洲祥等大变形动力固结理论
D c ,经过简化提出一个一维小变形固结波动模型,即式(50)和式(65). 固结波具有频散和耗散特征,其极限相位速度满足式(60)和式(58).
(2)采用分离变量法,得到了单面排水和瞬时加载条件下无量纲固结波定解问题的解析解答,即式(94),可为理论应用分析和校核数 值解法的精度提供可靠的依据. 固结波解析解即式(94)数学结构反映了动力学中过阻尼(
Φ )和欠阻尼(
D c )两种机理的贡献.
(3)单面排水和瞬时加载情况下固结波分析结果表明:当无量纲数
a 达到某些较大值时,无量纲超静孔压
a 可能出现阶跃和波动现象;而当
D c 为某些较小数值时,对应固结波响应结果可以解释Mandel-Cryer效应的部分机理. 超静孔压发展的本质是固结波传播.
(4) Terzaghi经典固结理论系统分析结果表明:(a) Terzaghi模型方程其实可以部分反映渗透性和压缩性变化. (b)早期Terzaghi固结模型与后期Terzaghi固结模型可能不同,
而Terzaghi(1943) 和Terzaghi(1960)的解释相互矛盾. (c)当坐标理解为普通土体坐标时,早期Terzaghi模型就成为等同于后期模型的小变形模型,但会出现系数{Invalid MML}兼作压缩系数和体积压缩系数的错误. (d)当坐标理解为固相体积坐标时,早期Terzaghi模型就是一种与后期模型不同的大变形模型,此时系数{Invalid MML}将仅表示压缩系数. (e)不同时期Terzaghi固结模型的固结系数涉及4种定义和2种坐标性质,可统一于式(138). (f)经大变形诠释的早期Terzaghi固结模型比后期小变形模型在理论上更先进.
(5)鉴于经典一维固结理论上述复杂背景,固结波模型在形式上可拓展至相应的4种表述结果.
(6)固结波模型具有丰富的内涵:常规缩尺固结试验在理论上存在物理力学参数与固结波响应两种因素之间的不确定性矛盾; 通过微观土力学视角的固结研究宜重视尺寸效应. 土力学中可能隐含一种量子效应.
(7)在一定{Invalid MML}范围内,抛物型经典一维固结理论结果在不同程度上近似于双曲型固结波模型结果. 未来固结波理论发展,可以逐步考虑非线性、固相惯性和多场多相耦合,同时加强试验研究.
致谢 感谢审稿专家提出的15条宝贵建议;感谢国家自然科学基金委和评审专家在固结理论与应用方向给予的资助和支持. 清华大学王高明和北京交通大学周旭宽同学提供了部分德语文献帮助. University of Texas at Austin的胡靖博士生、University of Natural Resources and Life Sciences (BOKU) Austria的吴伟教授、University of Newcastle Australia的王善勇教授等也为文献检索付出时间和帮助. 俄罗斯留学生 Tsa bel Serge (Tsaybel Sergey)翻译了俄语著作[54-56]若干章节. 北京交通大学李涛教授百忙中口译了德语文献[
3 ]有关部分. 长安大学周勇军教授推荐桥梁/结构动力学文献并用心答复若干专业问题. 河海大学雷国辉教授热情提供了待刊论文. 北京交通大学赵成刚教授鼓励作者不断取得新成果,李伟华教授就Biot动力固结理论给以有益讨论. 如有可能,愿本文能作为作者同济大学博士后出站暨在北京交通大学从教十周年(2008.05-2018.05)纪念,同时谨献给父亲丁 勤君、母亲赵吉香和伯父丁勤民,感谢给予的爱和教诲. 最后谨对编委会和编辑部等老师们的高效工作,集体致敬.
The authors have declared that no competing interests exist.
[1] Lambe TW Whitman RV . Soil Mechanics New York: Wiley , 1969 : 406 -422 [2] Lambe TW Whitman RV . Soil Mechanics, SIVersion New York: John Wiley & Sons , 1979 : 406 -422 [3] Terzaghi K Erdbaumechanik auf Bodenphysikalischer Grundlage Leipzig und Wien: Franz Deuticke , 1925 : 140 -152 [本文引用: 8] [4] Poskitt TJ Discussion: The origins of the theory of consolidation: the Terzaghi-Fillunger dispute Geotechnique , 1997 , 47(4 ): 893 -895 [5] de Boer R Schiffman RL Gibson RE The origins of the theory of consolidation: The Terzaghi-Fillunger dispute Geotechnique , 1996 , 46(2 ): 175 -186 [6] Gibson RE England GL Hussey MJL The theory of one-dimensional consolidation of saturated clays. I. Finite non-linear consolidation of thin homogeneous layers Geotechnique , 1967 , 17(3 ): 261 -273 [7] Znidarcic D Schiffman RL On Terzaghi’s concept of consolidation Geotechnique , 1982 , 32(4 ): 387 -389 [本文引用: 2] [8] Lee K Szalwinski CM Discussion on ‘On Terzaghi’s concept of consolidation’ Geotechnique , 1984 , 34(1 ): 130 -134 [9] Terzaghi K. Theoretical Soil Mechanics. New York: John Wiley & Sons Inc. , 1943 : 265 -296 [本文引用: 25] [10] Terzaghi K Jelinek R. Theoretische Bodenmechanik Berlin/Heidelberg: Springer-Verlag , 1954 : 268 -300 [本文引用: 4] [11] Terzaghi K Peck RB Mesri G Soil Mechanics in Engineering Practice, 3rd ed New York: Wiley , 1996 : 223 -236 [12] 龚晓南 , 谢康和 . 土力学 . 北京: 中国建筑工业出版社, 2002 : 92 -109 [本文引用: 1] (Gong Xiaonan Xie Kanghe . Soil Mechanics. Beijing: China Architecture & Building Press, 2002 : 92 -109 (in Chinese)) [本文引用: 1] [13] 钱家欢 . 土力学 . 南京: 河海大学出版社, 1988 : 72 -101 [本文引用: 1] (Qian Jiahuan . Soil Mechanics .Nanjing: Hohai University, 1988 : 72 -101 (in Chinese)) [本文引用: 1] [14] 李广信 , 张丙印 , 于玉贞 . 土力学 , 第2版. 北京: 清华大学出版社, 2013 : 153 -164 [本文引用: 1] (Li Guangxin Zhang Bingyin Yu Yuzhen . Soil Mechanics,2nd ed. Beijing: Tstinghua Unviersity Press, 2013 : 153 -164 (in Chinese)) [本文引用: 1] [15] 赵成刚 , 白冰 . 土力学原理, 第2版 . 北京: 北京交通大学出版社,清华大学出版社, 2017 : 175 -186 [本文引用: 1] (Zhao Chenggang Bai Bing. Principles of Soil Mechanics, 2nd ed. Beijing: Beijing Jiaotong University Press, Tsinghua University Press, 2017 : 175 -186 (in Chinese)) [本文引用: 1] [16] 李广信 . 高等土力学,第2版 . 北京: 清华大学出版社, 2016 : 319 -361 [本文引用: 1] (Li Guangxin . Advanced Soil Mechanics, 2nd ed. Beijing: Tsinghua University Press, 2016 : 319 -361 (in Chinese)) [本文引用: 1] [17] 陈仲颐 , 周景星 , 王洪瑾 . 土力学 . 北京:清华大学出版社, 1994 : 143 -157 [本文引用: 1] (Chen Zhongyi Zhou Jingxing Wang Hongjin . Soil Mechanics. Beijing: Tsinghua Universtiy Press, 1994 : 143 -157 (in Chinese)) [本文引用: 1] [18] 高大钊 . 土力学与基础工程 . 北京: 中国建筑工业出版社, 1999 : 92 -102 [本文引用: 1] (Gao Dazhao. Soil Mechanics and Foundation Engineering. Beijing: China Architecture & Building Press, 1999 : 92 -102 (in Chinese)) [本文引用: 1] [19] Kaliakin V Soil Mechanics: Calculations, Principles and Methods. Oxford: Butterworth-Heinemann , 2017 : 377 -418 [本文引用: 1] [20] 洪毓康 . 土质学与土力学,第2版. 北京: 人民交通出版社, 1995 : 106 -119 [本文引用: 1] (Hong Yukang. Soil Science and Soil Mechanics, 2nd ed. Beijing: China Communications Press, 1999 : 106 -119 (in Chinese)) [本文引用: 1] [21] 张克恭 , 刘松玉 . 土力学 .北京:中国建筑工业出版社, 2001 : 104 -110 [本文引用: 1] (Zhang Kegong Liu Songyu . Soil Mechanics. Beijing: China Architecture & Building Press, 2001 : 104 -110 (in Chinese)) [本文引用: 1] [22] Das BM. Advanced Soil Mechanics , 4th ed. Boca Raton: CRC Press, 2014 : 303 -402 [本文引用: 1] [23] 袁大军 , 丁洲祥 , 朱合华 . 对经典小变形固结理论固结系数的辨析 岩土力学 , 2009 , 30(6 ): 1649 -1652, 1657 (Yuan Dajun Ding Zhouxiang Zhu Hehua Analysis of consolidation coefficients in calssic small-strain consolidation theory Rock and Soil Mechanics 2009 , 30(6 ): 1649 -1652, 1657 (in Chinese)) [24] Biot MA Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range The Journal of the Acoustical Society of America , 1956 , 28(2 ): 168 -178 [25] Biot MA Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range The Journal of the Acoustical Society of America , 1956 , 28(2 ): 179 -191 [26] Biot MA Mechanics of deformation and acoustic propagation in porous media Journal of Applied Physics , 1962 , 33(4 ): 1482 -1498 [27] Biot MA General theory of three-dimensional consolidation Journal of Applied Physics , 1941 , 12(2 ): 155 -164 [28] Olson RE Settlement of embankments on soft clays Journal of Geotechnical and Geoenvironmental Engineering , 1998 , 124(8 ): 659 -669 [29] Yin JH Graham J Elastic visco-plastic modelling of one-dimensional consolidation Geotechnique , 1996 , 46(3 ): 515 -527 [30] Liu JC Griffiths DV A general solution for 1D consolidation induced by depth- and time-dependent changes in stress Geotechnique , 2015 , 65(1 ): 66 -72 [31] Verruijt A. An Introduction to Soil Mechanics. Extras Online: Springer International Publishing AG 2018 , 2018: 123 -155 [32] Chai JC Zhou Y . Method for considering the effect of nonuniform consolidation International Journal of Geomechanics 2018 , 18(2 ): 04017151-1-9[33] 丁洲祥 , 龚晓南 , 谢永利 . 欧拉描述的大变形固结理论 力学学报 , 2005 , 37(1 ): 92 -99 (Ding Zhouxiang Gong Xiaonan Xie Yongli Acta Mechanica Sinica 2005 , 37(1 ): 92 -99 (in Chinese)) [34] 钱学森 . 物理力学介绍 物理通报 , 1957 , 7(4 ): 193 -200 (Qian Xuesen Introduction to physical mechanics Physics Bulletin 1957 , 7(4 ): 193 -200 (in Chinese)) [35] 陈纪修 , 於崇华 , 金路 . 数学分析 , 第2版,下册. 北京: 高等教育出版社, 2004 : 353 -383 (Chen Jixiu Yu Chonghua Jin Lu . Mathematical Analysis, 2nd ed., Part B. Beijing: Higher Education Press, 2004 : 353 -383 (in Chinese)) [36] 张文生 . 微分方程数值解——有限差分理论方法与数值计算 . 北京: 科学出版社, 2015 : 262 -277 (Zhang Wensheng. Numerical Solutions to PDEs:Finite Difference Methods and Numerical Calculation . Beijing: Science Press, 2015 : 262 -277 (in Chinese)) [37] 龚晓南 . 高等土力学 . 杭州: 浙江大学出版社, 1996 : 91 -149 (Gong Xiaonan . Advanced Soil Mechanics. Hangzhou: Zhejiang University Press, 1996 : 91 -149 (in Chinese)) [38] 孙建渊 , 王灏 . 输水管道水锤效应作用下斜拉桥结构动力响应研究 土木工程学报 , 2017 , 50(2 ): 82 -87 (Sun Jianyuan Wang Hao Study on dynamic response of cable-stayed bridge under water hammer action in water pipeline China Civil Engineering Journal 2017 , 50(2 ): 82 -87 (in Chinese)) [39] 刘晶波 , 宝鑫 , 谭辉 等 . 波动问题中流体介质的动力人工边界 力学学报 , 2017 , 49(6 ): 1418 -1427 (Liu Jingbo Bao Xin Tan Hui et al .Dynamical artificial boundary for fluid medium in wave motion problems Chinese Journal of Theoretical and Applied Mechanics 2017 , 49(6 ): 1418 -1427 (in Chinese)) [40] Xu C Song J Du X et al .A local artificial-boundary condition for simulating transient wave radiation in fluid-saturated porous media of infinite domains International Journal for Numerical Methods in Engineering , 2017 , 112: 529 -552 [41] de Boer R Ehlers W Liu Z One-dimensional transient wave propagation in fluid-saturated imcompressible porous media Archive of Applied Mechanics , 1993 , 63(1 ): 59 -72 [42] Schanz M Cheng AHD Transient wave propagation in a one-dimensional poroelastic column Acta Mechanica , 2000 , 145(1-4 ): 1 -18 [43] 丁洲祥 . 一维渗透力与浮力 力学学报 , 2017 , 49(5 ): 1154 -1162 (Ding Zhouxiang One-dimensional seepage force and buoyancy Chinese Journal of Theoretical and Applied Mechanics 2017 , 49(5 ): 1154 -1162 (in Chinese)) [44] 钱家欢 , 殷宗泽 . 土工原理与计算, 第2版. 北京: 中国水利水电出版社, 1996 : 199 -237 [本文引用: 2] (Qian Jiahuan Yin Zongze. Principles and Calculation of Geotechnical Engineering, 2nd ed. Beijing: China Water & Power Press, 1996 : 199 -237 (in Chinese)) [本文引用: 2] [45] 丁洲祥 , 朱合华 , 谢永利 等 . 基于非保守体力的大变形固结有限元法 力学学报 , 2009 , 41(1 ): 91 -97 (Ding Zhouxiang Zhu Hehua Xie Yongli et al .Finite-strain consolidation finite-element method subjected to non-conservative body force Journal of Theoretical and Applied Mechanics 2009 , 41(1 ): 91 -97 (in Chinese)) [46] 仇玉良 , 丁洲祥 . 一维小变形主、次固结耦合理论模型分析 岩土力学 , 2012 , 33(7 ): 1957 -1964 (Qiu Yuliang Ding Zhouxiang Study of coupling theory of one-dimensional small-strain primary and secondary consolidation model Rock and Soil Mechanics 2012 , 33(7 ): 1957 -1964 (in Chinese)) [47] Terzaghi K. From Theory to Practice in Soil Mechanics. New York: John Wiley & Sons , Inc. , 1960 : 106- 133 -146 [本文引用: 1] [48] Taylor DW Fundamentals of Soil Mechanics. New York, Wiley , 1948 : 208 -249 [49] 高大钊 , 袁聚云 . 土质学与土力学,第3版. 北京: 人民交通出版社, 2001 : 107 -117 (Gao Dazhao Yuan Juyun. Soil Science and Soil Mechanics, 3rd ed. Beijing: China Communications Press, 2001 : 107 -117 (in Chinese)) [50] 钱建固 , 袁聚云 , 赵春风 等 . 土质学与土力学,第5版. 北京: 人民交通出版社股份有限公司, 2015 (Qian Jiangu Yuan Juyun Zhao Chunfeng et al. Soil Science and Soil Mechanics, 5th ed. Beijing: China Communications Press, 2015 (in Chinese)) [51] 崔托维奇 HA. 土力学, 第3版. 吴光轮译 . 北京: 地质出版社, 1956 : 392 -428 [本文引用: 1] ( Tsytovich HA . Soil Mechanics, 3rd ed. Wu Guanglun, Translator . Beijing: Geological Publishing House, 1956 : 392 -428 (in Chinese)) [本文引用: 1] [52] 丁洲祥 , 朱合华 , 丁文其 . 大变形固结理论连续性条件的严格表述 同济大学学报(自然科学版) , 2009 , 37(4 ): 471 -474 (Ding Zhouxiang Zhu Hehua Ding Wenqi A strict form of continuity condition in large strain consolidation theory Journal of Tongji Universtiy ( Natrural Science )2009 , 37(4 ): 471 -474 (in Chinese)) [53] ASCE . Soil Mechanics Nomenclature Manual of Engineering Practice , 1941 , 22[54] Tsytovich NA Mekhanika gruntov Moskva , 1940 : 204 -221 [55] Tsytovich NA Mekhanika gruntov ( Kratki kurs. Moskva, Vysshaya Shkola , 1983 : 171 -201 [56] Tsytovich NA Mekhanika gruntov Moskva , 1963 : 503 -513 [57] de Boer R Development of porous media theories: a brief historical review Transport in Porous Media , 1992 , 9(1-2 ): 155 -164 [58] Fillunger P Erdbaumechanik? Vienna: Selbst-verlag des Verfassers , 1936 [本文引用: 2] [59] Tani ME Hydrostatic paradox of saturated media Geotechnique , 2007 , 57(9 ): 773 -777 [60] 宋佳 , 许成顺 , 杜修力 等 . 不同渗透性饱和土中三类体波的传播性质研究与参数分析 中国科学: 技术科学 , 2017 , 47(7 ): 774 -784 (Song Jia Xu Chengshun Du Xiuli et al .Effect of permeability on the velocities and attenuation properties of three body waves in satuared soil Scientia Sinica Technologica 2017 , 47(7 ): 774 -784 (in Chinese)) [61] Voyiadjis GZ Song CR The Coupled Theory of Mixtures in Geomechanics with Applications. The Netherlands: Springer- Verlag Berlin Heidelberg , 2006 : 15 -21 [62] Zienkiewicz OC Chang CT Bettess P Drained, undrained, consolidating and dynamic behaviour assumptions in soils Geotechnique , 1980 , 30(4 ): 385 -395 [63] Zienkiewicz OC Shiomi T Dynamic behaviour of saturated porous media; The generalized Biot formulation and its numerical solution International Journal for Numerical and Analytical Methods in Geomechanics , 1984 , 8: 71 -96 [64] Zienkiewicz OC Basic formulation of static and dynamic behaviours of soil and other porous media Applied Mathematics and Mechanics , 1982 , 3(4 ): 457 -468 [65] GB/T50123-1999 . 土工试验方法标准. 北京: 中国计划出版社, 1999 : 83 -93 (GB/T50123-1999 . Standard for soil test method. Beijing: China Planning Press, 1999 : 83 -93 (in Chinese)) [66] Duncan JM Limitations of conventional analysis of consolidation settlement Journal of Geotechnical Engineering , ASCE 1993 , 119(9 ): 1333 -1359 [67] Mesri G Funk JR . Settlement of the Kansai international airport Journal of Geotechnical and Geoenvironmental Engineering , 2015 , 141(2 ): 04014102-1-16[68] 赵亚溥 . 纳米与介观力学 . 北京: 科学出版社, 2014 (Zhao Yapu. Nano and Mesoscopic Mechanics. Beijing: Science Press, 2014 (in Chinese)) [69] 69 马彤辉 . 涂层基体在脉冲激光辐照下的非傅里叶效应分析. [硕士论文] 北京: 北京交通大学 , 2016 (Ma Tonghui Analysis on non- Fourier effect of coating and substrate irradiated with intense laser. [MSc Thesis] Beijing: Beijing Jiaotong Universtiy , 2016 (in Chinese)) [70] Ma XB Ye SL Scattering of thermal waves by a heterogeneous subsurface spheroid inclusion including non-Fourier effects Thermochimica Acta , 2014 , 597: 65 -70 [71] 71 李政阳 . 一维热波晶体的热传导特性研究. [硕士论文] 北京: 北京交通大学 , 2017 (Li Zhengyang The properties of heat conduction in the one dimensional thermal wave crystal. [Master Thesis] Beijing: Beijing Jiaotong University , 2017 (in Chinese)) [72] 顾樵 . 数学物理方法 . 北京: 科学出版社, 2012 : 98 -131 (Gu Qiao. Mathematical Methods for Physics. Beijing: Science Press, 2012 : 98 -131 (in Chinese)) [73] 梁昆淼 . 数学物理方法,第4版 . 北京: 高等教育出版社, 2010 : 143 -180 (Liang Kunmiao. Mathematical Methods for Physics, 4th ed. Beijing: Higher Education Press, 2010 : 143 -180 (in Chinese)) [74] 过增元 , 曹炳阳 . 基于热质运动概念的普适导热定律 物理学报 , 2008 , 57(7 ): 4273 -4281 (Guo Zengyuan Cao Bingyang A general heat conduction law based on the concept of motion of thermal mass Acta Physica Sinica 7 ): 4273 -4281 (in Chinese)) [75] 赵成刚, 李舰, 宋朝阳 等 . 土力学理论需要发展与变革 岩土工程学报 , 2018 , 40(8 ): 录用待刊 (Zhao Chenggang, Li Jian, Song Zhaoyang , et al . Soil mechanics theory needs reform and development Chinese Journal of Geotechnical Engineering 2018 , 40(8 ): in print (in Chinese)) [76] 王路君,艾智勇 . 衰变热源作用下饱和多孔介质热固结问题的扩展精细积分法 力学学报 , 2017 , 49(2 ): 324 -334 (Wang Lujun, Ai Zhiyong . EPIM for thermal consolidation problems of saturated porous media subjected to a decaying hear source Chinese Journal of Theoretical and Applied Mechnics 2017 , 49(2 ): 324 -334 . [77] 张常光, 赵均海, 代岩 . 硬壳层非饱和软基路堤的填土高度研究 力学学报 , 2016 , 48(2 ): 484 -494 (Zhang Changguang, Zhao Junhai, Dai Yan . Investigation on filling height of embankment on saturated soft ground with stiff crust Chinese Journal of Theoretical and Applied Mechnics 2016 , 48(2 ): 484 -494 . [78] 关驰,谢海建,楼章华 . 成层非饱和覆盖层中气水两相扩散模型 力学学报 , 2013 , 45(2 ): 171 -176 (Guan Chi, Xie Haijian, Lou Zhanghua . Gas-water two-phase diffusion model for unsaturated layered cover systems Chinese Journal of Theoretical and Applied Mechnics 2013 , 45(2 ): 171 -176 . [79] 陈庆, 朱合华,闫治国 ,等 . 基于自洽法的电化学沉积修复饱和混凝土细观描述 力学学报 , 2015 , 47(2 ): 367 -371 (Chen Qing, Zhu Hehua, Yan Zhiguo ,et al . Micro-scale description of the saturated concrete repaired by electrochemical deposition method based on self-consistent method Chinese Journal of Theoretical and Applied Mechnics 2015 , 47(2 ): 367 -371 .


 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT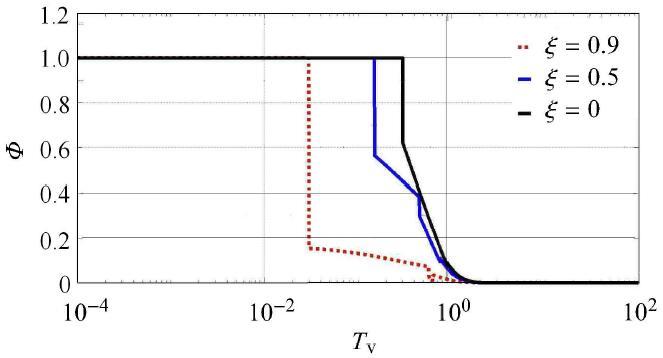 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT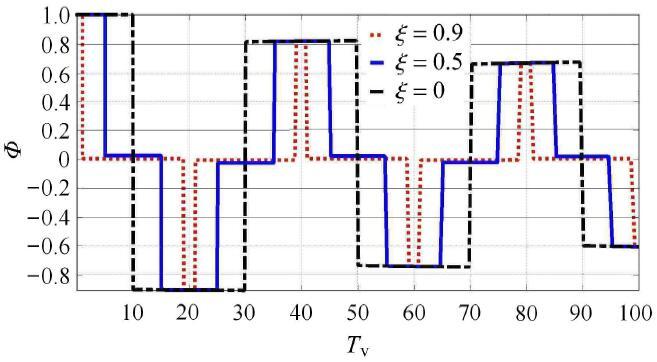 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT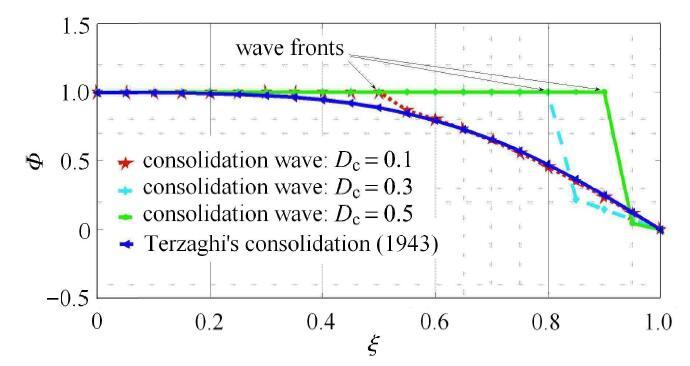 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT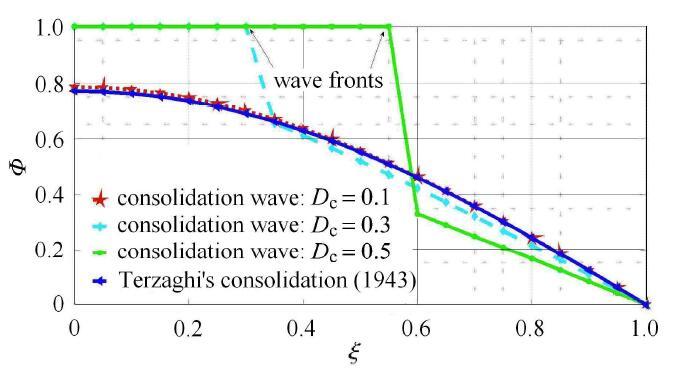 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT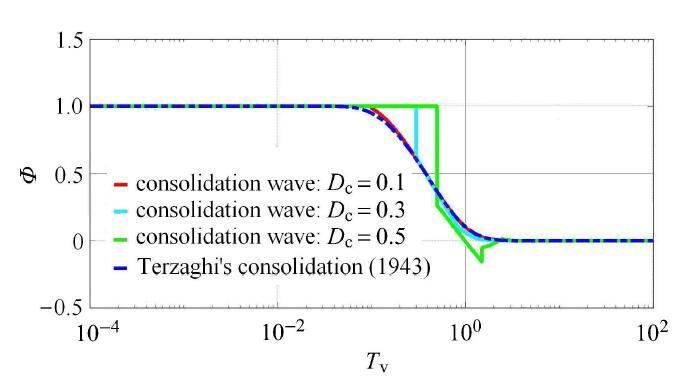 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT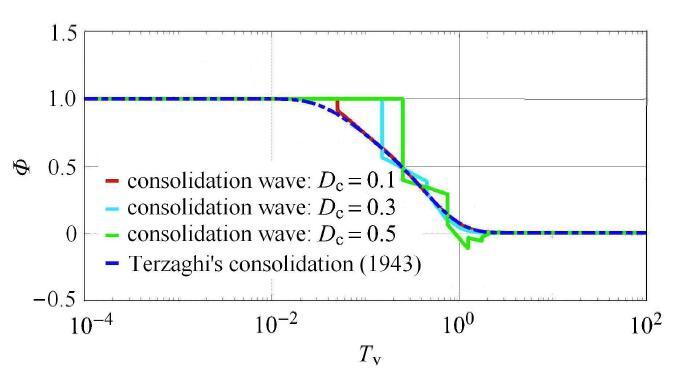 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT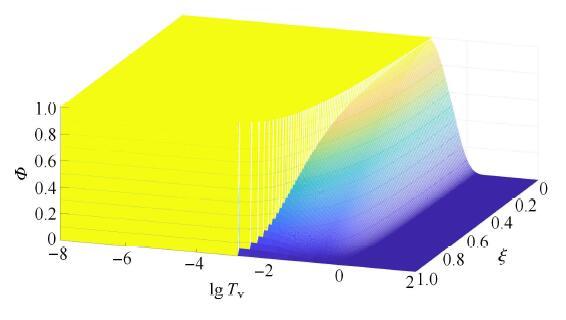 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT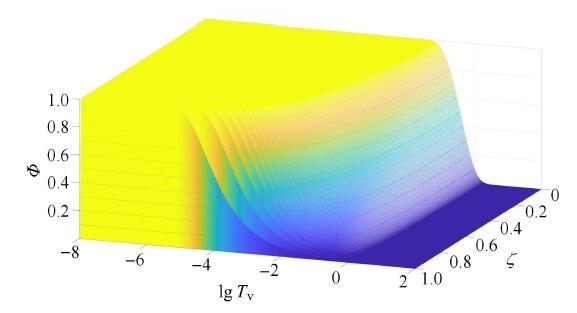 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT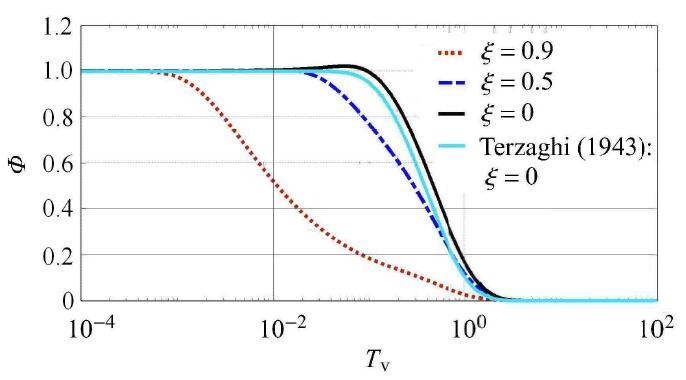 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT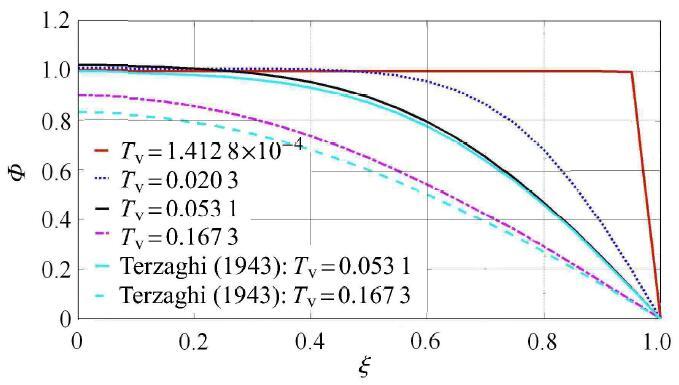 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT