兰州理工大学工程力学系,兰州 730050
A GENERALIZED THERMOELASTIC PROBLEM WITH NONLOCAL EFFECT AND MEMORY- DEPENDENT DERIVATIVE
ZhangPei, HeTianhu中图分类号:O343.6
文献标识码:A
通讯作者:
收稿日期:2018-03-19
接受日期:2018-03-21
网络出版日期:2018-06-10
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (1370KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
经典的热弹耦合理论[1]克服了非耦合理论中不考虑温度场与变形场的耦合影响的缺陷,但同时,它又继承了非耦合理论的另 一个不足：所预测的热传播速度是无限大的[2],这与实验结果[3]是相悖的. 为了克服这一缺陷,****们对热传导方程进行了修正,提出了非傅里叶 热传导理论模型,如：C-V热波模型[4,5]、抛物型两步模型[6]、双曲型两步模型[7]等. Lord和Shulman[8]引入C-V模型 建立了L-S型广义热弹性理论. 受C-V模型和L-S理论的启发,许多用于描述热以有限速度传播的广义热弹理论相继涌现,比如：引入两个热松弛时间的G-L广义 热弹性理论[9]、不考虑能量损耗的G-N广义热弹性理 论[10]、双温度广义热弹性理论[11]、双相滞后广义热弹性理论[12]、广义热弹动力学理论[13]、 惯性熵热弹性理论[14]和热质量热弹性理论[15]等.近年来,由于在极端环境下热传导、生物组织黏弹特性和随机动力学[16,17]等方面研究上的成功应用,分数阶微积分学受到越来越多的关注. 在广义热弹性领域,已经有不同形式的基于分数阶积分修正的分数阶广义热弹性理论[18,19,20]被提出并在不同模型中得到应用[21,22]. Diethelm[23]改进了Caputo型 分数阶微分,得到
式中
$K(t - p) = \dfrac{(t - p)^{n - \alpha - 1}}{\Gamma (n - \alpha )}$
n是整数且$\alpha $满足$n - 1 < \alpha \leqslant n$，$K(t - p)$是核函数，$\Gamma$是伽马函数，$f^{(n)}$是函数$f$的$n$阶微分. 上述定义具有直观的物理意义, 即$f(t)$的$\alpha $阶分数阶微分依赖整个积分域[$a$, $t$]上所有$f^{(n)}(t)$的影响. 这种影响称为``记忆依赖影响''，核函数$K(t - p)$可视为每一时刻$f^{(n)}(t)$影响的比重. 因为这一特性，Caputo分数阶微分便可用于描述一些系统或物理过程的瞬时变化率受过去情形的影响. Wang和Li[24]认为，对于任何给定的正数$a$和核函数， 式(1)不能反映出当时间$t$取值较大时候的记忆影响. 受此启发，他们提出了"记忆依赖微分"， 函数$f$的一阶记忆依赖微分算子可表示为如下形式
${\rm D}_\omega f (t) = \dfrac{1}{\omega }\int_{t - \omega }^t K (t - \xi ){f}'(\xi ) d\xi (2)$
式中,
Yu等[25]将记忆依赖微分算子用于改进C-V传热方程,从而得到新的热传导方程,并提出了基于上述热传导方程的新的记忆依赖广义热弹性理论,当
此时,若取
相对于分数阶热传导模型,引入记忆依赖算子有以下几个优势：首先,记忆依赖模型有其明确的物理意义,其精髓就是记忆依赖算子的定义, 它能用于描述“瞬时变化率受过去情形影响” 的一些系统和物理过程的响应;第二,记忆依赖模型的公式是基于整数阶的微积分运算,相比于分数阶模型在运算时更加便利;最后, 对于不同情形下选取的不同核函数(类似不同过程选取不同分数阶参数),时间延迟因子也可以根据需要自由选择,从而提供了更多可能 性来得到更加真实的材料力学行为,因此,它 更加 灵活,因为分数阶模型主要的影响参数只有一个分数阶系数. 基于记忆依赖广义热弹性理论,已有以下研究：Yu等[28]研究了一维半无限体受热冲击时的响应;Lotfy等[29]引入双温度 研究了光辐射半导体材料的广义热弹问题;Ezzat等[30,31]在其基础上发展了双相滞后记忆依赖模型和进行了 热弹--磁流体动力学方面的研究;Shaw[32]研究了记忆依赖模型下物理量求解的不连续性.
纵观上述的广义热弹性理论,可以发现,这些理论的“广义”主要体现在对热传导方程的改进,即对经典理论的傅里叶定律引进一些相关 的材料常数,例如：热松弛时间、温度变化率、相位滞后、分数阶算子和记忆依赖算子等等,而对应的弹性方程还是维持了经典的形式. 虽然可以很好地适用于尺寸相对较大的结构,但在一些微尺寸结构中,比如某一材料的外部与内部特征长度接近的情况下,其合理性却遭到 了挑战. 这种情况下,就需要引入可以描述材料内外部特征尺寸的相关材料参数来建立新的非经典弹性关系,应用较为广泛的相关理论有： Eringen[33]提出的非局部理论、Aifantis[34]的梯度理论和Yang等[35]改进的偶应力理论. 其中, Eringen的非局部理论得到了广泛的应用.
Eringen认为, 材料中一点
$\sigma _{ij} ({\pmb r}) = \int_V K_r \left( {{\pmb r}, {\pmb r}',\chi } \right)\pi _{ij} ({\pmb r}' ) d V \left({\pmb r}' \right) (4)$
$\pi _{ij} ({\pmb r}' ) = \lambda \varepsilon _{kk} ({\pmb r}' ) \delta _{ij} + 2\mu \varepsilon _{ij} \left({\pmb r}' \right) (5)$
$\varepsilon _{ij} ({\pmb r}' ) = \dfrac{1}{2}\left( {\dfrac{\partial u_j ({\pmb r}' ) }{\partial {r}'_i } + \dfrac{\partial u_i ({\pmb r}' ) }{\partial {r}'_j }} \right) (6)$
式中
核函数
$\left[ {1 - (e_0 a)^2\nabla ^2} \right]\sigma _{ij} ({\pmb r}) = \pi _{ij}({\pmb r}' ) $(7)
考虑非局部效应,Yu等[28] 建立了新的G-L非局部广义热弹性理论并研究了一维半无限大体的瞬态热冲击问题; Li等[36]研究了非局部广义热扩散问题. 总体来看,同时考虑记忆依赖微分和非局部理论的研究数量还是相对较少,对于移动热源作用的两端固定杆件模型的瞬态响应研究还未发现.
本文基于同时考虑记忆依赖和非局部效应的广义热弹性理论,研究了受移动热源作用的两端固定杆的动态响应,并考查了不同核函数下时间延迟因子和非局部因子对响应的影响, 以期对微尺度下考虑非局部效应的弹性体的瞬态热响应的预测提供新的参考依据.
1 基本方程
在经典耦合热弹性理论中,基本方程如下.运动方程
几何方程
$\varepsilon _{ij} = \dfrac{1}{2}(u_{i,j} + u_{j,i} ) $(9)
本构方程
$\sigma _{ij} = \lambda \varepsilon _{kk} \delta _{ij} + 2\mu \varepsilon _{ij} - \gamma \theta \delta _{ij} $(10)
$\rho \eta = \gamma {\kern 1pt} \varepsilon _{kk} + \dfrac{\rho C_E }{T_0 }\theta $(11)
傅里叶热传导方程
$q_i = - \kappa \theta _{,i} (12)$
热量运输方程
当考虑非局部效应时, 式(10)变为
$\left[ {1 - \left( {e_0 a} \right)^2\nabla ^2} \right] \sigma _{ij} = \lambda \varepsilon _{kk} \delta _{ij} + 2\mu \varepsilon _{ij} - \gamma \theta \delta _{ij} $(14)
应用记忆依赖微分的新热传导方程为
$q_i + \omega D_\omega q_i = - \kappa \theta _{,i} $(15)
这里核函数取Wang和Li[25]给出的形式
$K( t - \xi ) = \left\{ \begin{array}{l} 1 \\ 1 - \dfrac{t - \xi }{\omega } \\ \Big(1 - \dfrac{t - \xi }{\omega } \Big ) ^{2} \end{array} \right. (16)$
对比记忆依赖微分和非局部弹性本构关系的形式,发现记忆依赖微分可看作 “时间尺度上的非局部效应”,那么令它也满足归一性条件,可得到一改进的核函数形式
$K( t - \xi ) = \left\{ \begin{array}{l} 1 \\ 2\Big (1 - \dfrac{t - \xi }{\omega }\Big) \\ 3\Big (1 - \dfrac{t - \xi }{\omega }\Big ) ^{2} \end{array} \right. (17) $
式中,ui是位移矢量分量,
2 建立模型的控制方程
考虑一个长为
显示原图|下载原图ZIP|生成PPT图1有限长杆件示意图
-->Fig. 1The sketch of the finite rod
-->
根据所选模型的几何形状, 可以视其为一维问题,所以各物理量只是坐标
$\left[ {1 - (e_0 a)^2\dfrac{\partial ^2}{\partial x^2}} \right]\sigma = (\lambda + {2}\mu )\dfrac{\partial u}{\partial x} - \gamma \theta (18)$
$ (\lambda + {2}\mu )\dfrac{\partial ^2u}{\partial x^2} - \gamma \dfrac{\partial \theta }{\partial x} = \rho \left[ { {1} - (e_0 a)^2\dfrac{\partial ^2}{\partial x^2}} \right]\dfrac{\partial ^2u}{\partial t^2} $(19)
$ \kappa \dfrac{\partial ^2\theta }{\partial x^2} = \left( {1 + \omega D_\omega } \right)\left( {\rho C_E \dfrac{\partial \theta }{\partial t} + \gamma T_0 \dfrac{\partial ^2u}{\partial x\partial t} - Q} \right) $(20)
引入下列无量纲量对方程进行无量纲化
$\left.\begin{array}{ll} \{ x^\ast ,u^\ast \} = c_0 \eta _0 \{x, u\},, \ \ \eta _0 = \dfrac{\rho C_E }{\kappa } \\ \{t^\ast ,\omega ^\ast \} = c_0^2 \eta _0 \{t,\omega \} \\ \theta ^\ast = \dfrac{\theta }{T_0 },, \ \ \sigma ^\ast = \dfrac{\sigma }{\mu },, \ \ Q^\ast = \dfrac{Q}{\kappa T_0 \eta _0 } \\ \left( {e_0 a} \right)^\ast = c_0 \eta _0 \left( {e_0 a} \right) ,, \ \ c_0^2 = \dfrac{\lambda + 2\mu }{\rho } \end{array}\right\} $(21)
方程(18)~方程(20)变为(去掉星号)
$ \left[ {1 - (e_0 a)^2\dfrac{\partial ^2}{\partial x^2}} \right]\sigma = \beta ^2\dfrac{\partial u}{\partial x} - b\theta (22)$
$\dfrac{\partial ^2u}{\partial x^2} - \dfrac{b}{\beta ^2}\dfrac{\partial \theta }{\partial x} = \left[ {1 - (e_0 a)^2\dfrac{\partial ^2}{\partial x^2}} \right]\dfrac{\partial ^2u}{\partial t^2} (23)$
$ \left( { {1} + \omega D_\omega } \right)\left( {\dfrac{\partial \theta }{\partial t} + g\dfrac{\partial ^{2}u}{\partial x\partial t} - Q} \right) = \dfrac{\partial ^{2}\theta }{\partial x^{2}} (24)$
式中,$\beta ^2 = (\lambda + 2\mu ) / \mu $，$b = \gamma T_0 / \mu $，$g = \gamma / \rho C_E $.
初始条件
$\left.\begin{array}{ll} u(x,0) = \dot {u}(x,0) = 0 \\ \theta (x,0) = \dot {\theta }(x,0) = 0 \end{array}\right\} (25)$
边界条件
$\left.\begin{array}{ll} u(0,t) = u(l_0 ,t) = 0 \\ \dfrac{\partial \theta (0,t)}{\partial x} = \dfrac{\partial \theta (l_0 ,t)}{\partial x} = 0 \end{array}\right\} $(26)
移动热源取以下无量纲形式
这里
3 拉普拉斯变换求解
应用下列拉普拉斯变换公式$\left.\begin{array}{ll} {\rm L} \left[ {f(t)} \right] = \bar {f}(s) = \int_0^\infty {{\rm e}^{ - st}f(t)d t} \\ Re(s) > 0 \end{array}\right\} (28)$
方程(22)~方程(24)化为
$\left[ {1 - (e_0 a)^2\dfrac{d^2}{dx^2}} \right]\bar {\sigma } =\beta ^2\dfrac{d \bar {u}}{dx} - b\bar {\theta } (29)$
$\beta ^2\left[ {(1 + (e_0 a)^2s^2)\dfrac{d ^2}{d x^2} - s^2} \right]\bar {u} = b\dfrac{d \bar {\theta }}{d x} (30)$
$\left( {1 + G_0 } \right)\left( {s\bar {\theta } + g s\dfrac{d \bar {u}}{d x} - \alpha {\rm e}^{ - (s / \upsilon )x}} \right) = \dfrac{d ^2\bar {\theta }}{d x^2} (31)$
式中
${\rm L}\left\{ {\omega D_\omega f(t)} \right\} = F(s)G_0 (s) (32)$
$ G_0 (s) = \left\{ \!\!\begin{array}{ll} 1 - {\rm e}^{ - s\omega }, & {K = 1} \\ 1 - \dfrac{1 - {\rm e}^{ - s\omega }}{\omega s} , & {K = 1 - \dfrac{t - \xi }{\omega }} \\ \Big(1 - \dfrac{2}{\omega s}\Big) + \dfrac{2(1 - {\rm e}^{ - s\omega })}{\omega ^2s^2 }, & K = \Big(1 - \dfrac{t - \xi }{\omega } \Big )^2 \end{array}\!\! \right. $(33)
$ F(s) = L\left( {\dfrac{\partial \bar {\theta }}{\partial t} + g\dfrac{\partial ^2\bar {u}}{\partial t\partial x} - Q} \right)= \\ s\bar {\theta } + gs\dfrac{d \bar {u}}{d x} - \alpha {\rm e}^{ - (s / \upsilon )x} ,, \ \ \ \alpha _0 = Q_0 / \upsilon (34)$
边界条件化为
$\left.\begin{array}{l} \bar {u}(0,s) = \bar {u}(l,s) = 0 \\ \dfrac{d \bar {\theta }(0,s)}{d x} = \dfrac{d \bar {\theta }(l,s)}{d x} = 0 \end{array}\!\!\right\} (35)$
从方程(30)和(31)中消去
$\dfrac{d ^4\bar {u}}{d x^4} - m_1 \dfrac{d ^2\bar {u}}{d x^2} + m_2 \bar {u} = m_3 {\rm e}^{ - (s / \upsilon )x} (36) $
式中
$\begin{array}{l} m_1 = (1 + G_0 )s + \dfrac{\beta ^2s^2 + (1 + G_0 )bgs}{\beta ^2\left[ {1 + (e_0 a)^2s^2} \right]} \\ m_2 = \dfrac{(1 + G_0 )s^3}{1 + (e_0 a)^2s^2}, \ \ m_3 = \dfrac{(1 + G_0 )bs\alpha _0 }{\beta ^2\upsilon \left[ {1 + (e_0 a)^2s^2} \right]} \end{array} $
方程(36)的通解为
$ \bar {u} = C_1 {\rm e}^{ - k_1 x} + C_2 {\rm e}^{k_1 x} + C_3 {\rm e}^{ - k_2 x} + \\ C_4 {\rm e}^{k_2 x} + C_5 {\rm e}^{ - (s / \upsilon )x} (37) $
这里
$k^4 - m_1 k^2 + m_2 = 0 $(38)
所以
$\left.\begin{array}{ll} k_1 = \sqrt {\dfrac{m_1 + \sqrt {m_1^2 - 4m_2 } }{2}} \\ k_2 = \sqrt {\dfrac{m_1 - \sqrt {m_1^2 - 4m_2 } }{2}} \end{array}\!\! \right \}(39) $
同样地,从方程(30)和(31)中消去
$\dfrac{d ^4\bar {\theta }}{d x^4} - m_1 \dfrac{d ^2\bar {\theta }}{d x^2} + m_2 \bar {\theta } = m_4 {\rm e}^{ - (s / \upsilon )x} (40) $
式中
方程(40)的解为
式中
将式(37)和式(41)代入式(30),可得
$\left.\begin{array}{l} C_{11} = - A_1 C_1 ,C_{22} = A_1 C_2 \\ C_{33} = - A_2 C_3 ,C_{44} = A_2 C_4 \\ C_{55} = \beta ^2s\left\{ {\upsilon ^2 - [1 + (e_0 a)^2s^2] } \right\}C_5 /b\upsilon \end{array}\!\!\right\} $(42)
式中
将式(37)和式(41)代入边界条件(35),可得
$\left.\begin{array}{l} C_1 = B_2 D_1 C_5 ,, \ \ C_2 = - B_2 D_2 C_5 \\ C_3 = - B_1 D_3 C_5 ,, \ \ C_4 = B_1 D_4 C_5 \end{array}\right\} $(43)
式中
$ D_1 = \dfrac{{\rm e}^{k_1 l} - {\rm e}^{ - (s / \upsilon)l}}{{\rm e}^{k_1 l} - {\rm e}^{ - k_1 l}} $
$D_2 = \dfrac{{\rm e}^{ - k_1 l}- {\rm e}^{ - (s / \upsilon )l}}{{\rm e}^{k_1 l} - {\rm e}^{ - k_1 l}}$
$D_3 = \dfrac{{\rm e}^{k_2 l} - {\rm e}^{ - (s / \upsilon)l}}{{\rm e}^{k_2 l} - {\rm e}^{ - k_2 l}} $
$D_4 = \dfrac{{\rm e}^{ - k_2 l}- {\rm e}^{ - (s / \upsilon )l}}{{\rm e}^{k_2 l} - {\rm e}^{ - k_2 l}}$
$B_i = \dfrac{k_i^2 - s^2 / \upsilon ^2}{k_1^2 - k_2^2 } \ \ \ \ (i = 1,2) $
至此,完成问题在拉氏域的求解,将
$ \bar {u} = B_2 D_1 C_5 {\rm e}^{ - k_1 x} - B_2 D_2 C_5 {\rm e}^{k_1 x} - \\ B_1 D_3 C_5 {\rm e}^{ - k_2 x} + B_1 D_4 C_5 {\rm e}^{k_2 x} + C_5{\rm e}^{ - (s / \upsilon )x} (44)$
无量纲温度表达式
$ \bar {\theta } = - A_1 B_2 D_1 C_5 {\rm e}^{ - k_1 x} - A_1 B_2 D_2 C_5 {\rm e}^{k_1 x} + \\ A_2 B_1 D_3 C_5 {\rm e}^{ - k_2 x} + A_2 B_1 D_4 C_5 {\rm e}^{k_2 x} + \\ \dfrac{\beta ^2s[\upsilon ^2 - (1 + (e_0 a)^2s^2)]}{b\upsilon }C_5 {\rm e}^{ - (s / \upsilon )x} (45)$
再将式(44)和式(45)代入式(29),得
$ \bar {\sigma } = E_1 {\rm e}^{ - k_1 x} + E_2 {\rm e}^{k_1 x} + E_3{\rm e}^{ - k_2 x} + \\ E_4 {\rm e}^{k_2 x} + E_5 {\rm e}^{ - (s / \upsilon )x}(46)$
式中
$ E_1 = \dfrac{ - \beta ^2p^2B_2 D_1 C_5 }{k_1 }$
$E_2 = \dfrac{ - \beta ^2p^2B_2 D_2 C_5 }{k_1 }$
$E_3 = \dfrac{\beta ^2p^2B_1 D_3 C_5 }{k_2 }$
$E_4 = \dfrac{\beta ^2p^2B_1 D_4 C_5 }{k_2 }$
$E_5 = - \beta ^2s\upsilon C_5 $
因为在拉氏域得到的表达式的形式冗长且复杂,很难得到解析的反变换解. 因此,这里采用Brancik[37]提出的一种基于快速反变换技术的拉普拉斯反变换程序进行数值求解.
4 算例及讨论
前言中提到,记忆依赖微分可视为分数阶微分的衍生,不同分数阶参数$\begin{array}{l} \lambda = 7.76\times 10^{10},{\rm N}/{\rm m}^2,, \ \ T_0 =293,{\rm K}, \ \ \upsilon = 2,, \ \ l_0 = 10 \\ \mu = 3.86\times 10^{10},{\rm N}/{\rm m}^2,, \ \ Q_0 = 10,, \ \ \rho =8,954,{\rm kg}/{\rm m}^3 \\ \alpha _t = 1.78\times 10^{ - 5},{ k}^{-1} \end{array} $
4.1 核函数影响
4.1.1 线性核函数本小节 研究线性核函数形式
在图2 (a)中,无量纲温度首先上升,经典耦合理论所反映的热干扰区域明显较大且不为零(即使值很小). 相较经典耦合理论的结果,时间延迟因子不为零时的两条分布曲线分别在
显示原图|下载原图ZIP|生成PPT图2线性核函数下结果图示
-->Fig. 2The distribution of non-dimensional physical quantities under linear kernel function
-->
在图2 (b)中,因为细杆两端固定,所以两个端点处的位移始终为0. 随着时间延迟因子增大,最大位移值增大.
在图2(c)中,可以看到细杆中的应力始终呈压应力状态,这主要是因为细杆两端固定,热膨胀变形受阻,从而产生压应力,应力峰值在
4.1.2 非线性核函数
本节 研究经典和改进的非线性核函数形式$K(t - \xi ) =\Big (1 - \dfrac{t - \xi}{\omega }\Big)^2$和$K(t - \xi ) = 3\Big (1 - \dfrac{t - \xi }{\omega}\Big)^2$下, 时间延迟因子$\omega = 0.03$和$\omega = 0.05$对物理量分布的影响情况, 非局部因子取$e_0 a = 0$, 时间取$t =2$时刻, 所得结果见图3.
从图3(a)中无量纲温度的分布 发现,对于非线性核函数的两种经典和改进的形式下,不同时间延迟因子对温度分布的影响的区别主要体现在不同的峰值上,另外热波 传播的距离也受轻微影响,经典核函数下受影响较小,改进后的核函数形式下受影响较大. 同样地情况也体现在图3(b)和图3(c)中.
显示原图|下载原图ZIP|生成PPT图3非线性核函数下结果图示
-->Fig. 3The distribution of non-dimensional physical quantities under non-linear kernel function
-->
因此,时间延迟因子可作为新的控制参数来模拟不同的响应. 且它在和修正的核函数的组合中影响更加明显.
4.2 非局部影响
本节 研究非局部因子对各无量纲量分布的影响. 计算中, 选取3个不同的非局部因子值$e_0a = 0$(不考虑非局部影响情形), $e_0 a = 0.05$和$e_0 a =0.1$, 同时, 时间延迟因子和核函数分别取$\omega = \;0.03$和改进的线性形式$K(t- \xi ) = 2\Big(1 - \dfrac{t - \xi }{\omega }\Big)$, 时间取$t = 2$, 所得结果见图4.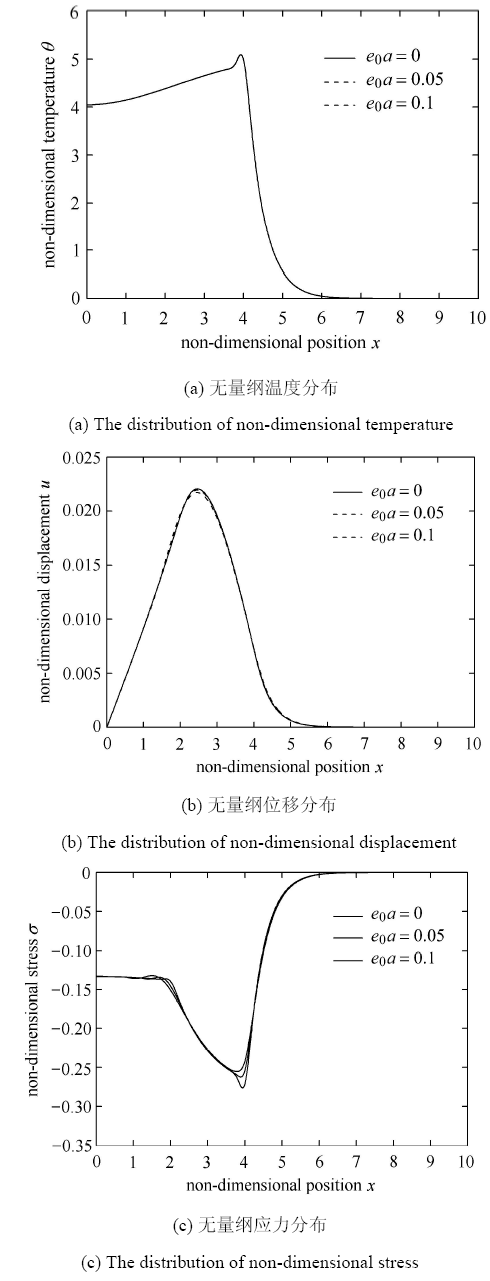
显示原图|下载原图ZIP|生成PPT图4非局部影响结果图示
-->Fig. 4The distribution of non-dimensional physical quantities under nonlocal effect
-->
考虑改进的核函数形式后,在图4(a)中,对于不同的非局部因子,所得无量纲温度的分布曲线是重叠的,即非局部因子对无量纲温度无 明显影响. 从图4(b)中可见,随着
5 结 论
本文基于同时考虑记忆依赖算子和非局部效应的广义热弹性理论,研究了受移动热源作用的两端固定杆模型,并类比非局部弹 性关系中核函数归一化条件改进了记忆依赖微分中的核函数项,分别得到了在不同类型核函数下时间延迟因子 和非局部因子对无量 纲温度、位移和应力的分布规律的影响. 通过以上分析和计算,得到以下结论：(1) 对比经典热弹耦合理论,记忆依赖广义热弹性理论所以测得热传播速度是有限的.
(2) 不同的响应分析可选取不同的核函数和时间延迟因子的组合来计算. 时间延迟因子可作为一个新的参数来预测不同的结果,且它在改进的核函数下影响更明显.
(3) 非局部因子对无量纲温度的分布几乎无影响,相反的,对位移和应力的影响显著,位移、应力的峰值随非局部因子增大而减小.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . . |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . . [PhD Thesis]. |
| [22] | . . |
| [23] | |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . |
| [33] | . |
| [34] | . |
| [35] | . |
| [36] | . |
| [37] | // |
