横断山区水土资源利用与经济增长的匹配关系

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2021-12-29

彭立^,¹^,², 邓伟^,¹^,², 谭静³, 林磊³

1. 四川师范大学地理与资源科学学院,成都 610068

2. 中国科学院、水利部成都山地灾害与环境研究所,成都 610041

3. 西南财经大学中国西部经济研究中心,成都 610074

Restriction of economic development in the Hengduan Mountains Area by land and water resources

PENG Li^,¹^,², DENG Wei^,¹^,², TAN Jing³, LIN Lei³

1. College of Geography and Resources, Sichuan Normal University, Chengdu 610101, China

2. Institute of Mountain Hazards and Environment, CAS, Chengdu 610041, China

3. China Western Economic Research Center, Southwestern University of Finance and Economics, Chengdu 610074, China

通讯作者: 邓伟(1957-), 男, 辽宁沈阳人, 博士, 研究员, 研究方向为山区发展战略、山区资源环境与国土空间发展。E-mail: dengwei@imde.ac.cn

收稿日期:2019-05-14修回日期:2020-07-3网络出版日期:2020-09-25

基金资助:

国家重点基础研究发展计划.2015CB452706
中国科学院科技服务网络计划.KFJ-STS-QYZD-060

Received:2019-05-14Revised:2020-07-3Online:2020-09-25

Fund supported:

National Basic Research Program of China.2015CB452706
Science and Technology Service Network Initiative of CAS.KFJ-STS-QYZD-060

作者简介 About authors
彭立(1983-), 男, 山东滕州人, 博士, 研究员, 主要从事山区水土资源利用与乡村发展研究。E-mail: pengli@imde.ac.cn

摘要
水土资源不仅是山区生态系统服务供给的一部分,同时也是山区经济发展的重要投入要素。本文以横断山区为研究对象,利用基尼系数法评估水土资源和经济发展之间的匹配状况,同时基于个体随机效应模型建立拓展的Cobb-Douglas生产函数模型实现了经济增长对水土要素的敏感性分析,引入经济增长阻尼模型定量测算了水土资源对横断山区经济发展的制约程度。结果表明：① 2006—2015年横断山区水资源、土地资源与GDP的区域基尼系数波动范围分别为0.260~0.298和0.389~0.424,水资源对不同产业的满足程度相对合理,而对土地资源的利用与经济发展较不匹配,尤其是第二、三产业;② 敏感性分析结果表明,横断山区土地资源的产出弹性是水资源2倍左右,土地资源的累计贡献率明显高于水资源,土地资源要素对经济增长贡献大于水资源要素。③ 水土资源增长阻尼平均水平分别为0.012和0.022,说明水资源和土地资源对横断山区经济发展均产生明显的约束作用,且受土地资源的限制较大。研究表明中国山区发展需要更加重视水土资源开发利用与经济增长需求的匹配,充分挖掘水土资源的利用潜力提高供给可以降低其对经济增长的制约程度。
关键词： 水土资源;基尼系数;增长阻尼;面板模型;横断山区

Abstract

As a part of the supply of ecosystem services, land and water resources are an important factor restricting economic development in mountainous areas. Taking the Hengduan Mountains Area as a case study, we evaluated the degree of matching between land and water resources and economic development using the Gini coefficient method. Furthermore, the sensitivity of economic growth to land-water factors was analyzed by establishing an extended Cobb-Douglas function based on the individual stochastic effect model. In addition, the growth drag model was introduced to measure the restriction of land-water resources on economic development in the study area quantitatively. The research produced several important results: (1) From 2006 to 2015, the fluctuation ranges of the Gini coefficient between land and water resources and gross domestic product (GDP) in the study area were 0.265-0.298 and 0.389-0.424, respectively. The satisfaction by water resources in different industries was relatively reasonable, but the utilization of land resources for economic development was not satisfactory, especially in the secondary and tertiary industries. (2) The sensitivity analysis results showed that the elasticity of land resources in the region was about twice that of water resources. The cumulative contribution rate of land resources was significantly higher than that of water resources, and the contribution of land resources to economic growth was greater than that of water resources. (3) The average growth drag values of land and water resources were 0.012 and 0.022, respectively, indicating that both land and water resources had obvious restraining effects on the economic development, which was greatly restricted by land resources. The research showed that effective development of mountainous areas in China should focus on the sufficient land-water resources demanded by economic growth. Utilizing the potential of land-water resources and increasing their supply can reduce restriction on economic growth and promote sustainable development.

Keywords：land and water resources;Gini coefficient;growth drag;panel data model;Hengduan Mountains Area

PDF (2602KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
彭立, 邓伟, 谭静, 林磊. 横断山区水土资源利用与经济增长的匹配关系. 地理学报[J], 2020, 75(9): 1996-2008 doi:10.11821/dlxb202009013
PENG Li, DENG Wei, TAN Jing, LIN Lei. Restriction of economic development in the Hengduan Mountains Area by land and water resources. Acta Geographica Sinice[J], 2020, 75(9): 1996-2008 doi:10.11821/dlxb202009013

1 引言

水资源和土地资源是国土空间开发的基础性资源。水资源禀赋和开发利用的合理性在很大程度上影响着其他资源的利用方式,土地资源的面积、质量和开发程度则决定了生产的效率,水土资源的管理利用状况对经济社会稳步发展具有重要影响。山区是中国经济发展的重要载体,也是自然资源和生态系统服务的主要来源。中国山区占地面积达到了中国国土的69%,耕地面积占40%,拥有70%的淡水资源^[1]。随着城镇化、工业化和农业现代化的快速推进,水土资源的限制与压力与日俱增,水土资源的合理配置已成为山区经济可持续发展面临的重要问题。

水土资源与社会经济要素的匹配是合理配置水土资源的目标,很多****为水土资源与社会经济要素的匹配程度进行了一系列研究,主要的研究思路可分为以下几种：① 水土资源和聚落的空间匹配性分析,通常基于遥感、GIS空间分析手段来实现^[2,3,4]。② 基于耦合协调度模型或者水土匹配指数的研究,通过构建耦合度评价、水土资源匹配测算等模型分析经济社会发展与水土资源开发之间的耦合效应及其时空分异^[5,6]。③ 基于基尼系数法等间接手段测算区域水土资源和经济的匹配性。例如张吉辉等利用中国31个省（直辖市、自治州）2004—2009年的水资源数据,引入人口、土地面积、水资源禀赋等指标测算出国内省市间的水资源—经济发展水平基尼系数^[7]。张晓涛等^[8]、武萍等^[9]采用区域基尼系数法,以省市级行政区为研究对象,分析了经济发展和水资源、土地资源和劳动力的匹配情况^[8,9]。在经济学中,基尼系数能够反映出总体的不公平性,可以将总的差异分解成不同因子的差异,从而分析不同因子对总的差异的影响^[10]。为此,本文试图引入基尼系数作为指标以评估横断山区水土资源和经济发展之间的匹配状况。

为解决水土资源和经济发展的不匹配问题,国内外****们开始关注国土空间发展受水土资源的约束程度。Nordhaus等首先将包括土地在内的自然资源纳入Solow模型之中,分别建立存在资源约束和不存在资源约束的两个新古典经济增长模型,基于这两个模型稳态条件下的人均产出增长率之差,构建出自然资源的“增长阻尼”模型,并运用这一模型考察了资源和土地对美国经济的影响^[11]。Bruvoll等提出自然环境约束会引发环境治理的社会成本,并且利用动态资源环境应用模型计算和预测了挪威由环境尾效带来的福利损失程度^[12]。Romer等将在不受资源限制情况下经济增长速度与受约束的增长速度的差值定义为“增长阻尼”,并提出了利用Cobb-Douglas生产函数测算“增长阻尼”的具体方法^[13]。Thorvaldur等借鉴Nordhaus的增长阻尼模型,认为对自然资源的依赖影响了当前的制度和宏观经济结果^[14]。国内****对自然资源的增长阻尼也进行了一系列实证研究,对增长阻尼模型进行了改进和完善。曹雪等^[15]、Yang等^[16]、Liu等^[17,18]在Romer的模型上逐渐形成了针对中国问题的分析框架,基于中国省域或市域数据计算的增长阻尼都证明了中国经济发展受到水土资源的影响^{[15,16,17,18]}。理论上看,山区的水土资源对经济增长的影响可能会更大,亟待定量揭示。

在中国供给侧结构性改革的大背景下,通过优化生产要素配置促进经济增长成为主要思路。横断山区自然资源较为丰富但经济发展滞后,贫困现象明显,《中国农村扶贫开发纲要（2011—2020年）》划定的集中连片特困地区涉及横断山区域的有乌蒙山区、滇西边境山区以及四川省西北地区等。以凉山州为例,17个县市中的11个是国家扶贫开发工作重点县。相当一部分地区,因“水”贫困、因“土”贫困的现象明显。另一方面,作为长江上游生态屏障一部分,在国家主体功能区规划中,横断山区众多区县被划定为国家重点生态功能区,承担着为国家提供战略性生态系统服务的角色。因此,探索有限的资源配置在经济系统中的作用,对于缓解发展和保护之间的矛盾具有现实意义。本文以横断山区为研究对象,从山区水资源、土地资源两个角度出发,借鉴经济学中的基尼系数评估横断山区10个市（州）的水资源—土地资源—GDP匹配程度,并在此基础上借助并改进经典的Cobb-Douglas生产函数计算出横断山区发展的增长阻尼,定量水土资源限制的差异性。本文对水土资源限制经济发展的程度进行量化分析,对进一步优化水土资源与社会经济要素的配置,促进山区经济发展具有指导意义。

2 研究方法与数据来源

2.1 研究区域概况

横断山区位于青藏高原东部、四川盆地西部和云贵高原西北部,是中国地形第一、第二阶梯的过渡地带。在地貌上由一系列纵贯南北的山脉与河谷组成,境内有怒江、澜沧江、金沙江、雅砻江等水系,海拔高差大且由西北向东南递减。横断山区南北跨约10个纬度,受东南季风、西南季风和微地貌所控制,降水量有明显的季节差异和内部空间差异。横断山区土地利用以林草地为主,占到86.05%（2015年）,适宜农业的耕地资源较少,主要分布在坡地和河谷地带。受地形海拔控制,横断山区的可利用建设资源极其匮乏,山地聚落的分布呈现分散、小片、破碎的特点。

横断山区的范围确定有多种方法^[19,20,21],本文重在关注经济地理层面,首先考虑社会经济数据的完整性,其次是地貌单元的准确性。因此,在尽量考虑行政单元和地貌单元的大体一致性的原则下,为便于进行计量研究,本文借鉴相关研究^[22,23],将研究区范围调整确定为甘孜州、阿坝州、凉山州、攀枝花、丽江市、大理州、怒江州、迪庆州、楚雄州、昆明市,共10个市（州）（图1）。

图1

新窗口打开|下载原图ZIP|生成PPT
图1研究区域范围

Fig. 1Location of the Hengduan Mountains Area

2.2 数据来源及指标选择

针对Cobb-Douglas生产函数,本文将劳动力、资本、水资源、土地资源作为基本投入指标,经济产值作为产出指标。借鉴其他****指标选取和处理方式,选取国民生产总值（GDP）作为经济增长的表征;劳动（L）采用社会从业人员数据;资本（K）采用永续盘存法估算。为了消除通货膨胀的影响且保持数据的一致性,对GDP及资本数据以起始年2006年为基期,采用价格指数进行可比价格调整。

在水资源指标的选取上,基于研究目的和数据可获得性,本文选取工业用水、农业用水、生活用水三者总和衡量水资源投入量。水资源数据来自于历年云南省和四川省水资源公报。在土地资源指标的选取上,学术界所采用的指标差异较大,部分****将耕地面积、林业用地面积、可利用草地面积这3类土地面积加总作为土地资源投入量^[24]。考虑到山区土地资源对产业部门的增长贡献,本文结合横断山区土地利用结构的特点,使用建设用地与耕地面积二者之和来表示土地资源总量。土地数据来自于相关市州历年的土地利用变更调查数据。本文的经济及其他数据来源于《中国城市统计年鉴》《四川省统计年鉴》《云南省统计年鉴》等。主要涉及2006—2015年的按三次产业分的地区生产总值、固定资产投入额、劳动力等。

2.3 研究方法

2.3.1 部分模型指标处理 本文的指标处理主要包括2个方面：① 对经济相关指标进行价格指数的调整;② 对于固定资本存量用永续盘存法进行估算。

由于经济相关指标数据来源于各省统计年鉴,而统计年鉴数据均是按照当年价格计算,为了排除由于物价水平变化带来的误差,更准确的反应GDP实际的变化,本文按统计年鉴中提供的2006—2015年价格指数进行调整（下述固定资本存量价格按相同方法处理）,以各地2006年实际价格进行衡量。对于固定资本存量K,由于统计年鉴并没有该数据,本文采用永续盘存法^[25]进行估算,基本公式为：

（1）

K_{t} = K_{t - 1} (1 - δ) + (I_{t} + I_{t - 1} + I_{t - 2}) / 3

式中：K_t为t时期固定资本存量;K_t_-1为t-1时期固定资本存量;δ为折旧率;I_t为t时期新增固定资本投资;L_t_-1为t-1时期新增固定资本投资;L_t_-2为t-2时期新增固定资本投资。

柯善咨等^[26]结合中国实际情况确定永续盘存法所依赖的4个关键因素：固定资产投资建设周期、固定资产价格加权指数、加权折旧年限和初始资本存量。根据不同折旧年限计算得到的2组资本存量序列数据可以作为资本存量数据的上下限。本文采取同样的假定,以2006年的不变价格计算I_t,假定固定资本折旧率

δ

为0.05。同时采取Marshall^[27]提出的估算初始资本存量

K_{0}

的方法进行初始资本存量估算：

（2）

K_{0} = I_{0}^{'} (\frac{1 + g}{g + δ})

式中：

I_{0}^{'}

为初始年固定资本投资额;g为不变价投资

I_{0}^{'}

的平均增长率。

2.3.2 横断山区水土资源基尼系数计算方法 为探讨研究区水土资源与GDP的匹配程度,本文参考基尼系数的算法和应用案例^[28,29],结合水土资源在横断山区的分布特征,构建了区域基尼曲线。

选取水土资源总量作为基本匹配对象,以GDP作为匹配分级对象,分别计算出横断山区10个市（州）的单位体积水土资源所对应GDP,该相对值即为水土资源与GDP匹配水平分级排序的指标;并按照该指标从低到高对区划单元进行排序;同时,分别计算10个市（州）水土资源和GDP占横断山区总量的累积百分比,定义横轴为GDP的累积比例,纵轴为行政单位的水土资源累积比例,拟合出洛伦兹曲线。然后利用定积分求得0~1基尼曲线与45°线所夹图形的面积A,基尼系数G = 2A。

参照经济学上的基尼系数评价居民收入公平程度的划分方法,本文将横断山区水土资源与GDP的匹配程度划分为5个等级^[30],具体划分如表1所示。

Tab. 1
表1
表1水土资源与GDP匹配程度划分
Tab. 1Classification of the matching degree between land and water resources and GDP

基尼系数区间	(0, 0.2)	[0.2, 0.3)	[0.3, 0.4)	[0.4, 0.5)	[0.5, 1)
匹配程度	高度匹配	相对匹配	一般	较不匹配	极不匹配

新窗口打开|下载CSV

2.3.3 横断山区水土资源增长阻尼模型推导 Cobb-Douglas生产函数主要通过各要素在总产出中的占比来反映要素替代弹性,Romer基于Cobb-Douglas生产函数考察了自然资源对经济增长的约束,建立了增长阻尼（Growth Drag）方程^[13]：

（3）

Y (t) = K {(t)}^{α} T {(t)}^{β} S {(t)}^{γ} [A (t) L {(t)]}^{1 - α - β - γ} (α, β, γ > 0,1 - α - β - γ > 0)

式中：Y(t)表示总产出;K(t)表示资本投入;T(t)表示土地资源;S(t)表示水资源;A(t)表示技术进步;L(t)表示劳动投入;t表示时间;α、β、γ分别表示资本生产弹性、土地生产弹性、水资源生产弹性。

Romer认为自然资源的约束会引致劳动力平均资源利用量的下降,从而在不受资源限制情况下经济增长速度与受约束的增长速度的差值可以定义为“增长阻尼”。对本文而言,其值等于不存在水土资源限制的增长速度与存在水土资源限制的增长速度之间的差额。

对（3）式进行变形,两边取对数得到：

（4）

\ln Y (t) = α \ln K (t) + β \ln T (t) + γ \ln S (t) + (1 - α - β - γ) \ln A (t) L (t)

在经济学中变量对时间求导得到变量的增长率,（4）式两边变量同时对时间求导数,可以得到Y、K、T、S、A、L的增长率函数,分别用g_Y(t)、g_K(t)、g_T(t)、g_S(t)、g_A(t)、g_L(t)表示,推得经济增长率方程：

（5）

g_{Y} (t) = α g_{K} (t) + β g_{T} (t) + γ g_{S} (t) + (1 - α - β - γ) [g_{A} (t) + g_{L} (t)]

资本累积方程为

? K_{t} = s Y_{t - 1} - (1 - δ) K_{t - 1}

,要使K的增长率

? K_{t}

K_{t - 1}

不变,则

? K_{t}

K_{t - 1}

等于

Y_{t - 1}

K_{t - 1}

,假定经济保持均衡增长,在平衡的增长路径上有g_Y(t)等于g_K(t),移项得出总产出增长率：

（6）

g_{Y} (t) = \frac{(1 - α - β - γ) (g_{L} (t) + g_{A} (t)) + β g_{T} (t) + γ g_{S} (t)}{1 - α}

在不受自然资源约束的情况下,经济的稳态增长率等于劳动增长率n,同样土地、水资源的增长率等于n,（6）式可以化简：

（7）

g_{Y} (t) = \frac{(1 - α - β - γ) (n + g_{A} (t)) + (β + γ) n}{1 - α}

根据增长阻尼系数的推导过程,可以得出本文所需的土地资源的阻尼系数和水资源阻尼系数。假定其它资源均不受约束,土地资源对经济的阻尼系数：

（8）

Dra g_{T} = \frac{β (n - g_{T} (t))}{1 - α}

同理可得水资源对经济的阻尼系数：

（9）

Dra g_{S} = \frac{γ (n - g_{S} (t))}{1 - α}

2.3.4 面板模型回归检验 为了测度水土资源约束引致的增长阻尼,本文选择2006—2015年横断山区10个市或州的平衡短面板数据,利用拓展的Cobb-Douglas生产函数建立模型并进行回归。

首先需进行个体效应的检验,由于同一个市（州）不同年份数据之间一般存在自相关的扰动项,而普通标准误大约是聚类稳健标准误的一半,故选取“最小二乘虚拟变量模型（LSDV）”检验法进行判别。同时需要将混合回归作为参照系,提出假设H0： all ui = 0,i = 1, 2, 3l,即原假设认为选择混合回归更优。结果显示绝大部分地区的个体虚拟变量p值小于0.01,即1%水平上显著,“所有个体虚拟变量都为0的原假设H0被拒绝,即结果认为模型存在个体效应,不应使用混合回归。

3 结果分析

3.1 横断山区水土资源—经济的匹配性分析

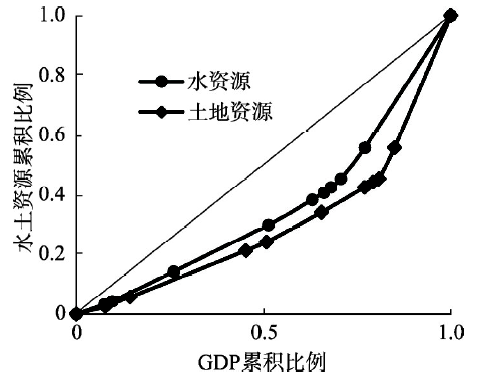
3.1.1 横断山区水土资源—GDP基尼系数 本文将收集到的研究区域内10个市（州）2006—2015年的水资源使用量、土地资源使用量、GDP等数据进行整理和加工,计算这10个市（州）各自单位水资源和土地资源所对应的GDP。根据基尼系数构建方法绘制洛伦兹曲线,从而得出横断山区水土资源与GDP的匹配现状。

图2中,水资源—GDP洛伦兹曲线与45°线所构成的面积为0.145,根据基尼系数的含义,得到2015年横断山区水资源与GDP的区域基尼系数为0.29,这一数值表示该区域国民经济中的水资源利用相对匹配和均衡。同样计算得到横断山区土地资源与GDP的区域基尼系数为0.4,表示该区域国民经济中的土地资源利用较不均衡,这一数值位于警戒线附近。在两条洛伦兹曲线中,横断山区土地资源—GDP的洛伦兹曲线更远离绝对平均线,意味着水资源的均衡性要优于土地资源,土地资源对经济增长的匹配程度较低。

图2

新窗口打开|下载原图ZIP|生成PPT
图22015年横断山区水土资源—GDP洛伦兹曲线

Fig. 2Water resources, land resources and GDP Lorenz curve in the Hengduan Mountains Area in 2015

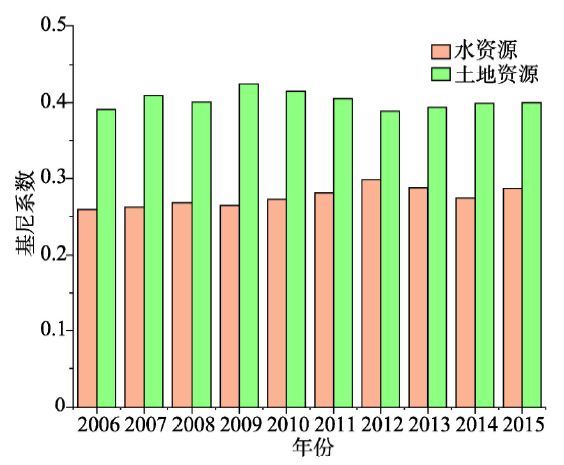
图3中显示的是2006—2015年水资源的产业基尼系数和土地资源的产业基尼系数逐年变化。从测算结果可以发现,总体上横断山区水资源与GDP匹配的基尼系数变化比较平稳,2006—2015年均在0.260~0.298间波动,2012年达到最高点后稍有回落,总体处于相对匹配的区间,总的来说该区域的水资源与产业发展的匹配程度是较为合理,水资源能够满足经济发展的需要。从测算结果可以看出,横断山区土地资源与GDP匹配的基尼系数近年来一直在0.4左右变化,与GDP的匹配程度较差,明显低于水资源与GDP的匹配程度。这与横断山区海拔高、地势起伏度大、开发困难的特点相一致。

图3

新窗口打开|下载原图ZIP|生成PPT
图32006—2015年横断山区水土资源基尼系数

Fig. 3Gini coefficients of water resources, land resources and GDP in the Hengduan Mountains Area from 2006 to 2015

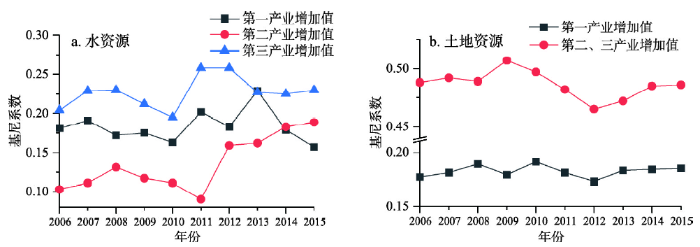
3.1.2 横断山区水土资源分产业部门的基尼系数 在整体揭示水土资源与GDP的基尼系数的基础上,进一步考虑不同国民经济产业部门划分对水资源的利用的差别,可对水资源量在不同产业中的使用进一步区分,以揭示不同产业水资源利用水平的均衡性。参照上述方法选取农业用水、工业用水、生活用水作为基本匹配对象,以第一产业、第二产业、第三产业生产总值作为匹配分级对象,可以计算出横断山区不同产业的水资源基尼系数,结果如图4所示。具体到三大不同的产业,横断山区第一产业中水资源—产业匹配十分均衡,基尼系数数值仅在2011年和2013年超过0.2,其余年份都小于0.2。第二产业区域基尼系数在三个产业部门中是最小的,历年数据均低于0.2。第三产业的基尼系数较第一、二产业明显偏高,除2010年之外,基尼系数值都在[0.2, 0.3]区间内,即各地第三产业对水资源的利用水平更不均衡。

图4

新窗口打开|下载原图ZIP|生成PPT
图42006—2015年横断山区水土资源分产业部门的基尼系数

Fig. 4Gini coefficients of different industries in the Hengduan Mountains Area from 2006 to 2015

通过类似方法,本文进一步计算出2006—2015年土地资源分别与第一、二、三产业生产总值对应的基尼系数,考虑到二、三产业所使用的土地类型绝大多数为建设用地以及数据的可操作性^[31],本文将二、三产业增加值合并后与建设用地面积进行基尼系数测算。从图4可以看出耕地的基尼系数较小,即耕地与第一产业增加值的匹配性比较均衡。建设用地与第二、三产业值的基尼系数一度接近0.5,各地在第二、三产业的发展上差异很大,利用水平极不均衡,这可能是由于横断山区内部地貌分异所带来的适宜建设用地资源的巨大差异所导致的。

3.2 横断山区水土资源增长阻尼

3.2.1 面板模型回归结果 对2006—2015年横断山区的各地市生产总值、固定资本存量、水资源、土地资源等变量先取对数再做面板回归分析,具体来说选择个体随机效应模型建立拓展的Cobb-Douglas生产函数模型,模型结果如表2所示。

Tab. 2
表2
表2拓展的Cobb-Douglas生产函数模型结果
Tab. 2Results of the extended Cobb-Douglas production function model

变量	系数	z值	个体效应检验
lnK	0.226^**	5.89	固定效应VS随机效应卡方值9.42 Prob > chi2 = 0.0935
lnL	0.485^**	2.89
lnT	0.193^**	3.15
lnS	0.112	0.65

注：^**表示通过1%显著性检验。

新窗口打开|下载CSV

由表2可见,仅有水资源的显著性低于10%,其余变量均在1%显著,变量回归效果较好。结果表明资本存量、劳动力、土地资源和水资源与产出密切相关,其中水资源和土地资源的产出弹性都较大,即可以通过水资源和土地资源变量来解释GDP增长。横断山区资本的产出弹性约为0.226,劳动的产出弹性约为0.485,接近不考虑水土资源约束时的资本劳动产出比（1∶2）,在横断山区整体产出增加值中,劳动要素的对经济增长的弹性远大于资本、水资源和土地资源等要素的产出弹性,说明横断山区经济整体仍处于劳动密集型。土地资源和水资源的产出弹性分别是0.193和0.112,即土地资源要素对GDP增长贡献大于水资源要素,这可能源于横断山区水资源相对土地资源更为丰富,更为稀缺的土地资源变动反而能够带来更多的边际产出变动。

GDP的产出弹性可以表征为敏感性,即当投入要素诸如固定资本存量、劳动力、土地资源、水资源4个变量分别增加1个单位或者减少1个单位时GDP的单位变化量。可以看出,在横断山区适当增加水资源供应量和土地开发量均能在一定程度上促进GDP的增长。此外,横断山区劳动力和资本存量对GDP有更高的积极效应,GDP在资本存量和劳动力上表现得更为敏感,意味着该地区的发展仍然可以依靠资本和劳动力的投入,这也证明了其经济发展的阶段还较低。

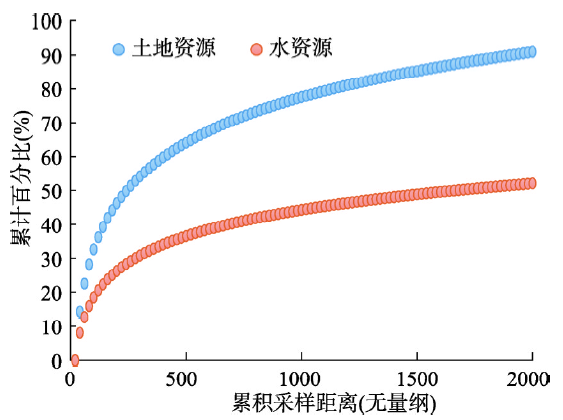
在控制其他变量不变的前提下,基于表2率定的生产函数,利用GDP产出的累积要素贡献率进行弹性效应分析可以得出水土资源要素贡献的差异对比（图5）。很明显,水土资源对GDP的增长有重大贡献,其中土地资源的累计贡献率的比率明显高于水资源,这与前述土地资源的产出弹性是水资源的2倍左右的结论是基本一致的,进一步证明了在横断山区,土地资源要素对GDP增长的贡献弹性高于水资源要素。

图5

新窗口打开|下载原图ZIP|生成PPT
图5水土资源的GDP累积贡献率对比

Fig. 5Relationship between water-land resources and cumulative contribution rate

3.2.3 水土资源阻尼系数 进一步对水土资源的变化率进行计算,结合面板回归模型的计量结果,根据公式（8）和公式（9）分别求得横断山区各市（州）土地资源和水资源的增长阻尼值（图6）,由此可以看出横断山区水土资源增长阻尼的内部特征。另外,将土地资源和水资源的增长阻尼值相加得到水土资源阻尼值（图6）,发现所有市（州）的“增长阻尼”系数均为正值,说明水资源和土地资源约束对横断山区经济发展确实存在一定的增长阻尼。这也表明水资源和土地资源的增量供给在当前阶段能够促进经济增长,横断山区的经济发展整体还处于低水平阶段,合理增加水资源和土地资源的供给都能够带来更多的经济产出。从内部差异来看,昆明的水土资源整体阻尼最大（0.041）,怒江的水土资源整体阻尼最小（0.024）。

图6

新窗口打开|下载原图ZIP|生成PPT
图62006—2015年横断山区各市(州)水资源和土地资源增长阻尼

Fig. 6Growth drag comparison between water and land resources in the Hengduan Mountains Area

从图6可看出,水资源对横断山区各市（州）经济形成的增长阻尼差异性较大,土地资源对经济形成的增长阻尼差距较小。水土资源增长阻尼平均水平分别为0.012和0.021,说明该区域经济发展速度比在没有受到水土资源限制的情况下年均降低1.2%和2.1%。另外,各市（州）土地资源的阻尼系数总是大于水资源的阻尼系数,这可能与横断山区的地形条件导致土地资源普遍难以有效利用有关。这说明水资源对经济增长的限制影响小于土地资源的限制影响,与前述土地资源的产出弹性大于水资源的规律相一致。参为了进一步探索土地资源增长阻尼的空间分布特征,参考阻尼特征以及其他相关研究的结果^[32,33],本文以0.01（明显低于其他城市的阻尼系数）和0.02（明显高于其他城市的阻尼系数）为分割点,将阻尼系数>0.02的市州划分为高增长阻尼区域,阻尼系数0.01~0.02的城市划分为中增长阻尼区域,阻尼系数0~0.01的市州城市划分为低增长阻尼区域。针对土地资源,除了迪庆州和攀枝花是处于中增长阻尼类型的城市以外,其他8各市州均属于高增长阻尼类型,说明横断山区的经济增长普遍受到土地资源的约束。

4 政策与启示

水土资源针对横断山区的经济增长研究不能忽视其重要的生态地位,作为中国长江上游生态屏障的一部分,在国家主体功能区规划中,相当大一部分县（区）被定位为国家重点生态功能区。因此,一方面横断山区承担着为国家提供战略性生态系统服务的角色,另一方面其内部也存在自身社会经济发展的强烈内在需求,尤其是部分区域仍属于深度贫困区,亟需区域持续地益贫式经济增长。对于山区而言,水资源和土地资源的不仅仅是生态系统的重要组分,同时也是经济系统的重要投入要素。实质上,对经济系统中的水土要素的投入进行优化,通过引导产业转型和产业集聚提高水土资源的利用效率,既能促进经济增长,也能提升国家重点生态功能区的生态保护效果和可持续性。

在中国城镇化这个大背景下,山区的城镇化进程为资源利用、资本投入、劳动力就业提供了新机遇。重视合理的山区城镇化带来的经济增长及链式影响,对于区域的经济增长具有重要意义。城镇化将农村剩余劳动力带入城镇,是劳动力、资源等生产要素在城镇聚集,逐步形成区域增长极,并将信息,资本等向农村转移,这种扩散和回流最终导致了区域经济的整体发展。因此,横断山区的经济增长,生态保护等都离不开城镇化这一背景。

从研究结果来看,横断山区水土资源的对经济增长的阻尼较大,这意味着未来经济增长仍然可以从资源利用的优化提升中获得更大的驱动力。由于横断山区土地资源的累计贡献率的比率明显高于水资源,土地资源的优化利用是重点。根据横断山区实际,未来应该以土地整理为抓手,推动部分地区的农地规模化经营,推动边际土地利用和撂荒地的转型增效;同时,针对城乡聚落用地的应该提升集约化程度,通过新村综合体和重点城镇建设,提高产业用地的单位产出,吸引环境友好型的投资项目,提升集聚经济的效益。在当前中国的自然资源管理改革的大背景下,资源管理注重“公平效率”、强调“永续利用”、融合“三资一体”、构建“有效市场”。水土资源在重塑自然资源管理新格局中起着核心的作用,其中使资源利用在经济系统中达到相对充分是区域资源管理和经济增长共同的目标。

另外,根据研究结果,横断山区劳动力和资本存量对GDP有更高的积极效应,意味着该地区的发展仍然可以依靠资本和劳动力的投入带来积极的增长红利。在资本投入方面,依然需要国家重大项目的投入和民间资本的双轮驱动。值得关注的是,由于横断山区拥有大量的国家重点生态功能区,目前针对国家重点生态功能区的大量财政转移支付资金,可以适当扩展和调整项目的性质和范围,将生态保护与相关产业链接起来,推动生态产业的打造,提升地方政府和利益相关方的直接经济收益。在劳动力投入方面,劳动力的产出弹性在横断山区经济增长中贡献最大,因此未来本区域仍然需要大量的劳动力投入,这说明需要重视劳动力数量的投入和保证,不过在空心化的大趋势下存在较大的挑战。另一方面,也需要重视教育和技能培训带来的劳动力质量提升,以多方面提升劳动生产率。

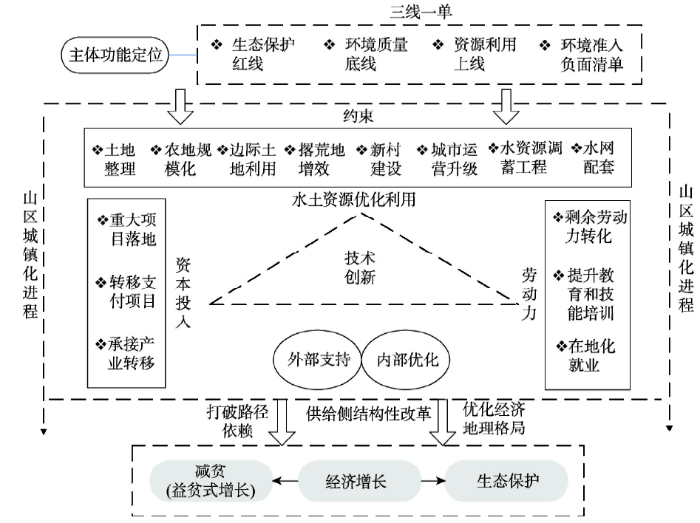
需要强调的是,由于横断山区重要的生态地位,其经济社会发展布局需要在生态文明战略的指导下,以国家主体功能区定位为导向,在三线一单（生态保护红线、环境质量底线、资源利用上线和环境准入负面清单）的严格控制下,科学地利用自然资源和国土空间,遵循市场原则,健全资源环境有偿使用和生态补偿机制^[36],实现经济发展和生态保护的合理权衡。一方面避免对生态环境的破坏,另一方面实现经济增长的涓滴化,推动区域贫困问题的减缓（图7）。

图7

新窗口打开|下载原图ZIP|生成PPT
图7横断山区经济发展的驱动机制

Fig. 7The driving mechanism for the economic growth of the Hengduan Mountains Area

5 结论与讨论

水土资源是经济发展的重要投入要素,本文首先利用基尼系数法评价横断山区水资源—土地资源—GDP之间的匹配状况,2015年横断山区水资源与GDP、土地资源与GDP的区域基尼系数分别为0.29和0.4,说明该区域水资源对经济增长的匹配程度相对较高,而土地资源对经济增长的满足程度相对较低。通过产业划分后的基尼系数可以看出,横断山区第三产业水资源与GDP的基尼系数略大,但也在相对匹配的区间内,而各产业土地资源与GDP的基尼系数普遍较低,尤其是第二、三产业的基尼系数较大且与总体基尼系数的变化趋势一致,表明横断山区土地资源对各次产业的发展需求均无法满足,其中以对第二、三产业的不匹配为主要表现。

本文基于Romer的增长阻尼模型,定量测算出横断山区水土资源对横断山区经济发展的制约程度。结果表明,水资源和土地资源对经济发展产生明显的约束作用,增长阻尼分别为0.012和0.022。水资源对经济增长的影响小于土地资源的影响,土地资源的累计贡献率明显高于水资源,同时其敏感性更强。受限于山地地形,大部分地区土地开发利用受到限制,导致耕地、可利用建设用地资源较少,故土地资源对经济的增长阻尼较大,而横断山区水资源相对充足,故水资源引致的经济发展的增长阻尼相对较小。这表明,目前土地资源要素对经济增长贡献的重要性大于水资源。但是不可忽视的是,由于横断山区内部存在较大的自然地理分异,水资源的分布并不均衡,部分地区工程性缺水现象在山区也是较普遍的现象。因此,不管从经济系统还是生态系统来讲,对水资源的保护与利用仍需重视。

总之,从发展经济学的视角出发,以横断山区为代表的中国山区发展需要更加重视水土资源利用与经济增长需求的匹配,在顾及由山区生态功能、生态脆弱性等特点所决定的水土资源利用限制的前提下,科学合理配置山区水土资源的利用,充分挖掘水土资源的利用潜力提高供给,不仅仅具有生态效益,而且可以降低对经济增长的制约程度。通过本文的有关分析,可以从以下途径减小水土资源对经济增长的约束。一是增加资本和劳动的有效供给,利用技术进步和资本替代水土资源。二是改变和集约土地利用方式,通过提升产出效率增加土地资源供给。

本文尝试从理论和实证2个方面分析了水土资源对山区经济发展的影响,但还存在一定的不足之处：① 研究假定技术水平是不变的,没有考虑技术进步的持续提高会动态改变水土资源的利用效率;② 水土资源调控机制有待进一步深化,不同产业的耗水量和土地资源需求量差异很大,而产业结构更多是受到当地资源禀赋的影响,并不能完全依靠改变产业结构来提升水土资源的利用效率。这些问题都值得进一步探讨。

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Deng

Wei

, Tang

Wei

. General directions and countermeasures for urbanization development in mountain areas of China
Mountain Research, 2013,31(2):168-173.

[本文引用: 1]

[ 邓伟, 唐伟. 试论中国山区城镇化方向选择及对策
山地学报, 2013,31(2):168-173.]

[本文引用: 1]

[2]

Sawaya

, Olmanson

, Heinert

, et al. Extending satellite remote sensing to local scale: Land and water resources monitoring using high revolution imagery
Remote Sensing of Environment, 2003,88(1/2):144-156.

DOI:10.1016/j.rse.2003.04.006 URL [本文引用: 1]

[3]

Xu Y

, Mo X

, Cai Y

. Analysis on groundwater table draw down by land use and the quest for sustainable use in the Hebei Plain in China
Agricultural Water Management, 2005,75(1):38-53.

[本文引用: 1]

[4]

Yang

Yanzhao

, Zhang

Weike

, Feng

Zhiming

, et al. Land use change induced land and water resources balance: A case study on the Xiliaohe watershed
Journal of Natural Resources, 2013,28(3):437-449.

[本文引用: 1]

[ 杨艳昭, 张伟科, 封志明, 等. 土地利用变化的水土资源平衡效应研究: 以西辽河流域为例
自然资源学报, 2013,28(3):437-449.]

[本文引用: 1]

[5]

Dong

Wen

, Yang

, Zhang

Yufang

. Coupling effect and spatio-temporal differentiation between oasis city development and water-land resources
Resources Science, 2013,35(7):1355-1362.

[本文引用: 1]

[ 董雯, 杨宇, 张豫芳. 绿洲城镇发展与水土资源开发的耦合效应及其时空分异
资源科学, 2013,35(7):1355-1362.]

[本文引用: 1]

[6]

Wang

Wei

, Lv

Ningjiang

, Wang

Xin

, et al. Study on spatial matching pattern of water and soil resources in Yellow River delta
Journal of Water Resources & Water Engineering, 2014,25(2):66-70.

[本文引用: 1]

[ 王薇, 吕宁江, 王昕, 等. 黄河三角洲水土资源空间匹配格局探析
水资源与水工程学报, 2014,25(2):66-70.]

[本文引用: 1]

[7]

Zhang

Jihui

, Li

Jian

, Tang

Yan

. Analysis of the spatio-temporal matching of water resource and economic development factors in China
Resources Science, 2012,34(8):1546-1555.

[本文引用: 1]

[ 张吉辉, 李健, 唐燕. 中国水资源与经济发展要素的时空匹配分析
资源科学, 2012,34(8):1546-1555.]

[本文引用: 1]

[8]

Zhang

Xiaotao

, Yu

Fawen

. Analysis of the matching status between economic development and water resources in the Yellow River Basin
China Population, Resources and Environment, 2012,22(10):1-6.

[本文引用: 2]

[ 张晓涛, 于法稳. 黄河流域经济发展与水资源匹配状况分析
中国人口·资源与环境, 2012,22(10):1-6.]

[本文引用: 2]

[9]

Ping

, Zhang

Hui

, Xing

Yan

. Study on the matching of water resources utilization in Qinghai Province
China Population, Resources and Environment, 2018,28(7):46-53.

[本文引用: 2]

[ 武萍, 张慧, 邢衍. 青海省水资源利用的匹配性研究
中国人口·资源与环境, 2018,28(7):46-53.]

[本文引用: 2]

[10]

Liu

Chunla

, Liu

Weidong

, Lu

Dadao

, et al. A study of provincial differences in China's eco-compensation framework
Acta Geographica Sinica, 2015,70(12):1897-1910.

[本文引用: 1]

[ 刘春腊, 刘卫东, 陆大道, 等. 2004—2011年中国省域生态补偿差异分析
地理学报, 2015,70(12):1897-1910.]

[本文引用: 1]

[11]

Nordhaus W

, Stavins R

, Weitzman M

. Lethal model 2: The limits to growth revisited
Brookings Papers on Economic Activity, 1992(2):1-59.

URLPMID:12287537 [本文引用: 1]

The author examines some major concerns about global economic growth from both theoretical and empirical points of view, using

[12]

Brvoll

, Glomsrod

, Vennemo

. Environmental drag: Evidence from Norway
Ecological Economics, 1999,30(2):235-249.

[本文引用: 1]

[13]

Romer

. Advanced Macroeconomics. 2nd ed. Shanghai: Shanghai University of Finance & Economics Press, 2001.

[本文引用: 2]

[14]

Thorvaldur

, Gyl?

. Natural resources and economic growth: The role of investment
The World Economy, 2006,29(8):1091-1115.

[本文引用: 1]

[15]

Cao

Xue

, Jin

Xiaobin

, Zhou

Yinkang

. Amendment of "Growth Drag" to economy based on ecological footprint model: A case study of Nanjing City
China Population, Resources and Environment, 2011,21(3):558-561.

[本文引用: 2]

[ 曹雪, 金晓斌, 周寅康. 资源环境对南京市经济发展的“增长阻尼”
中国人口·资源与环境, 2011,21(3):558-561.]

[本文引用: 2]

[16]

Yang

, Wu

Cifang

. Study of Chinese economic "growth drag" caused by land resource in the perspective of the modified two-level ces production function
Chinese Journal of Population, Resources and Environment, 2012,10(4):39-43.

[本文引用: 2]

[17]

Liu Y

, Xie Y

. Measuring the dragging effect of natural resources on economic growth: Evidence from a space-time panel filter modeling in China
Annals of the Association of American Geographers, 2013,103(6):1539-1551.

[本文引用: 2]

[18]

Liu Y

. Economic growth drag in the central China: Evidence from a panel analysis
Applied Economics, 2013,46(14):2163-2174.

[本文引用: 2]

[19]

Shi Z

, Deng

, Zhang S

. Spatio-temporal pattern changes of land space in Hengduan Mountains during 1990-2015
Journal of Geographical Sciences, 2018,28(4):529-542.

[本文引用: 1]

[20]

Zongxing

, He

Yuanqing

, Xin

Huijuan

, et al. Spatio-temporal variations of temperature and precipitation in Mts. Hengduan region during 1960-2008
Acta Geographica Sinica, 2010,65(5):563-579.

[本文引用: 1]

[ 李宗省, 何元庆, 辛惠娟, 等. 我国横断山区1960—2008年气温和降水时空变化特征
地理学报, 2010,65(5):563-579.]

[本文引用: 1]

[21]

, Fu

, Shen

, et al. Monitoring snow cover variability (2000-2014) in the Hengduan Mountains based on cloud-removed MODIS products with an adaptive spatio-temporal weighted method
Journal of Hydrology, 2017,551:314-327.

[本文引用: 1]

[22]

Chen

Tiantian

, Peng

, Liu

Shaoquan

, et al. Relationships of relief degree of topography with population and economy in Hengduan mountain area based on GIS
Journal of University of Chinese Academy of Sciences, 2016,33(4):505-512.

[本文引用: 1]

[ 陈田田, 彭立, 刘邵权, 等. 基于GIS的横断山区地形起伏度与人口和经济的关系
中国科学院大学学报, 2016,33(4):505-512.]

[本文引用: 1]

[23]

Shi

Zhenqin

, Deng

Wei

, Zhang

Shaoyao

. Spatial pattern and spatio-temporal change of territory space in Hengduan Mountains region in recent 25 years
Geographical Research, 2018,37(3):607-621.

[本文引用: 1]

[ 时振钦, 邓伟, 张少尧. 近25年横断山区国土空间格局与时空变化研究
地理研究, 2018,37(3):607-621.]

[本文引用: 1]

[24]

Xie

Shuling

, Wang

Zheng

, Xue

Junbo

. An analysis of the "Growth Drag" of water and land resources in China's economic development
Management World, 2005,7(4):22-25.

[本文引用: 1]

[ 谢书玲, 王铮, 薛俊波. 中国经济发展中水土资源的“增长尾效”分析
管理世界, 2005,7(4):22-25.]

[本文引用: 1]

[25]

Yuming

. Calculation and analysis the total factor productivity of Provinces and municipalities in the country
Economists, 2002,18(3):115-121.

[本文引用: 1]

[ 叶裕民. 全国及各省区市全要素生产率的计算和分析
经济学家, 2002,18(3):115-121.]

[本文引用: 1]

[26]

Shanzi

, Xiang

Juan

. Estimation of the fixed capital stocks in Chinese cities for 1996-2009
Statistical Research, 2012,29(7):19-24.

[本文引用: 1]

[ 柯善咨, 向娟. 1996—2009年中国城市固定资本存量估算
统计研究, 2012,29(7):19-24.]

[本文引用: 1]

[27]

Marshall

, Mariam

. Measurement of capital stocks, consumption of fixed capital, and capital services
Report on a Presentation to the Central American Ad Hoc Group on National Accounts, 2005.

[本文引用: 1]

[28]

Ali H

, Sami S

. Inequality, Economic Growth and Natural Resources Rent: Evidence from the Middle East and North Africa
Basingstoke: Palgrave Macmillan, 2016.

[本文引用: 1]

[29]

Qiao

Kun

, Zhu

Wenquan

, Hu

Deyong

, et al. Examining the distribution and dynamics of impervious surface in different functional zones of Beijing
Acta Geographica Sinica, 2017,72(11):100-113.

[本文引用: 1]

[ 乔琨, 朱文泉, 胡德勇, 等. 北京市不同功能区不透水地表时空变化差异
地理学报, 2017,72(11):100-113.]

[本文引用: 1]

[30]

Jantzen R

, Volpert

. On the mathematics of income inequality: Splitting the Gini index in two
American Mathematical Monthly, 2012,119(10):824-837.

[本文引用: 1]

[31]

Xin

, Zhang

Ruiping

, Ou

Minghao

, et al. Study on construction land contribution to secondary & service industry and its spatial correlation
China Population, Resources and Environment, 2011,21(9):64-68.

[本文引用: 1]

[ 李鑫, 张瑞平, 欧名豪, 等. 建设用地二三产业增长贡献及空间相关性研究
中国人口·资源与环境, 2011,21(9):64-68.]

[本文引用: 1]

[32]

Zeng

Wei

. The influence of land resources on urban economic growth
Resources Science, 2014,36(7):1317-1326.

[本文引用: 1]

[ 曾伟. 土地资源对城市经济增长的影响分析: 理论与实证
资源科学, 2014,36(7):1317-1326.]

[本文引用: 1]

[33]

Wang

Jiating

. Study on the land resource growth drag in China's regional economic growth
Economic Geography, 2010,30(12):2067-2072.

[本文引用: 1]

[ 王家庭. 中国区域经济增长中的土地资源尾效研究
经济地理, 2010,30(12):2067-2072.]

[本文引用: 1]

[34]

Mao

Hanying

. Theories and methods of optimal control of human-earth system
Acta Geographica Sinica, 2018,73(4):608-619.

[ 毛汉英. 人地系统优化调控的理论方法研究
地理学报, 2018,73(4):608-619.]