HTML
--> --> -->ENSO predictability is largely impacted by the air-sea interaction process in the tropical Pacific Ocean (McPhaden, 2003). Great efforts are made to explore the predictors and optimal forcing of El Ni?o events in the tropical Pacific Ocean (Moore et al., 2006; Bunge and Clarke, 2014; Lopez and Kirtman, 2014; Duan and Hu, 2016). Recently, more and more studies have suggested that information from outside the tropical Pacific Ocean, like from the subtropical Pacific Ocean (Matei et al., 2008; Lu et al., 2017) and the Atlantic Ocean (Rodríguez-Fonseca et al., 2009; Ham et al., 2014), also plays a vital role in influencing ENSO predictions. Besides the sea temperatures in the Pacific Ocean, the oceanic state in the tropical Indian Ocean also influences the ENSO forecast in the Pacific Ocean (Behera and Yamagata, 2003; Luo et al., 2010). Lim and Hendon (2017) pointed out that strong negative Indian Ocean Dipole (IOD) events acted as a promoter of the weak La Ni?a during 2016. The ENSO simulation from Coupled General Circulation Model (CGCM) including both the tropical Pacific Ocean and the Indian Ocean tends to be more realistic than considering the tropical Pacific Ocean only (Yu et al., 2002). In statistical forecasting models, using Indian Ocean Dipole Mode Index (DMI) as a predictor can also significantly improve the ENSO forecasting skill (Izumo et al., 2010, 2014). The Indian Ocean Dipole can affect the strength of the Walker Circulation in autumn and lead to the development of ENSO events. Gear-like coupling between the Indian and Pacific oceans (GIP) is one of the atmospheric bridge theories developed to interpret the interactions between the air-sea interaction phenomena over the tropical Pacific and the Indian Ocean (Wu and Meng, 1998). A positive rotating GIP normally has an anticlockwise monsoon anomaly (westerly wind anomaly at the low-level and easterly wind anomaly at the upper-level) over the tropical Indian Ocean and a clockwise Walker Circulation anomaly (easterly wind anomaly at the low-level and westerly wind anomaly at the upper-level) over the tropical Pacific Ocean, while a negative GIP consists of a clockwise wind anomaly over the Indian Ocean and an anticlockwise Walker Circulation anomaly in the tropical Pacific Ocean. Meng and Wu (2000) have also verified that the ENSO events in the tropical Pacific Ocean can be triggered via GIP since the zonal wind anomaly in the tropical Indian Ocean can influence the air-sea coupling system in the Pacific Ocean. Along with the atmospheric bridge over the tropical oceans, the Indonesian Throughflow (ITF), the only oceanic channel connecting the tropical Indian Ocean and the tropical Pacific Ocean, also stands out as one of the dynamical mechanisms behind the IOD forcing influencing the ENSO-related SSTA (Yuan et al., 2011, 2013; Zhou et al., 2015).
From the perspective of error growth, the influence of sea temperature in the tropical Indian Ocean on ENSO predictions cannot be ignored. Two types of initial errors of sea temperature in the tropical Indian Ocean have been explored and found to be most likely to yield the Spring Prediction Barrier (SPB) of El Ni?o prediction (Zhou et al., 2019), suggesting the possibility that applying targeted observation strategies in the locations of the initial errors can further improve El Ni?o prediction skill (Zhou et al., 2020). Investigations of error evolution mechanisms show that for Type-1 initial error with positive IOD-like structure, the ITF plays a dominant role in influencing SSTA in the tropical Pacific Ocean, but for Type-2 initial error, the atmospheric bridge works as the main way to impact El Ni?o prediction. Each study mentioned above focused on the influences of IO-related initial errors on the predictability of El Ni?o events. However, as the negative phase of ENSO, La Ni?a events can also modulate the East Asian winter and summer monsoons (Huang et al., 2004; Xue et al., 2015), modulate the Mei-yu Rainfall over the Yangtze River Valley (Wang et al., 2012), and lead to severe wintertime droughts in northern China (Gao and Yang, 2009). Besides, the influences of La Ni?a events are worldwide. La Ni?a events can also influence sea temperature in the Atlantic Ocean (Wu et al., 2020) and snow accumulation in the Andes (Cortés and Margulis, 2017), leading to climatic anomalies in Europe (Ding et al., 2017). So, it is urgent to study the predictability of La Ni?a events and improve La Ni?a prediction skill. Given the influences of the initial state of the tropical Indian Ocean on the predictability of El Ni?o events, it is natural to ask: Will the initial errors of sea temperature in the tropical Indian Ocean influence La Ni?a predictability? Do the initial errors that are most likely to induce the SPB for La Ni?a and El Ni?o predictions share similar spatial structures? What is the mechanism behind the error evolutions? What is the implication of the targeted observation strategy for La Ni?a forecasts? All of these questions are addressed in this study.
In this paper, section 2 gives a brief description of the model and data. The experimental design is shown in section 3. The initial errors that are most likely to induce the SPB during La Ni?a prediction are investigated in section 4. The characteristics of the error evolutions and their dynamical mechanisms are analyzed in detail in section 5. In section 6, the implications of applying targeted observations in the tropical Indian Ocean are studied. The summary and discussion are presented in section 7.
As a coupled model, the CESM’s simulations of the sea temperature states (i.e., the climatology state and standard deviations) in the tropical Indian Ocean and the Pacific Ocean are in good agreement with the observations. ENSO dominates as the leading mode in the tropical Pacific Ocean, explaining nearly 51% of the total variances of the SST during the winter. The power spectrum of the Ni?o-3 index from the simulation shows a period of three to six years. Six typical La Ni?a events simulated by this model are shown in Fig. 1. These typical La Ni?a events which start cooling in Jan(0), usually reach their peak in Oct(0) and decay afterwards. Finally, these La Ni?a events change to the normal state in May(1). Here, “0” and “1” represent the La Ni?a year and the following year, respectively. This seasonal feature indicates that the CESM provides reasonable simulation of La Ni?a events’ phase-locking feature. In the Indian Ocean, the dipole mode (i.e., positive sea temperature anomalies in the tropical western Indian Ocean and negative anomalies in the tropical eastern Indian Ocean) works as the leading mode and can explain 64% of the total variance.
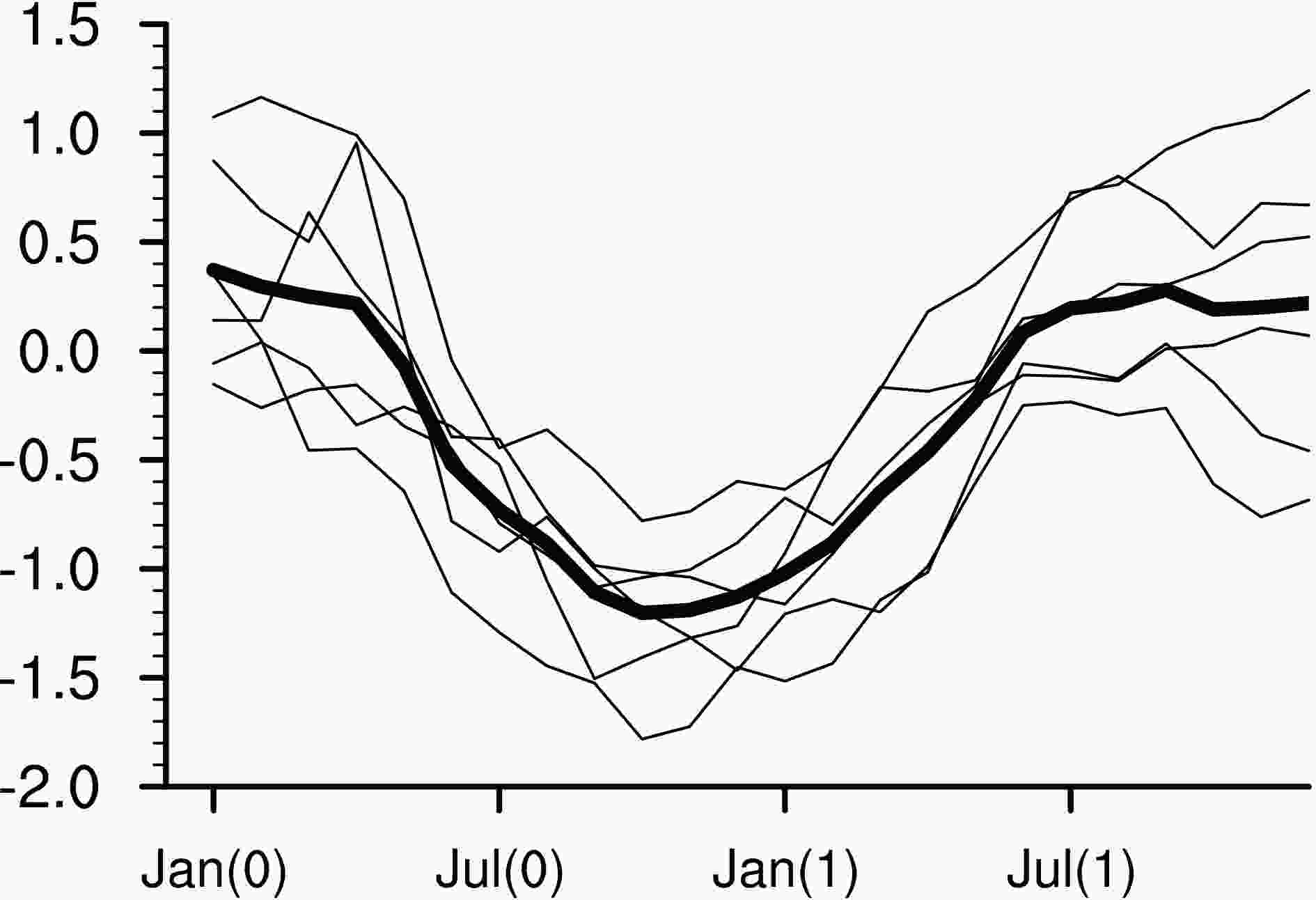Figure1. Ni?o-3 index (units: °C) of six La Ni?a events from CESM1.0.3. The thin lines represent the six La Ni?a events and the thick line is the mean of the six events (here, “0” and “1” signify the La Ni?a year and the next year, respectively).The atmospheric bridge and the ITF are suggested as the most important ways for initial errors in the tropical Indian Ocean to impact the SSTA predictions in the tropical Pacific Ocean. So, the CESM’s ability to simulate both the atmospheric bridge (GIP) and the ITF is investigated. In the climatological simulation, the rising branch of the atmospheric bridge is located over the western Pacific Ocean and the eastern Indian Ocean, where SSTs are warm; meanwhile, two sinking branches appear in the eastern Pacific Ocean and the tropical western Indian Ocean. Regarding the ITF, the volume transport along the IX01 line is commonly used to present the ITF. The IX01 XBT (expendable bathythermograph) line, which is part of XBT network of the Indian Ocean Observing System (IndOOS) (Hermes et al., 2019), almost crosses the Fremantle-Sunda Straits, which is a connection between the tropical Pacific Oceans and the Indian Ocean. On average, the ITF calculated from the CESM simulations is 10.7 Sv, and it usually peaks in the summer and decays in the winter, showing a seasonally dependent feature. These features simulated by the CESM are very consistent with the ITF observations (Gordon, 2005; Tillinger and Gordon, 2009).
Besides the CESM’s good performance on the simulations mentioned above, it can also simulate the role of the atmospheric bridge and the ITF in the IOD forcing that influences the SSTA in the tropical Pacific Ocean. Following the example of Yuan et al. (2013), analysis of the lag correlations between the IOD index with the SSTA in the tropical oceans is also carried out, and just like FGOALS-g2 (Xu et al., 2013), the CESM can simulate the ITF’s role in IOD forcing influencing the SSTA associated with the ENSO, but the atmospheric bridge’s role is overestimated when compared with the observations. The ITF’s contributions are also further examined with sensitivity experiments carried out with the CESM (Zhou et al., 2015).
In short, the CESM can be used to study the influence of the initial errors in the tropical Indian Ocean on the predictability of La Ni?a.
A number of sensitivity experiments are then carried out for the selected La Ni?a events in an attempt to explore the IO-related initial errors that are most likely to yield the SPB. Here, IO-related initial errors are obtained by the following steps: First, for each typical La Ni?a event simulated from the coupled model, the differences between the sea temperatures in the tropical Indian Ocean (40°–130°E, 10°S–10°N; 0–400 m, ranging from the 1st to 30th level in the ocean model) of the start month and every other month during the four years before the start month are obtained as the initial errors. Thus, for each La Ni?a event, 24 initial perturbations can be chosen. Taking simulation 0061-01 from the model as an example, the 24 initial errors are 0057-02, 0057-04, 0057-06, …, 0060-10, and 0060-12. These initial errors are marked as T′, and their norms can be calculated according to
In order to have a deeper understanding of the common features of the SPB-related initial errors, the evolution of the averaged prediction errors induced by both SPB-related and non_SPB-related initial errors are shown (the thick black line in Figs. 2a1 and 2b1). For SPB-related initial errors, the prediction errors increase rapidly during May(0) to Sep(0), eventually reaching very large values, indicating that April?May?June (AMJ) and July?August?September (JAS) are the seasons with quickest error increases during the forecasts. For non_SPB-related initial errors, the growth rates of the prediction errors during these seasons are quite small. Additionally, most of the predicted Ni?o-3 index errors induced by the SPB-related initial errors are positive and keep growing during the predictions, as seen in Fig. 2b1. These SPB-related initial errors tend to lead to La Ni?a events being underpredicted in terms of their magnitudes, and sometimes they even result in a forecast missing a La Ni?a event entirely.
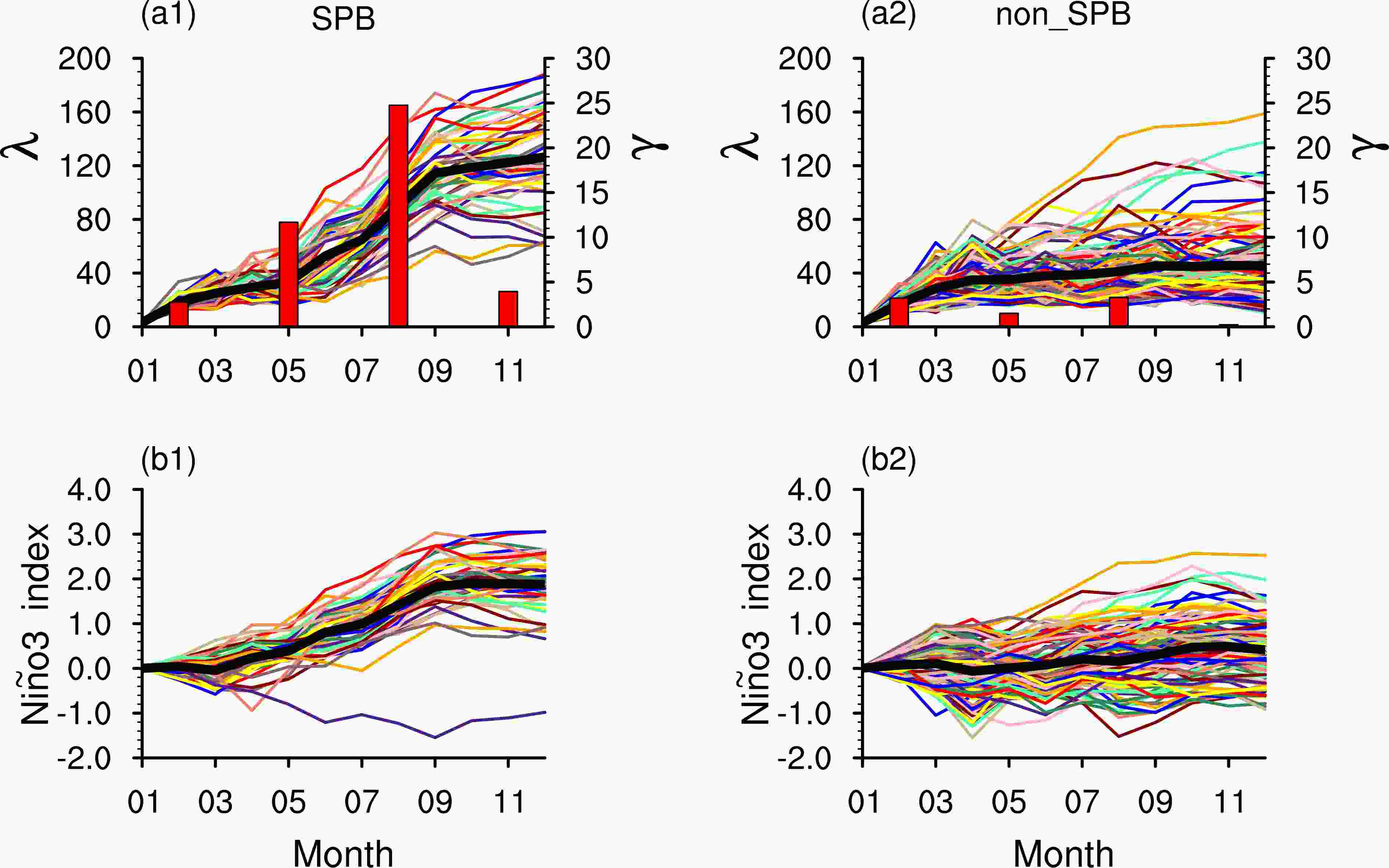Figure2. (a1) The prediction errors (λ) caused by each SPB-related conditional initial error (colored curves) for the six La Ni?a events with the start month Jan (0) (the average is in bold black), where the average of the seasonal growth rates of prediction errors (γ) are also plotted in histograms; (a2) same as (a1), but for non_SPB-related conditional initial errors; (b1) and (b2) show the corresponding Ni?o-3 index errors (units: °C, colored curves) when compared with the control run and their averaged mean (bold black) for SPB-related and non_SPB-related conditional initial errors, respectively.Cluster analysis is applied to diagnose the common spatial features of the SPB-related initial errors obtained above, and two types of SPB-related initial errors are found, as shown in Fig 3. Among all 45 SPB-related initial errors, 18 are Type-1 initial errors (Fig. 3a1). We can see that Type-1 initial errors have a positive IOD-like spatial structure with positive sea temperature errors in the tropical western Indian Ocean and negative values in the east; while for the Type-2 initial errors, as shown in Fig. 3a2, the structure is almost opposite to that of the Type-1 initial errors (i.e., with negative errors in the western basin and positive errors in the east). These dipole-like features not only occur on the surface of the Indian Ocean, but also prevail in the subsurface regions (as shown in Figs. 3b1 and b2). The sea temperature errors in the subsurface can also modulate the influence on the sea surface temperature by vertical mixing and entrainment processes (Zhang and Zebiak, 2002; Zhu et al., 2020).
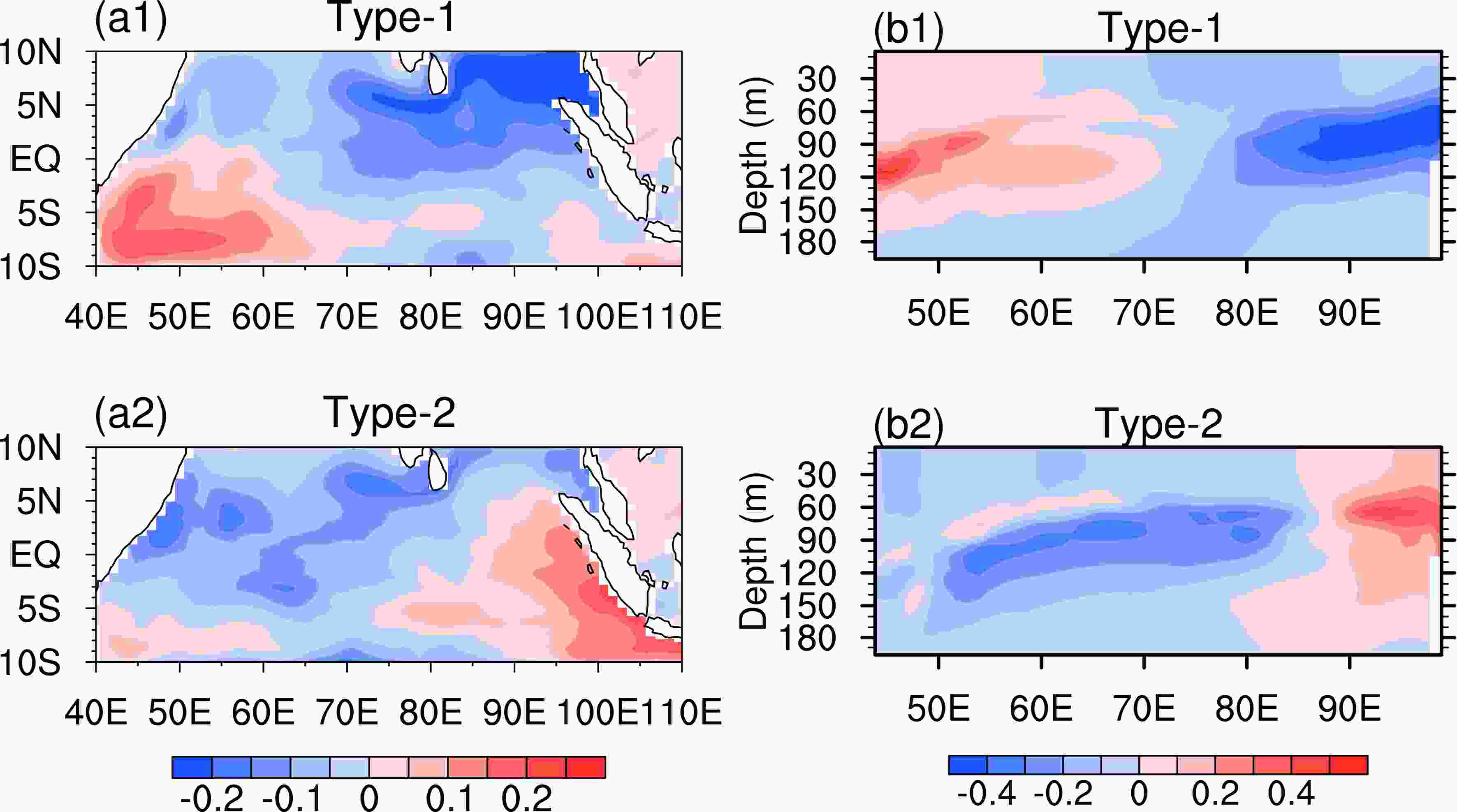Figure3. The SST and the vertical sea temperature (averaged by meridian 5°N to 5°S) components of the Type-1 (a1 and b1) and Type-2 (a2 and b2) SPB-related initial errors for Jan (0).The error evolutions of sea temperature Type-1 initial errors along the tropical oceans are composited in Fig. 4. When Type-1 initial errors are superimposed in the tropical Indian Ocean, the sea temperature errors exhibit a positive IOD-like pattern, and the magnitudes of the sea temperature errors are increased. In the tropical Pacific Ocean, the positive errors of sea temperature first appear in the eastern Pacific Ocean at the start month and continue growing afterwards. At the end of the predictions, the prediction errors in the tropical Indian Ocean and the tropical Pacific Ocean are positive IOD-like and El Ni?o-like, respectively.
Figure4. The composite monthly sea temperature component (averaged meridional over 5°N to 5°S) for the evolutions of Type-1 initial error with the start month Jan(0) (the regions covered by dots indicates those of statistical significance (>95%). The evolution of sea temperature errors is highlighted as black arrow.For SPB-related Type-2 initial error, the composited error evolutions are displayed in Fig. 5. Unlike the evolution of Type-1 initial error, when Type-2 initial error is added in the tropical Indian Ocean, negative IOD-like sea temperature error patterns do not stay there through the end of the prediction. In fact, the positive errors in the eastern Indian Ocean diminish and turn to negative values during Apr(0), while negative errors in the western Indian Ocean convert to positive errors. This positive IOD-like pattern dominates in the tropical Indian Ocean in the end. Meanwhile in the tropical Pacific Ocean, positive sea temperature errors first show in the western Pacific Ocean. These positive errors keep growing and propagate to the east Pacific Ocean, resulting in an El Ni?o-like error state in the end.
Figure5. As in Fig. 4, but for Type-2 initial error.To sum up, in the tropical Indian Ocean, when SPB-related Type-1 initial error is added in the tropical Indian Ocean, the errors tend to keep growing with this kind of spatial structure, just like a positive IOD event experiencing a growing phase evolution; while for SPB-related Type-2 initial errors with a negative IOD-like mode, the prediction errors tend to decay and ultimately change to a positive IOD-like state. In the tropical Pacific Ocean, the sea temperature errors induced by the SPB-related Type-1 initial error experience localized developments in the eastern Pacific Ocean. Meanwhile, the prediction errors of sea temperature induced by Type-2 initial error usually first appear in the western Pacific Ocean and then propagate to the east.
It is clear that both kinds of SPB-related initial errors experience quite different evolutions in the two oceans. Why are they different and what are the dynamic mechanisms behind the error evolutions? Zhou et al. (2019) suggested that during El Ni?o predictions, either the ITF or the atmospheric bridge plays a vital role in IO-related initial errors influencing the SST predictions in the tropical Pacific Ocean. We cannot help wondering: Do these dynamical mechanisms still work in the La Ni?a predictions? Which role do they play in each kind of error evolutions? In order to make these clear, the roles of both the ITF and the atmospheric bridge (GIP) are studied.
First, we look into the role of the ITF. The averaged volume transport of the ITF anomalies calculated along the IX01 line for SPB-related Type-1 and Type-2 initial errors are ?0.13 Sv and ?0.50 Sv, respectively. Zhou et al. (2015) performed sensitivity experiments with the atmospheric bridge shut down, resulting in ITF anomalies induced by positive and negative IOD forcing of 6.18 Sv (positive) and ?6.21 Sv (negative), respectively. It is clearly shown that the ITF anomalies induced by both Type-2 initial error in this study and that from negative IOD forcing are both negative, implying that the ITF may play a leading role in the evolution of Type-2 initial error. Since the ITF volume is defined as the amount of warm water transported from the warm pool area in the western Pacific Ocean to the Indian Ocean, negative ITF error indicates that less warm water is transported from the western Paci?c Ocean to the Indian Ocean, or anomalously warm water in the tropical eastern Indian Ocean penetrates into the western Paci?c Ocean (Zhou et al., 2015), which may also be the dynamical mechanism of Type-2 initial error influencing the SST prediction in the Pacific Ocean.
In order to have a deeper understanding of the dynamical mechanisms, composited error evolutions of Type-2 initial error are plotted and shown in Fig. 6. It is clearly seen that positive sea surface height errors are induced by the positive sea temperature errors in the tropical eastern Indian Ocean, leading to local downwelling anomalies there. These downwelling anomalies further penetrate into the western Paci?c Ocean, resulting in positive sea temperature errors. And, these positive errors of sea temperature keep traveling to the equatorial eastern Paci?c Ocean, preserving an El Ni?o-like error pattern at the end of the prediction. So, the ITF’s role in Type-2 initial errors influencing the SSTA predictions associated with La Ni?a is clear. But how about the role of the atmospheric bridge? Actually, according to the GIP theory, which is one of the popular atmospheric bridge theories, the positive errors in the eastern Indian Ocean tend to induce updraft errors over the Indian Ocean and downdraft errors over the Pacific Ocean, leading to negative SSTA prediction errors in the tropic Pacific Ocean. Meanwhile, positive SSTA prediction errors are the main errors during the whole prediction. So, it is the ITF, rather than the atmospheric bridge, that plays the leading role in Type-2 initial error influencing the La Ni?a predictions.
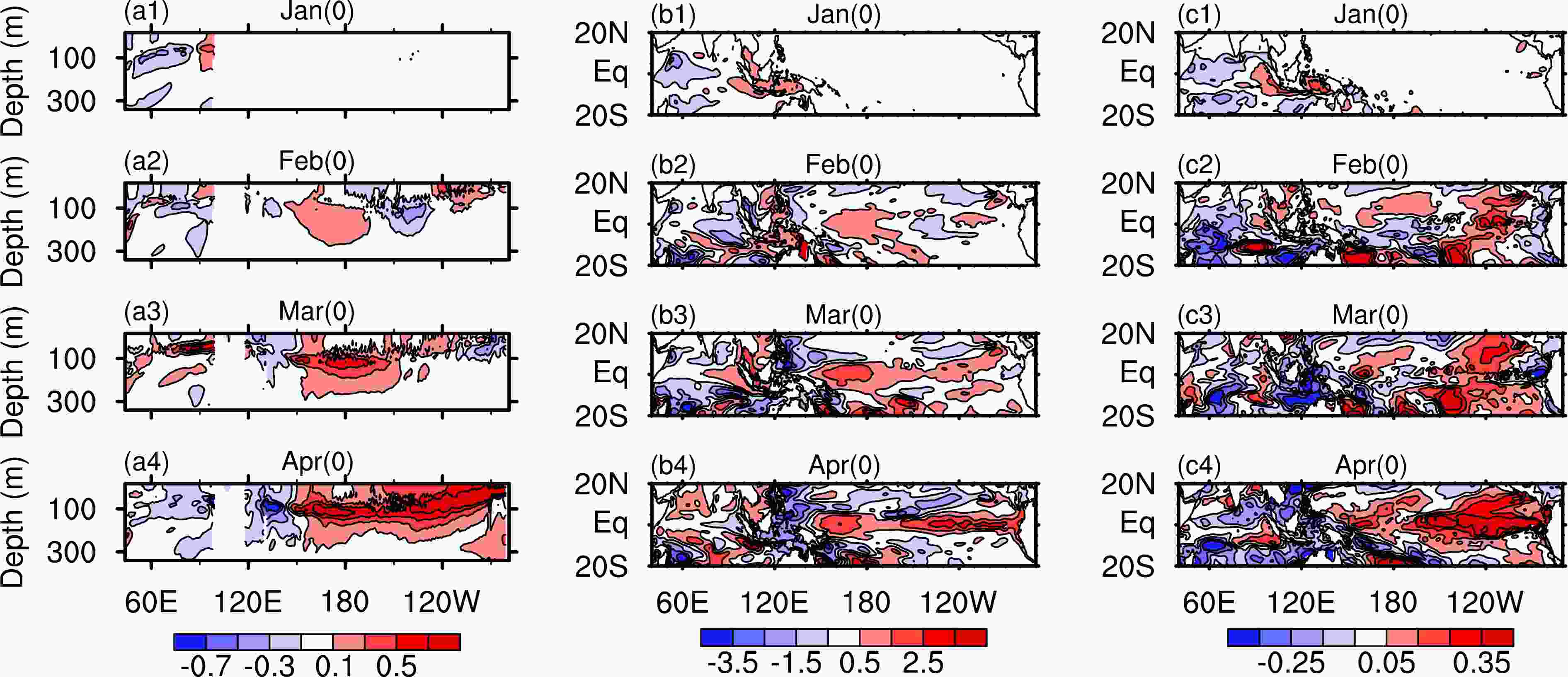Figure6. Composited evolution of Type-2 initial error from Jan(0) to Apr(0) with the components of (a) the vertical sea temperature errors in tropical Indian Ocean and the Pacific Ocean over the equator, (b) the SSH errors, and (c) the SST errors.When it comes to the SPB-related Type-1 initial error, the induced ITF errors are also negative, which is of the opposite sign to the ITF anomalies induced by the negative IOD forcing when the atmospheric bridge was shut down (Zhou et al., 2015). According to Zhou et al. (2015), when positive IOD-like errors influence the SST predictions in the tropical Pacific Ocean through the ITF, the negative SST errors usually dominate in the tropical Pacific Ocean throughout the predictions, rather than inducing positive errors there. Thus, it is very unlikely for the ITF to play the chief role in IO-related initial errors influencing SSTA prediction in the Pacific Ocean since we have positive prediction errors of sea temperature in the Pacific Ocean during the La Ni?a forecasts. So, we must study the role of the atmospheric bridge. Evolutions of wind errors induced by the Type-1 initial errors are plotted in Fig. 7. It is shown that during Jan(0), when positive IOD-like errors of sea temperature are superimposed in the tropical Indian Ocean, downdraft errors appear both in the western Pacific Ocean and the eastern Indian Ocean. According to the GIP theory, these downdraft errors can lead to updraft errors in the central and eastern Pacific Ocean during Jan(0) and Feb(0). Those downdraft errors further induce positive errors of sea temperature in the eastern Pacific Ocean, resulting in many La Ni?a events being missed by forecasts. Therefore, SPB-related Type-1 initial errors in the Indian Ocean usually influence the sea temperature in the tropical Pacific Ocean mainly by virtue of the GIP.
Figure7. Wind error evolutions induced by the Type-1 initial error during Jan (0) and Feb (0) (averaged by meridian 5°N to 5°S). The updraft and downdraft branches are highlighted as red arrows.To sum up, Type-1 and Type-2 SPB-related initial errors in the tropical Indian Ocean mainly influence the sea temperature predictions in the Pacific Ocean via GIP and the ITF, respectively.
Figure8. The sensitive area (shaded in red) of targeted observations in the tropical Indian Ocean for the La Ni?a predictions.The results of the targeted observations sensitivity experiments are shown in Table 1. The bulk of non-sensitive area in the tropical Indian Ocean is about 2.22 × 107 km3, which is four times larger than the sensitive area. Although the area is much larger, adopting the targeted observation strategy in the non-sensitive area provides little help toward achieving better La Ni?a predictions. Surprisingly, the prediction skill is reduced (?0.14%) in general. From Sensi-1, where targeted observation strategies are applied inside the sensitive area, La Ni?a prediction skill can be improved by 20.59%. The averaged benefit is defined following Zhou et al. (2020) (i.e., β= improvement of La Ni?a prediction skill / volume of the area with targeted observations applied). Here, β measures the effectiveness of adopting targeted observation strategies since it can represent the prediction skill improvement per km3 for a certain area. In this study, the effectiveness β from both Sensi-1 and Sensi-2 are calculated. β of Sensi-1 is very large, reaching up to 399.90; β of Sensi-2 is ?0.06 on average. Although the sensitive area occupies a very small area of the tropical Indian Ocean, it is very effective to adopt targeted observation strategy there to reduce the prediction errors of the La Ni?a forecasts.
| Sensi-1 | Sensi-2 | |
| Prediction errors for Exp-ref (Err0) | 101.32 | 101.32 |
| Predictions errors with targeted observations (Err) | 80.46 | 101.46 |
| The improvement for El Ni?o events ($1 - { { {\rm{Err} } } }/{ { {\rm{Er} }{ {\rm{r} }_0} } }$) | 20.59% | ?0.14% |
| The bulk of sensitive area (107 km3) | 0.52 | 2.22 |
| Averaged benefit for the targeted observation β (10?7 km?3) | 399.90 | ?0.06 |
Table1. The averaged prediction errors and the averaged benefits of the targeted observation strategy conducted inside/outside the sensitive area for La Ni?a predictions.
Prediction errors of sea temperature from the control run, Sensi-1, and Sensi-2 are shown in Fig. 9. In the control run, without any targeted observations applied, positive sea temperature errors dominate as the main feature at the end of the forecasts, as shown in Fig. 9a. In Fig. 9b, where targeted observation strategies are applied inside the sensitive area, positive prediction errors of sea temperature are still there, but both the magnitude and the area of the errors are reduced. As in Fig. 9c, when targeted observation strategies are adopted outside the sensitive area, the spatial pattern and the magnitude of the prediction errors are much like those from the control run, implying little improvements of La Ni?a prediction skill. The differences of prediction errors between these different sensitivity experiments support the former conclusion that adopting targeted observation strategies in the sensitive area in the Indian Ocean can significantly reduce the prediction errors and improve the forecast skill of La Ni?a events.
Figure9. Prediction errors in Dec(0) in the tropical oceans for La Ni?a predictions starting from Jan(0), (a) for predictions superimposed with the whole initial errors in the tropical Indian Ocean, (b–c) for predictions with targeted observation strategy conducted inside/outside the sensitive area in the tropical Indian Ocean, respectively.The predicted SSTA are also shown in Fig. 10. Figure 10a shows the “true state” of typical La Ni?a events, with negative SSTA prevailing in the tropical Pacific Ocean. When SPB-related initial errors exist in the tropical Indian Ocean, the La Ni?a event mode is disappeared due to the large influences from the IO-related initial errors. When targeted observation strategies are adopted outside the sensitive area in the Indian Ocean, as in Fig. 10d, predicted SSTA shows larger negative SSTA in the tropical Pacific Ocean when compared with that from Fig. 10b, showing some improvement. However, when targeted observation strategies are adopted inside the sensitive area in the tropical Indian Ocean (Fig. 10c,), the predicted SSTA in the tropical Pacific Ocean shows a typical La Ni?a mode pattern with a relatively reduced magnitude, implying that the prediction skill for La Ni?a events is significantly improved.
Figure10. Predicted SSTA in Dec(0) in the tropical oceans for La Ni?a predictions starting from Jan(0), (a) for the “true state” of La Ni?a events, (b) for predictions superimposed with the whole initial errors in the tropical Indian Ocean, (c–d) for the predictions with targeted observation strategy conducted inside/outside the sensitive area in the tropical Indian Ocean, respectively.In short, La Ni?a prediction is sensitive to the sea temperature errors in the sensitive area which resides in the eastern tropical Indian Ocean, and it is very useful to apply targeted observations in this sensitive area, instead of other places, to obtain better La Ni?a forecasts.
Two types of optimal conditional initial errors in the tropical Indian Ocean that have the largest influences on La Ni?a predictions are explored in this study. Type-1 and Type-2 SPB-related initial errors, with positive and negative IOD-like structures respectively, are both very similar to the SPB-related initial errors in the tropical Indian Ocean of the El Ni?o predictions discovered by Zhou et al. (2019). Therefore, the Type-1 initial errors calculated from both the El Ni?o events and La Ni?a predictability studies are marked as “Type-1 initial error,” and same for Type-2 initial errors. A brief summary is presented in Table 2. For El Ni?o forecasts, both Type-1 and Type-2 initial errors tend to have negative prediction errors of sea temperature in the tropical Pacific Ocean; the ITF and the atmospheric bridge play leading roles in IO-related Type-1 and Type-2 initial errors influencing the SSTA associated with ENSO prediction, respectively. When it comes to the La Ni?a forecasts, both types of IO-related initial errors tend to result in positive errors of sea temperature in the tropical Pacific Ocean, and IO-related Type-1 and Type-2 initial errors incline to influence the ENSO predictions by virtue of the atmospheric bridge and the ITF, respectively.
| Prediction errors induced by the IO-related initial errors | Dynamic mechanism for Type-1 initial errors | Dynamic mechanism for Type-2 initial errors | |
| El Ni?o events | Negative initial errors | ITF | Atmospheric bridge |
| La Ni?a events | Positive initial errors | Atmospheric bridge | ITF |
Table2. A brief table of the influences of IO-related initial errors (both Type-1 and Type-2) on the SSTA predictions in the Pacific Ocean, and the possible main dynamical mechanisms behind them.
Even though these IO-related Type-1 and Type-2 initial errors for both El Ni?o and La Ni?a predictions have much in common, there are still some differences that cannot be neglected. For SPB-related Type-1 initial errors of El Ni?o, the positive errors dominate between 10°S and 10°N in the western Indian Ocean, while for Type-1 initial errors of La Ni?a, the positive errors only appear in the southern Western Indian Ocean. Ojha and Gnanaseelan (2015) suggest that a north-south dipole is the dominant mode in the subsurface. Unfortunately, the region for the initial errors in the tropical Indian Ocean is not big enough to include the whole southern pole in the subsurface in our study. More studies should be carried out if we want to figure out the similarity between the SPB-related Type-1 initial errors of La Ni?a and the subsurface dipole.
For the IO-related initial errors that have the largest influence on El Ni?o predictions with start month Jan(0), all the predictions tend to underestimate the magnitude of the La Ni?a events. This is also the case for most of the sensitivity experiments carried out during the study of La Ni?a predictions, with one exception represented by the purple line in Fig. 2b. Why is this initial error so special? Is it just a random case? Or may it have any implications? Two types of SPB-related initial errors are revealed in the tropical Indian Ocean, and the roles of both the ITF and the atmospheric bridge are analyzed. Are they independent? Can their influences be quantified? These questions will need to be answered in the future with more carefully designed sensitivity experiments and analyses.
In this study on La Ni?a predictability, we only use the traditional Ni?o-3 index to represent La Ni?a events. However, ENSO events are diverse, including both EP-type and CP-type (Kao and Yu, 2009; Kug et al., 2009) events, and prediction barriers exist for them both (Ren et al., 2016; Tian et al., 2019). So, more studies should be carried out to explore the different influences of IO-related initial errors on the two different types of ENSO events.
It can be concluded that both positive and negative IOD-like initial errors have the largest influences on the predictions of ENSO events, leading to the SPB phenomena. Mu and Jiang (2011) pointed out that the optimally growing initial errors in the onset predictions of blocking events and the optimal precursors that trigger the onsets have a lot in common. And the optimal precursors and the conditional nonlinear optimal perturbation always share similar structures (Mu et al.,, 2014, 2017). So, what is the optimal precursor of ENSO events in the tropical Indian Ocean? Will the optimal precursor in the tropical Indian Ocean share similar structures with these SPB-related initial errors? What’s more, ensemble forecasts are one of the most useful ways to improve ENSO prediction skill, and a good ensemble forecast relies on good ensemble initial errors. So, could this kind of IO-related initial error that grows fastest be considered as one of the ensemble initial errors in order to improve the ensemble forecast skill? These questions can be explored in the future studies.
According to the large value area of these SPB-related initial errors, the sensitive area in the tropical Indian Ocean for La Ni?a forecasts is revealed. And adopting targeted observation strategies in this sensitive area can significantly decrease the prediction errors of La Ni?a forecasts. Zhou et al. (2020) have also identified the sensitive area in the Indian Ocean for El Ni?o forecasts. It can be noticed that, both kinds of sensitive areas mainly reside in the equatorial eastern Indian Ocean. So, whether this region can be treated as the common sensitive area for ENSO predictions is also one of our concerns. What’s more, due to the large computational cost, sensitivity experiments of the targeted observations are only carried out with the SPB-related cases. Since most cases are not SPB-type, whether the sensitive area still works is another interesting question. So further studies should be carried out to answer these questions. Also because of the huge computational cost, only sensitivity experiments starting from Jan(0) are completed. More sensitivity experiments starting from other start months, such as Apr(0), Jul(0), and so on, should be completed to explore the influences of IO-related initial errors on SSTA forecasts during La Ni?a predictions bestriding its decaying phase.
The National Marine Environmental Forecast Center has an operational global SST forecast model, which also shows good performance for ENSO prediction (Zhang et al., 2018, 2019). Though the conclusions from this paper are all based on the “perfect model” assumption, it is still of our interests to apply them to operational forecasts to see how it works in real time. What are the influences of the initial errors of sea temperature in the tropical Indian Ocean on real La Ni?a predictions? Will the sensitive area identified in this study remain effective in operational forecast models? ENSO prediction skill can be further improved once these questions are answered with sensitivity experiments carried out with the operational forecast model.
In this study, we simply assume the model is perfect, so no model errors are considered. However, due to an overly strong Bjerknes feedback simulated in the equatorial Indian Ocean, most Coupled Model Intercomparison Project Phase Three (CMIP3) and CMIP5 models (including the CESM we used in this study) have IOD bias (Cai and Cowan, 2013). Moreover, like many other coupled models, the CESM also has an overly strong variability of sea surface temperature in the eastern Indian Ocean because of its exaggerated sensitivity to thermocline variations (Wieners et al., 2019). Our conclusions may be model-dependent since we only use the CESM, which is also flawed, to complete the sensitivity experiments. If we can reduce the model errors in ENSO predictions following the strategy of Tao et al. (2020) (i.e., using the Nonlinear Forcing Singular Vector (NFSV) approach), ENSO prediction skill may be further improved.
Acknowledgements. This study was supported by the National Key R&D Program of China (Grant No. 2019YFC1408004), together with the National Natural Science Foundation of China (Grant Nos. 41930971, 41805069, 41606031) and the Office of China Postdoctoral Council (OCPC) under Award Number 20190003
