魏志强, 吴英毅, 国金宇
中国科学院大学数学科学学院, 北京 100049
2015年11月07日 收稿; 2016年01月07日 收修改稿
基金项目: 国家自然科学基金（11471308）资助
通信作者: 魏志强 ?E-mail:wei1988321@163.com

摘要: HCMU度量是紧黎曼面上带奇点的extremal度量.研究它的存在性十分重要.通过研究Chen和Wu（Pacific J Math，2009，240（2）：267-288）给出的S²上HCMU度量存在的充分必要条件，证明当S²上至少有（N-1）个鞍点时，一定存在non-CSC HCMU度量，其中N是所有锥奇点的个数.
关键词: 极值度量紧黎曼面HCMU度量锥奇点
Existence of a class HCMU metric on S²
WEI Zhiqiang, WU Yingyi, GUO Jinyu
School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China


Abstract: HCMU metric is an extremal K?hler metric with singularities on a compact Riemann surface. It is important to study the existence of HCMU metrics. Through studying the sufficient and necessary condition of Chen and Wu(Pacific J Math, 2009, 240(2):267-288) for the existence of HCMU metrics on S², we show that there must exist a non-CSC HCMU metric on S² which has N conical singularities and at least (N-1) saddle points.
Key words: extremal metriccompact Riemann surfaceHCMU metricconical singularity
一般意义上的extremal K?hler度量最早由Calabi^[1]提出, 目的是在一个紧K?hler流形的固定K?hler类中找到“最好”的度量.具体地, 设M为一个紧K?hler流形, 在一个固定的K?hler类中, extremal K?hler度量是下述Calabi能量的临界点

$\mathscr{C}\left( g \right) = \int_M {{R^2}{\rm{d}}g, } $

这里R是K?hler类中度量g的数量曲率. $\mathscr{C}\left( g \right)$(g)的Euler-Lagrange方程是

${{R}_{, \alpha \beta }}\text{=}0, 1\le \alpha, \beta \le di{{m}_{\mathbb{C}}}M, $

(1)

这里R_{, αβ}是R的2阶(0, 2)型协变导数.因此称在一个紧K?hler流形M上满足(1)的度量为extremal K?hler度量.当M是紧Riemann面时, Calabi^[1]证明extremal K?hler度量就是常曲率(CSC)度量.自然地, 问题是如果在紧Riemann面上extremal K?hler度量有奇点, 是不是仍然是常曲率度量？答案是否定的.在紧Riemann面上带奇点的extremal K?hler度量通常被称为HCMU(the Hessian of the Curvature of the Metric is Umbilical)度量. Chen^[2]给出只带cusp奇点的HCMU度量的分类, 其中在球面上确实存在非常曲率的HCMU度量.下文简称非常曲率的HCMU度量为non-CSC HCMU度量.之后, Chen^[3]研究带锥奇点的non-CSC HCMU度量, 并给出一个这种HCMU度量存在的障碍性定理.Chen等^[4]给出带锥奇点的non-CSC HCMU度量都是由一些结构简单的带锥奇点的non-CSC HCMU度量拼起来的，这种结构最简单的带锥奇点的non-CSC HCMU度量称为football.还给出任意2个football能拼在一起的充要条件.Lin和Zhu^[5]用ODE的方法在S²上构造一类称为exceptional HCMU度量, 这类度量锥奇点的锥角度都是2nπ的形式, 其中n是正整数, 并且这些锥奇点都是高斯曲率K的鞍点. Chen和Wu^[6]推广了文献[5]中的结论, 给出S²上non-CSC HCMU度量的具体构造.
本文将利用上述这些结果研究这样一个问题:设p₁, …, p_N是S²给定的N个锥点, 对应的锥角度分别为2πα₁, …, 2πα_N, 其中α_k>0(k=1, …, N)且不为1.设α₁, …, α_N中有I个整数, 当N-I满足什么条件时, S²上一定存在non-CSC HCMU度量.
1 预备知识1.1 HCMU度量, 锥奇点和cusp奇点设M是一个紧致无边的Riemann面, p₁, …, p_N是M上的N个点.设g是M\P上的光滑保角度量, 其中P={p₁, …, p_N}.如果g满足

${\Delta _g}K + {K^2} = C, $

(2)

其中K为g的Gauss曲率, C为实常数, 则称g为M上的extremal Hermitian度量.式(2)在局部复坐标系(U, z)下等价于

$\frac{{\partial {K_{, zz}}}}{{\partial \;\bar z}} = 0, $

(3)

见文献[3].如果g在局部复坐标系下满足

${K_{, zz}} = 0, $

(4)

则称g为HCMU(the Hessian of the curvature of the metric is umbilical)度量.明显HCMU度量一定是extremal Hermitian度量, 并且HCMU度量就是extremal K?hler度量在M\P上的直接推广.在下文中, 我们一直假设extremal Hermitian度量和HCMU度量有有限的面积和有限的Calabi能量, 即

$\int_{M\backslash P} {{\rm{d}}g < + \infty, \int_{M\backslash P} {{K^2}{\rm{d}}g < + \infty .} } $

(5)

下面介绍锥奇点和cusp奇点的定义.
定义1.1 ??设M是Riemann面, p∈M.又设(U, z)为p附近的复坐标系且z(p)=0，g为U\{p}上的光滑度量.如果$g = {{\rm{e}}^{2\varphi }}{\left| {\;{\rm{d}}z\;} \right|^2}$, 并且φ-(α-1)ln|z|(α>0)在p处连续, 称p为g的锥奇点并且g在p处有锥角度2πα.
定义1.2 ??设M是Riemann面，p∈M.又设(U, z)为p附近的复坐标系且z(p)=0, g为U\{p}上的光滑度量.如果$g = {{\rm{e}}^{2\varphi }}{\left| {\;{\rm{d}}z\;} \right|^2}$, 并且${\lim _{z \to 0}}\frac{{\varphi + \ln \left| z \right|}}{{\ln \left| z \right|}} = 0$, 称p为g的cusp奇点.
当HCMU度量满足(5), 则它的奇点或者是锥奇点或者是cusp奇点^[7-8].
1.2 带锥奇点的non-CSC HCMU度量的基本性质, football分解与粘合设M是一个紧致无边的Riemann面, p₁, …, p_N是M上的N个点, 记P:={p₁, …, p_N}.设g是M\P上的光滑保角度量.设(U, z)为M\P上的局部复坐标系, 则g在U上可以写成

$g = {e^{2\varphi }}{\left| {{\rm{d}}z} \right|^2}, $

于是M\P上的高斯曲率为K=-e^-2φΔφ, 这里$\Delta = 4\frac{{{\partial ^2}}}{{\partial z\partial \bar z}}$.如果g是M\P上的HCMU度量, 即式(4)成立, 这等价于

$\nabla K = \sqrt {-1} {{\rm{e}}^{-2\varphi }}{K_{\overline z }}\frac{\partial }{{\partial z}}$

为M\P上的全纯向量场, 这也等价于

$V = \frac{1}{2}\left( {\sqrt {-1} {{\rm{e}}^{-2\varphi }}{K_{\overline z }}\frac{\partial }{{\partial z}}-\sqrt { - 1} {{\rm{e}}^{ - 2\varphi }}{K_z}\frac{\partial }{{\partial \;\bar z}}} \right)$

为M\P上的Killing向量场.进一步, 如果g是non-CSC HCMU度量, $\nabla K$和V都是非平凡的.
现在假设g为non-CSC HCMU度量, p₁, …, p_N为g的锥奇点, 并且g在这些锥奇点的锥角度分别为2πα₁, …, 2πα_N, 这里α₁, …, α_N都为正实数并且都不为1, 因为Lin和Zhu^[5]证明如果HCMU度量在某点处的锥角度为2π, 则度量在该点处是光滑的, 即该点实际上不是度量的奇点. Chen^[3]通过研究V以及V的积分曲线得到下列重要结论:
命题1.1^[3]??Gauss曲率可以连续地延拓到整个M上.
命题1.2^[3]?? V的奇点个数有限, 并且V的奇点集一定是K的鞍点集和K的局部极值点集的并集, 这里K的鞍点是指存在2条以上V的积分曲线在该点相交.
命题1.3^[3]??K的鞍点必为g的锥奇点, 并且K的鞍点锥角度为2πα形式, 这里α为整数, 进一步, V在K的鞍点处的旋转指标为α-1.
命题1.4^[3]?? g的锥奇点除了K的鞍点外, 都是K的局部极值点. K的光滑临界点都是局部极值点, 即K的局部极值点分成2类:一类是g除鞍点外的锥奇点, 另一类是K的全部光滑临界点. V在K的任何一个局部极值点处的旋转指标都是1.
综合命题1.2，1.3和1.4对V应用Poincaré-Hopf指标定理有
定理1.1^[3] ??设$\left\{ {{p_1}, \cdots, {p_I}} \right\} \subset \left\{ {{p_1}, \cdots, {p_N}} \right\}\left( {0 \le I \le N} \right)$为K的鞍点集, 则M的Euler示性数为

${\chi ^{\left( M \right)}} = \sum\limits_{i = 1}^I {\left( {1-{\alpha _i}} \right) + \left( {N-I} \right) + s, } $

(6)

其中，S表示K的光滑临界点的个数.
由定理1.1, 如果K没有鞍点, 即I=0, 则χ^(M)=N+S>0, 因此, M一定是为球面, 于是2=χ^(M)=N+S, 即K只有2个局部极值点分别在最大、最小值点处.这种HCMU度量实际上是旋转对称的, 称为football.如图 1所示.
Fig. 1

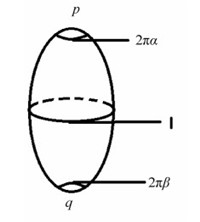	Download: JPG larger image
图 1 Football Fig. 1 Football

其中, p和q分别表示K的最大、最小值点, 且度量在这2点处的锥角度分别为2πα和2πβ, α>β>0:数字1表示纬线, 即V的积分曲线.具体地,

$g = {\rm{d}}{u^2} + {f^2}\left( u \right){\rm{d}}{\theta ^2}\;\;\left( {0 \le u \le l, 0 \le \theta \le 2{\rm{\pi }}} \right)$

这里f(u)满足基本性质:$f\left( 0 \right) = f\left( l \right) = 0;f'\left( 0 \right) = \alpha, f'\left( l \right) =-\beta ;f\left( u \right) > 0, u \in \left( {0, l} \right)$.为了方便, 记这样的football为S_{{α, β}}².此外, 在文献[3]中, Chen还给出利用football构造复杂一些non-CSC HCMU度量的方法.例如:取2个相同的football $S_{\{ \frac{1}{2}, \frac{1}{3}\} }^2$, 如图 2所示.
Fig. 2

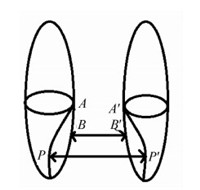	Download: JPG larger image
图 2 2个football粘合 Fig. 2 Gluing of two footballs

分别从K的最小值点沿经线剪开相同的距离, 然后分别将经线P和P′, Q和Q′粘在一起, 于是得到一个新的non-CSC HCMU度量, 这个HCMU度量有锥角度$2{\rm{\pi }}\frac{1}{2}, 2{\rm{\pi }}\frac{1}{2}, 4{\rm{\pi, 2\pi }}\frac{2}{3}, A\left( {A'} \right)$是K的鞍点, 锥角度为4π.
在文献[4]中, Chen等继续了Chen在文献[3]中的研究并得到下面一些结果.
命题1.5^[4]??带锥奇点的non-CSC HCMU度量, 任何K的局部极值点都是K的最大值点或者最小值点.如果记K₁和K₂分别为K的最大值和最小值, 则K₁>0, K₁>K₂>-(K₁+K₂).
定理1.2^[4]??带锥奇点的non-CSC HCMU度量都可以沿着有限多条从K的最大值点到K的最小值点的测地线(这些测地线与V垂直)将底流形剖分成有限多片, 而每一片都与某个football等距.
定理1.3^[4]?? 2个football $S_{\left\{ {{\alpha _1}, {\beta _1}} \right\}}^2$与$S_{\left\{ {{\alpha _1}, {\beta _1}} \right\}}^2$能沿着经线或者经线的一段粘起来的充要条件是

$\frac{{{\alpha _1}}}{{{\beta _1}}} = \frac{{{\alpha _2}}}{{{\beta _2}}}, \frac{{{\alpha _1}}}{{{\alpha _2}}} = \frac{{{A_1}}}{{{A_2}}}.$

这里A₁和A₂分别表示$S_{\left\{ {{\alpha _1}, {\beta _1}} \right\}}^2$与$S_{\left\{ {{\alpha _2}, {\beta _2}} \right\}}^2$的面积.
1.3 球面S²上non-CSC HCMU度量的存在与具体构造Lin和Zhu^[5]研究$\nabla K$并构造了S²上一类称为exceptional HCMU度量.即下面定理.
定理1.4^[5] ??设${p_1} = \infty, {p_2} = {z_2}, \cdots, {p_N} = {z_N}$是${{s}^{2}}=\mathbb{C}\cup \left\{ \infty \right\}$上N个点, 且α₁≥2, …, α_N≥2是N个整数, 设

$\alpha = {\alpha _1} + \sum\limits_{i = 2}^N {\left( {{\alpha _i}-1} \right)} .$

则$g = {{\rm{e}}^{2\varphi }}{\left| {{\rm{d}}z} \right|^2}$是S²上在p_i处的锥角度为2πα_i的exceptional HCMU度量的充要条件是存在一个正数k, 一个非零复数B, 和$\mathbb{C}$一个次数为(α+1)的多项式f(z), 满足f(z)有不同的零点γ_l，3k≤α+1, 和

$\sum\limits_{l = 1}^k {\frac{{-2a}}{{z-{\gamma _l}}}} + \sum\limits_{l' = k = 1}^{\alpha + 1} {\frac{2}{{z-{\gamma _{l'}}}}} = \frac{{B\prod\nolimits_{i = 2}^n {{{\left( {z - {z_i}} \right)}^{{\alpha _i} - 1}}} }}{{\prod \begin{array}{l}\alpha + 1\\l = 1\end{array} \left( {z - {\gamma _l}} \right)}}, $

其中a=(α+1-k)/k.更进一步, K和φ由下面方程确定

$\begin{array}{l}\frac{1}{{{{\left( {K + \frac{{\left( {a-2} \right)\beta }}{{2a-1}}} \right)}^a}}}\left( {\beta-K} \right){\left( {K + \frac{{\beta \left( {a + 1} \right)}}{{2a - 1}}} \right)^{a - 1}} = \\A\prod\limits_{l = 1}^k {{{\left| {z - {\gamma _l}} \right|}^{ - 2a}}\prod\limits_{l' = k + 1}^{\alpha + 1} {{{\left| {z - {\gamma _{l'}}} \right|}^2}, } } \end{array}$

和

$\varphi = \frac{1}{2}\ln \left[{\left( {\frac{1}{{{{\left| {F\left( z \right)} \right|}^2}}}} \right)\left( {-\frac{1}{3}{K^3} + cK + c'} \right)} \right], $

其中A>0是某一个常数, 且

$\begin{array}{*{20}{c}}{\beta = \sqrt c \left( {2a - 1} \right)/\sqrt {{a^2} - a + 1} ,}\\{\;c' = \frac{{\left( {a + 1} \right)\left( {a - 2} \right){\beta ^3}}}{{3{{\left( {2a - 1} \right)}^2}}},}\\{F\left( z \right) = {{\left( {z - {z_2}} \right)}^{ - \left( {{\alpha _2} - 1} \right)}} \cdots {{\left( {z - {z_N}} \right)}^{ - \left( {{\alpha _N} - 1} \right)}}f\left( z \right),}\\{\;\;f\left( z \right) = {B^{ - 1}}\frac{{ - 3a\left( {a - 1} \right){\beta ^2}}}{{{{\left( {2a - 1} \right)}^2}}}\prod\limits_{l = 1}^{\alpha + 1} {\left( {z - {\gamma _l}} \right).} }\end{array}$

在文献[6]中, Chen和Wu将上面定理推广到S²上non-exceptional度量的存在性与具体构造, 即下面定理:
定理1.5^[6] ??设${p_1} = \infty, {p_2} = {z_2}, \cdots, {p_N} = {z_N}$是${{s}^{2}}=\mathbb{C}\cup \left\{ \infty \right\}$上N个点，设α₁, …, α_N≥N是N个正实数, 且α₁≥2, …, α_j≥2是j个整数, 则
· S²存在一个HCMU度量使得p₁, p₂, …, p_N是锥奇点, 锥角度分别为2πα₁, …, 2πα_N且
· p₁, p₂, …, p_j是K的所有鞍点.
等价于
· $S=2+\sum\limits_{{{i}'}}^{j}{{{\alpha }_{{{i}'}}}-N\ge 0}$, 且
·存在j+1, …, N的置换δ, 整数l满足0≤l≤N-j, 整数t满足0≤t≤S和$\left\{ {{\beta }_{1}}, \cdots, {{\beta }_{S}} \right\}\subset \mathbb{C}\backslash \left\{ {{z}_{2}}, \cdots {{, }_{{{z}_{N}}}} \right\}$使得

$\begin{array}{c}{\alpha _{\delta \left( 1 \right)}} + {\alpha _{\delta \left( 2 \right)}} + \cdots + {\alpha _{\delta \left( l \right)}} + t > {\alpha _{\delta \left( {l + 1} \right)}} + \\\; \cdots + {\alpha _{\delta \left( {N-j} \right)}} + S-t, \end{array}$

和

$\begin{array}{*{20}{c}}{\sum\limits_{k = 1}^l {\frac{{{\alpha _{\delta \left( k \right)}}}}{{z - {z_{\delta \left( k \right)}}}} + \sum\limits_{k' = l + 1}^{N - j} {\frac{{\left( {a - 1} \right){\alpha _{\delta \left( {k'} \right)}}}}{{z - {z_{\delta \left( {k'} \right)}}}} + } } }\\{\;\;\sum\limits_{m = 1}^t {\frac{1}{{z - {\beta _m}}}} + \sum\limits_{m' = t + 1}^s {\frac{{a - 1}}{{z - {\beta _{m'}}}}} }\\{ = \frac{{B\prod\nolimits_{i'}^j {{{\left( {z - {z_{i'}}} \right)}^{{\alpha _{i'}} - 1}}} }}{{\prod\nolimits_{k = j + 1}^N {\left( {z - {z_k}} \right)\prod\nolimits_{m = 1}^s {\left( {z - {\beta _m}} \right)} } }},}\end{array}$

其中B≠0，$a-1 =-\frac{{{\alpha _{\max }}}}{{{\alpha _{\min }}}}$.这里

$\begin{array}{c}{\alpha _{\max }} = {\alpha _{\delta \left( 1 \right)}} + {\alpha _{\delta \left( 2 \right)}} + \cdots + {\alpha _{\delta \left( l \right)}} + t, \\{\alpha _{\min }} = {\alpha _{\delta \left( {l + 1} \right)}} + \cdots + {\alpha _{\delta \left( {N-j} \right)}} + S-t.\end{array}$

2 主要结论与证明现在返回到我们要研究的问题, 即当S²上给定了N个锥奇点和N个锥角度时, 锥角度满足什么样的条件时一定存在non-CSC HCMU度量.我们的结论是当锥奇点个数与K的鞍点个数相差不超过1时一定存在, 即下面定理.
定理2.1 ??设${p_1} = \infty, {p_2} = {z_2}, \cdots, {p_N} = {z_N} = 0$是${{s}^{2}}=\mathbb{C}\cup \left\{ \infty \right\}$上任意N≥3个不同的点, α₁, …, α_N是N个不为1的正实数, 若α₁, …, α_N-1是整数.则S²\{p₁, …, p_N}上一定存在non-CSC HCMU度量g, 使得p₁, …, p_N是g的锥奇点, 锥角度分别是2π α₁, …, 2πα_N且p₁, …, p_N-1是g的高斯曲率K的鞍点.
证明 ??因为α₁, …, α_I为整数, 其中I=N-1.由障碍定理知若满足条件的non-CSC HCMU度量存在, 则一定存在鞍点.现在我们证明S²上一定存在以p₁, …, p_I为鞍点的non-CSC HCMU度量.由障碍定理, 有

$2 = \sum\limits_{i = 1}^I {\left( {1-{\alpha _i}} \right) + \left( {N-I} \right) + s, } $

其中S为光滑极值点的个数.由于I=N-1, 所以

$S = \sum\limits_{i = 1}^I {\left( {{\alpha _i}-1} \right) + 1 \ge 3.} $

首先给出几个引理
引理2.1 ??若存在ω₁, …, ω_S-1, B使得方程

$\begin{array}{*{20}{c}}{\frac{{{\alpha _N}}}{{z - {z_N}}} + \frac{\lambda }{{z - \beta }} + \sum\limits_{m = 1}^{S - 1} {\frac{1}{{z - {\omega _m}}}} }\\{ = \frac{{B\prod\nolimits_{i = 2}^I {{{\left( {z - {z_i}} \right)}^{{\alpha _i} - 1}}} }}{{\left( {z - {z_N}} \right)\left( {z - \beta } \right)\prod\nolimits_{m = 1}^{S - 1} {\left( {z - {\omega _m}} \right)} }},}\end{array}$

(7)

成立, 其中z₂, …, z_N, β是提前给定的互不相等的复数, α₁, …, α_N是N个不为1的正实数, 且α₁, …, α_N-1是整数, I=N-1, $S = \sum\limits_{i = 1}^I {\left( {{\alpha _i}- 1} \right) + 1, \lambda =- \left[{\sum\limits_{i = 1}^I {\left( {{\alpha _i}-1} \right) + {\alpha _N}} } \right]} $.则B≠0, ω_m≠β, m=1, …, S-1且
1)若对任意m，ω_m≠z_i，i=2, …, I, 则ω_m≠z_N, m=1, …, S-1, 且ω₁, …, ω_S-1互不相等.
2)若存在m₀, i₀, 使得ω_m0=z_i0, 则ω₁, …, ω_S-1中有且只有α_i0个等于z_i0.
证明 ??若B=0，则(7)右边为零, 对左边求在点z_N的系数应该有α_N+l₀=0, 其中l₀是ω₁, …, ω_S-1中等于z_N的个数.这是不可能的.从而B≠0.
若存在m₀, 使得ω_m0=β, 代入(7)并通分可知左边分母的次数比右边分母的次数低, 这是不可能的.因此结论成立.
1)若ω₁, …, ω_S-1中存在l₁>0个与z_N相等, 不妨设ω₁, …, ω_l1=z_N.代入(7)并通分可知左边分母的次数低于右边分母的次数, 因此这是不可能的.类似的可证ω₁, …, ω_S-1互不相等.
2)若存在m₀, j₀, 使得ω_m0=z_j0, 不妨设若存在ω₁=z₂, 则ω₁, …, ω_S-1中有且只有α₂个等于z₂.因为若ω₁, …, ω_S-1中等于z₂的个数大于α₂，代入(7)通分知左边分母的次数低于右边分母的次数.若ω₁, …, ω_S-1中等于z₂的个数小于α₂, 代入(7)可知左边关于z₂的留数为零, 这是不可能的.因此结论成立.
引理2.2 ??对$\mathbb{C}$上给定的互不相同复数z₂, …, z_N=0和正实数α₁, …, α_N, 其中α₁, …, α_I(I=N-1)是不为1的整数, 一定存在$\beta \in \backslash \left\{ {{z_2}, \cdots, {z_N}} \right\}$和ω₁, …, ω_S-1以及B满足(7).
证明 ??令

$\begin{array}{c}\frac{{{\alpha _N}}}{{z-{z_N}}} + \frac{\lambda }{{z-\beta }} + \sum\limits_{m = 1}^{S-1} {\frac{1}{{z - {\omega _m}}}} \\ = \frac{{\sum\nolimits_{k = 1}^S {{b_k}{z^{S - k}}} }}{{\left( {z - {z_N}} \right)\left( {z - \beta } \right)\prod\nolimits_{m = 1}^{S - 1} {\left( {z - {\omega _m}} \right)} }}, \end{array}$

(8)

则

$\begin{array}{c}{b_1} =- \left[{{\alpha _N}\beta + \lambda {z_N} + \left( {{z_N} + \beta } \right)\left( {S-1} \right)-{\sigma _1}} \right], \\{b_2} = \left[{{\alpha _N}\beta + \lambda {z_N} + \left( {{z_N} + \beta } \right)\left( {S-2} \right){\sigma _1}-2{\sigma _2}} \right], \\3 \le k \le S - 1, {b_k} = {\left( { - 1} \right)^k}\left\{ {\left[{{\alpha _N}\beta + \lambda {z_N} + } \right.} \right.\\\;\;\;\;\;\;\;\left. {\;\left( {{z_N} + \beta } \right)\left( {S-k} \right)} \right]{\sigma _{k -1}} + \\\;\;\;\;\;\left. {{z_N}\beta \left( {S -k + 1} \right){\sigma _{k -2}} - k{\sigma _k}} \right\}\\\left. {{b_s} = {{\left( { - 1} \right)}^S}{\alpha _N}\beta {\sigma _{S - 1}} + \lambda {z_N}{\sigma _{S - 1}} + {z_N}\beta {\sigma _{S - 1}}} \right].\end{array}$

其中$\sum {_{1 \le {i_1} < \cdots < {i_j} \le S-1}\left( {{\omega _{{i_1}}} \cdots {\omega _{{i_j}}}} \right) = {\sigma _j}} $.
由于z_N=0, 若令σ₀=1, σ_S=0.则

$\begin{array}{l}{b_k} = {\left( {- 1} \right)^k}\left[{\left( {{\alpha _N} + S-k} \right)\beta {\sigma _{k-1}}-} \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {k{\sigma _k}} \right], k = 1, \cdots, S.\end{array}$

(9)

又

$\begin{array}{*{20}{l}}{\prod\limits_{i = 2}^I {{{\left( {z - {z_i}} \right)}^{{\alpha _i} - 1}} = } }\\{\prod\limits_{i = 2}^I {\left[ {\sum\limits_{j = 0}^{{\alpha _i} - 1} {{{\left( { - 1} \right)}^{{\alpha _i} - 1 - j}}z_j^{{\alpha _i} - 1 - j}C_{{\alpha _i} - 1}^j{z^j}} } \right]} }\\{ = \sum\limits_{l = 0}^{\alpha - {\alpha _1}} {\left[ {{{\left( { - 1} \right)}^{\alpha - {\alpha _1} - l}}\sum\limits_{l = {j_2} + \cdots + {j_I}} {\left( {z_2^{{\alpha _2} - 1 - {j_2}}C_{{\alpha _2} - 1}^{{j_2}} \cdots z_I^{{\alpha _I} - 1 - {j_I}} \cdot } \right.} } \right.} }\\{\left. {\left. {C_{{\alpha _I} - 1}^{{j_I}}} \right)} \right]{z^l} = \sum\limits_{l = 0}^{\alpha - {\alpha _1}} {{d_l}{z^l}.} }\end{array}$

其中

$\begin{array}{l}{d_l} = {\left( {-1} \right)^{\alpha-{\alpha _1}-l}}\\\sum\limits_{l = {j_2} + \cdots + {j_I}} {\left( {z_2^{{\alpha _2} - 1 - {j_2}}C_{{\alpha _2} - 1}^{{j_2}} \cdots z_I^{{\alpha _I} - 1 - {j_I}}C_{{\alpha _I} - 1}^{{j_I}}} \right), } \\\alpha = {\alpha _1} + \sum\limits_{i = 2}^I {\left( {{\alpha _i} - 1} \right) = S.} \end{array}$

则

$B\sum\limits_{l = 0}^{\alpha-{\alpha _1}} {{d_l}{z^l} = \sum\limits_{k = 1}^S {{b_k}{z^{S-k}}.} } $

即

$B\sum\limits_{l = 0}^{S-{\alpha _1}} {{d_l}{z^l} = \sum\limits_{k = 1}^{{\alpha _1}-1} {{b_k}{z^{S-k}} + \sum\limits_{k = {\alpha _1}}^S {{b_k}{z^{S - k}}.} } } $

所以

${b_k} = \left\{ \begin{array}{l}0, k = 1, \cdots, {\alpha _1}-1.\\B\;{d_{S-k}}, k = {\alpha _1}, \cdots, S.\end{array} \right.$

(10)

由(9)和(10)得

$k{\sigma _k} = \left\{ \begin{array}{l}\left( {{\alpha _N} + S-k} \right)\beta {\sigma _{k-1}}, k = 1, \cdots, {\alpha _1}-1.\\{\left( { - 1} \right)^{k + 1}}B{d_{S - k}} + \left( {{\alpha _N} + S - k} \right)\beta {\sigma _{k - 1}}, \\k = {\alpha _1}, \cdots, S.\end{array} \right.$

所以

$\begin{array}{l}{\sigma _k} = \\\left\{ \begin{array}{l}C_{{\alpha _N} + S - 1}^k{\beta ^k},k = 1, \cdots ,{\alpha _1} - 1.\\C_{{\alpha _N} + S - 1}^k{\beta ^k} - B{\left( { - 1} \right)^k}\frac{{{d_{S - k}}}}{k}\\- B\sum\limits_{l = {\alpha _1}}^{k - 1} {{{\left( { - 1} \right)}^l}{d_{S - l}}{\beta ^{k - l}}} \\\frac{{\left( {{\alpha _N} + S - k} \right)\left( {{\alpha _N} + S - k + 1} \right) \cdots \left( {{\alpha _N} + s - l - 1} \right)}}{{l\left( {l + 1} \right) \cdots k}},\\k = {\alpha _1}, \cdots ,S.\end{array} \right.\end{array}$

(11)

因此由σ_S=0, 而β≠0, 所以β必须满足

$\begin{array}{l}{\left( {-1} \right)^s}\frac{{{d_0}}}{S} + \sum\limits_{l = {\alpha _1}}^{S-1} {{{\left( {-1} \right)}^l}{d_{S - l}}{\beta ^{S - l}}} \\\frac{{\left( {{\alpha _N}} \right)\left( {{\alpha _N} + 1} \right) \cdots \left( {{\alpha _N} + S - l - 1} \right)}}{{l\left( {l + 1} \right) \cdots S}} \ne 0.\end{array}$

(12)

由于式(12)左边是关于β的多项式, 次数不超过S-α₁.从而左边多项式的根个数有限, 因此一定存在$\beta \in \mathbb{C}\backslash \left\{ {{z}_{2}}, \cdots, {{z}_{N}} \right\}$和非零B, 使得σ_S=0.再由式(11), 所以存在ω₁, …, ω_S-1使得式(7)成立.
引理2.3 ??对$\mathbb{C}$上给定的互不相同复数z₂, …, z_N=0和不为1的正实数α₁, …, α_N, 其中α₁, …, α_I(I=N-1)是整数, 一定存在$\beta \in \mathbb{C}\backslash \left\{ {{z}_{2}}, \cdots, {{z}_{N}} \right\}$使得方程(7)有解B, ω₁, …, a_S-1满足ω₁, …, ω_S-1与z₂, …, z_I不相等.
证明 ??首先证明对不同的β₁, β₂使得对应的B, ω₁, …, ω_S-1和$\widetilde B, {\widetilde \omega _1}, \cdots, {\widetilde \omega _{S-1}}$满足$\left\{ {B, {\omega _1}, \cdots, } \right.\left. {{\omega _{S-1}}} \right\} \cap \left\{ {\widetilde B, {{\widetilde \omega }_1}, \cdots, {{\widetilde \omega }_{S-1}}} \right\} = \emptyset $, 因为

$\begin{array}{l}\frac{{{\alpha _N}}}{{z-{z_N}}} + \frac{\lambda }{{z-{\beta _1}}} + \sum\limits_{m = 1}^{S-1} {\frac{1}{{z - {\omega _m}}}} \\ = \frac{{B\prod\nolimits_{i = 2}^I {{{\left( {z - {z_i}} \right)}^{{\alpha _i} - 1}}} }}{{\left( {z - {z_N}} \right)\left( {z - {\beta _1}} \right)\prod\nolimits_{m = 1}^{S - 1} {\left( {z - {\omega _m}} \right)} }}, \\\frac{{{\alpha _N}}}{{z - {z_N}}} + \frac{\lambda }{{z - {\beta _2}}} + \sum\limits_{m = 1}^{S - 1} {\frac{1}{{z - {{\widetilde \omega }_m}}}} \\ = \frac{{\widetilde B\prod\nolimits_{i = 2}^I {{{\left( {z - {z_i}} \right)}^{{\alpha _i} - 1}}} }}{{\left( {z - {z_N}} \right)\left( {z - {\beta _2}} \right)\prod\nolimits_{m = 1}^{S - 1} {\left( {z - {{\widetilde \omega }_m}} \right)} }}, \end{array}$

相减得

$\begin{array}{l}\frac{\lambda }{{z-{\beta _1}}}-\frac{\lambda }{{z-{\beta _2}}} + \sum\limits_{m = 1}^{S - 1} {\frac{1}{{z - {\omega _m}}} - \sum\limits_{m = 1}^{S - 1} {\frac{1}{{z - {{\widetilde \omega }_m}}}} } \\ = \frac{{B\prod\nolimits_{i = 2}^I {{{\left( {z - {z_i}} \right)}^{{\alpha _i} - 1}}} }}{{\left( {z - {z_N}} \right)\left( {z - {\beta _1}} \right)\prod\nolimits_{m = 1}^{S - 1} {\left( {z - {\omega _m}} \right)} }} - \\\frac{{\widetilde B\prod\nolimits_{i = 2}^I {{{\left( {z - {z_i}} \right)}^{{\alpha _i} - 1}}} }}{{\left( {z - {z_N}} \right)\left( {z - {\beta _1}} \right)\prod\nolimits_{m = 1}^{S - 1} {\left( {z - {{\widetilde \omega }_m}} \right)} }}, \end{array}$

由于上式左边关于z在点z_N是解析的, 而右边z_N是一个极点, 矛盾.这就是说方程(7)的解是由参数β唯一决定.
现证明引理2.3, 由于z₂, …, z_I是有限个点, 若某一个ω_m0=z_j0, 若这样参数β存在则只能唯一.因此使得参数β对应的ω₁, …, ω_S-1与z₂, …, z_I中某些项是相等的只能是有限多.而参数β取值范围是无限的, 从而结论成立.
设${{S}^{2}}=\mathbb{C}\cup \left\{ \infty \right\}, {{P}_{1}}=\infty, {{P}_{i}}={{z}_{i}}, i=2, \cdots, N\cdot \beta \in \mathbb{C}\backslash \left\{ {{z}_{2}}, \cdots, {{z}_{N}} \right\}$是任意给定的一点.由文献[7]中定理2.5, 存在以p₁, …, p_I为鞍点, 以p_N为最大值点, 以β为最小值点的non-CSC HCMU度量的充分条件是
1) α_i≥2, i=1, …, I且为整数.由假设知这已经满足.
2) $\exists T, 0\le T\le S$，使得α_N+T>S-T.这里取T=S-1, 其中$S=\sum\nolimits_{i=1}^{I}{\left( {{\alpha }_{i}}-1 \right)+1}$.故也满足.
3)存在$\left\{ {{\omega }_{1}}, \cdots, {{\omega }_{S-1}} \right\}\subset \mathbb{C}\backslash \left\{ \beta, {{z}_{2}}, \cdots, {{z}_{N}} \right\}$, 使得下面式子成立:

$\begin{align} & \frac{{{\alpha }_{N}}}{z-{{z}_{N}}}+\frac{\lambda }{z-\beta }+\sum\limits_{m=1}^{S-1}{\frac{1}{z-{{\omega }_{m}}}} \\ & =\frac{B\prod\nolimits_{i=2}^{I}{{{\left( z-{{z}_{i}} \right)}^{{{\alpha }_{i}}-1}}}}{\left( z-{{z}_{N}} \right)\left( z-\beta \right)\prod\nolimits_{m=1}^{S-1}{\left( z-{{\omega }_{m}} \right)}}, \\ \end{align}$

(13)

其中$\lambda =-\frac{{{\alpha }_{\max }}}{{{\alpha }_{\min }}}=-\left[\Sigma _{i=1}^{I}\left( {{\alpha }_{i}}-1 \right)+{{\alpha }_{N}} \right]$.
综合引理2.1, 2.2和2.3，定理2.1得证.
推论2.1 ??设p₁, p₂, …, p_N是S²上任意N≥3个不同的点, α₁, …, α_N是N个不为1的正实数, 若α₁, …, α_N中有N-1整数, 不妨设α₁, …, α_N-1是整数.则S²\{p₁, …, p_N}上一定存在non-CSC HCMU度量g, 使得p₁, …, p_N是g的锥奇点, 锥角度分别是2πα₁, …, 2πα_N且p₁, …, p_N-1是g的高斯曲率K的鞍点.
证明 ??因为S²上的任意3点都可以经过M?bius变换变成$\infty $, 1, 0, 这里只要把p₁, p_N变成$\infty $, 0即可.
注：由引理2.2知存在$\beta \in \mathbb{C}\backslash \left\{ {{z}_{2}}, \cdots, {{z}_{N}} \right\}$和ω₁, …, ω_S-1满足式(7), 但由引理2.1, 此时ω₁, …, ω_S-1中的某些项可能与给定的z₂, …, z_I中某些是相等的.事实上由定理2.5可知这个时候仍然存在non-CSC HCMU度量, 但p₁, …, p_N-1不全是高斯曲率的鞍点.因为若ω₁, …, ω_S-1中存在与z₂, …, z_I中的某些项相等, 不妨设z₂, …，z_k, 则ω₁, …, ω_S-1中有且只能有α₂, …, α_k个分别与z₂, …z_k相等.代入式(13)可得

$\begin{align} & \sum\limits_{i=2}^{k\ \ }{\frac{{{\alpha }_{i}}}{z-{{z}_{i}}}+\frac{{{\alpha }_{N}}}{z-{{z}_{N}}}+\frac{{{\lambda }'}}{z-\beta }+\sum\limits_{m=1}^{{S}'-1}{\frac{1}{z-{{{{\omega }'}}_{m}}}=}} \\ & \frac{B\prod\nolimits_{i=k+1}^{I}{{{\left( z-{{z}_{i}} \right)}^{{{\alpha }_{i}}-1}}}}{\left( z-{{z}_{N}} \right)\left( z-\beta \right)\prod\nolimits_{i=2}^{k}{\left( z-{{z}_{i}} \right)\prod\nolimits_{m=1}^{{S}'-1}{\left( z-{{{{\omega }'}}_{m}} \right)}}}, \\ \end{align}$

(14)

其中${\lambda }'=\lambda, {S}'=S-\sum\nolimits_{i=2}^{k}{{{\alpha }_{i}}, {{{{\omega }'}}_{m}}, m=1, \cdots, {S}'}$表示ω₁, …, ω_S-1中不与z_i, i=2, …, N中相等的项.式(14)说明若存在ω₁, …, ω_S-1满足式(13), 但是ω₁, …, ω_S-1中某些项与z_i, i=2, …, N中某些项相等的话, 我们同样可以得到non-CSC HCMU度量.
3 后续的讨论由定理2.1的证明过程我们发现只要给定的整数越多, S²上存在non-CSC HCMU度量的可能性越大.事实上当给定的鞍点与所有锥奇点的个数相差大于等于3时, 就不一定存在non-CSC HCMU度量, 文献[7]中给出不存在non-CSC HCMU度量的例子, 这个例子是锥点个数与鞍点个数的差为3, 因此我们后续将研究鞍点与锥点相差2的时候是否可以得到类似的结论.
参考文献

[1]	Calabi E. Extremal K?hler metrics[C]//Seminar on Differential Geometry, Ann of Math Stud 102. Princeton:Princeton Univ Press, 1982:259-290.
[2]	Chen X X. Extremal Hermitian metrics on Riemann surfaces[J].Calc Var, 1999, 8:191–232.DOI:10.1007/s005260050123
[3]	Chen X X. Obstruction to the existence of metric whose curvature has umbilical Hessian in a K-surface[J].Communications in Analysis and Geometry, 2000, 8(2):267–299.DOI:10.4310/CAG.2000.v8.n2.a2
[4]	Chen Q, Chen X X, Wu Y Y. The structure of HCMU metric in a K-surface[J].International Mathematics Research Notices, 2005, 16:941–958.
[5]	Lin C S, Zhu X H. Explicit construction of extremal Hermitian metric with finite conical singularities on S2[J].Communications in Analysis and Geometry, 2002, 10(1):177–216.DOI:10.4310/CAG.2002.v10.n1.a8
[6]	Chen Q, Wu Y Y. Existence and expilicit construction of HCMU metrics on S2 and T2[J].Pacific Journal of Mathematics, 2009, 240(2):267–288.DOI:10.2140/pjm
[7]	Chen X X. Weak limits of Riemannian metrics in surfaces with integral curvature bound[J].Calc Var, 1998, 6:189–226.DOI:10.1007/s005260050089
[8]	Wang G F, Zhu X H. Extremal Hermitian metrics on Riemann surfaces with singularities[J].Duke Math Journal, 2000, 104(2):181–210.DOI:10.1215/S0012-7094-00-10421-8