张亚坤, 唐国平
中国科学院大学数学科学学院, 北京 100049
摘要: G为阶数小于6的非平凡群，p为整除群G的阶数的素数，确定k≥2时K₂($\mathbb{Z}$G/p^k$\mathbb{Z}$G)的结构。
关键词: K₂-群Dennis-Stein符号群环
Let G be a finite abelian p-group, and Γ the maximal $\mathbb{Z}$-order of $\mathbb{Z}$G in $\mathbb{Q}$G. By Propo sition 2.2 in Ref.[1], Γ is the integral clo sure of $\mathbb{Z}$G in $\mathbb{Q}$G, and |G|Γ$\subseteq $$\mathbb{Z}$G$\subseteq $Γ. When 1 < |G| < 6, we find that calculation of K₂($\mathbb{Z}$G/p^k$\mathbb{Z}$G)(k≥2) is equivalent to calcula tion of K₂ of K₂($\mathbb{Z}$G) and K₂(Γ), which are listed in Table 1. A brief in troduction to the explicit structures of K₂($\mathbb{Z}$G) and K₂(Γ) can be found in Ref.[2].
Table 1

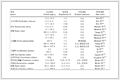Table 1 Structures of K2($\mathbb{Z}$G) and K2(Γ) G Γ K2($\mathbb{Z}$G) K2(Γ) C2 $\mathbb{Z}$2 (C2)2 (C2)2 C3 $\mathbb{Z}$⊕$\mathbb{Z}$[ζ3] C2 C2 C4 $\mathbb{Z}$2⊕$\mathbb{Z}$[i] (C2)2 (C2)2 C5 $\mathbb{Z}$⊕$\mathbb{Z}$[ζ5] C2 C2 (C2)2 $\mathbb{Z}$4 (C2)6 (C2)4

Table 1 Structures of K2($\mathbb{Z}$G) and K2(Γ)

For simplicity, for any positive integer k≥2, we define

$\mu \left(k \right)=\left\{ \begin{align} & {{\left({{C}_{2}} \right)}^{2}}, \ \ \ \ \ \ \ \ \ \ \ \ k=2, \\ & {{\left({{C}_{2}} \right)}^{2}}\oplus {{C}_{4}}, \ \ \ \ \ k\ge 3. \\ \end{align} \right.$

We summarize our results in Table 2.
Table 2

Table 2 Main results (k≥2) G K2($\mathbb{Z}$G/pkΓ) K2($\mathbb{Z}$G/pk$\mathbb{Z}$G) C2 (C2)2 (C2)2 C3 C3 C3 C4 μ(k) μ(k) C5 C5 C5 (C2)2 * (C2)6

Table 2 Main results (k≥2)

1 PreliminariesLemma 1.1??Let $\mathscr{O}$ be a totally imaginary Dedekind domain of arithmetic type with field of function $\mathbb{F}$. Let p^s=|μ_p($\mathbb{F}$)|, where μ_p($\mathbb{F}$) is the p-th power roots unity in the field $\mathbb{F}$. Then for any integer m > 1, SK₁($\mathscr{O}$, m$\mathscr{O}$) is a cyclic subgroup of μ($\mathbb{F}$) of order l, where

$\text{or}{{\text{d}}_{p}}\left( l \right)={{\left[ \text{or}{{\text{d}}_{p}}\left( m \right)-\frac{1}{p-1} \right]}_{\left[ 0, s \right]}}, $

i.e., ord_p(l) is in the interval [0, s], and is the greatest integer≤$\left( \text{or}{{\text{d}}_{p}}\left( m \right)-\frac{1}{p-1} \right)$.
Proof??This follows directly form Corollary 4.3 in Ref.[3].
Lemma 1.2??Let 1 < |C_p^r| < 6. Then for any integer k≥r≥1.

${{K}_{2}}\left( \mathbb{Z}{{C}_{{{p}^{r}}}}/{{p}^{k}}\Gamma \right)\cong \underset{i=0}{\overset{r}{\mathop{\oplus }}}\, {{K}_{2}}\left( \mathbb{Z}\left[ {{\zeta }_{{{p}^{i}}}} \right]/\left( {{p}^{k}} \right) \right).$

Proof??Let R=$\mathbb{Z}$C_p^r, I=p^kΓ such that k≥r. By Proposition 2.2.(b) in Ref.[1], we have I$\subseteq $R. Then the Cartesian square

$\begin{matrix} R & \to & R\text{/}I \\ \downarrow & {} & \downarrow \\ \Gamma & \to & \Gamma /I \\\end{matrix}$

gives rise to a nature commuative diagram with exact rows
By Corrollary 1.6 in Ref.[4], K₂(R) maps onto K₂(Γ). Hence, it is indicated in Table 1 that φ₂ is an isomorphism induced by inclusion. According to Theorem 1.3 in Ref.[1], φ₁ is a surjection and φ₄ is an isomorphism. Since both of SK₁(R) and SK₁(Γ) are trivial, φ₅ is an isomorphism. A diagram chasing shows that φ₃ is an isomorphism. Hence,

${{K}_{2}}\left( \mathbb{Z}{{C}_{{{p}^{r}}}}\text{/}{{p}^{k}}\Gamma \right)\cong {{K}_{2}}\left( \Gamma \text{/}{{p}^{k}}\Gamma \right).$

According to Corollary 2.10 in Ref.[5], $\mathbb{Q}$C_p^r is isomorphic to a direct sum of cyclotomic field

$\mathbb{Q}{{C}_{p^r}}\cong \underset{i=0}{\overset{r}{\mathop{\oplus }}}\, \mathbb{Q}\left( {{\zeta }_{{{p}^{i}}}} \right).$

By Proposition 2.2 in Ref.[1], $\Gamma \cong \underset{i=0}{\overset{r}{\mathop{\oplus }}}\, \mathbb{Z}\left( {{\zeta }_{{{p}^{i}}}} \right)$. Thus the result follows.
2 Main resultsIt is well known that K₂($\mathbb{Z}$/(2^k))=C₂(k≥2). If $\mathbb{Z}$[ζ_pⁱ] is totally imaginary, by Lemma 3.4, Theorem 3.8 and 5.1 in Ref.[6], and Corollary 4.3 in Ref.[3],

${{K}_{2}}\left( \mathbb{Z}\left[ {{\zeta }_{{{p}^{i}}}} \right]/\left( {{p}^{k}} \right) \right)\cong S{{K}_{1}}\left( \mathbb{Z}\left[ {{\zeta }_{{{p}^{i}}}} \right], \left( {{p}^{k}} \right) \right).$

$\mathbb{F}$or k≥2, using Lemma 1.1 and Lemma 1.2, we deduce that K₂($\mathbb{Z}$C₂/2^kΓ)=(C₂)², K₂($\mathbb{Z}$C₃/3^kΓ)=C₃, K₂($\mathbb{Z}$C₅/5^kΓ)=C₅, K₂($\mathbb{Z}$C₄/2^kΓ)=(C₂)²⊕C₄(k≥3), and K₂($\mathbb{Z}$C₄/4Γ)=(C₂)³.
Note that, for any integer s≥r, p^r+sΓ$\subseteq $p^s$\mathbb{Z}$C_p^r$\subseteq $p^sΓ. Hence, according to Proposition 1.1 in Ref.[7], K₂($\mathbb{Z}$C_p^r/p^r+sΓ) maps onto K₂($\mathbb{Z}$C_p^r/p^s$\mathbb{Z}$C_p^r) and K₂($\mathbb{Z}$C_p^r/p^s$\mathbb{Z}$C_p^r) maps onto K₂($\mathbb{Z}$C_p^r/p^sΓ). Therefore, we deduce that for k≥2, K₂($\mathbb{Z}$C₂/(2^k))=(C₂)², K₂($\mathbb{Z}$C₃/(3^k))=C₃, K₂($\mathbb{Z}$C₅/(5^k))=C₅, K₂($\mathbb{Z}$C₄/(2^k))=(C₂)²⊕C₄(k≥3), and K₂($\mathbb{Z}$C₄/(4))=(C₂)³ since, by Lemma 4.1.(a) in Ref.[7], K₂($\mathbb{Z}$C₄/(4)) has an exponent of 2.Summarizing, we have proven the theorems as follows.
Theorem 2.1??K₂($\mathbb{Z}$C₂/(2^k))(k≥2) is an elementary abelian 2-group of rank 2.
Theorem 2.2??$\mathbb{F}$or any integer k≥2,

${{K}_{2}}\left( \mathbb{Z}{{C}_{4}}/\left( {{2}^{k}} \right) \right)=\left\{ \begin{align} & {{\left( {{C}_{2}} \right)}^{3}}, \ \ \ \ \ \ \ \ \ \ \ k=2, \\ & {{\left( {{C}_{2}} \right)}^{2}}\oplus {{C}_{4}}, \ \ \ \ k\ge 3. \\ \end{align} \right.$

Theorem 2.3??$\mathbb{F}$or any integer k≥2 and p=3, 5, K₂($\mathbb{Z}$C_p/(p^k)) is a cyclic group of order p.
The method mentioned above is not suitable for the case when G=(C₂)². However, we have the result as follows.
Theorem 2.4??Let (C₂)²=〈σ〉×〈τ〉 be an elementary abelian 2-group of rank 2. Then K₂($\mathbb{Z}$(C₂)²/(2^k))(k≥2) is an elementary abelian 2-group of rank 6 with generators

$\begin{align} & \left\{ -1, -1 \right\}, \left\{ \sigma , -1 \right\}, \left\{ \tau , -1 \right\}, \left\{ \sigma , \tau \right\}, \\ & \left\langle \sigma -1, \tau \left( \sigma +1 \right) \right\rangle \ \text{and}\ \left\langle \tau \text{-}1, \sigma \left( \tau +1 \right) \right\rangle . \\ \end{align}$

Proof??According to Theorem 1.10 in Ref.[7], SK₁($\mathbb{Z}$(C₂)², (2^k)) is trivial. $\mathbb{F}$rom the relative K-theory exact sequence associated to the pair ($\mathbb{Z}$(C₂)², (2^k)), K₂($\mathbb{Z}$(C₂)²) maps onto K₂($\mathbb{Z}$(C₂)²/(2^k)). We deduce from the result of Ref.[2] that K₂($\mathbb{Z}$(C₂)²/(2^k)) is an elementary abelian 2-group of rank at most 6.
Besides, from Proposition 1.1 in Ref.[1], K₂($\mathbb{Z}$(C₂)²/(2^k)) maps onto K₂($\mathbb{F}$₂(C₂)²). Obviously, the kernel contains {-1, -1}, {σ, -1}, and {τ, -1}, while by the result on page 272 in Ref.[7], they are nontrivial and linearly independent. Based on Theorem 4 and Example 3 in Ref.[8], K₂($\mathbb{F}$₂(C₂)²) is an elementary abelian 2-group of rank 3 with generators {1+σ+τ, σ}, {1+σ+τ, τ}, and {σ, τ}. Therefore, the 2-rank of K₂($\mathbb{F}$₂(C₂)²) is at least 6.
Hence, K₂($\mathbb{Z}$(C₂)²/(2^k)) is isomorphic to K₂($\mathbb{Z}$(C₂)²). In Ref.[2], the explicit structure of K₂($\mathbb{Z}$(C₂)²) is given. The result follows.
References

[1]	Alperin R C, Dennis R K, Stein M R. SK1 of finite abelian groups.[J]. Invent Math, 1985, 82(1): 1-18.
[2]	Yang Z G, Tang G P, Liu H. On the structure of K2($\mathbb{Z}$[C2×C2])[J]. J Pure Appl Algebra, 2017, 221(4): 773-779. DOI:10.1016/j.jpaa.2016.08.001
[3]	Bass H, Milnor J, Serre J P. Solution of the congruence subgroup problem for SLn(n≥3) and Sp2n(n≥2)[J]. Publications Mathématiques de I'IHéS, 1967, 33: 59-137. DOI:10.1007/BF02684586
[4]	Stein M R. Excision and K2 of group rings[J]. J Pure Appl Algebra, 1980, 18(2): 213-224. DOI:10.1016/0022-4049(80)90130-9
[5]	Karpilovsky G. Commutative group algebras[M]. New York: Marcel Dekker Inc, 1983.
[6]	Dennis R K, Stein M R. K2 of discrete valuation rings[J]. Adv Math, 1975, 18(2): 182-238. DOI:10.1016/0001-8708(75)90157-7
[7]	Alperin R C, Dennis R K, Oliver R, et al. SK1 of finite abelian groups.Ⅱ[J]. Invent Math, 1987, 87(2): 253-302. DOI:10.1007/BF01389416
[8]	Magurn B A. Explicit K2 of some finite group rings[J]. J Pure Appl Algebra, 2007, 209(3): 801-811. DOI:10.1016/j.jpaa.2006.08.001