三元肥效模型异方差诊断及其可行广义最小二乘回归建模研究

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2021-12-26

孔庆波, 章明清, 李娟, 许文江, 章赞德, 姚建族. 三元肥效模型异方差诊断及其可行广义最小二乘回归建模研究[J]. 中国农业科学, 2018, 51(4): 728-737 https://doi.org/10.3864/j.issn.0578-1752.2018.04.012
KONG QingBo, ZHANG MingQing, LI Juan, XU WenJiang, ZHANG ZanDe, YAO JianZu. Heteroskedasticity Diagnosis and Feasible Generalized Least Squares Regression Modeling of Ternary Fertilizer Efficiency Model[J]. Scientia Acricultura Sinica, 2018, 51(4): 728-737 https://doi.org/10.3864/j.issn.0578-1752.2018.04.012

0 引言

【研究意义】肥料效应函数法是中国测土配方施肥技术的一个重要分支体系。但根据田间肥效试验结果,应用普通最小二乘法（OLS）建立肥效模型的成功率明显偏低,严重制约了该法的计量精确性和实用价值。因此,探讨如何提高田间肥效试验建模成功率具有意义。【前人研究进展】在常用肥效模型中,二次多项式肥效方程能较好地反映作物产量和施肥量之间的数量关系,模型计算和参数估计简便易行,是研究和应用最多的模型种类^[1,2,3]。但在施肥实践中,OLS法回归分析建立的一元肥效模型典型式仅占60%左右,二元肥效模型典型式则只有40.2%^[4,5],而三元肥效模型的典型式更低至23.6%^[6]。针对肥效模型在应用中存在的建模成功率偏低的问题,国内外****就肥效模型选择与其适用性^[7,8,9]、试验设计与参数估计方法^[10,11,12]、类特征肥效模型构建^[13,14,15]及非典型式推荐施肥优化方法^[12]等方面进行了深入研究,提出了许多改进措施,但至今未能得到较好地解决。当前广泛应用的“3414”设计方案的肥效试验结果既使采用蒙特卡洛（Monter Carlo）建模法,二元和三元模型典型式比率也仅有56.7%和37.3%^[12]。这种成败几乎各半的建模结果,困扰着计量施肥研究和应用。虽然任何田间试验都可能存在失误从而导致失败,但是,在不同肥料之间、肥料与其他产量限制因子之间存在着复杂的联应关系,我们没有理由认为其余的过半数试验均是失误。【本研究切入点】随着回归分析理论的发展和完善,人们发现,当回归方程随机误差项的方差存在显著水平差异时,普通最小二乘法回归建模就不再适用^[16]。此时其参数估计值就不再具有最小方差的优良性,模型参数显著性的t检验、回归方程显著性的F检验和拟合优度R²检验等都将失去可靠性,同时拟合参数具有较大的方差,回归方程预测能力也将失效,结果导致肥效模型失去实用价值。【拟解决的关键问题】本文利用近年来“3414”试验设计方案完成的早稻氮磷钾田间肥效试验结果,探讨三元二次多项式肥效模型的异方差诊断方法和可行广义最小二乘回归建模法（FGLS）在消除或缓解异方差危害方面的应用效果,为提高三元肥效模型建模可靠性和成功率提供一种新方法。

1 材料与方法

1.1 早稻氮磷钾肥效试验资料的收集整理

近年来,在水稻测土配方施肥工作中,福建在福州市、宁德市、南平市、三明市、龙岩市、莆田市、漳州的龙海市以及平和县、泉州的南安市等水稻主产区的主要项目县先后完成了171个氮磷钾田间肥效试验。这些试验均采用“3414”设计方案^[17],即（1）N₀P₀K₀;（2）N₀P₂K₂;（3）N₁P₂K₂;（4）N₂P₀K₂;（5）N₂P₁K₂;（6）N₂P₂K₂;（7）N₂P₃K₂;（8）N₂P₂K₀;（9）N₂P₂K₁;（10）N₂P₂K₃;（11）N₃P₂K₂;（12）N₁P₁K₂;（13）N₁P₂K₁;（14）N₂P₁K₁。其中,“2”水平为试验前的当地推荐施肥量,“0”水平表示不施肥,“1”水平和“3”水平的施肥量分别为“2”水平的50%和150%。本研究选择8个代表性试验点的田间试验结果来探讨三元二次多项式肥效模型的异方差诊断方法及其应对技术。这些试验点基础土样的主要理化性状采用常规方法^[18]测定,处理（6）的施肥量采用当地推荐施肥量（表1）,试验设计方案和田间管理与文献[17]相同。8个试验点的产量结果见表2。
Table 1
表1
表1早稻8个代表性试验点的供试土壤主要理化性状及其处理（6）氮磷钾施肥量
Table 1Main physical and chemical properties of soils in 8 representative experience sites and fertilization rate in 6^th treatment in early rice

序号 No.	试验地点 Experimental site	土属 Soil genus	土壤理化性状 Physical and chemical properties of the soil					处理(6)施肥量 Fertilizer of 6^th treatment (kg·hm^-2)
序号 No.	试验地点 Experimental site	土属 Soil genus	pH	有机质 OM (g·kg^-1)	碱解氮 Alkali. N (mg·kg^-1)	有效磷Avail. P (mg·kg^-1)	速效钾 Avail. K (mg·kg^-1)	N	P₂O₅	K₂O
1	蒲城县Pucheng County	灰泥田Plaster field	4.8	31.8	186	14.0	124	150	60	105
2	永定县Yongding County	黄泥田Yellow mud field	5.2	6.6	113	13.5	64	150	60	105
3	新罗区Xinluo District	灰泥田Plaster field	5.5	25.6	213	24.0	194	150	52.5	105
4	永安市Yongan City	黄泥田Yellow mud field	5.5	25.9	105	28.1	85	150	60	105
5	永定县Yongding County	黄泥田Yellow mud field	4.8	34.7	275	27.4	41	150	60	105
6	永安市Yongan City	灰泥田Plaster field	5.3	33.1	126	16.8	62	150	60	105
7	仙游县Xianyou County	黄泥田Yellow mud field	5.4	20.8	128	19.0	58	165	66	99
8	仙游县Xianyou County	灰沙田Plaster field	5.4	21.1	116	17.0	60	165	49.5	115.5

新窗口打开
Table 2
表2
表2早稻8个代表性试验点各施肥处理的稻谷产量
Table 2Rice grain yield of each fertilizer treatment in 8 representative experiments in early rice

序号 No.	处理号及其稻谷产量Treatments number and its rice grain yield (kg·hm^-2)
序号 No.	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	4461	5501	6393	4218	6240	6857	4802	3936	5807	5622	5025	5625	5880	5820
2	6529	4796	7748	6054	8067	9567	8798	5883	7704	8947	9567	8883	9225	9292
3	5379	7355	7844	7029	7524	7979	7709	7089	7775	7559	7434	6899	7280	7085
4	4528	5663	6863	5727	7056	7203	6758	5186	6990	5963	6539	6353	5946	6546
5	5532	7032	7257	6131	6788	7257	7500	6113	6975	6788	6788	6549	6807	6320
6	3930	4211	5786	4535	5850	6380	4560	4301	5715	5610	6200	5891	6120	5891
7	4800	5355	6705	6675	7125	7095	7020	6000	6870	6675	7095	7050	7005	7050
8	4800	5700	6945	6900	7350	7395	7305	6495	6945	7050	6855	6705	6645	6795

新窗口打开

1.2 多元线性回归模型的异方差及其诊断

经典线性回归分析针对模型随机误差项$\hat{u}$的一个重要假设是$\hat{u}$在不同观测点具有相同方差,即误差项$\hat{u}$的方差是一个等于σ²的常数^[16]。但是,这种等方差假设在实际问题中往往难以得到满足。当回归模型存在严重异方差时,普通最小二乘法就丧失了实用价值^[19,20]。异方差的定性诊断方法是模型残差分析^[16]。当回归模型的误差项具有同方差时,残差图上n个点的散布是随机的,无任何规律。如果存在异方差,残差图上点的分布就会呈现出一定的变化趋势,如残差值增大或减小等。
因线性回归模型的异方差有多种不同表现形式^[19],其定量诊断方法也有多种不同方法。本研究选择常用的怀特（White）检验、帕克（Park）检验和冠因克-巴塞特检验（Koenker-Basett,KB检验）等,具体使用方法可参考相关专著^[19]。

1.3 可行广义最小二乘回归建模法

目前常用的三元二次多项式肥效模型可用矩阵形式表示为：
$\hat{Y}$=Xβ+$\hat{u}$ （1）
式中,$\hat{Y}$表示拟合产量;X表示肥效试验设计矩阵,β表示肥效模型参数向量,$\hat{u}$表示模型拟合残差向量。用普通最小二乘法（OLS）进行回归分析时,模型参数的计算式为：
$\hat{\beta }$=(X′X)^-1X′Y （2）
式中,Y表示各施肥处理的试验产量向量。针对异方差问题,数理统计学家已经提出了消除或缓解线性回归模型异方差的许多方法^[19,21],但应用较广泛的方法是可行广义最小二乘法（FGLS）或称之为可行加权最小二乘法（FWLS）。这种方法是对原回归模型（1）式加权,使之变成一个新的不存在异方差性的模型,然后采用OLS估计其参数^[19]。因此,FGLS就是对加了权重的残差平方和实施OLS,即：
∑W_iu_i²=∑W_i[Y_i-βX)]²→min （3）
式中,W_i为给定的第i个处理产量的权数。如何获得各处理产量的W_i?一种可行的方法是对原模型进行OLS估计,得到随机误差项的近似估计量$\hat{u}$,以此构建权数估计量。即：w=（${{\hat{u}}_{1}}^{2}$,${{\hat{u}}_{2}}^{2}$,…,${{\hat{u}}_{n}}^{2}$）,进而构造权矩阵W,然后用OLS估计新模型。记参数估计量为${{\hat{\beta }}^{*}}$,即FGLS的参数估计量计算式为：
${{\hat{\beta }}^{*}}$=(X′W^-1X)^-1X′W^-1Y （4）
这就是原模型（1）式的可行广义最小二乘估计,它是无偏和有效的估计量^[16]。因为${{\hat{\beta }}^{*}}$是β的最佳线性无偏估计量,因此,FGLS的总离差平方和SST*、回归平方和SSR*以及残差平方和SSE*的计算式分别为：
SST*=Y′W^-1Y （5）
SSR*=Y′W^-1X(X′W^-1X)^-1X′W^-1Y （6）
SSE*=SST*-SSR* （7）
进而可以计算得到FGLS回归模型的F值和拟合优度R²等统计检验参数。上述的具体数学原理和计算方法可参阅相关专著^[16,21-22]。

1.4 肥效模型典型性判别方法

假设三元二次多项式肥效模型的数学形式如下：
$\hat{Y}$=b₀+b₁N+ b₂P+ b₃K+ b₄N²+ b₅P²+ b₆K²+ b₇NP+ b₈NK+ b₉PK+ε （8）
式中,N、P、K分别表示N、P₂O₅和K₂O施肥量（kg·hm^-2）;ε为拟合残差（kg·hm^-2）;$\hat{Y}$为拟合产量（kg·hm^-2）。根据无约束最优化方法^[6],若函数f (N, P, K)在点X处的一阶梯度向量g(X) （其中,X=（N, P, K））等于零向量;同时,若肥效函数的Hesse矩阵G(X )为负定,则此函数有极大值。对式（8）的三元二次多项式肥效模型而言,Hesse矩阵G(X)的各阶主子式假设为G₁、G₂和G₃,则它们的行列式值分别为：G₁=2b₄;G₂=4b₄b₅-b₇²;G₃=2(4b₄b₅b₆+b₇b₈b₉-b₄b₉²- b₅b₈²-b₆b₇²)。因此,各类三元肥效模型的典型性判别方法如下：①若g(X* )=0,且G₁<0,G₂>0,G₃<0,则矩阵G(X )为负定,肥效模型具有全局最高产量点。同时,若g(X*)=0所代表的点X*对应的N、P、K数值均落在试验设计的施肥量范围内,则该肥效模型属于典型式。②若G(X*)为负定,但点X*对应的N、P、K数值有一个或一个以上超过试验设计施肥量,则该肥效模型属于推荐施肥量外推的非典型式。③若g(X*)=0,而且G1>0,G2>0,G3>0,则Hesse矩阵G (X )为正定,此函数有全局最低产量点,肥效型属于存在最低产量点的非典型式。④若g(X*)=0,G₁、G₂和G₃不满足正定和负定的条件而且不等于零,则Hesse矩阵为不定,点X*为驻点,该肥效模型属于无最高产量点的非典型式。

1.5 肥效模型异方差检验和参数估计的计算机实现

三元二次多项式肥效模型的异方差检验、OLS和FGLS回归建模均涉及到繁杂的数学计算,本研究采用MATLAB软件来完成相关工作,其中,OLS法回归诊断调用regstats功能函数,OLS回归分析调用regress功能函数,FGLS法则调用fgls功能函数。根据上述统计学原理,在MATLAB软件平台上编写计算程序完成异方差检验及其绘图。

2 结果

2.1 OLS法回归分析及其肥效模型典型性判别

根据表1的8个试验点施肥量和表2相应的14个处理试验产量结果,应用OLS进行回归分析（表3）。结果表明,1号和2号的两个试验点未达到统计显著水平,试验资料不可用;3—8号的6个试验点,回归模型均达到统计显著水平。因为通过显著性检验的三元二次多项式肥效模型有典型式和3种不同类别的非典型式^[6],因而,通过显著性检验的6个回归模型还需进一步进行典型性判别（表3）,以便确定推荐施肥方法。结果显示,尽管3号试验点肥效模型的一次项参数符号为正,二次项参数符号为负,满足了植物营养的一般规律,但是,该肥效模型不存在最高产量点,边际产量导数法推荐施肥的结果不可靠。4号试验点有最高产量点,边际产量导数法推荐施肥量没有外推,但是,P的一次项参数为负数,属于参数符号不合理的非典型式。5号试验点有最高产量点,N、P、K的一次项和二次项参数的符号满足植物营养的一般规律,但钾肥的最高施肥量超过试验设计施肥量,属于推荐施肥结果远外推的非典型式。6—8号试验点的肥效模型存在最高产量点,模型一次项和二次项参数的符号正常,边际产量导数法推荐施肥量在试验设计施肥量范围内,属于典型肥效模型。
Table 3
表3
表3三元二次多项式肥效模型的OLS回归分析
Table 3OLS regression analysis of ternary quadratic polynomial’s fertilizer response model

序号 No.	统计指标 Statistical index							建模结论 Modeling conclusion
序号 No.	F	R²	P	MSe	PS	MY	RF	建模结论 Modeling conclusion
1	5.67	0.9273	0.0551	1.7071×10⁵	-	-	-	未达统计显著水平NRSS
2	2.84	0.8645	0.1640	1.0563×10⁶	-	-	-	未达统计显著水平NRSS
3	6.24	0.9335	0.0467	8.7928×10⁵	Y	N	-	无最高产量点No Max. yield
4	6.69	0.9377	0.0414	1.2214×10⁵	N	Y	-	参数不合理Irrational parameters
5	11.16	0.9617	0.0166	3.5249×10⁴	Y	N	N	施肥量外推Extrapolated application rate
6	16.02	0.9730	0.0085	6.2805×10⁵	Y	Y	Y	典型式Typical model
7	13.61	0.9684	0.0115	5.3412×10⁴	Y	Y	Y	典型式Typical model
8	27.35	0.9840	0.0030	2.4950×10⁴	Y	Y	Y	典型式Typical model

“PS” means parameters symbols,“MP” means Maximum yield, “RF” means recommended fertilization; “NRSS” means no reaching statistically significant lever. “Y” means normal, “N” means abnormal. The same as Table 5“PS”表示参数符号;“MY”表示有最高产量点,“RF”表示推荐施肥量;NRSS表示未达统计显著水平;“Y”表示正常状态,“N”表示异常状态。表5同

新窗口打开
因此,采用目前常用的OLS回归建模,1号和2号试验点属于未达统计显著水平的肥效模型,3—5号试验点建立的肥效模型属于非典型式,只能弃之不用;只有6—8号试验点的肥效模型满足植物营养学的一般肥效规律,属于三元典型肥效模型。

2.2 肥效模型的异方差及其统计检验

OLS回归建模要求模型随机误差项具有相同方差,否则,回归建模结果就不可靠^[16],在应用上易对肥效试验结果产生误判。为此,需对表2的8个试验资料进行回归诊断。以各处理的试验产量为X轴,OLS拟合残差为Y轴,绘制图1的残差散点图。结果表明,无论是统计未达显著水平的1号试验点肥效模型（图1-a）,还是3号试验点的非典型肥效模型（图1-b）或者8号试验点的典型肥效模型（图1-c）,随着水稻产量水平提高,其拟合残差均呈现逐渐散开的漏斗状分布趋势,表明都不满足随机分布的假设。结果预示着14个处理产量的拟合残差方差不相等,且随着产量水平提高而增大,但1号试验点随着稻谷产量水平增加,拟合残差的增加绝对值最大,3号试验点则其次,8号试验点拟合残差绝对值的变化幅度最小。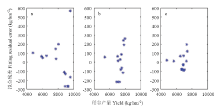

显示原图|下载原图ZIP|生成PPT
图1三元肥效模型拟合残差图
a：统计不显著模型（1号试验点）,b：非典型式模型（4号试验点）,c：典型式模型（7号试验点）
-->Fig. 1Model fitting residual graph of ternary fertility efficiency
a: Model of no reaching statistically significant lever (No. 1 test point), b: Atypical model (No. 4 test point), c:Typical model (No. 7 test point)
-->

图1的拟合残差图给出了三元肥效模型异方差的定性分析结果,要回答异方差的严重程度,还需要做定量分析（表4）。由于异方差在线性回归模型中可能有不同的表现形式^[19],在不同的定量检验方法中,只要有一种检验结果达到统计显著水平,就说明回归模型存在该种形式的异方差。结果表明,拟合残差绝对值变化幅度最小的8号试验点的OLS回归模型异方差未达显著水平,其余7个试验点建立的OLS回归方程至少有一种异方差模型达到统计显著水平,即存在严重的异方差。
Table 4
表4
表4肥效模型异方差的统计检验
Table 4Statistical test of model’s heteroscedasticity

序号 No.	怀特检验White test			冠因克-巴塞特(KB)检验KB test			帕克检验Park test			检验结论 Statistical conclusion
序号 No.	X²计算值 Calculated value	X²临界值 Critical value (P<0.05)	显著性 Sign.	F值 F value	P值 P value	显著性 Sign.	F值 F value	P值 P value	显著性 Sign.	检验结论 Statistical conclusion
1	4.0773	9.4877	N	3.6370	0.0807	N	6.2747	0.0277	Y	存在异方差EH
2	8.8535	9.4877	N	1.9847	0.1843	N	8.7512	0.0120	Y	存在异方差EH
3	11.006	9.4877	Y	1.6796	0.2327	N	1.4467	0.2523	N	存在异方差EH
4	9.5601	9.4877	Y	3.4481	0.0880	N	6.0049	0.0306	Y	存在异方差EH
5	12.695	9.4877	Y	0.5445	0.4748	N	2.7423	0.1236	N	存在异方差EH
6	3.5147	9.4877	N	2.2892	0.1562	N	6.9213	0.0219	Y	存在异方差EH
7	9.4429	9.4877	N	5.1458	0.0426	Y	4.0790	0.0663	N	存在异方差EH
8	5.9743	9.4877	N	2.0541	0.1773	N	3.6984	0.0785	N	没有异方差NH

“Sign” means significance lever, “Y” means reaching statistically significant lever, “N” means no reaching statistically significant lever; “EH” means existence heteroscedous, “NH” means no existence heteroscedous“Sign.”表示显著性;“Y”表示显著,“N”表示不显著。“EH”表示存在异方差,“NH”表示不存在异方差

新窗口打开

2.3 可行广义最小二乘法对肥效模型建模结果的影响

根据表4的异方差检验结果,1—7号试验点肥效模型存在统计显著水平的异方差,表3的OLS回归建模结果就失去了可靠性。为此,采用可行广义最小二乘法回归建模（表5）。
Table 5
表5
表5可行广义最小二乘法回归建模结果
Table 5Modeling results using feasible generalized least squares regression

序号 No.	统计指标 Statistical index							建模结论 Modeling conclusion
序号 No.	F	R²	P	MSe	PS	MY	RF	建模结论 Modeling conclusion
1	369.4	0.9985	0.0000	1.8385	Y	Y	Y	典型式Typical model
2	133.8	0.9959	0.0001	1.5989	Y	Y	Y	典型式Typical model
3	1545.4	0.9997	0.0000	1.4617	Y	Y	Y	典型式Typical model
4	822.7	0.9993	0.0000	1.4832	Y	Y	Y	典型式Typical model
5	3267.1	0.9998	0.0000	1.4258	Y	Y	Y	典型式Typical model
6	802.4	0.9993	0.0000	2.1569	N	Y	N	非典型式Atypical model
7	2000.3	0.9997	0.0000	1.4946	Y	Y	Y	典型式Typical model
8	3295.8	0.9998	0.0000	2.0512	Y	Y	Y	典型式Typical model

新窗口打开
结果显示,可行广义最小二乘法明显改善了肥效模型的建模效果。1号和2号试验点的F值和拟合优度R²由OLS法的未达到显著水平提高到极显著水平,而且肥效模型转化为典型式。其他6个试验点的肥效模型F值和拟合优度R²同样得到显著的提升;3号、4号和5号试验点分别由OLS法的无最高产量点的、P项参数符号不合理、推荐施肥量外推的非典型式转化为典型式。但是,OLS法属于典型式的6号试验点,尽管模型存在异方差,若采用FGLS法则导致回归模型由典型式变为非典型式,结果反而变劣。对异方差未达显著水平差异的8号试验点,采用FGLS回归也能提高拟合优度,模型同样是典型式。
因此,在8个代表性试验点中,采用FGLS法回归建模,显著提高了肥效模型的拟合优度和典型式的出现几率,明显地提高了建模成功率。
FGLS法为什么能提高建模成功率呢?比较1号、3号和8号试验点的两种参数估计方法,FGLS回归建模明显地降低了肥效模型各个参数的方差（表6）;表5和表3的均方误差（MSE）结果也表明,FGLS回归建模大幅度降低了误差均方。结果说明FGLS大幅度提高了肥效模型的拟合精度和模型预测能力,从而提高了肥效模型的可靠性。
Table 6
表6
表6OLS与FGLS回归的参数方差比较
Table 6Parameter variance compare between the regression methods of OLS and FGLS

方法 Method	试验点 Sites	模型参数 Model parameter
方法 Method	试验点 Sites	b₀	b₁	b₂	b₃	b₄	b₅	b₆	b₇	b₈	b₉
OLS	1	169090	122.69	766.79	250.38	0.0009	0.0339	0.0036	0.0279	0.0091	0.0570
	3	87092	63.193	515.86	128.97	0.0004	0.0298	0.0019	0.0188	0.0047	0.0383
	8	157	3.850	12.832	5.499	0.009	0.103	0.019	0.070	0.030	0.101
FGLS	1	138500	83.248	356.87	137.21	0.0005	0.0193	0.0018	0.0182	0.0042	0.0362
	3	70329	43.238	247.32	72.234	0.0003	0.0174	0.0010	0.0124	0.0022	0.0246
	8	136	3.068	8.567	3.967	0.007	0.076	0.013	0.055	0.020	0.078

Others trial sites had the same results with the conclusion of the Table 6, and the data were omitted其他试验点的模型参数方差状况与表中数据相似,略去计算结果

新窗口打开

2.4 消除异方差后的肥效模型推荐施肥量

根据FGLS回归建模得到的典型肥效模型,结合N、P₂O₅、K₂O和稻谷价格分别为4.3、5.0、6.0和2.0元/kg的市场均价,应用边际产量导数法计算推荐施肥量（表7）。OLS回归建模能得到典型肥效模型的7号和8号试验点,两种建模方法所得肥效模型的推荐施肥量和预测产量水平十分相近;1—5号试验点,由OLS回归建模未达显著水平或是非典型肥效模型,用FGLS回归建模转化成了典型肥效模型,其推荐施肥量和预测产量水平也符合现有经验认识,尤其是,1号、3号和5号试验点的基础土壤碱解氮含量分别为186、213、275 mg·kg^-1（表1）,接近或超过早稻高产临界指标^[17],3个试验点的氮肥推荐用量明显低于常规推荐水平。结果表明,FGLS回归建模的推荐施肥量是可靠的。
Table 7
表7
表7OLS肥效模型与FGLS肥效模型推荐施肥量的比较
Table 7Compare the recommended fertilization rate between the fertilizer response model of OLS and FGLS

序号No.	OLS回归建模OLS regression modeling								FGLS回归建模FGLS regression modeling
	最高施肥量Max.(kg·hm^-2)				经济施肥量Eco. (kg·hm^-2)				最高施肥量Max. (kg·hm^-2)				经济施肥量Eco. (kg·hm^-2)
	N	P₂O₅	K₂O	产量Yield	N	P₂O₅	K₂O	产量Yield	N	P₂O₅	K₂O	产量Yield	N	P₂O₅	K₂O	产量Yield
1	-	-	-	-	-	-	-	-	97	45	77	6671	75	42	61	6620
2	-	-	-	-	-	-	-	-	241*	88*	175*	10036	193	72	136	9906
3	-	-	-	-	-	-	-	-	88	76	96	7829	12	86	63	7709
4	-	-	-	-	-	-	-	-	147	53	86	7181	124	44	77	7131
5	-	-	-	-	-	-	-	-	132	129*	113	7599	58	105	87	7450
6	162	46	105	6498	93	43	66	6361	-	-	-	-	-	-	-	-
7	165	58	88	7346	137	49	76	7286	169	62	89	7305	139	50	77	7240
8	168	66	119	7301	144	54	92	7219	171	54	123	7299	145	48	93	7217

“Max.” and “Eco.” means the maximum application rate and economical application rate in recommendation fertilization respectively. Data with “*” in table indicates extrapolated results“Max.”表示最高施肥量,“Eco.”表示经济施肥量。带“*”号的数据表示外推结果

新窗口打开

2.5 肥效模型异方差出现几率及其FGLS法效果评价

为了评价FGLS对三元肥效模型的建模效果,利用福建省早稻测土配方施肥项目在全省各地主要项目县完成的171个“3414”设计方案的氮磷钾田间肥效试验结果,逐个进行回归分析,统计结果见表8。FGLS大幅度提高了三元肥效模型的拟合优度,每个试验点的R²和F值均达到统计显著水平,而OLS则有16%试验点的肥效模型未达统计显著水平。
Table 8
表8
表8不同参数估计方法对肥效模型建模结果的影响
Table 8Effects of modeling results by using different methods of estimate parameters in fertilizer response model

建模方法 Modeling method	试验数 Trials (n)	异方差模型比例Proportion of heteroscedastic model (%)	未达到统计显著水平的模型比例 Proportion of no reaching significant level’s model (%)	达到统计显著水平的模型比例Proportion of reaching significant level’s model (%)
				无最高产量点 Inexistence max. yield	有最高产量点Existence max. yield
				无最高产量点 Inexistence max. yield	参数符号不合理 PS unreasonable	推荐施肥量外推 RF extrapolation	典型模型 Typical model
OLS	171	25.15	16.02	36.59	14.44	5.26	27.68
FGLS	171	-	0	41.67	15.61	7.28	34.99

PS: Means parameter symbol; RF: Means recommendation fertilizationPS表示参数符号;RF表示推荐施肥量

新窗口打开
模型典型性判别分析表明,在3种非典型肥效模型类型中,无论是OLS还是FGLS回归建模,无最高产量点的非典型肥效模型所占比例高达40%左右,其次是参数符号不合理的非典型肥效模型所占试验点比例大致15%,而氮磷钾推荐施肥量属于外推的非典型肥效模型所占比例6%左右,两种方法的结果差异很小;OLS回归建模的典型肥效模型占试验点数的27.68%,而FGLS回归建模的典型肥效模型比例达到34.99%,比OLS回归建模提高了7.31个百分点。

3 讨论

3.1 多项式肥效模型产生异方差的原因

在经典回归建模理论中,针对线性回归方程随机误差项$\check{u}$的一个重要假设是$\check{u}$在不同观测点具有同方差性。异方差将导致严重后果^[16],包括：（1）尽管OLS参数估计的无偏性仍然成立,并且基于此的产量预测也是无偏的,但参数估计值的方差不再是最小的,即最小二乘法失去了有效性,对大样本也是如此。（2）由于异方差的影响,造成难以正确估计模型参数的标准误,且无法辨别是正的还是负的偏差,导致回归模型的 t 统计量和F统计量失去了可靠性。（3）由于参数估计量不是有效的,从而对产量的预测也将不是有效的。二次多项式肥效模型是建立在经典正态线性回归模型理论基础上的,要正确建立肥效模型就必须遵守回归分析理论的基本假设^[19]。长期以来,我们在建立作物肥效模型时,大都忽略了回归分析理论有关同方差性等条件的基本假设,这是目前建模成功率低^[4,5,6]的重要原因之一。
总结本研究结果并结合专业特点,多项式肥效模型产生异方差的主要原因有：（1）随着试验设计和田间试验管理水平的提高,肥效模型的误差方差σ²可能会减少。反之,若田间试验操作或管理出现失误,可能导致部分处理出现异常产量结果,使模型误差方差σ²出现非常数;（2）由于田间土壤肥力水平存在空间异质性,可能导致部分试验处理出现异常产量值,导致出现异方差;（3）多项式肥效模型属于经验回归模型,对某些试验点来说可能导致模型设定不正确;（4）在多数情况下,当土壤养分肥力较低时,作物产量处于低产水平,此时通过施肥可迅速提高产量,而因施肥造成减产或平产的可能空间很小,即产量方差较小;但在高产阶段,通过施肥可能继续增产,也可能不再增产,甚至可能因过量施肥造成减产,即产量变化的可能空间较大,此时方差必然较大。从这个意义上讲,依据不同施肥量和产量建立的经验肥效模型必然带有异方差性质。福建的171个早稻氮磷钾肥效试验结果表明,这种异方差性达到统计显著水平的试验点占到试验总数的25%左右（表8）。因此,通过控制试验田土壤空间异质性、提高试验管理水平,降低试验产量异常值的出现几率,是消减异方差和提高建模成功率的重要途径。

3.2 多项式肥效模型异方差的检验方法

针对异方差的严重危害性,在现代回归分析理论中已经研究提出了多种异方差定量诊断方法^[19]。本研究选择怀特（White）检验、冠因克-巴塞特（KB）检验、帕克（Park）检验等3种常用的异方差定量检验方法,探讨三元肥效模型异方差性质。结果表明,不同试验点建立的三元二次多项式肥效模型,误差项的异方差有不同的表现形式。由于目前还难以明确在什么试验条件下会出现哪种形式的异方差,因而,在实用上,通常同时选用几种不同异方差检验方法进行检验。只要有一种检验方法达到统计显著水平,就说明肥效模型存在该种形式的异方差。
当前,构建异方差定量检验方法的共同思路是,检验随机误差项的方差与回归模型自变量或因变量观测值之间的相关性及其数学形式^[19],各种检验方法正是在这个思路下发展起来的。本文选用3种常用的检验方法,它们各有自己的特色和优点。其中,怀特检验不仅能够检验异方差的存在,同时在多变量的情况下,还能够判断出是哪一个变量引起的异方差。帕克检验的优点是不但能确定有无异方差性,而且还能给出异方差的具体函数形式。冠因克-巴塞特检验的一个优点是即使回归模型中的误差项不是正态分布的,它仍能适用。因此,这三种方法都是检验肥效模型异方差的有效方法。

3.3 多项式肥效模型异方差的修正方法

用普通最小二乘法估计肥效模型参数时,对参数的估计是以产量拟合残差平方和最小为条件的。在最小化过程中,对每个施肥处理的产量拟合残差平方所提供的信息的重要程度是同等看待的,它们在决定肥效模型参数的过程中所起的作用是相同的,或者说取了相同的权数,即权数都为1。这在同方差条件下,因不同施肥处理的作物产量水平在偏离均值程度上是相同的,这样做是合理的。但是,在异方差条件下,由于各施肥处理的产量水平在偏离均值程度上相差很大,这样做就未必合理。
本研究针对三元二次多项式肥效模型异方差问题,采用FGLS回归建模。该法是对原模型加权,即：对较小OLS拟合残差平方的施肥处理产量赋予较大的权数,对较大OLS拟合残差平方的施肥处理产量赋予较小的权数,使回归模型转化成不存在异方差性的新模型,然后再次采用OLS估计其参数。结果表明,与OLS回归建模方法相比,FGLS方法能将绝大部分试验点的试验结果由OLS方法的未达统计显著水平转化为达到统计显著水平,或者将部分试验点的非典型式模型转化为典型肥效模型（表3和表5）,明显提高了建模成功率。
在对付线性回归模型异方差上,除了FGLS外,“OLS+稳健标准误”也是常用方法^[22]。该法是在异方差情况下,仍然采用OLS,但对OLS估计量的标准差进行修正。与OLS估计比较,肥效模型参数估计值没有变化,但是参数估计值的方差和标准差变化明显。经过这种修正的模型参数标准差,模型参数的显著性检验和模型产量预测等方面就变为有效的。那么,究竟是使用“OLS+稳健标准误”还是FGLS?从肥效模型角度看,我们总是希望将OLS建模出现的非典型模型尽可能多地转化为典型肥效模型。由于“OLS+稳健标准误”方法的模型参数没有变化,显然不能实现这一目标,而FGLS方法则能把部分非典型肥效模型转化为典型式。从这个意义上讲,FGLS方法具有优势。同时,表7的建模结果使我们注意到,OLS回归建模是典型肥效模型的试验资料,若采用FGLS回归建模,可能出现非典型式,使结果变劣。因此,在实际工作中,我们也不应对异方差反应过度^[19]。如果OLS方法能得到典型肥效模型,就无需考虑其他修正方法。
福建171个早稻氮磷钾肥效试验资料的总结结果表明,FGLS回归建模的三元典型肥效模型比例仅达到34.99%,只比OLS回归建模提高7.31个百分点。究其原因,多项式肥效模型不仅存在异方差,而且还存在严重的多重共线性^[23]问题,制约了OLS法的有效性^[19],对FGLS回归建模也不例外。只有较好地克服了这两个建模问题,才可能较大幅度地提高建模成功率。如何同时克服多项式肥效模型的异方差和多重共线性问题,提出最优建模策略,则有待于未来的进一步研究。

4 结论

根据171个早稻“3414”设计的氮磷钾田间肥效试验结果,现代回归分析理论的可行广义最小二乘法建模技术是消除三元二次多项式肥效模型异方差的有效方法。该法明显减小模型各个参数的方差,改善了肥效模型的拟合精度和模型预测能力,进而提高了田间肥效试验资料的建模成功率。
The authors have declared that no competing interests exist.