郭军, 曲亮, 窦套存, 王星果, 沈曼曼, 胡玉萍, 王克华^,中国农业科学院家禽研究所,江苏扬州 225125

Using Random Regression Models to Estimate Genetic Parameters on Body Weights in Layers

GUO Jun, QU Liang, DOU TaoCun, WANG XingGuo, SHEN ManMan, HU YuPing, WANG KeHua^,Poultry Institute, Chinese Academy of Agricultural Sciences, Yangzhou 225125, Jiangsu

通讯作者: 王克华,E-mail： sqbreeding@126.com

责任编辑: 林鉴非
收稿日期:2019-05-19接受日期:2019-10-28网络出版日期:2020-06-01

基金资助:

江苏现代农业产业技术体系建设项目.JATS[2018]247 现代农业产业技术体系建设专项资金.CARS-40-K01 江苏省农业重大新品种创制项目.PZCZ201729

Received:2019-05-19Accepted:2019-10-28Online:2020-06-01
作者简介 About authors
郭军,Tel：0514-85599012;E-mail：guojun. yz@gmail.com。









摘要
【目的】通过分析勒让德多项式阶数对最大似然值、残差的影响,优化随机回归模型,评估蛋鸡资源群体体重遗传潜能和选择时机,为蛋鸡资源群体育种方案提供参数。【方法】收集东乡绿壳蛋鸡与白莱航鸡F₂资源群体体重数据26 532条。系谱数据包含5 871只鸡,其中4 174只鸡有5条记录,802只鸡有4条记录,128只鸡没有记录。数据清洗包括去除离群值数据、去除翅号重复个体、去除性别不明个体、去除少于4条记录个体。经整理,剩余25 483条体重数据,其中绿壳蛋鸡2 223条,白莱航鸡696条,F₁代6 002条,F₂代16 562条。应用SPSS软件中一般线性模型分析非加性遗传因素对体重的影响,确定将批次、性别列入动物模型固定效应。应用随机回归模型分析蛋鸡早期体重方差组分、遗传参数、随机回归系数矩阵特征向量。随机回归动物模型中包括一般固定效应、固定回归项及随机回归项三类效应。研究中,以批次-性别作为固定效应,以周龄体重作为固定回归项,将加性遗传效应和永久环境效应作为随机回归项。经AIC、BIC筛选,随机回归模型中加性遗传效应宜嵌入5阶勒让德多项式、永久环境效应宜嵌入5阶勒让德多项式、固定回归项宜嵌入2阶勒让德多项式。残差做异质化处理,分为5个水平,即每次观测设定一个残差初始值,观测间隔期残差以线性回归计算。【结果】蛋鸡资源群体1—9周龄体重遗传力为0.46—0.63,重复力为0.88—0.92,遗传相关系数为0.32—0.99,永久环境相关系数为0.34—0.99。遗传相关系数随着周龄间隔增大而减小,相邻周龄遗传相关系数较高。遗传方差、永久环境方差以及残差随年龄增加而增加。加性遗传效应随机回归系数矩阵前三个特征值依次为1 976.91、161.95、42.22,前三个特征值合计解释99%遗传变异。【结论】随机回归模型可用于蛋鸡早期体重遗传评估及选育。对加性遗传系数矩阵第二特征方程系数进行选择可以改变个体生长曲线,选择时机宜在3—6周龄。蛋鸡资源群体早期体重遗传力略高于其它群体同类研究结果。
关键词： 体重;随机回归模型;遗传力;特征值;蛋鸡

Abstract
【Objective】 This study was to assess the effect of the orders of Legendre polynominals on the size of the maximum likelihood and the error, to optimize the random regression model, to evaluate the genetic potential and selection knot of layer resource population and to provide parameters for optimal layer breeding scheme for resource population. 【Method】The data set consisted of 26 532 items collected from the layer resource population, which set up by White Leghorn reciprocal crossing with the blue eggshell chickens. The pedigree consisted of 5 871 individuals, including 4 147 chickens with 5 records, 802 chickens with 4 records and 128 chickens without records. The standard of data cleaning included: i. removing outlier; ii. eliminating repeated individuals; iii. getting rid of unknown sexed individuals; iv. individuals with less than 4 records were also excluded. After data cleaning procedures, 25 483 records on body weight could be used in the next step, 2 223 of which collected from blue shelled chickens, 696 of which collected from White Leghorn, 6 002 of which collected from F₁ generation and 16 562 of which collected from F₂ generation. The influence of the nongenetic factors on body weights was analyzed by GLM in SPSS. The fixed effects of animal model included batch and sex factors. Using the random regression model, variance components, genetic parameters and eigenvectors were obtained. The model included general fixed effect and fixed regression, random regression. In this study, batch-sex was the fixed effects, and a fixed regression was fitted for week age body weight effects; the direct additive genetic, permanent environment were the random effects. Comparing with AIC and BIC values, the best model should embed 2nd Legendre polynomials into fixed effects, 5th Legendre polynomials into additive genetic effects and permanent environmental effects. Heterogeneous residual variance was grouped into 5 levels. Each observation was set an initial estimate. The residual variance between the neighboring observations was treated as a linear regression. 【Result】 For the body weights on resource population, heritability was ranged from 0.46 to 0.63, repeatability varied from 0.88 to 0.92, the genetic correlation was ranged from 0.32 to 0.99, and permanent environmental correlation was varied from 0.34 to 0.99. The genetic correlations among the weeks reduced with the intervals increased, high correlations occurred between the neighboring weeks. The genetic variance, permanent environmental variance and residual variance increased with ages. The first three eigenvalues of additive genetic effects was 1 976.91, 161.95, and 42.22, respectively, and these eigenvalues could explain 99% of total variations. 【Conclusion】The genetic parameters on the early body weights in laying chickens were estimated with a random regression model. The individual growth curve could be altered by selection on the coefficients associated with the second eigenfunction. The right time seemed to select on 3 to 6 week. Estimates of heritability in the resource population were larger than the results in the literatures.
Keywords：body weight;random regression model;heritability;eigenvalue;layer


PDF (508KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
郭军, 曲亮, 窦套存, 王星果, 沈曼曼, 胡玉萍, 王克华. 应用随机回归模型估计蛋鸡体重遗传参数[J]. 中国农业科学, 2020, 53(11): 2297-2304 doi:10.3864/j.issn.0578-1752.2020.11.015
GUO Jun, QU Liang, DOU TaoCun, WANG XingGuo, SHEN ManMan, HU YuPing, WANG KeHua. Using Random Regression Models to Estimate Genetic Parameters on Body Weights in Layers[J]. Scientia Acricultura Sinica, 2020, 53(11): 2297-2304 doi:10.3864/j.issn.0578-1752.2020.11.015

0 引言

【研究意义】体重是蛋鸡选育目标之一。为节约生产成本、减少饲料消耗,蛋鸡体重应在满足产蛋性能需要的前提下尽量减少^[1]。ANDERSON等比较分析了1958—2011年北卡随机交配群体与商品蛋鸡群体生产性能评测试验,结果表明商品蛋鸡早期体重持续降低^[2]。绿壳蛋鸡已在我国商品化生产,然而绿壳蛋鸡体重遗传力等参数尚未见报到,影响了绿壳蛋鸡选择准确性。【前人研究进展】蛋鸡体重可以重复测量,并随测量时间呈现连续递进变化,此类性状称为纵向性状,也称动态性状^[3]、函数值性状^[4]。以随机回归模型解析动态性状遗传参数是当前流行趋势。近年来,利用随机回归模型评估家禽体重研究取得一些进展。BEGLI等以艾维因肉鸡与伊朗地方鸡F₂资源群体为素材,评估体重与饲料利用效率性状^[5]。同样针对肉鸡,MEBRATIE等应用随机回归模型分析了科宝肉鸡体重性状,结果显示遗传背景随生长阶段推移而改变^[6]。ROVADOSCKI等^[7]以随机回归模型分析了散养条件下巴西4个试验品系体重遗传参数。RAFAT等^[8]应用随机回归模型解析了火鸡2—32周龄体重遗传力、遗传相关系数,发现随机回归模型不需要校正数据,还比传统模型提供了更多信息。除了鸡和火鸡之外,应用随机模型还评估了肉用鹌鹑和蛋用鹌鹑体重性状^[9,10,11,12]。【本研究切入点】综上所述,多个团队以随机回归模型评估了肉用家禽体重性状。针对蛋鸡尚未见应用随机回归模型评估体重性状。【拟解决的关键问题】本研究以白莱航鸡与东乡绿壳蛋鸡F₂资源群体为素材,收集2010—2013年体重数据,剖分方差组分,解析遗传参数,分析特征值及特征方程。研究结果将为绿壳蛋鸡选育提供支持。

1 材料与方法

1.1 试验动物

体重数据采集自江苏省家禽研究所邵伯基地（江苏省扬州市江都区邵伯镇小街2号）F₂蛋鸡资源群体,有关群体构建信息详见文献[13]。简言之,以东乡绿壳蛋鸡、白莱航鸡为亲本,经正反交获得F₁代、F₂代,其中F₁代出雏1 581只鸡,F₂代出雏3 749只鸡。亲代出雏时间为2011年8月21日,F₁出雏时间为2012年7月5日,F₂出雏时间为2013年2月5日。试验鸡出雏时戴翅号,翻肛鉴别雌雄。育雏1—9周龄期间,隔周称重,称重前禁食12 h。

1.2 统计分析

1.2.1 数据整理 蛋鸡资源群体体重原始数据共有26 532条记录,其中1周龄5 303条、3周龄5 280条、5周龄5 310条、7周龄5 275条、9周龄5 353条。数据清洗包括去除翅号重复个体、去除离群值、去除性别不明个体、去除少于4条记录个体。经数据清洗后,资源群体体重数据集剩余25 483条记录。其中绿壳蛋鸡2 223条,白莱航鸡696条,F₁代6 002条,F₂代16 562条。系谱数据包含5 871只鸡,其中4 174只鸡有5条记录,802只鸡有4条记录,128只鸡没有记录。以ANOVA分析批次、性别、母亲体重对蛋鸡体重的影响,确定影响体重的非加性遗传因素。表1列出资源群体体重表型值信息。

Table 1
表1
表1蛋鸡资源群体体重数据统计
Table 1Statistics on body weights in the resource population

世代 Generation	1周龄体重 1st-week BW	3周龄体重 3rd-week BW	5周龄体重 5th-week BW	7周龄体重 7th-week BW	9周龄体重 9th-week BW
绿壳蛋鸡公鸡Blue shelled cocks	48.53b±5.24	107.40b±14.51	167.13b±27.25	301.11b±47.41	469.60b,c±68.73
绿壳蛋鸡母鸡Blue shelled hens	46.29 a±5.14	97.05a±12.56	147.23a±24.11	260.84a±37.50	396.74a±52.44
白莱航鸡公鸡White leghorn cocks	69.54f±6.80	162.88g±14.94	268.08f±28.13	473.17f±38.15	634.12g±67.65
白莱航鸡母鸡White leghorn hens	66.02e±6.75	145.29e±13.31	236.76d±23.36	397.29e±36.25	539.40e±55.33
F1代公鸡Cocks in F1 generation	47.05a±7.74	141.15d±20.34	273.07f±31.35	382.72e±48.58	569.77f±67.75
F1代母鸡Hens in F1 generation	45.64a±7.35	130.03c±19.90	241.94d±29.27	331.45c±39.61	478.98c±58.73
F2代公鸡Cocks in F2 generation	62.91d±5.82	152.26f±19.45	252.52e±34.15	393.87e±56.56	522.68d±71.82
F2代母鸡Hens in F2 generation	60.61c±5.33	139.27d±15.96	225.19c±28.33	353.03d±47.51	458.44b±56.63

Different letters in same column indicate significant difference among groups as determined by SNK multiple comparisons(P<0.05)
体重平均值标为SNK两两比较结果,不同字母表示差异显著（P<0.05）

新窗口打开|下载CSV

1.2.2 遗传模型 用WOMBAT软件估计方差组分、遗传参数,并预测育种值^[14]。残差处理影响遗传评估结果准确性。本研究以不同水平处理残差,即异质残差方法。首先,以单性状动物模型按周龄分别分析体重数据,残差相近的划为同一水平。依据单性状模型分析结果,确定残差水平以及初始设定值。然后,以随机回归模型评估资源群体体重性状,当参数向量变化小于10^-8、对数似然值变化小于5×10^-4时,运行达到收敛标准,完成计算。随机回归模型数学表达式为,

${{y}_{ikl}}=FE+\sum\limits_{m=0}^{{{n}_{1}}}{{{b}_{l}}{{\phi }_{m}}({{t}^{*}})}+\sum\limits_{m=0}^{{{n}_{2}}}{{{a}_{km}}}{{\phi }_{m}}({{t}^{*}})+\sum\limits_{m=0}^{{{n}_{3}}}{{{p}_{km}}}{{\phi }_{m}}({{t}^{*}})+{{e}_{ikl}}$

式中,y_ikl是第i批次第l周龄第k只鸡体重;FE是固定效应,包括性别效应和世代效应;b_l是第l周龄第m个固定回归系数;a_km是第k只鸡加性效应第m个随机回归系数;p_km是第k只鸡永久环境效应第m个随机回归系数;t^*是标准化的时间,取值在-1和+1之间;φ_m是嵌入的勒让德多项式;e_ikl是残差效应;n₁、n₂、n₃是嵌入固定效应、加性遗传以及永久环境效应勒让德多项式阶数。

1.2.3 方差参数及特征方程 计算遗传参数过程包括方差组分剖分、标准误计算以及特征方程分析。遗传、永久环境方差计算公式为,

$\sigma _{a}^{2}={{\phi }^{'}}{{K}_{a}}\phi $

$\sigma _{pe}^{2}={{\phi }^{'}}{{K}_{pe}}\phi $

式中,$\sigma _{a}^{2}$、$\sigma _{pe}^{2}$为蛋鸡体重加性遗传、永久环境方差。$\phi $为勒让德多项式回归系数矩阵,由标准化的时间与勒让德多项式相乘。K_a、K_pe为随机回归系数矩阵,由Wombat软件获得。

遗传相关标准误计算公式为,

$S{{E}_{{{r}_{{{A}_{xy}}}}}}=\frac{1-r_{A}^{2}}{\sqrt{2}}\sqrt{\frac{SE(h_{x}^{2})SE(h_{y}^{2})}{h_{x}^{2}h_{y}^{2}}}$

式中,SE为标准误,r_A为x与y日龄遗传相关,h²为遗传力,x、y分别为日龄。

K矩阵的特征值及特征向量通过R计算获得,其计算代码为eigen(K).为获得特征方程,需计算$\Lambda E$,E为特征向量,$\Lambda $为勒让德多项式系数矩阵^[15]。5阶多项式系数矩阵为,

${{\Lambda }_{5}}=\left[ \begin{matrix} \text{0}\text{.7071} & 0 & -0.7906 & 0 & 0.7950 \\ 0 & 1.2247 & 0 & -2.8063 & 0 \\ 0 & 0 & 2.3717 & 0 & -7.9550 \\ 0 & 0 & 0 & 4.6771 & 0 \\ 0 & 0 & 0 & 0 & 9.2808 \\\end{matrix} \right]$

1.2.4 模型比较 使用赤池弘次信息准则（Akaike’s information criterion,AIC）以及贝叶斯信息准则（Bayesian Information Criterion,BIC）选择最优模型。AIC、BIC分别写作,

AIC=-2lgL+2p

BIC=-2lgL+plg(N-r)

其中,L为模型最大似然值的对数,p为模型参数数量,N为观察值总数,r为固定效应指示矩阵阶数。

AIC、BIC都对过多参数进行惩罚,相对而言BIC惩罚程度更大。优先选择AIC、BIC值偏小的模型^[16]。

2 结果

2.1 固定因子确定

由表1可知,蛋鸡体重标准差随周龄增加而增加。同周龄体重SNK多重比较可知,白莱航公鸡较重,绿壳蛋鸡母鸡较轻。经SPSS直方图、P-P图及Q-Q图分析体重数据符合正态分布。ANOVA分析表明,公鸡体重高于同周龄母鸡体重（P<0.001）,同周龄世代之间存在显著差异（P<0.05）。因此,动物模型将批次（世代）和性别列入固定效应。

2.2 模型选择

依据表2列出的AIC、BIC选择标准,遗传模型加性遗传效应宜包含5阶勒让德多项式,永久环境模型宜包含5阶勒让德多项式,固定效应宜包含2阶勒让德多项式。设定异质性残差是由于生理条件、健康状态以及一些未知因素导致的不同周龄体重上的差异。残差设定为5个水平,即每次观测设定一个残差初始值,观测间隔期残差以线性回归计算。

Table 2
表2
表2蛋鸡体重遗传模型比较
Table 2Comparison of models on body weight in laying chickens

加性遗传效应阶数 Orders of additive genetic effects	永久环境效应阶数 Orders of PE effects	参数个数 The number of parameters	最大对数似然值 Maximum lgL	AIC	BIC
2	2	11	-84372	168766	168855
2	3	14	-83807	167642	167755
2	4	18	-83776	167589	167734
2	5	23	-83734	167514	167514
2	6	29	-83734	167526	167760
3	3	17	-83627	167288	167426
3	4	21	-83599	167240	167410
3	5	26	-83553	167157	167367
3	6	32	-83553	167169	167428
4	4	25	-83515	167081	167283
4	5	30	-83419	166899	167142
4	6	36	-83419	166911	167202
5	5	35	-83052	166173	166456
5	6	41	-83052	166185	166517
6	6	47	-83052	166197	166577

新窗口打开|下载CSV

2.3 遗传参数估计

随机回归模型以无限维形式呈现方差-协方差矩阵,表3按周龄给出体重方差组分及遗传参数。加性遗传方差、永久环境方差及残差演变趋势基本一致,即随周龄增加而增加。加性遗传方差大于同周龄永久环境方差。加性遗传方差和永久环境方差标准误都很小,大部分变异系数在10%以内,表明方差参数估值比较精确。

Table 3
表3
表3蛋鸡体重方差组分和遗传参数
Table 3Variance component and genetic parameters on body weight in resource population

周龄 Weeks	加性遗传方差 Additive variance	永久环境方差 Permanent environmental variance	残差 Residual	表型方差 Phenotypic variance	遗传力 Heritability	永久环境方差占比 $\sigma _{pe}^{2}/\sigma _{p}^{2}$	重复力 Repeatability
1	18.91±1.44	14.76±0.85	3.99	37.67±1.01	0.50±0.03	0.39±0.03	0.891
2	158.36±13.51	70.01±8.23	22.85	251.21±9.07	0.63±0.04	0.28±0.04	0.91
3	214.60±14.83	153.93±8.80	41.70	410.23±10.50	0.52±0.03	0.38±0.02	0.90
4	538.68±32.11	349.48± 18.39	87.74	975.89±24.30	0.55±0.02	0.36±0.02	0.91
5	925.68±55.51	528.66± 30.59	133.77	1588.11±40.61	0.58±0.02	0.33±0.02	0.92
6	1275.48±86.87	694.50± 47.56	264.02	2233.99±57.81	0.57±0.03	0.31±0.03	0.88
7	1882.89±152.26	1100.43± 85.98	394.26	3377.59±95.76	0.56±0.03	0.33±0.03	0.88
8	2471.92±216.91	1798.51±126.09	498.20	4768.62±135.92	0.52±0.03	0.38±0.03	0.90
9	2797.48±238.06	2731.94±147.03	602.13	6131.55±159.58	0.46±0.03	0.45±0.03	0.90

Considering the standard error of repeatability approached zero, this item was omitted
重复力标准误接近于0,故省略

新窗口打开|下载CSV

表3列出蛋鸡资源群体1—9周龄体重遗传力和重复力。绿壳蛋鸡与白莱航鸡资源群体体重遗传力为0.46—0.63,最高值出现在第2周。除第2周之外,遗传力走势趋向两头低中间高的钟型。蛋鸡资源群体早期体重遗传力为中等偏高,表明该群体体重性状具有较多遗传潜能。永久环境效应占比与遗传力走势不同,呈现两头高中间低的形势。蛋鸡体重重复力维持在0.90左右,表明蛋鸡体重比较稳定,还表明重复测量差异主要来自个体间差异。

各周龄体重遗传相关系数、永久环境相关系数见表4,相邻周龄遗传相关系数和永久环境相关系数较高,两种相关系数随着周龄间隔增大而减小。各周龄永久环境效应为中等到高等相关,表明永久环境对体重有重要影响。

Table 4
表4
表4不同周龄蛋鸡体重遗传相关系数(对角线下)及永久环境相关系数(对角线上)
Table 4Estimated values of genetic (below the diagonal) and permanent environmental correlations (above the diagonal) on body weight

周龄 Weeks	周龄 Weeks
	1	2	3	4	5	6	7	8	9
1		0.59±0.05	0.65±0.03	0.59±0.03	0.54±0.03	0.48±0.05	0.38±0.05	0.34±0.05	0.42±0.04
2	0.68±0.02		0.76±0.03	0.49±0.05	0.43±0.05	0.48±0.06	0.52±0.06	0.54±0.05	0.50±0.05
3	0.86±0.01	0.71±0.02		0.93±0.01	0.87±0.01	0.77±0.02	0.62±0.03	0.57±0.03	0.71±0.02
4	0.71±0.02	0.32±0.03	0.90±0.01		0.97±0.00	0.85±0.01	0.64±0.03	0.57±0.03	0.76±0.02
5	0.68±0.02	0.33±0.03	0.89±0.01	0.99±0.00		0.94±0.01	0.77±0.02	0.71±0.02	0.86±0.01
6	0.70±0.02	0.54±0.03	0.91±0.01	0.91±0.01	0.95±0.00		0.94±0.01	0.90±0.01	0.98±0.00
7	0.67±0.02	0.72±0.02	0.86±0.01	0.74±0.01	0.80±0.01	0.95±0.00		0.99±0.00	0.97±0.00
8	0.66±0.02	0.73±0.02	0.82±0.01	0.67±0.02	0.73±0.01	0.90±0.01	0.99±0.00		0.96±0.00
9	0.67±0.02	0.40±0.04	0.78±0.02	0.82±0.01	0.86±0.01	0.89±0.01	0.85±0.01	0.87±0.01

新窗口打开|下载CSV

2.4 特征方程分析

加性遗传随机回归系数矩阵特征值依次为：1 976.91、161.95、42.22、16.72、0.22,所占百分比为89.94、7.37、1.92、0.76、0.01。第4特征值及后面的特征值占比少于1%,对蛋鸡早期生长的贡献很少,故忽略不计。如图1所示,加性遗传第1特征方程近乎线性,全程为正值。第2特征方程呈现余弦波走势,19—46日龄以及邻近第9周为正值,其余为负值。第3特征方程为波浪状,1—7周龄为正值,第8周为负值且呈急剧下降。永久环境随机回归系数矩阵特征值依次为：1 341.10、124.70、35.51、1.53、0.57,所占百分比为89.20、8.29、2.36、0.10、0.04。

图1

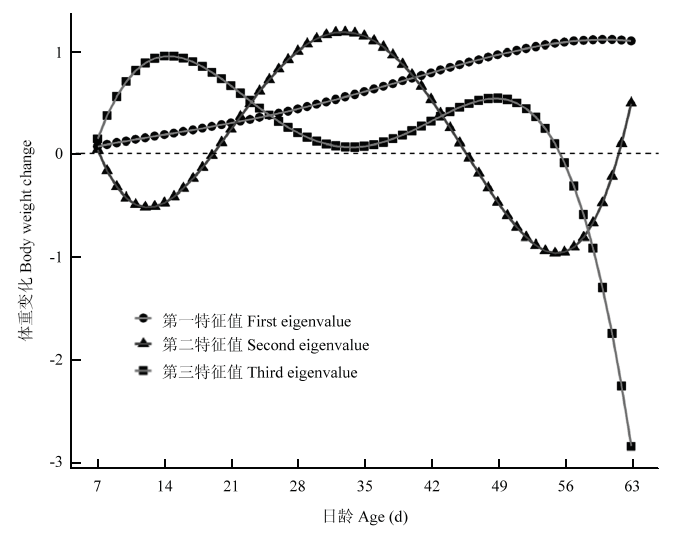新窗口打开|下载原图ZIP|生成PPT
图1体重遗传关系矩阵前3个特征值及相应特征方程

Fig. 1Three largest eigenvalues of the eigenfunctions on body weight

3 讨论

传统上,畜禽遗传评估以多性状动物模型分析重复测量育种数据。与多性状动物模型相比,随机回归模型的优点在于：①可以利用特征值系数有效改变性状曲线;②以较少的参数拟合方差-协方差矩阵;③能够利用不完整记录^{[15, 17]}。本研究利用蛋鸡资源群体体重动态数据,以动物模型估计遗传参数,分析早期体重遗传潜能以及选择时机。为实现研究主旨,需要掌控好两个关键点,即模型的优化和特征方程的建立。

特征方程可用于选育蛋鸡体重。加性遗传系数矩阵特征值具有生物学意义,它是遗传变异在各个维度的最大选育潜力。本研究中,随机回归模型赋予加性遗传系数矩阵时间属性,因而通过特征向量建立以时间为自变量的特征方程。加性遗传系数矩阵第一特征值反应蛋鸡线性生长趋势。蛋鸡体重第一特征方程在1—9周时间段内为正值,表明选择任意时间点体重也搭车选择其他时间点,无论选择增加体重还是选择减少体重。应用随机回归模型分析鹌鹑体重,结果表明加性遗传效应系数矩阵第1特征值及其特征向量约占总变异87%,与本研究结果相当^[18]。BOLIGON等^[16]分析了内洛尔牛初生重至成年体重遗传参数变化,结果表明第1特征值约占总变异的90%。ABEGAZ等^[19]以随机回归模型分析了埃塞俄比亚奥罗绵羊体重遗传变异规律,结果表明第1特征值约占总遗传变异83%,与本文结果相近。然而,肉牛体重遗传评估结果表明,第1特征值解释了96%遗传变异^[20]。肉牛上的研究结果不同于其它物种,或许归因于遗传背景,也可能因为肉牛体重遗传评估时使用了降维处理方式,即忽略AIC、BIC选择,强行将随机回归系数矩阵降阶。加性遗传系数矩阵第二特征值可用于改变个体生长发育曲线。然而,考虑到第2特征值在遗传变异中的占比,选择该系数的遗传进展将会缓慢。MEYER等^[21]指出,特征值占比高于5%的选择都有意义,因而可以对资源群体加性遗传系数矩阵第二特征值进行选择。本团队应用随机回归模型还分析了蛋鸡资源群体蛋黄重^[13]、蛋壳强度^[22],但第二特征值占比低于5%,表明这两个性状不适合特征值选择。其他特征值因为总变异占比较少,选育时可忽略。

随机回归模型多项式阶数对于遗传参数、方差组分估计值很重要。POOL等认为,3阶勒让德多项式足以满足遗传评估生长或泌乳曲线的需要^[23]。高阶多项式不仅对计算能力提出更高要求,还带来标准误增大。育种实践中,BLUP方法容错性能较好,即使参数存在轻微偏差,也不至于影响育种值排序。然而,BROTHERSTONE等^[24]认为当数据分析难于收敛时,高阶多项式比低阶多项式效率更高。LEGARRA等^[25]认为降低多项式维数可能造成端值异常。本研究主旨在于估计遗传参数,故遗传模型应用高阶勒让德多项式。分析结果显示两个端值遗传力未出现异常。同一群体的另外两个性状,蛋黄重和蛋壳强度,由于应用低阶多项式处理,导致端值遗传力偏大^[13,22]。总之,随机回归模型的优化取决于研究目的。如果估计遗传参数,选择高阶多项式;如果预测育种值,考虑低阶多项式。

早期体重不仅与鸡的维持需要有关,还与个体健康程度、均匀度存在关联,因而国内外****针对早期体重开展了遗传评估工作。DRUYAN等^[26]分析了安卡肉鸡早期体重遗传参数,7、14、19日龄体重遗传力分别为0.56、0.54、0.63,与本研究结果相近。MOGHADAM等^[27]以多性状动物模型分析了肉鸡猝死、腹水与体重的关系,获得考尼仕鸡4周龄体重遗传力为0.45,白洛克鸡遗传力为0.35的研究结果,低于本文报告的结果。GAYA等^[28]以多性状动物模型分析罗斯肉鸡38日龄体重,获得其遗传力为0.40,低于本研究结果。本研究团队以如皋黄鸡为试验材料,应用REML方法评估其6周龄体重加性遗传力为0.33,低于本研究结果^[29]。以上鸡早期体重遗传分析结果存在差异,究其原因,与遗传背景不同有关,也与研究模型以及固定效应设置有关。本文遗传参数估计值略高于其它研究结果,与所用素材来自F₂杂交群体有关。

4 结论

随机回归模型可用于蛋鸡早期体重选育。研究结果表明：1）动物模型嵌入5阶勒让德多项式可以拟合加性遗传效应和永久环境效应;2）遗传相关和特征方程分析表明资源群体可是进行体重早期选择,通过选择特征值系数可以改变个体生长曲线,选择时机宜在3—6周龄;3）蛋鸡资源群体体重重复力在0.90左右,表明2—3次测量即可准确预测今后的体重水平;4）蛋鸡资源群体早期体重遗传力略高于其他群体同类研究结果。后续研究将进一步加强数据采集分析工作。如果体重数据能够包括9周龄之后记录,就能获知加性遗传第一特征方程能否回落,第二特征方程能否持续余弦波走势,对蛋鸡资源群体的选育工作提供更多支持。

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] GOODMAN B, GODFREY G F . Heritability of body weight in the domestic fowl
Poultry Science, 1956,35(1):50-53.
DOI:10.3382/ps.0350050URL [本文引用: 1]

[2] ANDERSON K, HAVENSTEIN G, JENKINS P, OSBORNE J . Changes in commercial laying stock performance, 1958-2011: Thirty-seven flocks of the North Carolina random sample and subsequent layer performance and management tests
World's Poultry Science Journal, 2013,69(3):489-514.
DOI:10.1017/S0043933913000536URL [本文引用: 1]

[3] 杨运清, 李仁杰, 李淑玲 . 动态性状遗传参数的估计方法
畜牧兽医学报, 1996(5):412-416.
URL [本文引用: 1]

YANG Y Q, LI R J, LI S L . An estimation method for genetic parameters of dynamic traits
Acta Veterinaria et Zootechnica Sinica, 1996(5):412-416.(in Chinese)
URL [本文引用: 1]

[4] JAFFRéZIC F, PLETCHER S D . Statistical models for estimating the genetic basis of repeated measures and other function-valued traits
Genetics, 2000,156(2):913-922.
[本文引用: 1]

[5] BEGLI H E, TORSHIZI R V, MASOUDI A A, EHSANI A, JENSEN J . Longitudinal analysis of body weight, feed intake and residual feed intake in F-2 chickens
Livestock Science, 2016,184:28-34.
[本文引用: 1]

[6] MEBRATIE W, SHIRALI M, MADSEN P, SAPP R L, HAWKEN R, JENSEN J . The effect of selection and sex on genetic parameters of body weight at different ages in a commercial broiler chicken population
Livestock Science, 2017, 204:78-87.
[本文引用: 1]

[7] ROVADOSCKI G A, PETRINI J, RAMIREZ-DIAZ J, PERTILE S F N, PERTILLE F, SALVIAN M, IUNG L H S, RODRIGUEZ M A P, ZAMPAR A, GAYA L G, CARVALHO R S B, COELHO A A D, SAVINO V J M, COUTINHO L L, MOURAO G B . Genetic parameters for growth characteristics of free-range chickens under univariate random regression models
Poultry Science, 2016,95(9):1989-1998.
[本文引用: 1]

[8] RAFAT S A, NAMAVAR P, SHODJA D J, JANMOHAMMADI H, KHOSROSHAHI H Z, DAVID I . Estimates of the genetic parameters of turkey body weight using random regression analysis
Animal, 2011,5(11):1699-1704.
DOI:10.1017/S1751731111000929URL [本文引用: 1]

[9] MOTA L F M, MARTINS P, LITTIERE T O, ABREU L R A, SILVA M A, BONAFE C M . Genetic evaluation and selection response for growth in meat-type quail through random regression models using B-spline functions and Legendre polynomials
Animal, 2018,12(4):667-674.
[本文引用: 1]

[10] KARAMI K, ZEREHDARAN S, TAHMOORESPUR M, BARZANOONI B, LOTFI E . Genetic evaluation of weekly body weight in Japanese quail using random regression models
British Poultry Science, 2017,58(1):13-18.
[本文引用: 1]

[11] BARBIERI A, ONO R K, CURSINO L L, FARAH M M, PIRES M P, BERTIPAGLIA T S, PIRES A V, CAVANI L, CARRENO L O D, FONSECA R . Genetic parameters for body weight in meat quail
Poultry Science, 2015,94(2):169-171.
[本文引用: 1]

[12] SILVA L P, RIBEIRO J C, CRISPIM A C, SILVA F G, BONAFE C M, SILVA F F, TORRES R A . Genetic parameters of body weight and egg traits in meat-type quail
Livestock Science, 2013,153(1-3):27-32.
DOI:10.1016/j.livsci.2013.01.014URL [本文引用: 1]

[13] 郭军, 王克华, 曲亮, 沈曼曼, 马猛, 窦套存, 胡玉萍 . 应用随机回归模型分析蛋鸡蛋黄质量遗传参数
南京农业大学学报, 2016,39(1):145-149.
[本文引用: 3]

GUO J, WANG K H, QU L, SHEN M M, MA M, DOU T C, HU Y P . Genetic parameters for yolk weight in resource population with random regression model
Journal of Nanjing Agricultural University, 2016,39(1):145-149. (in Chinese)
[本文引用: 3]

[14] MEYER K . WOMBAT—A tool for mixed model analyses in quantitative genetics by restricted maximum likelihood (REML)
Journal of Zhejiang University Science B, 2007,8(11):815-821.
DOI:10.1631/jzus.2007.B0815URL [本文引用: 1]

[15] KIRKPATRICK M, LOFSVOLD D, BULMER M . Analysis of the inheritance, selection and evolution of growth trajectories
Genetics, 1990,124(4):979-993.
[本文引用: 2]

[16] BOLIGON A A, MERCADANTE M E Z, FORNI S, L?BO R B, ALBUQUERQUE L G, . Covariance functions for body weight from birth to maturity in Nellore cows
Journal of Animal Science, 2010,88(3):849-859.
DOI:10.2527/jas.2008-1511URL [本文引用: 2]

[17] SCHAEFFER L . Application of random regression models in animal breeding
Livestock Production Science, 2004, 86(1/3):35-45.
[本文引用: 1]

[18] AKBAS Y, TAKMA C, YAYLAK E . Genetic parameters for quail body weights using a random regression model
South African Journal of Animal Science, 2004,34(2):104-109.
[本文引用: 1]

[19] ABEGAZ S, VAN WYK J B, OLIVIER J J, . Estimates of (co) variance function for growth to yearling in Horro sheep of Ethiopia using random regression model
Archives Animal Breeding, 2010,53(6):689-700.
DOI:10.5194/aab-53-689-2010URL [本文引用: 1]

[20] ARANGO J, CUNDIFF L, VAN VLECK L D . Covariance functions and random regression models for cow weight in beef cattle
Journal of Animal Science, 2004,82(1):54-67.
DOI:10.2527/2004.82154xURL [本文引用: 1]

[21] MEYER K, KIRKPATRICK M . Restricted maximum likelihood estimation of genetic principal components and smoothed covariance matrices
Genetics Selection Evolution, 2005,37(1):1.
DOI:10.1186/1297-9686-37-1-1URL [本文引用: 1]
Principal component analysis is a widely used 'dimension reduction' technique, albeit generally at a phenotypic level. It is shown that we can estimate genetic principal components directly through a simple reparameterisation of the usual linear, mixed model. This is applicable to any analysis fitting multiple, correlated genetic effects, whether effects for individual traits or sets of random regression coefficients to model trajectories. Depending on the magnitude of genetic correlation, a subset of the principal component generally suffices to capture the bulk of genetic variation. Corresponding estimates of genetic covariance matrices are more parsimonious, have reduced rank and are smoothed, with the number of parameters required to model the dispersion structure reduced from k (k + 1)/2 to m (2 k - m + 1)/2 for k effects and m principal components. Estimation of these parameters, the largest eigenvalues and pertaining eigenvectors of the genetic covariance matrix, via restricted maximum likelihood using derivatives of the likelihood, is described. It is shown that reduced rank estimation can reduce computational requirements of multivariate analyses substantially. An application to the analysis of eight traits recorded via live ultrasound scanning of beef cattle is given.

[22] GUO J, MA M, QU L, SHEN M M, DOU T C, WANG K H . Estimation of genetic parameters related to eggshell strength using random regression models
British Poultry Science, 2015,56(6):645-650.
DOI:10.1080/00071668.2015.1113503URL [本文引用: 2]

[23] POOL M, MEUWISSEN T . Reduction of the number of parameters needed for a polynomial random regression test day model
Livestock Production Science, 2000,64(2/3):133-145.
DOI:10.1016/S0301-6226(99)00166-9URL [本文引用: 1]

[24] BROTHERSTONE S, WHITE I, MEYER K . Genetic modelling of daily milk yield using orthogonal polynomials and parametric curves
2000,70(3):407-415.
[本文引用: 1]

[25] LEGARRA A, MISZTAL I, BERTRAND J . Constructing covariance functions for random regression models for growth in Gelbvieh beef cattle
Journal of Aanimal Science, 2004,82(6):1564-1571.
[本文引用: 1]

[26] DRUYAN S, SHLOSBERG A, CAHANER A . Evaluation of growth rate, body weight, heart rate, and blood parameters as potential indicators for selection against susceptibility to the ascites syndrome in young broilers
Poultry Science, 2007,86(4):621-629.
DOI:10.1093/ps/86.4.621URL [本文引用: 1]

[27] MOGHADAM H K, MCMILLAN I, CHAMBERS J R, JULIAN R J, TRANCHANT C C . Heritability of sudden death syndrome and its associated correlations to ascites and body weight in broilers
British Poultry Science, 2005,46(1):54-57.
[本文引用: 1]

[28] GAYA L G, FERRAZ J B S, REZENDE F M, MOUR?O G B, MATTOS E C, ELER J P, MICHELAN FILHO T, . Heritability and genetic correlation estimates for performance and carcass and body composition traits in a male broiler line
Poultry Science, 2006,85(5):837-843.
[本文引用: 1]

[29] 窦套存, 王克华, 曲亮, 沈曼曼, 胡玉萍, 郭军 . 如皋黄鸡42日龄体重母体遗传效应评估
山西农业大学学报(自然科学版), 2014,34(6):511-517.
[本文引用: 1]

DOU T C, WANG K H, QU L, SHEN M M, HU Y P, GUO J . Maternal genetic effects of body weight in Rugao Yellow Chicken
Journal of Shanxi Agricultural University(Nature Science Edition), 2014,34(6):511-517. (in Chinese)
[本文引用: 1]