民用型倾转旋翼机必须满足发动机失效后安全飞行的FAA条款[1]。旋翼机通常出现的发动机失效情况分为单发失效和双发失效。发动机失效/故障后,倾转旋翼机可选择继续飞行或着陆,取决于倾转旋翼机总重、倾转旋翼机剩余功率及单发失效时的飞行状态及条件;双发失效时,倾转旋翼机必须进行着陆飞行;发动机失效时,倾转旋翼机驾驶员此时需合理使用发动机的剩余功率,综合考虑飞行状态及外部条件,以规划飞行策略及飞行路径。飞行试验风险大、费时耗资, 而数值优化技术可以相对低成本、快速地给出最优的操纵策略,可以为飞行试验提供参考。
基于最优控制方法的直升机低速回避区(H-V曲线)及飞行轨迹数值优化的研究已开展了大量工作[2-5],但国内外对倾转旋翼机发动机失效后的低速回避区、飞行轨迹及操纵策略的研究相对较少。倾转旋翼机的发动机失效后飞行轨迹研究需面临倾转旋翼机操纵冗余问题,同时短舱倾转过渡也会有不同影响。
Carlson等[6-8]以旋翼拉力系数、短舱倾角、纵向杆为控制变量,解决倾转旋翼机操纵冗余的问题,建立纵向二维刚体飞行动力学模型,系统阐述了倾转旋翼机发动机失效后飞行轨迹优化问题, 并结合安全着陆要求,对倾转旋翼机低速回避区进行了充分的研究。国内严旭飞和陈仁良[9-10]引入混合操纵模式,依此建立倾转旋翼机纵向二维飞行动力学模型,并基于最优控制理论研究了倾转旋翼机短距起飞单发失效着陆的最优化轨迹及倾转过渡过程的操纵策略优化。
本文引入XV-15倾转旋翼机混合操纵方式,建立倾转旋翼机发动机失效飞行动力学模型,考虑倾转旋翼机性能、操纵和安全着陆等要求,基于最小回避区的思想,建立适当的目标函数和约束,形成发动机失效后安全着陆的轨迹优化最优控制模型;采用间断有限元法和序列二次规划(SQP)算法进行求解。计算了XV-15倾转旋翼机单发、全发失效后低速回避区,分析了不同飞行重量、操纵要求对低速回避区的影响,给出了相应的高悬停点、拐点、低悬停点的最优化飞行轨迹。
1 倾转旋翼机发动机失效飞行动力学模型 1.1 倾转旋翼机增广纵向刚体飞行动力学模型 倾转旋翼机具备纵向对称特征,2台发动机以传动轴共同驱动2副旋翼,倾转旋翼机单发、双发失效后,左右旋翼仍以相同转速同步运转;另外不考虑横向运动,倾转旋翼机的发动机失效后飞行及操纵都应当在纵向平面内。因此,建立倾转旋翼机二维纵向刚体飞行动力学模型,可写为
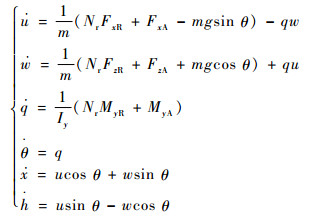 | (1) |
式中:旋翼个数Nr=2;u和w分别为体轴系中纵向速度和垂向速度;q为俯仰角速度;θ为俯仰角;x为水平位移;h为高度;Iy为倾转旋翼机俯仰惯性距;FxR、FzR和MyR分别为旋翼纵向、垂向的力和俯仰力矩;FxA、FzA和MyA分别为机体所有气动面产生的纵向力、垂向力和俯仰力矩;m为倾转旋翼机总重;g为重力加速度。
旋翼气动力的计算采用叶素理论、均匀入流模型、准定常一阶挥舞运动[11]。考虑旋翼尾迹对机翼的干扰,将机翼划分为2个区域:滑流区(受旋翼尾流直接影响)和自由流区(不受旋翼尾流直接影响)。自由流区的机翼气动力模型与常规飞机机翼类似,滑流区的机翼气动力模型需要考虑旋翼在机翼处的诱导速度和滑流区的面积;不考虑旋翼尾迹、机体对尾翼的气动干扰[6]。各部件的气动力和力矩系数来自于XV-15的吹风数据[11]。
倾转旋翼机发动机失效后,发动机可用轴功率改变,必然影响旋翼转速,因此功率平衡方程可写为
 | (2) |
式中:Ps为可用轴功率;Pr为全机需用功率;IR为旋翼转动惯量;Ω为旋翼转速;POEI/AEI为单发、全发失效后的发动机功率;τp为发动机功率时间常数。
由于倾转旋翼机的操纵特点,引入混合操纵模式,以解决操纵冗余问题, 该混合操纵可将倾转旋翼机的操纵量缩减至3个,由总距杆量δXCOL、纵向杆δXLN、短舱倾转角δIN表述左右旋翼桨根总距θ0、纵向周期变距θs和升降舵偏转角θe,方程如下:
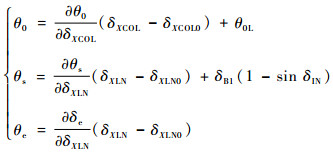 | (3) |
式中:δXCOL0为总距杆零位;?θ0/?δXCOL为总距系数,与δIN相关;旋翼总距补偿角θ0L与δIN相关;δXLN0为纵向杆零位;?θs/?δXLN为旋翼纵向周期变距系数,与δIN相关;δB1为补偿量;?δe/?δXLN为升降舵偏转系数,与δIN相关[12]。
左右旋翼横向周期变距θc为0,为避免数值优化计算过程中的“bang-bang”现象,采用操纵量的一阶导数作为控制变量,并将原有操纵量作为新的状态变量[9]。
因此,倾转旋翼机发动机失效的飞行动力学模型可表述如下:
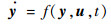 | (4) |
式中:y=[u, w, q, θ, x, h, Ω, Ps, δXCOL, δXLN, δIN]为状态变量矩阵;
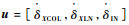
1.2 飞行动力学模型验证 以XV-15倾转旋翼机为研究对象,图 1给出了短舱倾转角为90°(直升机模式)、襟翼/副翼角度为40°/25°和短舱倾转角为75°、襟翼/副翼角度为40°/25°的2种飞行模态下,不同前飞速度V的配平结果。本文模型配平状态与GTRS模型结果[12-13]进行对比分析,建立的倾转旋翼机二维纵向刚体飞行动力学模型较为准确,可用于后续的飞行轨迹优化研究。
 |
| 图 1 不同模型的配平状态数据对比 Fig. 1 Comparison results of trim from different models |
| 图选项 |
2 倾转旋翼机发动机失效最优控制模型 2.1 最优控制模型建模 对于给定的外界环境条件和直升机总重量,可能存在由直升机飞行高度和飞行速度的组合来描述的不安全区域,在这个不安全区域内飞行时如果出现发动机失效,即使具有一定飞行技术的驾驶员也不能使直升机安全着陆,该不安全区域被定义为回避区,回避区的边界曲线也被称为高度-速度曲线(H-V曲线)。图 2给出了倾转旋翼机发动机失效后的高度-速度曲线示意图。
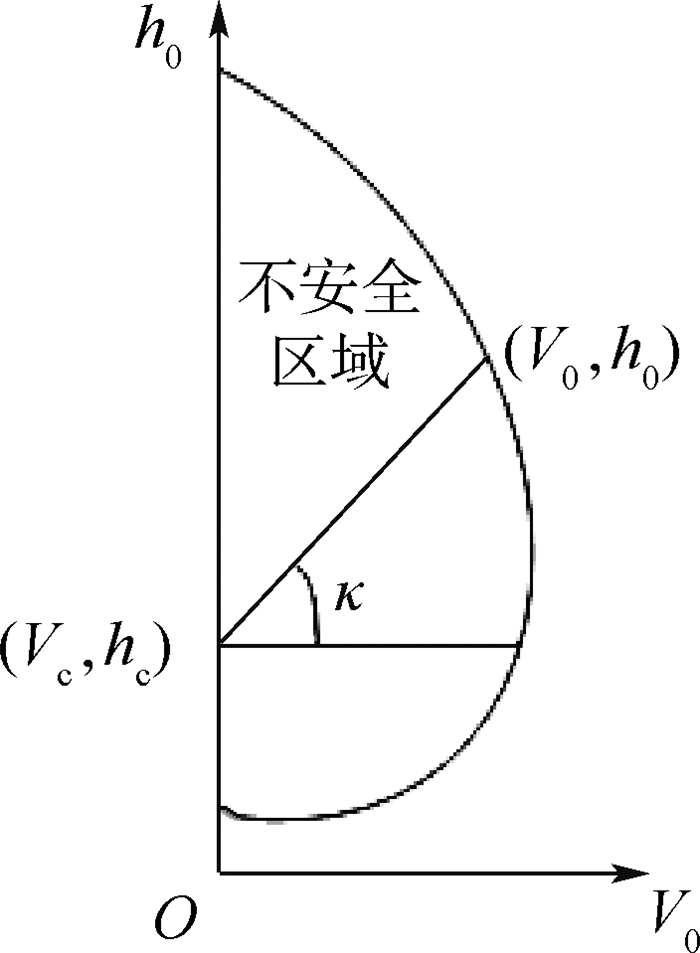 |
| 图 2 经典旋翼机低速回避区示意图 Fig. 2 Classical low-speed avoidance zone of rotorcraft |
| 图选项 |
按照最小化回避区的思想,将H-V曲线求解问题转换为安全着陆最优控制问题[6, 8, 14]。假定一条由(V0, h0)组合的曲线,该曲线上任意一点都满足发动机失效后安全着陆飞行要求, 以逼近不安全区域的边界;在给定的倾转旋翼机重量和安全飞行要求下,使该曲线所含区域最小化,即为最小化回避区思想。因此在计算该曲线时,可转化为该曲线上任意一点(V0, h0)至低速回避区内参考点的(Vc, hc)距离最小;同时倾转旋翼机发动机失效后,需要考虑驾驶员操纵负荷,飞行过程中以相对平滑的操纵为佳;且需保持机体在合适的范围内运动。因此,倾转旋翼机H-V曲线上任意一点的目标函数为
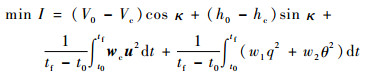 | (5) |
式中: t0为初始时刻;tf为末端时刻;wc为控制矩阵的加权向量;w1、w2为机体姿态加权系数。
状态方程为倾转旋翼机飞行动力学模型方程(4);将图 2中(V0, h0)作为额外优化变量,通过夹角κ进行约束, 以避免最优控制模型的局部最优解。倾转旋翼机发动机失效轨迹优化初始边界条件应为飞行器当前稳态飞行状态,因此飞行轨迹优化的初始条件为
 | (6) |
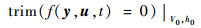 | (7) |
末端约束为发动机失效后倾转旋翼机安全着陆的限制条件,因此设定为
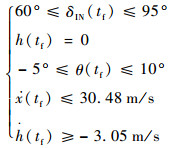 | (8) |
在着陆飞行过程中,由于倾转旋翼机的操纵系统限制及结构限制,在优化计算中需要对操纵杆量、倾转角度、短舱倾转角速度[6]进行约束;考虑驾驶员的操纵负荷等问题, 需要对操纵速率进行限制;旋翼转速、机体俯仰角和俯仰角速率也同样需要进行约束。因此路径约束如下:
 | (9) |
2.2 无量纲与缩放化处理 数值优化计算过程中,由于状态变量和控制变量的量纲不同及数值之间量级差别较大,会导致数值求解误差过大。需要对最优控制模型进行无量纲缩放化处理,其中飞行动力学方程(4)可写成如下形式:
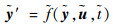 | (10) |
式中:
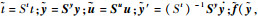
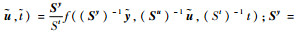
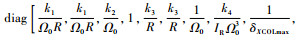
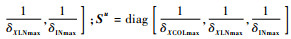
2.3 最优控制模型数值解法 倾转旋翼机发动机失效着陆过程是连续动态最优控制问题,状态变量和控制变量较多,解析法无法适用。本文采用间断有限元法进行离散化[4, 15-16],将连续动态最优控制问题转化为非线性规划(NLP)问题,并采用序列二次规划算法进行求解[17]。
间断有限元法具有较高数值分辨率,能使离散化计算更为灵活和高效。{Γh}是时间域Γ上的一个剖分,每个剖分称为K。t0≡t0 < t1 < … < tn-1 < tn≡tf, n>1,n个区间,每个区间Ti=[ti, ti+1],长度为hi, i=0, 1, …, n-1。多数情况下,tf未知,为方便处理,将时间域投影到单位时间域上:(t0, tf)→(0, 1)。
控制方程在每一时间剖分K上的弱形式为
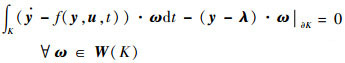 | (11) |
式中:ω为测试函数;λ为单元边界函数;W为测试函数空间。
对上述弱形式进行积分,并采用有限元法进行离散:
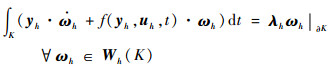 | (12) |
式中:(yh, uh, λh)∈(Yh, Uh, Λh)。有限元空间Yh、Uh、Wh可取为如下的形式:
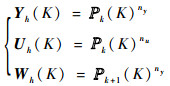 | (13) |
式中:

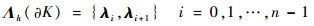 | (14) |
通量场值
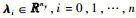
 | (15) |
控制函数u(t)只有单元区间函数,并没有类似于状态变量的通量值,因此只有单元内部变量。在单元节点处,一般有
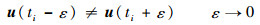 | (16) |
这就是间断有限元法。前文讨论的约束都是对状态变量的约束。对于控制变量,只有单元内部节点,而没有单元节点,往往会导致控制变量的断点值跑到约束之外,因此,对于控制变量的端点值,使用插值方法插出端点值,作为不等式约束加入最优化问题。
应用间断有限元法离散最优控制问题,式(12)可表示为残差形式:
 | (17) |
离散形式中的tf反映了单元时间步长hi也是未知的,因此在非线性规划问题中,优化变量X为
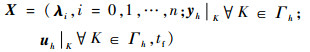 | (18) |
优化变量包含了单元内部状态变量值、单元内部控制变量值和末时间值。使用式(17),在每个单元内将控制方程离散化。同时,将最优控制的边界和约束方程式(6)~式(9)进行离散化形成非线性规划的约束方程。将目标函数(5)用优化变量X表示,构建出非线性规划模型。
2.4 最优控制模型验证计算 以XV-15为研究对象,图 3给出了本文模型与文献[6]计算结果的对比。飞行初始高度为12.192 m,初始速度为9.167 m/s,飞行重量为6 350 kg;文献[6]中,以旋翼拉力系数CT、短舱倾转角δIN、纵向杆位移量S为控制变量,并基于旋翼拉力系数CT建立旋翼气动力与功率模型,该方法虽极大简化了计算量,但无法反映出机体运动、旋翼参数及旋翼操纵量等对旋翼拉力和旋翼需用功率的影响。文献[6]飞行动力学模型与本文飞行动力学模型存在明显差异。
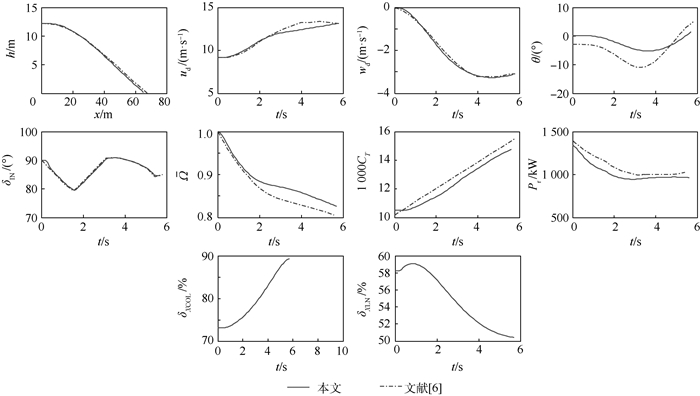 |
| 图 3 不同模型的单发失效状态最优化轨迹 Fig. 3 Optimal trajectory of different models in one engine inoperative (OEI) condition |
| 图选项 |
因此进行对比计算时,采用了特殊设置,路径约束中不对控制变量u进行限制,将优化末端时间固定为tf=5.8 s;并跟踪文献[6]中的短舱倾转角倾转过程δINobj,取消目标函数方程式(5)中最小距离项,目标方程设置为
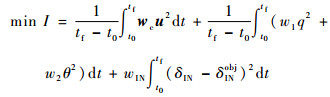 | (19) |
式中:wIN为跟踪加权系数。
从图 3中可以看出,wIN=1 000时,短舱倾转角的倾转过程基本与文献[6]一致,同时飞行轨迹、纵向地速ud、垂向地速wd基本重合,其他优化变量, 如无量纲旋翼转速Ω、旋翼拉力系数CT、需用功率Pr较为接近,机体俯仰角θ由于飞行动力学模型不同导致初始平衡态数据不一致,但在着陆飞行过程中的变化趋势基本一致;本次计算验证了本文建立的最优控制模型的可行性。
3 倾转旋翼机低速回避区 3.1 单发失效H-V曲线 基于第2节最优控制模型和数值优化算法,研究了不同高度和速度组合下的单发失效后着陆飞行轨迹和操纵策略。图 4中给出了倾转旋翼机重量m分别为5 896、6 123、6 350、6 804 kg及6 350 kg直升机模式下的XV-15倾转旋翼机单发失效后的H-V曲线。显示同一重量下,本文计算的低速回避区相对文献[6]中H-V曲线偏小,差异化较大;主要是由于建立的飞行动力学方程存在较大差异,最优控制模型中的差异性在2.4节中就有所体现。
 |
| 图 4 倾转旋翼机单发失效H-V曲线 Fig. 4 H-V diagram of tiltrotor in OEI condition |
| 图选项 |
由图 4看出,随着倾转旋翼机重量减小,低速回避区收缩。可推断,XV-15倾转旋翼机的起飞重量较低时,单发失效后的回避区很小,甚至消失,倾转旋翼机在起飞过程中极大保证了安全性,该起飞重量下XV-15倾转旋翼机在任意高度和速度组合下,单发失效后都能够安全着陆。在实际的起飞过程中,具有一个很小的爬升速度,虽然一定的爬升速度有利于安全着陆,但考虑到单发失效会出现在任意高速和速度,因此较为合理的XV-15垂直起飞时的最大安全重量应当在5 896 kg左右。
在起飞重量为6 804 kg时,低速回避区的拐点为(12.25 m/s, 15.35 m),即倾转旋翼机在大起飞重量进行起飞时,不宜采用垂直起飞模式,在爬升过程中一旦出现单发失效,较大概率没有足够的前飞速度以保证倾转旋翼机的安全着陆飞行。另一角度而言,倾转旋翼机采用滑跑起飞模式能够有效提高其最大起飞重量,滑跑起飞的离地高度和进入爬升的状态应规避该重量下的低速回避区。
起飞重量为6 350 kg的直升机模式下,低速回避区的区域大于同一重量下倾转过渡的低速回避区。由于短舱进行倾转时,能够快速有效地改变旋翼气动力的方向(见图 5)。短舱倾转旋转过程中,体轴系下旋翼对机体重心的前向力FxR迅速增加,倾转旋翼机能够获得更多的前飞速度;而直升机模式下,倾转旋翼机为获得足够前飞速度,需进行更大角度的俯冲,最终需求足够的高度和更多的时间以调整着陆姿态和速度。因此同一重量下,直升机模式下的单发失效低速回避区比正常倾转模式下的区域大。
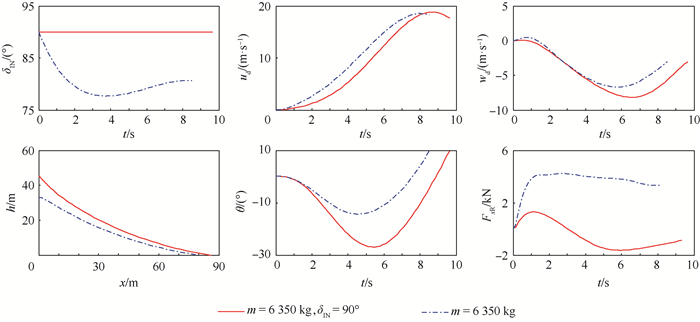 |
| 图 5 单发失效时高悬停点飞行轨迹及操纵时间历程(m=6 350 kg) Fig. 5 Flight trajectory and history of control of high hover point in OEI condition (m=6 350 kg) |
| 图选项 |
3.2 全发失效H-V曲线 对于双发旋翼飞行器,双发失效是极为罕见的,但仍然有必要进行双发失效的研究,以了解潜在的危险区域。对于双发失效的飞行器,以保证人员安全性为主,极端情况下,允许一定的飞行器损伤。因此,全发失效后安全着陆的飞行轨迹优化,限制条件可适当放宽,优化量调整为
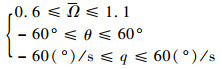 | (20) |
图 6给出了不同重量下倾转旋翼机的全发失效低速回避区曲线。图 6显示,全发失效状态下,倾转旋翼机的低速回避区随重量减小而递减,但飞行重量对于回避区的影响有限,即XV-15以最小起飞重量起飞时,全发失效的低速回避区依然存在且相对较大。双发失效时,倾转旋翼机的起飞重量对H-V曲线中的低悬停点高度基本无影响, 且下边界对高度变化并不敏感。最小起飞重量m=5 443 kg时, 低悬停点高度为1.59 m, 非常接近地面,该重量下H-V曲线的拐点速度达到26 m/s。在大概率发生双发失效情况下,倾转旋翼机不应采用垂直起飞模式,此时需采用滑跑起飞模式,倾转旋翼机在地面滑行加速至一定的起飞速度再进行爬升飞行。
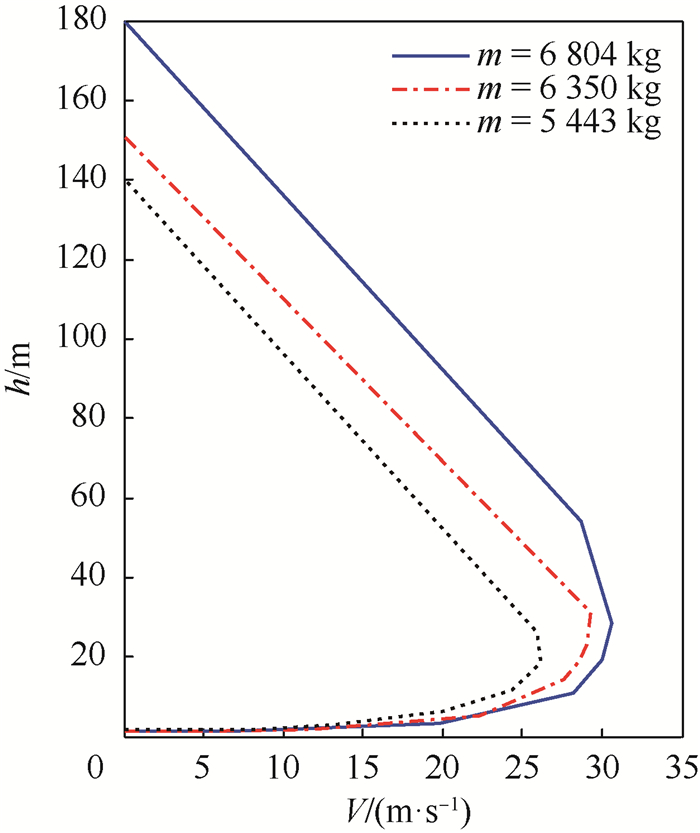 |
| 图 6 倾转旋翼机全发失效H-V曲线 Fig. 6 H-V diagram of tiltrotor in AEI condition |
| 图选项 |
图 7给出了起飞重量m=5 443 kg时低悬停点、拐点、高悬停点的飞行轨迹和操纵时间历程。在低悬停点时发生双发失效,倾转旋翼机处于垂直下降状态,在极短的时间内完成着陆过程,前飞速度及机体姿态基本无变化。拐点处的飞行过程中,倾转旋翼机初始具备较大前飞速度、较低的飞行高度,此过程需将部分前飞的动能用于维持滞空和调整姿态的时间,因此初始采取降低总距,减缓旋翼转速下降,后拉杆及短舱倾转角后倾,阻止掉高度,随后缓慢提总距和前推杆,缓慢下降高度。倾转旋翼机在高悬停点处,初始前飞速度为0或很小,需要由飞行高度提供足够的势能以保障安全着陆飞行。倾转旋翼机初始阶段增加前飞速度以消耗高度势能,随后调整飞行,达到安全着陆的要求;因此在初始2 s内倾转旋翼机采取降低总距、短舱前倾,以迅速进入俯冲阶段,降低飞行高度,促使飞行速度迅速增加,在此过程中旋翼转速急速下降,总距下放,导致旋翼拉力下降;随后在俯冲过程中提总距,短舱缓慢后倾,促使倾转旋翼机拉起,前飞速度迅速增加,下降率回调,达到安全触地速度和角度。
 |
| 图 7 全发失效时飞行轨迹及操纵时间历程(m=5 443 kg) Fig. 7 Flight trajectory and history of control in AEI condition (m=5 443 kg) |
| 图选项 |
4 结论 1) 本文以XV-15倾转旋翼机为研究对象,进行了基于最优控制理论的倾转旋翼机单发/全发失效的低速回避区研究,针对不同的飞行重量,给出了相应的H-V曲线。
2) 单发失效低速回避区曲线显示,XV-15倾转旋翼机采用垂直起飞模式的最大安全飞行重量为5 896 kg左右;采用滑跑起飞则可有效提升最大起飞重量。
3) 针对同一重量下,分析了倾转旋翼机不同飞行模式对低速回避区的影响,表明单发失效后倾转旋翼机短舱运动,能够有效减小低速回避区域。
4) XV-15倾转旋翼机全发失效低速回避区最小拐点速度达26 m/s, 在较大概率发生全发失效时,倾转旋翼机不宜采取垂直起飞模式。
5) 单发/双发失效后每一安全着陆飞行,都将倾转旋翼机需用功率降低至剩余功率的水平,并合理规划使用剩余功率、高度势能和动能。
参考文献
| [1] | Federal Aviation Administration.Airworthiness standards: Transport category rotorcraft: CFR-PART 29[S].Washington, D.C.: Federal Aviation Administration, 2019. |
| [2] | SHARMA V.Optimal sideways operation of a category-A helicopter from an elevated helipad[C]//American Helicopter Society 52nd Annual Forum, 1996: 852-866. |
| [3] | JHEMI A A.Optimal flight of a helicopter in engine failure[D].Minneapolis: University of Minnesota, 1999. https://www.researchgate.net/publication/33750359_Optimal_flight_of_a_helicopter_in_engine_failure |
| [4] | BOTTASSO C L, CROCE A, LEONELLO D, et al. Optimization of critical trajectories for rotorcraft vehicles[J]. Journal of the American Helicopter Society, 2005, 50(2): 165-177. DOI:10.4050/1.3092853 |
| [5] | 孟万里.直升机单台发动机失效后飞行轨迹优化研究与应用[D].南京: 南京航空航天大学, 2014. MENG W L.Study and application of trajectory optimization for helicopter flight after one engine failure[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2014(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1015951833.htm |
| [6] | CARLSON E B.Optimal tiltrotor aircraft operations during power failure[D].Minneapolis: University of Minnesota, 1999. https://www.researchgate.net/publication/33687892_Optimal_tiltrotor_aircraft_operations_during_power_failure |
| [7] | CARLSON E B, ZHAO Y Y. Optimal short takeoff of tiltrotor aircraft in one engine failure[J]. Journal of Aircraft, 2002, 39(2): 280-289. DOI:10.2514/2.2925 |
| [8] | CARLSON E B, ZHAO Y Y. Prediction of tiltrotor height-velocity diagrams using optimal control theory[J]. Journal of Aircraft, 2003, 40(5): 896-905. DOI:10.2514/2.6865 |
| [9] | 严旭飞, 陈仁良. 倾转旋翼机动态倾转过渡过程的操纵策略优化[J]. 航空学报, 2017, 38(7): 520865. YAN X F, CHEN R L. Control strategy optimization of dynamic conversion procedure of tilt-rotor aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(7): 520865. (in Chinese) |
| [10] | 严旭飞, 陈仁良. 倾转旋翼机短距起飞单发失效着陆的轨迹优化[J]. 哈尔滨工业大学学报, 2017, 49(10): 38-44. YAN X F, CHEN R L. Trajectory optimization of tilt-rotor aircraft landing in short takeoff after one engine failure[J]. Journal of Harbin Institute of Technology, 2017, 49(10): 38-44. DOI:10.11918/j.issn.0367-6234.201604113 (in Chinese) |
| [11] | TALBOT P D, TINLING B E.A mathematical model of a single main rotor helicopter for piloted simulation[R].Washington, D.C.: NASA, 1982. |
| [12] | FERGUSON S W.A mathematical model for real time flight simulation of a generic tilt rotor aircraft: NASA CR166536[R].Washington, D.C: NASA, 1988. |
| [13] | 曹芸芸.倾转旋翼飞行器飞行动力学数学建模方法研究[D].南京: 南京航空航天大学, 2012. CAO Y Y.Research on mathematical modeling method for tilt rotor aircraft flight dynamic[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2012(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1014005312.htm |
| [14] | 严旭飞, 池骋, 陈仁良, 等. 变转速旋翼直升机单发失效低速回避区分析[J]. 航空学报, 2018, 39(10): 122107. YAN X F, CHI C, CHEN R L, et al. Analysis of low-speed height-velocity diagram of variable speed rotor helicopter in one engine inoperative situation[J]. Acta Aeronautics et Astronautica Sinica, 2018, 39(10): 122107. (in Chinese) |
| [15] | BETTS J T. Practical methods for optimal control using nonlinear programming[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2001. |
| [16] | BOTTASSO C L, SCORELLETTI F.Trajectory optmization strategies for simulation of the ADS-33 mission task elements[C]//European Rotorcraft Forum, 2008: 1-21. |
| [17] | GILL P E, MURRAY W.User's guide for SNOPT Version 7: Software for large-scale nonlinear programming[Z/OL].San Diego: University of California, 2011: 4-29.https://web.stanford.edu/group/SOL/guides/sndoc7.pdf. |
