与相控阵(Phased Array, PA)不同，频率分集阵列(Frequency Diverse Array, FDA)通过在阵元间引入远小于载频f₀的频差Δf控制相邻阵元的相差从而形成具有时间-角度-距离相关性的波束指向^[1-2]。文献[3-5]系统综述了目前FDA领域研究的主要进展以及亟待解决的关键技术问题。对于收发共型的一维均匀线性频率分集阵列(Uniform Linear Array Frequency Diverse Array, ULA-FDA)，在接收端可通过基于频域滤波及基于正交波形2种方法实现信号分离，从而得到基于梳状滤波器的FDA(Frequency Diverse Array Based on Frequency Filter, FDA-BFF)和多输入多输出FDA(Frequency Diverse Array based on Multiple-Input Multiple-Output, FDA-MIMO)接收机结构^[6-8]。支援干扰机可通过在防区外释放强噪声或密集假目标信号的方式在作战区域形成一定的干扰扇面，以掩护作战飞机突防。此时，作战飞机与干扰机处于不同的空间位置，可通过空域滤波技术最大化目标方向接收增益，同时对干扰方向增益置零。基于FDA的自适应波束形成方法中双边最小方差无失真响应(Two-Side Minimum Variance Distortionless Response, TS-MVDR)波束形成器能够有效降低经典最小方差无失真响应(Minimum Variance Distortionless Response, MVDR)波束形成器的计算复杂度，但当估计的导向矢量存在误差时，波束形成器的输出性能会严重下降。
针对这一问题，本文在将重叠子阵结构代替ULA-FDA作为接收阵列的基础上，采用可变加载约束的最速下降线性约束最小方差(Steepest Descent Linear Constrained Minimum Variance, SD-LCMV)算法计算导向矢量失配时的最优权矢量，实现了阵列方向图主瓣的纠偏和保形。最后，仿真验证了本文分析的正确性。
1 模型假设 图 1为ULA-FDA的基本结构。

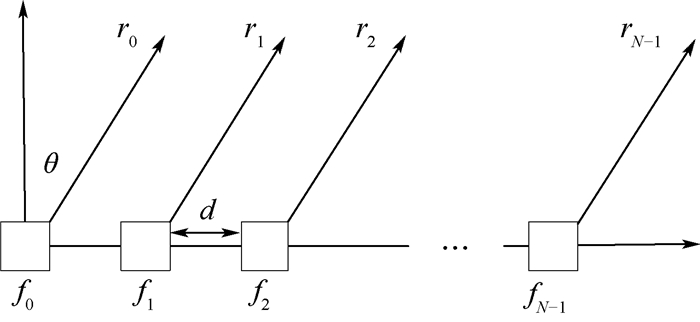图 1 ULA-FDA基本结构 Fig. 1 Basic configuration of ULA-FDA

图选项

窄带条件下，设载波频率为f₀，则第n个阵元对空辐射信号的载频为

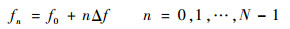(1)

第n个阵元发射信号可表示为

(2)

阵元n发射的信号到达远场点观测点(R, θ)的信号表达式为

(3)

式中：阵元n到目标点的距离r_n=R－ndsin θ，R为参考阵元到目标点的距离，d为阵元间距; c为光速。一般地，阵元n与阵元n－1发射的信号传播到远场点观测点(R, θ)时所形成的相位差为

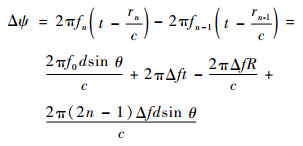(4)

当Δf=0时，，FDA退化为PA。式(4)中的第1项表示阵元信号在观测点处的相位差，这是由阵元间传播距离差引起的；第2项表明Δψ是时间的函数，针对FDA方向图特性研究的文献中多取t=0 s，以研究静止状态下的FDA特性；第3项表明Δψ与距离R及频偏Δf相关，这一项是FDA辐射方向图具有距离相关性的基础；由于f₀?N·Δf; 第4项在运算中经常可以忽略。综上所述，式(4)可简化为

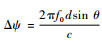
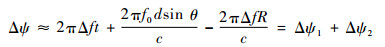(5)

式中：Δψ₁=2πΔft为两相邻阵元初始信号因脉宽产生的时变相位差；为电磁波传播过程中由于频差及波程差造成的相位差，该相位差与距离、角度呈线性关系。
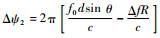
采用如图 1所示的阵列作为收发共型阵，信号在发射端经赋相或加权后向空间辐射，经目标二次反射回接收阵列，在接收端通过采用不同的滤波方式可以构成相应的发射-接收机结构。文献[8-9]中对带限相干处理、全波段相干处理、全波段伪相干处理这3种FDA阵列接收端信号处理机制与FDA-PA、FDA-BFF、FDA-MIMO接收机结构的对应关系做了详细的分析。本文基于文献中关于FDA阵列3种接收端信号处理机制的分析，对基于PA雷达、FDA-BFF以及FDA-MIMO结构的MVDR波束形成器的干扰抑制性能做进一步的分析。
1.1 MVDR算法模型 假设一PA雷达包含M个全向阵元，目标位于空间(R_s, θ_s)处，另有Z个干扰源，空间位置分别为(R_i, θ_i), i=1, 2, …, Z，则PA的接收信号可表示为

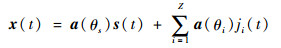(6)

式中：s(t)为有用信号；J(t)=[j₁(t), j₂(t), …, j_Z(t)]为干扰信号集；a(θ)为PA的接收导向矢量，即

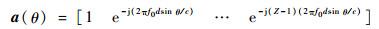(7)

阵列输出可表示为

(8)

式中：w^H为接收端加权矢量；n(t)为接收机噪声矢量。MVDR波束形成准则可表述为^[10]

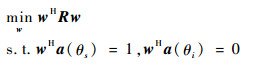(9)

求解式(9)，可得对应的加权矢量为

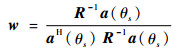(10)

式中：R=E[x_J(t)x_J^H(t)]，x_J(t)=J(t)+n(t)。数字波束的输出性能常用输出信干噪比(SINR)表示，即

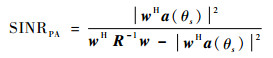(11)

1.2 MVDR算法应用 将FDA-BFF、FDA-MIMO接收机结构的导向矢量代入式(10)，即可求得相应的最优加权矢量。对FDA-BFF结构，阵列输出为

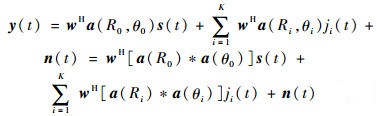(12)

式中：a(R)=[1??e^j(2πΔfR/c)??…??e^{j(N－1)(ΔfR/c)}]；a(θ)=[1??e^{－j(2πf₀dsin θ/c)}??…??e^{－j(N－1)(2πf₀dsin θ/c)}]；*表示Hadamard积。将导向矢量代入式(10)，得接收端加权矢量为

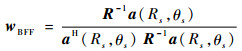(13)

输出信干噪比可为

(14)

对FDA-MIMO结构，阵列输出可表示为

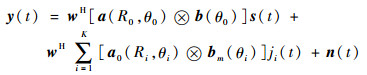(15)

式中：?表示克罗内克积；b(θ)=a(θ)。由式(15)可得，相比于PA雷达和FDA-BFF结构，FDA-MIMO结构具备二维空域的干扰抑制能力，只要干扰与目标在距离、角度一维可分辨，就能够在保持目标增益的同时对干扰进行抑制，干扰抑制能力更强。此时，接收端加权矢量可表示为

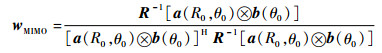(16)

输出信干噪比可表示为

(17)

1.3 TS-MVDR算法在FDA-MIMO中的应用 为解决式(10)在FDA-MIMO中直接应用算法复杂度过高的问题，充分利用MIMO导向矢量中的克罗内克结构，采用TS-MVDR^[8]进行最优权矢量求解，即将MIMO波束形成过程虚拟为发射波束形成和接收波束形成2个过程，两过程中的导向矢量分别为a(R, θ)和b(θ)，利用式(9)分别求取对应过程的最优权矢量，再求取两最优权矢量的克罗内克积作为最终的权重矢量，该过程可描述为

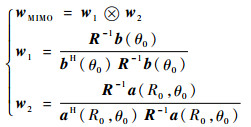(18)

假设FDA-MIMO拥有N个阵元，MVDR波束形成器需通过式(15)求解N²个系数向量；而TS-MVDR相当对单一子阵、子列分别进行MVDR波束形成，最后通过克罗内克积综合为一个权矢量，仅需求解2N个系数向量，大大降低了计算量。
2 子阵FDA结构分析 图 1所示基本FDA阵列在阵元间引入固定的频偏增量，其“S型”的方向图中存在着距离-角度耦合的问题，这一耦合是由于频偏增量与阵元间距的线性递增同步而导致的^[11-12]。通过在阵元间引入非线性频偏增量或者将阵列结构划分为不同的子阵结构都可以打破这种同步，从而实现方向图的距离-角度解耦^[13-16]。图 2为单边子阵、中心对称子阵、重叠子阵以及交叉子阵FDA的阵列结构^[17-19]。

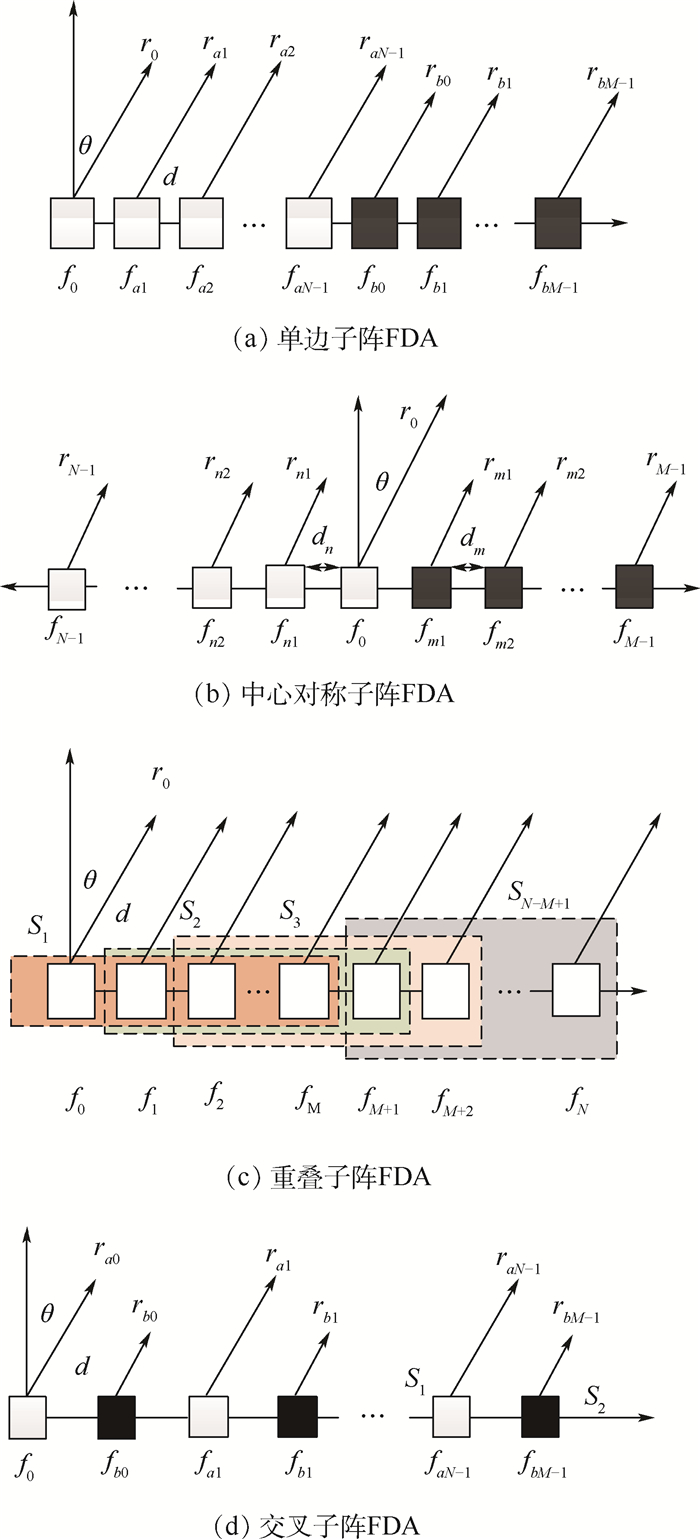图 2 子阵FDA结构 Fig. 2 Configuration of subarray-based FDAs

图选项

本文采用旁瓣最低的重叠子阵FDA结构代替基本的ULA-FDA作为收发共型阵，同时将正弦形式的非线性频偏增量引入重叠正弦FDA阵列。图 2(c)的重叠子阵FDA中从参考阵元开始依次构建阵元数为M的子阵列，相邻子阵间不完全重叠。假定ULA-FDA阵列阵元数为N，子阵的阵元数为M，则可以构建出N－M+1个子阵列。第l个子阵在远场位置处的信号形式为

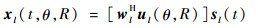(19)

式中:s_l(t)为第l个子阵的发射波形; w_l为权矢量；u_l为导向矢量，即

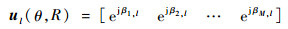(20)

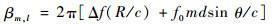(21)

3 可变加载约束SD-LCMV算法 MVDR波束性器假定干扰的空间位置已知，但实际中干扰源位置的估计必定存在一定的误差，在导向矢量出现失配的情况下，MVDR波束形成器在抑制主瓣干扰的过程中会出现主瓣偏移和畸变，副瓣升高以及输出信干噪比降低的问题。当估计的导向矢量存在误差时，真实的期望信号会被当作干扰抑被制，MVDR波束形成器收敛到估计的导向矢量上，以a表示估计的导向矢量，即w^Ha=1和w^Ha=0^[20-21]：

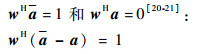(22)

可变加载约束SD-LCMV算法通过对权重矢量的范数设置一个上界约束，从而提高波束形成器的稳健性能。将式(9)的优化问题模型改写为

(23)

式中:δ表示约束上界。采用拉格朗日乘子法构造代价函数：

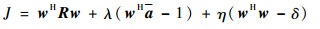(24)

采用最速下降方向即负梯度方向作为搜索方向，得到权矢量的迭代公式为

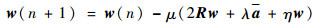(25)

式中：μ为迭代步长。将式(25)代入约束条件w^H(n+1)a=1，可求得λ的表达式为

(26)

将式(26)代入式(25)中，得到权重迭代公式为

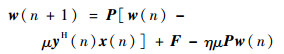(27)

式中：P=I－a(a^Ha)^－1a^H，F=a(a^Ha)^－1，将式(27)代入约束条件||w(n+1)||²=w^H(n+1)·w(n+1)≤δ中可得关于η的一元二次方程为

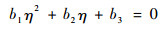(28)

其中：

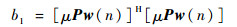(29)

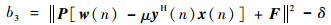(30)

(31)

求解可得η。式中：Re[]表示取实部。同时，根据式(32)在最速下降方向上搜索真实导向矢量：

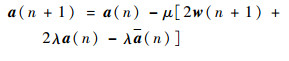(32)

4 仿真分析 假设阵元间距d=c/(2f₀)，f₀=10 GHz，Δf=10 kHz，t=0 s，仿真验证本文分析的有效性。
仿真1??3种阵列的干扰抑制特性分析。
本例中考虑30阵元的FDA阵列，假设目标位置为(30 km, 30°)，干扰位于(32 km, 31°)，基于PA、FDA-BFF结构的MVDR阵列方向图分别如图 3和图 4所示。改变干扰位置，设干扰位于(32 km, 42°)处，得基于MVDR的FDA-BFF阵列方向图如图 5所示。对于FDA-MIMO结构，由于MIMO的结构复杂性，MVDR波束形成器并不适用于大规模的FDA-MIMO阵列。当干扰位于(32 km, 31°)，当阵元数分别为9、30时，基于FDA-MIMO结构的MVDR波束形成器的阵列方向图如图 6和图 7所示。图 8仿真了干扰位于(33 km, 31°)时基于TS-MVDR的FDA-MIMO阵列方向图。

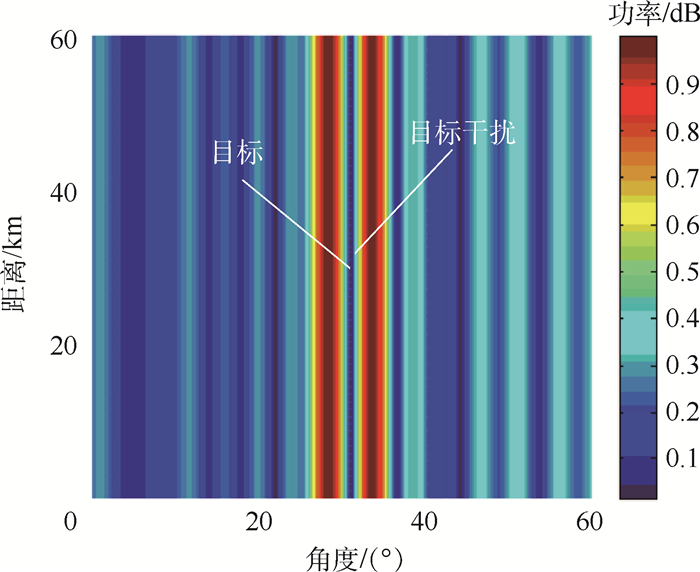图 3 PA的阵列方向图(N=30) Fig. 3 PA beampattern (N=30)

图选项

图 4 基于MVDR的FDA-BFF阵列方向图(N=30) Fig. 4 FDA-BFF beampattern based on MVDR (N=30)

图选项

图 5 基于MVDR的FDA-BFF阵列方向图(N=30) Fig. 5 FDA-BFF beampattern based on MVDR (N=30)

图选项

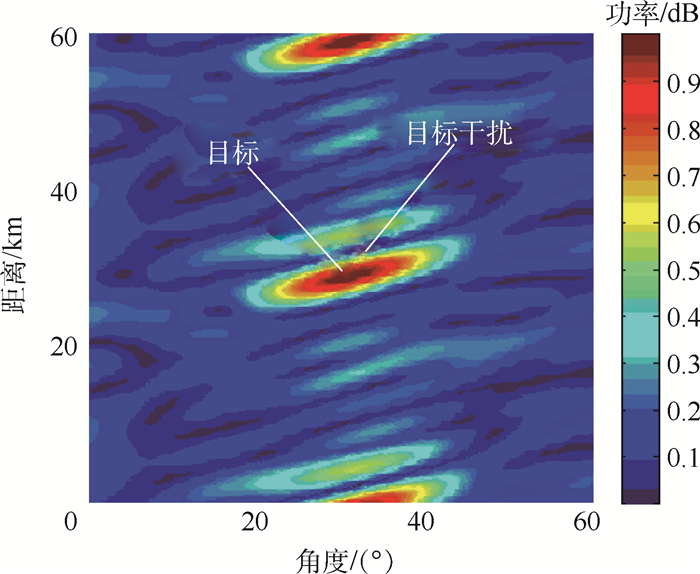图 6 基于MVDR的FDA-MIMO阵列方向图(N=9) Fig. 6 FDA-MIMO beampattern based on MVDR (N=9)

图选项

图 7 基于MVDR的FDA-MIMO阵列方向图(N=30) Fig. 7 FDA-MIMO beampattern based on MVDR (N=30)

图选项

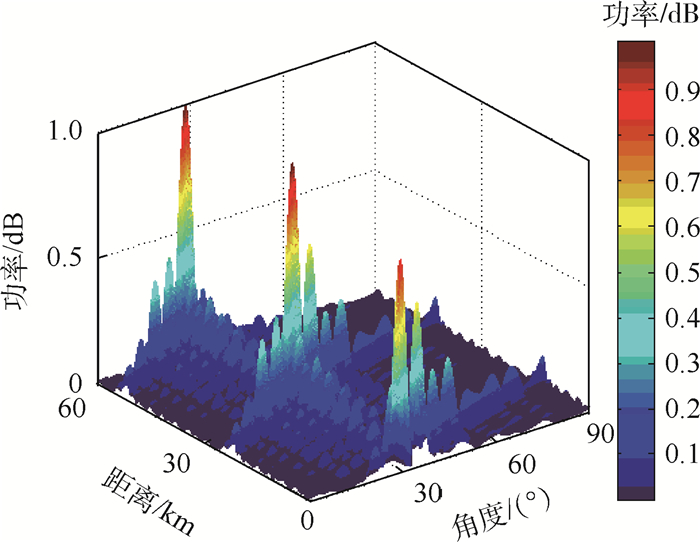图 8 基于TS-MVDR的FDA-MIMO阵列方向图(N=30) Fig. 8 FDA-MIMO beampattern based on TS-MVDR (N=30)

图选项

一般情况下，PA结构可以在干扰角度形成一条仅与角度相关而与距离无关的“零陷带”。但当干扰与目标角度接近时，由图 3可知，PA的阵列方向图会出现主瓣畸变的问题。由于FDA阵元间频偏增量的原因，图 4中的FDA-BFF结构的波束指向具有距离角度二维相关性，可在(32 km, 31°)干扰位置处形成零陷的同时，在目标位置处保持增益。由图 5可知，当干扰的空间位置满足FDA-BFF结构波束的距离-角度耦合关系时，即干扰位于FDA-BFF的空域主瓣内时，FDA-BFF形成的主瓣在目标位置处依然发生了畸变，波束形成器输出性能也出现了下降。
由图 6和图 7可知，当N=9时，通过应用一维MVDR能够得到在目标处增益最大，在干扰处增益置零的方向图；但当N=30时，虽然在干扰位置处仍能形成零陷，但方向图出现较大程度畸变，无法找到相应的主瓣区域。由图 8可看出，利用TS-MVDR算法进行波束形成，在阵元数较大的情况下方向图不会出现严重的畸变；但当干扰与目标角度相近时，仍会产生主瓣畸变。这是因为TS-MVDR本质上是对算法计算量的优化，当干扰与目标角度相近时，在对单一子阵、子列分别进行MVDR波束形成的过程中已经存在主瓣畸变的问题，求取克罗内克积的过程对主瓣畸变问题没有优化作用。
仿真2??4种子阵FDA的发射方向图对比。
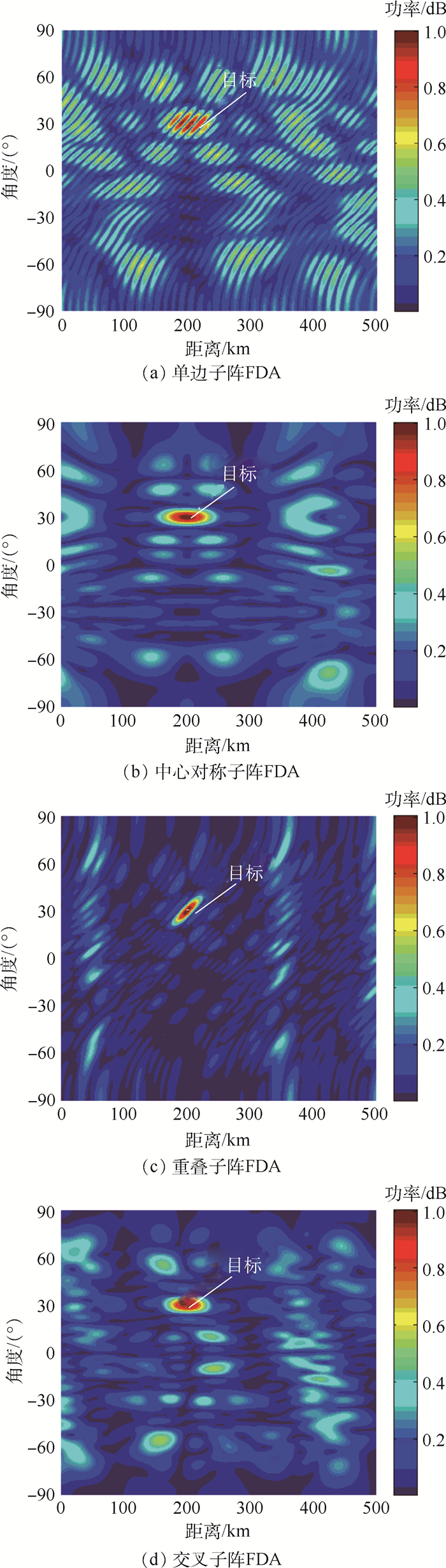
本文的核心是采用非线性频偏增量的重叠子阵FDA代替基本ULA-FDA作为收发共型阵，在导向矢量存在失配时通过SD-LCMV算法求取最优导向矢量。本例中对比分析4种子阵FDA结构的发射方向图特性。假设基本ULA-FDA的阵元数为20，每个子阵的阵元数为10，频偏增量Δf=2 kHz。图 9为当目标位于(200 km, 30°)时4种子阵FDA结构的发射方向图。为进一步优化，将正弦形式的非线性频偏引入到4种子阵结构中得到图 10所示的发射方向图。

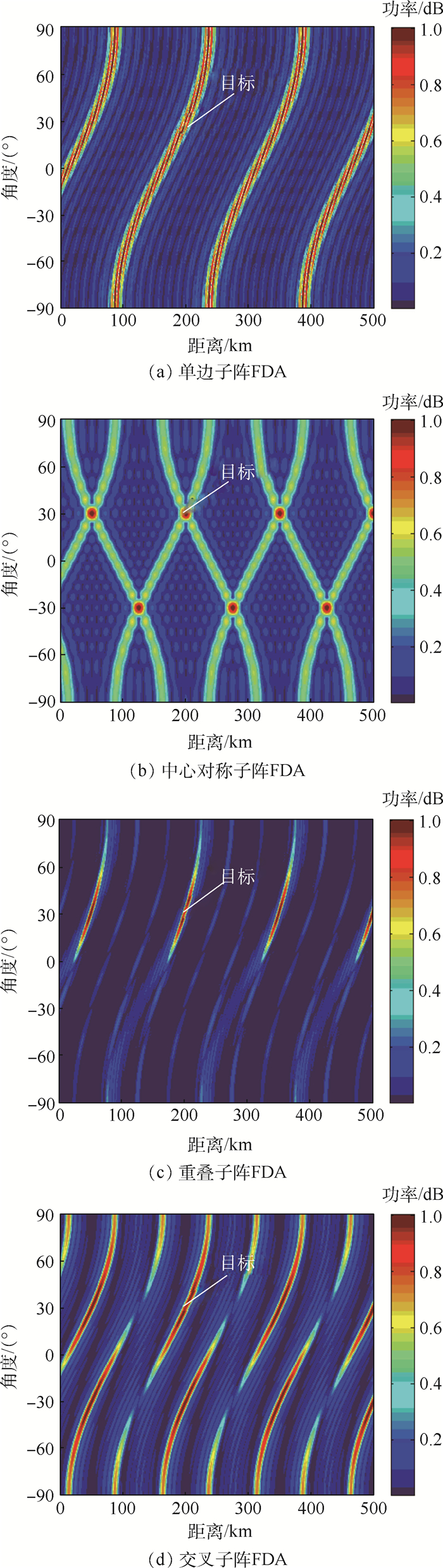图 9 子阵FDA发射方向图 Fig. 9 Transmit beampattern of subarray-based FDA

图选项

图 10 采用正弦频偏的子阵FDA发射波束图 Fig. 10 Transmit beampattern of subarray-based FDA with sinusoidal frequency offset

图选项

与PA波束指向只与角度相关而与距离无关不同，FDA通过在阵元间引入一个固定的频偏增量增加了雷达的自由度，形成了具有距离-角度相关性的波束指向。当基本FDA的“S型”方向图中固有的距离-角度耦合会给波束的精确控制等带来一系列的问题。如图 9所示，仅将基本的ULA-FDA阵列划分为4种子阵FDA不能有效地实现距离-角度解耦。通过将非线性频偏增量引入到阵列中得到图 10所示的发射方向图。图 10中4种子阵FDA都可在目标位置处形成点状的波束指向，对比主瓣宽度和旁瓣大小，重叠子阵FDA具有最优特性。因此，本文后续分析基于重叠子阵sin-FDA阵列的MVDR波束形成器的干扰抑制特性。
仿真3??ULA-FDA与重叠子阵sin-FDA的方向图对比。
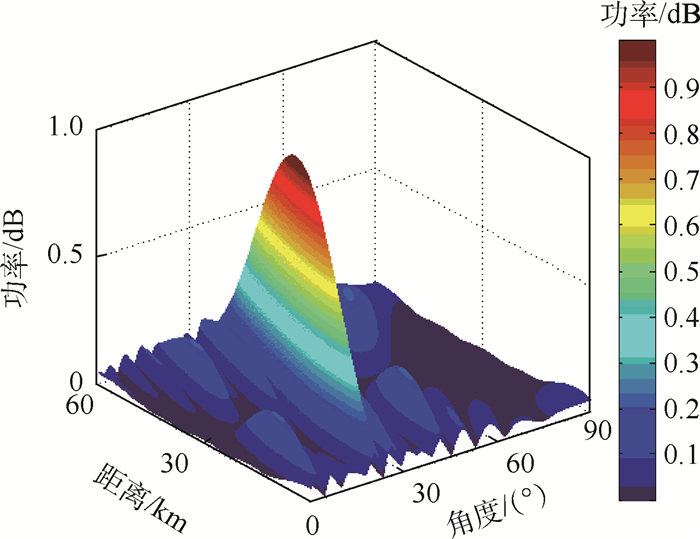
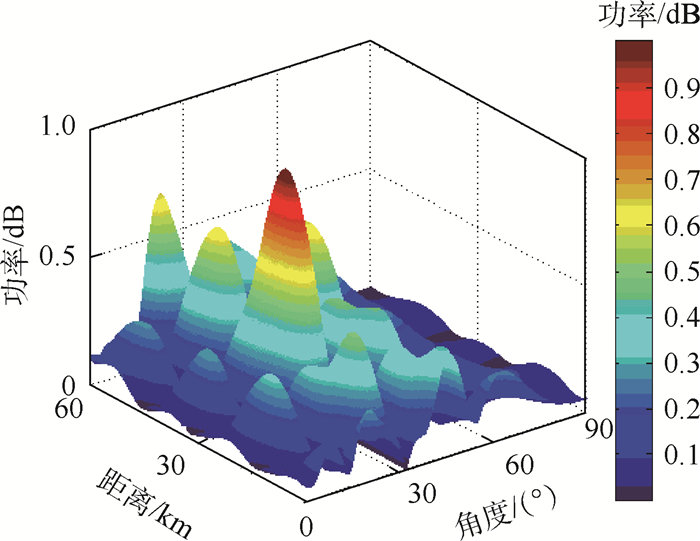
阵元数为20的ULA-FDA阵列可以构成11个阵元数为10的重叠子阵，远场目标位置处的场强为各子阵场强的叠加。与图 11中基本ULA-FDA发射阵列的多峰值方向图不同，图 12中重叠子阵sin-FDA发射方向图的波束主瓣在目标位置处可以形成点状的发射波束，能够有效消除静态方向图中的距离-角度耦合。此外，基于中心对称、交叉子阵以及单边子阵结构的FDA发射方向图都可以实现指向目标位置的点状波束。将重叠子阵sin-FDA结构作为接收阵列，得到如图 13所示的阵列方向图。与图 8不同，图 13中得到单峰值的重叠sin-FDA-MIMO的阵列方向图。当导向矢量失配时波束形成器的性能会出现下降，针对这一问题本文引入SD-LCMV算法计算导向矢量失配时的最优权矢量。

图 11 ULA-FDA发射方向图 Fig. 11 ULA-FDA transmit beampattern

图选项

图 12 重叠子阵sin-FDA发射方向图 Fig. 12 Overlapping subarray-based sin-FDA transmit beampattern

图选项

图 13 重叠子阵sin-FDA阵列方向图 Fig. 13 Overlapping subarray-based sin-FDA beampattern

图选项

仿真4??导向矢量失配时的干扰抑制特性。
本例中考虑导向矢量存在2°指向误差，频偏增量Δf=2 kHz，阵元数为20的PA、FDA-BFF及重叠子阵sin-FDA阵列其干扰位于(33 km, 32°)时的情况。
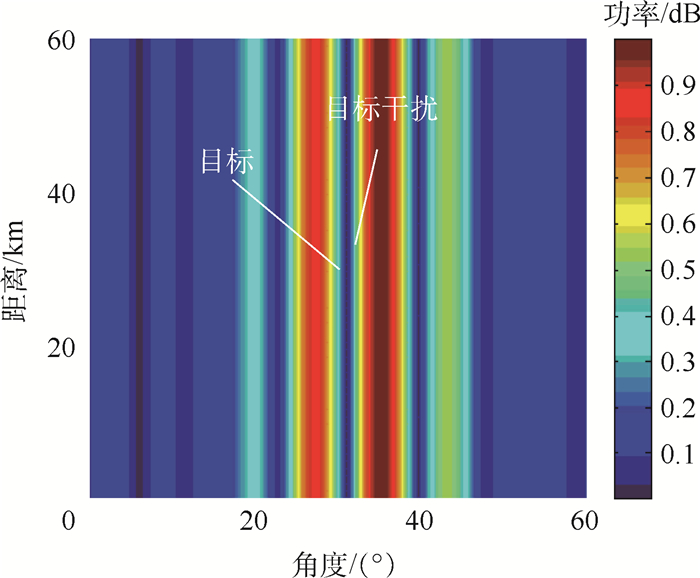
图 14~图 16分别为存在2°指向误差，导向矢量失配情况下基于PA、FDA-BFF及重叠子阵sin-FDA的MVDR波束形成器的阵列方向图。如图 14和图 15所示，当存在指向误差时，MVDR波束形成器会收敛到存在误差的估计导向矢量上，主瓣产生明显偏移。2种算法在干扰位置处都能形成有效零陷，但基于FDA-BFF的MVDR波束形成器形成的零陷较浅，干扰抑制效果有待进一步提高。本文方法能够有效纠正主瓣的偏移，避免畸变的出现。同时期方向图仅在目标位置处形成单一主瓣峰值，这也为后续关于目标参数估计的一系列分析中的模糊消除奠定了重要基础。图 17中本文方法的输出SINR高于其他2种结构。基于FDA-BFF的MVDR波束形成器存在SINR输出的性能“凹口”，出现凹口的原因是因为主瓣畸变。

图 14 存在指向误差时的PA阵列方向图 Fig. 14 PA beampattern with pointing error

图选项

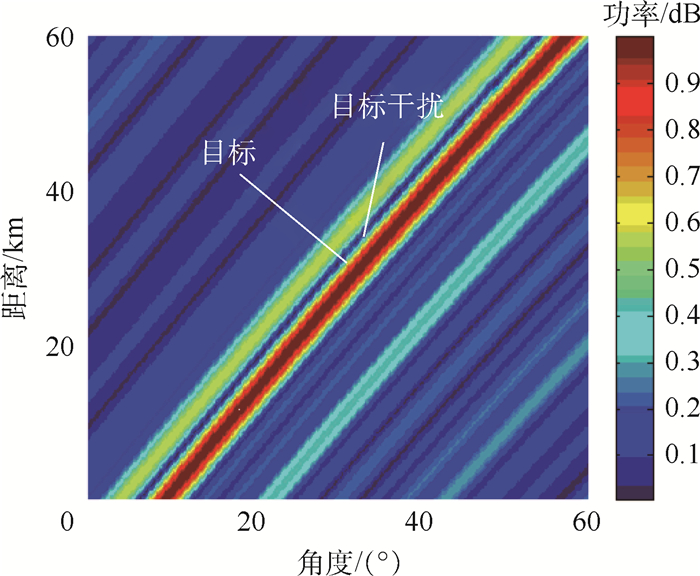图 15 存在指向误差时的FDA-BFF阵列方向图 Fig. 15 FDA-BFF beampattern with pointing error

图选项

图 16 存在指向误差时的重叠子阵sin-FDA阵列方向图 Fig. 16 Overlapping subarray-based sin-FDA beampattern with pointing error

图选项

图 17 3种机制的SINR比较 Fig. 17 SINR comparison among three architectures

图选项

5 结论 1) 分析了干扰与目标位置接近时，MVDR波束形成器在阵元数较大、导向矢量失配时出现的主瓣畸变问题。
2) 对比了4种子阵FDA的阵列方向图特性，得到将正弦频控函数引入重叠子阵FDA中可以得到较为理想的主瓣宽度及旁瓣特性。
3) 对比验证了与ULA-FDA阵列相比，重叠子阵sin-FDA阵列的发射方向图与阵列方向图具有的解距离-角度耦合特性。
4) 仿真验证了当导向矢量存在指向误差时，通过SD-LCMV算法的修正，基于重叠子阵sin-FDA的阵列方向图能够在抑制干扰的同时实现主瓣纠偏和保形。

参考文献

[1]	WANG W Q, SHAO H Z, CHEN H. Frequency diverse array radar:Concept, principle and application[J]. Journal of Electronics & Information Technology, 2016, 38(4): 1000-1011.
[2]	WANG W Q. Overview of frequency diverse array in radar and navigation applications[J]. IET Radar, Sonar & Navigation, 2016, 10(6): 1001-1012.
[3]	王文钦, 陈慧, 郑植, 等. 频控阵雷达技术及其应用研究进展[J]. 雷达学报, 2018, 7(2): 153-166. WANG W Q, CHEN H, ZHENG Z, et al. Advances on frequency diverse array radar and its applications[J]. Journal of Radars, 2018, 7(2): 153-166. (in Chinese)
[4]	许京伟, 朱圣棋, 廖桂生, 等. 频率分集阵雷达技术探讨[J]. 雷达学报, 2018, 7(2): 167-182. XU J W, ZHU S Q, LIAO G S, et al. An overview of frequency diverse array radar technology[J]. Journal of Radars, 2018, 7(2): 167-182. (in Chinese)
[5]	陈小龙, 陈宝欣, 黄勇, 等. 频控阵雷达空距频聚焦信号处理方法[J]. 雷达学报, 2018, 7(2): 183-193. CHEN X L, CHEN B X, HUANG Y, et al. Frequency diverse array radar signal processing via space-range-Doppler focus (SRDF) method[J]. Journal of Radars, 2018, 7(2): 183-193. (in Chinese)
[6]	张昭建, 谢军伟, 盛川, 等. 频率分集阵列接收机结构设计及方向图分析[J]. 华中科技大学学报, 2017, 45(6): 15-20. ZHANG Z J, XIE J W, SHENG C, et al. Frequency diverse array receiver architectures design and pattern analysis[J]. Huazhong University of Science & Technology, 2017, 45(6): 15-20. (in Chinese)
[7]	JONES A M.Frequency diverse array receiver architectures[D].Dayton, OH: Wright State University, 2011.
[8]	冯晓宇, 谢军伟, 张晶, 等. 频控阵波束特性及波形控制研究[J]. 空军工程大学学报(自然科学版), 2018, 19(3): 42-48. FENG X Y, XIE J W, ZHANG J, et al. Research on waveform properties and beam control of frequency diverse array[J]. Journal of Air Force Engineering University (Natural Science Edition), 2018, 19(3): 42-48. DOI:10.3969/j.issn.1009-3516.2018.03.008 (in Chinese)
[9]	王博, 谢军伟, 张晶, 等. 基于非线性频偏的频控阵波束控制研究[J]. 北京理工大学学报, 2019, 39(3): 311-319. WANG B, XIE J W, ZHANG J, et al. Study of frequency diverse array beam control based on nonlinear frequency offset[J]. Transactions of Beijing Institute of Technology, 2019, 39(3): 311-319. (in Chinese)
[10]	张小飞. 阵列信号处理及MALTAB实现[M]. 北京: 电子工业出版社, 2015: 50-51. ZHANG X F. Array signal processing and MATLAB realization[M]. Beijing: Electronic Industry Press, 2015: 50-51. (in Chinese)
[11]	王哲.频控阵波束的距离角度依赖特性研究[D].成都: 电子科技大学, 2018. WANG Z.Research on range-angle-dependent characteristics of frequency diversearray beampattern[D].Chengdu: University of Electronic Science and Technology of China, 2018(in Chinese).
[12]	王博, 谢军伟, 张晶, 等. 子阵结构FDA阵列模糊函数建模与研究[J]. 空军工程大学学报(自然科学版), 2019, 20(4): 90-96. WANG B, XIE J W, ZHANG J, et al. Modeling and research of ambiguity function based on subarray-based FDA[J]. Journal of Air Force Engineering University(Natural Science Edition), 2019, 20(4): 90-96. (in Chinese)
[13]	WANG W Q. Subarray-based frequency diverse array radar for target range-angle estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(4): 3057-3067.
[14]	XU Y H, SHI X W, XU J W, et al. Range-angle-decoupled beampattern synthesis with subarray-based frequency diverse array[J]. Digital Signal Processing, 2017, 64: 49-59.
[15]	WANG Z H, MU T, SONG Y L, et al. Beamforming of frequency diverse array radar with nonlinear frequency offset based on logistic map[J]. Progress in Electromagnetics Reasearch, 2018, 64: 55-63.
[16]	XU Y H, SHI X W, LI W T, et al. Flat-top beampattern synthesis in range and angle domains for frequency diverse array via second-order cone programming[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1479-1482.
[17]	WANG Z, WANG W Q, SHAO H. Range-azimuth decouple beamforming for frequency diverse array with costas-sequence modulated frequency offsets[J]. Eurasip Journal on Advances in Signal Processing, 2016, 2016(1): 124.
[18]	项喆, 陈伯孝, 杨明磊. 频率分集雷达最优频率间隔选择方法[J]. 西安电子科技大学学报, 2017, 44(4): 12-17. XIANG Z, CHEN B X, YANG M L. Frequency increment optimization method for frequency diverse radar[J]. Journal of Xidian University, 2017, 44(4): 12-17. (in Chinese)
[19]	KHAN W, QURESHI I M, BASITAND A, et al.Transmit/received beamforming for MIMO log-frequency diverse array radar[C]//Proceedings of the International Bhurban Conference on Applied Science & Technlogy.Piscataway, NJ: IEEE Press, 2016: 689-693.
[20]	路成军, 盛卫星, 韩玉兵, 等. 基于可变加载的稳健并行波束形成算法[J]. 南京理工大学学报, 2013, 37(3): 371-377. LU C J, SHENG W X, HAN Y B, et al. Robust parallel beamforming algorithm based on variable loading[J]. Journal of Nanjing University of Science and Technology, 2013, 37(3): 371-377. (in Chinese)
[21]	LI Y C, CHEN C, ZENG W H, et al. Robust adaptive beamforming algorithm based on steering vector estimation[J]. Chinese Journal of Radio Science, 2015, 31(1): 188-193.