当前,国内外****对电动汽车充电行为的研究很多。国内研究大多基于传统车辆行驶数据模拟电动汽车的运行规律,考虑不同情况下充电行为的差异,分析电动汽车充电负荷的计算方法。文献[5]考虑电动汽车的空间动态转移特性下充电行为的差异,预测不同类型电动汽车的空间分布,并建立具体详细的负荷预测模型。文献[6]基于居民出行调研统计数据构建出行链,提出一种涉及电动汽车充电频率的负荷计算方法。文献[7]利用蒙特卡罗法模拟电动汽车的出行特性,提出一种考虑气温影响的电动汽车充电负荷计算方法。文献[8]考虑充电起始时间和日行驶里程2个影响因素,用蒙特卡罗仿真方法求得电动汽车功率需求,建立电动汽车功率需求的统计学模型。文献[9]基于调研数据分析不同类型电动汽车的充电行为,提出基于蒙特卡罗模拟的电动汽车充电负荷计算模型。文献[10]根据北京市机动车行驶规律,探讨对充电需求的影响因素(用户行驶开始时间、结束时间和行驶里程),采用蒙特卡罗法建立通勤用电动汽车充电需求模型。
国外对电动汽车充电行为的研究也非常重视,文献[11]发现消费者通常选择在晚上充电,但在高峰期,消费者更有可能使用快速充电桩。文献[12]以燃油汽车数据类比电动汽车数据,采用Logit模型进行分析,表明初始电荷状态、充电时间、起点与充电站的距离对电动汽车的路径选择有影响。文献[13]针对私家车GPS数据,考虑每个停车事件中电池的实际充电状态、停车持续时间、停车类型和车辆传动系,引入新的随机方法更精确地预测负荷。文献[14]基于对私家车GPS行驶数据的统计分析,分析电动汽车在不同场景下的充电时间分布特性,利用排队论模型预测电动汽车的负荷需求。文献[15]采用实际运营的插入式电动汽车的数据,提出基于回归和时间序列方法的组合模型,预测电动汽车充电时长。文献[16]利用3种不同的电动汽车充电数据来估算电动汽车的潜在电力需求,并模拟其对电网的影响。文献[17]基于排队理论分析电动汽车到站信息,提出电动汽车充电需求的随机模型,对电动汽车充电负载波动进行实时更清晰的短期预测。文献[18]研究电动汽车对低压配电网的影响,针对2种充电方案进行建模,评估电动汽车对变压器负载、馈线负载、电压偏差和总系统损耗的影响。
综上所述,由于缺少真实的电动汽车数据,现有研究大多采用蒙特卡罗模拟或人工调查的方法进行分析验证。但是,人工调查数据的准确率较低,而且数据的样本量不足;而模拟的数据多假定充电条件,忽视了电动汽车充电行为的自主选择性,很难反应真实情况,缺乏说服力;少部分采用的实际数据主要来自于美国的插入式电动汽车,由于中国交通和充电环境与美国不同,充电行为特征也是不同的。多数对充电行为的研究只分析了充电过程,忽略了放电过程对充电行为的影响。另外,部分考虑充电行为影响因素的文献只考虑了单一因素的影响,且着重研究电动汽车充电对于电网等其他问题的影响[19-20],忽略了这些影响因素对充电行为本身的影响。
本文从实际出发,根据北京市私家电动汽车的历史车联网数据,针对电动汽车充电行为不确定性,引入出行链的概念,以“链”的形式将电动汽车的时间维、空间维联系在一起,将电动汽车的充电过程和放电过程构建成一个整体,考虑电动汽车充电行为的多种潜在影响因素,统筹兼顾天气、旅程开始时间、出行链时长、出行链距离、旅程速度、起始电荷状态、上一次出行链状态等,通过模型确定充电行为的显著影响因素,并基于显著影响因素对出行链是否充电进行建模和预测。
1 数据准备 本文采用电动汽车车联网数据。由于电动汽车充电行为与其出行规律紧密相关,为了更全面地分析电动汽车充电行为,引入出行链的概念。出行链是指用户为完成某项活动,按照时间顺序在不同区域间转移的连接形式[21]。本节首先对车联网数据进行简单描述,然后对数据集进行处理,得到基于出行链的充电行为数据,最后对充电行为数据进行总结分析。
1.1 电动汽车数据处理 本文所采用的电动汽车车联网数据由北京市130辆私家电动汽车行驶实况数据构成,共涵盖约5 000万组行车数据信息,数据时间主要集中在2015年8月,平均每辆车约有15 d的数据,每组行车数据平均时间间隔为10 s;内容主要包括终端编号、充放电状态、续驶里程、动力电池SOC、放电电流、经度、纬度、里程和采集时间等。
首先对采集到的行车数据信息进行预处理,规范数据格式,填补缺失数据,剔除错误信息。然后根据动力电池电荷状态的变化情况,分别提取充电数据和放电数据。最后根据数据的结构组成特点及经验分析,规定车辆停止时间大于1 h,则本次充放电过程或放电过程结束,实现单次充电过程和放电过程的识别。
在电动汽车的充放电过程中,上一次放电过程的结束时间、结束位置、荷电状态等对本次充电过程的开始时间、充电时长、充电位置等有很大的影响,因此将充电过程和放电过程结合起来可以更全面地分析充电行为。由于通常情况下出行链描述居民从家出发再返回家的一个过程[22],过程中包含大量的时间、空间和活动类型信息,而且这些信息之间是相互联系和相互作用的。基于出行链的研究更能体现电动汽车充电过程和放电过程的关联性。
因此接下来通过经纬度在地图上匹配电动汽车的放电(即行驶)过程,然后根据经验将数据中晚上使用常规充电的充电地点视为家的所在地,根据时间和空点连续性对单次放电过程和充电过程进行匹配,以家为起讫点构建车辆出行链模型。同时记录单条出行链充电的次数、旅程起始点、总距离、总时间、旅行速度、起始电池核电量,以及每次快速充电的起始点、充电时长、充电量等。
1.2 充电行为数据总结 通过1.1节对电动汽车数据的处理可以看出,在出行链中的充电过程绝大多数都为快速充电,剔除2条使用常规充电的出行链数据,得到120辆电动汽车的3 002条出行链信息,按快速充电情况分为以下4种:无充电、快速充电1次、快速充电2次及快速充电3次,如表 1所示。可以看到,发生快速充电行为的出行链远小于无快速充电行为,说明大部分情况下,电池电量能够满足旅程所需,用户习惯回到家后使用常规充电方式充电。
表 1 基于出行链的充电行为分布 Table 1 Distribution of charging behavior based on trip chains
| 充电次数 | 0 | 1 | 2 | 3 |
| 出行链分布 | 2 378 | 410 | 167 | 47 |
表选项
2 充电行为的潜在影响因素 本文更关心的是不同影响因素所引起的充电行为本身的差异。目前大多数对充电行为的研究多设定固定的充电模式或者假设在某个目的地充电,但实际用户也存在旅程中的充电行为。本文采用充电出行链频次(即指定情况下或一定时间内有充电行为的出行链数量)作为统计量,分析不同潜在影响因素所引起的基于出行链的充电频次差异情况。
对于充电行为的研究,最先考虑的便是天气问题,一方面当温度过高或过低时,司机会使用空调或者暖气,这将增加单位里程耗电量,增加电动汽车的充电需求。另一方面,遇到雨、雪等恶劣天气,会影响车辆的行驶速度,进一步影响电动汽车的充电行为。本文数据均发生在2015年8月,此时天气如表 2所示。可见,气温差异并不明显,空调或暖气的使用并无差异,而且只存在部分小雨天气,未出现恶劣天气,因此天气的影响并不明显。
表 2 2015年8月部分北京天气情况 Table 2 Some weather conditions in Beijing in August 2015
| 日期 | 最高气温/℃ | 最低气温/℃ | 天气 |
| 2015-08-01 | 31 | 23 | 阴转小到中雨 |
| 2015-08-02 | 30 | 23 | 多云转阴 |
| 2015-08-03 | 30 | 23 | 阵雨转多云 |
| 2015-08-04 | 33 | 22 | 晴转多云 |
| 2015-08-05 | 32 | 22 | 多云转雷阵雨 |
| 2015-08-06 | 31 | 22 | 多云 |
表选项
用户行驶过程中是否会充电往往取决于电动汽车电池现有剩余电量是否足以完成接下来的行程,起始电池核电量是非常重要的因素。由于本文所采用车辆充满电时的续航里程均在145~150 km之间,差异并不大,因此采用电池起始电荷状态对充电行为进行分析,电池电荷状态简称SOC,主要用来反映电池的剩余容量,其数值上定义为剩余容量占电池容量的比值。随起始电荷状态的变化,充电出行链频次分布如图 1所示。可以看出,起始电荷状态越高,有充电行为的出行链频次越低。
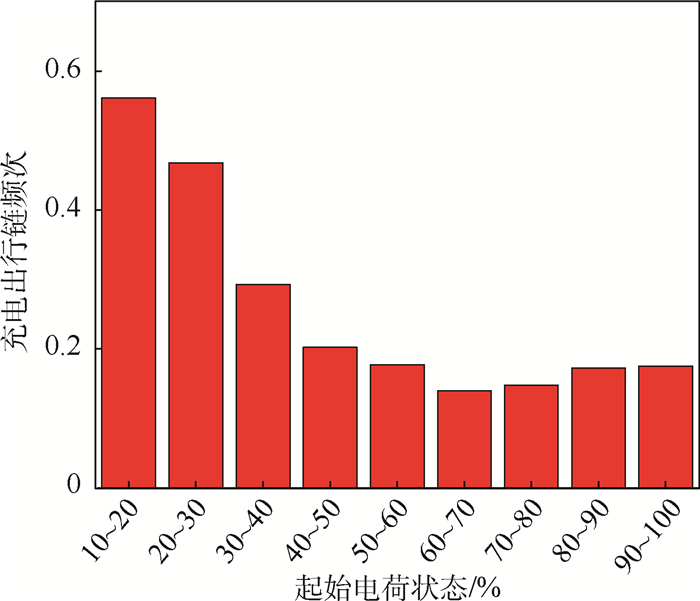 |
| 图 1 起始电荷状态的影响 Fig. 1 Influence of initial state of charge |
| 图选项 |
基于出行链的充电行为研究,旅程开始的时间被认为是必要的因素,电动汽车用户往往在晚上出行链结束时,到达住宅区后选择常规充电模式充电,因此越晚开始的旅程,中途选择快速充电的可能性越小。图 2显示了一天24个时段出行的电动汽车充电频次变化情况。可以看出,上午开始的出行链充电的可能性更大。
 |
| 图 2 旅程开始时间的影响 Fig. 2 Influence of journey start time |
| 图选项 |
在研究车辆充电行为时,出行链距离和时长的影响也很重要。对于出行链距离,以50km为出行链距离区间,计算出每个距离区间内的充电出行链频次,如图 3所示,可以看出,出行链的充电频次和距离呈线性正相关关系。对于出行链时长的分析,将有充电行为和无充电行为的数据分成2个系列,绘制成折线图(见图 4)。可以看到,有充电行为和无充电行为的出行链时长相差较大,有充电行为的出行链时长相对较大,平均在30 000~40 000 s,而无充电行为的出行链时长平均在5 000 s,相差一个数量级,因此出行链时间越长,充电的可能性就越大。
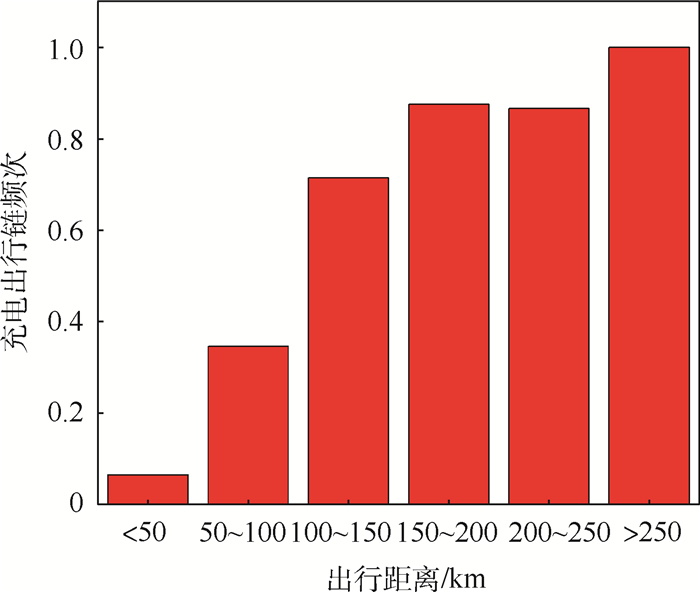 |
| 图 3 出行链距离的影响 Fig. 3 Influence of trip chain distance |
| 图选项 |
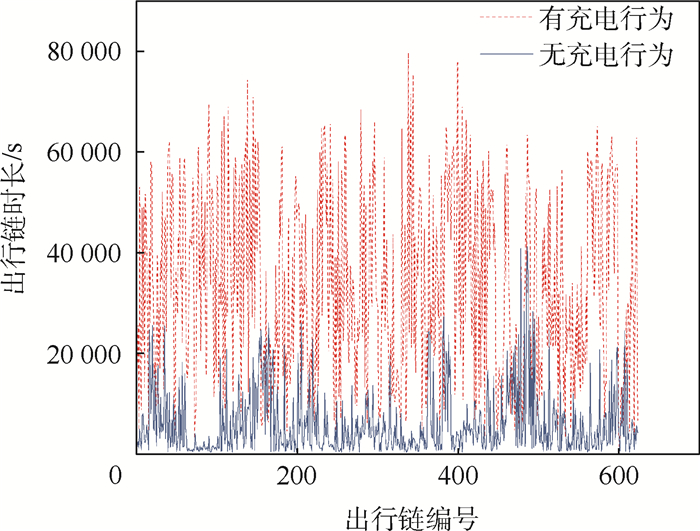 |
| 图 4 出行链时长的影响 Fig. 4 Influence of trip chain duration |
| 图选项 |
在研究车辆里程耗电量时,车辆速度是首先被考虑的因素,同样,对于出行链的充电行为,旅程平均速度也是一个重要的影响因素。首先计算各个出行链的平均速度,然后将平均速度从小到大归一化到[0, 1],即将最大平均速度视为1,最小平均速度视为0,以0.05为一个区间绘制直方图(见图 5)。可见,不同速度区间的出行链数量呈正态分布,当平均速度很小时,随着平均速度的增加,充电的出行链个数随之增加,当平均速度在0.30~0.35时达到最大,之后随着平均速度的增大,充电的出行链个数越来越少。
 |
| 图 5 旅程速度的影响 Fig. 5 Influence of journey speed |
| 图选项 |
将有充电行为的出行链状态计为1,无充电行为的出行链状态计为0,则上一次和本次的出行链的状态组合有:0-0、0-1、1-0、1-1,将这4种组合的出行链个数占比绘制成如图 6所示的饼状图。可以看出,0-0即上一次和本次出行链均无充电行为,占77%,这说明大部分私家车用户选择常规充电模式充电,只有少部分用户使用快速充电方式;1-1即上一次和本次出行链均充电,占16%,说明有快速充电习惯的用户下次出行链也充电的概率更大。
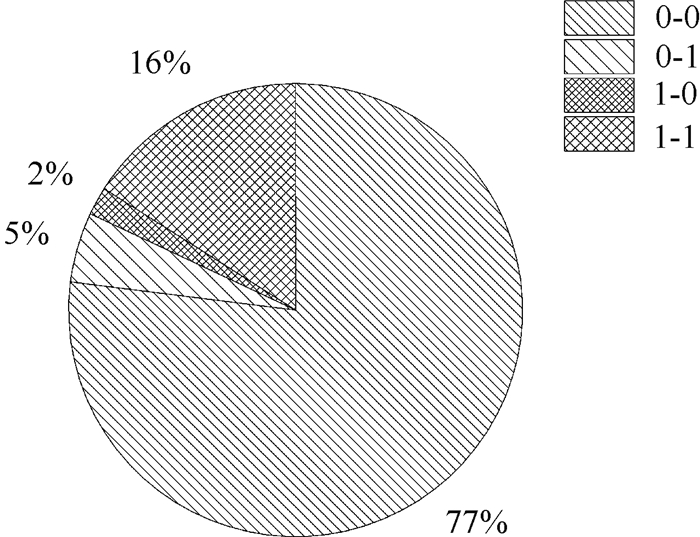 |
| 图 6 上一次出行链状态的影响 Fig. 6 Influence of last trip chain state |
| 图选项 |
基于上述分析,影响出行链充电行为的潜在影响因素主要包括天气、旅程开始时间、出行链时长、出行链距离、旅程速度、起始电荷状态及上一次出行链状态。
3 充电行为的显著影响因素 本文选取logistic回归模型分析确定充电行为的显著影响因素,该模型对自变量的分布要求不高,适用范围广,既能够很好地解决非线性问题,又可以解决多个自变量的问题,筛选出对因变量有显著影响的因素。
3.1 logistic回归模型 logistic回归分析是一种广义的线性回归分析模型,二元logistic回归模型则指因变量分为2类,取值0或1。本文研究出行链的充电行为,将其视为二分类数据,用数字“0”代表没有充电行为的出行链,并将充电次数为1、2、3的旅程一起并称为有充电行为的出行链,用数字“1”代表。出行链的充电行为模型可以表示为
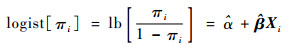 | (1) |
式中: πi为第i条出行链有充电行为的概率,1-πi为第i条出行链没有充电行为的概率;
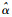
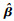
3.2 显著影响因素的确定 对第2节提到的潜在影响因素进行汇总和简单描述,并将因素变量数字化,如表 3所示。从表 2可以看到,2015年8月北京的天气呈现晴、晴转多云、晴转阴、多云、多云转阴、多云转雷阵雨、雷阵雨、阴转小到中雨、雷阵雨转中雨、阵雨等多种情况,为了便于分析,将其划分为晴天和雨天,视为二分类数据,晴天用0表示,雨天用1表示。将旅程开始时间按照早晚划分,只取开始时间对应的小时数,则旅程开始时间被分为0-1,1-2,…,23-24等24个时段。对于出行链的时长,只计入旅程放电时间,不计充电时间,并统一换算为以s为单位的数据。出行链距离则是整个出行链中车辆行驶的总距离,以km为单位。旅程速度为出行链距离与时长的比值,单位统一为km/h, 直接录入速度数据。起始电荷状态在数值上定义为剩余容量占电池容量的比值,其值的范围在0~100之间。上一次出行链状态是指目标出行链之前一次出行链的充电状态,将其视为二分类数据,数字0表示无充电行为,数字1表示有充电行为。
表 3 出行链充电行为的潜在影响因素 Table 3 Potential influential factors affecting charging behavior of travel chain
| 因素变量 | 描述 | 取值 |
| 天气 | 目标出行链所在日的天气情况 | 分晴雨天,晴天为0,雨天为1 |
| 旅程开始时间 | 目标出行链开始行驶的时间 | 24 h制,只取出发对应的小时数 |
| 出行链时长 | 目标出行链中车辆行驶的总时长 | 只计放电过程时间,不计充电时间 |
| 出行链距离 | 目标出行链中车辆行驶的总距离 | 旅程中车辆行驶的距离,单位km |
| 旅程速度 | 目标出行链中车辆的平均行驶速度 | 出行链距离/时长,不计充电时间 |
| 起始电荷状态 | 目标出行链开始时电池的电荷状态 | 开始时剩余容量/电池容量,取值0~100 |
| 上一次出行链状态 | 目标出行链之前一次出行链充电行为 | 取值0和1,1为有充电,0为无充电 |
表选项
使用SPSS软件,把表 3列出的所有潜在影响因素变量都放入模型进行回归,为了更好地拟合模型,根据回归结果剔除影响不显著的因素,保留显著性水平在0.05以下的统计意义上显著的参数,各因素的显著性水平如表 4所示。表中:B为回归系数和截距(常数项),可以是负数(负相关时回归系数出现负值);SE为标准误差;Wals为卡方值,等于B除以其标准误差(SE)的平方值;df为自由度;P为显著性;Exp(B)称为OR,等于B值的返自然对数。
表 4 基于潜在影响因素的模型分析结果 Table 4 Model analysis results based on potential influential factors
| 因素变量 | B | SE | Wals | df | P | Exp(B) |
| 旅程开始时间 | 0.032 | 0.017 | 3.485 | 1 | < 0.01 | 1.033 |
| 出行链时长 | 0 | 0 | 76.843 | 1 | < 0.01 | 1.000 |
| 出行链距离 | 0.012 | 0.004 | 7.817 | 1 | < 0.01 | 1.004 |
| 旅程速度 | 0.043 | 0.011 | 16.509 | 1 | >0.05 | 1.044 |
| 起始电荷状态 | -0.053 | 0.004 | 161.159 | 1 | < 0.01 | 0.949 |
上一次出行链 状态 | 1.212 | 0.204 | 35.309 | 1 | < 0.01 | 3.359 |
| 天气 | 0.384 | 0.310 | 1.530 | 1 | >0.05 | 1.468 |
| 常量 | -2.651 | 0.428 | 38.438 | 1 | < 0.01 | 0.071 |
表选项
从表 4中可以看出,旅程速度和天气是影响不显著的因素。旅程速度受用户自身影响较大,且有距离和时长的比值确定,相对来说对充电行为的影响并不显著;本文数据均发生在2015年8月,天气变化并不明显,只存在晴雨天差别,没有冰雪等恶劣天气,所以天气的影响并不显著。
旅程开始时间、出行链时长、出行链距离、起始电荷状态和上一次出行链状态这5个变量达到显著性水平,且在0.01水平上显著。不同时段开始的出行链,途中充电的概率也大不相同,电动汽车用户往往在晚上出行链结束时,到达住宅区后选择常规充电模式充电,则出行链越晚开始中途快速充电的可能性越小。出行链的距离和时长直接可以判断电动汽车的电量能否完成本次出行链,出行链的距离和时间越长,电动汽车充电的可能性越大。电动汽车电池起始电荷状态是否足以完成接下来的行程,是用户行驶过程中是否会充电的关键。根据电动汽车用户的规律,有快速充电习惯的用户会经常途中充电,因此上一次出行链充电的用户,目标出行链也充电的概率更大。
从回归系数(B)可以看出,各自变量对因变量解释的变化方向,起始电荷状态的系数是负数,说明起始电荷状态越低越容易发生充电行为。综上,最终保留的显著影响因素为:旅程开始时间、出行链时长、出行链距离、起始电荷状态和上一次出行链状态。
4 充电行为预测模型 将3.2节确定的显著影响因素重新输入logistic回归模型,得到基于显著影响因素的各因素变量系数,根据系数确定充电行为的预测模型,将剩余数据集的显著影响因素变量输入充电行为的预测模型,并对模型实现的预测效果进行验证。
4.1 模型建立 将确定的显著影响因素重新输入logistic回归模型,确定各因素变量系数
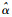
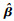
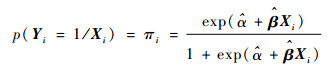 | (2) |
式中:Yi为第i条出行链的充电行为。如果车辆i有充电行为,则
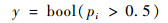 | (3) |
通过式(3)计算,最终判定pi>0.5为有充电行为的出行链。
4.2 预测结果 将确定的显著影响因素(旅程开始时间、出行链时长、出行链距离、起始电荷状态和上一次出行链状态)的数据重新输入logistic回归模型,并经过校正,确定各自变量对因变量的影响强度,得到基于显著影响因素的充电行为回归模型,具体结果如表 5所示。可以看出,旅程开始时间、出行链时长、起始电荷状态和上一次出行链状态这4个变量在0.01水平上显著,出行链距离的影响在0.05水平上显著。
表 5 基于显著影响因素的模型分析结果 Table 5 Model analysis results based on significant influential factors
| 因素变量 | B | SE | Wals | df | P | Exp(B) |
| 旅程开始时间 | 0.030 | 0.018 | 2.919 | 1 | < 0.01 | 1.030 |
| 出行链时长 | 0 | 0 | 69.012 | 1 | < 0.01 | 1.000 |
| 出行链距离 | 0.022 | 0.004 | 38.200 | 1 | < 0.05 | 1.023 |
| 起始电荷状态 | -0.052 | 0.004 | 163.219 | 1 | < 0.01 | 0.957 |
上一次出行 链状态 | 1.120 | 0.201 | 31.071 | 1 | < 0.01 | 3.065 |
| 常量 | -1.704 | 0.357 | 22.822 | 1 | < 0.01 | 0.182 |
表选项
用3.1节得到的回归模型进行4.1节的变形,利用式(2)计算目标出行链有充电行为的概率,通过布尔函数公式(3)对剩余数据集的出行链充电行为进行判定,并对预测模型实现效果进行验证,得到的验证结果如表 6所示。充电行为整体的预测准确率达到84.77%,表示模型对出行链是否充电的行为识别度较高,预测效果较好。另外可明显看出,对无充电行为的出行链的识别率高于有充电行为。
表 6 充电行为预测模型验证结果 Table 6 Model verification results for charging behavior prediction
| 有无充电 出行链 | 实际 个数 | 预测 个数 | 预测准确 个数 | 准确 率/% | 预测 误差/% |
| 充电出行链 | 126 | 120 | 92 | 76.67 | 23.33 |
| 无充电出行链 | 281 | 287 | 253 | 88.15 | 11.85 |
| 整体出行链 | 407 | 407 | 345 | 84.77 | 15.23 |
表选项
为了比较单一和多个显著影响因素的预测模型,并将模型结果可视化,本文采用受试者工作特征曲线作图,该曲线简称ROC曲线,是根据一系列不同的二分类方式以真阳性率(灵敏度)为纵坐标,假阳性率(1-特异度)为横坐标绘制的曲线。ROC曲线简单、直观,通过图示可观察分析方法的准确性,并可用肉眼作出判断。单一和多个显著影响因素的充电行为预测模型结果的ROC曲线如图 7所示。结果表明,基于多个显著影响因素对充电行为预测的准确率更高,通过计算,基于多显著影响因素的曲线下面积(AUC)为0.893,AUC较大预测效果较好。
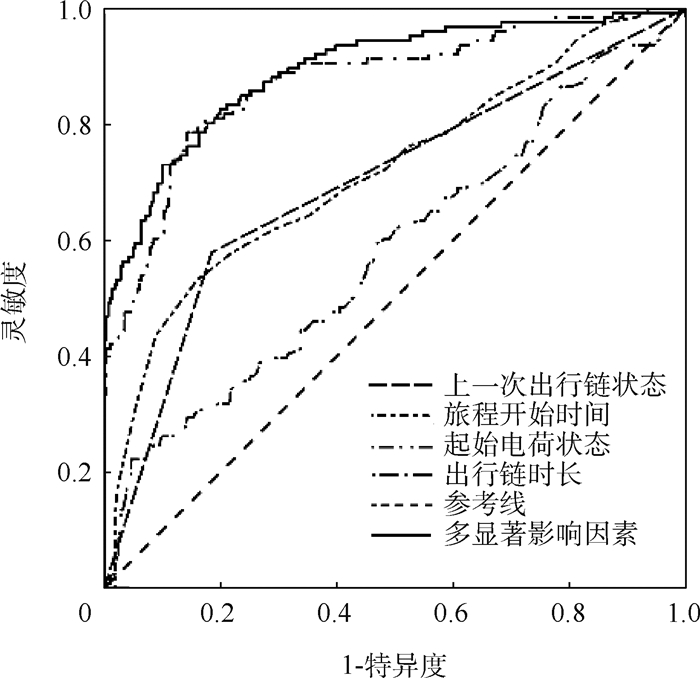 |
| 图 7 充电行为预测模型的ROC曲线 Fig. 7 ROC curves of charging behavior prediction model |
| 图选项 |
为了比较不同天气、不同情况下预测结果的差别,对不同情况下的预测结果分别绘制ROC曲线图,在对2种或2种以上预测情况进行比较时,以直观地鉴别优劣,靠近左上角的ROC曲线所代表的预测方法更准确,也可通过分别计算ROC曲线下的面积(AUC)进行比较,AUC越大预测效果越佳。
将预测结果中晴天和雨天2种数据划分开,分别绘制ROC曲线,如图 8所示。可以看出,ROC曲线相差较大,通过计算得到晴天和雨天的ROC曲线下面积分别为0.911和0.805,进一步说明该模型对晴天的预测效果更佳。
 |
| 图 8 不同天气情况下充电行为预测模型的ROC曲线 Fig. 8 ROC curves of charging behavior prediction model under different weather conditions |
| 图选项 |
5 结论 本文基于出行链理论研究了电动汽车充电行为的影响因素,通过作图对各潜在影响因素做出了详细分析,并确定了电动汽车充电行为的显著影响因素,基于显著影响因素建立预测模型,对电动汽车的充电行为进行预测和验证。
1) 分析了天气、旅程开始时间、出行链时长、出行链距离、旅程速度、起始电荷状态、上一次出行链状态对电动汽车充电行为本身的影响。越晚开始的出行链中途快速充电的可能性越小;出行链的距离和时间越长,电动汽车充电的可能性越大;随着旅程速度的增加,充电频次的变化呈正态分布,电池起始电荷状态越低充电的频次越高;有快速充电的用户有惯性行为,上一次出行链充电的用户,目标出行链充电的概率更大。
2) 通过logistic回归模型分析,确定了本文中电动汽车充电行为的显著影响因素,包括旅程开始时间、出行链时长、出行链距离、起始电荷状态和上一次出行链状态。
3) 基于显著影响因素建立预测模型,基于多个影响因素对充电行为预测的准确率达到84.77%;根据天气可以得出不同情况下的预测结果略有差别,对晴天的预测准确率更高。
本文虽然已经考虑了大多数因素,但由于数据的局限性,温度、天气、道路等级等因素尚未考虑;另外本文仅仅对单条出行链是否充电进行了预测,没有对具体的充电时间、充电时长进行建模和预测。为使本文提出的预测模型的准确率更高,接下来可以搜集更全面的数据,并将温度、恶劣天气、道路等级等因素考虑其中;在此基础上继续对充电次数、充电时间等进行预测,并进一步对出行链中的快速充电行为进行建模优化,为更准确地进行充电负荷预测、充电设施布设、电网规划建设奠定基础。
参考文献
| [1] | BOULANGER A G, CHU A C, MAXX S, et al. Vehicle electrification:Status and issues[J]. Proceedings of the IEEE, 2011, 99(6): 1116-1138. DOI:10.1109/JPROC.2011.2112750 |
| [2] | 张文亮, 武斌, 李武峰, 等. 我国纯电动汽车的发展方向及能源供给模式的探讨[J]. 电网技术, 2009, 33(4): 1-5. ZHANG W L, WU B, LI W F, et al. Discussion on development trend of battery electric vehicles in China and its energy supply mode[J]. Power System Technology, 2009, 33(4): 1-5. DOI:10.3969/j.issn.1674-0629.2009.04.001 (in Chinese) |
| [3] | 高赐威, 张亮. 电动汽车充电对电网影响的综述[J]. 电网技术, 2011, 35(2): 127-131. GAO C W, ZHANG L. A survey of influence of electric vehicle charging on power grid[J]. Power System Technology, 2011, 35(2): 127-131. (in Chinese) |
| [4] | 胡泽春, 宋永华, 徐智威. 电动汽车接入电网的影响与利用[J]. 中国电机工程学报, 2012, 32(4): 1-10. HU Z C, SONG Y H, XU Z W. Impacts and utilization of electric vehicles integration into power systems[J]. Proceedings of the CSEE, 2012, 32(4): 1-10. (in Chinese) |
| [5] | 张艳娟, 苏小林, 闫晓霞, 等. 基于电动汽车时空特性的充电负荷预测[J]. 电力建设, 2015, 36(7): 75-81. ZHANG Y J, SU X L, YAN X X, et al. A method of charging load forecast based on electric vehicle time-space characteristics[J]. Electric Power Construction, 2015, 36(7): 75-81. DOI:10.3969/j.issn.1000-7229.2015.07.010 (in Chinese) |
| [6] | 陈丽丹, 聂涌泉, 钟庆. 基于出行链的电动汽车充电负荷预测模型[J]. 电工技术学报, 2015, 30(4): 216-225. CHEN L D, NIE Y Q, ZHONG Q. A model for electricvehicle charging load forecasting based on trip chains[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 216-225. DOI:10.3969/j.issn.1000-6753.2015.04.027 (in Chinese) |
| [7] | 王海玲, 张美霞, 杨秀. 基于气温影响的电动汽车充电需求预测[J]. 电测与仪表, 2017, 54(23): 123-128. WANG H L, ZHANG M X, YANG X. Electric vehicle charging demand forecasting based on influence of weather and temperature[J]. Electrical Measurement and Instrumentation, 2017, 54(23): 123-128. DOI:10.3969/j.issn.1001-1390.2017.23.020 (in Chinese) |
| [8] | 田立亭, 史双龙, 贾卓. 电动汽车充电功率需求的统计学建模方法[J]. 电网技术, 2010, 34(11): 126-130. TIAN L T, SHI S L, JIA Z. A statistical model for charging power demand of electric vehicles[J]. Power System Technology, 2010, 34(11): 126-130. (in Chinese) |
| [9] | 罗卓伟, 胡泽春, 宋永华, 等. 电动汽车充电负荷计算方法[J]. 电力系统自动化, 2011, 35(14): 36-42. LUO Z W, HU Z C, SONG Y H, et al. Study on plug-in electric vehicles charging load calculating[J]. Automation of Electric Power Systems, 2011, 35(14): 36-42. (in Chinese) |
| [10] | 杨冰, 王丽芳, 廖承林. 大规模电动汽车充电需求及影响因素[J]. 电工技术学报, 2013, 28(2): 22-27. YANG B, WANG L F, LIAO C L. Research on powercharging demand of large-scale electric vehicles and its impacting factors[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 22-27. DOI:10.3969/j.issn.1000-6753.2013.02.003 (in Chinese) |
| [11] | MOON H B, PARK S Y, JEONG C, et al. Forecasting electricity demand of electric vehicles by analyzing consumers' charging patterns[J]. Transportation Research Part D:Transport and Environment, 2018, 62: 64-79. DOI:10.1016/j.trd.2018.02.009 |
| [12] | ASHTARI A, BIBEAU E, SHAHIDINEJAD S, et al. PEV charging profile prediction and analysis based on vehicle usage data[J]. IEEE Transactions on Smart Grid, 2012, 3(1): 341-350. DOI:10.1109/TSG.2011.2162009 |
| [13] | STEEN D, CARLSON O, BERTLING L. Assessment of electric vehicle charging scenarios based on demographical data[J]. IEEE Transactions on Smart Grid, 2012, 3(3): 1457-1468. DOI:10.1109/TSG.2012.2195687 |
| [14] | ALIZADEH M, SCAGLIONE A, DAVIES J, et al. A scalable stochastic model for the electricity demand of electric and plug-in hybrid vehicles[J]. IEEE Transactions on Smart Grid, 2014, 5(2): 848-860. DOI:10.1109/TSG.2013.2275988 |
| [15] | WANG J, LIU K, YAMAMOTO T. Improving electricity consumption estimation for electric vehicles based on sparse GPS observations[J]. Energies, 2017, 10(1): 129. DOI:10.3390/en10010129 |
| [16] | SCH?UBLE J, KASCHUB T, ENSSLEN A, et al. Generating electric vehicle load profiles from empirical data of three EV fleets in Southwest Germany[J]. Journal of Cleaner Production, 2017, 150: 253-266. DOI:10.1016/j.jclepro.2017.02.150 |
| [17] | YANG Y, YAO E, YANG Z, et al. Modeling the charging and route choice behavior of BEV drivers[J]. Transportation Research Part C:Emerging Technologies, 2016, 65: 190-204. DOI:10.1016/j.trc.2015.09.008 |
| [18] | FERNANDEZ L P, ROMáN T G S, COSSENT R, et al. Assessment of the impact of plug-in electric vehicles on distribution networks[J]. IEEE Transactions on Power Systems, 2011, 26(1): 206-213. DOI:10.1109/TPWRS.2010.2049133 |
| [19] | HüBNER M, ZHAO L, MIRBACH T, et al.Impact of large-scale electric vehicle application on the power supply[C]//2009 IEEE Electrical Power & Energy Conference (EPEC).Piscataway, NJ: IEEE Press, 2009: 1-6. |
| [20] | IKEGAMI T, OGIMOTO K, YANO H, et al.Balancing power supply-demand by controlled charging of numerous electric vehicles[C]//2012 IEEE International Electric Vehicle Conference.Piscataway, NJ: IEEE Press, 2012: 1-8. |
| [21] | BOWMAN J L, BEN-AKIVA M E. Activity-based disaggregate travel demand model system with activity schedules[J]. Transportation Research Part A:Policy and Practice, 2001, 35(1): 1-28. DOI:10.1016/S0965-8564(99)00043-9 |
| [22] | 温剑锋, 陶顺, 肖湘宁, 等. 基于出行链随机模拟的电动汽车充电需求分析[J]. 电网技术, 2015, 39(6): 1477-1484. WEN J F, TAO S, XIAO X N, et al. Analysis on charging demand of EV based on stochastic simulation of trip chain[J]. Power System Technology, 2015, 39(6): 1477-1484. (in Chinese) |
