为了得到高精度的码伪距测量值,国内外****研究采用不同方法提高码跟踪环精度。文献[4]提出了采用载波多普勒的估计值辅助伪码环的环路架构;文献[5]提出一种自适应带宽的码跟踪环设计方案,通过实时调整环路滤波器带宽提升码跟踪环性能;文献[6]采用补偿迭代思想对码跟踪环进行了改造,并改进提高了伪距测量方法;文献[7]提出利用三点二次插值法处理相关谱谱峰数据在低采样率情况下提高码相位测量精度,并与两点、三点线性内插法进行了对比;文献[8]以相关峰值点为分界点对相关峰两侧分别做最小二乘拟合,以两直线交点的横坐标与零相偏参考值的差值作为码相位的估值,得到比最小二乘同步法和三点二次插值法更加稳定和精确的估值结果;文献[9]提出最小二乘提高码相位测量精度;文献[10]在其基础上,给出了一种累加最小二乘法的实现结构,使最小二乘法的适用范围更广、精度更高。但以上方法都是以两信号的相关函数及相关峰为基础,需要两路或者更多路复制码信号进行相关计算,存在一定局限性。
针对以上问题,本文以互功率谱相位为研究对象,采用相位条纹法,在延迟锁定环的基础上,提出一种高精度的码相位测量方法。
1 相位条纹法原理 1981年,Piersol[11]提出了用相位参数估计延时的方法,通过测量互功率谱的相位谱回归直线斜率来估计延时。雷达技术中常用相位条纹法测量同一信号经反射后到达两相关接收机的时间延时。两路信号分别记为f1(t)和f2(t),其中, f2(t)=f1(t-τ),τ为信号到达两接收机的时延。对两路信号进行互相关计算,设
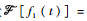
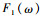
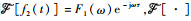
 | (1) |
式中:R12(t)为f1(t)和f2(t)的互相关函数。因此,互功率谱密度的相位为
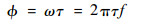 | (2) |
由式(2)可知,当时延τ一定的情况下,两路信号互功率谱密度的相位?与频率f存在线性关系,且斜率只与信号时延τ有关。考虑到计算出的互功率谱密度相位?的取值范围为[-π, π],所以?~f直线被切割为周期性的条纹,每条条纹斜率为2πτ,如图 1所示。
 |
| 图 1 延迟1 s的两路相同信号互功率谱相位条纹 Fig. 1 Cross-correlation power spectrum phase stripes of two same signals with a delay of 1 s |
| 图选项 |
图 1中条纹间隔T0为
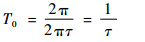 | (3) |
条纹频率f0(即每1 Hz频带内条纹数)为
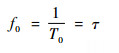 | (4) |
因此,通过统计相位条纹的出现频率,即可测量出信号的时延。
2 相位条纹法测量码相位 在GPS接收机中,接收的卫星信号与本地NCO生成的伪码信号也可视为存在待测时延的两路相关信号,且伪码信号有足够宽的频带,有利于在频域中生成足够多的条纹,便于测量条纹出现的频率,测量出的条纹频率即是码相位测量值,可以用于组装码伪距。卫星信号经射频前端下变频之后,进入跟踪环路。当跟踪环路进入稳定跟踪状态后,采用Ⅰ支路混频器输出的信号(已经消除载波相位误差和多普勒频移),与伪码NCO生成的即时支路伪随机码计算互功率谱密度,通过统计出现的相位条纹频率,即可获得码相位测量值。码跟踪环结构及相位条纹法结构(虚线部分)如图 2所示。图中:SIF(n)为经过接收机射频前端处理采样后的中频数字信号;i和q分别表示混频后的两支路信号;E、P和L分别为超前、即时和滞后复制码;δcp为码环鉴别器输出的码相位测量结果。
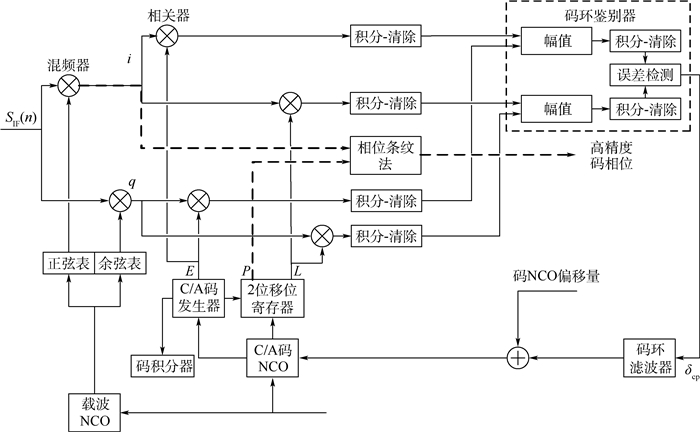 |
| 图 2 典型接收机码跟踪环路及相位条纹法结构 Fig. 2 Structure of typical receiver code tracking loop and phase stripe method |
| 图选项 |
2.1 互功率谱相位的计算 设经混频后的中频信号为f1(t),本地生成的伪码信号为f2(t)。分别进行傅里叶变换,得到
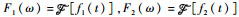
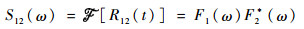 | (5) |
其相位为复数S12(ω)的辐角主值:
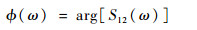 | (6) |
2.2 傅里叶变换时延提取和时延补偿法 计算出互功率谱的相位后,获取码相位测量值的关键就是提取相位条纹的频率。经实验验证,由于导航信号信噪比较低,直接采用直线拟合效果较差,傅里叶变换法提取条纹是更优的方式。该方法是对相位条纹?(f)再次进行傅里叶变换,当条纹频率为f0时,条纹间隔T0=1/f0,单个条纹?1(f)可以表示为
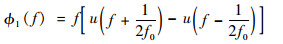 | (7) |
对式(7)进行傅里叶变换,得到单个条纹的幅度谱为
 | (8) |
式中:ψ为相位条纹函数?1(f)的角频率。
当条纹以T0为周期重复出现时,周期性的多条相位条纹的傅里叶变换幅度谱为
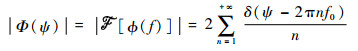 | (9) |
式中:δ为冲激函数。
由式(9)可知,两信号的互功率谱相位条纹?(f)经过再次傅里叶变换后得到幅度谱|Φ(ψ)|,当n=1时,|Φ(ψ)|的函数值为最大值,此时ψ=2πf0,即在

考虑到接收机进入到稳定跟踪状态后,本地码NCO生成的伪随机码已经经过了延迟锁定环的调整,与接收信号之间的时延远小于一个码片长度。由式(4)得,条纹频率f0与时延τ成正比,时延τ越大,条纹数量越多。更多的条纹数使得傅里叶变换法提取条纹的结果更接近式(9)计算的理论值。因此,为了提高频带内条纹数量,便于傅里叶变换法提取更精确的条纹频率,应提前采用时延补偿法,将本地信号额外延迟一个固定时间τ0,使待测时延变为(τ+τ0),其中τ0≥τ。用傅里叶变换法测出补偿后的两信号时延,再减去补偿时延τ0,即可获得原始时延即码相位测量值。
2.3 时域折叠法提高信噪比 接收信号中包含的噪声也会对条纹频率的提取造成一定程度的影响。当GPS卫星处于天顶方向(仰角90°)时,信号经过射频前端处理,进入跟踪环路后,噪声带宽为C/A码信号的带宽2.046 MHz,此时信噪比(SNR)约为-16.5 dB[2]。而当卫星处于低仰角(约5°)时,中频信号信噪比约为-24.5 dB。较低的信噪比使得相位条纹淹没在噪声之中,给提取条纹频率带来很大的困难。
时域折叠原理如图 3所示。
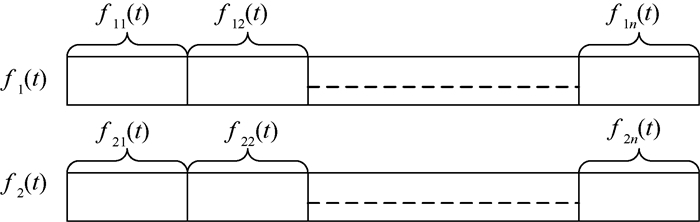 |
| 图 3 时域折叠法示意图 Fig. 3 Schematic diagram of time domain folding method |
| 图选项 |
两段信号数据均被分为均匀的n段数据段,分别表示为f11(t), f12(t),…,f1n(t)和f21(t), f22(t),…,f2n(t)。经过分段后,将每段数据叠加求和,得到时域折叠后的信号数据f′1(t)和f′2(t)为
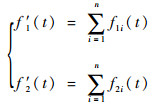 | (10) |
GPS信号中,导航电文的数据码码长为20 ms,伪码周期仅为1 ms。也就是在20 ms内,可以忽略导航电文对伪码相位的影响。在此条件下,对接收信号进行每段1 ms时长的时域折叠,可以有效减小噪声功率,提高信噪比。当折叠段数为10段时,信噪比将提高约10 dB。经时域折叠提高信噪比之后的两路信号f′1(t)和f′2(t)再计算互功率谱相位,即可得到较为清晰的相位条纹。
2.4 相位条纹法实现步骤 相位条纹法测量码相位的完整步骤如图 4所示,该方法需要接收机射频前端下变频的中频卫星信号,以及跟踪环路进入稳定跟踪状态后的本地复制载波和本地复制码。首先,将中频信号和本地复制载波经过混频器,滤除载波和多普勒频移,得到接收输入信号f1(t)。本地复制码作为本地输入信号f2(t),经过时延补偿,得到f2(t-τ0),与接收信号f1(t)之间间隔一个较大的时延。其次,分别对接收信号和本地码信号进行式(10)所示的相同时长的信号时域折叠,得到高信噪比的信号f′1(t)和f′2(t-τ0),并保持两路信号的相关性。然后,通过式(5)和式(6),计算两信号的互功率谱相位,生成相位条纹。对相位条纹再次进行式(9)所示的傅里叶变换,可以得到二次变换幅度谱|Φ(ψ)|最大值对应的条纹频率,即两信号的间隔时延为(τ+τ0)。最后,从测量时延中减去补偿的时延量,即可获得比延迟锁定环更高精度的码相位测量值τ。
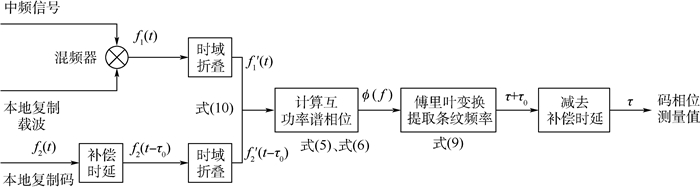 |
| 图 4 相位条纹法流程图 Fig. 4 Flowchart of phase stripe method |
| 图选项 |
3 仿真实验 采用MATLAB软件编程对第2节方法进行仿真实验,仿真参数如表 1所示。表中,码速率的单位cps表示码片每秒。通过软件编程,模拟生成卫星信号下变频之后的中频信号、本地载波信号和码信号。经2.4节的步骤后,仿真结果如图 5~图 8所示。
表 1 仿真参数 Table 1 Simulation parameters
| 参数 | 数值 |
| 信号长度/ms | 10 |
| 中频载波频率/MHz | 4[13] |
| 伪码长度/bit | 1 023 |
| 码速率/Mcps | 1.023 |
| 采样频率/MHz | 100 |
| 设定待测时延/ns | 10 |
| 补偿时延/ns | 1 000 |
| 时域折叠段数 | 10 |
表选项
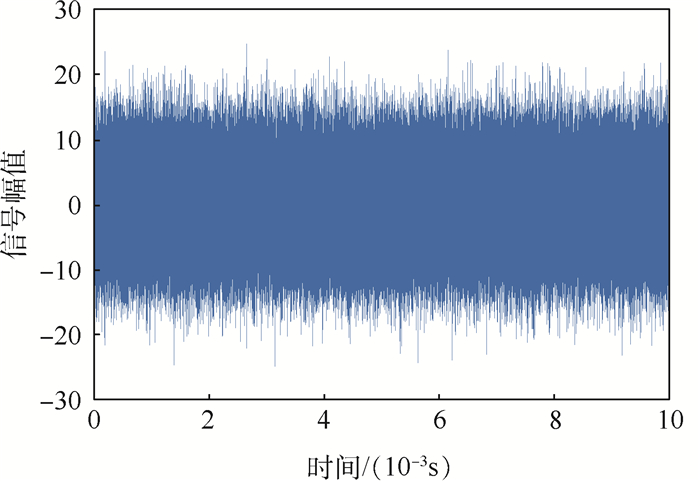 |
| 图 5 输入的中频信号 Fig. 5 Input IF signal |
| 图选项 |
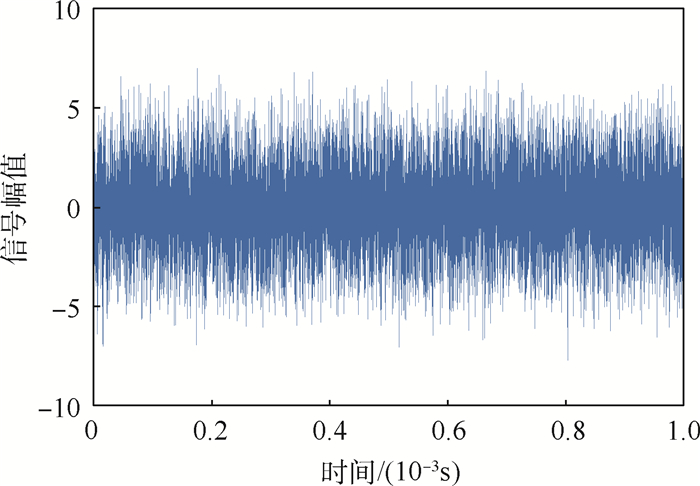 |
| 图 6 时域折叠后的信号 Fig. 6 Folded signal in time domain |
| 图选项 |
 |
| 图 7 接收信号与本地码信号的互功率谱相位条纹 Fig. 7 Cross-correlation power spectrum phase stripes between received signal and local code signal |
| 图选项 |
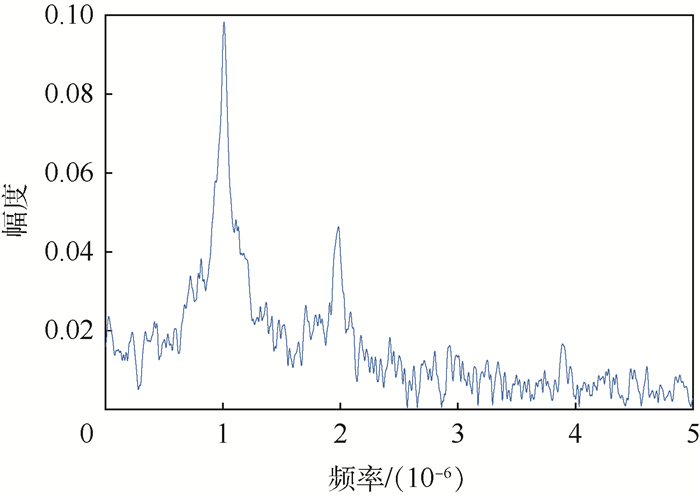 |
| 图 8 条纹频率 Fig. 8 Stripe frequency |
| 图选项 |
图 5为模拟经过射频前端处理之后进入跟踪环路的中频信号,有效信号已经完全淹没在噪声中;图 6为中频信号经过与本地载波信号混频,并进行时域折叠后的信号,可以发现噪声幅度明显减小,有效地提高了信号信噪比。
图 7为图 6中的信号与本地码信号的互功率谱相位,低频段有明显的倾斜条纹,高频段的条纹被淹没在噪声中。其中部分集中在0相位的数据点是互功率谱幅值较小的数据,为了防止由于MATLAB软件的舍入误差造成极大的相位偏差而被设为0相位。图 8为采用傅里叶变换法提取条纹频率时,对图 7的数据进行再次傅里叶变换后的功率谱幅度,最大值对应频率即为测得时延。将此结果减去补偿时间,即可得到码相位测量值。
采用以上程序,对于不同的信噪比情况,分别进行1 000次蒙特卡罗仿真模拟,并与相同情况下延迟锁定环的测量误差进行对比。延迟锁定环常用的3种码鉴相器算法中,相比于非相干前减后幅值法和非相干前减后功率法,相干点积功率法的运算量较小,且得到的码相位测量值最为准确[14]。此处选取采用相干点积功率法鉴相器的延迟锁定环进行对比,其码相位测量误差均方差(RMSE)计算式为[2, 15]
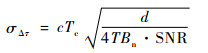 | (11) |
式中:c为光速;Tc为伪码码宽,此处取值C/A码码宽, 即
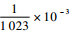
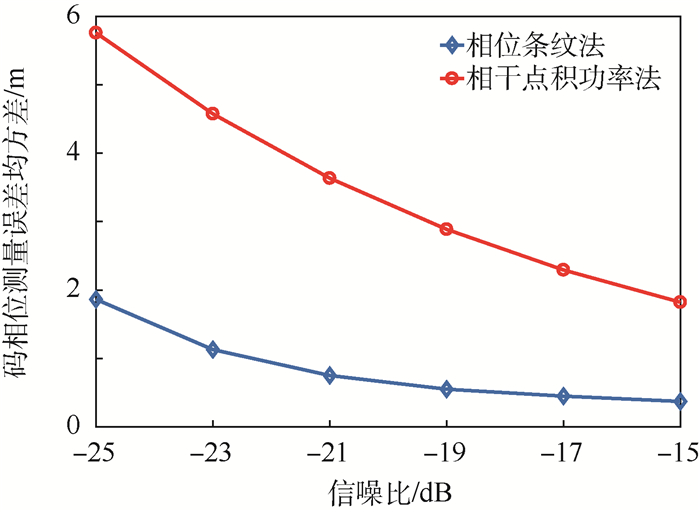 |
| 图 9 码相位测量误差均方差对比 Fig. 9 RMSE of code phase measurement error comparison |
| 图选项 |
表 2 码相位测量误差均方差结果 Table 2 RMSE results of code phase measurement error
| 信噪比/dB | 码相位测量误差均方差/m | |
| 相位条纹法 | 相干点积功率法 | |
| -15 | 0.371 1 | 1.821 7 |
| -17 | 0.448 7 | 2.293 3 |
| -19 | 0.549 7 | 2.887 1 |
| -21 | 0.750 4 | 3.634 7 |
| -23 | 1.129 2 | 4.575 8 |
| -25 | 1.863 2 | 5.760 6 |
表选项
4 结论 1) 根据本文的仿真实验结果,当卫星处于天顶方向,接收信号信噪比为-15 dB时,码相位测量误差均方差可以达到约0.37 m,约为一个码片宽度(293 m)的0.13%,比延迟锁定环测量误差均方差1.82 m提高了约80%。
2) 随着信噪比的下降,测量误差会逐渐增大。而当卫星处于低仰角(约5°)时,信噪比下降至约-25 dB,测量误差均方差增大到1.86 m,为码片宽度的0.63%,但仍比延迟锁定环测量误差均方差5.76 m提高约68%。
3) 与传统跟踪环路相比,本文方法少量增加了接收机处理器的计算量和计算时间,显著提高了码伪距的测量精度,且不存在整周模糊度的问题。在接收机的实际应用中,可以用较低的成本提供高精度的码伪距测量值,具有十分广泛的应用价值。同时也能为高精度测距和定位提供一定的参考作用。
为使本文方法能更加准确、高效地实现码相位测量,仍需要优化部分参数和细节计算。
参考文献
| [1] | 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2017. XIE G. Principles of GPS and receiver design[M]. Beijing: Publishing House of Electronics Industry, 2017. (in Chinese) |
| [2] | 鲁郁. 北斗/GPS双模软件接收机原理与实现技术[M]. 北京: 电子工业出版社, 2016. LU Y. BeiDou/GPS dual-mode software receiver principle and implementation technology[M]. Beijing: Publishing House of Electronics Industry, 2016. (in Chinese) |
| [3] | MISRA P, ENGE P. Global positioning system:Signals, measurements, and performance[M]. 2nd ed. Warszawa: Ganga-Jamuna Press, 2006. |
| [4] | 罗柳镇.高精度卫星测距技术研究与实现[D].南京: 南京理工大学, 2016: 37-43. LUO L Z.Research and realization of high precision satellite ranging technology[D].Nanjing: Nanjing University of Science and Technology, 2016: 37-43(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10288-1017056980.htm |
| [5] | 刘盟超, 赵丙风. GNSS接收机自适应带宽伪码跟踪环路设计[J]. 无线电通信技术, 2017, 43(4): 64-66. LIU M C, ZHAO B F. Design of adaptive bandwidth DLL for GNSS receivers[J]. Radio Communications Technology, 2017, 43(4): 64-66. DOI:10.3969/j.issn.1003-3114.2017.04.15 (in Chinese) |
| [6] | 邓中亮, 赵洋, 尹露, 等.一种提高伪距测量精度方法研究[C]//第六届中国卫星导航学术年会论文集.北京: 中国卫星导航系统管理办公室学术交流中心, 2015: 4. DENG Z L, ZHAO Y, YIN L, et al.An improved pseudo-range measurement method research[C]//6th China Satellite Navigation Conference(CSNC).Beijing: Academic Exchange Centre of China Satellite Navigation Office, 2015: 4(in Chinese). |
| [7] | 龚国辉, 李思昆. 提高DSSS信号PN码相位测量精度的三点二次插值法[J]. 通信学报, 2007, 28(2): 130-133. GONG G H, LI S K. Improving DSSS signal PN code phase measurement precision by 3-points quadratic interpolation[J]. Journal on Communications, 2007, 28(2): 130-133. DOI:10.3321/j.issn:1000-436X.2007.02.021 (in Chinese) |
| [8] | 罗海军, 彭卫东, 李明阳, 等. 基于分段直线拟合的伪随机码相位测量法[J]. 计算机测量与控制, 2015, 23(3): 727-729. LUO H J, PENG W D, LI M Y, et al. Method of phase measurement of PN codes based on piecewise linear fitting[J]. Computer Measurement and Control, 2015, 23(3): 727-729. DOI:10.3969/j.issn.1671-4598.2015.03.015 (in Chinese) |
| [9] | 胡修林, 张俊, 杨灵. 直接序列扩频通信系统中PN码相位的精确测量方法[J]. 电讯技术, 2005, 45(3): 128-131. HU X L, ZHANG J, YANG L. A method for accurately measuring the phase of PN code in DSSS systems[J]. Telecommunication Engineering, 2005, 45(3): 128-131. DOI:10.3969/j.issn.1001-893X.2005.03.029 (in Chinese) |
| [10] | 张波, 郭英, 齐子森, 等. PN码相位精确测量的累加最小二乘法[J]. 北京航空航天大学学报, 2016, 42(10): 2265-2270. ZHANG B, GUO Y, QI Z S, et al. Precise measurement of PN code phase by accumulative least square method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(10): 2265-2270. (in Chinese) |
| [11] | PIERSOL A G. Time delay estimation using phase data[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1981, 29(3): 471-477. DOI:10.1109/TASSP.1981.1163555 |
| [12] | 熊庆旭, 刘锋, 常青. 信号与系统[M]. 北京: 高等教育出版社, 2011. XIONG Q X, LIU F, CHANG Q. Signals and systems[M]. Beijing: Higher Education Press, 2011. (in Chinese) |
| [13] | BRAASCH M S, VAN DIERENDONCK A J. GPS receiver architectures and measurements[J]. Proceedings of the IEEE, 1999, 87(1): 48-64. DOI:10.1109/5.736341 |
| [14] | 王松瑞.北斗二代接收机捕获跟踪算法研究与实现[D].西安: 西安电子科技大学, 2017: 37-38. WANG S R.Research and implementation of the BD-Ⅱ receiver acquisition and tracking algorithm[D].Xi'an: Xidian University, 2017: 37-38(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10701-1017300627.htm |
| [15] | VAN DIERENDONCK A J, FENTON P, FORD T. Theory and performance of narrow correlator spacing in a GPS receiver[J]. Navigation, 1992, 39(3): 265-283. DOI:10.1002/navi.1992.39.issue-3 |
