近年来,光场技术进一步发展,利用微透镜阵列,单相机一次曝光能同时完成光线的位置和方向信息(即光场)的记录。因此,在传统显微成像系统的基础上加装微透镜阵列构成显微光场成像系统[7],可以实现单相机一次曝光记录物空间的光场信息,进一步利用图像处理技术可以得到物空间的三维坐标信息[8],因此光场显微成像结合粒子图像测速技术(光场Micro-PIV),通过单个光场相机有望实现微尺度瞬时三维速度场的测量。微尺度流场中,示踪粒子的三维坐标信息的准确重建是光场Micro-PIV技术实现瞬时三维速度场测量的关键。示踪粒子的成像过程可表示为示踪粒子的光强分布与成像系统的点扩散函数(PSF)的卷积[9],因此可通过反卷积进行示踪粒子三维重建。反卷积算法主要有线性反卷积法[10]、盲反卷积法[11]和Lucy-Richardson(L-R)算法[12]。线性反卷积法对噪声敏感度高且无法复原高频信息,重建精度低;盲反卷积法虽然精度高,但需在迭代重建的同时更新PSF,计算量大,耗时长;L-R算法能够按照泊松噪声统计标准对给定PSF的退化图像进行反卷积迭代推演,当给定的PSF足够精确时,可以准确而快速地完成三维重建。但准确获得PSF是L-R算法完成示踪粒子三维重建的关键。
现有的PSF模型可分为两大类:基于几何光学的PSF模型和基于波动光学的PSF模型。由于显微光场成像系统衍射无法忽略,同时系统中微透镜阵列的引入,导致现有的基于几何光学和波动光学的PSF模型均不适用于光场Micro-PIV中PSF的确定。因此,需要建立适合显微光场成像系统的PSF模型。目前,PSF可通过理论计算和实验测量方法确定。对于显微光场成像系统,实验测量方法要求粒子直径小于衍射限制,同时,当系统参数变化时,需要重新进行实验测量,导致PSF确定过程极为耗时。而理论计算方法没有上述限制,且系统参数变化时,只需改变PSF模型中相应的参数,即可计算出新的PSF。
针对光场Micro-PIV中PSF的确定,本文基于波动光学建立了显微光场成像PSF模型,进行了数值模拟,获得了理论的PSF图像。构建了光场Micro-PIV实验装置,实验确定了显微光场成像系统的PSF图像,进一步通过L-R算法实现了微尺度三维流动中示踪粒子的三维重建,对PSF理论计算模型的准确性进行了验证。
1 光场Micro-PIV 光场的概念最早由Gershun[13]提出,用来描述光在三维空间中的辐射传输特性。当光线在传播过程中保持能量不变时,可表示为四维光场。对于四维光场的表征,主要采用双平面法,表达形式为L(u, v, s, t),其中(u, v)和(s, t)分别表示光线与2个相互平行的平面的坐标交点。基于光场理论,在传统显微镜与相机传感器之间加装微透镜阵列,可组成显微光场成像系统,从而记录待测对象的光场信息。图 1为显微光场成像原理示意图。其中,微透镜阵列位于筒镜后焦面处,相机传感器位于微透镜阵列后焦面处。测量体内任意一点S发出光线,经过显微镜内物镜与筒镜的作用,会聚于微透镜阵列C处,每个微透镜把接收的光线按其传播方向分散到相机传感器的不同像素点上,因此可通过单光场相机实现四维光场信息采集。
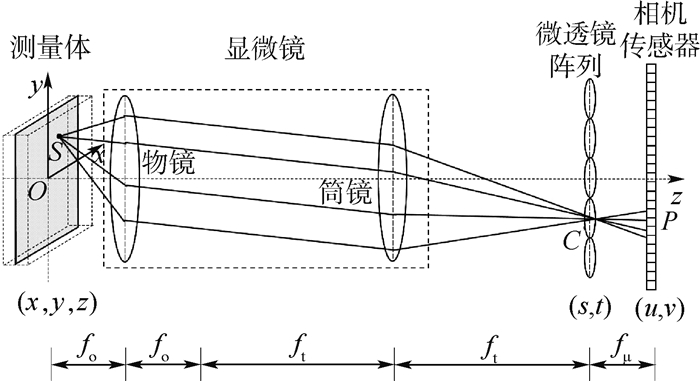 |
| 图 1 显微光场成像原理示意图 Fig. 1 Schematic diagram of microscopic light field imaging |
| 图选项 |
基于显微光场成像的Micro-PIV系统原理如图 2所示。光场Micro-PIV系统主要由激光器(激光波长λ0=532nm)、显微镜、微注射泵、光场相机系统和计算机组成。通过光场Micro-PIV系统获得时间间隔为Δt的2张示踪粒子的光场图像后,通过L-R算法反卷积重建出示踪粒子的三维坐标信息,再利用互相关算法获得瞬时三维速度场。L-R算法的迭代公式可表示为[11]
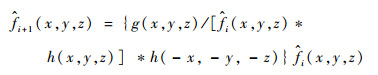 | (1) |
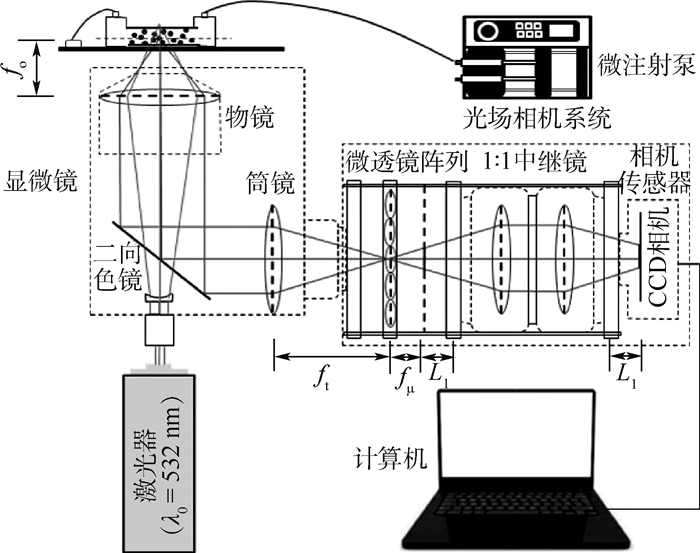 |
| 图 2 光场Micro-PIV系统原理图 Fig. 2 Schematic diagram of light field Micro-PIV system |
| 图选项 |
式中:

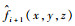
从式(1)可见,显微光场成像系统的PSF是光场Micro-PIV通过L-R算法完成三维重建的前提。准确获得显微光场成像系统的PSF图像之后,反卷积问题将转换为线性复原问题。
2 显微光场成像PSF模型 点光源是最基本的光源单位,对于复杂的光源,可以将其视为众多点光源的叠加。现以点光源为例,分析其在显微光场成像系统中的成像过程。以物镜的焦点为原点,系统光轴为z轴,建立如图 1所示坐标系。其中,z=0表示物镜焦平面,z>0表示离焦且靠近物镜,z < 0表示离焦且远离物镜。测量体内任一点光源发出的球面波在系统中的传播过程可分为以下3个部分:
1) 球面波经过显微镜内物镜和筒镜到达微透镜阵列。显微镜可视为衍射受限光学系统,点光源S(x, y, z)发出的发散球面波投射到物镜上,经显微镜变换为筒镜上的会聚球面波,根据基于波动光学的标量衍射理论[14],到达微透镜阵列的球面波的波阵面U(x, y, z)可表示为
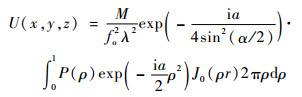 | (2) |
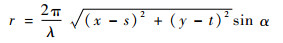 | (3) |
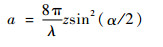 | (4) |
式中:x、y、z为点光源的三维坐标;r和a分别为物面径向和轴向光学坐标;fo为物镜焦距;λ为荧光波长;M为物镜的放大倍率;α为物镜孔径角的半数,sin α=NA,NA为物镜的数值孔径;ρ为物镜孔径的规格化径向坐标;P(ρ)为归一化光瞳函数;J0(·)为零阶贝塞尔函数;s、t为微透镜阵列面坐标。
2) 球面波透过微透镜阵列。微透镜阵列可简化为疏状函数,本文采用的微透镜孔径为正方形,因此微透镜阵列的透过率函数T(x, y, z)可表示为
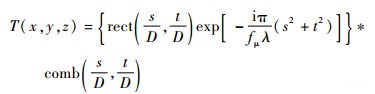 | (5) |
式中:rect(·)和comb(·)分别为矩形函数和梳状函数;fμ和D分别为微透镜的焦距和孔径。
球面波穿过微透镜阵列后,其波阵面U′(x, y, z)为
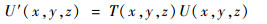 | (6) |
3) 球面波传播到相机传感器面。球面波传播到相机传感器面可视为菲涅尔衍射,到达相机传感器面的波阵面U″(x, y, z)可表示为
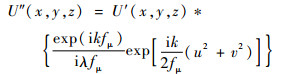 | (7) |
式中:k为波矢,k=2π/λ;u、v为传感器面坐标。
通过傅里叶变换,式(7)可表示为
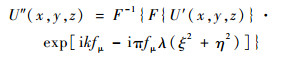 | (8) |
式中:ξ和η分别为传感器面上坐标u和v的空间频率,ξ=u/(λfμ), η=v/(λfμ);F(·)和F-1(·)分别为傅里叶变换和傅里叶逆变换。
因此,测量体内点光源S(x, y, z)发出的球面波到达相机传感器面的光强分布h(x, y, z)为
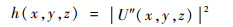 | (9) |
光学系统的PSF定义为输入物为一点光源时其输出像的光强分布,因此,h(x, y, z)即为光场Micro-PIV系统的PSF。
3 实验系统 为了验证本文建立的PSF模型,基于图 2所示的光场Micro-PIV系统原理,搭建了光场Micro-PIV实验系统,如图 3所示。其中,光场相机系统由微透镜阵列、1:1中继镜和CCD相机组成,各部件通过笼板和笼杆加以固定。显微镜可控制载物台与物镜距离,精度为1μm,因此可确定测量体所处深度范围。显微镜内的二向色镜用于过滤被反射的激光,以提高光场图像的信噪比。显微光场成像系统参数如表 1所示,改变系统参数主要通过更换显微镜物镜和相应的微透镜阵列来实现。实验所用微流控芯片为矩形层流芯片,其长直微通道截面宽度为150μm,深度为50μm。实验时,含有示踪粒子的溶液经微注射泵注入到微流控芯片中,示踪粒子被激光激发出峰值波长为584nm的荧光,粒子激发的荧光经显微光场成像系统成像于相机传感器面,通过计算机可实时记录含有示踪粒子的光场图像。
 |
| 图 3 光场Micro-PIV实验系统 Fig. 3 Light field Micro-PIV experimental system |
| 图选项 |
表 1 显微光场成像系统参数 Table 1 Microscopic light field imaging system parameters
| 设备 | 参数 | 数值 |
| 显微镜 | 物镜放大倍率M | 10 |
| 物镜数值孔径NA | 0.3 | |
| 物镜焦距fo/mm | 20 | |
| 筒镜焦距ft/mm | 200 | |
| CCD相机 | 分辨率npx×npy | 2352×1768 |
| 像素大小Pp/μm | 5.5 | |
| 微透镜阵列 | 微透镜孔径D/μm | 136 |
| 微透镜焦距fμ/μm | 2260 | |
| 荧光粒子 | 荧光波长λ/nm | 584 |
表选项
4 结果分析 4.1 仿真结果 参照表 1所示的显微光场成像系统参数,利用式(2)~式(9),计算不同深度的轴上点(x=0, y=0)的PSF,结果如图 4所示。图 4为深度z=0~80μm时光轴上点的模拟PSF图像。可以发现,除焦面附近(z=0~20μm)外,轴上点的PSF已经不再是圆斑,而是由离散的点斑组成。这是因为系统中加入了微透镜阵列,轴上的点发出的光线会被微透镜按照其传播方向折射到微透镜覆盖的不同像素点上,从而形成离散的点斑。当深度不同时,轴上点光源发出的球面波到达微透镜阵列时会有不同的波阵面,且会经过不同数量的微阵列,因此不同深度的轴上点会产生不同的PSF图像,由此可以通过PSF反演出深度信息。
 |
| 图 4 光轴上不同深度点的模拟PSF图像 Fig. 4 Simulated PSF image of points at different depth on optical axis |
| 图选项 |
图 5为点光源处于深度z=50μm时不同水平位置处PSF仿真结果。图 5(b)给出了位于同一深度(z=50μm)不同水平位置的点的PSF图像,各点的具体位置如图 5(a)所示,图 5(c)为同一深度不同微透镜对应位置点的PSF图像。图 5(a)中一个色块对应一个微透镜,边长为D/M,其中S0为轴上点,S1~S8为离轴点。通过比较图 5(b)中S0~S8的PSF图像可以发现,当测量体内的点处于同一深度不同位置时,其PSF图像不一致,即PSF图像不满足平移不变性。通过比较图 5(c)中S1和S′1的PSF图像可以发现,当点光源处于不同微透镜的对应位置时,如图 5(a)中的S1和S′1,点光源形成的PSF图像一致。这是因为当点光源产生值为D/M的位移时,其产生的球面波到达微透镜阵列时会形成值为D的位移,而D恰为微透镜孔径的大小,因此同一深度的PSF图像满足周期分布,周期为D/M,即
 | (10) |
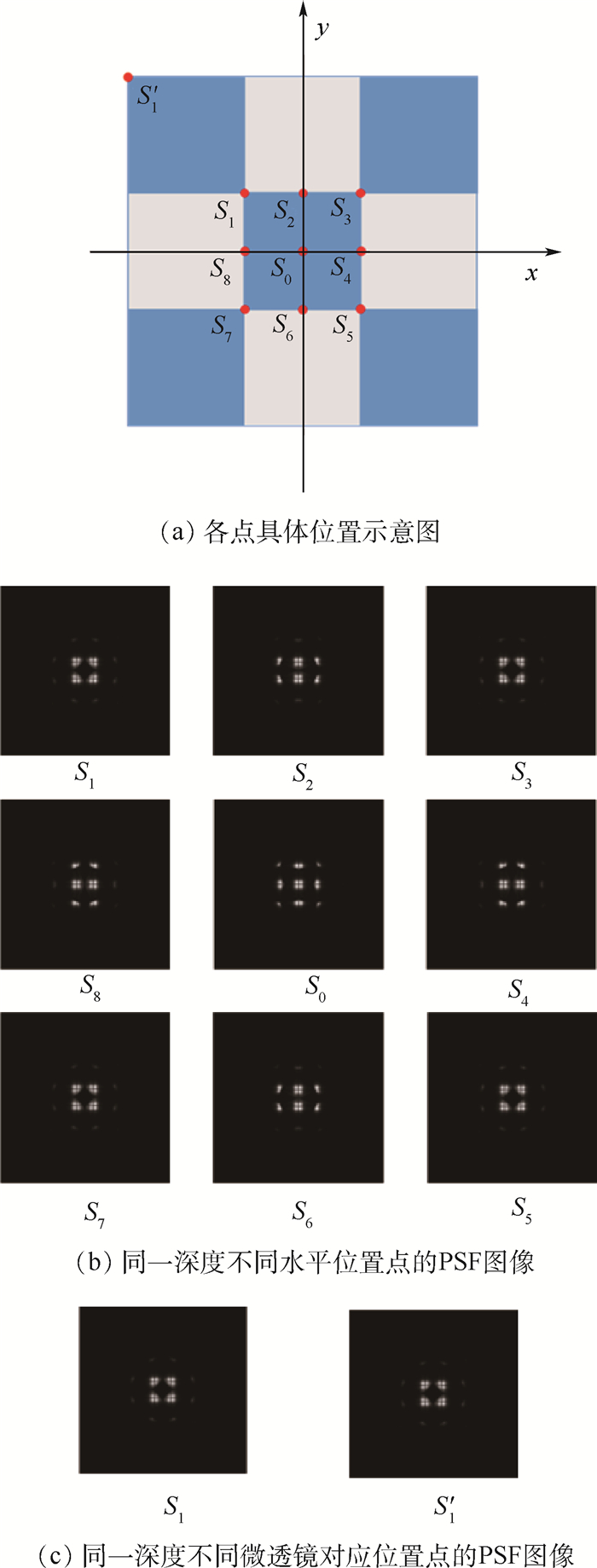 |
| 图 5 深度z=50μm时不同水平位置处PSF仿真结果 Fig. 5 PSF simulation results at different horizontal positions when depth z=50μm |
| 图选项 |
式中:m、n为正整数。
从式(10)可见,只需计算同一深度中心微透镜区域各点的PSF图像,再经过平移,即可获得同一深度任意点的PSF图像。通过PSF所处微透镜区域及其图像,可以反演出水平位置信息。
结合图 4和图 5,可见本文所建立的显微光场成像系统PSF模型可以模拟出点光源处于不同水平位置不同深度时的PSF图像,PSF反映了测量体内任意点的三维坐标信息。
4.2 模型验证 基于搭建的光场Micro-PIV实验系统,实验获取了粒径为2的示踪粒子的光场图像。深度处于z=0~80μm的轴上点的PSF图像如图 6所示。
 |
| 图 6 光轴上不同深度点的实际PSF图像 Fig. 6 Actual PSF image of points at different depth on optical axis |
| 图选项 |
从图 6可以发现,当粒子深度逐渐增加时,PSF图像先呈圆斑(z=0~20μm),然后变为离散的点斑,且PSF图像占据的微透镜阵列数随着离焦距离增大而增大,这与模拟的PSF图像表现一致。
通过比较图 4和图 6中对应的PSF图像,发现其形状与大小基本一致。
为了进一步评价PSF模型的准确性,本文从图像相似度与三维重建两方面进行了验证。首先通过结构相似性(SSIM)算法[15]进行模型验证,SSIM算法计算公式为
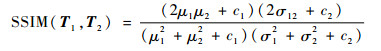 | (11) |
式中:SSIM(T1, T2)为图像相似度函数值,T1和T2分别为比较的2张图像矩阵;μ1和μ2分别为T1和T2的平均值;σ12为T1、T2的协方差;σ12和σ22分别为T1和T2的方差;c1=(k1L)2, c2=(k2L)2为用来维持稳定的常数,L为像素值的动态范围,k1=0.01, k2=0.03。相似度函数值越接近1,表明比较的2张图片相似度越高。
对图 4和图 6中对应的PSF图像进行图像相似度计算,结果如表 2所示。可以看出,在相同条件下,模型得到的模拟PSF图像与光场Micro-PIV系统的实际PSF图像计算得到的图像相似度函数值均大于0.94,可以认为2组图像具有较好的一致性,证明了本文建立的基于波动光学的显微光场成像PSF模型的准确性。
表 2 图像相似度函数值 Table 2 Image similarity function values
| 深度/μm | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| 相似度函数值 | 0.9838 | 0.9820 | 0.9740 | 0.9661 | 0.9586 | 0.9581 | 0.9556 | 0.9463 | 0.9426 |
表选项
进一步以计算获得的PSF为已知量,对实验获得的单个粒子和不同粒子浓度下的流场的光场图片,利用L-R算法进行反卷积重建,结果如图 7~图 9所示。图 7为单个示踪粒子的实验光场图片和重建结果,示踪粒子的三维坐标为(61.5μm, 61μm, 50μm)。从图 7(b)~(d)可见,重建粒子大致为橄榄球形,在水平和竖直方向均有一定的拉伸,水平拉伸为1μm,竖直拉伸为4.3μm,这是由于在拉伸区域内,任意点光源发出的光线经系统成像后形成的图像相似,系统无法准确识别,使得重建后出现拉伸。虽然重建存在拉伸,但重建粒子的中心点的三维坐标为(61μm, 60.5μm, 50.5μm),与实际三维坐标仅有一个像素的误差,在误差允许范围之内,即通过L-R算法和本文建立的PSF模型可以完成单个示踪粒子的三维坐标信息的重建。图 8和图 9分别为低粒子浓度(0.025g/L)和高粒子浓度(0.25g/L)的重建结果。低粒子浓度下,示踪粒子形成的PSF图像相互影响较小,而高粒子浓度下,示踪粒子形成的PSF图像相互影响较大,PSF图像相互叠加。但在高、低示踪粒子浓度下,L-R算法结合PSF模型,可实现示踪粒子的重建,获取示踪粒子的三维坐标信息,也进一步验证了基于波动光学的显微光场成像PSF模型的准确性。
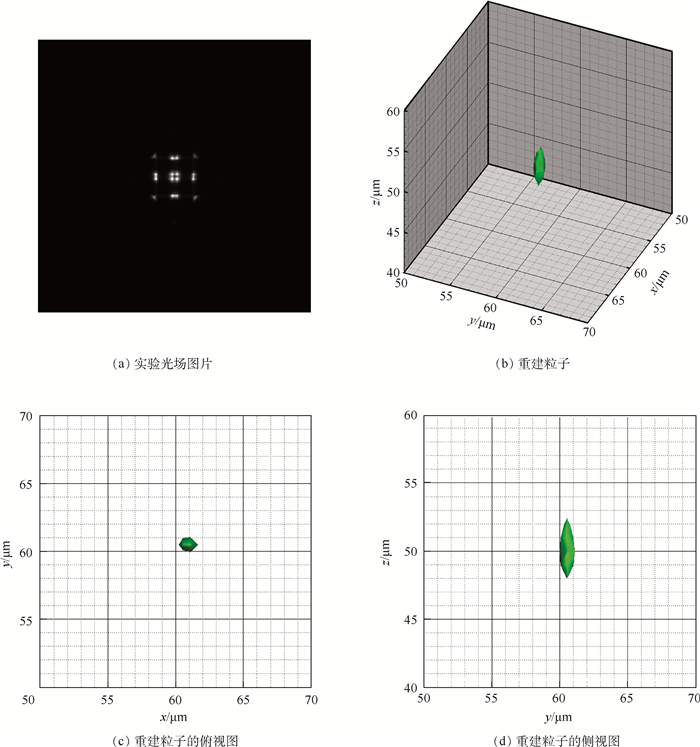 |
| 图 7 单个粒子实验光场图片及重建结果 Fig. 7 Single particle experimental light field image and reconstruction results |
| 图选项 |
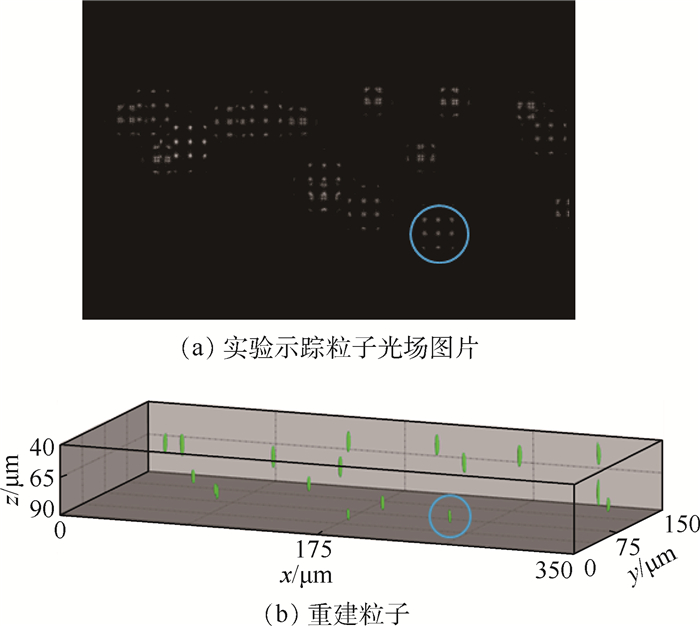 |
| 图 8 低粒子浓度(0.025g/L)实验重建结果 Fig. 8 Low particle concentration (0.025g/L) experimental reconstruction results |
| 图选项 |
 |
| 图 9 高粒子浓度(0.25g/L)实验重建结果 Fig. 9 High particle concentration (0.25g/L) experimental reconstruction results |
| 图选项 |
5 结论 1) 本文建立了基于波动光学的显微光场成像系统PSF模型,得到了系统的模拟PSF图像,仿真结果表明,通过PSF可以获得测量体内任意点的三维坐标信息。
2) 搭建了光场Micro-PIV实验系统,实验获取了系统的实际PSF图像,对模拟PSF图像和实际PSF图像利用SSIM算法进行了相似度计算,结果表明两者具有较高的相似性,验证了PSF模型的准确性。
3) 对不同示踪粒子光场图片利用L-R算法进行了反卷积计算,结果表明,利用本文建立的PSF模型可完成三维重建,并可获得示踪粒子的准确三维坐标信息,进一步验证了PSF模型的准确性。
参考文献
| [1] | 葛洋, 姜未汀. 微通道换热器的研究及应用现状[J]. 化工进展, 2016, 35(s1): 10-15. GE Y, JIANG W T. The research progress and application of the micro-channel heat exchanger[J]. Chemical Industry and Engineering Progress, 2016, 35(s1): 10-15. (in Chinese) |
| [2] | LOUSSIF N, ORFI J. Simultaneously developing laminar flow in an isothermal micro-tube with slip flow models[J]. Heat & Mass Transfer, 2014, 50(4): 573-582. |
| [3] | PRAKASH S. Microfluidic devices in nanotechnology[M]. New York: Wiley, 2010. |
| [4] | RAFFEL M, WILLERT C E, SCARANO F, et al.Micro-PIV[M]//RAFFEL M, WILLERT C E, WERELEY S T, et al.Particle Image Velocimetry.Berlin: Springer, 2018: 241-258. |
| [5] | LINDKEN R, WESTERWEEL J, WIENEKE B. Stereoscopic micro particle image velocimetry[J]. Experiments in Fluids, 2006, 41(2): 161-171. DOI:10.1007/s00348-006-0154-5 |
| [6] | SHINOHARA K, SUGⅡ Y, JEONG J H, et al. Development of a three-dimensional scanning microparticle image velocimetry system using a piezo actuator[J]. Review of Scientific Instruments, 2005, 76(10): 106109. DOI:10.1063/1.2114889 |
| [7] | LEVOY M, REN N, ADAMS A, et al.Light field microscopy[C]//ACM SIGGRAPH 2006.New York: ACM, 2006: 924-934. |
| [8] | LV H, GU K, ZHANG Y, et al.Light field depth estimation exploiting linear structure in EPI[C]//IEEE International Conference on Multimedia & Expo Workshops.Piscataway, NJ: IEEE Press, 2015: 1-6. |
| [9] | WANG Z, BOVIK A C, LU L.Why is image quality assessment so difficult?[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing.Piscataway, NJ: IEEE Press, 2011: 3313-3316. |
| [10] | ATTENDU J M, ROSS A. Time domain nearfield acoustical holography with three-dimensional linear deconvolution[J]. Journal of the Acoustical Society of America, 2018, 143(3): 1672-1683. DOI:10.1121/1.5027841 |
| [11] | LEVIN A, WEISS Y, DURAND F, et al. Understanding blind deconvolution algorithms[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(12): 2354-2367. DOI:10.1109/TPAMI.2011.148 |
| [12] | PONTI M, HELOU E S, FERREIRA P J S G, et al. Image restoration using gradient iteration and constraints for band extrapolation[J]. IEEE Journal of Selected Topics in Signal Processing, 2016, 10(1): 71-80. DOI:10.1109/JSTSP.2015.2493978 |
| [13] | GERSHUN A. The light field[J]. Studies in Applied Mathematics, 1939, 18(1-4): 51-151. |
| [14] | GU M. Advanced optical imaging theory[M]. Berlin: Springer, 2000. |
| [15] | WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment:From error visibility to structural similarity[J]. IEEE Transactions on Image Process, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |
