Huang等[2]提出的超限学习机(Extreme Learning Machine,ELM)因快速的计算速度、突出的全局近似能力,已被应用于处理包括时间序列预测在内的复杂非线性问题[3-4]。为了适应在线序贯学习需要,Huang等[5]提出了ELM的在线学习版本,即OS-ELM(Online Sequential Extreme Learning Machine);2011年,Huang等[6]又利用核技巧对ELM进行扩展,提出了核超限学习机(Kernel ELM,KELM),其能够以更快的学习速度实现与支持向量机(Support Vector Machine,SVM)相似的(回归和二分类任务)或更好的(多分类任务)泛化性能。
然而,由于OS-ELM并非属于基于核的方法,处理非线性问题的性能并不突出;KELM作为一种离线的批学习方法,其模型更新需花费大量时间与存储空间,显然无法满足在线状态预测对实时性的要求。因此,发展一种基于核方法的增量算法或序贯算法显然是一种更好的选择[7]。
文献[8]基于分块矩阵的求逆公式提出了KELM的增量学习方法,即KB-IELM,首次将KELM扩展到在线应用。KB-IELM的模型阶数随训练样本的增加而线性增长,计算成本随之超线性增加。为解决此问题,放弃冗余信息、选择更有价值的样本去构造并更新模型成为普遍共识[9-10],这就是模型的稀疏化过程。文献[11]将这些有价值的样本称作元(atoms),由此构成的子集称作字典(dictionary)。
近年来,大量稀疏化方法被引入KELM在线学习中。文献[12-13]提出一种基于传统滑动时间窗的KELM在线学习方法,该方法使用时间窗内的样本构造字典,其模型复杂度和泛化性能直接依赖于时间窗宽度;文献[7]提出一种基于近似线性独立(Approximate Linear Dependency,ALD)准则的KELM在线学习方法,该方法虽然提升了模型泛化性能,但是复杂度较高[14],且需要预设一个误差阈值。文献[15-16]分别基于瞬时信息测量和积累一致性测量提出包括“构造”、“修剪”在内的两步稀疏化方法,实现了对训练样本有区别的取舍。但是,瞬时信息的计算依赖于一系列概率密度函数,而往往这些概率密度函数却不易计算;积累一致性仅仅依赖于系统输入的特征,而没有考虑系统输出。文献[17]在使用瞬时信息测量作为稀疏准则的基础上,同时引入时变正则化因子,虽然保证了模型在不同的非线性区域拥有不同的结构风险,但增加的正则化因子的寻优过程大大影响了在线应用的计算效率。另外,以上所有稀疏化方法都或多或少引入了额外的计算量。
迄今为止,所有基于KELM的增量学习或在线学习方法,均将纳入模型的有效样本(字典内的样本)视为等价值,在对动态的非线性映射建模时,这种样本间“权重均衡”的做法显然是不合理的,时间越近的样本应该在建模时拥有更大的参考价值[18-19]。基于此,本文提出了一种具有遗忘因子的KELM在线稀疏学习方法(Online Sparse KELM with Forgetting Factor,FF-OSKELM)。该方法通过引入遗忘因子重新定义KELM的目标函数,使字典内时间越近的样本在建模时具有越高的权重,在此基础上,重新推导了一个统一的学习框架,在使快速留一交叉验证(Fast Leave-One-Out Cross-Validation,FLOO-CV)误差实现字典稀疏化的同时,进行核权重向量的同步更新。通过实例分析表明,本文方法具有很高的时效性、预测准确性和稳定性,适用于解决在线状态预测问题。
1 核超限学习机 假设有一数据流S={(x1, y1), (x2, y2), …},xi为一个d维的输入向量,yi为对应的输出值。则ELM模型定义为[2]
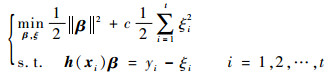 | (1) |
式中:β=[β1, β2, …, βL]T为模型输出权重向量;h(xi)=[h1(xi), h2(xi), …, hL(xi)]为隐层神经元对输入样本xi的映射向量;ξi为对应于第i个样本的训练误差;c为正则化参数,并且c∈R+。
基于KKT优化条件求解式(1)的优化问题,可得输出权重为
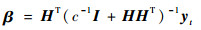 | (2) |
式中:yt=[y1, y2, …, yt]T为输入样本对应的目标值向量;H=[hT(x1), hT(x2), …, hT(xt)]T为输入样本的映射矩阵。
应用Mercer条件定义核矩阵Ω=HHT,Ω(i, j)=h(xi)·hT(xj)=k(xi, xj),可得ELM的核化形式为
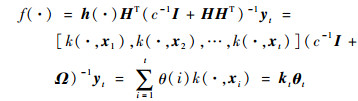 | (3) |
式中:kt为当前时刻的核估计向量,并且有kt=[k(·, x1), k(·, x2), …, k(·, xt)];θt=[θ1, θ2, …, θt]T为t时刻的核权重向量,且θt=(c-1I+Ωt)-1yt。
由此可见,KELM是一系列核函数的线性组合,其中每个样本xi的地位是等同的,这对动态变化的非线性映射建模是不合适的,并且当t→∞时,方法的计算负担显然将无法承受。因此,改进的方法至少需要关注以下3个方面:①考虑样本xi时间差异性的KELM的重新定义;②在重新定义的KELM的基础上,构成稀疏字典的有效样本的选择;③核权重向量θt的更新。
2 改进的在线核超限学习机 2.1 具有遗忘因子的KELM 定义1 假设数据流S={(x1, y1), (x2, y2), …},xi为一个d维的输入向量,yi为对应的输出值。则具有遗忘因子的ELM定义为
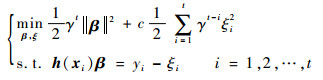 | (4) |
与式(1)相比,式(4)引入了参数γ,称之为遗忘因子,并且0 << γ < 1。
解优化方程式(4),得到输出权重为
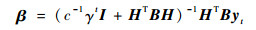 | (5) |
式中:E=diag{γt-1, γt-2, …, 1}。
根据矩阵求逆公式:
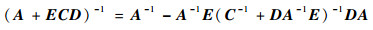 | (6) |
令
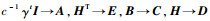
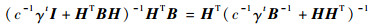 | (7) |
把式(7)代入式(5),得到
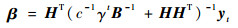 | (8) |
进一步,令
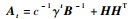
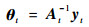 | (9) |
此时,具有遗忘因子的ELM的核化形式(以下简称FF-KELM)为
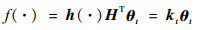 | (10) |
2.2 基于FLOO-CV误差的字典选择 设在时刻t稀疏字典为Dt={k(·, xit)}i=1m,{x1t, x2t, …, xmt} ?{x1, x2, …, xt},字典大小为m。基于式(9),两端同时乘以m阶矩阵At,得到[20]
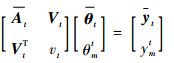 | (11) |
式中:
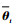
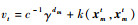
当使用前m-1个样本构成的稀疏矩阵对xmt进行预测时,FF-KELM输出权值为
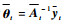
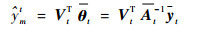 | (12) |
由式(11),有
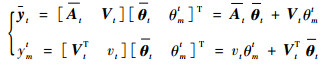 | (13) |
把式(13)代入式(12),有
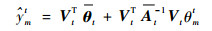 | (14) |
根据式(13)和式(14),FF-KELM对样本(xmt, ymt)的FLOO-CV误差估计为
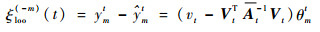 | (15) |
根据式(11)中At的分块形式,利用块矩阵逆公式,得到
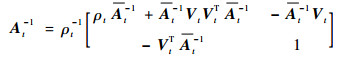 | (16) |
式中:
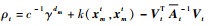
若令diag(At-1)i表示At-1第i行第i列元素,则式(15)进一步简化为
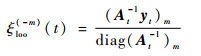 | (17) |
结合式(16)、式(17)可知,t时刻第m个样本对应的遗忘因子对ξloo(-m)(t)的影响只体现在ρt上。文献[20]表明,式(11)中交换元素的顺序对方程的解不会造成影响,由上述推导可知,该结论在FF-KELM中依然成立,故Dt中每个元素的FLOO-CV误差可表示为
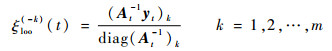 | (18) |
设Et=[ξloo(-1)(t), ξloo(-2)(t), …, ξloo(-m)(t)],其代表时刻t的泛化误差向量,则平均泛化误差εt为
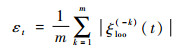 | (19) |
在t+1时刻,当新样本(xt+1, yt+1)到达时,根据式(10)模型对其输出预测值表示为
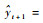
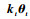
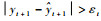
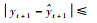
2.3 核权重向量在线更新 本节将核权重向量的更新过程分为构造和修剪2个阶段,新样本(xi+1, yi+1)到来后,依据阶段不同采用不同的处理方式。
当当前字典的规模mt小于预设规模m时,为构造阶段。在此阶段,设时刻t字典为Dt={k(·, xi)}i=1t,令At=c-1γtB-1+HHT。则在时刻t+1,对于新样本(xt+1, yt+1),Dt+1=Dt∪k(·, xt+1),且有
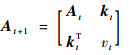 | (20) |
式中:
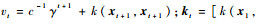
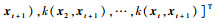
与式(16)类似,进一步有
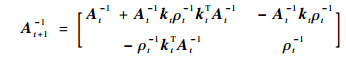 | (21) |
式中:
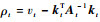
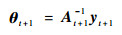 | (22) |
式中:
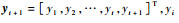
当字典的大小达到预定规模,即mt=m时,下一时刻进入修剪阶段。此时,为使字典规模保持恒定,在加入新样本前应当先删除一个样本,该样本在字典中的索引可表示为
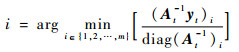 | (23) |
将At写成如图 1所示的形式。
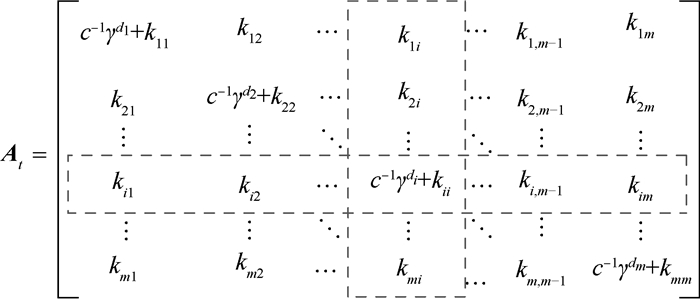 |
| 图 1 矩阵变换前的At Fig. 1 At before matrix transformation |
| 图选项 |
图 1中:d1 < d2 < … < di < … < dm, i为通过式(23)得到的样本索引。将At中的第i行移到第1行,第
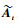
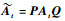
 | (24) |
 | (25) |
显然,
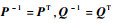
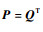
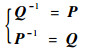 | (26) |
由式(26),可得
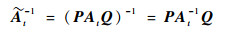 | (27) |
令
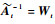
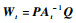
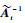
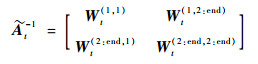 | (28) |
再将
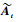
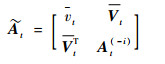 |
式中:
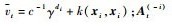
根据块矩阵逆公式对
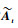
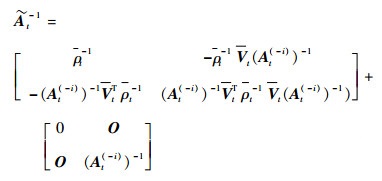 | (29) |
式中:
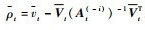
联合式(28)和式(29),有
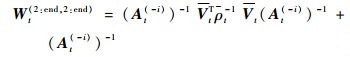 | (30) |
式(30)等号右侧第1项可以写成
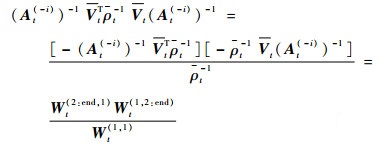 | (31) |
将式(31)的结果代入式(30)中,得到
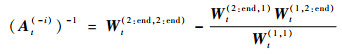 | (32) |
在时刻t+1,经过2.2节的字典选中,当新样本(xt+1, yt+1)作为有价值的节点需要插入字典中时,有
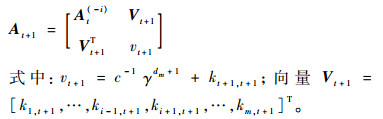 |
式中:
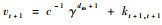
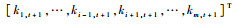
通过块矩阵求逆公式得到At+1的逆矩阵为
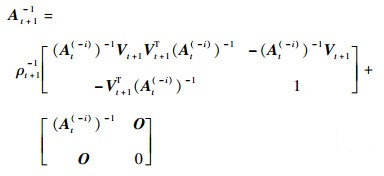 | (33) |
式中:
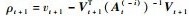
联合式(27)、式(28)、式(32)、式(33),可得At+1-1与At-1的递推关系,实现字典以快速留一交叉验证的方式删除一个样本后剩余样本的递推更新。进一步,可得核权重向量的更新公式,即
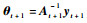
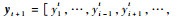
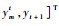
3 方法流程与复杂性分析 3.1 方法流程 将本文提出的FF-OSKELM方法流程总结如下。
步骤1??初始化。设置模型参数,包括字典规模m, 遗忘因子γ,核参数σ,令mt=1,t=1,Dt={k(·, x1)},计算
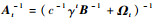

步骤2??新样本(xt+1, yt+1)到达,若mt < m,执行步骤3,否则执行步骤4。
步骤3??使用式(21)更新At+1-1,使用式(22)更新
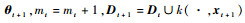
步骤4??使用式(10)计算
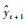
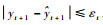
步骤5??使用式(23)确定下标i,删除第i个字典后的字典记为
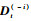
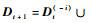
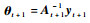
3.2 复杂性分析 以下对方法的2个主要过程简要分析其复杂性。
在核权重向量更新过程中,在构造阶段,计算kt的时间复杂度为O(mt),而计算At+1-1的时间复杂度为O(mt2);在修剪阶段,计算
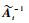
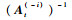
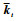
在使用FLOO-CV误差进行字典关键节点选择过程中,计算预测值
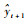
一般说来,字典规模m不会太大,因此本文方法可以满足在线应用的需求。
4 实验分析 仿真实验从计算复杂度、预测精度、预测稳定性3个方面进行设计。计算复杂度通过训练时间和测试时间来衡量,预测精度通过均方根误差(Root Mean Square Error,RMSE)来度量,最大绝对预测误差(Maximal Absolute Prediction Error,MAPE)和平均相对误差率(Mean Relative Error Rate,MRPE)则作为预测稳定性的衡量指标。
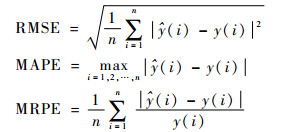 |
本文所有方法均采用高斯核作为核函数,即
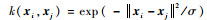
4.1 非平稳Mackey-Glass混沌时间序列预测 本节首先使用Mackey-Glass混沌时间序列来证明本文方法的有效性。可以通过如下时延差分方程得到:
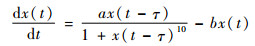 |
初始条件与文献[17]完全相同,即a=0.2,b=0.1,τ=17,x(0)=1.2,当t < 0时,x(t)=0,步长Δ=0.1,通过四阶Runge-Kutta方法解方程,在此基础上,加上正弦曲线0.3 sin(2 πt/3 000)以得到新的时间序列。设置采样间隔Ts=10Δ,规定时间嵌入维数等于10,由此获得了与文献[17]完全相同的数据集,包含1 191组样本数据,前991组用于训练,后200组用于测试。
本节实验中分别用ReOS-ELM[21]、KB-IELM[8]、FOKELM[12]、FF-KB-IELM(在KB-IELM基础上引入本文的遗忘因子)、FF-FOKELM(在FOKELM基础上引入本文的遗忘因子)、ALD-KOS-ELM[7]、NOS-KELM[17]与本文FF-OSKELM方法对比。ReOS-ELM采用Sigmoid函数作为激活函数,即
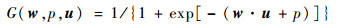 |
式中:p为偏量。
实验中所有方法的对应参数均与文献[17]一致,如表 1所示,其预测结果如表 2所示。由表 2可知:①由ReOS-ELM和其他方法的对比可知,在大多数情况下(ReOS-ELM的实验结果具有随机性),从精度上看,基于核的在线预测方法优于ReOS-ELM;从训练时间上看,ReOS-ELM勉强与KB-IELM相当,但远远差于带稀疏化过程的方法;ReOS-ELM的预测稳定性是最差的。②由KB-IELM和FF-KB-IELM及FOKELM和FF-FOKELM的对比可知,加上遗忘因子后,原有方法无论是在精度还是在训练及预测时间上都小有提升,这是因为遗忘因子的引入使模型在学习过程中能够不同程度地忘记过时数据,进而降低其在学习过程中的不利影响,同时更快地适应新到数据。③得益于遗忘因子及基于FLOO-CV误差的稀疏字典选择,本文方法在训练时间、精度及预测稳定性3个方面都远远超过KB-IELM,即使与文献[17]的NOS-KELM方法相比,本文方法也具有明显优势。在同样的数据集、硬件平台、算法参数的条件下,其保持预测时间极短的同时,训练时间缩短了92%,训练和预测精度分别提升了67%、65%,MAPE及MRPE分别提升了58%、63%。
表 1 实验1参数设置 Table 1 Parameter setup in Experiment 1
| 方法 | 正则化参数c | 核参数σ | 其他参数 |
| ReOS-ELM | 2×103 | L=50 | |
| KB-IELM | 10 | 10 | |
| FF-KB-IELM | 10 | 10 | γ=0.999 |
| FOKELM | 2×104 | 10 | z=50 |
| FF-FOKELM | 2×104 | 10 | z=50, γ=0.999 |
| ALD-KOS-ELM | 1×103 | 10 | b=0.000 01 |
| NOS-KELM | 2×104 | 10 | m=50, δ=0.01, η=0.8 |
| FF-OSKELM | 2×104 | 10 | m=50, γ=0.999 |
| 注:L为ReOS-ELM中隐层神经元个数;z为FOKELM中时间窗长度;ALD-KOS-ELM中的b表示ALD准则需要设置的阈值;NOS-KELM中的δ和η均是梯度下降法中运用动态学习率时需要设置的常数,详细请参见相关文献[17]。 | |||
表选项
表 2 实验1预测结果 Table 2 Prediction results of Experiment 1
| 方法 | 训练 | 测试 | |||||
| 时间/s | RMSE | 时间/s | RMSE | MAPE | MRPE | ||
| ReOS-ELM | 7.940 5 | 0.019 5 | 0.00 11 | 0.018 6 | 0.050 0 | 0.012 1 | |
| KB-IELM | 8.665 9 | 0.017 5 | 0.010 7 | 0.015 3 | 0.042 0 | 0.010 8 | |
| FF-KB-IELM | 8.632 2 | 0.015 3 | 0.010 1 | 0.013 2 | 0.037 5 | 0.009 4 | |
| FOKELM | 0.092 2 | 0.026 8 | 4.446 5×10-4 | 0.012 2 | 0.031 7 | 0.008 3 | |
| FF-FOKELM | 0.088 6 | 0.025 9 | 3.314 5×10-4 | 0.011 0 | 0.028 6 | 0.007 4 | |
| ALD-KOS-ELM | 0.146 4 | 0.011 2 | 3.716 0×10-4 | 0.010 9 | 0.025 0 | 0.008 1 | |
| NOS-KELM | 0.565 0 | 0.010 4 | 2.405 9×10-4 | 0.009 3 | 0.026 3 | 0.006 3 | |
| FF-OSKELM | 0.045 4 | 0.003 4 | 3.512 2×10-4 | 0.003 3 | 0.011 0 | 0.002 3 | |
| 注:ELM输入层初始权重的随机性导致ReOS-ELM的实验结果具有很大的随机性,表中只列出了ReOS-ELM一次实验的结果。 | |||||||
表选项
图 2为ALD-KOS-ELM、NOS-KELM、FF-OSKELM这3种使用了稀疏化过程的方法参与训练的样本数随时间变化的关系。可以发现:①只有不到1/10的训练样本被FF-OSKELM模型所使用,这说明基于FLOO-CV误差的字典稀疏化方法有很好的稀疏效果(虽然本节实验中ALD-KOS-ELM参与训练的样本量更少,但其严重依赖额外的阈值参数),也从另一个方面对训练时间的缩短给出了合理解释。②随着训练步数的增加,实际参与训练的样本数量趋于稳定,不会无限增加。说明在本文方法下,实验中的时间序列的输入模式是有限的,这也和大部分正常工作的非线性系统的工作状态相吻合。
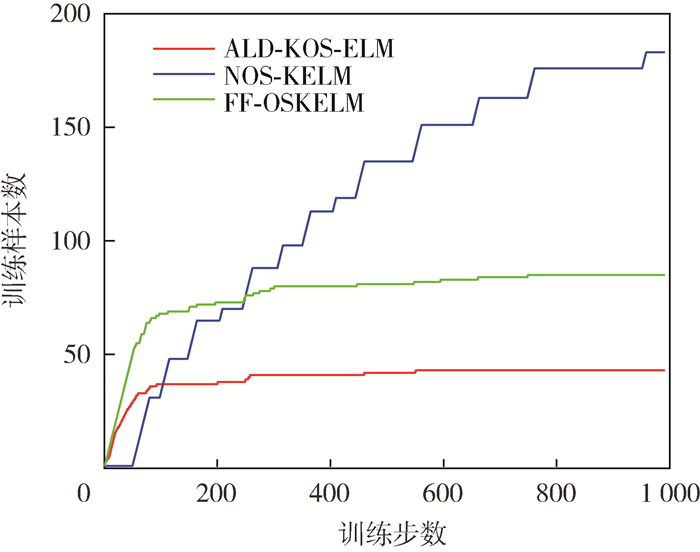 |
| 图 2 对Mackey-Glass混沌时间序列学习的训练样本数 Fig. 2 Number of learned samples for chaotic Mackey-Glass time series |
| 图选项 |
图 3和图 4为FOKELM、KB-IELM、ALD-KOS-ELM、FF-OSKELM这4种方法对Mackey-Glass混沌时间序列的学习曲线及预测曲线。由图 3可以看到,FF-OSKELM性能更强,其主要优势体现在随着训练步数(训练样本数)的增加,相比于其他方法,可以收敛到一个更加精确的阶段。
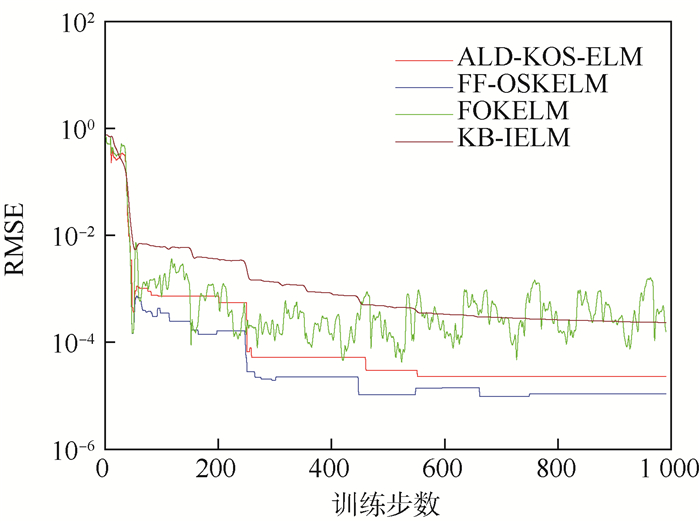 |
| 图 3 不同方法的学习曲线(实验1) Fig. 3 Learning curves of different methods (Experiment 1) |
| 图选项 |
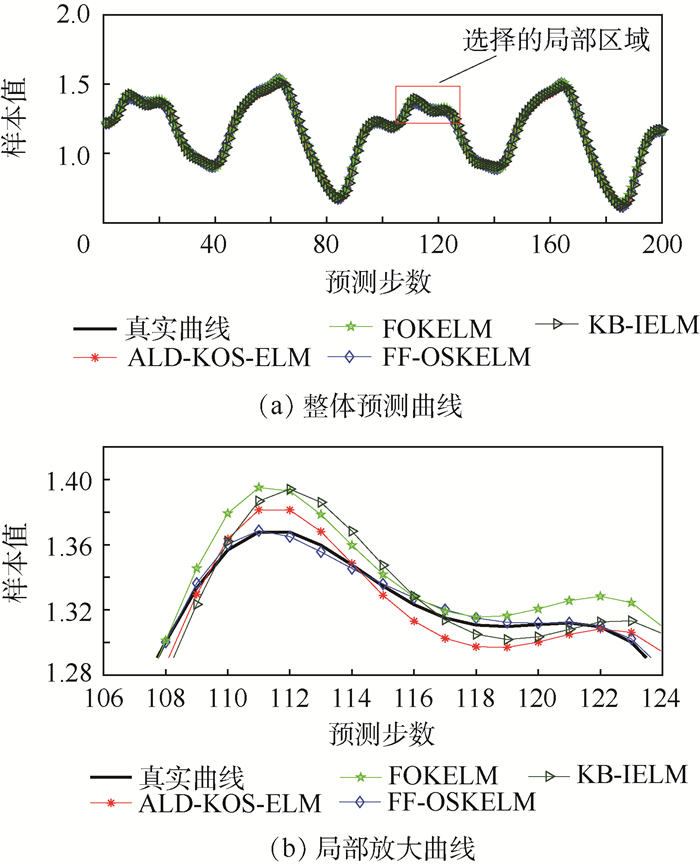 |
| 图 4 不同方法的预测曲线(实验1) Fig. 4 Prediction curves of different methods (Experiment 1) |
| 图选项 |
图 4(a)表明,所有方法大体上均能有效跟踪目标序列,进一步,由图 4(b)的局部放大图可知,相比其他方法,FF-OSKELM预测误差更小,具有最佳的动态跟踪能力。考虑到FF-OSKELM更好的时效性,因此本文提出的方法用于时间序列预测具有相当的优势。
4.2 基于飞参数据的飞机发动机状态预测 本文方法具有一定的通用性,适用于时间序列数据的预测。以某型直升机发动机为例,选取了发动机扭矩等6个主要监测项目,原始数据取自该型机的飞参系统。图 5为某飞行时间段内发动机排气温度与滑油压力的变化曲线。
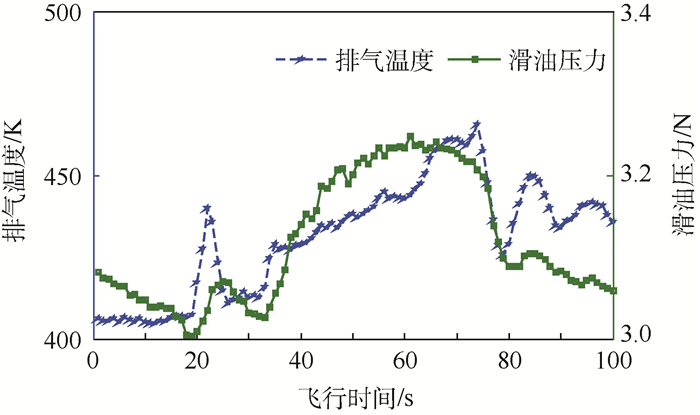 |
| 图 5 某发动机排气温度与滑油压力变化曲线 Fig. 5 Curves of exhaust gas temperature and oil pressure of an aero-engine |
| 图选项 |
每间隔1 s进行采样,每个监测项目获取100组样本。为证明本文方法的优势,样本的预处理方法与相关参数的设置与文献[15]相同,即:时间嵌入维数设为3,由此获得97组新样本(前67组用于训练,后30组用于测试),实验中各方法的参数设置如表 3所示。4.1节结果表明,ReOS-ELM、KB-IELM及FF-KB-IELM各项性能较其他方法相差甚远,因此本节实验只选择FOKELM、ALD-KOS-ELM及NOS-KELM这3种方法与本文方法FF-OSKELM进行比较。
表 3 实验2参数设置 Table 3 Parameter setup in Experiment 2
| 监测项目 | 正则化 参数c | 核参数 σ | m | 阈值δ |
| 发动机扭矩 | 2×104 | 5×104 | 30 | 2×10-5 |
| 发动机转速 | 2×104 | 1×109 | 30 | 2×10-8 |
| 排气温度 | 2×104 | 1×107 | 30 | 2×10-9 |
| 滑油温度 | 2×104 | 2×105 | 30 | 2×10-9 |
| 滑油压力 | 2×104 | 2×104 | 30 | 2×10-9 |
| 燃油瞬时流量 | 2×103 | 2×105 | 30 | 2×10-6 |
| 注:阈值δ为ALD-KOS-ELM的参数,m为其他3种方法的参数,表示字典规模或时间窗长度。 | ||||
表选项
将后30组测试样本全部作为预测数据,表 4为4种方法分别对6个监测项目的预测结果,其中各监测项目中的最优指标以加粗字体标出。可以看到:①从训练时间上看,FOKELM在某些监测项目上要略优于本文方法,这是因为本节实验中训练样本极少且已有样本的“规律性”不明显,意味着样本的价值性更高,导致更多的样本被纳入字典中进行训练,增加了包括本文方法在内的3种具有稀疏化过程的方法的训练时间。②对于绝大部分监测项目,即便在训练样本如此稀少而预测步长如此大的不利条件下,本文方法在预测精度和预测稳定性上依然拥有相当程度的优势。
表 4 实验2预测结果 Table 4 Prediction results of Experiment 2
| 监测项目 | 方法 | 训练 | 测试 | ||||
| 时间/s | RMSE | RMSE | MAPE | MRPE | |||
| 发动机扭矩 | FOKELM | 0.006 8 | 0.846 3 | 1.453 8 | 3.342 7 | 0.166 5 | |
| ALD-KOS-ELM | 0.006 9 | 0.784 6 | 1.020 5 | 2.581 4 | 0.110 8 | ||
| NOS-KELM | 0.045 0 | 0.710 8 | 1.457 0 | 3.421 6 | 0.167 5 | ||
| FF-OSKELM | 0.005 7 | 0.653 0 | 1.304 1 | 3.062 2 | 0.150 7 | ||
| 发动机转速 | FOKELM | 0.003 1 | 333.634 4 | 241.756 6 | 627.155 1 | 0.007 2 | |
| ALD-KOS-ELM | 0.011 4 | 91.332 5 | 167.500 5 | 451.946 1 | 0.005 2 | ||
| NOS-KELM | 0.053 4 | 156.557 5 | 276.815 6 | 684.522 2 | 0.007 9 | ||
| FF-OSKELM | 0.004 4 | 82.935 1 | 132.873 9 | 385.796 6 | 0.004 0 | ||
| 排气温度 | FOKELM | 0.005 6 | 4.859 3 | 7.474 8 | 19.777 0 | 0.012 5 | |
| ALD-KOS-ELM | 0.031 0 | 4.192 1 | 5.402 7 | 13.672 6 | 0.009 3 | ||
| NOS-KELM | 0.038 8 | 5.386 8 | 7.648 3 | 20.021 0 | 0.012 8 | ||
| FF-OSKELM | 0.005 2 | 3.286 17 | 3.855 3 | 9.694 2 | 0.006 7 | ||
| 滑油温度 | FOKELM | 0.004 3 | 0.183 7 | 0.321 1 | 0.511 7 | 0.008 1 | |
| ALD-KOS-ELM | 0.044 4 | 0.044 7 | 0.160 4 | 0.250 0 | 0.004 2 | ||
| NOS-KELM | 0.062 6 | 0.218 9 | 0.701 0 | 0.985 9 | 0.018 5 | ||
| FF-OSKELM | 0.004 7 | 0.031 7 | 0.108 5 | 0.180 9 | 0.002 8 | ||
| 滑油压力 | FOKELM | 0.004 6 | 0.111 5 | 0.105 4 | 0.140 0 | 0.030 9 | |
| ALD-KOS-ELM | 0.035 0 | 0.061 4 | 0.040 7 | 0.056 3 | 0.012 5 | ||
| NOS-KELM | 0.039 1 | 0.077 5 | 0.050 4 | 0.075 7 | 0.015 2 | ||
| FF-OSKELM | 0.025 7 | 0.036 7 | 0.028 0 | 0.045 7 | 0.008 4 | ||
| 燃油瞬时流量 | FOKELM | 0.033 5 | 3.353 4 | 7.456 0 | 18.800 3 | 0.031 7 | |
| ALD-KOS-ELM | 0.012 2 | 2.419 3 | 6.589 6 | 23.668 6 | 0.024 4 | ||
| NOS-KELM | 0.057 4 | 2.619 0 | 7.698 1 | 18.667 9 | 0.033 6 | ||
| FF-OSKELM | 0.007 8 | 2.163 2 | 6.508 9 | 23.396 4 | 0.024 1 | ||
| 注:因为方法的测试时间均过于短暂,已能满足绝大部分在线应用需求,此表不再将之作为对比项。 | |||||||
表选项
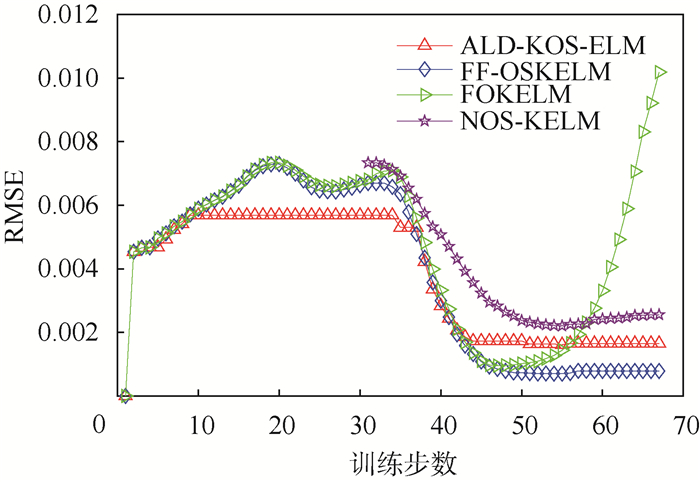
以预测发动机未来30个单位时间内的滑油压力为例,4种方法的学习曲线如图 6所示。其中,NOS-KELM因为需要使用前30个样本进行初始化,所以从第31个样本开始计算测试的均方根误差。可以看到,FF-OSKELM收敛精度要优于ALD-KOS-ELM和NOS-KELM。尽管FOKELM在训练的某些阶段表现出了与FF-OSKELM相当的性能,但其收敛性并不稳定,在某些阶段内,甚至有可能出现随着训练样本的增加性能反而持续下降的趋势。
 |
| 图 6 不同方法的学习曲线(实验2) Fig. 6 Learning curves of different methods (Experiment 2) |
| 图选项 |
当预测步数为30时,4种方法对滑油压力的预测曲线如图 7所示。显然,与其他3种方法相比,FF-OSKELM匹配效果最好。相应地,图 8显示了对滑油压力的绝对预测误差(Absolute Pre- diction Error,APE)曲线。图中:红色虚线为参考线。对比可知,FF-OSKELM整体上拥有最低的预测误差。
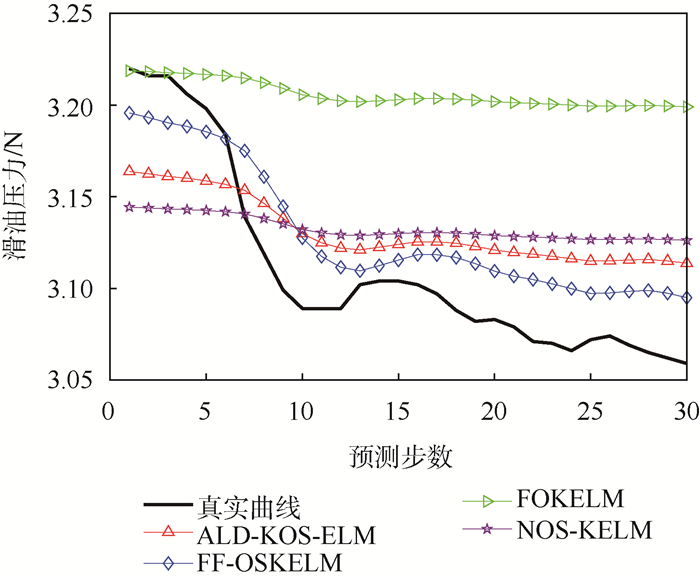 |
| 图 7 滑油压力预测曲线 Fig. 7 Prediction curves of oil pressure |
| 图选项 |
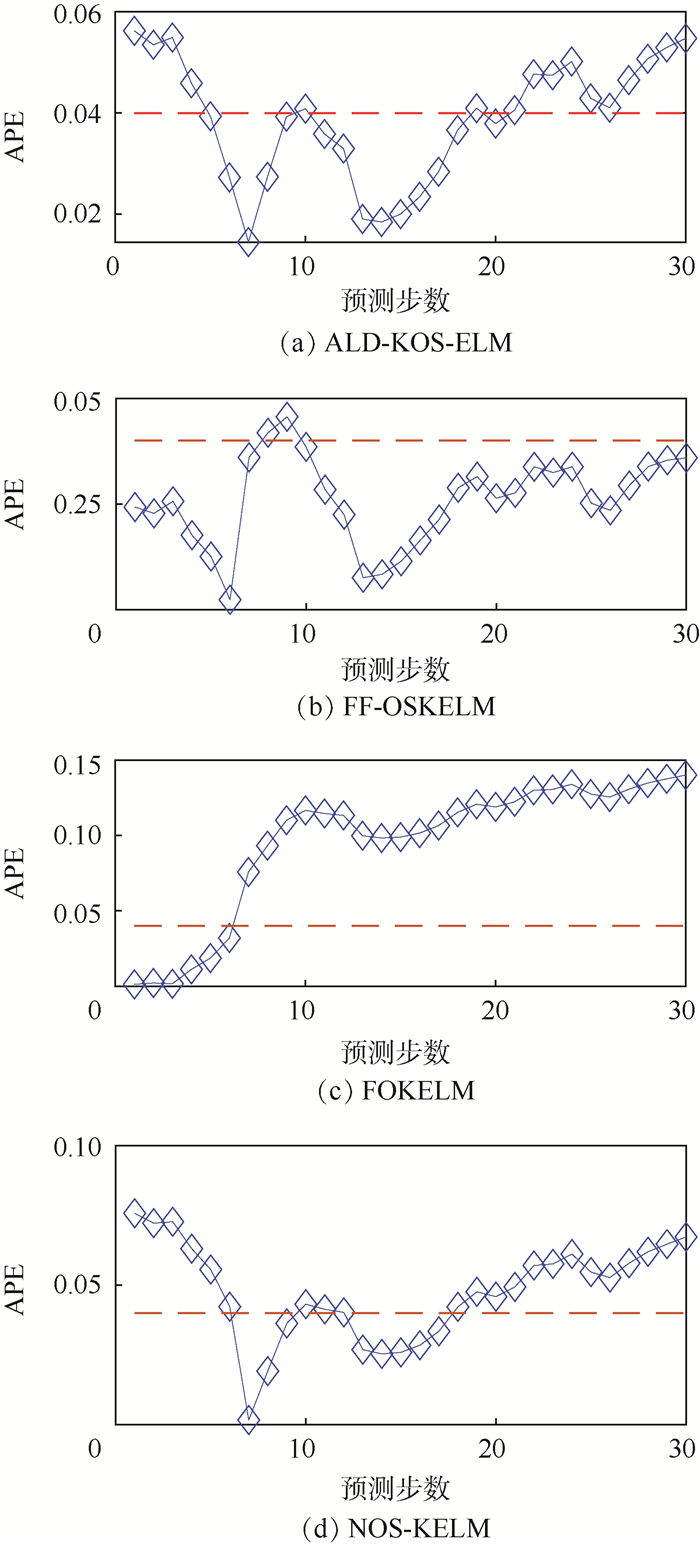 |
| 图 8 滑油压力绝对预测误差曲线 Fig. 8 Absolute prediction error curves of oil pressure |
| 图选项 |
5 结论 本文考虑在线预测中样本的时间差异性,定义了具有遗忘因子的核超限学习机(FF-KELM)。在此基础上,针对其模型膨胀问题,给出了FF-KELM的在线版本(FF-OSKELM),并将之运用于某型直升机发动机的状态预测,实验结果表明:
1) 相比于KB-IELM和FOKELM,遗忘因子的引入可以在原有方法的基础上进一步缩短训练时间,提升预测精度和预测稳定性。
2)在稀疏化方法上,同为无需引入额外阈值参数的自适应的稀疏方法,本文采用的FLOO-CV方法比NOS-KELM使用的瞬时信息测量的稀疏效果要更好,且没有引入额外的计算量。
3)在发动机性能参数的训练数据量仅为67而预测步长等于30的恶劣条件下,与FOKELM、ALD-KOS-ELM和NOS-KELM相比,本文方法预测时间几乎为0,在6个监测项目上的平均训练时间分别缩短了7.6%、62.0%和81.9%,平均预测均方根误差分别提升了44.0%、19.9%和50.9%,且整体上具有更好的预测稳定性,能满足在线状态预测要求。
参考文献
| [1] | TIAN Z, QIAN C, GU B, et al. Electric vehicle air conditioning system performance prediction based on artificial neural network[J]. Applied Thermal Engineering, 2015, 89: 101-104. DOI:10.1016/j.applthermaleng.2015.06.002 |
| [2] | HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine:Theory and application[J]. Neurocomputing, 2006, 70(1-3): 489-501. DOI:10.1016/j.neucom.2005.12.126 |
| [3] | YIN G, ZHANG Y T, LI Z N, et al. Online fault diagnosis method based on incremental support vector data description and extreme learning machine with incremental output structure[J]. Neurocomputing, 2014, 128: 224-231. DOI:10.1016/j.neucom.2013.01.061 |
| [4] | BILAL M, LIN Z P, LIU N. Ensemble of subset online sequential extreme learning machine for class imbalance and concept drift[J]. Neurocomputing, 2015, 149: 316-329. DOI:10.1016/j.neucom.2014.03.075 |
| [5] | LIANG N Y, HUANG G B, SARATCHANDRAN P, et al. A fast and accurate online sequential learning algorithm for feedforward networks[J]. IEEE Transactions on Neural Networks, 2006, 17(6): 1411-1423. DOI:10.1109/TNN.2006.880583 |
| [6] | HUANG G B, ZHOU H, DING X, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B:Cybernetics, 2011, 42(2): 513-529. |
| [7] | SCARDAPANE S, COMMINIELLO D, SCARPINITI M, et al. Online sequential extreme learning machine with kernels[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(9): 2214-2220. DOI:10.1109/TNNLS.2014.2382094 |
| [8] | GUO L, HAO J H, LIU M. An incremental extreme learning machine for online sequential learning problems[J]. Neurocomputing, 2014, 128: 50-58. DOI:10.1016/j.neucom.2013.03.055 |
| [9] | YU X, RASHID M, FENG J, et al. Online glucose prediction using computationally efficient sparse kernel filtering algorithms in type-1 diabetes[J]. IEEE Transactions on Control Systems Technology, 2018, 99: 1-13. |
| [10] | HAN M, ZHANG S, XU M, et al. Multivariate chaotic time series online prediction based on improved kernel recursive least squares algorithm[J]. IEEE Transactions on Cybernetics, 2018, 49(4): 1160-1172. |
| [11] | HONEINE P. Analyzing sparse dictionaries for online learning with kernels[J]. IEEE Transactions on Signal Processing, 2015, 63(23): 6343-6353. DOI:10.1109/TSP.2015.2457396 |
| [12] | ZHOU X R, LIU Z J, ZHU C X. Online regularized and kernelized extreme learning machines with forgetting mechanism[J]. Mathematical Problems in Engineering, 2014, 2014: 1-11. |
| [13] | ZHOU X R, WANG C S. Cholesky factorization based online regularized and kernelized extreme learning machines with forgetting mechanism[J]. Neurocomputing, 2016, 174: 1147-1155. DOI:10.1016/j.neucom.2015.10.033 |
| [14] | RICHARD C, BERMUDEZ J C M, HONEINE P. Online prediction of time series data with kernels[J]. IEEE Transactions on Signal Processing, 2009, 57(3): 1058-1067. DOI:10.1109/TSP.2008.2009895 |
| [15] | 张伟, 许爱强, 高明哲. 基于稀疏核增量超限学习机的机载设备在线状态预测[J]. 北京航空航天大学学报, 2017, 43(10): 2089-2098. ZHANG W, XU A Q, GAO M Z. Online condition prediction of avionic devices based on sparse kernel incremental extreme learning machine[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(10): 2089-2098. (in Chinese) |
| [16] | 张伟, 许爱强, 高明哲. 一种基于积累一致性测量的在线状态预测算法[J]. 上海交通大学学报, 2017, 51(11): 1391-1398. ZHANG W, XU A Q, GAO M Z. An online condition prediction algorithm based on cumulative coherence measurement[J]. Journal of Shanghai Jiaotong University, 2017, 51(11): 1391-1398. (in Chinese) |
| [17] | ZHANG W, XU A Q, PING D F, et al. An improved kernel-based incremental extreme learning machine with fixed budget for nonstationary time series prediction[J]. Neural Computing & Applications, 2019, 31(3): 637-652. |
| [18] | LIM J S, LEE S, PANG H S, et al. Low complexity adaptive forgetting factor for online sequential extreme learning machine (OS-ELM) for application to nonstationary system estimations[J]. Neural Computing & Applications, 2013, 22(3-4): 569-576. |
| [19] | 郭威, 徐涛, 于建江, 等. 基于M-estimator与可变遗忘因子的在线贯序超限学习机[J]. 电子与信息学报, 2018, 40(6): 94-101. GUO W, XU T, YU J J, et al. Online sequential extreme learning machine based on m-estimator and variable forgetting factor[J]. Journal of Electronics & Information Technology, 2018, 40(6): 94-101. (in Chinese) |
| [20] | 张英堂, 马超, 李志宁, 等. 基于快速留一交叉验证的核极限学习机在线建模[J]. 上海交通大学学报, 2014, 48(5): 641-646. ZHANG Y T, MA C, LI Z N, et al. Online modeling of kernel extreme learning machine based on fast leave-one-out cross-validation[J]. Journal of Shanghai Jiaotong University, 2014, 48(5): 641-646. (in Chinese) |
| [21] | HUYNH H T, WON Y. Regularized online sequential learning algorithm for single-hidden layer feedforward neural networks[J]. Pattern Recognition Letters, 2011, 32(14): 1930-1935. DOI:10.1016/j.patrec.2011.07.016 |
