对于高超声速流动过程中的热力学非平衡分子能级分布,一般认为分子的振动、转动能级满足各自温度下的Boltzmann分布,而电子能级则会明显偏离电子温度的Boltzmann分布,后来也有人认为振转能级也会偏离Boltzmann分布[5]。对于无法用温度简单描述的能级分布情况,目前主要采用碰撞-辐射(Collisional-Radiative,CR)模型计算能级分布[6-7]。CR模型通过计算各类能够影响能级数密度的微观过程速率,从而建立控制方程,来计算各能级分布。求解过程中,认为能级分布计算可以与流场计算解耦,同时假设能级变化处于准稳态(QSS)。影响CR模型精度的最大因素就是对各能级跃迁微观过程速率的描述。许多人通过量子力学ab initio的方法或实验测量的方法获取这些跃迁的速率,但是不同方法得到的速率一般都有巨大差异[8-9]。
本文针对1991年Sharma和Gillespie[10]通过电弧驱动激波管(Electric Arc-driven Shock-Tube, EAST)实验获得的高超声速流平衡和非平衡状态下的辐射光谱,基于QSS假设下的CR模型,分析了不同的氮气碰撞激发、辐射跃迁速率模型得到的N2、N2+分子电子能级分布及紫外辐射光谱。并将理论计算光谱与实验测量结果进行了对比分析,找出了与实验结果最为接近的速率计算模型。
1 理论模型 1.1 碰撞-辐射模型 对于不满足Boltzmann分布的分子能级分布,一般采用建立速率方程的方法计算各能级的数密度。速率方程需要考虑影响多种能级的激发、退激过程,包括电子碰撞激发、重粒子碰撞激发、自发辐射跃迁、碰撞离解。
建立速率方程如下:
 | (1) |
式中:Ni为i能级数密度,cm-3;Ne为电子数密度,cm-3;K(i, j)为碰撞跃迁速率,cm3/s;N+为离子数密度,cm-3; K(i, c)为碰撞离解速率,cm3/s;A(i, j)为自发辐射跃迁速率,s-1。
对该方程的求解基于QSS假设,认为各类激发过程的速率一般远大于i能级数密度的变化率,因此认为
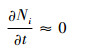 | (2) |
速率方程简化为一般的代数方程,可方便地进行求解。
1.2 碰撞激发速率模型 基于麦克斯韦速度分布率,N2、N2+与电子和重粒子碰撞的激发速率系数可表示为
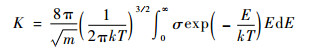 | (3) |
式中:m为碰撞粒子质量;T为温度;σ为激发截面积;E为碰撞能量; k为Boltzmann常数。Park[6, 11]在1984年公布的NEQAIR代码中使用类氢粒子的非弹性碰撞模型计算了碰撞激发截面积,并得到了激发速率系数。2008年,Park[12-13]基于实验测量数据对激发截面积进行了修正。1999年,Teulet等[14]基于WTCS(Weighted Total Cross Section)方法计算了双原子分子与电子碰撞的激发和离解速率。2006年,Johnston[15]基于Teulet的理论模型,结合最新的实验测量结果选取了一套分子与电子、重粒子碰撞激发、离解的速率系数。
以对N2+ 1-谱带辐射影响很大的N2+(X)+M?N2+(B)+M(M包括电子和重粒子)过程为例,各不同激发速率系数随温度的变化规律如图 1所示, 图中横轴表示平动温度T=振动温度Tr =电子温度Te。
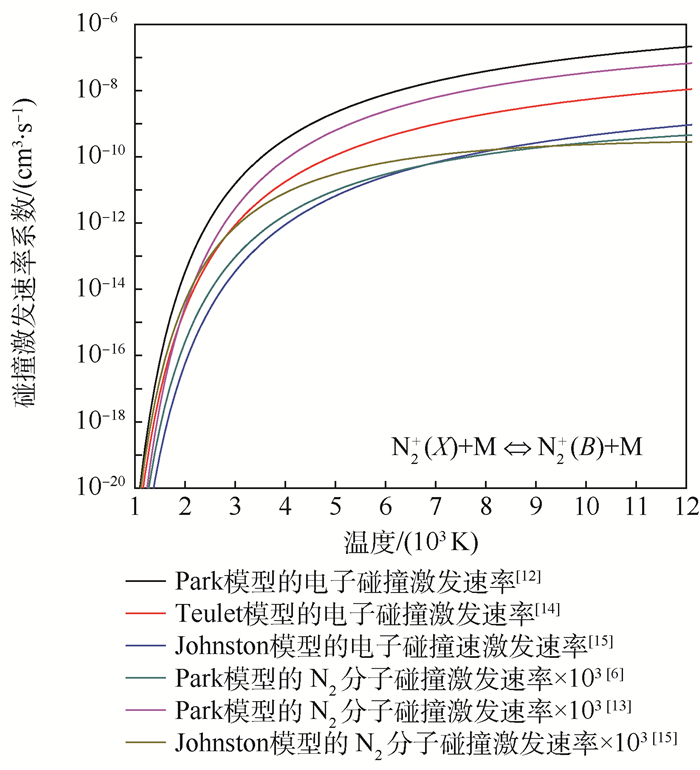 |
| 图 1 N2+(X-B)电子态的碰撞激发速率系数随温度的变化 Fig. 1 Variation of electron collision excitation rate coefficient from N2+(X-B) state with temperature |
| 图选项 |
在本文分析的激波管实验中,重粒子的数密度比电子约大3个量级。从图 1可以看出,重粒子碰撞激发的效果与电子碰撞同等重要,需要同时考虑[16]。对于不同的速率系数模型,同一状态下的激发速率系数差别是很大的。如果激发速率过大,仿真结果将始终处于平衡状态,无法反映恰当的非平衡效应发生过程。而如果激发速率过小,针对平衡态的仿真结果也将偏离Boltzmann分布,背离真实情况。
2 理论仿真和对比 Sharma和Gillespie[10]基于EAST激波管模拟了纯氮气的高超声速流动,实验采用0.64 MJ40 kV电容器组供电,激波速度达到6.2 km/s,初始压力为133 Pa,高度约为47 km大气的压力。实验通过设置2套光谱仪实现在一次激波实验中测量2个不同延时的光谱。第1处光谱测量延时为辐射峰值前40~50 ns,约在激波后1 cm处,曝光时间为200 ns,代表流动非平衡区域;第2处光谱测量延时为为辐射峰值后2.5~3 μs,约在激波后30 cm处,曝光时间为2.5 μs,代表流动平衡区域。光谱测量的范围从300~440 nm,光谱分辨率达到0.5 nm,主要测量到了N2+的1-谱带及N2的2+谱带,还有部分杂质CN的影响。针对测量到的辐射谱带,本文主要电子能级的分布如表 1所示。
表 1 计算考虑电子能态 Table 1 Electronic states in calculation
| 能态 | 电子态 | Ee/cm-1 | 简并度 |
| N2 | X1Σg+ | 0 | 1 |
| A3Σu+ | 49754 | 3 | |
| B3Πu | 59306 | 6 | |
| C3Πu | 88977 | 6 | |
| N2+ | X2Σg+ | 0 | 2 |
| A2Πu | 9167 | 4 | |
| B2Σu+ | 25461 | 4 | |
| C2Σu+ | 64608 | 4 |
表选项
本文模型仅考虑分子电子能级的Non-Boltzmann分布,认为振转能级均满足Boltzmann分布。
2.1 平衡区辐射光谱 基于流场计算结果,平衡区温度为6 464 K。基于分子电子能级的Boltzmann分布, 采用逐线法[17]计算分子的辐射光谱与实验测量结果对比如图 2所示。
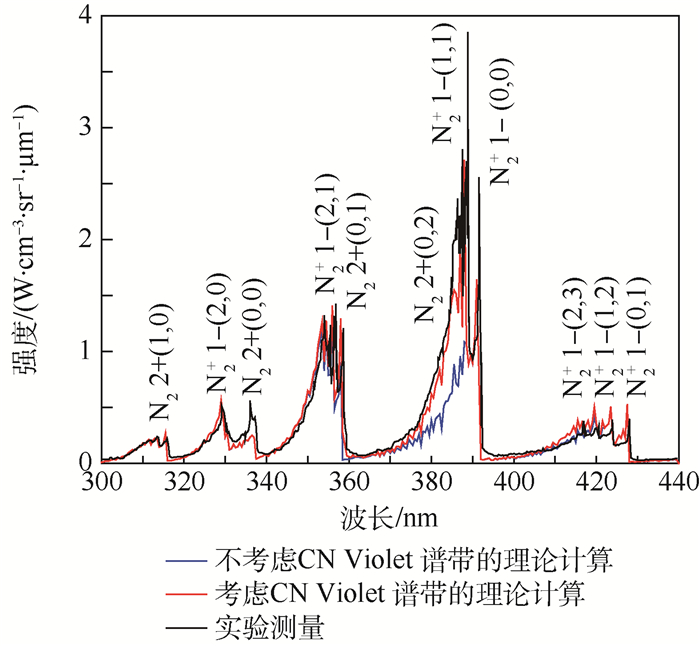 |
| 图 2 平衡区测量与计算辐射光谱 Fig. 2 Measured and calculated radiation spectra in equilibrium area |
| 图选项 |
在380~390 nm的位置,辐射光谱受到激波管中常见的杂质CN的Violet谱带影响,本文假设CN物质的量浓度为8.5×10-6,得到了与实验结果较为匹配的辐射光谱。
采用CR模型对平衡态下的能级分布开展计算,得到能级分布如表 2所示,Nie为能级i三温度Boltzmann分布下的能级数密度,Ni为能级i非平衡能级数密度。
表 2 不同理论模型计算的平衡区分子能级分布 Table 2 Molecular energy level distribution in equilibrium region calculated by different theoretical models
| 能态 | Nie/cm-3 | Park模型 | Johnston模型 | |||
| Ni/cm-3 | Ni/Nie | Ni/cm-3 | Ni/Nie | |||
| N2+(X) | 1.36×1013 | 1.36×1013 | 1.00 | 1.36×1013 | 1.00 | |
| N2+(A) | 4.68×1012 | 4.67×1012 | 1.00 | 4.68×1012 | 1.00 | |
| N2+(B) | 4.03×1010 | 3.97×1010 | 0.99 | 2.35×1010 | 0.58 | |
| N2(X) | 3.24×1017 | 3.24×1017 | 1.00 | 3.24×1017 | 1.00 | |
| N2(A) | 3.64×1013 | 2.92×1013 | 0.80 | 3.66×1013 | 1.01 | |
| N2(B) | 6.32×1012 | 5.11×1012 | 0.81 | 6.28×1012 | 0.99 | |
| N2(C) | 2.55×1011 | 2.04×1011 | 0.80 | 2.52×1010 | 0.10 | |
表选项
可见对于N2+,Park模型具有足够大的碰撞激发速率,可以在平衡态下计算得到满足Boltzmann的数密度分布。Johnston模型对于低能态的能级处理较好,只在B2Σu+能级上存在一定误差。对于N2,Park模型认为C3Πu能级具有很高的能量,极易发生离解,其能级分布满足与N原子的Saha方程,其他能级才使用CR模型计算。而Park模型得到的结果在各能级均存在一定的误差,而Johnston模型针对低能级具有较好的精度,但是针对C3Πu电子态则有极大的误差。
2.2 非平衡区辐射光谱 针对激波层非平衡区,平动温度为11 605 K,N2的振动温度为8 098 K,N2+的振动温度为9 364 K,电子温度与振动温度一致。
在激波管实验中非平衡区域的物理状态下,不同模型碰撞激发速率系数如表 3所示。
表 3 不同模型碰撞激发速率系数的计算结果 Table 3 Calculation results of collision excitation rate coefficient by different models
| cm3·s-1 | ||||||
| N2+反应过程 | 碰撞激发速率系数 | N2反应过程 | 碰撞激发速率系数 | |||
| Park模型 | Johnston模型 | Park模型 | Johnston模型 | |||
| N2+(X)+e-?N2+(A)+e- | 2.9×10-7 | 1.7×10-11 | N2(X)+e-?N2(A)+e- | 9.1×10-13 | 1.4×10-12 | |
| N2+(X)+e-?N2+(B)+e- | 4.9×10-8 | 3.2×10-10 | N2(X)+e-?N2(B)+e- | 3.3×10-13 | 4.7×10-13 | |
| N2+(X)+e-?N2+(C)+e- | 3.6×10-9 | 3.2×10-11 | N2(X)+e-?N2(C)+e- | - | 1.3×10-15 | |
| N2+(A)+e-?N2+(B)+e- | 8.8×10-7 | 8.1×10-11 | N2(A)+e-?N2(B)+e- | 2.4×10-9 | 9.4×10-10 | |
| N2+(A)+e-?N2+(C)+e- | 2.7×10-8 | 8.3×10-11 | N2(A)+e-?N2(C)+e- | - | 1.1×10-10 | |
| N2+(B)+e-?N2+(C)+e- | 2.5×10-7 | 4.3×10-10 | N2(B)+e-?N2(C)+e- | - | 6.3×10-9 | |
| N2+(X)+e-?N+N++e- | 4.2×10-12 | 1.6×10-13 | N2(X)+e-?N+N++e- | 1.2×10-16 | 4.1×10-15 | |
| N2+(A)+e-?N+N++e- | 1.5×10-11 | 1.7×10-12 | N2(A)+e-?N+N++e- | 3.8×10-13 | 1.7×10-10 | |
| N2+(B)+e-?N+N++e- | 1.1×10-10 | 3.2×10-12 | N2(B)+e-?N+N++e- | 1.6×10-12 | 1.8×10-11 | |
| N2+(C)+e-?N+N++e- | 3.9×10-9 | 1.0×10-10 | N2(C)+e-?N+N++e- | - | 6.3×10-9 | |
| N2+(X)+M?N2+(A)+M | 1.1×10-12 | 3.0×10-12 | N2(X)+M?N2(A)+M | 5.6×10-14 | 2.5×10-17 | |
| N2+(X)+M?N2+(B)+M | 4.1×10-13 | 1.9×10-13 | N2(X)+M?N2(B)+M | 1.7×10-14 | 0 | |
| N2+(X)+M?N2+(C)+M | 3.2×10-14 | 0 | N2(X)+M?N2(C)+M | - | 0 | |
| N2+(A)+M?N2+(B)+M | 8.1×10-13 | 0 | N2(A)+M?N2(B)+M | 5.8×10-12 | 4.5×10-12 | |
| N2+(A)+M?N2+(C)+M | 8.2×10-14 | 0 | N2(A)+M?N2(C)+M | - | 0 | |
| N2+(B)+M?N2+(C)+M | 3.8×10-13 | 0 | N2(B)+M?N2(C)+M | - | 1.5×10-12 | |
| N2+(X)+M?N+N++M | 8.8×10-14 | 6.9×10-18 | N2(X)+M?N+N++M | 4.6×10-15 | 0 | |
| N2+(A)+M?N+N++M | 3.6×10-13 | 2.1×10-16 | N2(A)+M?N+N++M | 3.2×10-11 | 0 | |
| N2+(B)+M?N+N++M | 4.4×10-12 | 5.3×10-16 | N2(B)+M?N+N++M | 1.7×10-10 | 0 | |
| N2+(C)+M?N+N++M | 2.5×10-10 | 1.4×10-14 | N2(C)+M?N+N++M | - | 0 | |
表选项
Park模型认为N2的C3Πu能级由于具有接近离解限的电子能级,其能级分布应该与N原子达到离解平衡,满足Saha方程,不需要参与到速率方程的求解中。因此并没有计算与C3Πu能级相关的激发速率。
各模型计算的N2+1-谱带、N2 2+及1+谱带跃迁的高低电子能级数密度如表 4所示。
表 4 不同理论模型计算的非平衡区分子电子能级数密度 Table 4 Molecular electron energy level density in nonequilibrium region calculated by different theoretical models
| 能态 | Nie/cm-3 | Park模型 | Johnston模型 | |||
| Ni/cm-3 | Ni/Nie | Ni/cm-3 | Ni/Nie | |||
| N2+(X) | 1.22×1014 | 1.12×1014 | 0.92 | 1.23×1014 | 1.01 | |
| N2+(A) | 6.31×1013 | 6.31×1013 | 1.00 | 6.23×1013 | 0.99 | |
| N2+(B) | 1.13×1012 | 1.13×1012 | 1.00 | 3.96×1011 | 0.35 | |
| N2(X) | 4.33×1017 | 4.44×1017 | 1.03 | 4.33×1017 | 1.00 | |
| N2(A) | 4.56×1014 | 4.43×1013 | 0.10 | 3.99×1014 | 0.88 | |
| N2(B) | 1.21×1014 | 3.64×1012 | 0.03 | 1.05×1014 | 0.87 | |
| N2(C) | 7.47×1012 | 5.05×1010 | 0.01 | 1.37×1012 | 0.18 | |
表选项
按上述能级分布计算的辐射光谱与实验测量结果的对比如图 3所示。
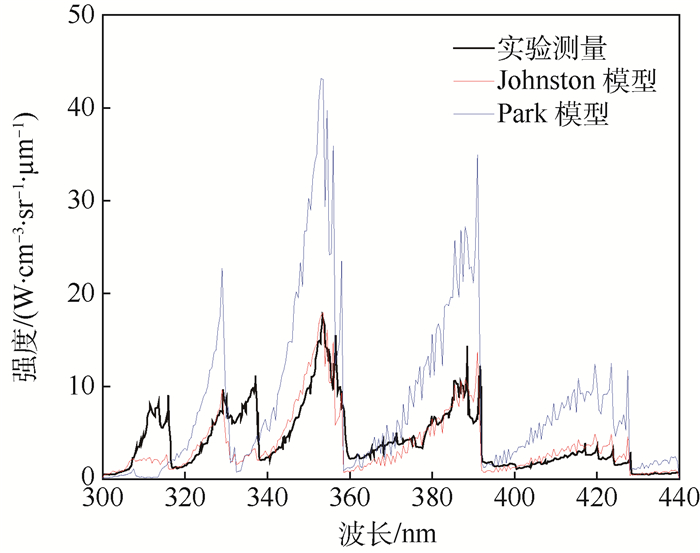 |
| 图 3 不同理论模型计算的非平衡区域辐射光谱与实验测量结果比较 Fig. 3 Comparison of nonequilibrium radiation spectra calculated by different theoretical models with experimental measurements |
| 图选项 |
Park模型对于N2+的碰撞激发速率计算过大,导致在非平衡区域N2+依然按平衡态分布,使得N2+的辐射光谱远大于测量光谱。Johnston模型计算得到数密度与测量光谱匹配较好。而对于N2的C3Πu态,2个模型过于低估其数密度分布,导致N2的辐射光谱远低于测量光谱。
2.3 速率系数 Park模型对于N2+的激发速率计算过大,致使在平衡和非平衡区域N2+的能级均呈现Boltzmann分布,而对于N2的激发速率计算过小,致使平衡区N2能级分布达不到Boltzmann分布,而非平衡区高态能级分布过低。
Johnston模型对于N2+非平衡区的辐射有精确的计算,在平衡区对B2Σu+能级的数密度计算稍微偏低。而对于N2的不管是平衡还是非平衡区域,Johnston模型都过低的仿真了C3Πu态的能级分布。这是由于Johnston模型认为N2分子从C3Πu到B2Σu+电子态自发跃迁过程的速率系数高达2.6×107 s-1。而Park模型认为该速率只有5 880 s-1。对于该过程速率的过高估计使得C3Πu态很快发生向下跃迁,能级数密度远低于真实情况。如果采用Park模型的爱因斯坦系数替换Johnston模型原有的系数,所得结果如表 5所示。
表 5 修改后的速率模型计算的分子电子能级数密度 Table 5 Molecular energy level density calculated by modified rate model
| 能态 | 平衡区 | 非平衡区 | |||||
| Nie/cm-3 | Ni/cm-3 | Ni/Nie | Nie/cm-3 | Ni/cm-3 | Ni/Nie | ||
| N2+(X) | 1.36×1013 | 1.36×1013 | 1.00 | 1.22×1014 | 1.23×1014 | 1.01 | |
| N2+(A) | 4.68×1012 | 4.68×1012 | 1.00 | 6.31×1013 | 6.23×1013 | 0.99 | |
| N2+(B) | 4.03×1010 | 2.35×1010 | 0.58 | 1.13×1012 | 3.96×1011 | 0.35 | |
| N2(X) | 3.24×1017 | 3.24×1017 | 1.00 | 4.33×1017 | 4.33×1017 | 1.00 | |
| N2(A) | 3.64×1013 | 3.70×1013 | 1.02 | 4.56×1014 | 3.87×1014 | 0.85 | |
| N2(B) | 6.32×1012 | 6.36×1012 | 1.01 | 1.21×1014 | 1.01×1014 | 0.83 | |
| N2(C) | 2.55×1011 | 2.66×1011 | 1.04 | 7.47×1012 | 5.22×1012 | 0.70 | |
表选项
将Park模型的爱因斯坦系数代入Johnston模型后,在平衡区能够得到Boltzmann分布。在非平衡区按照表 5的能级分布,计算得到的光谱如图 4所示。
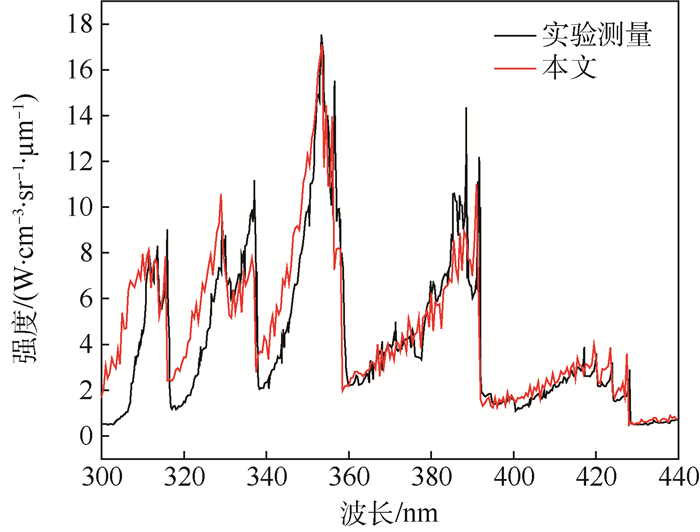 |
| 图 4 采用修改模型计算的非平衡区域辐射光谱与实验测量结果比较 Fig. 4 Comparison of radiation spectra of nonequilibrium area calculated by modified model with experimental measurement results |
| 图选项 |
经过修改之后采用Johnston参数的CR模型可以得到更接近实验结果的辐射光谱,尤其在谱带峰值位置与实验测量结果有较好匹配,只在谱带侧翼偏差较大,如300~310 nm波段。
3 结论 1) 通过比较激波管中激波不同位置的光谱,可以发现在激波头部位置确实存在热力学非平衡的区域。在这个能量刚刚被剧烈激发的区域,不仅电子、振动、转动各自由度之间能量无法平衡,电子能级的高能态也没有被充分激发,能级分布只有3温度Boltzmann分布的35%(N2+B2Σu+)和70%(N2C3Πu)。
2) 为描述激波中的非平衡过程,需要引入对微观过程精细计算的CR模型,而CR模型的精度就很大程度上依赖于各微观过程速率的精度。通过本文的工作可以发现,Park模型对各类碰撞激发过程的速率都有过高的计算,使得即使在非平衡区域也很难仿真出偏离Boltzmann的能级分布。Johnston模型通过收集各类实验与仿真的激发速率得到相对较好的速率参数集,但是对N2(C)?N2(B)+hv自发跃迁过程爱因斯坦系数的错误设置极大地影响了仿真的光谱结果。本文发现,综合Park模型的爱因斯坦系数和Johnston模型的碰撞激发速率可以得到与激波管实验最为匹配的理论计算结果。
3) 本文的计算只考虑电子能级的非Boltzmann分布,振动和转动能级均认为其满足于各组分的振动温度和平动温度的Boltzmann分布。本文理论计算的振动跃迁峰值与实验测量结果匹配得较好,说明在计算的物理状态下N2+和N2电子激发态的振动能级分布基本满足Boltzmann分布。但在各振动跃迁谱带的翼侧,即高振动能级主要贡献的谱段,理论计算与测量结果存在一定偏差。N2+的1-谱带的侧翼辐射偏差较小,而N2 2+谱带的侧翼,尤其是300~310 nm波段理论计算偏差较大。
参考文献
| [1] | PARK C. Review of chemical kinetic problems for future NASA missions, Ⅰ.Earth entries[J]. Journal of Thermophysics and Heat Transfer, 1993, 7(3): 385-398. DOI:10.2514/3.431 |
| [2] | PARK C, HOWE J T, JAFFE R L, et al. Review of chemical-kinetic problems of future NASA missions, Ⅱ:Mars entries[J]. Journal of Thermophysics and Heat Transfer, 1994, 8(1): 9-23. |
| [3] | ANNALORO J, BULTEL A, OMALY P.Elaboration of a collisional-rediative model for CO2-N2-Ar plasma flows: Appliction to atmospheric Martian entries[C]//42nd AIAA Thermophysics Conference.Reston: AIAA, 2011: 3954. |
| [4] | CRUDEN B A, PRABHU D, MARTINEZ R, et al.Absolute radiation measurement in Venus and Mars entry conditions[C]//10th AIAA/ASME Joint Thermophysics and Heat Transfer Conference.Reston: AIAA, 2010: 092407. |
| [5] | LAUX C O, PIERROT L, GESSMAN R J. State-to-state modeling of a recombining nitrogen plasma experiment[J]. Chemical Physics, 2012, 398(1): 46-55. |
| [6] | PARK C.Calculation of nonequilibrium radiation in the flight regimes of aeroassisted orbital transfer vehicles[C]//AIAA 22nd Aerospace Sciences Meeting.Reston: AIAA, 1984: 1-13. |
| [7] | LEMAL A, JACOBS C M, PERRIN M Y, et al.Simulation of shock tube radiation measurements with a collisional-radiaitve model[C]//51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aeroespace Exposition.Reston: AIAA, 2013: 1-9. |
| [8] | LEE E S, PARK C, CHANG K S.Shock-tube determination of CN formation rate in a CO-N2 mixture[C]//45th AIAA Aerospace Sciences Meeting and Exhibit.Reston: AIAA, 2007: 1-13. |
| [9] | PANESI M, MAGIN T E, BOURDON A, et al.Analysis of the FIRE Ⅱ flight experiment by means of a collisional radiative model[C]//46th AIAA Aerospace Sciences Meeting and Exhibit.Reston: AIAA, 2008: 1-15. |
| [10] | SHARMA S P, GILLESPIE W. Nonequilibirum and equilibrium shock front radiation measurements[J]. Journal of Thermophysics and Heat Transfer, 1991, 5(3): 257-265. DOI:10.2514/3.259 |
| [11] | PARK C. Nonequilibrium hypersonic aerothermodynamics[M]. New York: Wiley, 1989. |
| [12] | PARK C.Rate parameters for electronic excitation of diatomic Molecules Ⅰ.Electron-impact processes[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings.Reston: AIAA, 2008: 1206. |
| [13] | PARK C.Rate parameters for electronic excitation of diatomic Molecules Ⅱ.Heavy particle-impact processes[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings.Reston: AIAA, 2008: 1446. |
| [14] | TEULET P, SARRETTE J P, GOMES A M. Calculation of electron impact inelastic cross sections and rate coefficients for diatomic molecules.application to air molecules[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 1999, 62(5): 549-569. DOI:10.1016/S0022-4073(98)00129-0 |
| [15] | JOHNSTON C O.Nonequilibrium shock-layer radiative heating for earth and titan entry[D].Blacksburg: Virginia Polytechnic Institute and State University, 2006: 116-126. https://www.researchgate.net/publication/253796496_Nonequilibrium_shock-layer_radiative_heating_for_Earth_and_Titan_entry |
| [16] | 吴杰, 董雁冰. 热力学非平衡分子辐射中的重粒子影响[J]. 红外与激光工程, 2012, 41(11): 2981-2985. WU J, DONG Y B. Impact of heavy particles in radiation from thermally nonequilibrium molecules[J]. Infrared and Laser Engineering, 2012, 41(11): 2981-2985. DOI:10.3969/j.issn.1007-2276.2012.11.023 (in Chinese) |
| [17] | ARNOLD J O, WHITING E E, LYLE G C. Line-by-line calculation of spectra from diatomic molecules and atoms assuming a voigt line profile[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 1969, 9(6): 775-798. DOI:10.1016/0022-4073(69)90075-2 |
