在半导体封装器件引线失效预测方面,国内外开展的理论模型研究主要包括:电-热几何模型、疲劳损伤分析模型和寿命预测模型三大方面[3]。在电-热几何模型方面,相关研究发现,引线几何形状不同,产生的疲劳区域会不同,从而影响器件整体寿命[4],且从概率统计角度也发现,器件受几何形状的影响较大[5]。在疲劳损伤分析模型方面,由于热循环产生的应力对器件疲劳损伤影响较大[6],因此相关研究运用有限元计算和近红外测试[7]及热阻抗计算等方法[8]进行热分析,然后通过得到的温度场计算应力应变,再根据相应寿命预测模型推算寿命。研究发现,在热循环载荷下,引线根部为应力集中区域,最易发生疲劳损伤[9],科研人员提出了一些传统高周疲劳损伤模型以及时间速率敏感的时域模型用于寿命预测[10-11]。在寿命预测模型方面,主要有基于温度加速试验的Arrhenius预测模型[12]和基于应力-应变的Coffin-Manson模型2种,其中应力-应变法又分为有限元法和解析法[13]。有限元法较依赖Coffin-Manson准则校准程度。研究发现,通过试验数据来校准会使预测结果更准确[14]。例如,通过体积平均累积塑性应变和损伤数据来校准该模型[15],但老化试验费时费力。因此,相关研究提出若不考虑二次硬化和动态重结晶[16],可采用一种材料依赖的损伤裂纹扩展模型在规律时间间隔点估计界面损伤状态[17],从而省却一些不必要的老化试验。而解析法计算量小,准确度取决于材料应力-应变关系是否合理。但两者在特定条件下可以达到同样的预测精度。
本文以“数学建模-物理分析-试验设计-案例验证”并行的研究方法展开具体研究。首先,根据设计LED的加速循环电载荷老化试验,提出了一种基于电流加速模型的加速因子提取方法;其次,从加速寿命与引线应变幅的关系入手,基于仿真模拟方法得到加速电流应力条件下LED金引线的平均失效时间与应变幅的关系;最终,基于修正Coffin-Manson模型完成对LED金引线疲劳断裂失效寿命的预测和试验验证。
1 基于电流加速模型的寿命预测 传统寿命预测模型是通过加速寿命与加速因子相乘得到的。加速因子的准确性依赖于加速因子提取公式是否合理,以及各影响系数的准确度。因此,传统加速因子提取的准确性一般不高,而加速寿命则由试验获得,其准确性较高。本节遵循“老化机理不变原则”设计了3种加速电流应力的LED加速寿命测试试验,提出电流加速模型提取电流加速因子,预测LED额定电流条件下的使用寿命。
1.1 电流加速模型及加速因子提取 基于传统电压加速模型计算加速因子的方法如下:
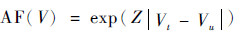 | (1) |
式中:AF为加速因子;Z为电压影响系数;Vt为测试状态下的电压值,V;Vu为参考工作状态下的电压值,V。
由于该模型多用于普通电子器件加速因子的粗略估算,精度不高。作为本文研究对象的LED通常为恒流驱动元件,其工作压降变化较小,因此电压不宜作为加速条件。因此, LED的功率循环测试通常是指电流载荷循环变化测试过程。在此过程中,输入电功率部分转化为光,部分转化为热,而热变化引起黏弹体对引线应力的影响也发生了变化。因此,本文综合考虑以上因素,提出对传统电压加速模型进行修订。
首先,根据二极管的I-V方程,即
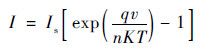 | (2) |
式中:I为正向电流;Is为反向饱和电流;v为正向偏压;q为电子电荷;K为玻尔兹曼常量;T为开氏温度;n为理想因子,当反向饱和电流较小时,该值可通过I-V曲线截距获得,本文根据测得样品I-V曲线取截距值得到n = 2.67。当环境温度为105℃时,KT/q = 0.032 37 V。
由于本次试验中LED外加电压量级大于10-1,且需要考虑内阻,因此整体压降为
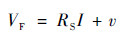 | (3) |
式中:RS为LED内阻。
综合式(2)、式(3)可得整体器件压降VF为[18]
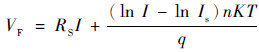 | (4) |
反向饱和电流Is通常与二极管PN结种类以及温度有关[19],与正向电流无关,根据式(4)可得
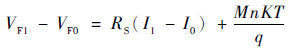 | (5) |
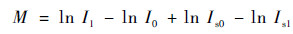 | (6) |
式中:VF1为压力电压;VF0为参考电压;I1为压力工作电流;I0为参考工作电流;Is1为芯片在压力电流工作条件下达到的温度对应的反向饱和电流;Is0为芯片在参考电流工作条件下达到的温度对应的反向饱和电流。
结合式(1)可得
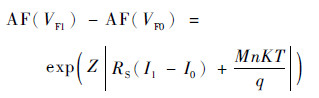 | (7) |
再将式(7)改写为
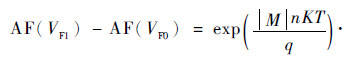 | (8) |
令AF(I) = D(AF(VF1)-AF(VF0)),则
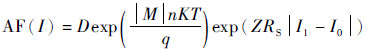 | (9) |
综合式(8)和式(9)可知,前者为两电压加速因子的差值,后者为电流加速因子值。因此要使两式相等,必须引入比例系数D,用以表征电流加速因子与电压加速因子之间关系的常数。
由于电流变化会引起LED结温变化,而温度变化又会引起反向饱和电流的变化,因此在给定电流下的LED正向压降并不相同。本文引入电压修正系数Zx修正电压变化引起的误差。
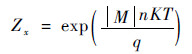 | (10) |
则式(9)可简写为
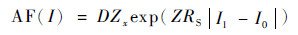 | (11) |
式(11)即为本文最终改进后的电流加速因子提取模型。
虽然反向饱和电流与正向电流无关,但LED生成的热会影响反向饱和电流,因此本文测试反向饱和电流时,采用让样品在各种压力电流下稳定工作一段时间,然后迅速加反向电压来获取反向饱和电流值。表 1为3种正向电流条件下的测试结果。
表 1 三种正向电流条件下的测试结果 Table 1 Test results under conditions of three forward currents
| 正向电流I/mA | 器件内阻RS/Ω | 压力反向饱和电流Is1/(10-9A) | 参考反向饱和电流Is0/(10-10A) | 理想因子n |
| 800 | 4.78 | 1.4 | 2 | 2.67 |
| 900 | 4.37 | 2.3 | 2 | 2.67 |
| 1000 | 4.04 | 2.9 | 2 | 2.67 |
表选项
本文分别通过控制电流和电压,对样品做加速试验,记录参考电流以及电压下的寿命值为317 s;然后分别增加样品工作电流为0.1 A和工作电压为0.1 V时,记录寿命分别为153 s和264 s。假设参考电流或电压下的加速因子为1,则增加0.1 V或0.1 A后的加速因子分别为1.20和2.07。此时电流加速因子和电压加速因子与参考加速因子之差的比率D为10.04。本文取近似值D = 10为比例系数。
Z为电压影响系数,即式(1)描述曲线中每一点切线斜率。本文将式(1)近似为三段线,如图 1所示,图中端点横坐标依次为实测参考电流和3种压力电流对应的电压值,纵坐标为通过老化试验获得的加速因子,则3种压力电压下Z可近似为每段线斜率,即1.61、8.65、9.76。将表 1数据代入式(6)和式(10)计算可得:3种正向电流(800、900、1 000 mA)加速应力条件下的修正系数Zx = 3.97,3.76,3.65。其中,参考额定工作电流为700mA。将试验测试数据代入修正模型式(11)可以得到,电流800 mA时的加速因子为AF800 = 4.65;900 mA时的加速因子为AF900 = 21.24;1 000 mA时的加速因子为AF1 000 = 68.31。
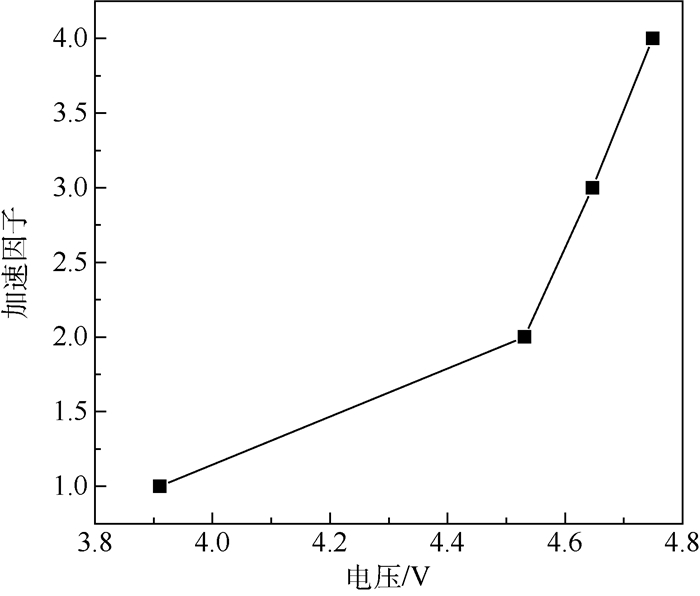 |
| 图 1 基于电压加速模型的加速因子提取 Fig. 1 Extracted acceleration factors based on voltage acceleration model |
| 图选项 |
1.2 功率循环老化试验 如图 2所示,本文选用1 W大功率正装封装LED为研究对象,其额定工作电流为700 mA。引线为30 μm的金线,连接芯片和电极,并被硅胶(无荧光粉)包裹。
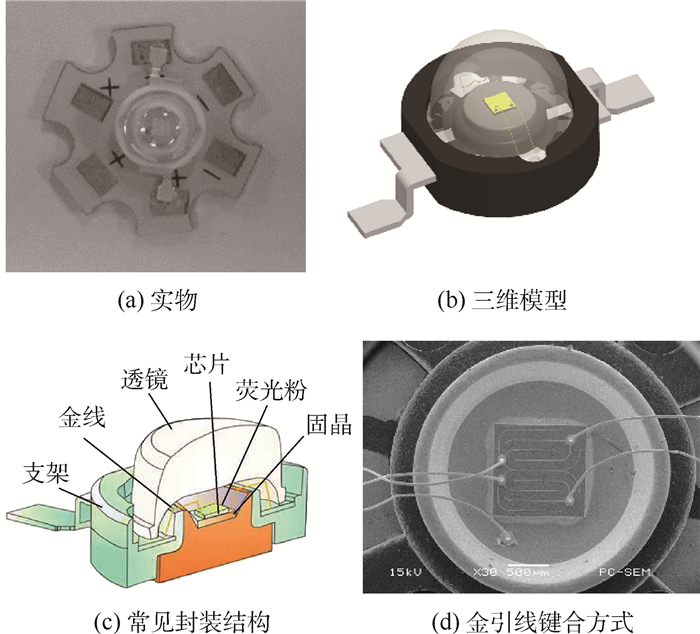 |
| 图 2 本文所选大功率LED样品 Fig. 2 High-power LEDs used in this paper |
| 图选项 |
本文采用功率循环老化试验对试验样品进行加速老化测试。试验平台如图 3所示,该平台由3台功率循环电源与配套夹具、3台电压巡检仪、1台PC和1台恒温箱组成。每台功率循环电源可分别为30个样品单独供电。装载样品的夹具放置于高温恒温箱中。夹具与功率循环电源之间为电源线连接,夹具与电压巡检仪之间为数据线连接。本文通过电压巡检仪采集每颗LED的正向电压信号,通过正向电压信号判断和记录LED的失效时间。为了保证每个样品的老化条件和负载条件一致,每个样品均为并联单独供电,若有样品失效也不会影响其他样品的电驱动参数。本次试验样品总共为60颗,分为4组不同电流条件,分别为参考额定工作电流700 mA下和加速条件800、900、1 000 mA下各15颗。恒温箱温度设定为105℃,功率循环电源的循环周期设置为1 s。
 |
| 图 3 LED功率循环老化试验平台装置图 Fig. 3 Power cycling aging test platform for LEDs |
| 图选项 |
1.3 实测失效寿命和加速寿命预测结果对比 据试验统计,700、800、900和1 000 mA四种电流条件下的样品失效模式均为引线断裂。依据电压巡检仪记录数据可统计得到4种试验条件下63%样品失效的平均失效时间分别为1 765、400、82和26 h。如表 2所示,根据1.1节计算得到的加速因子可得额定工作电流条件下的3个预测寿命值。将其与试验统计寿命值比较,绝对误差分别为5.38%、1.30%和0.62%。由此可见,本文针对功率循环下大功率LED金引线失效模式提出的电流加速模型预测精度较高。
表 2 加速寿命测量结果和预测结果对比 Table 2 Comparison of accelerated lifetime testing results and prediction results
| 正向电流/mA | 63%平均失效时间/h | 加速因子 | 预测寿命/h | 700mA试验寿命/h | 绝对误差/% |
| 800 | 400 | 4.65 | 1860 | 1765 | 5.38 |
| 900 | 82 | 21.24 | 1742 | 1765 | 1.30 |
| 1000 | 26 | 68.31 | 1776 | 1765 | 0.62 |
表选项
2 基于Coffin-Manson的寿命预测 金引线失效是正装大功率LED器件失效的主要原因之一,其中以引线断裂和焊点脱落2种情况最为常见。功率循环测试使得LED样品封装材料的温度随之发生循环变化,不同温度下硅胶会处于不同的力学状态而产生较大的热应力变化。本节首先通过仿真模拟计算应力分布,找到最可能失效的部位与方式;然后,基于Coffin-Manson模型预测失效寿命,并与试验测量结果进行对比;最后,通过失效分析手段观察1.2节试验中失效样品的引线断裂情况,并与仿真模拟结果进行对比。
2.1 有限元模型构建 由图 4可知,大功率LED的模型主要由塑料壳、硅胶、金线、电极、芯片、热沉等组成。塑料壳的材料为环氧树脂;LED芯片材料简化为蓝宝石(氧化铝);封装硅胶为黏弹性材料;热沉、芯片和电极材料为线性材料;金线的直径为30 μm。如图 4所示,本文采用1/4模型来减小计算量,对重点研究部位即硅胶与金线进行非线性参数设定。设定外表面空气自然对流系数为6W/(m2·℃),对称面绝热,底部施加固定约束。
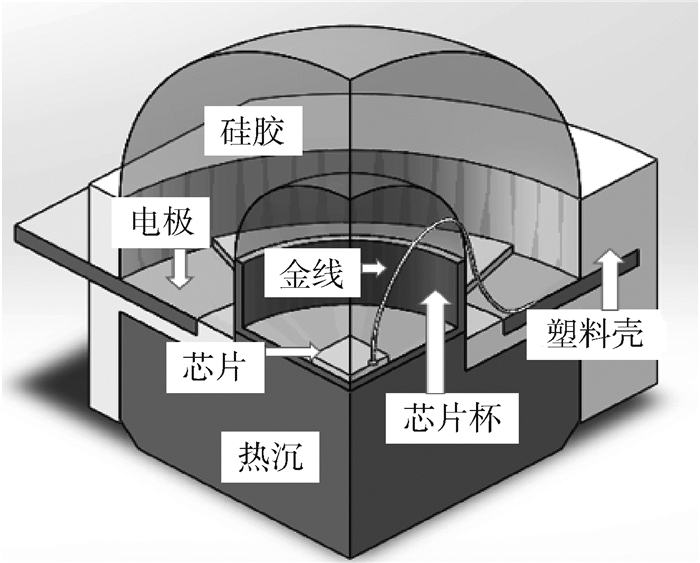 |
| 图 4 大功率LED的仿真模型 Fig. 4 Simulation model of high-power LED |
| 图选项 |
2.2 非线性材料参数设定 金引线设定为双线性各向同性强化材料,其屈服准则服从von Mises准则,屈服强度为32.7 MPa,切线模量为0.6×103 MPa。由动态热机械分析(DMA)方法测得硅胶的黏弹性参数,得到剪切松弛储能模量主曲线和体积松弛储能模量主曲线,然后采用广义麦克斯韦模型(Prony级数)拟合得到有限元仿真需要的松弛时间、剪切松弛系数、体积松弛系数。松弛储能模量E(t)用Prony级数表示[20]为
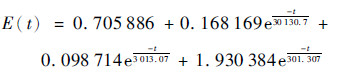 | (12) |
2.3 载荷与边界条件设定 如图 5所示,本文选取功率加载间隔为1 s,即通电1 s、断电1 s,峰值电流载荷分别为700、800、900和1 000 mA。芯片的发热功率值由电功率除去积分球测得的光功率得到,再将芯片的发热功率转换成单位体积下的热功率加载到芯片上,进行功率循环模拟。模拟环境温度设定为105℃。
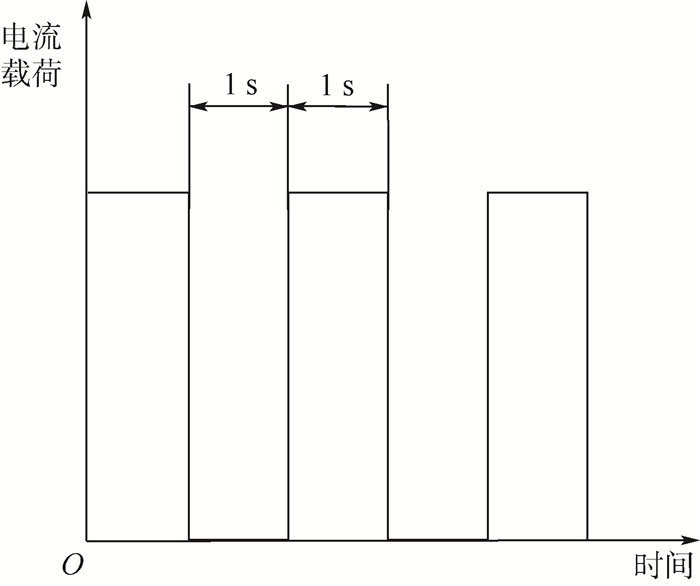 |
| 图 5 功率循环载荷示意图 Fig. 5 Schematic of power cycling loading |
| 图选项 |
2.4 金引线应力分布仿真结果 基于局部应变法的疲劳寿命预测是将疲劳寿命估算建立在应力集中部位的应力和应变局部估算上[21]。因此,可以认为引线是在此处断裂而导致整个器件失效的。对于大功率LED正装封装结构来说(见图 2(c)),LED芯片在功率循环载荷下周期性产热,产生的热量部分传导至硅胶,从而在硅胶内部产生一个周期变化的温度场。由于硅胶的材料表现为黏弹性,且弹性模量远小于引线,因此引线的受力主要是由硅胶发生形变导致的。图 6为在加速电流1 000 mA、环境温度105℃条件下的金引线应力分布仿真。结果显示,引线最大von Mises应力出现在与芯片连接一端的根部位置。
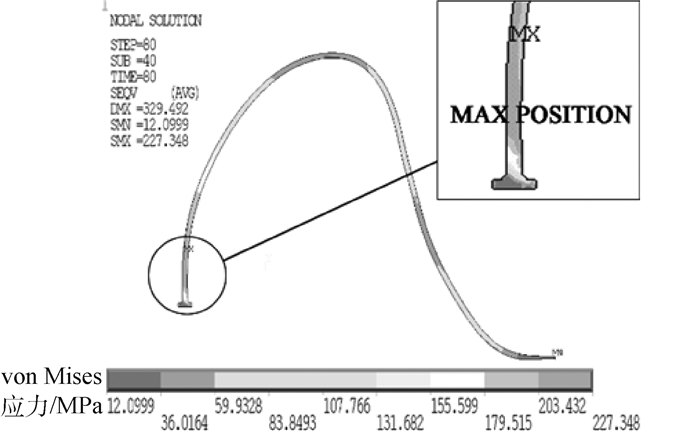 |
| 图 6 功率循环测试后金引线的von Mises应力仿真分布 Fig. 6 Simulated von Mises stress distribution of gold bonding wire after power cycling test |
| 图选项 |
为了验证仿真结果,本文将该加速老化条件下的失效样品取出,通过X-RAY检测(见图 7(a))发现引线跟芯片连接根部位置有明显褶皱痕迹。因此,可以判断此处应力变化较明显,是最可能产生断裂的位置。同时,采用封装硅胶溶解剂除掉引线周围的硅胶,再通过光学显微镜可以直观地观察到引线断裂的位置和状态。如图 7(b)所示,金引线断裂位置与仿真结果非常相似,出现在与芯片连接一端的根部附近。
 |
| 图 7 功率循环测试后LED失效样品图 Fig. 7 Failed LED sample after power cycling test |
| 图选项 |
2.5 金引线疲劳断裂寿命预测结果 19世纪60年代,Manson和Coffin在研究金属材料疲劳过程发现,塑性应变幅的对数与疲劳载荷反向次数的对数存在线性关系,提出了一种以塑性应变幅为参量的疲劳寿命描述法[22]。这就是著名的Coffin-Manson低周疲劳模型,是一个建立于大量试验数据基础上的经验公式。
本文对4种电流载荷条件做了金引线的塑性应变仿真计算,并将得到的应变幅汇总,如图 8所示。可知,随着时间增加,应变幅增大后趋于稳定;随着电流增加,引线最大应变幅也在增加。
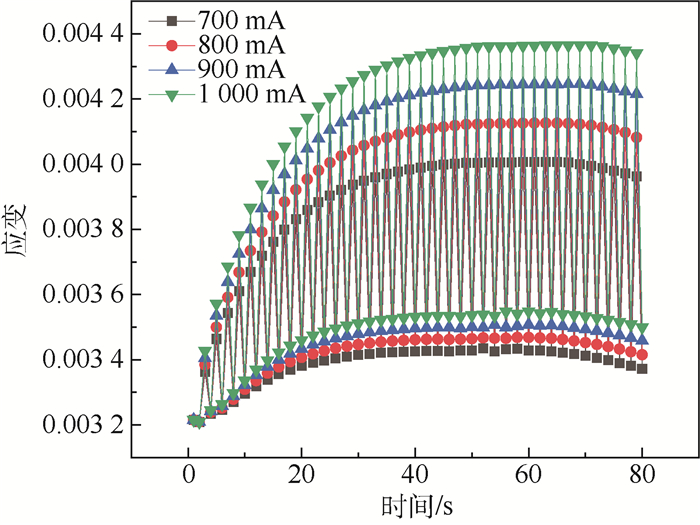 |
| 图 8 不同电流条件下金引线的塑性应变变化过程 Fig. 8 Changing process of plastic strain of gold bonding wire under different current conditions |
| 图选项 |
由于大电流条件下引线为应变疲劳,因此采用Coffin-Manson寿命预估模型方程[23],计算引线疲劳失效平均寿命,公式如下:
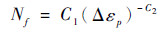 | (13) |
式中:Δεp为引线应变幅值;Nf为疲劳寿命。本文以800、900和1 000 mA电流条件下的3组加速失效寿命数据拟合Coffin-Manson关系式,拟合结果为C1 = 1.99×10-37, C2 = 12.38。将系数代入式(13),计算出700 mA电流条件下的预测寿命。结果如表 3所示,样品在700 mA额定工作电流条件下金引线的疲劳寿命仿真预测值与实测值的误差为6.912%,预测精度较高。
表 3 基于仿真的金引线疲劳寿命预测结果 Table 3 Gold bonding wire fatigue lifetime prediction results based on simulations
| 电流/mA | 应变幅 | 实测寿命/h | 预测寿命/h | 误差/% |
| 700 | 0.000590 | 1765 | 1887 | 6.912 |
| 800 | 0.000667 | 400 | ||
| 900 | 0.000757 | 82 | ||
| 1000 | 0.000840 | 26 |
表选项
3 结论 本文针对大功率正装LED封装的金引线失效,以“数学建模-物理分析-试验设计-案例验证”相结合的方式,分别提出基于电流加速模型和Coffin-Manson模型2种寿命预测方法。研究结果表明:
1) 结合设计相关试验与加速测试对传统电压加速模型进行修正,据此提出电流加速模型并提取加速因子,预测额定工作电流条件下金引线失效寿命值与试验测量值之间的平均误差为2.43%。
2) 通过研究样品失效机理,发现采用循环电载荷下金引线的失效机理为应变疲劳断裂,本文采用表征应变幅与寿命关系的Coffin-Manson模型,并基于加速测试条件下仿真计算的应变幅和对应老化试验寿命拟合模型系数,最终得到额定工作电流条件下金引线失效寿命的仿真预测值与实际测量值对比,误差为6.912%。由此可见,本文提出的2种方法均有较高的预测精度,能实现LED寿命及可靠性的快速、准确评估。
参考文献
| [1] | VAN DRIEL W D, FAN X J. Solidstate lighting reliability:Components to systems[M]. Berlin: Springer, 2012. |
| [2] | CHANG M H, DAS D, VARDE P V, et al. Light emitting diodes reliability review[J]. Microelectronics Reliability, 2012, 52(5): 762-782. DOI:10.1016/j.microrel.2011.07.063 |
| [3] | 鲁光祝.IGBT功率模块寿命预测技术研究[D].重庆: 重庆大学, 2012. LU G Z.Lifetime prediction for IGBT power module[D].Chongqing: Chongqing University, 2012(in Chinese). |
| [4] | MERKLE L, KADEN T, SONNER M, et al.Mechanical fatigue properties of heavy aluminium wire bonds for power applications[C]//Electronics System-Integration Technology Conference.Piscataway, NJ: IEEE Press, 2008: 1363-1368. |
| [5] | HU J M, PECHT M, DASGUPTA A. A probabilistic approach for predicting thermal fatigue life of wire bonding in microelectronics[J]. Journal of Electronic Packaging, 1991, 113(3): 275-285. DOI:10.1115/1.2905407 |
| [6] | HUA Y, LIN M, BASARAN C. Failure modes and FEM analysis of power electronic packaging[J]. Finite Elements in Analysis & Design, 2002, 38(7): 601-612. |
| [7] | SPENCER M L, LORENZ R D.Analysis and in-situ measurement of thermal-mechanical strain in active silicon power semiconductors[C]//Industry Applications Society Meeting.Piscataway, NJ: IEEE Press, 2008: 1465-1471. |
| [8] | 李志星, 张鑫宇, 平恩顺. 基于PFA的IGBT键合线失效机理及寿命预测[J]. 半导体技术, 2013, 38(9): 63-66. LI Z X, ZHANG X Y, PING E S. Failure mechanism and lifetime forecasting based on PFA for bonding wire in IGBT[J]. Semiconductor Technology, 2013, 38(9): 63-66. (in Chinese) |
| [9] | 姚二现, 庄伟东, 常海萍. IGBT模块功率循环疲劳寿命预测[J]. 电子产品可靠性与环境试验, 2013, 31(2): 12-17. YAO E X, ZHUANG W D, CHANG H P. Power cycle fatigue lifetime prediction of IGBT module[J]. Electronic Product Reliability & Environmental Testing, 2013, 31(2): 12-17. DOI:10.3969/j.issn.1672-5468.2013.02.004 (in Chinese) |
| [10] | YANG L, AGYAKWA P A, JOHNSON C M. A time-domain physics-of-failure model for the lifetime prediction of wire bond interconnects[J]. Microelectronics Reliability, 2011, 51(9-11): 1882-1886. DOI:10.1016/j.microrel.2011.07.052 |
| [11] | BIELEN J, GOMMANS J J, THEUNIS F.Prediction of high cycle fatigue in aluminum bond wires: A physics of failure approach combining experiments and multi-physics simulations[C]//International Conference on Thermal, Mechanical and Multiphysics Simulation and Experiments in Micro-Electronics and Micro-Systems.Piscataway, NJ: IEEE Press, 2006: 1-7. |
| [12] | MATSUNAGA T, UEGAI Y.Thermal fatigue life evaluation of aluminum wire bonds[C]//Electronics Systemintegration Technology Conference.Piscataway, NJ: IEEE Press, 2006: 726-731. |
| [13] | HAGER C, STUCK A, TRONEL Y, et al.Comparison between finite-element and analytical calculations for the lifetime estimation of bond wires in IGBT modules[C]//12th International Symposium on Power Semiconductor Devices and ICs.Piscataway, NJ: IEEE Press, 2000: 291-294. |
| [14] | CIAPPA M, FICHTNER W.Lifetime prediction of IGBT modules for traction applications[C]//IEEE International Proceedings on Reliability Physics.Piscataway, NJ: IEEE Press, 2000: 210-216. |
| [15] | ZHANG S U, BANG W L. Fatigue life evaluation of wire bonds in LED packages using numerical analysis[J]. Microelectronics Reliability, 2014, 54(12): 2853-2859. DOI:10.1016/j.microrel.2014.07.142 |
| [16] | AGYAKWA P A, CORFIELD M R, YANG L, et al. Microstructural evolution of ultrasonically bonded high purity Al wire during extended range thermal cycling[J]. Microelectronics Reliability, 2011, 51(2): 406-415. DOI:10.1016/j.microrel.2010.08.018 |
| [17] | YANG L, AGYAKWA P A, JOHNSON C M. Physics-of-failure lifetime prediction models for wire bond interconnects in power electronic modules[J]. IEEE Transactions on Device & Materials Reliability, 2013, 13(1): 9-17. |
| [18] | 林亮, 陈志忠, 童玉珍, 等. GaN基大功率倒装焊蓝光LED的I-V特性研究[J]. 半导体光电, 2007, 28(6): 766-768. LIN L, CHEN Z Z, TONG Y Z, et al. Research on current-voltage characteristics of GaN-based high power flip-chip blue LED[J]. Semiconductor Optoelectronics, 2007, 28(6): 766-768. DOI:10.3969/j.issn.1001-5868.2007.06.004 (in Chinese) |
| [19] | 李炳乾, 布良基, 甘雄文, 等. LED正向压降随温度的变化关系研究[J]. 光子学报, 2003, 32(11): 1349-1351. LI B Q, BU L J, GAN X W, et al. Research on the relationship of the change in forward voltage with temperature of light emitting diode[J]. Acta Photonica Sinica, 2003, 32(11): 1349-1351. (in Chinese) |
| [20] | 唐红雨, 杨道国, 张国旗, 等. 硅胶粘弹性对大功率LED可靠性的影响[J]. 电子元件与材料, 2013, 32(9): 51-55. TANG H Y, YANG D G, ZHANG G Q, et al. Influences of viscoelasticity of silicone on the reliability of high power light emitted diode[J]. Electronic Components & Materials, 2013, 32(9): 51-55. DOI:10.3969/j.issn.1001-2028.2013.09.015 (in Chinese) |
| [21] | 董月香. 疲劳寿命预测方法综述[J]. 大型铸锻件, 2006(3): 39-41. DONG Y X. General description of the fatigue life prediction method[J]. Heavy Casting and Forging, 2006(3): 39-41. DOI:10.3969/j.issn.1004-5635.2006.03.014 (in Chinese) |
| [22] | 郑战光, 蔡敢为, 李兆军, 等. 基于损伤力学阐释Manson-Coffin低周疲劳模型[J]. 中国机械工程, 2011, 22(7): 812-814. ZHENG Z G, CAI G W, LI Z J, et al. Interpretation of Manson-Coffin model of low cycle fatigue based on damage mechanics[J]. China Mechanical Engineering, 2011, 22(7): 812-814. (in Chinese) |
| [23] | ZHANG B, TAO G.An improved Coffin-Manson model for mid-power LED wire-bonding reliability[C]//IEEE International Symposium on the Physical and Failure Analysis of Integrated Circuits.Piscataway, NJ: IEEE Press, 2014: 78-82. |
