根据材料产生的塑性应变是否可以忽略不计,把疲劳损伤分为高周疲劳和低周疲劳[7]:高周疲劳的细观塑性应变通常可以忽略不计,特征为其失效断裂循环数NR会很高,NR大于10 000循环;而低周疲劳的损伤与循环塑性应变一起发展,故塑性应变不可以忽略,特征为其断裂循环数NR较低,NR小于10 000循环。现有的疲劳损伤演化模型主要分为2类:一类是通过实验数据拟合的疲劳损伤曲线直接构造疲劳损伤演化函数,建立疲劳损伤模型[8-10],其中以Chaboche疲劳损伤模型为代表,这种模型直接从实验数据出发,具有精确度高、普适性好等优点,但是其参数多,不易获取,并且没有很好的理论基础;另一类是通过利用连续损伤力学理论,以不可逆热力学理论框架,构造耗散势,导出疲劳损伤演化函数,建立疲劳损伤模型,然后根据实验数据进行验证和拟合参数[11-14],其中以Lemaitre疲劳损伤模型为代表,这种模型中的损伤与塑性应变相关,实质上属于延性损伤模型。这2类疲劳损伤模型虽然均有广泛的应用,然而实践表明它们并不适合于工程应用[15]。
本文利用不可逆热力学理论框架和损伤的微观力学,基于脆性损伤的机理,得到了一种新的脆性疲劳损伤模型。该模型具有推导严密、形式简单、参数少等优点。并根据实际情况,考虑初始损伤,对模型进行修正,最后通过实验数据确定参数并对模型进行验证,验证结果表明新模型比同类型疲劳损伤模型与实验结果符合的更好。
1 疲劳损伤模型 微裂纹的成核和增长及其结合而萌生的细观裂纹是脆性损伤的主要机理[11]。脆性损伤是一个不可逆的耗散过程,其间并未发生塑性变形。在脆性损伤中笔者可以根据微裂纹的图形来建立细观各向同性损伤变量和微裂纹表面密度之间的关系。而延性损伤的主要机理是因局部大塑性变形导致的微空穴的成核、增长和合并[11]。在延性损伤中本文需要建立损伤变量和微空穴密度之间的关系。所以脆性损伤和延性损伤在损伤演化模型构建方面是不同的。
本文主要基于脆性损伤机理来构建疲劳损伤模型。用微裂纹表征细观典型体元(Representative Volume Element, RVE)损伤,基于不可逆热力学理论框架和损伤的微观力学,用微裂纹的增长来表示细观RVE的损伤的演化,并假设经典的宏观疲劳裂纹的扩展规律(Paris公式)适用于细观RVE中的微裂纹扩展,从而建立起能代表宏观尺度的细观RVE的脆性疲劳损伤模型。
1.1 基于群体微裂纹密度的疲劳损伤变量的定义 考虑细观尺度L×L×L的立方体RVE。d×d×d立方体为微观元素,其中包含任意面积si和任意方向的微裂纹,n为裂纹数,如图 1所示。
 |
| 图 1 损伤的微观-细观单元 Fig. 1 Microscopic damage and meso-damage element |
| 图选项 |
G为相对应于裂纹面积s的应变能释放率,D为微元的损伤,Y为微元应变能密度释放率,则有
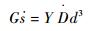 | (1) |
对于整个细观体积则有
 | (2) |
假定G=Gc时,微裂纹开始扩展,Y=Yc时,出现损伤。此外si=0→Di=0,对式(2)两边积分得到: Gc





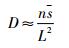 | (3) |
1.2 疲劳损伤演化模型 假定整个细观RVE所有微观元素的裂纹宽度均为e,同时令a为所有微观元素的裂纹长度的均值,即a=(

 | (4) |
利用Paris公式[16]:
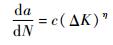 | (5) |
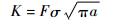 | (6) |
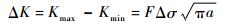 | (7) |
式中:da/dN为裂纹扩展速率,a为裂纹长度,N为交变载荷的循环次数;c和η为材料参数;F为几何形状因子;σ为名义应力幅值;K为名义应力强度因子值;Kmax和Kmin分别为裂纹处应力强度因子的最大值和最小值;Δσ为裂纹处应力幅值。假定微观元素微裂纹疲劳扩展规律符合Paris公式。对于微观元素所受的是有效应力,根据应变等效原理将Paris公式的名义应力替换成有效应力,即σ=σ/(1-D),相应的
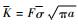
 | (8) |
对式(4)两边求导得
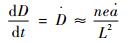 | (9) |
又可知
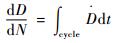 | (10) |
式中:cycle为一个循环。
将式(8)和式(9)代入式(10)得
 |
根据式(4)得
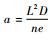

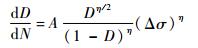 | (11) |
损伤边界条件为:初始条件N=0?D=0;破坏状态N=Nf?D=1,其中Nf为疲劳寿命。
根据损伤的边界条件,为了得到显式的解,将式(11)的分子Dη/2近似为(N/Nf)η/2代入式(11),两边积分得到
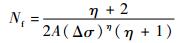 | (12) |
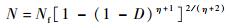 | (13) |
由式(13)得到
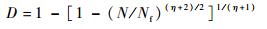 | (14) |
由于现实中材料初始状态下大多数是有损伤的,因此考虑初始损伤对疲劳损伤模型进行修正是有必要的,即修正后损伤边界条件:初始条件N=0?D=D0,D0为初始损伤;破坏状态N=Nf?D=1,根据修正后的损伤边界条件对式(14)进行线性修正,即
 | (15) |
在上述疲劳损伤模型的公式推导过程中,基于微观损伤机理建立的损伤模型,相对于传统宏观唯象的模型更加具有物理意义。
2 验证与分析 对于试件损伤度的测量,本文采用弹性模量衰减的方法测量疲劳损伤。
本文的实验构件及实验条件与文献[17-18]中提供的相一致,在文献[17]提供的疲劳实验数据的基础之上得到所提出的新的疲劳损伤演化模型的参数,然后通过该模型理论值、实验值与文献[17-18]的理论值进行对比分析。
实验构件:直径为6 mm的圆柱形试样,材料为12Cr1MoV钢。
实验条件:实验机型号为MTS880,载荷形式是拉压对称循环,三角波加载。
实验结果:根据测量弹性模量衰减的方法测量损伤值,疲劳实验所得到的一定循环比下的损伤量的实验结果见表 1。
表 1 D和N/Nf的实测值 Table 1 Test values of D and N/Nf
| 实验编号 | D | N/Nf |
| 1 | 0.15 | 0.35 |
| 2 | 0.18 | 0.40 |
| 3 | 0.20 | 0.60 |
| 4 | 0.25 | 0.80 |
| 5 | 0.50 | 0.95 |
| 6 | 1.00 | 1.00 |
表选项
根据实验数据,针对不考虑初始损伤的疲劳损伤演化方程即式(14)和考虑初始损伤的演化方程即式(15),分别利用非线性回归参数估计得到式(14)和式(15)的参数值,从而可以得出损伤量D与循环比N/Nf的关系式,如图 2所示。在图 2中,不考虑初始损伤的结果是由式(14)计算得到,而考虑初始损伤的结果是由式(15)得到。
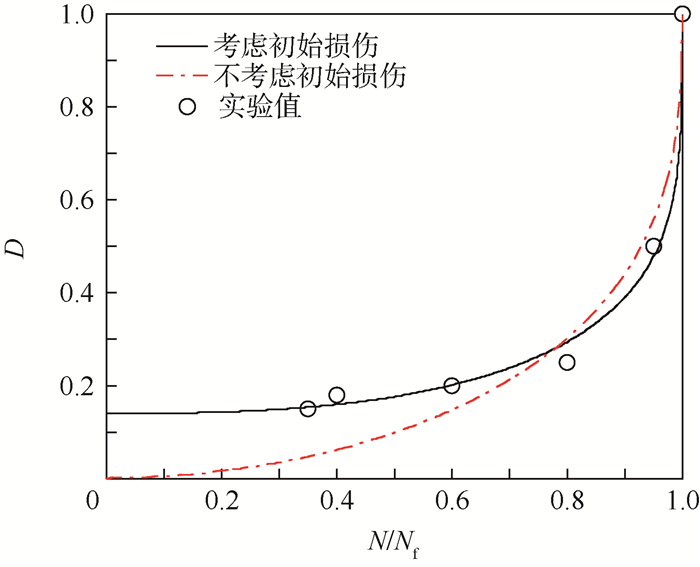 |
| 图 2 不考虑初始损伤、考虑初始损伤新模型与实验值的结果对比 Fig. 2 Comparison among new model without initial damage, new model with initial damage and experimental results |
| 图选项 |
利用非线性函数的最小二乘参数估计和参数估计对参数拟合,分别得到:不考虑初始损伤的疲劳损伤演化模型式(14)的参数η=1.919 2,其置信度为95%的置信区间为[1.030 3,2.808 1];考虑初始损伤的疲劳损伤演化模型式(15)的参数η=3.197 3,其置信度为95%的置信区间为[2.219 1,4.175 6],D0=0.138 6。
为了更好说明模型与实验数据的近似程度,用实验所测的值与其相对应的模型计算值的相关系数表示其近似的程度。由于实验数据的最后一个值对应于模型的边界条件,为了更好地表示模型与实验数据的近似程度,在计算其相关系数时去掉实验数据的最后一个值。不考虑初始损伤的疲劳损伤演化模型式(14)与实验数据的相关系数为0.968 4。考虑初始损伤的疲劳损伤演化模型式(15)与实验数据的相关系数为0.982 5。结合图 2,表明用初始损伤修正所得的疲劳损伤模型是合理的。
根据上面所得参数,考虑初始损伤的疲劳损伤演化模型式(15)可以表示为
 | (16) |
文献[17]认为金属构件的疲劳损伤主要属于机械损伤,其造成损伤的外因主要是有效当量应力幅造成的,基于Paris公式,构造损伤驱动力函数,所得疲劳损伤演化模型为D=1-(N/Nf)1/(η+1),经参数拟合得到
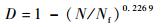 | (17) |
文献[18]基于Lemaitre模型进行推导,得到的疲劳损伤演化模型为:D=1-(N/Nf)Nfα,其中α为材料参数。经参数拟合得到
 | (18) |
现将考虑初始损伤的新模型即式(16)的理论值、实验值与文献[17]中模型即式(17)和文献[18]中模型即式(18)所提供的理论值进行对比,如图 3所示。在图 3中,理论值是由式(16)计算得到,文献[17]理论值是由式(17)得到,文献[18]理论值是由式(18)得到。
 |
| 图 3 新模型、文献[17]模型、文献[18]模型与实验值的结果对比 Fig. 3 Comparison among new model, model of Ref.[17], model of Ref.[18]and experimental results |
| 图选项 |
文献[17-18]所提出的疲劳损伤模型与实验数据的相关系数分别为0.959 9与0.966 4。结合图 3表明:新模型的理论值与实验值吻合的比较好,且比文献[17-18]所提供的理论值更加逼近实验值。特别是当N/Nf较小时,新模型要明显优于文献[17-18]所提供的理论值。这主要是因为新模型与文献[17]是应力控制的疲劳模型, 而文献[18]是应变控制的疲劳模型,新模型考虑了材料的初始损伤。三者是有一定差别的,其差别来源于模型的物理内涵与参数的拟合精度。其次从模型本身上来看,由式(11)可以得出
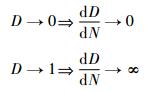 |
即疲劳过程初期,损伤趋近于0时,新模型的损伤增长缓慢,疲劳过程后期,损伤趋近于1时,新模型的损伤增长迅速,这符合疲劳损伤累积的一般规律,但是对于同类型的疲劳损伤模型一般并不满足:
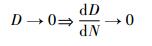 |
这也是新模型在疲劳过程的初期与实验的近似程度要明显优于同类型疲劳损伤模型的原因。同时,新模型在损伤初期采用不可逆热力学理论框架,基于损伤的微观力学,用微裂纹来表示损伤变量,实际是一种脆性各向同性损伤模型。因此,新模型能够应用于脆性材料疲劳损伤的寿命预测,物理内涵丰富。
本文中的实验和算例均采用拉压载荷加载,从而得到一种新的考虑初始损伤的脆性疲劳损伤模型。然而对于不同的加载路径,如纯扭及拉-扭等,新模型的适用性及外推的可能性(多维应力的等效处理)等方面工作需要以后继续完善。
3 结论 本文以不可逆热力学理论框架和损伤的微观力学为基础,基于脆性损伤的机理,建立了一种新的脆性疲劳损伤模型,该模型参数少,推导严密,且经实验验证,比同等类型的疲劳损伤模型更加符合实验结果。
1) 新模型包含了初始损伤变量,可以用来估算材料的初始损伤。
2) 新模型具有当材料损伤很小时,疲劳损伤增长缓慢的性质,而这是一般模型所不具有的性质。因此,新模型在疲劳过程的初期,损伤很小时,相比同类型疲劳损伤模型具有显著优势。同时新模型能够应用于脆性材料疲劳损伤的寿命预测。
3) 通过与实验对比分析,新模型与实验结果符合的比较好,且比文献[17-18]所提供的理论值更加逼近实验值,表明了本文所提出的新模型的合理性。
参考文献
| [1] | 国家自然科学基金委数理科学部. 力学学科发展研究报告[M].北京: 科学出版社, 2007: 89-92. Division of Mathematics and Physics, NSFC. Report on the development of mechanics[M].Beijing: Science Press, 2007: 89-92.(in Chinese) |
| [2] | WANG T J. A continuum damage model for ductile fracture of weld head affected zone[J].Engineering Fracture Mechanics, 1991, 40(6): 1075–1082.DOI:10.1016/0013-7944(91)90172-W |
| [3] | LEMAITRE J, DESMORAT R. Engineering damage mechanics[M].Berlin: Springer, 2005: 26-75. |
| [4] | KUMAR J, PRASAD K, KUMAR V. High-temperature low cycle fatigue damage assessment in near alpha IMI-834 titanium alloy[J].Fatigue and Fracture of Engineering Materials and Structures, 2011, 34(2): 131–138.DOI:10.1111/ffe.2011.34.issue-2 |
| [5] | 杨锋平, 孙秦, 罗金恒, 等. 一个高周疲劳损伤演化修正模型[J].力学学报, 2012, 44(1): 140–147. YANG F P, SUN Q, LUO J H, et al. A corrected damage law for high cycle fatigue[J].Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(1): 140–147.(in Chinese) |
| [6] | 关迪, 孙秦, 杨锋平. 一个修正的金属材料低周疲劳损伤模型[J].固体力学学报, 2013, 34(6): 571–578. GUAN D, SUN Q, YANG F P. A modified low cycle fatigue damage model for metals[J].Chinese Journal of Solid Mechanics, 2013, 34(6): 571–578.(in Chinese) |
| [7] | BRO? P. Contemporary fatigue damage aspects[J].Procedia Engineering, 2010, 2(1): 583–983.DOI:10.1016/j.proeng.2010.03.063 |
| [8] | CHABOCHE J L, LESNE P M. A non-linear continuous fatigue damage model[J].Fatigue and Fracture of Engineering Materials Structure, 1988, 11(1): 1–17.DOI:10.1111/ffe.1988.11.issue-1 |
| [9] | FATEMI A, YANG L. Cumulative fatigue damage and life prediction theories:A survey of the state of the art homogeneous materials[J].International Journal of Fatigue, 1998, 20(1): 9–34.DOI:10.1016/S0142-1123(97)00081-9 |
| [10] | GRANDA MARROQUíN L E, HERNáNDEZGóMEZ L H, URRIOLAGOITIACALDERóN G, et al. Cumulative damage evaluation under fatigue loading[J].Applied Mechanics and Materials, 2008, 13(14): 141–150. |
| [11] | LEMAITRE J. 损伤力学教程[M]. 倪金刚, 陶春虎, 译. 北京: 科学出版社, 1996: 85-94. LEMAITRE J.Damage mechanics tutorial[M].NI J G, TAO C H, translated.Beijing:Science Press, 1996:85-94(in Chinese). |
| [12] | WANG T J. Unified CDM model and local criterion for ductile fracture[J].Engineering Fracture Mechanics, 1992, 42(1): 177–183.DOI:10.1016/0013-7944(92)90289-Q |
| [13] | KUNC R, PREBIL I. Low-cycle fatigue properties of steel 42CrMo4[J].Materials Science and Engineering A, 2003, 345(2): 278–285. |
| [14] | CHANDRAKANTH S, PANDEY P C. An isotropic damage model for ductile material[J].Engineering Fracture Mechanics, 1995, 50(4): 457–465.DOI:10.1016/0013-7944(94)00214-3 |
| [15] | 杨晓华, 姚卫星, 段成美. 确定性疲劳累积损伤理论进展[J].中国工程科学, 2003, 5(4): 81–86. YANG X H, YAO W X, DUAN C M. The review of ascertainable fatigue cumulative damage rule[J].Engineering Science, 2003, 5(4): 81–86.(in Chinese) |
| [16] | 尹双增. 断裂·损伤理论及应用[M].北京: 清华大学出版社, 1992: 224-228. YIN S Z. Fracture and damage theories and their application[M].Beijing: Tsinghua University Press, 1992: 224-228.(in Chinese) |
| [17] | 郑战光, 蔡敢为, 李兆军. 一种新的疲劳损伤演化模型[J].工程力学, 2010, 27(2): 37–40. ZHENG Z G, CAI G W, LI Z J. A new model of fatigue damage evolution[J].Engineering Mechanics, 2010, 27(2): 37–40.(in Chinese) |
| [18] | 王卫国, 郑雯. 12Cr1MoV钢低周疲劳损伤研究[J].材料科学与工艺, 2005, 13(2): 193–195. WANG W G, ZHENG W. Research of low cycle fatigue damage of 12Cr1MoV steel[J].Materials Science and Technology, 2005, 13(2): 193–195.(in Chinese) |
