随着雷达技术的飞速发展，各种新功能、新体制的雷达层出不穷，以相控阵技术为核心的多功能雷达，因其具备较高的自适应能力、探测能力、抗干扰能力、高灵敏度、高可靠性以及同时多任务等诸多优越性能，得到了越来越广泛的应用^[1]。多功能雷达(Multi-Function Radar, MFR)通常采用灵活复杂的软件控制算法、电子波束控制等先进技术来实现同时多任务，能够完成搜索、捕获、跟踪、电子反对抗措施以及导弹制导等多种功能，其工作模式、功能状态具有规律变化的特性，因而如果能够获取MFR的状态转换，对于掌握该雷达运行规律、估计功能意图有着重要意义，同时也能够为决策者提供更充分可靠的支援情报。然而当前传统情报侦察系统所提供的情报信息有限，尚不能反映该体制雷达的状态转换信息。
近年来许多****对MFR的状态规律进行了深入探索，其中Visnevski等在形式语言与自动机的基础上提出了雷达句法模型，打破了传统的统计特征思想，以雷达句、短语、字的结构更全面充分地描述MFR的多功能特性，并利用该模型完成对MFR的识别、状态跟踪^[2-3]；刘海军等以句法模型为基础，研究了MFR辐射源的雷达字提取方法，并将概率思想引入识别算法中，取得了较好的识别效果^[4-5]；Arasaratnam等借助句法和OOMs (Observable Operator Models)，提出利用格子滤波(grid filter)来跟踪MFR辐射源状态的变化^[6]；马爽将生物数据处理中成熟的方法引入MFR辐射源识别中，提出一种MFR搜索规律重建方法^[7]，取得了较高的重建性能，然而并未对MFR的功能状态进行跟踪估计。上述对MFR的研究取得了一定的成果，但这些方法大都依靠脉冲样本图作为信号底层展开研究的，丢失了诸多的统计特征信息，并且大量脉冲样本图的提取、存储、匹配必将阻碍算法的运行速率；其次这些方法并没有考虑目标运动状态对MFR系统状态的影响。因而上述MFR状态分析模型，或多或少存在着估计准确率和鲁棒性的问题。
针对上述问题，在研究雷达句法和隐马尔可夫模型(Hidden Markov Model, HMM)^[8]的基础上，提出一种适用于MFR的层级识别模型，并在该模型基础上研究了一种基于HMM的状态转移估计方法。方法首先针对MFR辐射源构建了任务、状态、参数的层级模型，摒弃脉冲序列样本的方法，利用多个参数的统计特征信息作为模型底层；然后通过将MFR的内置状态转变作为HMM模型的隐藏序列，侦收的信号参数与目标机动信息作为观测序列，构建MFR-HMM模型；最后通过Baum-Welch、Viterbi算法^[8]优化模型参数、估计状态序列，进而利用D-S(Dempster-Shafer)证据理论对估计结果进行融合优化得到最终的MFR系统隐藏状态。
1 MFR辐射源层级模型 MFR系统内置的雷达资源管理软件可分为功能管理、任务调度和波形优选3个模块^[7]，是系统的控制中心，能够为各个功能分配所需的系统资源，选择合适的波形信号，并依据任务调度规则将不同功能的各个任务按照优先级生成任务序列，进而通过分时复用辅助MFR实现多个功能的并行独立工作。根据上述分析，可从MFR所执行的任务和发射信号着手，构建能够反映雷达运行机制和全面详尽描述信号特征的辐射源模型。
所建模型如图 1所示，分为任务、状态和参数3个层级。

图 1 雷达辐射源层级模型 Fig. 1 Hierarchical model of radar emitter

图选项

任务层C可以理解为MFR经过任务调度后生成的任务序列，由多个任务F组成。任务F代表雷达在一次波束照射时间内对某一目标或某空域所分配的任务，各个任务F之间相互独立，通过分时复用实现多个功能的并行工作。
状态层P代表能够反映雷达功能状态的工作模式，每种状态具备多个模式，各个模式由事先设定的多个固定脉冲列ω的有序组合构成，每个任务F至少由一个模式构成。以Mercury地基防空MFR为例，共有“搜索、截获、非自适应跟踪、距离分辨、跟踪保持”5种状态，所包含的模式有42种，其某个搜索任务可通过执行模式ω₁ω₂ω₄ω₅来实现。
参数层W作为核心层，描述了MFR信号特征且对识别有较大贡献的参数信息，由多个经事先编排的能够实现某种功能状态的固定脉冲列构成。参数层的各个脉冲列可用集合W表示，包含3个描述信息W_ωi={M^ω_i, T^ω_i, N^ω_i}。
M^ω_i为各个参数的统计描述信息，通过分析总结信号参数的变化规律，并参考文献[4]中辐射源联合参数建模方法，可将其描述为以下4种：
1) M^ω_i=x₀，参数值固定不变的描述(包含空集)。
2) M^ω_i=[x^L, x^U]，参数值为区间类型的描述。
3) M^ω_i={x₀, x₁, …, x_m}，参数值为枚举序列的描述。
4) M^ω_i=f(x)，参数值为函数类型的描述。
T为参数调制类型，利用常数0, 1, …, n表述，不同参数的T具备不同意义，0代表无调制。以常规脉冲描述字脉冲重复间隔(Pulse Recurrence Interval, PRI)、载频(Radio Frequency, RF)、脉宽(Pulse Width, PW)为例，各个参数的调制类型可表示为PRI：1—固定；2—参差；3—组变；4—抖动；5—滑变；6—调度；RF：1—固定；2—捷变；3—组变；PW：1—固定；2—多脉宽组合(多个)；3—抖动。
N^ω_i为某一脉冲序列的脉冲个数，在该段脉冲序列中，所有参数均保持其各自的调制样式不变。
对于每一个事先编排的固定脉冲列W而言，其所包含的参数特征并非一成不变的，可能含有多段内嵌脉冲列，其中每段内嵌脉冲列的各参数特征状态保持不变。下面通过模拟构建脉冲列W_ω1来详述模型的参数层，如图 2所示。

图 2 模拟生成的固定脉冲列Wω1 Fig. 2 Simulation of fixed pulse sequence Wω1

图选项

该固定脉冲列W_ω1中A、B分别代表 2段参数类型不同的内嵌脉冲列，下面仅以PRI、RF、PW三参数为例，说明参数层的表述：
设A段RF与PRI的调制方式为联合变化，第1组RF=3 588 MHz，PRI=350 μs，由5个脉冲构成，第2组RF=3 600 MHz，PRI=700 μs，由10个脉冲构成，第3组RF=3 653 MHz，PRI值为1 050 μs，由8个脉冲构成；PW为一个区间类型参数，区间值为1.5~1.8 μs。B段PRI为常规的固定样式，值为560 μs；RF为捷变样式，区间值为3 425~3 450 MHz；PW和A段相同，为区间参数1.5~1.8 μs，B段共计16个脉冲。则该脉冲列W_ω1描述为

(1)

(2)

(3)

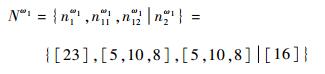(4)

在对参数层表述中，分割线“|”将不同段的内嵌脉冲列分隔开来，M^ω_i和T^ω_i中第1~3个参数依次对应特征PRI、RF、PW，而N^ω_i中n₁^ω₁和n₂^ω₁分别为脉冲列W_ω1第1、2段内嵌脉冲列的总个数，n₁₁^ω₁、n₁₂^ω₁分别为与第1段第1、2个参数特征对应的脉冲个数。
2 MFR-HMM模型 HMM是构建在马尔可夫模型基础上的双随机模型，通过寻找观测序列与隐藏状态之间的概率关系，在forward-backward^[9]、Baum-Welch^[10]和Viterbi算法^[11-12]的支撑下，能够解决HMM观测序列评估、模型优化学习、隐藏状态估计的问题^[13]。
对于MFR系统而言，如果将侦察接收机截获的信号视为观测序列，将MFR系统内部的功能状态视为隐藏状态，则MFR系统即可看作一个HMM模型^[14]，能够实现对MFR功能状态的估计。然而这样构建的HMM模型仅依靠侦收到的信号作为观测序列，丢失了对MFR系统状态转变影响巨大的因素——目标运动状态，导致反映信息不全面，估计精确度降低，同时由于目标运动状态作为己方信息，不存在侦收和识别误差的影响，在某些情况下可信度更高。针对该问题，结合目标运动状态，提出一种适应MFR系统的MFR-HMM模型，下面介绍该模型的构建方法。
2.1 HMM模型 一般地，HMM模型由以下5个参数描述^[15]：
1) 模型状态集S={S₁, S₂, …, S_N}，代表系统中的各个隐藏状态，N为模型状态总数。设某一时间t的系统状态为q_t，随着t的推移可得到状态序列Q={q₁, q₁, …, q_n}，n为序列长度。
2) 观测特征集V={v₁, v₂, …, v_M}，M为被观测到的特征数目。反映了系统输出，对于观测方，随时间t推移可得到观测序列O={o₁, o₂, …, o_n}。
3) 状态转移概率矩阵A=[a_ij]，a_ij=P(q_t+1=S_j|q_t=S_i)，1≤i, j≤N，代表了系统从状态S_i转变为S_j的概率(如果不能转变a_ij=0，否则a_ij＞0)。
4) 观测特征概率分布矩阵B=[b_j(k)]，b_j(k)=P(o_t=v_k|q_t=S_j), 1≤j≤N, 1≤k≤M，表示在状态S_j条件下，输出特征为v_k的概率。
5) 初始状态概率分布π={π_i}，π_i=P(q₁=S_i), 1≤i≤N，表示在初始化时间t=1时，系统状态为S_i的概率。
综合上述5个表征参数，HMM模型可表示为λ={S, V, A, B, π}。
2.2 目标运动状态 众所周知，MFR系统能够对周边环境进行感知，并对感兴趣的目标自适应地调整系统状态，而状态调整的依据除了系统自身运行机制的设定外，最重要的就是目标运动状态。下面从目标运动状态与MFR雷达管理系统之间的关系出发，分析影响系统状态的关键因素，并构建目标运动状态的观测特征集。
文献[16]对Mercury MFR的雷达管理系统进行了分析，指出MFR与目标之间的相互关系是导致MFR状态转移的主要原因。假设目标与MFR相距很远，且目标近似恒速运动，则MFR转变为持续跟踪状态的概率就会很低；如果目标加速地朝MFR进行机动，且相距较近，则MFR的雷达管理系统将会为该目标分配更多的资源，转变为跟踪状态的概率就会很高。基于此，从目标与MFR之间的径向距离、径向速度、径向加速度3个方面出发，将目标运动状态构建为MFR-HMM模型的观测特征。
可将t时刻MFR的目标描述为K_t={d_t, v_t, a_t}，其中d_t、v_t、a_t分别代表目标与MFR之间的径向距离、径向速度和径向加速度。对于每个参数，根据取值的不同划分为3个描述区间s₁、s₂、s₃，依次代表单参数因素对MFR的影响由高到低。对于d、v、a，s₁、s₂、s₃的含义如表 1所示。
表 1 描述区间s₁、s₂、s₃的含义 Table 1 Meanings of description interval s₁, s₂, s₃

参数	s1	s2	s3
d	近	中	远
v	高	中	低(包括逆向高速度)
a	大	中	小(包括逆向大加速度)

表选项






根据d、v、a 3个状态参数的不同取值，归属为不同的描述区间，可将目标划分为27个不同的运动状态L={L₁, L₂, …, L₂₇}，L={s_is_js_k}，1≤i, j, k≤3。这些目标运动状态即可与侦收到的模式一起构成MFR-HMM的观测特征集。
2.3 MFR-HMM模型构建 参考文献[3]，以Mercury水星MFR地基防空雷达为研究对象，简述MFR-HMM模型λ={S, V, A, B, π}的构成：
S={S₁, S₂, …, S₇}, 将MFR系统状态分为搜索(Search)、截获(Acquisition, ACQ)、非自适应跟踪(Non-Adaptive Track, NAT)、距离分辨(Range Resolution，RR)和跟踪保持(Track Maintenance, TM)共5种状态，其状态转移规律如图 3所示。

图 3 Mercury MFR状态转移图 Fig. 3 State transition diagram of Mercury MFR

图选项

V₁={v₁, v₂, …, v₄₂}，V₂={v₁, v₂, …, v₂₇}观测特征中包含雷达模式和目标运动状态2种类型，其中雷达模式参照Mercury MFR，共计42种，该雷达状态与模式之间关系如表 2所示；目标运动状态为27种，考虑实际中目标机动对MFR状态的影响，假定MFR状态与目标机动之间关系如表 3所示。为获得更为全面细致的观测描述，将V₁、V₂ 2种类型分别作为观测特征集，构建双链HMM。
表 2 按照状态分类的Mercury MFR模式 Table 2 Mercury MFR modes classified via state

MFR状态	雷达模式
Search	ω1ω2ω4ω5
	ω2ω4ω5ω1
	ω4ω5ω1ω2
	ω5ω1ω2ω4
	ω1ω3ω5ω1
	ω3ω5ω1ω3
	ω5ω1ω3ω5
ACQ	ω1ω1ω1ω1
	ω2ω2ω2ω2
	ω3ω3ω3ω3
	ω4ω4ω4ω4
	ω5ω5ω5ω5
NAT/TM	ω1ω6ω6ω6
	ω2ω6ω6ω6
	ω3ω6ω6ω6
	ω4ω6ω6ω6
	ω5ω6ω6ω6
RR	ω7ω6ω6ω6
	ω8ω6ω6ω6
	ω9ω6ω6ω6
ACQ/NAT/TM	ω6ω6ω6ω6
TM	ω7ω7ω7ω7
	ω8ω8ω8ω8
	ω9ω9ω9ω9
	ω1ω7ω7ω7
	ω2ω7ω7ω7
	ω3ω7ω7ω7
	ω4ω7ω7ω7
	ω5ω7ω7ω7
	ω6ω7ω7ω7
	ω1ω8ω8ω8
	ω2ω8ω8ω8
	ω3ω8ω8ω8
	ω4ω8ω8ω8
	ω5ω8ω8ω8
	ω6ω8ω8ω8
	ω1ω9ω9ω9
	ω2ω9ω9ω9
	ω3ω9ω9ω9
	ω4ω9ω9ω9
	ω5ω9ω9ω9
	ω6ω9ω9ω9

表选项






表 3 按照MFR状态分类的目标运动状态 Table 3 Target motion modes classified via state of MFR

MFR状态	目标运动状态
Search/ACQ	s3s2s2
	s3s2s3
	s3s3s2
	s3s3s3
	s3s1s1
	s3s1s2
	s3s1s3
	s3s2s1
	s3s3s1
Search/NAT/RR	s2s2s2
	s2s2s3
	s2s3s2
	s2s3s3
	s2s3s1
Search/RR/TM	s1s1s1
	s1s1s2
	s1s1s3
	s1s2s1
	s1s2s2
	s1s2s3
	s1s3s1
	s1s3s2
	s1s3s3
Search/NAT/RR	s2s1s1
	s2s1s2
	s2s1s3
	s2s2s1

表选项






3 状态转移估计方法 得到MFR-HMM模型后，想要估计出系统隐藏的状态转变，还需解决三方面的问题：一是模型不是最佳的，需要进一步优化；二是在最佳模型基础上，寻找解决状态估计的方法；三是由于所构建的MFR-HMM是双链HMM结构，在估计出状态序列后，为了充分发挥目标运动状态不受误差影响的特点，提高方法的准确率和鲁棒性，需要融合双链HMM的估计结果。这里分别采用Baum-Welch、Viterbi和D-S证据理论3种经典算法来解决上述问题。
3.1 模型优化 Baum-Welch算法作为EM(Expectation Maximization)算法的一个特例，主要用于解决HMM的模型优化问题。基本思路是通过不断寻求模型参数的最大似然估计(Maximum Likelihood Estimation, MLE)，使得P(O|λ′)≥P(O|λ)，λ和λ′分别为优化前后的模型，经反复迭代后即可得到最优模型。
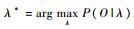
定义下列函数：
1) 前向变量α_t(i)=P(o₁o₂…o_t, q_t=S_i|λ)，表示前部分观测序列为o₁o₂…o_t，且t时刻状态为S_i的概率。将观测特征分布概率b代入可得

(5)

(6)

2) 后向变量β_t(i)=P(o_t+1o_t+2…o_n|q_t=S_i, λ)，表示结束部分序列为o_t+1o_t+2…o_n，且t时刻状态为S_i的概率。可以得到

(7)

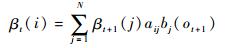(8)

3) 在模型λ和观测序列O条件下，t时刻系统状态为S_i的概率为

(9)

4) 在模型λ和观测序列O条件下，t、t+1时刻系统状态分别为S_i和S_j的概率。

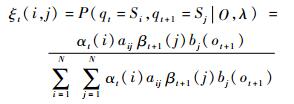(10)

模型优化的具体步骤如下：
1) 初始化λ=(π, A, B)。
2) 反复迭代，更新模型参数。

(11)

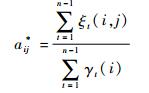(12)

(13)

式中：

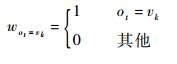3) 重复步骤2)，直至满足设定的收敛条件，完成优化得到模型λ^?。
3.2 状态序列估计 Viterbi算法以动态规划思想为基础，通过寻找单一的能够最佳解释观测序列的隐藏序列，来解决状态估计问题。因而在得到最佳模型λ^*后，已知观测序列O={o₁, o₂, …, o_n}，即可利用该算法对MFR系统的状态序列进行估计。
定义??从开始至某个时刻t，观测序列为{o₁, o₂, …, o_t}，且t时刻系统状态为S_i条件下，取得最佳状态序列的概率为δ_t(i)，即

(14)

则对于下一时刻t+1的δ_t+1(j)，可借助状态转移矩阵A和特征分布矩阵B获得，即

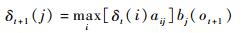(15)

依次迭代，并保存使得式(15) 成立的各个时刻t最佳状态S_i，即可得到最终状态序列。具体计算步骤如下：
1) 初始化t=1，δ₁(i)=π₁b_i(o₁)，ψ₁(i)=0，1≤i≤N，其中ψ₁(i)反映了开始前的状态值，设定为0。
2) 不断迭代，计算

(16)

(17)

式中：ψ_t(j)为能够产生式(16) 的前一时刻的最佳状态。
3) 处理最后一个序列，得到

(18)

式中：q_n^*为概率最大的状态。然后进行路径回溯，可得

(19)

通过路径回溯，即可估计出最终的状态序列Q^*={q₁^*, q₂^*, …, q_n^*}。
3.3 D-S证据理论 D-S证据理论是在Bayes理论基础上构建的决策融合方法，通过构建证据体、量化决策信任程度以及引入信任函数的方法来衡量决策信息的不确定程度。基本原理如下：
1) 构建证据体。以MFR状态估计为例，辨识框架可表示为Θ={S_i|i=1, 2, …, N}，S_i为决策为第i种状态的可能性。辨识框架中命题C的概率分布m:2^Θ→[0, 1]，则对空集的支持度为0，而对辨识空间中所有命题的支持度总和为1，即

(20)

则证据体可构建为(C, m(C))。
2) 构建信任函数和似真函数。若函数f_B:2^Θ→[0, 1]，同时满足

(21)

则f_B(C)为命题C的信任度，f_B为信任函数。类似的，若函数f_P:2^Θ→[0, 1]并满足

(22)

则f_P(C)为命题C的似真度，f_P为似真函数。
3) 按照D-S合成规则生成各个状态的概率，具体公式如下：

(23)

(24)

其中：m₁, m₂, …, m_n为不同证据源；k为冲突因子，代表不同证据源之间的冲突程度。然后选择概率最大的状态作为最终估计状态。
3.4 状态转移估计流程 综上所述，基于MFR-HMM模型的MFR状态转移估计流程如图 4所示。

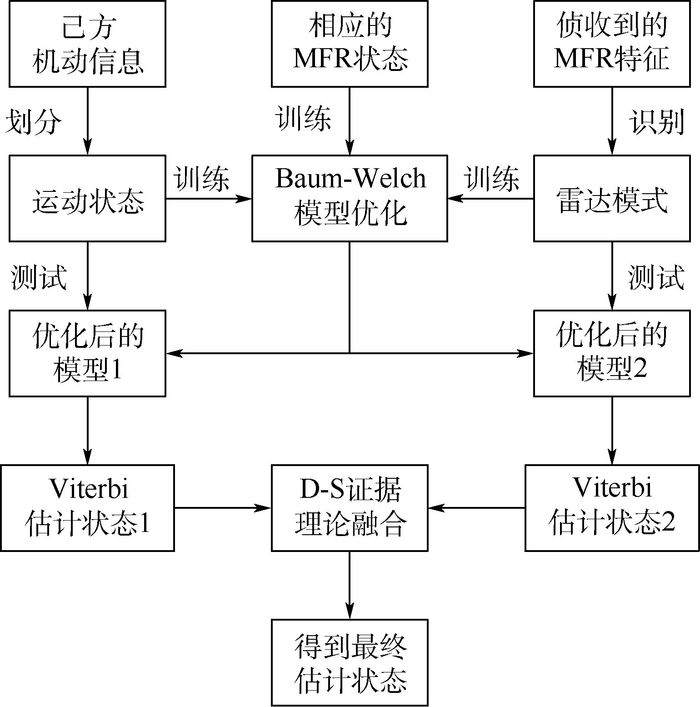图 4 状态转移估计流程 Fig. 4 Flow of radar state transfer estimation

图选项

可以将基于MFR-HMM的状态转移估计方法分为3个步骤：
1) 先验知识处理。对己方机动信息划分，得到运动状态；对侦收的MFR信号特征识别，得到雷达模式。然后分别结合相应的MFR状态作为训练数据，利用Baum-Welch算法得到优化后的模型1、2。
2) 状态估计。对测试数据也进行划分和识别，得到运动状态和雷达模式，在优化后的模型1、2的基础上，利用Viterbi算法进行估计，得到估计状态1、2。
3) 状态融合。通过D-S证据理论，融合2个HMM模型估计的状态1、2，得到最终结果。
4 实验 实验是在一定先验知识条件下展开的，包含两部分，分别验证所提出的MFR层级模型和基于MFR-HMM模型的状态转移估计方法的有效性。需要明确的是，第1组实验的以表 4中模拟的同部MFR的8种不同雷达模式作为对象进行识别；第2组实验以Mercury MFR的5种状态：搜索、截获、非自适应跟踪、距离分辨和跟踪保持作为估计对象。
表 4 雷达辐射源样本特征信息 Table 4 Sample feature information of radar emitters

雷达 模式	PRI/μs		RF/MHz		PW/μs		PA	DOA/(°)	样本 个数
	类型	取值	类型	取值	类型	取值
1	参差	[1 850, 1 880, 1 940] [1 060, 1 150, 1 100] [1 200, 1 250, 1 310]	组变	1 236/1 248/1 291	抖动	52.1±1.5	0.3~0.7	35~55	102
2	滑变	800/850/900/950/1 000	捷变	[3 850, 3 950]	固定	9.1	0.4~0.8	33~42	105
3	组变	1 125/1 276/1 342/1 497	组变	2 331/2 852/3 398/3 838	固定	15.9	0.5~0.9	16~30	104
4	固定	2 100	组变	2 300/2 400/2 500	多个	330.7/216.4/62.1	0.1~0.6	18~33	109
5	抖动	1 000±100	固定	2 925	抖动	50.6±1.5	0.2~0.7	33~58	100
6	调度	间隔544的脉冲5个 间隔690的脉冲7个 间隔依次为307, 343, 379, 398的脉冲4个 间隔为800±40的脉冲12个	固定	5 460	多个	1.5/2.5/3.2/7.3	0.4~1.0	23~39	109
7	抖动	1 500±150	捷变	[3 751, 3 950]	抖动	15.6±1.5	0.3~0.6	23~38	103
8	抖动	2 300±230	捷变	[3 322, 3 508]	固定	105.6	0.1~0.5	31~38	101

表选项






4.1 MFR层级模型有效性验证 模拟侦收到的同部MFR的8种不同雷达模式信号，特征信息如表 4所示, PA为脉冲幅度，DOA为到达方位角。
表 4中模式1和3的PRI与RF是对应联合变化的，模式1的骨架周期为27个脉冲，每个RF点对应一组PRI值，每组9个脉冲，每个PRI点3个脉冲；模式3的骨架周期为32个脉冲，每个RF对应一个PRI和8个脉冲。模式4的RF和PW是联合变化的，骨架周期为36个脉冲，每12个脉冲改变一次RF和PW值。模式6的PRI与PW联合变化，PRI调制类型为调度重频，包含4个预设的PRI单元，与4个脉宽值相对应，组合构成发射信号。
参照表 4所示的雷达样本信息，分别按照MFR层级模型、脉冲样本图模型以及统计参数模型仿真生成样本训练数据，测试数据相同，利用KNN(K-Nearest Neighbor)算法进行识别，不断改变测试数据的偏离误差(Error Deviation Level, EDL)，经过100次Monte Carlo，识别结果如图 5和表 5所示(选择PRI、RF、PW作为识别特征)。

图 5 不同模型条件下KNN识别准确率随偏离误差的变化 Fig. 5 Change of KNN recognition accuracy rate with EDL in different models

图选项

表 5 识别准确率对比 Table 5 Comparison of recognition accuracy rate

偏离误差/ %	识别准确率/%
	MFR层级模型	脉冲样本图模型	统计参数模型
0	99.64	97.87	83.17
8	96.18	92.59	75.95
16	93.19	88.69	72.19
24	85.57	80.26	66.22
32	74.60	68.96	58.53
40	64.71	60.39	52.05

表选项






从上述识别结果可以看出，随着参数EDL的逐渐增大，基于3种模型的识别准确率都呈下降趋势。其中统计参数模型由于缺失了各个参数的联合变化信息，识别准确率下降最快；脉冲样本图模型虽然对脉冲信息描述详尽，但缺失了统计信息，对于一些区间变化的特征描述不全面，因而识别准确率下降较快；所提出的MFR层级模型由于兼顾了统计参数和联合变化信息，识别准确率下降较慢，进而证实了该模型的有效性。
该MFR层级模型的构建是为了完成从侦收到的脉冲信号到雷达模式的识别，是后续状态估计的基础，因为所提出的MFR-HMM状态估计方法分别以识别出的雷达模式和目标运动信息作为观测特征进行估计，而后利用D-S证据理论融合得到最终的估计结果。因此如果前期识别模型构建的不恰当，必将影响雷达模式的识别准确率，从而影响状态估计的准确率。
4.2 基于MFR-HMM的状态转移估计方法有效性验证 以Mercury MFR为状态估计对象，参考图 3状态转换规律、表 2和表 3系统状态与观测特征的关系，按照图 6不同目标的概略机动轨迹，模拟生成4个目标的多批次机动信息，及其与之对应的MFR状态序列和观测序列，这里仅列举目标1的8个非连续机动状态下的观测特征、MFR状态，如表 6所示。

图 6 目标机动轨迹 Fig. 6 Target maneuver trajectory

图选项

表 6 目标1机动参数对应的观测特征和MFR状态 Table 6 Observational characteristics and MFR state of target 1's maneuver parameter

序 号	径向 距离/ km	径向速度/ (km·h-1)	径向 加速度/g	观测特征		MFR 状态
				运动 状态	雷达 模式
1	300.00	1 012.36	0.11	s3s1s2	ω4ω5ω1ω2	Search
2	273.53	1 167.26	-0.12	s3s1s3	ω3ω3ω3ω3	ACQ
3	219.81	896.37	2.13	s2s1s1	ω4ω6ω6ω6	NAT
4	171.96	427.68	2.16	s2s2s1	ω8ω6ω6ω6	RR
5	116.57	92.04	0.68	s1s3s2	ω3ω8ω8ω8	TM
6	135.93	-132.07	-1.16	s1s3s3	ω5ω9ω9ω9	TM
7	221.16	-973.28	-1.02	s2s3s3	ω9ω6ω6ω6	RR
8	280.72	-767.91	0.03	s3s3s2	ω3ω5ω1ω3	Search
????注：g=9.8 m/s2为重力加速度。

表选项






选取目标1机动时相应的状态序列和观测序列为训练数据，目标2、3、4作为测试数据，分别利用MFR-HMM模型、仅依靠侦获信息作为观测特征(observed-HMM)、仅依靠目标运动作为观测特征(motion-HMM) 3种HMM方法进行状态转移估计，如图 6所示。
1) 先验知识需求分析。在侦获到的模式信息存在10%识别错误率的条件下(识别错误率=错误识别模式个数/模式总个数)，逐步增加训练批次(目标1)，每批次包含连续的60个机动采样信息(实际中应该是实时连续获取的)，3种方法的估计准确率如图 7所示。

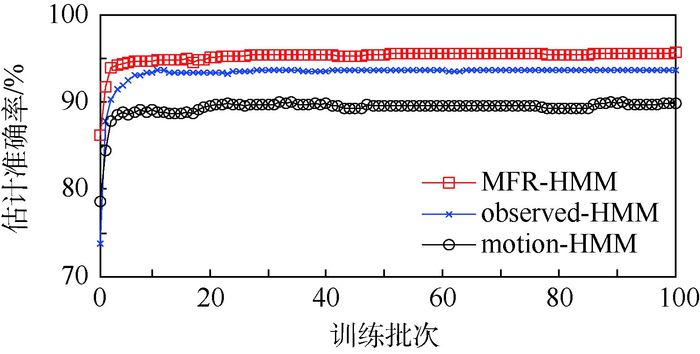图 7 估计准确率随先验信息的变化 Fig. 7 Change of estimation accuracy rate with prior information

图选项

从图 7中可以看出，随着训练数据的增加，当训练样本小于5批次时，3种方法的估计准确率都迅速提高，其中基于MFR-HMM方法的增速最快。当训练样本大于5批次时，3种方法都能够获得稳定的状态转移概率和观测特征分布概率，估计准确率达到稳定，此时基于MFR-HMM方法的估计准确率最高，可达95%。证实了该方法能够在较少先验知识的条件下，取得较好的状态转移估计效果。
2) 鲁棒性分析。在训练信息固定为50批的条件下，逐步增加所侦获模式信息的识别错误率，3种方法的估计准确率如图 8所示。

图 8 估计准确率随识别错误率的变化 Fig. 8 Change of estimation accuracy rate with recognition error rate

图选项

随着侦收模式识别错误率的增大，motion-HMM方法的估计准确率稳定不变，而MFR-HMM和observed-HMM方法的估计准确率都逐渐下降，其中基于MFR-HMM方法的准确率下降较缓。究其原因，主要因为目标运动状态作为己方信息，其获取不存在侦收或识别误差的影响。
当识别错误率小于42%时，MFR-HMM能够取得大于89.5%的估计准确率，高于另2种方法。当错误率大于42%时，虽然MFR-HMM的估计准确率逐步下降并将低于motion-HMM方法，但实际情况下，对侦收信息的识别错误率一般不超过20%，在该条件下所基于MFR-HMM状态转移估计方法能够取得大于93.16%的估计准确率，并具备较强的鲁棒性。
5 结论 1) 提出的MFR辐射源层级模型能够反映参数统计信息和联合变化规律，在相同识别算法的条件下，较模板匹配和脉冲样本图模型能够取得更为优越的识别准确率。
2) 提出的基于MFR-HMM的状态转移估计方法将目标运动状态信息同侦收到的模式信息一同作为HMM的观测特征，使得鲁棒性得到较大提升。
3) 方法通过构建双链HMM，利用D-S证据理论融合估计结果，先验知识需求较少，虽然一定程度上增加了时间消耗，但较D-S融合前能够取得更为优异的估计准确率。
为了更好地对目标雷达的状态意图进行预测，算法尚需解决依赖先验知识和非线性估计两大问题，同时这也是下一步工作的重心。

参考文献

[1]	贲德. 机载有源相控阵火控雷达的新进展及发展趋势[J].现代雷达, 2008, 30(1): 1–4. BEN D. Latest status & development trends of airborne AESA fire-control radar[J].Modern Radar, 2008, 30(1): 1–4.(in Chinese)
[2]	VISNEVSKI N.Syntactic modeling of multi-function radars[D].Hamilton:McMaster University, 2005:47-58.
[3]	VISNEVSKI N, KRISHNAMURTHY V, WANG A, et al. Syntactic modeling and signal processing of multifunction radars:A stochastic context-free grammar approach[J].Proceedings of the IEEE, 2007, 95(5): 1000–1025.DOI:10.1109/JPROC.2007.893252
[4]	刘海军. 雷达辐射源识别关键技术研究[D]. 长沙: 国防科学技术大学, 2010: 95-106. LIU H J.Researches on identification key technology for radar emitter[D].Changsha:National University of Defense Technology, 2010:95-106(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-90002-2010271175.htm
[5]	刘海军, 樊昀, 李悦, 等. 多功能雷达建模中的雷达字提取技术研究[J].国防科技大学学报, 2010, 32(2): 91–96. LIU H J, FAN Y, LI Y, et al. Research on extracting of radar words in modeling of multi-function radar[J].Journal of National University of Defense Technology, 2010, 32(2): 91–96.(in Chinese)
[6]	ARASARATNAM I, HAYKIN S, KIRUBARAJAN T, et al.Tracking the mode of operation of multi-function radars[C]//IEEE Conference on Radar.Piscataway, NJ:IEEE Press, 2006:233-238.
[7]	马爽. 多功能雷达电子情报信号处理关键技术研究[D]. 长沙: 国防科技大学, 2013: 101-125. MA S.Research on ELINT signal processing key technologies for multifunction radar research on extracting of radar words in modeling of multi-function radar[D].Changsha:National University of Defense Technology, 2013:101-125(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-90002-1015959319.htm
[8]	RYAN M S, NUDD G R. The Viterbi algorithm[J].Proceedings of the IEEE, 2015, 61(5): 268–278.
[9]	ATTOUCH H, PEYPOUQUET J, REDONT P. A dynamical approach to an inertial forward-backward algorithm for convex minimization[J].SIAM Journal on Optimization, 2014, 24(1): 232–256.DOI:10.1137/130910294
[10]	WELCH L R. Hidden Markov models and the Baum-Welch algorithm[J].IEEE Information Theory Society Newsletter, 2003, 53(2): 194–211.
[11]	周德强, 陈卫东. 基于Viterbi算法的扩频码与信息序列联合估计[J].飞行器测控学报, 2014, 33(5): 441–447. ZHOU D Q, CHEN W D. Joint blind estimation of spreading code and information sequence based on Viterbi algorithm[J].Journal of Spacecraft TT & C Technology, 2014, 33(5): 441–447.(in Chinese)
[12]	LIVANI H, JAFARZADEH S, EVRENOSOGLU C Y, et al. A unified approach for power system predictive operations using Viterbi algorithm[J].IEEE Transactions on Sustainable Energy, 2014, 5(3): 757–766.DOI:10.1109/TSTE.2014.2301915
[13]	刘韬. 基于隐马尔可夫模型与信息融合的设备故障诊断与性能退化评估研究[D]. 上海: 上海交通大学, 2013: 46-52. LIU T.Study of hidden Markov model and information fusion in equipment fault diagnosis and performance degradation assessment[D].Shanghai:Shanghai Jiao Tong University, 2013:46-52(in Chinese).
[14]	代鹂鹏, 王布宏, 蔡斌, 等. 基于SCFG建模的多功能雷达状态估计算法[J].空军工程大学学报(自然科学版), 2014, 15(3): 24–28. DAI L P, WANG B H, CAI B, et al. Latest status & development trends of airborne AESA fire-control radar[J].Journal of Air Force Engineering University(Natural Science Edition), 2014, 15(3): 24–28.(in Chinese)
[15]	章登义, 欧阳黜霏, 吴文李. 针对时间序列多步预测的聚类隐马尔科夫模型[J].电子学报, 2014, 42(12): 2359–2364. ZHANG D Y, OUYANG C F, WU W L. Cluster-based hidden Markov model in time series multi-step prediction[J].Acta Electronica Sinica, 2014, 42(12): 2359–2364.DOI:10.3969/j.issn.0372-2112.2014.12.004(in Chinese)
[16]	WANG A, KRISHNAMURTHY V. Signal interpretation of multifunction radars:Modeling and statistical signal processing with stochastic context free grammar[J].IEEE Transactions on Signal Processing, 2008, 56(3): 1106–1119.DOI:10.1109/TSP.2007.908949