国内外****对压电振动能量收集系统的机电耦合模型、能量收集电路设计、压电片尺寸等多方面进行了研究。Erturk和Inman[8]给出了压电单晶片与双晶片悬臂梁的分布参数模型及其在简谐基座激励下的封闭解。Badel等[9]开发了一种新型功率流优化方法,用于提高转化能量,相比于标准技术,此方法使得收集的电能提高了900%。Stewart等[10]研究指出,当压电片的长度占悬臂梁有效长度的2/3时,压电片的输出功率最大。
在压电能量收集方面,现有的研究多偏于理论模型[11-13]研究,也有少部分试验方面的验证[14]。这些研究多数针对带有集中质量块的悬臂梁和基座运动激励,而实际的机翼等振动结构不附加额外质量,且外激励不作用在基座,而是重力或气动力等非基座激励。本文结合压电材料的力电耦合理论和结构动力学理论,推导了基于压电陶瓷的悬臂梁能量收集装置的机电耦合方程,选取一阶模态进行分析,采用状态空间法进行时域求解,设计了试验装置,对理论建模进行了验证,对压电材料的发电能力进行了正确预测。
1 压电悬臂梁机电耦合建模 针对典型机翼结构,考虑悬臂梁根部固支,在根部附近上表面粘贴有压电片,悬臂梁稍部施加正弦激励力。为研究方便,采用经典的欧拉梁模型为研究对象。在压电铝梁(见图 1)上取长度为dx的微元(见图 2)进行分析。
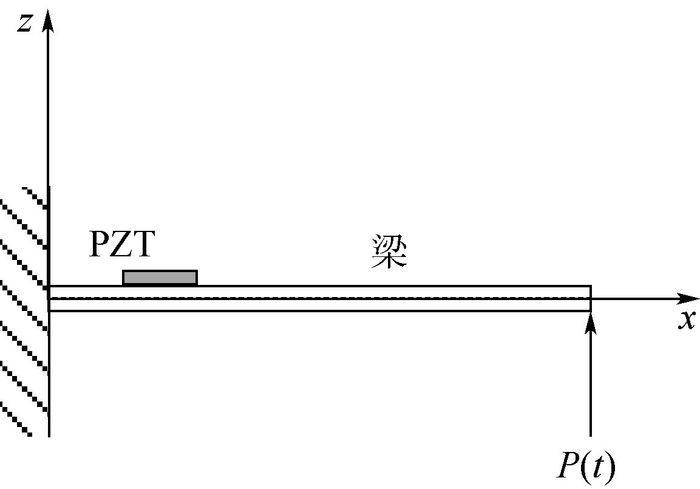 |
| 图 1 粘贴有压电片的欧拉梁示意图 Fig. 1 Schematic diagram of Euler beam with piezoelectric patch |
| 图选项 |
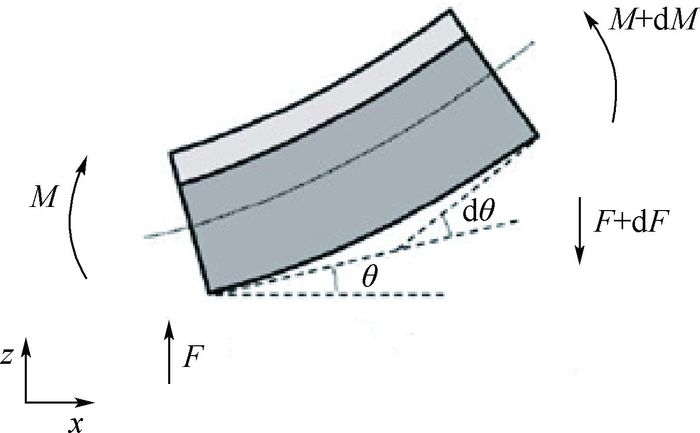 |
| 图 2 dx长度的悬臂梁微元受力分析 Fig. 2 Force analysis of a dx-length cantilever element |
| 图选项 |
图 2中:M为弯矩;F为力;θ为转角。对于该问题,边界条件为一端固支,自由端作用有集中力P(t)。基于欧拉伯努利梁理论假设,忽略重力影响,由振动理论[15]得微元段的力学平衡方程为
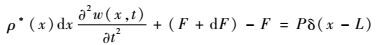 | (1) |
式中:ρ*(x)为压电梁的线密度;Pδ(x-L)表示在x=L处作用有集中力P;w(x, t)为梁的横向弯曲变形。
化简式(1) 得
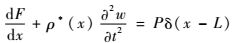 | (2) |
力矩平衡方程为
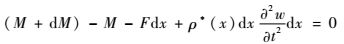 | (3) |
略去二阶小量得
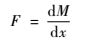 | (4) |
将式(4) 代入式(2) 得到压电悬臂梁振动微分方程为
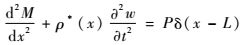 | (5) |
式中:
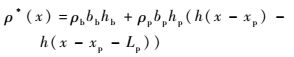 | (6) |
其中:ρb、bb和hb分别为压电悬臂梁基体的密度、宽度和高度;ρp、bp和hp分别为压电片的密度、宽度和高度;xp为压电片纵向位置;Lp为压电片的长度;h(x)为Heaviside函数,函数详细表达式见式(7);h(x-xp)-h(x-xp-Lp)表示压电片分布在xp≤x≤xp+Lp的范围内。
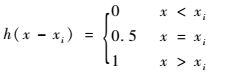 | (7) |
引入e型压电方程[16]:
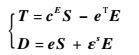 | (8) |
式中:T、D、E和S分别为应力矢量、电位移矢量、电场强度矢量和应变矢量;cE为恒电场条件下测得的弹性常数矩阵;εs为恒应变下测得的介电常数矩阵;e为压电弹性介质的压电应力常数矩阵。
由于31型压电薄片极化方向为3方向,所以E1=E2=0,同时压电片只受1方向的应力,故压电片的压电方程可简化为
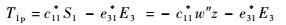 | (9) |
式中:T1p表示压电片上的应力。
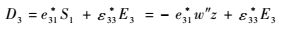 | (10) |
式中:D3为3方向的电位移。
压电悬臂梁的弯矩M可以表示为
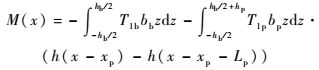 | (11) |
式中:T1b为压电悬臂梁基体的应力,其表达式为
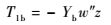 | (12) |
其中:Yb为悬臂梁基体的弹性模量。
把式(9) 代入式(11) 有
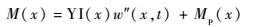 | (13) |
式中:Mp(x)为逆压电效应产生的弯矩;YI(x)为悬臂梁的弯曲刚度。
 | (14) |
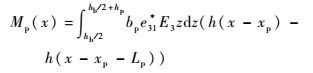 | (15) |
假设场强在压电片极化方向(3方向)均匀分布,则
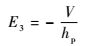 | (16) |
式中:V为电压。
把式(16) 代入式(15) 中有
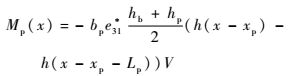 | (17) |
把式(13) 代入式(5) 中有
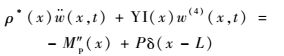 | (18) |
梁的横向位移可以表示为
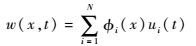 | (19) |
式中:Φi(x)为第i阶固有振型;ui(t)为第i阶振动模态响应。
根据模态振型的正交性质,每阶模态梁的振动方程可以表示为
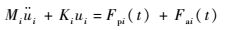 | (20) |
式中:Mi和Ki分别为第i阶模态质量和模态刚度;Fpi(t)为压电片通过逆压电效应产生的作用在机械结构上的模态力;Fai(t)为外部激励模态力。
 | (21) |
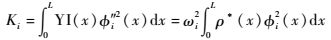 | (22) |
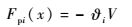 | (23) |
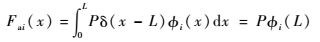 | (24) |
式中:ω为悬臂梁固有振动频率;
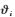
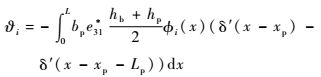 | (25) |
将式(23)、式(24) 代入式(20) 中可得
 | (26) |
对式(10) 沿长度方向积分得
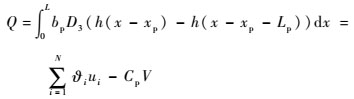 | (27) |
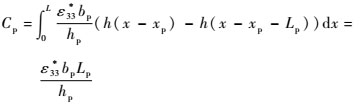 | (28) |
式中:Cp为压电片的电容;Q为由压电效应产生的电荷量。两边对时间求导可得
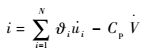 | (29) |
由欧姆定律可知
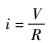 | (30) |
故式(29) 可变为
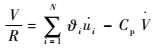 | (31) |
2 数值仿真 第1节推导了压电悬臂梁的机电耦合方程(见式(26) 和式(31)),本节将介绍如何求解该耦合方程。在求解之前先对方程进行简化,考虑到外激励频率一般比较低,因此结构在振动时一阶模态占主导。在研究时只取结构的第一阶模态,即w(x, t)=Φ(x)u(t),这样就将N维问题变为二维问题(见式(32))。
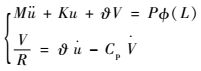 | (32) |
采用MSC.Nastran有限元软件进行模态分析。模态振型关于质量归一化,即M=1, K=ω2。并考虑实际结构阻尼,式(32) 可变为
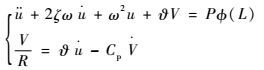 | (33) |
式中:ζ为阻尼比。写为状态空间方程的形式:
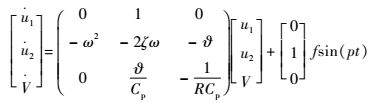 | (34) |
式中:PΦ(L)=fsin(pt)为稍部正弦变化的激振力的广义力形式。利用式(34) 可以在MATLAB中仿真得到正弦激励力下的压电片两端产生电压大小V。
压电悬臂梁结构的相关参数如表 1所示。
表 1 压电悬臂梁和压电片的几何参数及材料性能参数 Table 1 Geometry and material performance parameters of piezoelectric cantilever and piezoelectric patch
| 参数 | 数值 | |
| 铝制悬臂梁 | 压电片(PZT-5) | |
| 长/mm | 533 | 60 |
| 宽/mm | 30 | 30 |
| 高/mm | 5 | 0.5 |
| 弹性模量/GPa | 72 | 61 |
| 泊松比 | 0.3 | 0.35 |
| 密度/(kg·m-3) | 2 700 | 7 500 |
| 压电常数e31*/ (C·m-2) | -11.27 | |
| 电容/nF | 139 | |
表选项
2.1 输出电压随外激励频率变化规律 采用MSC.Nastran软件建立压电片和铝制悬臂梁的有限元模型,通过模态分析计算得到压电悬臂梁结构的一阶频率为15.985 Hz。在仿真分析时,阻尼比取0.03,正弦激励频率范围为10~20 Hz。外接电阻值取1 MΩ,输出电压曲线如图 3所示。可以看出,当外激励频率与压电悬臂梁固有振动频率接近时(15.4 Hz),输出电压达到峰值72.265 4 V。
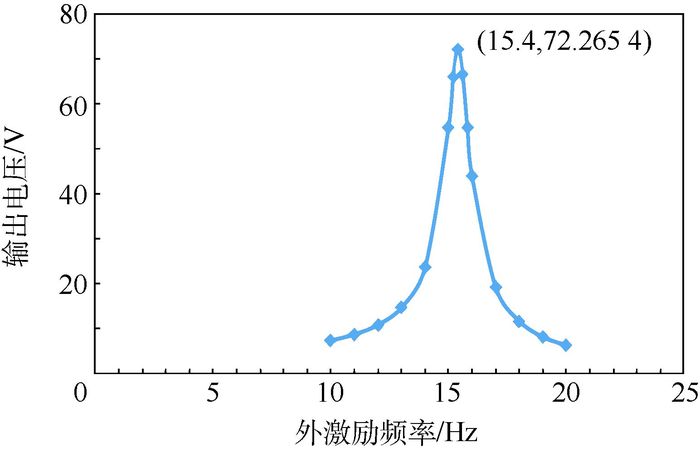 |
| 图 3 给定外接负载下的输出电压-外激励频率曲线 Fig. 3 Output voltage versus excitation frequency curve with given load |
| 图选项 |
2.2 输出电压随外接负载变化规律 2.1节分析了输出电压随外激励频率变化的规律,当激励频率为15.4 Hz时,输出电压达到峰值。本节将给出给定外激励频率下,输出电压随外接负载变化的规律仿真结果。外激励频率取15.4 Hz,外接电阻值范围为100~107 Ω,仿真曲线如图 4所示。可以看出,当外接电阻值达到1 MΩ左右时,输出电压达到最大值。
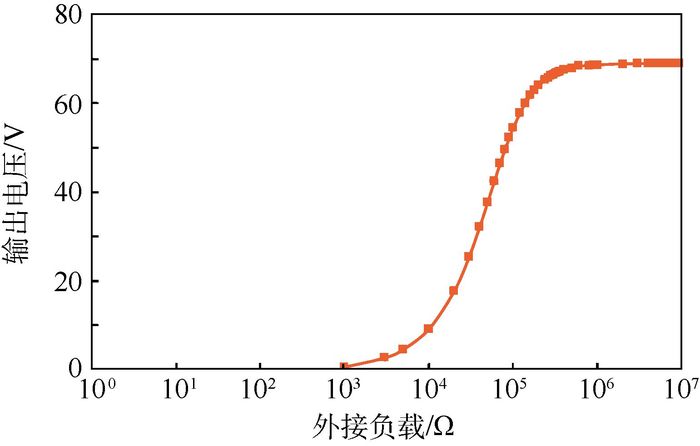 |
| 图 4 给定外激励频率下的输出电压-外接负载曲线 Fig. 4 Output voltage versus load curve withgiven excitation frequency |
| 图选项 |
3 试验验证 试验装置示意图如图 5所示。图中:xf为激振力距根部距离。建立了如图 6所示的试验装置实物图。在梁的根部贴有一片压电片,压电片的极化方向沿梁的厚度方向,在端部用激振器产生正弦激振力。外接可调负载的电阻箱。使用Labview编写采集界面,采用NI数据采集系统采集负载电压、翼尖加速度和激振力。
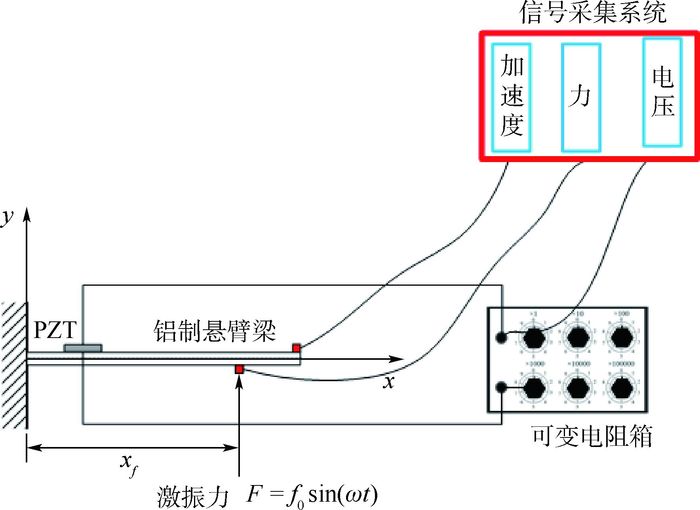 |
| 图 5 试验装置示意图 Fig. 5 Schematic diagram of test equipment |
| 图选项 |
 |
| 图 6 试验装置 Fig. 6 Test equipment |
| 图选项 |
本文分别进行了固定外接负载下不同外激励频率的输出电压试验和固定外激励频率下不同外接负载的输出电压试验,分别对第2节的仿真结果进行验证。
3.1 试验输出电压随外激励频率变化规律 试验时,把变阻箱的阻值调到1 MΩ,之后一直保持不变。改变激振力信号的外激励频率,即可测得不同外激励频率下的输出电压信号,由于NI数据采集系统的电压限制(最大电压为10 V),试验时必须控制输入的激振力幅值,图 7和图 8给出了外激励频率为15.4 Hz时的激振力-时间曲线和输出电压-时间曲线。为了便于试验结果分析,在进行试验数据处理时,将输出电压关于激振力的幅值归一化。试验结果如图 9所示。可以看出,当外激励频率为15.4 Hz时,单位激振力幅值的输出电压幅值约为73.69 V,与理论分析结果吻合很好。
 |
| 图 7 激振力-时间曲线 Fig. 7 Excitation force versus time curve |
| 图选项 |
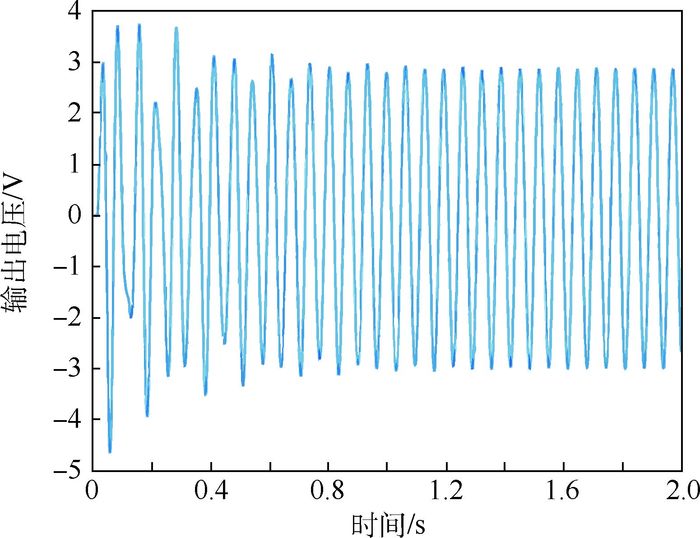 |
| 图 8 输出电压-时间曲线 Fig. 8 Output voltage versus time curve |
| 图选项 |
 |
| 图 9 给定外接负载下的输出电压-外激励频率曲线(试验) Fig. 9 Output voltage versus excitation frequency curve with given load (test) |
| 图选项 |
3.2 试验输出电压随外接负载变化规律 固定激振力的外激励频率为15.4 Hz,改变外接负载的阻值,即可得到不同负载下的输出电压值。试验时,外接负载的取值范围为100~107 Ω,试验结果如图 10所示。可以看出,当外接负载值为1 MΩ时,输出电压达到峰值。
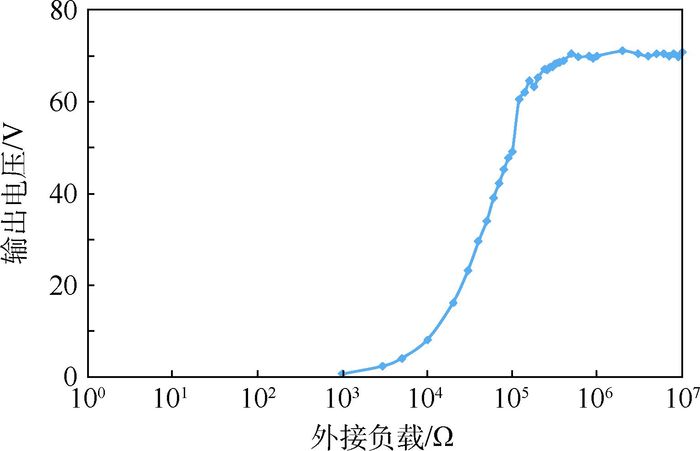 |
| 图 10 给定外激励频率下的输出电压-外接负载曲线(试验) Fig. 10 Output voltage versus load curve withgiven excitation frequency (test) |
| 图选项 |
4 试验结果对比及分析 图 11和图 12给出了仿真结果和试验结果的对比曲线。可以看出,仿真结果和试验结果吻合的非常好,误差小于5%。当外激励频率与压电悬臂梁一阶弯曲频率接近时,能量收集装置的电压达到峰值73 V/N。当外接负载达到1 MΩ以后,能量收集装置的电压达到峰值,且不再发生变化。
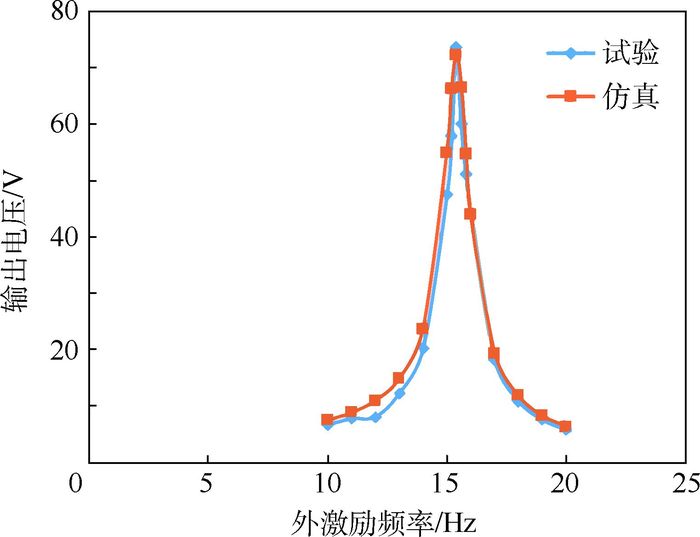 |
| 图 11 给定外接负载下输出电压-外激励频率仿真试验结果对比 Fig. 11 Simulation and test comparison of output voltage versus excitation frequency curve with given load |
| 图选项 |
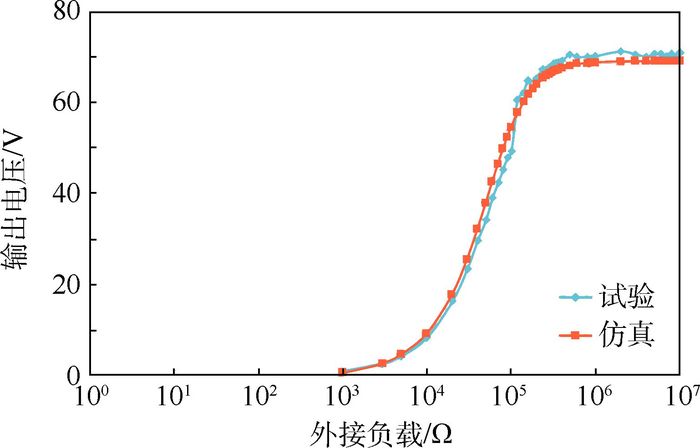 |
| 图 12 给定外激励频率下输出电压-外接负载仿真试验结果对比 Fig. 12 Simulation and test comparison of output voltage versus load curve with given excitation frequency |
| 图选项 |
5 结论 1) 输出电压-外激励频率、输出电压-外接负载仿真结果曲线与试验结果曲线吻合很好,仿真结果与试验结果的误差小于5%,说明压电悬臂梁的双向耦合分布参数的机电耦合模型能较为准确地反映其实际能量收集特性,为后续能量收集工作奠定了基础。
2) 激振器的附加质量和刚度会对系统的固有频率有影响,理论建模中未加以考虑,从而造成仿真结果与试验结果的误差。
3) 当外激励频率与压电悬臂梁一阶弯曲频率接近时,能量收集装置的电压达到峰值73 V/N。当外接负载达到1 MΩ以后,能量收集装置的电压达到峰值,且不再发生变化。
参考文献
| [1] | 王青萍. 基于压电臂梁的振动能量收集器的研究[D]. 武汉: 华中科技大学, 2010: 2-5. WANG Q P.Research on vibration energy harvester based on piezoelectric cantilever[D].Wuhan:Huazhong University of Science and Technology, 2010:2-5(in Chinese). |
| [2] | PRIYA S, INMAN D J. 能量收集技术[M]. 黄见球, 黄庆安, 译. 南京: 东南大学出版社, 2012: 1-100. PRIYA S, INMAN D J.Energy harvesting technologies[M].HUANG J Q, HUANG Q A, translated.Nanjing:Southeast University Press, 2012:1-100(in Chinese). |
| [3] | ARNOLD D. Review of microscale magnetic power generation[J].IEEE Transactions on Magnetics, 2007, 43(11): 3940–3951.DOI:10.1109/TMAG.2007.906150 |
| [4] | MITCHESON P, MIAO P, START B, et al. MEMS electrostatic micro-power generator for low frequency operation[J].Sensors and Actuators A, 2004, 115(2-3): 523–529.DOI:10.1016/j.sna.2004.04.026 |
| [5] | ANTON S R, SODANO H A. A review of power harvesting using piezoelectric materials[J].Smart Materials and Structures, 2007, 16(3): R1–R21.DOI:10.1088/0964-1726/16/3/R01 |
| [6] | JEON Y B, SOOD R, JEONG J H, et al. MEMS power generator with transverse mode thin film PZT[J].Sensors and ActuatorsA, 2005, 122(1): 16–22.DOI:10.1016/j.sna.2004.12.032 |
| [7] | UCHINO K. Piezoelectric actuators 2006[J].Journal of Electroceramics, 2008, 20(3-4): 301–311.DOI:10.1007/s10832-007-9196-1 |
| [8] | ERTURK A, INMAN D J. A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters[J].Journal of Vibration and Acoustics, 2008, 130(4): 41002.DOI:10.1115/1.2890402 |
| [9] | BADEL A, GUYOMAR D, LEFEUVRE E, et al. Piezoelectric energy harvesting using a synchronized switch technique[J].Journal of Intelligent Material Systems and Structures, 2006, 17(8-9): 831–839.DOI:10.1177/1045389X06057533 |
| [10] | STEWART M, WEAVER P M, CAIN M. Charge redistribution in piezoelectric energy harvesters[J].Applied Physics Letters, 2012, 100(7): 073901.DOI:10.1063/1.3685701 |
| [11] | 赵新强. 基于颤振机理的微型压电风致振动能量收集器基础理论与关键技术[D]. 重庆: 重庆大学, 2013: 10-20. ZHAO X Q.Basic theory and key technologies of micro piezoelectric wind-induced-vibration energy harvester based on flutter[D].Chongqing:Chongqing University, 2013:10-20(in Chinese). |
| [12] | WANG Y, INMAN D J. Experimental validation of a multifunctional wing spar design with sensing, harvesting and gust alleviation capabilities[J].IEEE/ASME Transactions on Mechatronics, 2013, 18(4): 1289–1299.DOI:10.1109/TMECH.2013.2255063 |
| [13] | WU Y N, LI D C, XIANG J W. Performance analysis and parametric design of an airfoil-based piezoaeroelastic energy harvester[J].European Journal of Lipid Science & Technology, 2014, 116(9): 1114–1128. |
| [14] | ANTON S R, ERTURK A, INMAN D J. Multifunctional unmanned aerial vehicle wing spar for low-power generation and storage[J].Journal of Aircraft, 2012, 49(1): 292–301.DOI:10.2514/1.C031542 |
| [15] | 方同, 薛璞. 振动理论及应用[M].西安: 西北工业大学出版社, 1998: 200-240. FANG T, XUE P. Vibrancy theory and applications[M].Xi'an: Northwestern Polytechnical University Press, 1998: 200-240.(in Chinese) |
| [16] | 王矜奉, 苏文斌, 王春明, 等. 压电振动理论及应用[M].北京: 科学出版社, 2011: 10-80. WANG J F, SU W B, WANG C M, et al. Theory and application of piezoelectric vibration[M].Beijing: Science Press, 2011: 10-80.(in Chinese) |
