捷联惯性导航系统(SINS)具有不依赖外界信息、抗干扰能力强、隐蔽性好、数据更新率高等优点,但其定位误差会随着时间积累;天文导航系统(CNS)具有导航误差不随时间积累、导航精度高的优点,但其数据更新率低,容易受到天气条件影响[2]。目前,SINS/CNS组合导航系统的组合方式一般可分为简单组合方式和基于最优估计的组合方式[3]。简单组合方式简单、可靠,但精度较低。基于最优估计的组合导航系统主要包括以下2类:① 利用红外地平仪或空间六分仪来直接敏感地平的组合导航系统[4-5],其利用地球敏感器提供的水平基准来获取高度角和方位角,但是由于地表的模糊性使得地平仪提供的水平基准精度较低,这与高精度的星敏感器不能相互匹配,从而影响了导航精度;② 基于校正陀螺漂移的SINS/CNS组合导航系统[6-7],其利用星敏感器高精度的测姿特性来修正陀螺漂移,仅对陀螺漂移引起的姿态误差有较好的修正效果,对加速度计偏置不能准确估计,因而不能有效地抑制速度和位置误差的发散。
基于星光折射间接敏感地平方法利用高精度的星敏感器测量星光折射角,通过大气折射模型及其误差补偿方法来间接测得地平信息,有效解决了低精度的地平基准问题,从而提高了导航精度[8-9]。星光折射间接敏感地平方法已经成为国内外****的研究热点,目前该方法已经开始应用到基于轨道动力学模型的航天器上[10-11]。但就目前的文献显示,在星光折射的研究中很少有分析折射星数目与导航精度的关系,事实上,二者之间存在着紧密的联系。
本文将星光折射间接敏感地平方法引入到SINS/CNS组合导航系统中,组成捷联惯性/天文(SINS/RCNS)组合导航系统,并将其应用于弹道导弹。在SINS/RCNS组合导航系统中,利用星光折射间接敏感地平方法获取高精度的地平信息,把根据折射得到的折射视高度引入到系统的量测中,修正了由加速度计偏置引起的导航误差;当使用多颗折射星时能够完全抑制位置误差的发散,满足了弹道导弹对射击精度的要求。
1 折射导航原理 根据大气的光学特性,星光通过地球的大气层时会发生折射。折射后的光线向地心方向弯曲,从而导致恒星的视位置比其真实位置偏高。如图 1所示,弹载星敏感器上观测到的折射光线相对于地球的折射视高度为ha,而实际上其在距离地面一个略低的折射高度hg,折射光线与未折射前星光方向间的夹角R为星光折射角。图 1中:Re为地球半径;r为导弹在地心惯性坐标系下的位置矢量;u为折射前的星光在地心惯性坐标下的单位矢量。r和u可表示为
 | (1) |
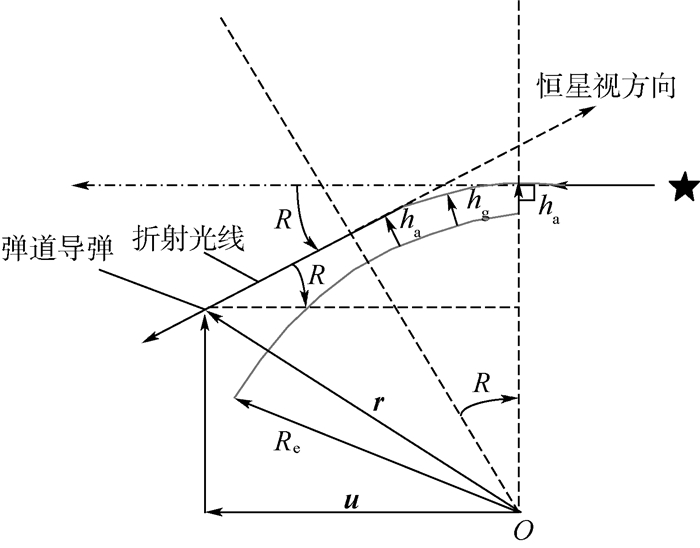 |
| 图 1 星光折射原理图 Fig. 1 Schematic diagram of starlight refraction |
| 图选项 |
式中:r=[x y z]T为导弹的位置矢量在地心惯性坐标系中的坐标;u=[sx sy sz]T为折射前星光的单位方向矢量在地心惯性坐标中的坐标,在恒星识别成功后可查星表得出。
SINS/RCNS组合导航系统需要2个星敏感器分别用来观测折射星和导航星。如图 2所示,一个星敏感器对准不发生折射的导航星,通过观测结果确定未折射的星光矢量在载体坐标系下的坐标P1和导弹姿态信息;另一个星敏感器对准折射星,由观测值可确定折射前后的星光矢量在载体坐标系中的坐标P3、P2。由P1和P2可得到两恒星星光之间的角距θ2,其与由恒星星历查得的标称值θ1不同,二者之差即为星光折射角R。
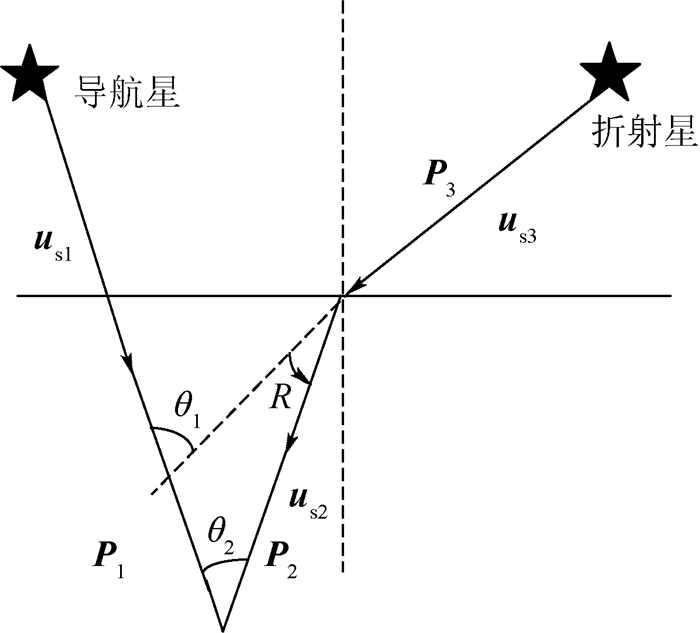 |
| 图 2 星光折射角的计算 Fig. 2 Calculation of starlight refraction angle |
| 图选项 |
得到星光折射角R后,根据图 1中的几何关系可得
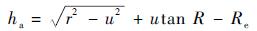 | (2) |
式(2) 反映了导弹与地球之间的位置关系,可以利用其修正因加速度计偏置导致的导航误差,抑制了导航误差的发散。
通过大气折射模型也可得到折射视高度的估计值,本文采用文献[12]提出的大气折射模型进行理论研究,其是在美国标准大气提供的数据的基础上建立了一个在高度20~50km连续变化的星光大气观测模型。
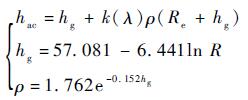 | (3) |
式中:hac为折射视高度的估计值,km;hg为折射高度,km;λ=0.7μm为光波波长;k(λ)=2.2517×10-7为散射系数,其只与光波的波长λ有关;ρ为大气密度,kg/m3;R为星光折射角,(″)。当高度大于20 km时,k(λ)ρ < 2×10-3。由于Rehg,可得hac≈hg+k(λ)ρRe
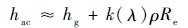 | (4) |
综合式(3)、式(4) 可得折射视高度估计值与星光折射角之间的关系为
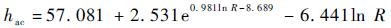 | (5) |
如果可以获取星光折射角,其对应的折射视高度估计值可由式(5) 计算得出。由式(2) 可以看出,折射视高度ha是导弹在地心惯性坐标系下位置矢量r的函数。因此,在现有的研究中常把折射视高度作为系统的量测变量[13]。
2 弹道导弹SINS/RCNS组合导航系统建模 2.1 系统的状态方程 本文所采用的状态方程是现有的建立在发射点惯性坐标系上的状态方程[14]:
 | (6) |
式中:F为状态转移矩阵;G为噪声驱动矩阵;状态变量X=[?x,?y,?z,δvx,δvy,δvz,δxc,δyc,δzc,εcx,εcy,εcz,▽cx,▽cy,▽cz]T分别代表平台失准角、相对于发射点惯性坐标系的速度误差、位置误差、陀螺常值漂移和加速度计常值偏置;系统噪声矩阵为w=[εsx, εsy, εsz, ▽sx, ▽sy, ▽sz]T,εsx、εsy、εsz为陀螺仪随机漂移,▽sx、▽sy、▽sz为加速计随机偏置。
2.2 系统的量测方程 SINS/RCNS组合导航系统量测方程由3部分组成,分别为姿态误差量测、位置误差量测和折射视高度误差量测。
2.2.1 姿态误差量测 姿态误差角为惯性导航系统输出的导弹相对于地心惯性坐标系的姿态角与星敏感器输出的相应姿态角之差。
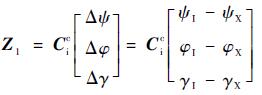 | (7) |
式中:Z1为姿态误差量测;Δψ、Δφ和Δγ为姿态误差角;ψI、φI和γI分别为由惯性导航系统输出的导弹在地心惯性坐标系中的航向角、俯仰角和横滚角;ψX、φX和γX分别为由星敏感器输出在地心惯性坐标系中相应的姿态信息;Cic为地心惯性坐标系到发射点惯性坐标系的姿态转换矩阵。θ和L分别为发射点的经度和纬度,A为发射角,则Cic可表示为
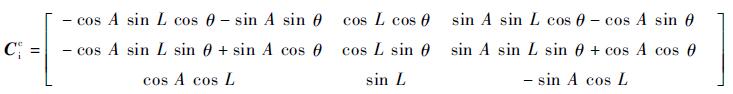 |
式(7) 中计算采用的是姿态误差角,而式(6) 中使用的是平台失准角。在以往的组合导航研究中,常常将姿态误差角视为平台误差角,但实际上二者并不是完全相同而有微小差别。应用到对导航精度要求高的载体时,计算时需要将二者区分开。本文采用文献[15]的方法来计算姿态误差角和平台失准角之间的关系,并对姿态误差角作泰勒公式展开处理,进而得到姿态误差量测的线性方程。具体关系如下:
 | (8) |
式中:Cbn为载体坐标到导航坐标系的转换矩阵。
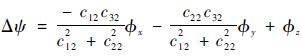 | (9) |
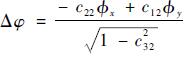 | (10) |
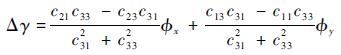 | (11) |
可得姿态误差角的量测方程为
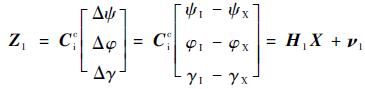 | (12) |
式中:H1为姿态误差量测矩阵;ν1为星敏感器的测量误差。
2.2.2 位置误差量测 位置误差为惯性导航系统输出的导弹在地心惯性坐标系中的位置矢量与天文导航系统输出的相应的位置矢量之差。
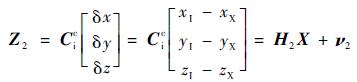 | (13) |
式中:H2为位置误差量测矩阵;rI=[xIyIzI]T为惯性导航系统输出的导弹在地心惯性坐标系中的位置矢量;rX=[xXyXzX]T为天文导航系统输出其在地心惯性坐标系中位置矢量;ν2为量测噪声。
2.2.3 折射视高度误差量测 由式(1)、式(2) 可知,r和u都包含着与地球位置相关的参数,因此它们必然包括惯性元件所积累的位置误差。式(5) 是一个经验公式,假定折射视高度的误差为νa,则真实高度hat可表示为
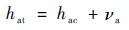 | (14) |
影响大气折射模型精度的最主要因素是大气密度。文献[16]指出,可以将平流层大气密度随纬度和季节变化的部分进行修正,有可能使平流层大气密度的估计误差小于1%,假定25km处的大气密度误差为1%(1σ),则1%(1σ)的密度误差和1%(1σ)折射量测误差引起的折射视高度的误差为76m。νa是由大气密度误差和量测误差引起的视高度误差,根据文献[16]中折射视高度误差计算公式可得νa=76m,可近似认为是均值为0、方差为E(νaνaT)=762m2的高斯白噪声。折射视高度误差可表示为
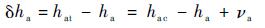 | (15) |
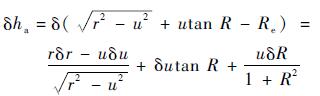 | (16) |
本文选用的导航坐标系为发射点惯性坐标系,式(16) 中导弹位置矢量所包含的参数都来自地心惯性坐标系,因此需要将地心惯性坐标系下的位置参数转换到发射点惯性坐标系。rc=[xc yc zc]T,r=[x y z]T分别表示导弹在发射点惯性坐标系和在地心惯性坐标系下的位置矢量,则二者之间存在如下关系:
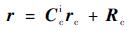 | (17) |
式中:Rc=[Rcx Rcy Rcz]T为发射点子午圈曲率半径在地心惯性坐标系中的投影;Cci=(Cic)T,同时令
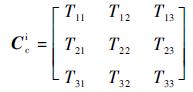 | (18) |
将式(18) 代入式(17) 可得
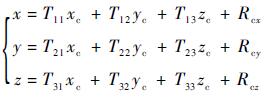 | (19) |
对式(19) 微分得到导弹的位置误差为
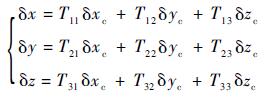 | (20) |
同样的,可以得到δr和δu。令l=
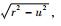
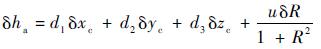 | (21) |
式中:
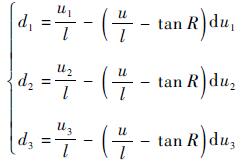 |
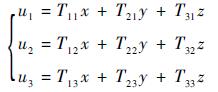 |
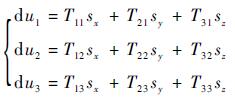 |
基于星光折射的量测方程为
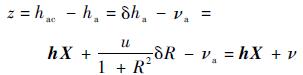 | (22) |
式中:h为使用一颗折射星时的量测矩阵;ν=
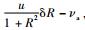
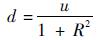 | (23) |
将式(23) 代入式(22) 得
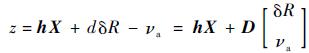 | (24) |
式中:D=[d -1]。
式(24) 等号两边同时乘以D-1得
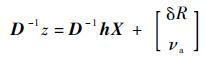 | (25) |
式中:D-1=DT(DDT)-1, 为广义逆矩阵。
定义z*=D-1z,h*=D-1h,ν*=[δR νa]T,可得折射视高度新的量测方程为
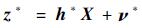 | (26) |
很明显,ν*是零均值高斯白噪声,满足了卡尔曼滤波方程对噪声的要求。当使用多颗折射星时,量测方程为
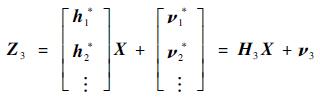 | (27) |
式中:H3和ν3分别为使用多颗折射星时量测矩阵和量测噪声。
综合式(7)、式(8) 以及式(27) 可得,组合导航系统总的量测方程为
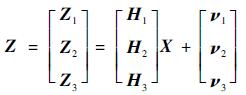 | (28) |
导航星识别成功之后,可以得到导弹的姿态信息及其星光矢量在载体坐标系中的位置矢量P1;折射星识别成功之后,可由三视场星敏感器输出折射星发生折射前后的星光矢量在载体坐标系中的位置矢量P3和P2。同时,根据星表可以得到折射前星光的单位矢量u,根据P1、P2可得到星光折射角R,根据R、r、u可得折射视高度。通过卡尔曼滤波对系统状态进行估计,并利用结果对捷联惯导进行修正。组合导航系统工作原理如图 3所示。
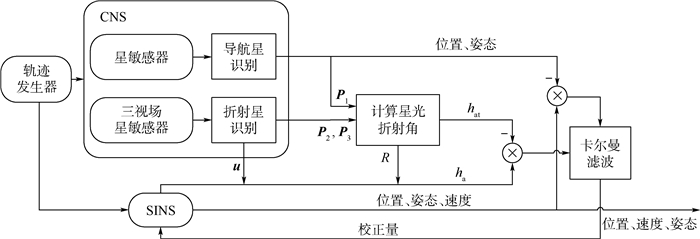 |
| 图 3 SINS/RCNS组合导航系统工作原理 Fig. 3 Operating principle of SINS/RCNS integrated navigation system |
| 图选项 |
2.3 系统的可观测性分析 系统状态的可观测程度决定着卡尔曼滤波的精度。因此,在模型建立之后对其进行可观测性分析是十分必要的。由式(6) 和式(28) 可知,本文构建的模型是线性系统,针对这种系统,Goshen-Meskin和Bar-Izhack[18-19]提出了线性定长系统可观测性分析定理(PWCS)来分析线性系统可观测状态的数目。根据PWCS,通过分析条带化可观测矩阵(SOM)的秩,可以得到状态矩阵中可观测状态的数目。表 1为使用不同数目折射星时SOM秩的变化。当使用折射星数目为0时,即为传统的基于校正陀螺漂移的SINS/CNS组合导航方法。随机在导弹飞行过程中选取3个时间段:180~180.5s(Ⅰ)、212~212.5s(Ⅱ)、284~284.5s(Ⅲ)。
表 1 使用不同数目折射星时对系统可观测性的影响 Table 1 Influence of using different numbers of refraction star on system observability
| 使用的折射星数目 | SOM秩 | ||
| Ⅰ时间段 | Ⅱ时间段 | Ⅲ时间段 | |
| 0 | 6 | 6 | 6 |
| 1 | 11 | 11 | 11 |
| 2 | 14 | 14 | 14 |
| 3 | 15 | 15 | 15 |
| 4 | 15 | 15 | 15 |
| 5 | 15 | 15 | 15 |
| 6 | 15 | 15 | 15 |
表选项
由表 1可知,随着使用折射星数目的增加,系统SOM的秩也在增加,说明系统的可观测性在不断增强。同时也能得出,当使用的折射星数目超过3颗时,SOM满秩,此时系统完全可观测。本文方法中,由于折射星的使用能够使系统的可观测性明显增强,当使用的折射星数目多于3颗时,系统完全可观测,卡尔曼滤波方程能够获得足够的状态信息,从而准确地估计加速度计偏置,导航精度将会得到很大提高。
3 仿真与分析 仿真初始条件:发射点坐标(116.34°E、39.98°N),垂直发射,仿真时间1100s,导弹飞出大气层时间为80s,发动机关机时间为160s;陀螺常值漂移和测量白噪声标准差分别为1(°)/h和0.5(°)/h;加速度计常值偏置和白噪声标准差分别为100μg和50μg。星敏感器在导弹飞出大气层后开始工作,由于恒星在天球上分布是不均匀的,而且在星图识别之前还要剔除双星、暗星等不符合要求的星,这可能得不到满足本文方法所需要的折射星数目,由PWCS可知,这会影响到系统的导航精度。为了获取足够的折射星,仿真实验中选用的星敏感器为三视场星敏感器,假定每个视场大小为40°,星敏感器精度为10″(1σ),星等敏感极限为7Mv。
图 4为本文方法与传统的基于校正陀螺漂移的SINS/CNS组合导航方法的姿态误差对比。图 5为使用1颗折射星时本文方法与传统组合导航方法位置误差比较。图 6为使用1颗折射星时本文方法各方向加速度计偏置的估计。
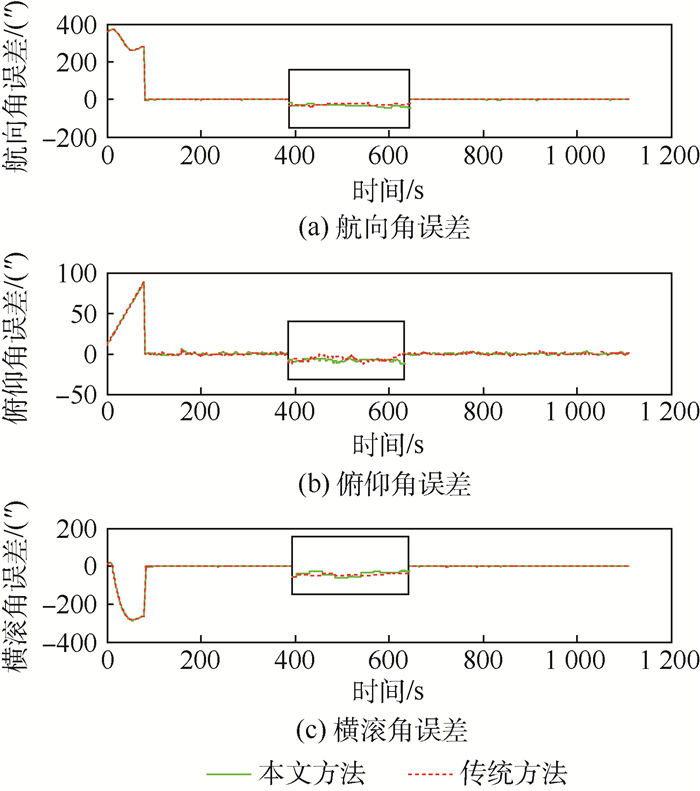 |
| 图 4 本文SINS/RCNS组合导航方法与传统SINS/CNS组合导航方法姿态误差对比 Fig. 4 Attitude error contrast between SINS/RCNS integrated navigation method and traditional SINS/CNS integrated navigation method |
| 图选项 |
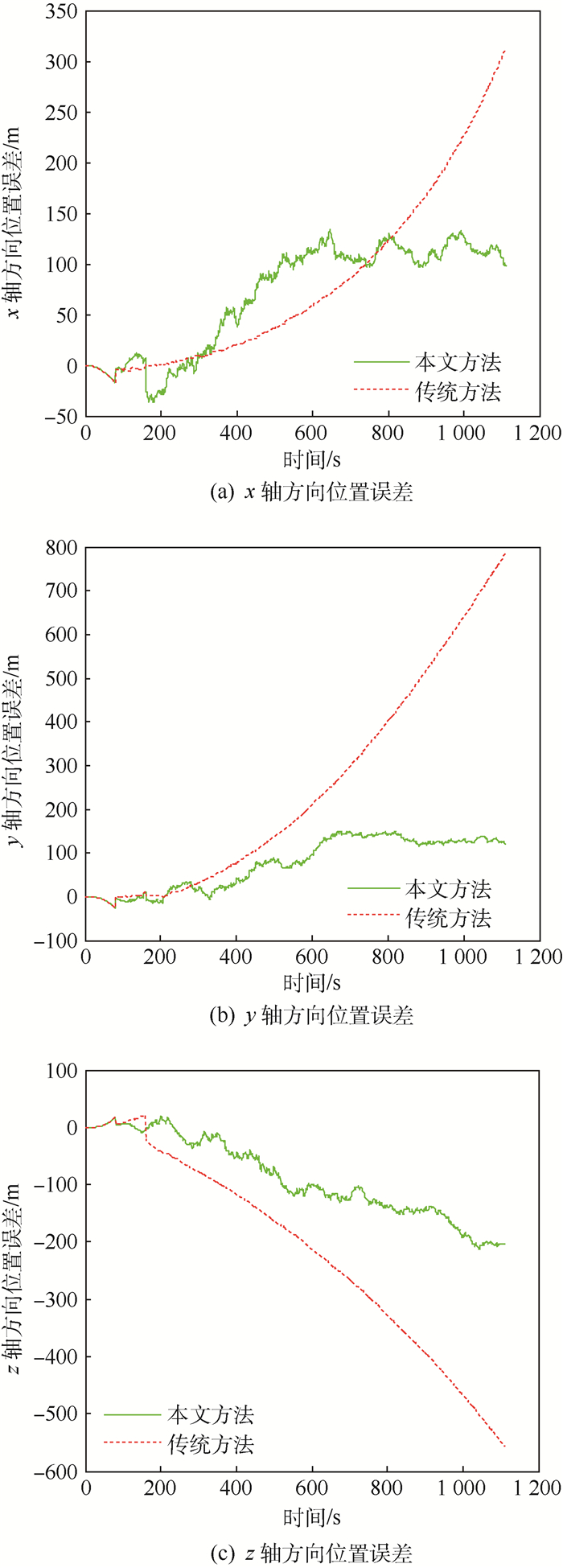 |
| 图 5 使用1颗折射星时本文SINS/RCNS组合导航方法与传统SINS/CNS组合导航方法比较 Fig. 5 Contrast between SINS/RCNS integrated navigation method by using one refraction star and traditional SINS/CNS integrated navigation method |
| 图选项 |
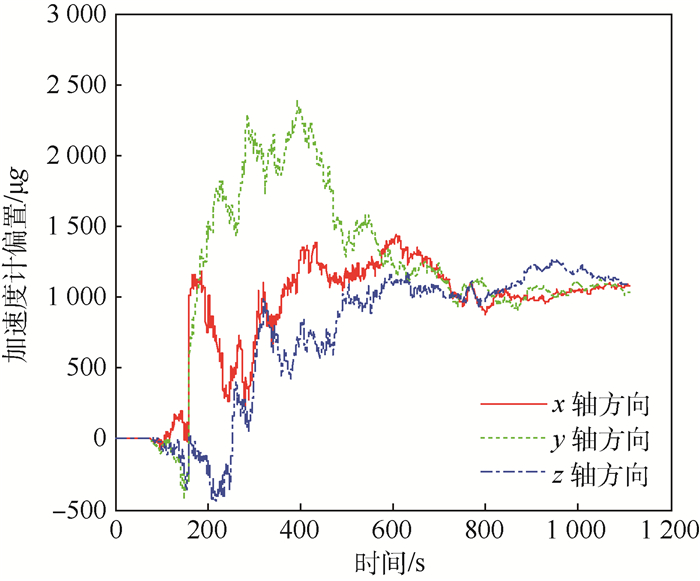 |
| 图 6 使用本文SINS/RCNS组合导航方法时加速度计偏置估计 Fig. 6 Estimation of accelerometer bias when using SINS/RCNS integrated navigation method |
| 图选项 |
仿真结果表明,本文方法与传统的基于校正陀螺漂移的SINS/CNS组合导航方法相比,二者姿态误差基本相同,继承了星敏感器高精度的测姿特性;由于传统方法不能准确地估计加速计偏置,导致了位置误差随着时间的推移而发散,本文方法因为折射星的使用使得量测方程中增加了与位置相关的折射视高度,增加了状态量的可观测数目,从而能够抑制位置误差的发散。图 5表明,当使用1颗折射星时,SINS/RCNS组合导航系统能在一定程度上抑制位置误差的发散,但仍不能彻底阻止其发散。这是因为仅使用1颗折射星时,不能彻底估计加速度计偏置,这与图 6的结果相一致。图 6表明,当使用1颗折射星时,本文方法能够在一定程度上估计加速计的偏置,但并不能精确估计其偏置,这是因为使用1颗折射星时系统不是完全可观测的。表 2为使用不同数目折射星时根据仿真结果得到的位置误差的均值与方差。
表 2 使用不同数目折射星时导航误差统计结果 Table 2 Navigation error statistical results when different numbers of refraction star are used
| 使用的折射星数目 | x轴位置误差/m | y轴位置误差/m | z轴位置误差/m | |||
| 均值 | 方差 | 均值 | 方差 | 均值 | 方差 | |
| 1 | 99.2 | 68.7 | 106.8 | 72.4 | -106.3 | 82.4 |
| 2 | 91.1 | 53.8 | 98.3 | 42.7 | -98.4 | 61.4 |
| 3 | 83.7 | 27.3 | 88.5 | 22.8 | -82.4 | 21.6 |
| 4 | 80.4 | 22.6 | 82.7 | 21.9 | -80.2 | 19.6 |
| 5 | 79.2 | 21.9 | 81.6 | 18.6 | -81.2 | 20.1 |
| 6 | 78.8 | 19.5 | 79.4 | 19.9 | -79.8 | 19.8 |
| 7 | 78.6 | 18.9 | 78.7 | 18.7 | -77.3 | 20.8 |
表选项
从表 2可得,导航精度随着使用折射星数目的增加而提高。折射星数目由1个增加到3个的过程中,导航精度都有较大提高。但当使用折射星数目多于3颗时,导航误差在不断减小直至趋于稳定,但变化幅度较小,这与可观测性分析结果一致。作为高速运载体,实时性是弹道导弹的一个重要技术指标,使用过多数目的折射星会带来额外的星图识别步骤和其他相关计算,这会给高速飞行的导弹带来影响。结合2.3节结论,在SINS/RCNS组合导航中,选择3颗折射星进行导航是比较理想的方案。
4 结论 1) 本文方法在姿态误差方面与传统的SINS/CNS组合导航方法相近,说明其继承了星敏感器测姿的高精度特性,有着良好的测姿精度。
2) 在位置误差方面,当使用1颗折射星时,本文方法较传统方法抑制了误差的发散,导航精度得到了一定的提高,但仍不能完全抑制位置误差的发散;使用3颗及3颗以上折射星时,系统的状态完全可观测,此时完全抑制了位置误差的发散,导航精度得到了很大提高。说明本文方法能有效解决对加速度计偏置估计的问题。
3) 本文选用的星敏感器的视场是为了验证方法的优越性而假定的理想模型,同时受到星敏感器技术和星图识别技术的限制,导弹在实际飞行过程中无法一直观测到3颗折射星。因此,在SINS/RCNS工程实际应用、少于3颗折射星情况的处理、星敏感器视场对选星的限制等方面还需要做进一步的研究。
参考文献
| [1] | 吕沧海, 冯艳, 师海涛. 中远程导弹组合导航技术[M].北京: 国防工业出版社, 2014: 1-3. LV C H, FENG Y, SHI H T. Middle-long-range missile integrated navigation technology[M].Beijing: National Defense Industry Press, 2014: 1-3.(in Chinese) |
| [2] | 全伟, 刘百奇, 宫晓琳, 等. 惯性/天文/卫星组合导航技术[M].北京: 国防工业出版社, 2011: 1-2. QUAN W, LIU B Q, GONG X L, et al. INC/CNS/GNSS integrated navigation technology[M].Beijing: National Defense Industry Press, 2011: 1-2.(in Chinese) |
| [3] | 王鑫, 王新龙. 弹道导弹SINS/CNS组合导航系统建模与性能仿真[J].航空兵器, 2015(2): 21–25. WANG X, WANG X L. System modeling and performance simulation on SINS/CNS integrated navigation system for ballistic missile[J].Aero Weaponry, 2015(2): 21–25.(in Chinese) |
| [4] | YANG L H, LI B, GE L. A novel SINS/CNS integrated navigation algorithm used in a ballistic missile[J].International Journal of Security and Its Applications, 2015, 9(9): 65–76.DOI:10.14257/ijsia |
| [5] | 张承, 熊智, 王融, 等. 直接敏感地平的空天飞行器惯性/天文组合方法[J].中国空间科学技术, 2013, 33(3): 64–71. ZHANG C, XIONG Z, WANG R, et al. New INS/CNS integrated algorithm on aerospace vehicle with directly sensing horizon[J].Chinese Space Science and Technology, 2013, 33(3): 64–71.(in Chinese) |
| [6] | JAMSHAID A, FANG J C. Realization of an autonomous integrated suite of strap-down astro-inertial navigation systems using unscented particle filtering[J].Computers and Mathematics with Applications, 2009, 57(2): 169–183.DOI:10.1016/j.camwa.2008.07.042 |
| [7] | QUAN W, FANG J C, XU F, et al. Hybrid simulation system study of SINS/CNS integrated navigation[J].IEEE Aerospace & Electronic Systems Magazine, 2008, 23(2): 17–24. |
| [8] | WANG X L, MA S. A celestial analytic positioning method by stellar horizon atmospheric refraction[J].Chinese Journal of Aeronautics, 2009, 22(3): 293–300.DOI:10.1016/S1000-9361(08)60102-8 |
| [9] | NING X L, FANG J C. A new autonomous celestial navigation method for the lunar rover[J].Robotics and Autonomous Systems, 2009, 57(1): 48–54.DOI:10.1016/j.robot.2008.02.006 |
| [10] | QIAN H M, SUN L, CAI J N, et al. A starlight refraction scheme with single star sensor used in autonomous satellite navigation system[J].Acta Astronautica, 2014, 96(1): 45–52. |
| [11] | 宁晓琳, 王龙华, 白鑫贝, 等. 一种星光折射卫星自主导航系统方案设计[J].宇航学报, 2012, 33(11): 1601–1610. NING X L, WANG L H, BAI X B, et al. A scheme design of satellite autonomous navigation system based on stellar refraction[J].Journal of Astronautics, 2012, 33(11): 1601–1610.DOI:10.3873/j.issn.1000-1328.2012.11.007(in Chinese) |
| [12] | WANG X L, XIE J, MA S. Starlight atmospheric refraction model for a continuous range of height[J].Journal of Guidance, Control, and Dynamics, 2010, 33(2): 634–637.DOI:10.2514/1.39499 |
| [13] | NING X L, WANG L H, BAI X B, et al. Autonomous satellite navigation using starlight refraction angle measurements[J].Advances in Space Research, 2013, 51(9): 1761–1772.DOI:10.1016/j.asr.2012.12.008 |
| [14] | XU F, FANG J C. Velocity and position error compensation using strap-down inertial navigation system/celestial navigation system integration based on ensemble neural network[J].Aerospace Science & Technology, 2008, 12(4): 302–307. |
| [15] | 宁晓琳, 蔡洪炜, 吴伟仁, 等. 月球车的惯性/天文组合导航新方法[J].系统工程与电子技术, 2011, 33(8): 1837–1844. NING X L, CAI H W, WU W R, et al. INS/CNS integrated navigation method for lunar rover[J].Systems Engineering and Electronics, 2011, 33(8): 1837–1844.(in Chinese) |
| [16] | 房建成, 宁晓琳. 天文导航原理及应用[M].北京: 北京航空航天大学出版社, 2006: 185-190. FANG J C, NING X L. Principle and application of celestial navigation[M].Beijing: Beihang University Press, 2006: 185-190.(in Chinese) |
| [17] | 秦永元, 张洪钺, 汪淑华. 卡尔曼滤波与组合导航原理[M].西安: 西北工业大学出版社, 2012: 80-84. QIN Y Y, ZHANG H Y, WANG S H. Kalman filter and principle of integrated navigation[M].Xi'an: Northwestern Polytechnical University Press, 2012: 80-84.(in Chinese) |
| [18] | GOSHEN-MESKIN D, BAR-IZHACK I Y. Observability analysis of piece-wise constant system-PartⅠ:Theory[J].IEEE Transactions on Aerospace and Electronics Systems, 1992, 28(4): 1056–1067.DOI:10.1109/7.165367 |
| [19] | GOSHEN-MESKIN D, BAR-IZHACK I Y. Observability analysis of piece-wise constant system-PartⅡ:Application to inertial navigation in-flight alignment[J].IEEE Transactions on Aerospace and Electronics Systems, 1992, 28(4): 1068–1075.DOI:10.1109/7.165368 |
