1948年,Taylor[3]率先提出了Taylor测试的基本原理,他利用圆柱形子弹撞击刚性靶板,通过子弹的最终变形获得了材料高应变率状态下的力学特性。同年,Whiffin[4]利用该方法对多种金属材料进行了试验分析,通过子弹的最终变形得到了材料动态屈服强度,此后多名****对Taylor模型进行了改进。例如,Hawkyard[5]利用能量守恒的办法代替动量定理对塑性波前进行了分析,得到的子弹变形模式比Taylor模型更加接近于试验结果。Jones等[6-7]同时也分析了应变率和应变强化效应对Taylor撞击结果的影响。另外还有不少****对Taylor测试进行了有限元仿真分析[8-10]。
除了金属材料,Taylor撞击还广泛用于测试聚合物[11-12]和泡沫材料[13-14]的动态力学性能,Lu等[13-14]是较早对多孔材料的Taylor撞击进行理论和试验研究的,他们通过多孔材料的压缩试验,指出压缩过程中密度与压缩应变呈线性关系,但这种线性关系只适用于压缩应变较小的情形。在本文中,通过引入多孔材料的塑性泊松比,对多孔泡沫材料压缩过程中的密度变化进行了详细推导,当塑性泊松比为常数时,密度表达式的一阶泰勒展开式可以退化到Lu等[13]的分析结果,当塑性泊松比为塑性应变和相对密度的函数时,本文进一步分析了泡沫材料相对密度对Taylor撞击响应的影响。
1 问题描述及基本方程 假设一个圆柱体泡沫子弹以初速度U撞击刚性靶板,撞击过程可分为3个阶段,图 1给出了撞击前、撞击中间阶段及子弹的最终变形。如图 1(a)所示,假设子弹的初始长度为L0,截面面积为A0,子弹为理想刚塑性材料,屈服应力σY,同时假设泡沫子弹的直径远大于孔隙直径,子弹可看作连续介质。当子弹撞击刚性靶板时,在撞击面上形成的塑性波立刻以速度v向子弹的自由端传播,如图 1(b)所示,塑性波前到达的区域立刻进入屈服,截面面积由A0变为A,子弹的密度由ρ0变为ρ,u为未变形区域的速度,z和h分别为未变形和变形区域的长度。如图 1(c)所示,撞击结束时子弹未变形和变形区域的长度分别为Z和H,Lf为子弹的总长度。
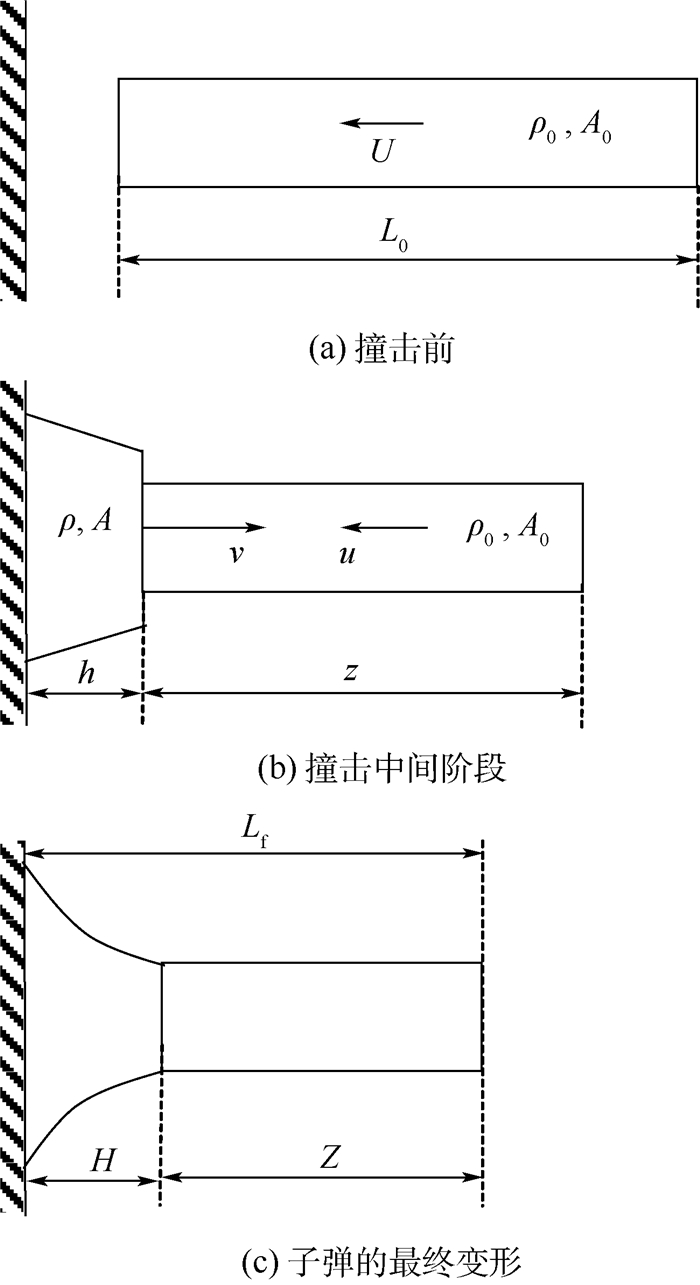 |
| 图 1 圆柱体泡沫子弹撞击刚性靶板前、撞击中间阶段及子弹的最终变形 Fig. 1 A cylindrical porous projectile striking on a rigid anvil before impact, in intermediate stage of deformation, and in final stage of deformation |
| 图选项 |
与Taylor模型一致,可得
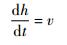 | (1) |
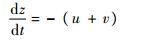 | (2) |
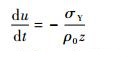 | (3) |
式中:t为时间。
由质量守恒可得连续方程:
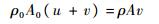 | (4) |
在塑性波前截面上,由冲量定理可得
 | (5) |
假设沿撞击方向有限长度dl0发生塑性变形后长度变为dl,截面面积由A0变为A,则变形前后的体积分别为
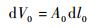 | (6) |
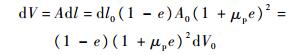 | (7) |
子弹压缩前后密度比可以写为
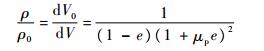 | (8) |
式中:V0为变形前的体积;V为变形后的体积;μp为塑性泊松比;e为塑性应变,其定义为
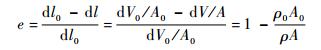 | (9) |
引入无量纲量:
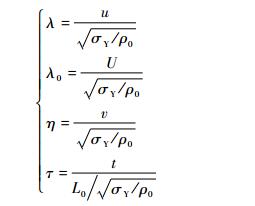 | (10) |
式中:λ和λ0分别为子弹未变形区域的无量纲瞬时速度及初始速度;η为塑性波前的无量纲速度,其初始值为η0;τ为无量纲时间。
1.1 子弹未变形区域的速度 联立式(4)和式(5)并将式(9)代入可得
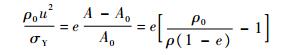 | (11) |
将式(8)和式(10)代入式(11)可得
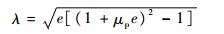 | (12) |
1.2 子弹未变形区域的长度 式(2)与式(3)相除得
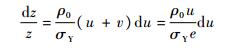 | (13) |
对式(11)两边求导,并将式(13)代入得
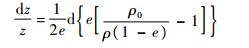 | (14) |
在子弹撞击刚性平面瞬时,子弹具有最大应变e0,将式(8)代入式(14),两端积分可得未变形区域长度z与应变e的关系:
 | (15) |
当撞击结束时,应变e=0,可以得到未变形区域的最终长度Z为
 | (16) |
1.3 子弹塑性变形区域的长度 式(1)与式(2)相除可得
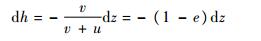 | (17) |
式(17)两边同除以L0可得
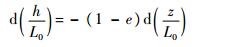 | (18) |
令式(15)中
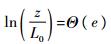
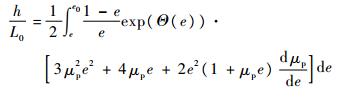 | (19) |
撞击结束时,应变e=0,此时可得塑性变形区的最终长度H为
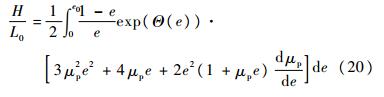 | (20) |
撞击结束时,Lf等于未变形区域和塑性变形区域的长度之和:
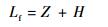 | (21) |
1.4 撞击持续时间 由式(3)和式(10)可得
 | (22) |
将式(12)和式(15)代入式(22),并结合初始条件τ=0时e=e0,两边积分得
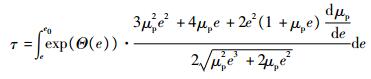 | (23) |
在撞击结束时e=0,代入到式(23)可以得到撞击持续时间τf:
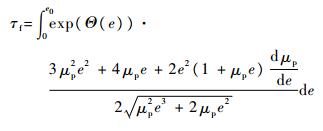 | (24) |
2 压缩密度比的退化 2.1 压缩密度比的一阶泰勒展开 由式(8),可得到压缩密度比的一阶泰勒展开式:
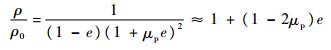 | (25) |
Lu等[14]通过多孔材料试验,认为子弹的压缩密度比与应变e满足
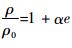
将式(25)代替式(8),类似推导可得到子弹未变形区域的无量纲瞬时速度λ、子弹未变形区域和变形区域的最终长度Z和H,以及无量纲撞击持续时间τf如下:
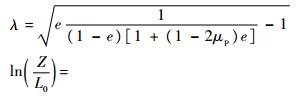 | (26) |
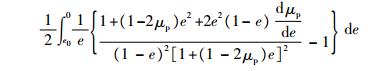 | (27) |
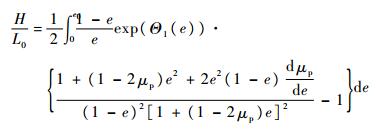 | (28) |
 | (29) |
式中:
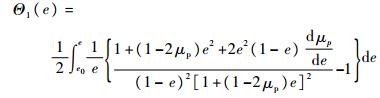 | (30) |
当μp为常数时,
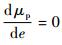
2.2 压缩密度比的二阶泰勒展开 由式(8),也可得到压缩密度比的二阶泰勒展开式:
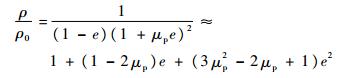 | (31) |
与2.1节类似,用式(31)代替式(8),得到的冲击响应结果为
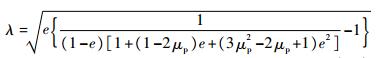 | (32) |
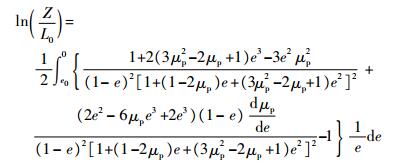 | (33) |
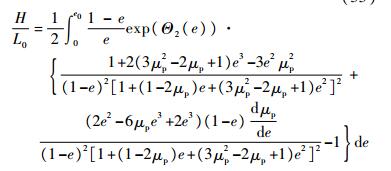 | (34) |
 | (35) |
其中:
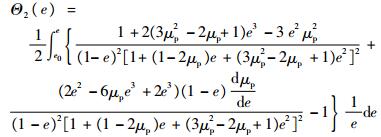 | (36) |
3 结果与讨论 3.1 塑性泊松比为常数 图 2给出了压缩密度比的一阶泰勒展开式与Lu等[13]模型的计算结果对比,这里取初始应变e0=0.3,同时取μp=0.25,对应于Lu等[13]模型中α=0.5。可以看出两者计算得到的冲击响应结果一致,这也说明一阶泰勒展开模型可以退化到Lu等[13]模型。
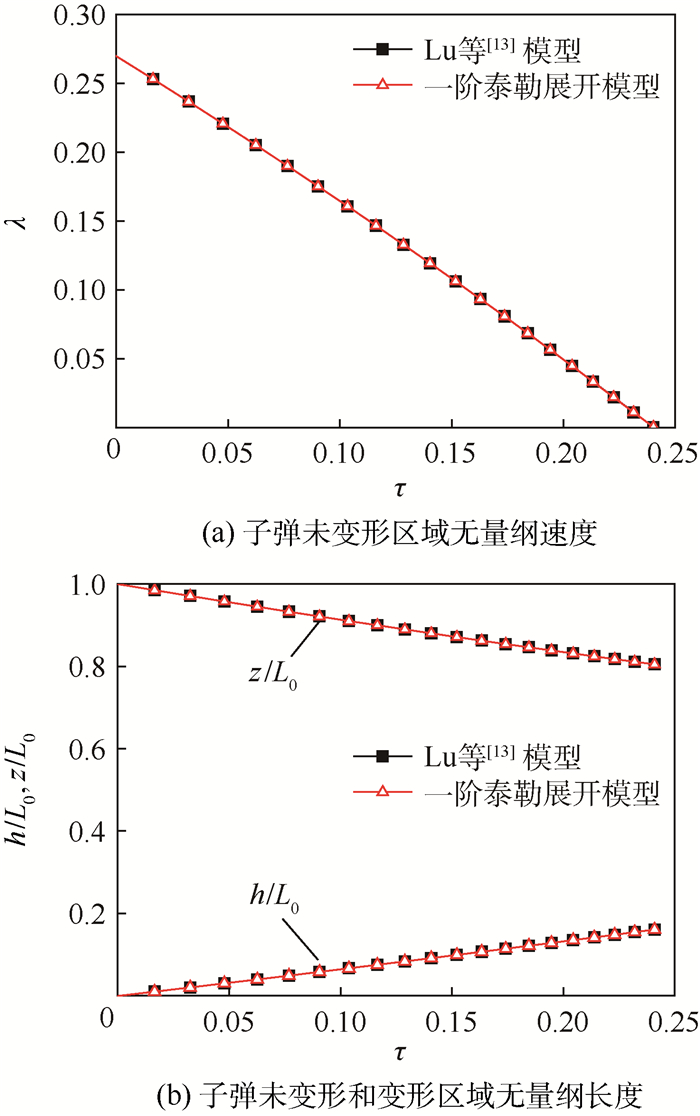 |
| 图 2 μp=0.25, e0=0.3时的冲击响应 Fig. 2 Impact responses when μp=0.25 and e0=0.3 |
| 图选项 |
3.2 塑性泊松比为压缩应变的函数 多孔材料的塑性泊松比并不为常数,与冲击速度和压缩应变有关,对于某闭孔金属泡沫材料,文献[15]通过数值模拟给出了如下低速冲击情况下的塑性泊松比与压缩应变的关系:
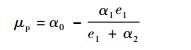 | (37) |
式中:e1为工程应变,满足e=ln(1+e1);α0、α1和α2为材料常数并满足:
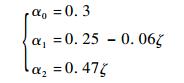 | (38) |
式中:ζ为泡沫子弹的相对密度,即金属泡沫的表观密度与相应金属材料的密度之比。
虽然式(37)是低速冲击条件下得到的数值模拟结果,但由文献[15]可知,冲击速度仅对塑性泊松比的峰值有较大影响,而该峰值对应的压缩应变很小,在Taylor撞击实验中,泡沫子弹的初始应变通常较大,此时冲击速度对塑性泊松比的影响较小,而在撞击后期,泡沫子弹的速度已较低,因此式(37)可以近似分析Taylor撞击问题。
由式(37),可以得到
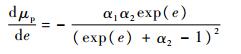 | (39) |
将式(37)分别代入到压缩密度比的原始表达式(8)及其一阶、二阶泰勒展开式(25)和式(31),可以分别得到对应的压缩密度比与压缩应变e的关系式。取泡沫材料的相对密度ζ=0.4,图 3给出了它们之间的关系,可以看出在压缩应变e较小时,压缩密度比与应变近似呈线性关系,这与Lu等[14]的试验结果一致,但当压缩应变e较大时,这种线性关系不再成立。
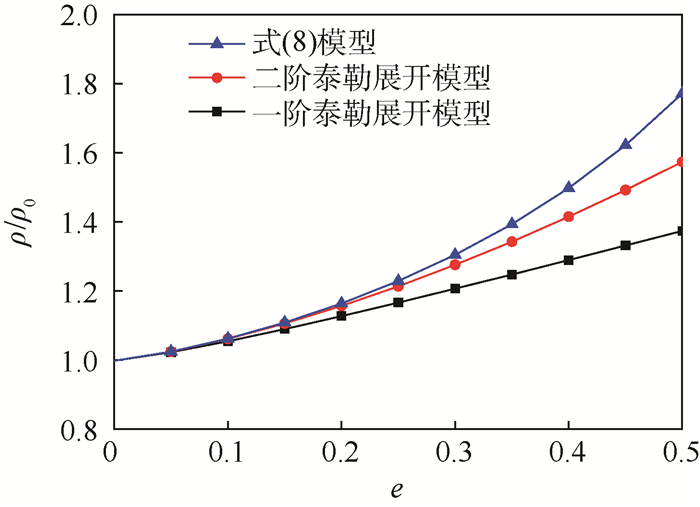 |
| 图 3 压缩密度比与压缩应变关系 Fig. 3 Relations between compressive density ratio and compressive strain |
| 图选项 |
图 4给出了由压缩密度比原始表达式(8)及其泰勒展开式(25)和式(31)得到的子弹的冲击响应历程,这里取泡沫材料的相对密度ζ=0.2,初始无量纲速度λ0=0.204 35,将λ0和式(37)分别代入到无量纲速度表达式(12)、式(26)和式(32)可以计算得到对应的初始应变e0,从而得到各参数随时间的变化规律。由图 4中可以看出它们具有相似的变化规律,而且随着展开阶次的增加,计算结果逐渐向压缩密度比原始表达式的结果靠近。
 |
| 图 4 不同压缩密度比模型的冲击响应比较(ζ=0.2, λ0=0.204 35) Fig. 4 Comparison of impact responses predicted by different compressive density ratio models (ζ=0.2, λ0=0.204 35) |
| 图选项 |
采用压缩密度比的原始表达式(8),并取初始无量纲速度λ0=0.204 35,可以计算出相对密度不同时泡沫子弹的冲击响应历程,如图 5所示。图中可以看出相对密度ζ不变时,子弹的塑性应变e、未变形区域长度z/L0和未变形区域的速度λ在冲击历程中逐渐减小,而变形区域的长度h/L0和塑性波前的速度η则随着时间的推移逐渐增大。同时可以看出,在同一时刻,随着相对密度ζ的增加,塑性应变e和子弹未变形区域长度z/L0减小,变形区域长度h/L0和塑性波前速度η则会增大,而未变形区域的速度λ则基本不变。
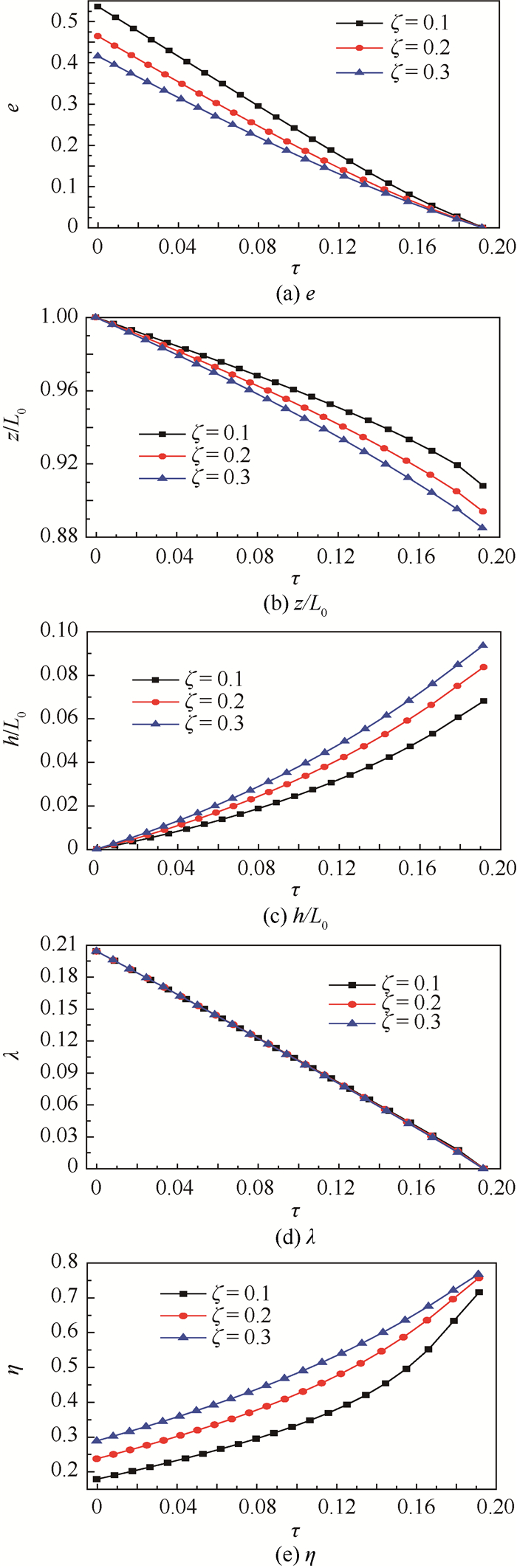 |
| 图 5 ζ不同时的冲击响应-时间曲线(λ0=0.204 35) Fig. 5 Impact responses versus time for different ζ (λ0=0.204 35) |
| 图选项 |
图 6给出了泡沫材料相对密度不同时子弹的冲击响应随无量纲初始速度λ0的变化规律,这里的压实应变取eD=0.8。可以看出ζ一定时,最大塑性应变e0、子弹最终的变形区域长度H/L0和冲击持续时间τf随着λ0的增加而增加,子弹最终的未变形区域长度Z/L0和子弹总剩余长度Lf /L0及塑性波前无量纲初始速度η0则随着λ0的增加而相应减小。在λ0一定时,随着ζ的增大,子弹最终的变形区域长度H/L0和初始塑性波前无量纲速度η0相应的增大,而最大塑性应变e0、子弹最终的未变形区域长度Z/L0则减小,冲击持续时间τf和子弹总剩余长度Lf /L0则基本保持不变。
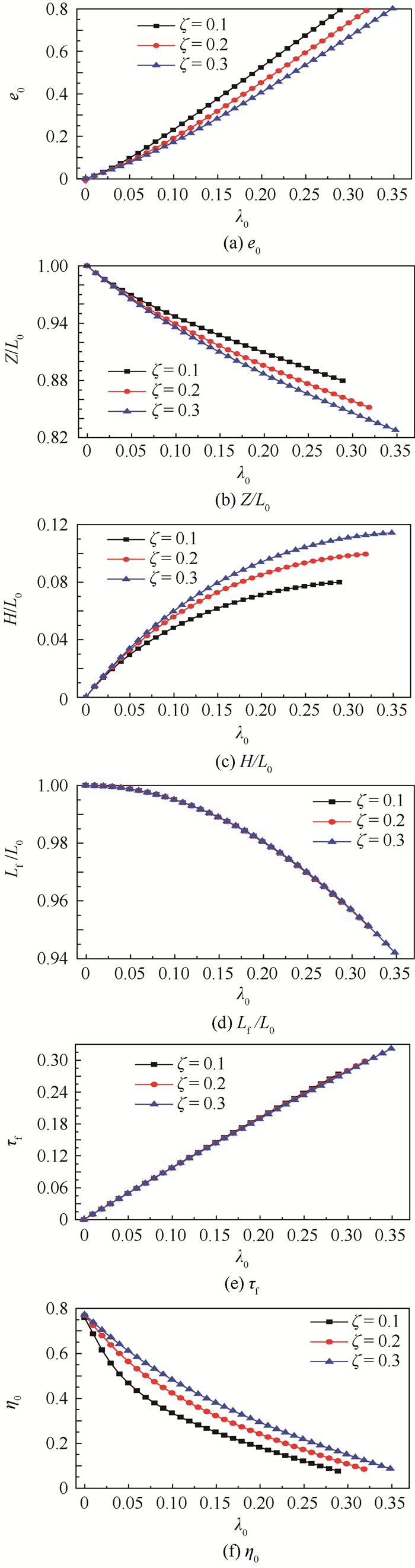 |
| 图 6 ζ不同时的最终冲击响应-λ0曲线 Fig. 6 Final impact responses versus λ0 for different ζ |
| 图选项 |
4 结论 本文通过引入塑性泊松比,从理论上推导了泡沫材料Taylor撞击中压缩密度比与压缩应变之间的关系,进而对泡沫子弹的Taylor撞击响应进行了分析,主要可以得到:
1)当塑性泊松比为常数时,压缩密度比的一阶泰勒展开式可以退化到Lu的分析模型。同时,通过分析发现,当压缩应变较小时,撞击过程中的压缩密度比与压缩应变近似呈线性关系,这与Lu的试验分析结果一致,但压缩应变较大时,这种线性关系将不再成立。而后又计算了压缩密度比二阶泰勒展开的结果,发现它们的冲击响应历程具有相似的变化规律,同时随着展开阶次的提高,计算结果将逐渐向着原始表达式的结果靠近。
2)当塑性泊松比为压缩应变的函数时,通过塑性泊松比与压缩应变和相对密度的关系式(37),分析了子弹相对密度对冲击响应的影响,发现相对密度会对泡沫子弹的冲击响应历程及最终变形产生影响,但对冲击响应持续时间影响较小。
3)子弹的初始速度会对子弹最终变形和冲击响应持续时间产生重要影响。
本文的分析结果对利用Taylor模型分析泡沫材料的动力学行为具有重要的指导意义。
参考文献
| [1] | LU G X, YU T X. Energy absorption of structures and materials[M].Cambridge: Woodhead Publishing Ltd, . |
| [2] | 余同希, 邱信明. 冲击动力学[M].北京: 清华大学出版社, 2011: 27-36.YU T X, QIU X M. Impact dynamics[M].Beijing: Tsinghua University Press, 2011: 27-36.(in Chinese) |
| [3] | TAYLOR G. The use of flat-ended projectiles for determining dynamic yield stress I:Theoretical considerations[J].Proceedings of the Royal Society of London A, 1948, 194(1038): 289–299.DOI:10.1098/rspa.1948.0081 |
| [4] | WHIFFIN A C. The use of flat-ended projectiles for determining dynamic yield stress II:Tests on various metallic materials[J].Proceedings of the Royal Society of London A, 1948, 194(1038): 300–322.DOI:10.1098/rspa.1948.0082 |
| [5] | HAWKYARD J B. A theory for the mushrooming of flat-ended projectiles impinging on a flat rigid anvil, using energy consideration[J].International Journal of Mechanical Sciences, 1969, 11(3): 313–333.DOI:10.1016/0020-7403(69)90049-6 |
| [6] | JONES S E, GILLIS P P, FOSTER JR J C, et al. A one-dimensional, two-phase flow model for Taylor impact specimens[J].Journal of Engineering Materials and Technology, 1991, 113(2): 228–235.DOI:10.1115/1.2903397 |
| [7] | JONES S E, DRINKARD J A, RULE W K, et al. An elementary theory for the Taylor impact test[J].International Journal of Impact Engineering, 1998, 21(1-2): 1–13.DOI:10.1016/S0734-743X(97)00036-5 |
| [8] | BRüIG M, DRIEMEIER L. Numerical simulation of Taylor impact tests[J].International Journal of Plasticity, 2007, 23(12): 1979–2003.DOI:10.1016/j.ijplas.2007.01.012 |
| [9] | TENG X, WIERZBICKI T, HIERMAIER S, et al. Numerical prediction of fracture in the Taylor test[J].International Journal of Solids and Structures, 2005, 42(9): 2929–2948. |
| [10] | MA X, ZHANG D Z, GIGUERE P T, et al. Axisymmetric computation of Taylor cylinder impacts of ductile and brittle materials using original and dual domain material point methods[J].International Journal of Impact Engineering, 2013, 54: 96–104.DOI:10.1016/j.ijimpeng.2012.11.001 |
| [11] | HUTCHINGS I M. Estimation of yield stress in polymers at high strain-rates using Taylor's impact technique[J].Journal of the Mechanics and Physics of Solids, 1978, 26(5): 289–301. |
| [12] | 胡文军, 张方举, 陈裕泽, 等. 聚碳酸酯的Taylor撞击实验及光塑性分析[J].高分子材料科学与工程, 2010, 26(10): 115–117.HU W J, ZHANG F J, CHEN Y Z, et al. Taylor impact test of polycarbonate and photoplastic analysis[J].Polymer Materials Science and Engineering, 2010, 26(10): 115–117.(in Chinese) |
| [13] | LU G X, WANG B, ZHANG T G. Taylor impact test for ductile porous materials part I:Theory[J].International Journal of Impact Engineering, 2001, 25(10): 981–991.DOI:10.1016/S0734-743X(01)00027-6 |
| [14] | WANG B, ZHANG J, LU G X. Taylor impact test for ductile porous materials part II:Experiments[J].International Journal of Impact Engineering, 2003, 28(5): 499–511.DOI:10.1016/S0734-743X(02)00105-7 |
| [15] | 王长峰.泡沬金属的动态压溃模型和率敏感性分析[D].合肥:中国科技大学, 2013.WANG C F.Dynamic crushing models and rate-sensitivity analysis of metallic foams[D].Hefei:University of Science and Technology of China, 2013(in Chinese).http://cdmd.cnki.com.cn/article/cdmd-10358-1013218144.htm |
