为将冲击信号从混合信号中提取出来,可以使用基于独立分量分析(Independent Component Analysis,ICA)的盲源分离(Blind Source Separation,BSS)方法[5, 6]。BSS方法是指在未知源信号与混合通道参数的情况下,仅根据观测信号的统计特征及观测数据恢复出源信号,其在损伤监测[2, 3, 5]、气象[7]、医学[8]以及通信领域[9]都有广泛的应用。正常情况下的BSS方法通常要求输入信号个数大于等于混合前源信号个数,即传感器阵列中,需要多个传感器测量序列作为输入,才能分离出独立的冲击信号与振动干扰信号。但是这种方法难以确定出不同传感器接收冲击信号的时间延迟,不能采用阈值时延法实现冲击定位。
为了充分利用源信号特征以及每个传感器的信息,实现传感器阵列对冲击信号定位,提出单通道伪多源采样方法与复域FastICA算法提取冲击信号,并结合阈值时延定位方法设计了联合冲击定位算法。其中,单通道伪多源采样方法利用单传感器的分时段信息构建多个观测信号作为复域FastICA算法的输入,进而分离出带相位信息的冲击信号;阈值时延定位方法根据冲击到达不同位置传感器的时间延迟,计算出实际冲击位置的坐标。
1 BSS预处理与单通道伪多源采样方法预先对阵列信号进行BSS处理,分离得到的源信号信息为接下来的单通道伪多源采样方法构造输入信号提供依据。
1.1 BSS预处理阵列信号BSS可在未知源信号与混合通道参数的情况下,仅根据观测信号的统计特征及观测数据恢复出源信号[10],其原理框图见图 1。
 |
| 图 1 BSS原理框图 Fig. 1 Block schematic of BSS |
| 图选项 |
BSS输入i路观测信号,恢复出j路信号(i≥j),但恢复出的信号具有幅值不确定性[6]。使用BSS对阵列传感器获取的N维含有噪声的信号进行预处理,能够分离出冲击信号与N-1路振动干扰信号。虽然对阵列信号进行BSS可以得到被测对象中是否包含冲击信号的综合信息,但是无法解算冲击定位所需的信号到达不同传感器的时间延迟。采用BSS对信号进行预处理的目的是得到冲击发生的大致时间段、干扰信号的种类和频率。一方面为单通道伪多源采样构造信号组提供依据;另一方面通过对分离出的环境噪声分析,便于确定减弱噪声的方法。
1.2 单通道伪多源采样方法一般情况下,信号在时域上是连续的。但是冲击信号的持续时间短,传感器采集到的信号序列中只有小部分包含冲击信号,绝大部分只含振动及噪声干扰。基于此振动冲击条件下的传感器观测序列实际上可分为冲击信号段与非冲击信号段,如图 2所示。可以通过分时段截取单个传感器的观测信号段,获得振动干扰信号与振动冲击混合信号。在实际应用中,将每个传感器不同时段的采集数据分为若干等长序列,并将其作为该传感器的多源观测数据,即单通道伪多源采样方法。通过计算各段的峭度判定采集信号的类型。
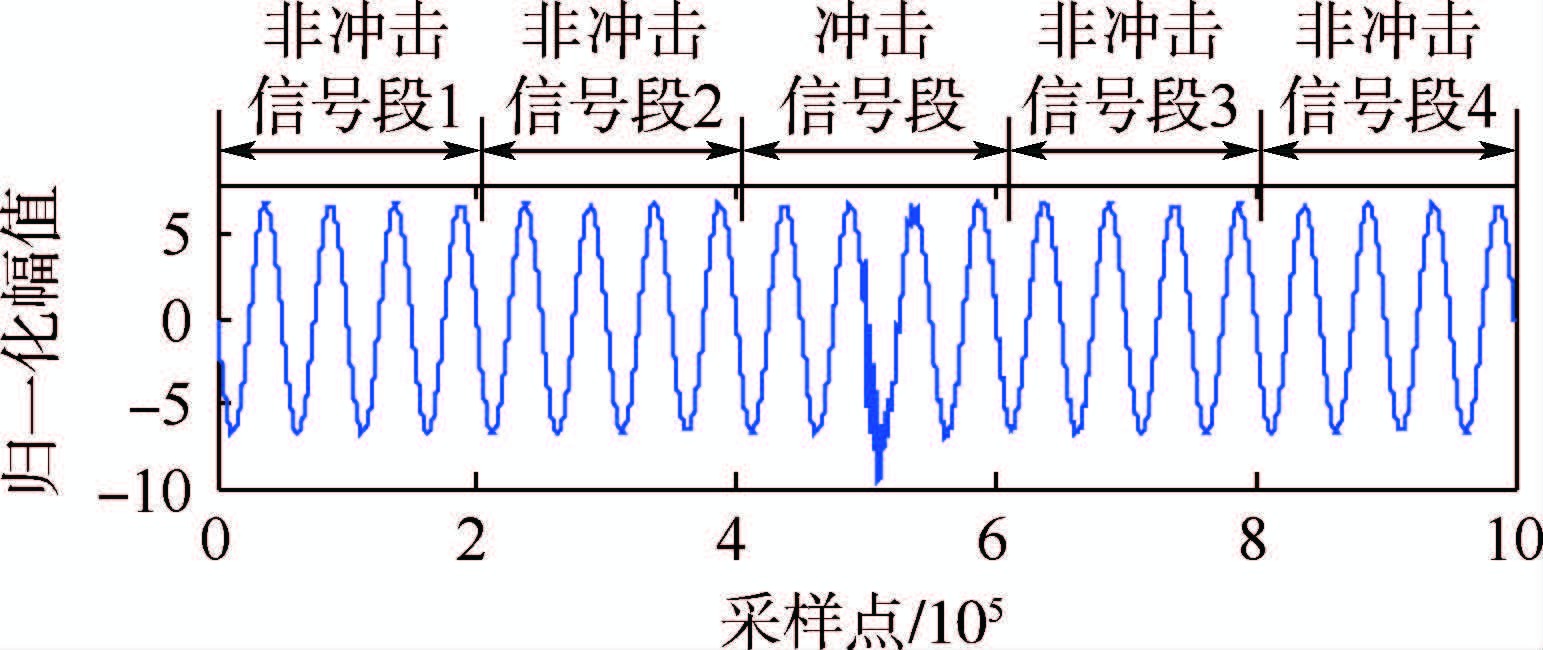 |
| 图 2 传感器观测序列分段 Fig. 2 Segmentations of sensor observation sequence |
| 图选项 |
峭度K是反映变量分布特性的数值统计量,其离散化计算公式为

式中:xi为信号值;x-为信号均值;N为采样点个数;σt为标准差。分别计算各段的峭度,结果发现,冲击信号段的峭度要明显大于非冲击信号段。
为获取冲击信号到达阵列中不同位置传感器的时间延迟,需要从单传感器的信号中分离带有相位信息的冲击信号,这属于传感器个数少于源信号个数的欠定BSS问题。解决此种相位信息提取问题,可采用复域FastICA算法,从频域角度对信号进行分离。而单通道伪多源采样方法的目的是解决欠定BSS问题,通过截取不同观测区间内的信号,构造出相位不同的信号作为复域FastICA算法的输入,用于分离单个传感器的冲击信号。具体实现过程及推导详见第2.2节。
2 复域FastICA算法提取冲击信号2.1 基于负熵的复域FastICA算法与实域FastICA算法相比,复域FastICA算法[11]考虑了信号的相位信息,其中待分离的独立成分以及混合矩阵为复数,但实域FastICA算法的基本公式及思想仍可用于复域情况。
BSS方法的基本公式为

式中:S为源信号矩阵;A为分离矩阵;X为观测信号矩阵。
随机变量x的负熵定义为
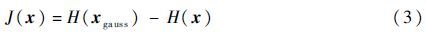
式中:J(x)为信号x的负熵;xgauss为与信号x具有相同方差的高斯随机变量;H(·)为信号的微分熵。根据中心极限定理,随机变量x的各分量之间统计独立性越强,x的非高斯性越强,负熵也就越大。可采用负熵作为代价函数衡量混合信号之间的分离程度。随着信号分离程度的提高,各信号之间的统计独立性也随之增加,负熵相应增加。因此,通过最大化负熵可得到最佳的分离信号。
由于复域变量的分布是球对称的,仅关注变量的模值,将实域的负熵定义迁移到复域内,采用仅依赖于模值的非高斯性度量JG(w)类比负熵[11]。

式中:G为光滑的偶函数;w为N维复权矢量,并且E(wHz2)=1,z为白化处理后的向量。
通过最大化JG就能获得一元独立成分。在正交约束的前提下,通过最大化N个一元非高斯性度量之和,估计出N个独立成分。同样,ICA模型对于复域信号可推出快速不动点算法,该算法可搜索到E(GwHz2)的极值。一元复域FastICA算法为

式中:g(·)可取的一种形式如式(6)所示:

其中:a1为任意常数;zi为z中元素。通过扩展,一元复域FastICA算法可以实现对多个信号的估计。
2.2 建立基于单通道伪多源采样的复域FastICA 算法提取冲击信号为论证基于单通道伪多源采样的复域FastICA算法从单传感器接收的混合信号中提取冲击信号的可行性,对振动环境下平板结构受到的冲击载荷信号进行建模。在相对较短的采样区间内,可假设结构中的振动干扰信号的频率不变。令传感器接收到的信号表示为

式中:ss(t)为冲击信号;sv(t)为振动干扰信号。
在结构内没有冲击信号传播时,传感器接收的信号仅包含振动干扰信号。存在冲击信号时,传感器获取的信号为两者的叠加。用基于单通道伪多源采样的复域FastICA算法来提取冲击信号的步骤可概括为以下3步:
1) 在无冲击情况下,任意获取不同相位的振动信号,信号个数为2T。如第1.1节所述,T为不同频率振动干扰信号个数;不失一般性但为方便推导,这里假设振动干扰信号个数为1,采集2段,分别记做x2(t)和x3(t)。
2) 在结构中存在冲击信号时,采集混合信号记为x1(t)。
3) 将x1(t)、x2(t)和x3(t)的傅里叶变换作为算法的输入进行信号分离。
x1(t)、x2(t)和x3(t)可表示为
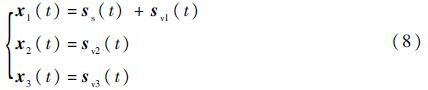
式中:
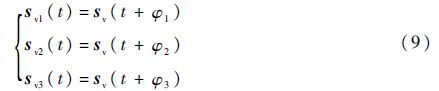
其中:φ1、φ2和φ3分别为sv1、sv2和sv3与sv的相位差。
对式(8)作傅里叶变换,得到

式中各项分别对应式(8)中各项的傅里叶变换。设

式中:

其中:Φ1为K1的相位。令

式中:a11和a12分别为2个相位差为90°的振动信号分量;Ω0为初始相位;θ1为合成信号相位,可表示为

将式(13)、式(14)代入式(12)有
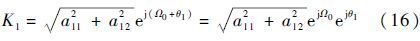
将式(15)代入式(16),得到
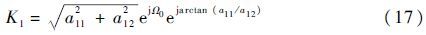
将欧拉公式ejα=sin α+j cos α代入式(17)得

化简后,式(18)可写为
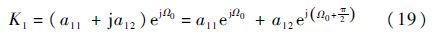
将式(19)代入式(11),有

令
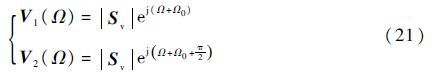
将式(21)代入式(20),有
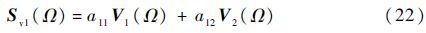
同理可表示出Sv2(Ω)、Sv3(Ω):

将式(22)~式(24)代入式(10)可得

用矩阵表示式(25)有
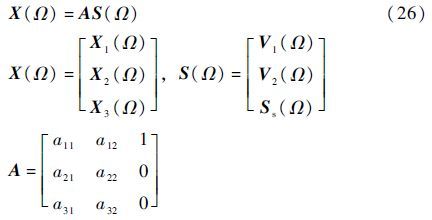
式中:aij(i=1,2,3;j=1,2)分别对应组成第i个信号的2个相位差为90°的振动信号分量的强度值。
根据式(26)可知,通过复域FastICA算法,可以将源信号x(t)的傅里叶变换X(Ω)分离得到冲击信号Ss和1组(每组2个)相位差为90°的振动干扰信号。更一般地,输入T(每组2个)组振动混合信号与1个振动冲击混合信号,可分离得到冲击信号和T组相位差为90°的非同频振动干扰信号。从而复域FastICA算法实现了单传感器混叠信号的分离。
复域FastICA算法虽然分离出了混叠信号,但其分离出的独立成分的顺序具有不确定性。为实现系统自动提取冲击信号,需要进行二次处理。分离出的信号可分为2类:异物撞击产生的冲击信号和振动干扰信号。分析2类信号的特征可知:冲击信号的幅值变化剧烈,持续时间短;振动干扰信号的幅值变化连续,能量分布均匀。针对此特点,同样选取峭度作为2类信号的区分标准,峭度较大的分量为冲击信号分量。
通过对阵列中传感器分别进行上述处理,可分别得到各个传感器接收到的冲击信号。因传感器距冲击点位置不同,各个信号间存在时间延迟,故可利用阈值时延定位方法求解冲击坐标。
3 阈值时延定位方法时延定位是根据同一信号到达不同位置传感器时间延迟的不同,利用时间差解算冲击位置的方法[12, 13]。本文从阵列信号中选取4个呈正方形布局(正方形边长为l)的传感器建立定位模型,如图 3所示。
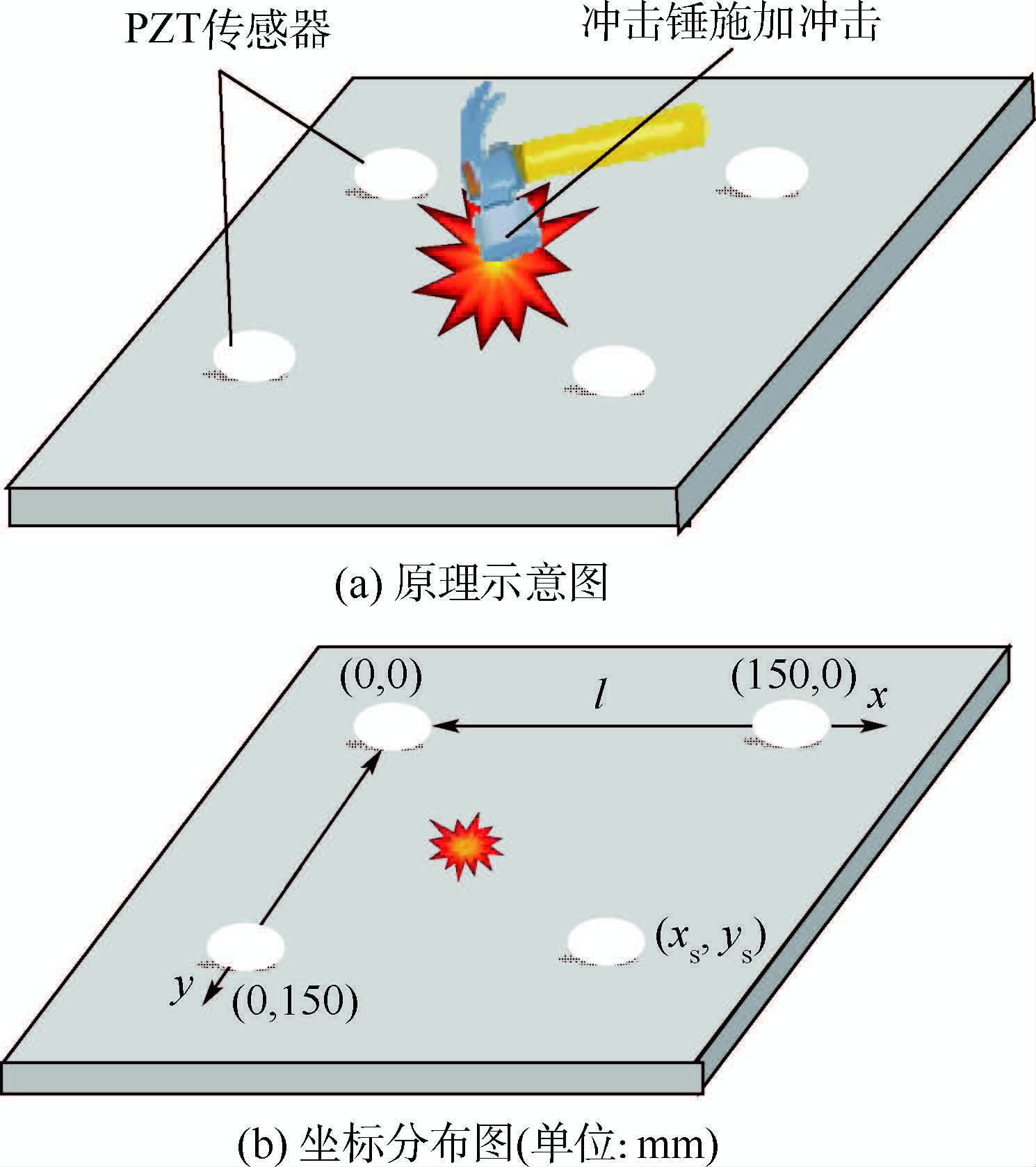 |
| 图 3 冲击定位示意图 Fig. 3 Schematic of impact location |
| 图选项 |
利用冲击信号到达4个传感器的时间差可推得冲击点坐标

式中:v为介质中声波传播速度;ti(i=A,B,C,D为传感器编号)为各传感器测得冲击信号到达时间。
冲击信号到达时间ti可以通过阈值法、互相关法[14]和短时均方根法[15]等多种方法得到。综合考虑精度及速度,本文选用阈值法,其原理简单,处理速度快。通过阈值法检测冲击信号的前沿,根据采样频率可以计算出冲击信号到达各个传感器的时间延迟,将时间延迟代入式(27)、式(28),可求解冲击坐标,实现平面冲击事件的定位。
综合单通道伪多源采样方法、复域FastICA算法及阈值时延定位方法设计了联合冲击定位算法,见表 1。
表 1 联合冲击定位算法Table 1 Combined impact location algorithm
| 输入:传感器阵列输出信号Q,介质中声波传播速度v 输出:冲击位置(xs,ys) |
| 1) 对传感器阵列输出Q做BSS预处理,得到冲击信号ss与T个不同频率振动干扰信号svi(i=1,2,…,T)的信息。 2) 在阵列中任选可构成正方形的4个传感器,正方形边长为l。 3) 对步骤2)中每个传感器的观测信号进行单通道伪多源采样,构造信号组Xj(j=1,2,3,4),其中每个信号组由1个冲击振动混合信号与2T个振动干扰信号构成。 4) 利用复域FastICA算法对Xj分别处理,得到冲击信号ssj(j=1,2,3,4)。 5) 利用阈值时延定位方法求得冲击信号到达步骤2)中各个传感器的时间延迟tj(j=1,2,3,4)和冲击事件的坐标(xs,ys)。 |
表选项
根据所选择的定位算法的不同,步骤2)中选取传感器个数有所不同;特别地,若已知源信号中的振动及噪声信息,可省略步骤1)。
4 数值仿真验证为验证基于单通道伪多源采样的复域FastICA算法以及设计的联合冲击定位算法的有效性,分别对其进行了数值仿真。
4.1 基于单通道伪多源采样的复域FastICA算法仿真仿真信号采用计算机生成的100 Hz正弦振动信号与采集的冲击信号混合,通过对混合信号不同观测区间截取,得到3路输入信号。图 4为利用单通道伪多源采样方法构建的输入信号。其中的冲击振动混合信号x1受振动信号影响,难以判定冲击信号前沿;x2、x3是有相位差的振动信号。图 5为复域FastICA算法分离得到的信号。其中y1、y3是分离出的振动信号,y2是分离出的冲击信号,与x1相比,其前沿较为明显。虽然因算法的幅值不确定性[6],使恢复出的冲击信号y2的幅值与混合信号x1中的冲击信号分量不等,但该不确定性并不影响对冲击前沿的判定。
 |
| 图 4 复域FastICA算法输入信号 Fig. 4 Input signals of complex domain FastICA algorithm |
| 图选项 |
 |
| 图 5 复域FastICA算法输出信号 Fig. 5 Output signals of complex domain FastICA algorithm |
| 图选项 |
4.2 联合冲击定位算法仿真建立定位仿真模型,其右向为x轴正方向,下向为y轴正方向,各传感器坐标如图 3所示,均使用归一化单位。考虑振动幅值影响,设定正弦信号幅值分别大于、小于冲击信号峰值2种情况,随机混合矩阵由软件生成,冲击点位置手动输入。仿真中,计冲击信号峰值为1,分别令振动信号幅值为0.05与5,模拟冲击点定为(15,125)。对A、B、C和D 4点分别得到的冲击振动混合信号序列使用联合冲击定位算法,求解冲击坐标。
为验证联合冲击定位算法稳定性,在2种条件下分别进行了20次重复实验。在弱振动条件下,定位的绝对偏差为(0.137 4,0.217 7),方差为(0.085 4,0.214 2);在强振动条件下,定位的绝对偏差为(0.296 4,0.302 4),方差为(0.306 7,0.352 4)。从仿真结果可以看出,算法精度及稳定度均较好;此外也证明了其求解冲击坐标的有效性。
5 实测实验验证5.1 实验方案设计为验证联合冲击定位算法在真实环境中的可行性,搭建了振动条件冲击定位实验平台。本实验平台由1块铝合金平板试件及传感元件、垂直振动台(杭州奥科环境试验设备有限公司,AK-W型)、电荷放大器(江苏东华测试技术股份有限公司,DH5863)、高速采集卡(凌华科技(中国)有限公司,AD9816)和工控机(凌华科技(中国)有限公司)组成。振动条件冲击定位实验平台如图 6(a)所示,冲击锤头如图 6(b)所示,其顶部为半球形,可视为点冲击源。
 |
| 图 6 实验平台及器材 Fig. 6 Experimental platform and equipments |
| 图选项 |
实验件通过紧固螺母与振动台固定在一起,尺寸为300 mm×300 mm×3 mm。传感元件选用PZT传感器,直径为20 mm,厚度为1 mm,安装坐标分别为(0 mm,0 mm)和(150 mm,0 mm),(150 mm,150 mm),(0 mm,150 mm)。实验件形状、PZT传感器位置及冲击示意图见图 3(b)。
5.2 实验结果及分析实验中,振动台振动频率设定为100 Hz,高、低调节参数分别为60、25,上位机数据采集软件采样频率为106 Hz,使用冲击锤在(70 mm,0 mm)位置敲击产生冲击,上位机保存4路PZT采集混合信号。
利用联合冲击定位算法分别处理4路传感器采集信号,混合信号如图 7所示。其中A、B、C和D分别对应4个PZT传感器采集信号。图 8为按照本文算法对A传感器求解得到的源信号。4路传感器分别求解得到的冲击信号见图 9,其中A1、B1、C1和D1分别对应于从4个传感器采集混合信号中恢复出的冲击信号。
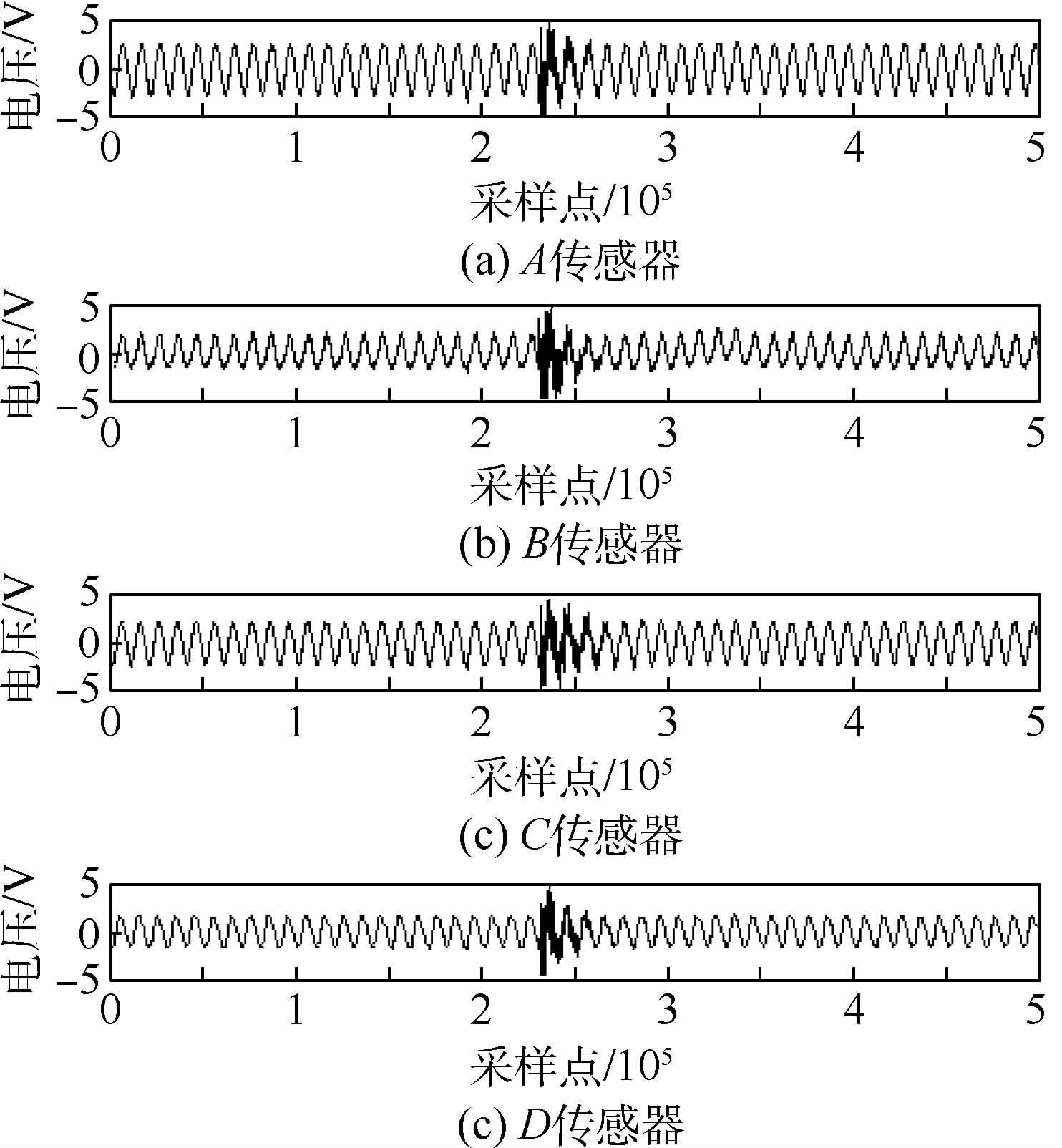 |
| 图 7 4路传感器观测信号 Fig. 7 Observed signals of four sensors |
| 图选项 |
 |
| 图 8 A传感器分离出的冲击与振动信号 Fig. 8 Impact and vibration signals separated from sensor A |
| 图选项 |
 |
| 图 9 4路传感器分离冲击信号 Fig. 9 Impact signals separated from four sensors |
| 图选项 |
利用阈值时延定位方法,结合采样频率及冲击起始点信息计算出冲击到达各传感器的时间延迟tj(j=1,2,3,4)分别为0.081 545、0.081 452、0.081 613和0.081 622 s,通过式(27)、式(28)解算出冲击事件的位置为(81.4 mm,4.8 mm),其在实验件上的位置见图 10,定位绝对误差约为12.4 mm,相对误差δ为

式中:Δ为绝对误差;L为实验件边长。相对误差求解为4%。
 |
| 图 10 实测定位实验结果 Fig. 10 Results of practical location experiment |
| 图选项 |
误差的原因一方面是对声波在介质中传播速度v的估计不够准确,在代入式(27)、式(28)求解时影响了定位结果。另一方面,实验中除去振动干扰外还有环境噪声存在,虽然在后期数据处理中采取了一定的消噪方法,但并未完全消除环境噪声的影响,对时间延迟的准确度造成了一定的影响。在接下来的工作中,可在获得冲击信号后对其进行更有针对性的消噪处理,以进一步提高定位精度。
6 结 论本文在提出单通道伪多源采样方法及复域FastICA算法提取冲击信号的基础上,结合阈值时延定位方法,设计了联合冲击定位算法,并在实验平台上对算法实用性进行了验证。研究结论如下:
1) 针对冲击信号特点,提出单通道伪多源采样方法,实现利用单传感器接收信号构造多个信号作为复域FastICA算法的输入信号,解决了观测信号个数少于待分离信号造成的欠定BSS问题。
2) 引入峭度作为信号类别的判断指标,实现了自动辨识传感器接收信号中的冲击段与非冲击段,自动辨识复域FastICA算法分离所得信号中的冲击信号与振动干扰信号。
3) 利用复域FastICA算法对单通道伪多源采样方法构造的信号进行分离,并对其提取冲击信号过程进行建模,从理论上证明了算法的可行性。
4) 在以上研究内容的基础上,设计了联合冲击定位算法,该算法输入为传感器阵列采集信号和冲击波速等信息,经过单通道伪多源采样、复域FastICA分离以及阈值时延定位过程,解算冲击在平面的坐标,并通过数值仿真验证了联合冲击定位算法的有效性。
5) 设计了振动条件冲击定位实验平台,在单振动干扰条件下,进行了4传感器阵列的冲击定位实验,定位误差在12 mm左右。
研究结果表明,基于单通道伪多源采样的复域FastICA算法可在振动环境下对冲击事件定位,精度满足实际工程需求,具有一定的工程实用价值。
参考文献
| [1] | DERRISO M M,CHANG F K.Future roles of structural sensing for aerospace applications:RTO-MP-AVT-141[R].Neuilly-sur-Seine:Air Force Research Lab Wright Patterson Afb Oh Air Vehicles Directorate,2006. |
| [2] | 苏永振,袁慎芳.基于独立分量分析的多源冲击定位方法[J].振动与冲击,2009,28(8):134-137. SU Y Z,YUAN S F.Impact of multi-source localization method based on independent component analysis[J].Journal of Vibration and Shock,2009,28(8):134-137(in Chinese). |
| Cited By in Cnki (19) | |
| [3] | IHN J B,CHANG F K.Pitch-catch active sensing methods in structural health monitoring for aircraft structures[J].Structural Health Monitoring,2008,7(1):5-19. |
| Click to display the text | |
| [4] | 耿荣生,沈功田,刘时风.基于波形分析的声发射信号处理技术[J].无损检测,2002,24(6):257-261. GENG R S,SHEN G T,LIU S F.Acoustic emission signal processing technology based on waveform analysis[J].Nondestructive Testing,2002,24(6):257-261(in Chinese). |
| Cited By in Cnki (138) | |
| [5] | 鲍鹏宇. 结构损伤监测信号处理方法研究[D].北京:北京航空航天大学,2013:65-82. BAO P Y.Research on methodology of structural damage monitoring signal processing[D].Beijing:Beihang University,2013:65-82(in Chinese). |
| [6] | 李舜酩. 振动信号的盲源分离技术及应用[M].北京:航空工业出版社,2011:24-42. LI S M.Blind source separation vibration signal technology and applications[M].Beijing:Aviation Industry Press,2011:24-42(in Chinese). |
| [7] | LIM Y,LEE J,OH H S,et al.Independent component regression for seasonal climate prediction:An efficient way to improve multimodel ensembles[J].Theoretical and Applied Climatology,2015,119(3-4):433-441. |
| [8] | ZHANG X,VIALATTE F B,CHEN C,et al.Embedded implementation of second-order blind identification (SOBI) for real-time applications in neuroscience[J].Cognitive Computation,2015,7(S1):56-63. |
| Click to display the text | |
| [9] | CASTELLA M,MOREAU E,ZARZOSO V.Advances in heuristic signal processing and applications[M].Berlin:Springer,2013:183-217. |
| [10] | COMON P,JUTTEN C.Handbook of blind source separation:Independent component analysis and applications[M].New York:Academic Press,2010:179-207. |
| [11] | BINGHAM E,HYVÄRINEN A.A fast fixed-point algorithm for independent component analysis of complex valued signals[J].International Journal of Neural Systems,2000,10(1):1-8. |
| Click to display the text | |
| [12] | KUNDU T. Acoustic source localization[J].Ultrasonics,2014,54(1):25-38. |
| Click to display the text | |
| [13] | CHEN J,HUANG Y,BENESTY J.Time delay estimation[M]//HUANG Y,BENESTY J.Audio signal processing for next-generation multimedia communication systems.Berlin:Springer,2004:197-227. |
| [14] | KNAPP C H,CARTER G C.The generalized correlation method for estimation of time delay[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1976,24(4):320-327. |
| Click to display the text | |
| [15] | CORRAL J L,MARTI J,REGIDOR S,et al.Continuously variable true time-delay optical feeder for phased-array antenna employing chirped fiber grating[J].IEEE Transactions on Microwave Theory and Techniques,1997,45(8):1531-1536. |
| Click to display the text |
