变重力场中散体颗粒堆的安息角及接触力分布

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2021-12-25

散体颗粒普遍存在于自然界中,如岩土、沙粒、矿石等.安息角是散体颗粒在重力的作用下发生运动、堆积和稳定后形成的最大倾斜角.近年来,受航天科学领域的影响,重力与散体颗粒安息角之间的关系引起了****们的广泛兴趣^{[1, 2, 3, 4, 5]},研究重力与安息角的关系有助于掌握类地星球表面的陨石撞击坑、碎石斜坡、颗粒流动、沙丘和火山堆成型等地质现象^{[6, 7]},也有助于掌握星球表层土质的力学性能^{[8, 9]},是人类进行原地勘探的前提和基础.安息角没有影响,Atwood-Stone和McEwen^[5]研究发现火星与地球表面沙丘的安息角相似,因此认为重力对安息角的影响不大.对研究结果中的差异,还没有很合理的解释,Kleinhans等^[3]提出,如果能得出颗粒堆内的接触力信息,将有助于揭示重力与安息角之间的关系.但是,目前的研究中主要是对安息角进行宏观测量,缺乏对颗粒堆微观力学信息的分析.颗粒堆内,颗粒相互接触而形成强度迥异的力链,力链支撑整个颗粒堆而保持稳定^{[10, 11, 12]}.然而,由于散体颗粒系统的离散性和随机性特点,经典的连续介质弹塑性理论不适用于颗粒堆的力学建模,因此不能准确地得出其微观力学信息.光弹性实验等手段可以对颗粒接触力的传导与分形进行定性描述,但是定量测量还有一定难度^{[13, 14]}.近年来,离散单元法(Discrete Element Method,DEM)逐渐发展成研究散体颗粒体系的重要数值试验工具^{[15, 16, 17, 18]},可以针对颗粒系统的非连续性质,方便地获得其微观力学信息.本文通过DEM建立散体颗粒的三维运动模型,模拟了不同重力场中散体颗粒的堆积过程,得出了颗粒堆的安息角以及力链结构,定量分析了接触力的概率分布规律,揭示了不同重力场中颗粒接触力的分布特点,与以往研究相比,从颗粒层面得出了颗粒堆内更多的力学信息.1 DEM建模1.1 颗粒运动模型散体颗粒的堆积运动属于密集颗粒运动,采用软球颗粒表示单个颗粒^[15].如图 1所示,质量为m_i、转动惯量为I_i的颗粒i在运动过程中主要受重力m_ig和接触力F_ij作用.当两个颗粒发生碰撞时,颗粒所受阻力为法向力F_ijⁿ,F_ijⁿ与法向变形位移及颗粒刚度相关.如果是偏心碰撞,则接触力产生切向分量F_ij^t,F_ij^t的极值为颗粒间的滑动摩擦力,当F_ij^t大于极值时,接触点产生滑动.颗粒间的接触力矩为T_ij,T_ij受滚动摩擦力矩的限制,T_ij大于滚动摩擦力矩后发生滚动.

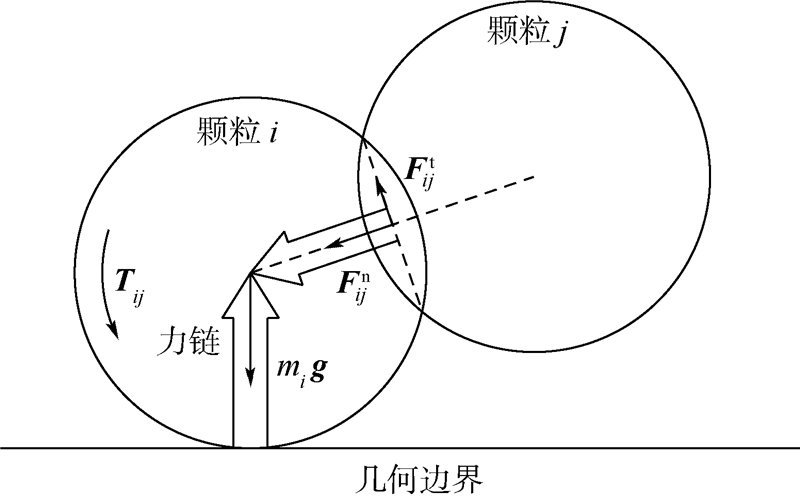
图 1 DEM颗粒模型示意图Fig. 1 Sketch of DEM model of particle

图选项

用连接颗粒中心和接触点的矢量表示力链^[11],矢量大小由线条的粗细表示,与接触点处接触力F_ij的大小成正比.单个颗粒i的运动控制方程为

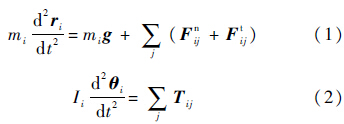
式中:r_i和θ_i分别为颗粒的位移与角位移;g为重力加速度.式(1)和式(2)中,接触力主要有3种计算模型^[15]:“线性接触力模型”、“Hertz-Mindlin模型”和“无滑移Hertz-Mindlin模型”.根据Alberto等^[17]的研究结果,密集颗粒运动中的接触力采用“无滑移Hertz-Mindlin模型”不但能保证计算精度,而且可以避免过多的计算量.因此,接触力采用“无滑移Hertz-Mindlin模型”计算,具体如下:

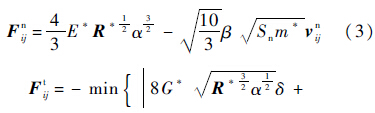
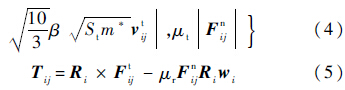
式中:颗粒等效半径

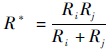;等效弹性模量

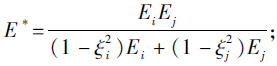等效质量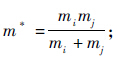

等效切向模量

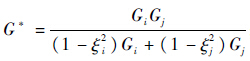;法向刚度S_n=2E^*(R^*α)^0.5,切向刚度S_t=8G^*(R^*α)^0.5;修正系数

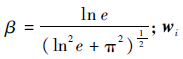为单位角速度矢量;α和δ分别为颗粒之间的法向、切向重叠量;v_ijⁿ和t_ijⁿ分别为颗粒之间相对速度的法向、切向分量；μ_r为滚动摩擦系数；μ_t为滑动摩擦系数.通过时间差分法可以对式(1)和式(2)进行求解^{[15, 16, 17, 18]},DEM基本算法不再赘述.模型中的参数变量为:颗粒的质量m、弹性模量E、泊松比ξ、恢复系数e、滚动摩擦系数μ_r和滑动摩擦系数μ_t.1.2 颗粒堆积过程颗粒为Nakashima等^[4]实验中采用的石英砂,从直径为d的出料口生成,在重力作用下堆积至直径为D的圆形底板上.DEM具体参数取值如表 1所示,其中:颗粒密度、弹性模量等参数采用文献^[4]测量值;为形成稳定的锥形颗粒堆,模型中μ_r-pb及μ_s-pb取值均大于测量值,显然,增大μ_r-pb和μ_s-pb的取值不会对颗粒堆安息角及内部接触力造成影响.表 1 模型参数 Table 1 Parameters of model

参数	数值
颗粒半径R/mm	6
颗粒密度ρ/(kg·m^-3)	2 090
颗粒-颗粒滑动摩擦系数μ_t-pp	0.154
颗粒-颗粒滚动摩擦系数μ_r-pp/mm	0.025
颗粒弹性模量E_p/MPa	57
颗粒-颗粒恢复系数e_pp	0.5
颗粒-底板恢复系数e_pb	0.3
颗粒泊松比ξ_p	0.25
底板泊松比ξ_b	0.3
底板弹性模量E_b/MPa	2 000
颗粒-底板滚动摩擦系数μ_r-pb/mm	0.3
颗粒-底板滑动摩擦系数μ_s-pb	1
底板直径D/mm	700
出料口直径d/mm	50
时间步长Δt/μs	43.4

表选项

颗粒堆积方式有“落雨式”和“点源式”两种^[4],模型中采用与多数自然现象较接近的“点源式”堆积方式.如图 2(a)所示,颗粒从出料口随机生成,受重力作用降落至底板,从底板中心开始堆积并逐渐向边缘扩展;如图 2(b)所示,颗粒扩展至底板边缘后堆积进入饱和状态,继续下落的颗粒将从底板的边缘滚落,随后关闭出料口直至形成稳定的颗粒堆,H为颗粒堆的高度.颗粒堆积过程中,出料口高度随颗粒堆积高度逐渐上移,以减轻颗粒降落时对安息角的冲击.颗粒堆安息角为

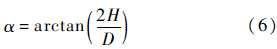
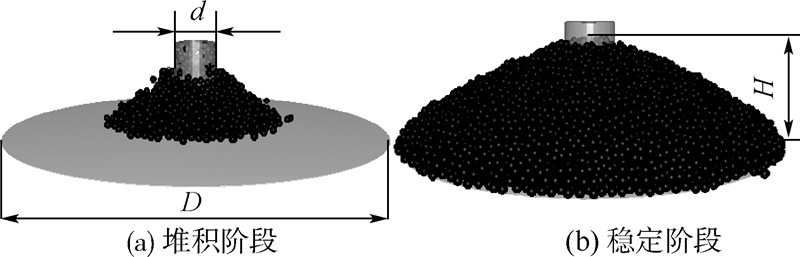图 2 “点源式”颗粒堆积过程Fig. 2 Particle accumulation of “point source type”

图选项

2 结果及讨论首先分析了地球重力场中(g=g₀)颗粒堆的力链结构.然后,模拟了g为0.167g₀(月球重力)、0.444g₀(火星重力)和2g₀时颗粒堆的安息角及接触力.2.1 颗粒堆的力链结构图 3为地球重力场中颗粒堆截面上接触力合力的力链结构.由图可知,与光弹性实验观测结果^[13]相似:即颗粒力链互相交接构成非均匀的力链网络,支撑颗粒堆保持稳定;力链强度沿着重力方向逐渐变强,但是力链网络的结构具有随机性,且强、弱力链会交替出现;底部接触力从颗粒堆的中心向边缘逐渐变弱,但是最大接触力不在中心位置,即存在实验中发现的“底部应力凹陷”和“拱桥桥应”^[11].重复模拟颗粒堆的安息角均约为23°,但是微观力链结构具有不可重复性.

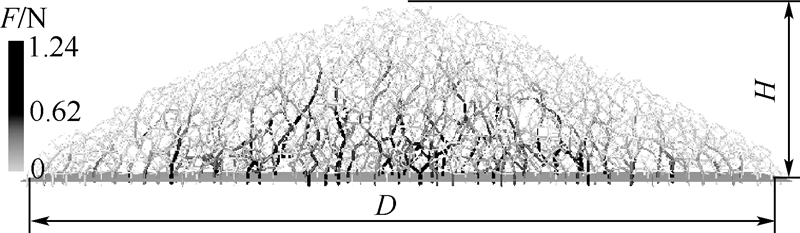图 3 颗粒堆截面上的力链Fig. 3 Force chain of granular pile in cross section

图选项

图 4为颗粒堆内接触力F_ij的概率密度函数P及累积分布函数(Cumulative Function Probability,CFP),图中,接触力的平均值为F_av.由图可知,接触力近似为对数正态分布,并且65%的接触力低于平均值,为弱力链,而大于平均值的接触力呈指数递减.结合图 3可知,颗粒堆内弱力链较多,是由于少数强力链贯穿于整个力链网络,并支持了颗粒堆大部分重量导致的.Thornton和Antony^[14]研究表明受压颗粒系统的接触力也符合这一分布规律,可以推测,颗粒系统内强、弱力链的比例不受外载荷的影响,是颗粒系统的固有性质.

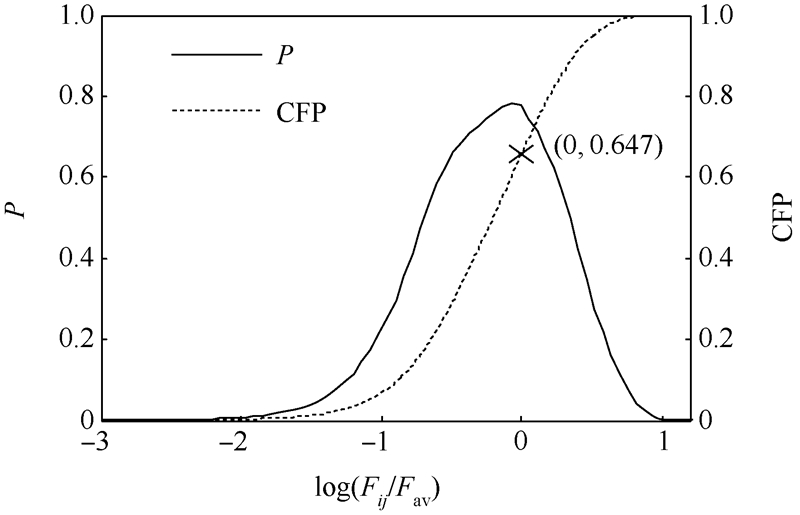图 4 接触力的概率分布Fig. 4 Probability distribution of contact-force

图选项

设η为接触点切向力与法向力的比值,即η=F_ij^t/F_ijⁿ.图 5为η的概率分布,由图可知:在0＜η＜μ_t-pp区域,P(η)为均匀分布;η=0.154=μ_t-pp处,P(η)出现脉冲峰值.η的均匀分布可能是由颗粒堆积过程的随机性导致的,这一特征与受压颗粒系统相同.当η=μ_t-pp时,表示接触点处于临界滑移状态,单轴实验中受压的颗粒系统约50%的接触点处于临界滑移^[8],而图 5表明颗粒堆内约70%的接触点处于临界滑移状态.根据颗粒的堆积过程可以推断:由于安息角是颗粒堆的临界稳定角,而颗粒堆是由颗粒沿着安息角一层一层堆积而形成,因此,与单轴实验的颗粒系统相比,颗粒堆内部有更多接触点处于临界滑移状态.

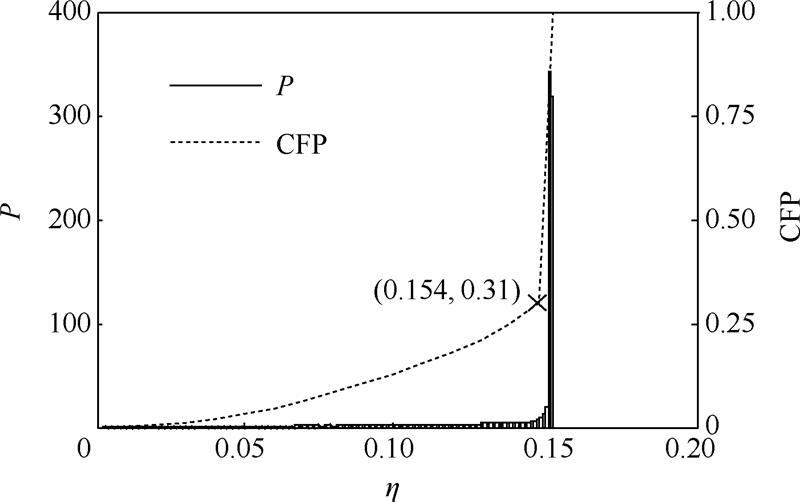图 5 η的概率分布Fig. 5 Probability distribution of η

图选项

2.2 不同重力场中的颗粒堆图 6为月球重力及火星重力作用下的颗粒堆的力链结构.虽然太阳系中类地星球的重力均小于地球^{[19, 20]},作为概念性研究,图中增加了g=2g₀的颗粒堆作为对比.由图可知,各重力场中颗粒堆的力链强度随着重力的增加而增大,但是几何轮廓与地球重力场中的相同,安息角均为23°,即安息角不受重力大小的影响.

图 6 不同重力场中颗粒堆的力链Fig. 6 Force chains of granular piles under variable g

图选项

图 7为不同重力场中颗粒堆接触力概率分布的对比.如图 7(a)所示,接触力随着重力的增大而增大,这是因为颗粒重力增加后,力链网络要形成力学平衡,接触力也必然增大.图 7(b)为无量纲化之后的接触力分布规律,图中,接触力除以颗粒重力mg进行无量纲化,由图可知,无量纲化之后接触力的概率密度函数高度相符,即接触力的概率密度函数与重力成比例关系.进一步分析η的分布规律,如图 7(c)所示,不同重力作用下,各颗粒堆η的分布规律一致,即接触点切向力与法向力比值的分布规律不受重力的影响.Radjai等^[12]研究发现不同尺寸规模颗粒系统之间的接触力概率分布具有相似性,由以上分析可知,不同重力场中颗粒堆的接触力概率分布也具有相似性.

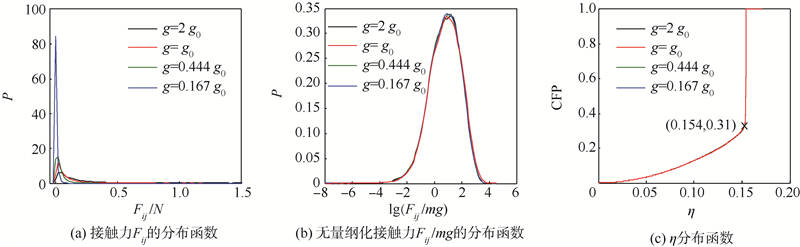图 7 各重力场中颗粒堆的接触力概率分布Fig. 7 Probability distributions of contact-force of granular piles under variable g

图选项

颗粒的粒径级配、粒径大小和粗糙度均会影响颗粒堆的接触力,从而改变安息角.表 2为6种不同物性参数的样本颗粒,其中,样本S₁和S₄的颗粒半径符合正态分布规律,且最大半径与最小半径之比为1.2,表中R表示样本颗粒的平均半径.根据DEM模型分别模拟了g为0.167g₀,0.444g₀,g₀和2g₀时各样本颗粒的堆积过程,安息角结果如表 3所示,由表可知,虽然各样本颗粒之间的安息角存在差异,但对于同一样本颗粒,4种重力下安息角的标准偏差均小于0.5°,表明各样本颗粒的安息角均不受重力大小的影响.
表 2 样本颗粒物性参数 Table 2 Physical parameters of sample particles

颗粒样本S	R/mm	μ_t-pp	μ_r-pp/mm
S₁	6	0.254	0.05
S₂	6	0.254	0.1
S₃	6	0.5	0.2
S₄	4	0.254	0.05
S₅	4	0.254	0.1
S₆	4	0.5	0.2

表选项

表 3 各样本颗粒堆的安息角 Table 3 Angles of repose of all samples( )

颗粒样本S	α				标准偏差
颗粒样本S	0.1g₀	0.4g₀	g₀	2g₀	标准偏差
S₁	23.8	24.5	24.1	24.0	0.06
S₂	29.7	29.8	30.1	29.5	0.06
S₃	33.3	33.2	33.7	33.0	0.1
S₄	24.3	25.0	24.8	24.6	0.1
S₅	29.4	30.0	30.1	30.9	0.38
S₆	35.5	35.8	36.2	36.0	0.07

表选项

图 8为各样本颗粒堆在不同重力场中的接触力概率分布,图中,接触力分别除以各样本颗粒的重力进行无量纲化.由图可知,各样本颗粒堆的接触力均近似为对数正态分布,并且,对于同一样本颗粒堆,接触力无量纲化之后的概率密度函数高度相符.另外,各样本颗粒堆的η的概率分布均为:η=μ_t-pp的接触点占约70%,而其余接触点的η在[0,μ_t-pp)之间均匀分布,而重力与η的分布规律无关,文中不再一一列出.可见,不同重力场中颗粒堆的接触力分布规律具有相似性,这一特征不受颗粒粒径级配、粒径大小和粗糙度的影响.

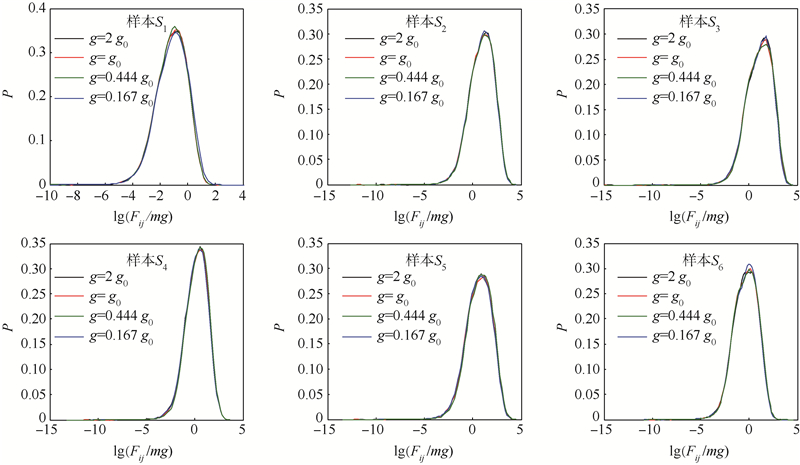图 8 各样本颗粒堆的接触力概率分布Fig. 8 Probability distributions of contact-force within granular piles for all samples

图选项

2.3 讨论颗粒堆由力链网络支撑而保持平衡,宏观呈现的倾斜角即为安息角.不同重力场中,颗粒堆力链的微观结构存在随机性差异,但是接触力的统计分布规律具有相似性,即接触力的强度随重力成比例增长,且接触点的η分布规律不受重力大小的影响.根据经典力学原理可知,力链的强度成比例增大后不改变力链网络节点的力学平衡,虽然颗粒堆积后的微观结构存在差异,但是整体结构的稳定性不变,即安息角不受影响.文中研究结果与Nakashima等^{[4, 19]}一致,即安息角不受重力大小的影响.近期,Horgan等^{[6, 7]}以安息角随着重力减小而增大为设想,对火星极地表面的沙丘地貌和地质结构进行了研究,但是,如果能进一步实验证明安息角与重力无关,则Horgan等^{[6, 7]}及其他****的相关研究结果需要重新评价.3 结论1) 散体颗粒堆积后,颗粒之间的接触力形成力链,力链结构呈非规则的网络状,且强、弱力链相互交替分布.其中,接触力强度呈对数正态分布,约65%接触力低于平均值,大于平均值的强力链呈指数递减.接触点中约70%处于临界滑移状态,其余接触点的切向力与法向力比值η在[0,μ_t-pp)区间为均匀分布.2) 不同重力场中,散体颗粒堆接触力的概率分布具有相似性,即接触力相对颗粒重力无量刚化后的概率密度函数高度相符,且接触点η的概率分布不受重力大小的影响.接触力分布规律的相似性特征不受颗粒粒径大小、粒径级配和粗糙度的影响.颗粒堆的微观结构存在随机性差异,但宏观安息角与重力的大小无关.
参考文献

[1]	Brucks A, Arndt T, Ottino J M, et al.Behavior of flowing granular materials under variable g[J].Physical Review E, 2007, 75(3):032301.
	Click to display the text
[2]	Hofmeister P G, Blum J, Heiβelmann D.The flow of granular matter under reduced gravity conditions[J].American Institute of Physics Conference Proceedings, 2009, 1145:71-74.
	Click to display the text
[3]	Kleinhans M G, Markies H, Postema F N.Static and dynamic angles of repose in loose granular materials under reduced gravity[J].Journal of Geophysical Research, 2011, 116:E11004.
	Click to display the text
[4]	Nakashima H, Shioji Y, Kobayashi T, et al.Determining the angle of repose of sand under low-gravity conditions using discrete element method[J].Journal of Terramechanics, 2011, 48(1):17-26.
	Click to display the text
[5]	Atwood-Stone C, McEwen A.Avalanche slope angles in low-gravity environments from active Martian sand dunes[J].Geophysical Research Letters, 2013, 40(12):2929-2934.
	Click to display the text
[6]	Horganical H H N, Bell J F.Seasonally active slipface avalanches in the north polar sand sea of Mars:Evidence for a wind related origin[J].Geophysical Research Letters, 2012, 39(9):L09201.
	Click to display the text
[7]	Sullivan R, Anderson R, Biesiadecki J, et al.Cohesions, friction angles, and other physical properties of Martian regolith from Mars exploration rover wheel trenches and wheel scuffs[J].Journal of Geophysical Research, 2011, 116:E02006.
	Click to display the text
[8]	Wong J Y.Predicting the performance of rigid rover wheels on extraterrestrial surfaces based on test results obtained on earth[J].Journal of Terramechanics, 2012, 49(1):49-61.
	Click to display the text
[9]	崔燚, 李雯, 王浚, 等.梯形齿车轮月面牵引性能的离散分析[J].北京航空航天大学学报, 2010, 36(3):253-256. Cui Y, Li W, Wang J, et al.Numerical analysis on traction performance of trapezia lugged wheel by distinct element method[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(3):253-256(in Chinese).
	Cited By in Cnki (4) \| Click to display the text
[10]	Guo Z G, Chen X L, Liu H F, et al.Theoretical and experimental investigation on angle of repose of biomass-coal blends[J].Fuel, 2014, 116:131-139.
	Click to display the text
[11]	Matuttis H G, Luding S, Herrmann H J.Discrete element simulation of dense packing and heaps made of spherical and non-spherical particles[J].Powder Technology, 2000, 109(1):278-292.
	Click to display the text
[12]	Radjai F, Jean M, Moreau J J, et al.Force distributions in dense two-dimensional granular systems[J].Physical Review Letters, 1996, 77(2):274-277.
	Click to display the text
[13]	Zhang L, Wang Y J, Zhang J.Force-chain distributions in granular system[J].Physical Review E, 2014, 89(1):012203.
	Click to display the text
[14]	Thornton C, Antony S J.Quasi-static shear deformation of a soft particle system[J].Powder Technology, 2000, 109(1-3):179-191.
	Click to display the text
[15]	Chung Y C, Liao H H, Hsiau S S.Convection behavior of non-spherical particles in a vibrating bed:Discrete element modeling and experimental validation[J].Powder Technology, 2013, 237:53-66.
	Click to display the text
[16]	高峰, 李雯, 孙刚, 等.模拟月壤可行驶性的离散元数值分析[J].北京航空航天大学学报, 2009, 35(4):501-504. Gao F, Li W, Sun G, et al.Numerical analysis on travelability of lunar soil simulant by means of distinct element method[J].Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(4):501-504(in Chinese).
	Cited By in Cnki (13) \| Click to display the text
[17]	Alberto D R, Francesco P D M.Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes[J].Chemical Engineering Science, 2004, 59(13):525-541.
	Click to display the text
[18]	Alizadeh E, Bertrand F, Chaouki J.Comparision of DEM results and Lagrangian experimental data for the flow and mixing of granules in a rotating drum[J].AIChE Journal, 2014, 60(1):60-75.
	Click to display the text
[19]	Blum J.Astrophysical microgravity experiments with dust particles[J].Microgravity Science Technology, 2010, 22(4):517-527.
	Click to display the text
[20]	Walton O R, Pamela C, Gill K S.Effects of gravity on cohesive of fine powders:Implications for processing Lunar regolith[J].Granular Matter, 2007, 9(5):353-363.
	Click to display the text