
式中:r为无量纲地心距;V为飞行器相对地球的无量纲速度;θ和φ分别为经度和纬度;γ和ψ分别为飞行航迹角和航向角;Ω为地球的自转角速度;σ为飞行器的倾侧角;L和D分别为无量纲的升力加速度和阻力加速度,具体计算公式如下:
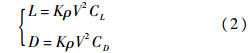
式中:K=0.5R0Sref/m,R0为地球半径,Sref为飞行器参考面积,m为飞行器质量;ρ为大气密度;CL和CD分别为升力系数和阻力系数.1.2 再入过程约束高超滑翔飞行器的再入飞行过程主要考虑热流密度约束Q、动压约束q和过载约束n的影响,具体计算公式如下所示[13, 14]:
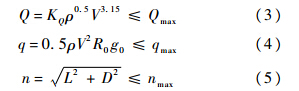
式中:KQ为与飞行器相关的常值参数;g0为海平面地球引力加速度;Qmax、qmax和nmax分别为热流密度约束、动压约束和过载约束的最大幅值,由高超声速飞行器本身的结构和材料所决定.式(3)~式(5)是再入滑翔飞行过程中必须满足的硬约束条件.1.3 再入终端约束不失一般性,引入如下能量形式的e作为自变量:
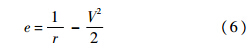
本文考虑的再入飞行终端约束主要包括终端高度约束、终端速度约束和终端经纬度约束,表达形式如下:
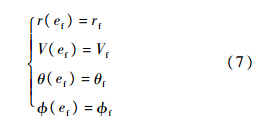
式中:rf、Vf、θf和φf分别为再入滑翔飞行器的给定终端状态.1.4 禁飞区约束禁飞区是指飞行轨迹不能从其上方经过的区域,通常由经纬度表征.本文采用无限高的圆柱模型来描述禁飞区约束,即再入滑翔轨迹与该圆柱不能相交,具体表达形式如下:

式中:(θZ,φZ)为禁飞区圆心;rZ为禁飞区半径.2 预测校正制导2.1 纵向制导律设计考虑到再入飞行器初始下降段的热保护要求,纵向制导设计采用升力式滑翔制导常用的二次函数分段标称攻角剖面,计算公式如下:
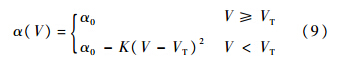
式中:α0为再入攻角初值;VT为飞行器攻角变化的临界马赫数;K为常值参数.通过对热流密度约束、动压约束和过载约束进行转化,可以在高度-速度平面建立再入飞行走廊的下边界,进而得到飞行器倾侧角的幅值限制,具体表达形式如下[15]:
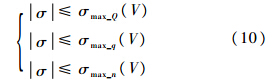
即在过程约束的作用下,倾侧角的最大幅值为
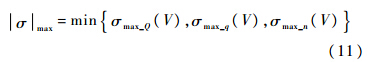
高超声速飞行器的再入点较高,导致初始下降段的气动力较小,因此该段采用开环制导方式.本文选择常值倾侧角σ0作为初始下降段的控制变量,其符号的具体计算公式如下:
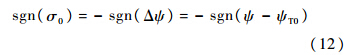
式中:ΨT0为再入初始状态的目标视线角;Δψ为航向角误差.进入滑翔段之后,在每个制导周期内,给定初始倾侧角σi的幅值,从当前状态对运动方程进行积分(倾侧角符号由侧向制导逻辑决定),则能够得到滑翔飞行终端时刻的待飞航程偏差:
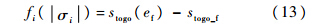
式中:待飞航程s选取星下点圆弧长度进行近似计算,具体计算公式如下:
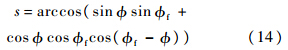
那么,使待飞航程误差f为零的倾侧角幅值可由割线法快速求解,具体计算公式如下[12]:
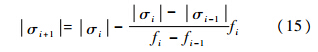
结合式(13)~式(15),即可求得当前制导周期内倾侧角指令的幅值.2.2 侧向制导律设计侧向制导律的主要作用是确定倾侧角指令的符号.为了躲避禁飞区约束,必须寻找合适的倾侧角反转逻辑.传统的侧向误差走廊仅仅考虑了航向角误差对倾侧角指令的影响,无法直接用于处理禁飞区约束.因此,本文设计一种侧向制导逻辑的切换机制,即:1) 当再入飞行器远离禁飞区时(这里认为飞行器与禁飞区圆心的水平距离大于其半径2倍的状态为远离禁飞区),采用传统的航向角误差走廊以实现飞行器的侧向运动控制,其具体形式如图 1所示;
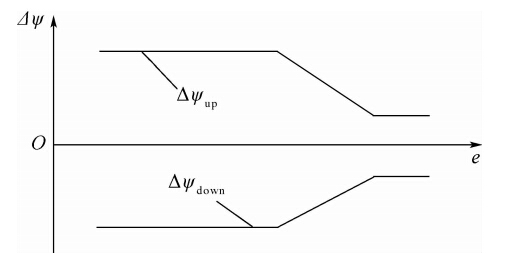 |
| 图 1 航向角误差走廊Fig. 1 Heading angle error corridor |
| 图选项 |
2) 当再入飞行器接近禁飞区时,根据禁飞区的位置和半径来确定当前时刻飞行航向角的导向区域,通过倾侧角反转对制导指令进行修正,使航向角位于该导向区域之内,进而完成禁飞区的规避控制.描述航向角导向区域的相关参数如图 2所示.图中C是飞行器的当前位置,T为目标点的位置,Z为禁飞区的圆心,rZ为禁飞区的半径.在地平面坐标系建立航向角导向区域的几何关系如下:
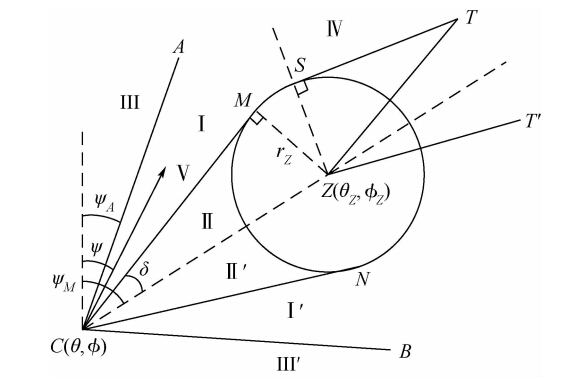 |
| 图 2 航向角导向区域Fig. 2 Heading angle orienting area |
| 图选项 |
1) 过C点作禁飞圆Z的切线CM、CN,记∠MCZ=∠NCZ=δ,则CM、CN构成航向角导向区域的内边界.2) 过C点设计漏斗形的几何区域CA、CB,使∠ACM=∠BCN=δ,则CA、CB构成航向角导向区域的外边界.3) 定义区域Ⅰ和Ⅰ′为航向角的导向区域,定义区域Ⅱ、Ⅱ′、Ⅲ和Ⅲ′为航向角的非导向区域.采用航向角导向区域来控制飞行器侧向运动的基本原理如下所述:1) 当CZ<2rZ时,侧向制导逻辑由传统的航向角误差走廊切换为航向角导向区域.2) 当目标落点位于CZ延长线的左侧时(例如位于T点),飞行器应紧靠禁飞区的左侧完成规避滑翔;当目标点位于CZ延长线的右侧时(例如位于T′点),飞行器应紧靠禁飞区的右侧完成规避滑翔.3) 以左侧规避滑翔为例,当飞行航向角(表征速度方向)位于导向区域Ⅰ时,倾侧角的符号保持不变;当飞行航向角越过导向区域的外边界CA时(即位于区域Ⅲ),倾侧角的符号变为正;当飞行航向角越过导向区域的内边界CM时(即位于区域Ⅱ),倾侧角的符号变为负.该制导逻辑的具体计算公式为
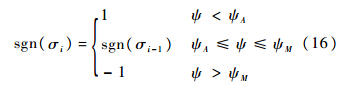
4) 当飞行器的当前位置C越过ZS的延长线而位于区域Ⅳ时(S为过T作禁飞圆切线的切点),认为禁飞区规避已经完成,侧向制导逻辑由航向角导向区域切换回航向角误差走廊,以保证滑翔飞行的落点精度,此时制导逻辑计算公式为
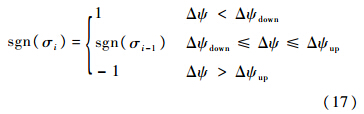
式中:Δψ=ψ-ψT为航向角误差,ψT为目标视线角;Δψup和Δψdown为航向角误差走廊的上下边界(如图 1所示).值得注意的是,本文设计的纵向制导律是通过预测滑翔轨迹的落点纵程进而实时地校正倾侧角指令幅值,因此纵向制导精度不受禁飞区约束的影响.侧向制导逻辑对最终滑翔飞行的落点精度起主要制约作用.在引入禁飞区约束后,通过增加倾侧角指令的反转次数以实现航向控制,而利用航向角导向区域的内边界约束(CM,CN)可以有效地规避禁飞区,利用外边界约束(CA,CB)可以限制飞行器在规避禁飞区时产生的航向偏移,进而保证了侧向制导精度.除此之外,完成禁飞区规避后,侧向制导逻辑由航向角导向区域切换至航向角误差走廊,进一步保证最终滑翔飞行的落点精度能够满足要求.3 仿真分析再入飞行器的初始状态见表 1,终端状态约束如下:目标位置(E90°,N30°),终端高度20 km,终端速度1 800 m/s.标称攻角剖面参数:K=0.11,α0=22°,VT=16 Ma.倾侧角指令的取值范围为-85°~85°.仿真计算机为Windows XP操作系统,主频3.0 GHz,内存2.0 GB.制导程序采用标准C/C++语言编写.表 1 飞行器初始再入状态Table 1 Initial reentry conditions of the vehicle
| 参数 | 高度/ km | 速度/ (m·s-1) | 经度/ (°) | 纬度/ (°) | 航迹角/ (°) | 航向角/ (°) |
| 数值 | 80.0 | 7 100.0 | 10.0 | -20.0 | -1.0 | 45.0 |
表选项
3.1 标准条件下制导方法仿真分析为了验证本文提出的制导算法具有可行性,设计以下3个仿真算例:算例1采用传统的预测校正制导方法;算例2和算例3采用考虑禁飞区规避的预测校正制导方法.其中,给定两个半径不同的禁飞区约束,其具体参数见表 2.表 2 标准条件下的禁飞区约束Table 2 No-fly zone constraints in standard conditions
| 禁飞区约束 | 中心位置 | 半径/km |
| 算例2 | (N10°,E60°) | 700 |
| 算例3 | (N10°,E60°) | 1 000 |
表选项
图 3(a)~图 3(c)给出了标准条件下(不考虑再入点散布误差)的制导仿真结果.通过对比得出以下结论:
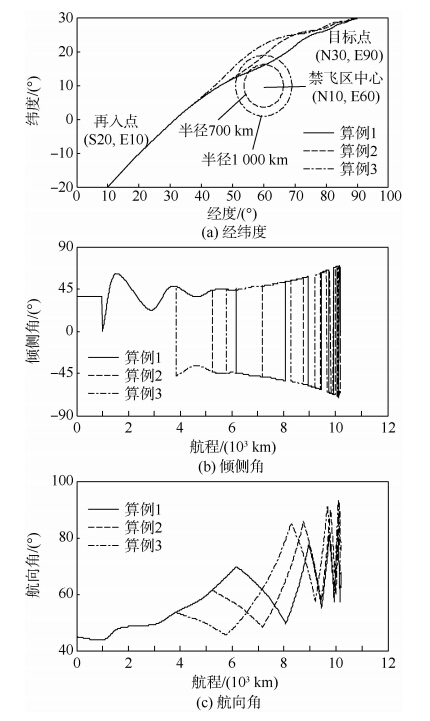 |
| 图 3 标准条件下制导仿真结果Fig. 3 Results of reentry guidance in standard condition |
| 图选项 |
1) 两种制导方法都能够满足预定航程要求,落点的经纬度误差均小于0.1°,与目标点的距离不超过10 km,符合再入制导的精度要求.2) 与算例1相比,本文提出的制导算法能够导引飞行器躲避半径不同的禁飞区约束,验证了该方法的可行性.3) 算例2和算例3表明,考虑禁飞区规避的制导算法能够根据禁飞区的位置和半径自适应地修正制导指令,提高了再入滑翔飞行的机动性.3.2 扰动条件下制导方法仿真分析再入滑翔飞行过程中,大气模型的不确定性和动力学系统的强扰动性都可能致使飞行器偏离初始轨迹和预定目标,进而导致飞行任务失败.为了验证考虑禁飞区规避的预测校正制导方法对各种参数偏差条件具有鲁棒性,针对不同初始扰动情况下的再入滑翔制导,进行了Monte Carlo仿真实验.给定两个位置不同的禁飞区约束,其具体参数见表 3.再入点初始散布偏差和飞行参数误差的分布类型及误差限见表 4.表 3 扰动条件下的禁飞区约束Table 3 No-fly zone constraints with dispersions
| 禁飞区约束 | 中心位置 | 半径/km |
| 禁飞区1 | (N1°,E45°) | 700 |
| 禁飞区2 | (N25°,E58°) | 700 |
表选项
表 4 再入点散布偏差和飞行参数误差Table 4 Dispersions of reentry interface and flight parameters
| 偏差项 | 分布类型 | 偏差限 |
| 高度偏差Δh/km | 均匀分布 | ±2.0 |
| 经度偏差Δθ/(°) | 均匀分布 | ±0.2 |
| 纬度偏差Δφ/(°) | 均匀分布 | ±0.2 |
| 速度偏差ΔV/(m·s-1) | 高斯分布 | ±100 |
| 航迹角偏差Δγ/(°) | 高斯分布 | ±0.3 |
| 航向角偏差Δψ/(°) | 均匀分布 | ±1.0 |
| 升力系数误差ΔCL/% | 高斯分布 | ±10 |
| 阻力系数误差ΔCD/% | 高斯分布 | ±10 |
表选项
图 4(a)~图 4(i)给出了扰动条件下的制导仿真曲线.图 4(j)给出了扰动条件下的落点散布统计.
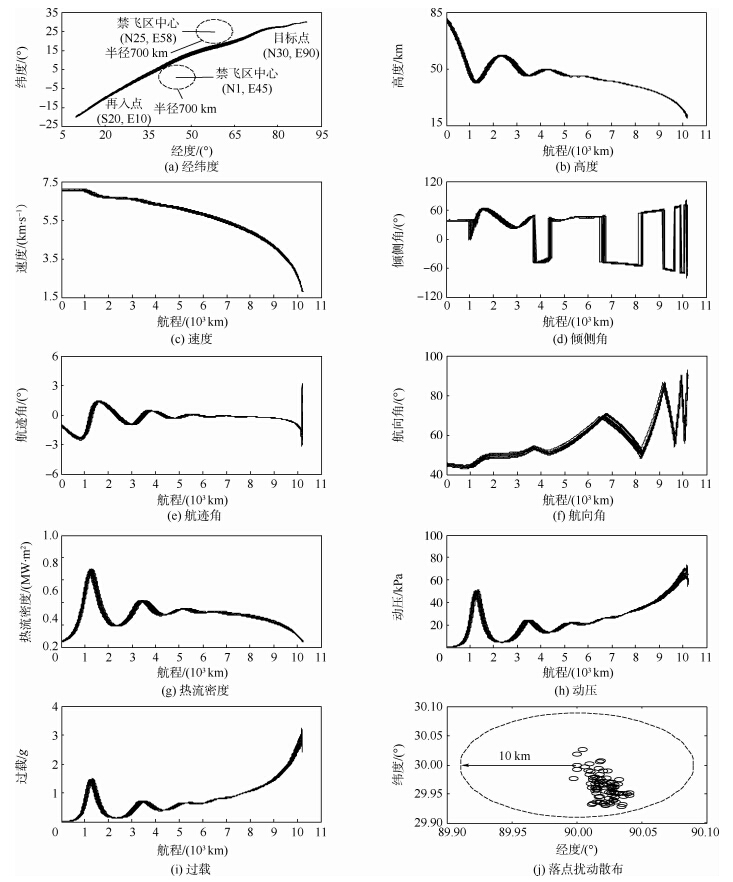 |
| 图 4 扰动条件下制导仿真结果Fig. 4 Results of reentry guidance with random dispersions |
| 图选项 |
通过分析得出以下结论:1) Monte Carlo仿真实验表明,考虑禁飞区规避的预测校正制导可以满足预定航程要求,其终端经纬度误差均小于0.1°,符合再入制导的精度要求.2) 经纬度扰动散布偏差表明,再入落点受到禁飞区约束的影响,主要集中在目标点的东南方,与目标点距离不超过10 km.3) 在再入点初始散布误差存在的情况下,滑翔飞行轨迹能够满足路径约束、终端约束和禁飞区约束的要求,然而,初始航向角偏差过大会对制导精度产生影响,因此应该尽量减小再入滑翔飞行的初始航向角偏差.4) 仿真结果表明,在飞行过程中引入升力系数误差和阻力系数误差,会在一定程度上影响纵向制导的精度,但预测校正制导仍然满足给定的精度需求,且没有对禁飞区规避产生影响,说明本文提出的算法具备可行性和鲁棒性.5) 对于传统的再入预测校正制导方法,倾侧角指令往往进行2~3次反转以实现航向控制.为了提升飞行器的横向机动性能,本文引入了禁飞区规避机制,且每添加一个禁飞区约束,倾侧角指令都需要增加2次反转.从Monte Carlo仿真结果可以发现,每一次制导指令反转时刻对应的飞行航程间隔均在200 km以上,因而不会超过飞行器的机动能力限制,进而保证了制导精度要求.4 结 论本文针对升力式高超声速飞行器再入制导问题,提出了一种考虑禁飞区规避的预测校正制导方法,研究分析和仿真结果表明:1) 本文提出的制导方法易于实现,且不改变传统预测校正制导的表达形式,不依赖于标准再入轨迹.2) 改进的侧向制导逻辑可以进行航向角误差走廊和航向角导向区域的切换,提高了倾侧角反转策略的灵活性.3) 标准条件下的仿真结果表明,与传统的预测校正制导相比,本文提出的制导方法能够有效地规避禁飞区约束.4) 扰动条件下的Monte Carlo仿真结果表明,本文提出的制导方法具有良好的鲁棒性.
参考文献
| [1] | Sarah N D,Nesrin S K.Survey of planetary entry guidance algorithms[J].Progress in Aerospace Sciences,2014,68:22-28. |
| Click to display the text | Cited By in Cnki (0) | |
| [2] | Zhao J,Zhou R,Jin X L.Progress in reentry trajectory planning for hypersonic vehicle[J].Journal of Systems Engineering and Electronics,2014,25(4):627-639. |
| Click to display the text | |
| [3] | Lu P.Predictor-corrector entry guidance for low-lifting vehicles[J].Journal of Guidance Control and Dynamics,2008,31(4):1067-1075. |
| Click to display the text | |
| [4] | 梁子璇,任章.基于在线气动参数修正的预测制导方法[J].北京航空航天大学学报,2013,39(7):853-857. Liang Z X,Ren Z.Predictive reentry guidance with aerodynamic parameter online correction[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(7):853-857(in Chinese). |
| Cited By in Cnki (1) | |
| [5] | Jorris T R,Cobb R G.Three-dimensional trajectory optimization satisfying waypoint and no fly zone constraints[J].Journal of Guidance Control and Dynamics,2009,32(2):551-572. |
| Click to display the text | |
| [6] | 谢愈,刘鲁华,汤国建,等.多约束条件下高超声速滑翔飞行器轨迹优化[J].宇航学报,2011,32(12):2499-2504. Xie Y,Liu L H,Tang G J,et al.Trajectory optimization for hypersonic glide vehicle with multi-constraints[J].Journal of Astronautics,2011,32(12):2499-2504(in Chinese). |
| Cited By in Cnki (6) | |
| [7] | Zhao J,Zhou R.Reentry trajectory optimization for hypersonic vehicle satisfying complex constraints[J].Chinese Journal of Aeronautics,2013,26(6):1544-1553. |
| Click to display the text | |
| [8] | Zhao J,Zhou R,Jin X L.Reentry trajectory optimization based on a multistage pseudospectral method[J].Scientific World Journal,2014,878193:1-13. |
| Click to display the text | |
| [9] | 雍恩米,钱炜祺,唐伟,等.考虑禁飞圆的滑翔式机动弹道与气动特性参数耦合设计[J].航空学报,2013,34(1):66-75. Yong E M,Qian W Q,Tang W,et al.Coupled design of maneuver glide reentry trajectory and aerodynamic characteristic parameters considering no-fly zone[J].Acta Aeronautica et Astronautica Sinica,2013,34(1):66-75(in Chinese). |
| Cited By in Cnki (2) | |
| [10] | 张科南,周浩,陈万春.高超声速飞行器多约束多种机动突防模式弹道规划[J].弹道学报,2012,24(3):85-90. Zhang K N,Zhou H,Chen W C.Trajectory planning for hypersonic vehicle with multiple constraints and multiple maneuvering penetration strategies[J].Journal of Ballistics,2012,24(3): 85-90(in Chinese). |
| Cited By in Cnki (1) | |
| [11] | Xie Y,Liu L H,Tang G J,et al.Highly constrained entry trajectory generation[J].Acta Astronautica,2013,88(1):44-66. |
| Click to display the text | |
| [12] | Xue S B,Lu P.Constrained predictor-corrector entry guidance[J].Journal of Guidance Control and Dynamics,2010,33(4):1273-1281. |
| Click to display the text | |
| [13] | 王青,莫华东,吴振东,等.基于能量的高超声速飞行器再入混合制导方法[J].北京航空航天大学学报,2014,40(5):580-585. Wang Q,Mo H D,Wu Z D,et al.Energy-based hybrid reentry guidance for hypersonic vehicles[J].Journal of Beijing University of Aeronautics and Astronautics,2014,40(5):580-585(in Chinese). |
| Cited By in Cnki | |
| [14] | Zhao J,Zhou R,Jin X L.Gauss pseudospectral method applied to multi-objective spacecraft trajectory optimization[J].Journal of Computational and Theoretical Nanoscience,2014,11(10):2242-2246. |
| Click to display the text | |
| [15] | Lu P,Xue S B.Rapid generation of accurate entry landing footprints[J].Journal of Guidance Control and Dynamics,2010,33(3): 756-767. |
| Click to display the text |
