摘要/Abstract
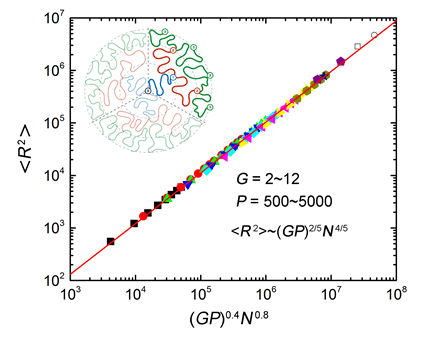
树枝形大分子是一种新型高分子材料,其浓度分布、末端官能团分布和分子尺寸决定了材料的性质.在柔性支化臂条件下,推导了均聚物树枝形大分子在溶剂中的自洽场理论,计算了不同代数G的树枝形大分子的链节浓度分布.计算结果表明:(1)在良溶剂(或绝热溶剂)中,柔性支化臂的树枝形大分子符合"dense-core"模型,链节浓度沿径向缓慢下降;(2)由于柔性链的折回构象,末端链没有向球形分子的外缘球壳层聚集的倾向;(3)不同代数的支化臂所受的拉伸强度不同,近中心处的第一代支化臂所受的拉伸程度最大;(4)自洽场计算与Flory平均场理论标度律估算结果一致,得到树枝形大分子在良溶剂中的分子尺寸具有标度律R~(GP)1/5N2/5,其中P是单个支化臂的聚合度,N是分子的总的链段数;(5)在G固定的情况下,该标度律简化为R~P3/5.
关键词: 树枝形大分子, 平均场理论, 自洽场理论, 标度律
Dendrimers are a class of novel polymer materials, which have received a lot of attention in past decades. The property of a dendrimer material strongly depends on the conformational details of the molecules, including the monomer density distribution, the functional end-group distribution, and the molecular size. In this paper, we consider a dendrimer composed of flexible and long spacers, immersed in the athermal or good solvent. A self-consistent field theory (SCFT) with a pre-averaged excluded volume potential is employed to calculate the density profiles of the segments and the radius of gyration R of the dendrimers. The stretched conformation of the spacers, and the scaling laws between the dendrimer size and its topologic parameters are analyzed. Our main results are:(1) The segment density of the dendrimers obeys the "dense-core" model, and decreases smoothly along the radial direction. (2) Due to the folding-back conformation, the local density of the end-segments is proportional to the local segment density. The density profile of the end-segments does not have a lifted peak at the outer layer of the spherical molecule. (3) The conformation of the spacers with lower generation numbers is strongly stretched in the central region where the segments are crowded. The first-generation spacers are mostly stretched. However, the spacers with higher generation numbers are much weakly stretched in the outer region. (4) Our self-consistent field theory calculations give the scaling law of the dendrimer size R~(GP)1/5N2/5, where G is the generation number of the dendrimer, P is the spacer segment number, and N is the total segment number. This agrees with the Flory mean field calculation for dendrimer based on full segment number. But it disagrees with the pioneer theories based on a linear side chains and the results from Monte Carlo simulations, which gave R~(GP)2/5N1/5. This disagreement is attributed to the limited bond length in simulations and the unlimited stretchable spacers in SCFT. (5) If G is fixed, the scaling law is simplified to R~P3/5 in good solvent, which agrees with the pioneer theories.
Key words: dendrimer, mean-field theory, self-consistent field theory, scaling law
PDF全文下载地址:
点我下载PDF
