
 , 丁桦2,3
, 丁桦2,3 1. 东北大学 轧制技术及连轧自动化国家重点实验室, 辽宁 沈阳 110819;
2. 东北大学 材料科学与工程学院, 辽宁 沈阳 110819;
3. 辽宁省轻量化用关键金属结构材料制备重点实验室, 辽宁 沈阳 110819
收稿日期:2020-08-05
基金项目:国家自然科学基金资助项目(51974084)。
作者简介:陈勇(1989-),男,河北唐山人,东北大学博士研究生;
张晓明(1965-),男,黑龙江青冈人,东北大学教授,博士生导师;
丁桦(1958-),女,安徽合肥人,东北大学教授,博士生导师。
摘要:对高锰TWIP钢进行不同温度(850~1 100 ℃)和应变速率(0.01, 0.1, 1, 5, 10 s-1)的绝热压缩试验, 研究试验钢高温热变形行为. 分析了变形温度和应变速率对流动特性的影响, 建立了应变补偿型本构方程, 并采用三种标准统计参数对应变补偿型本构方程的精确度进行了评估. 结果表明: 流动应力对变形温度和应变速率的敏感程度很高, 且随着变形温度的提高或应变速率的降低, 流动应力呈下降趋势; 应变速率对动态再结晶过程有着很复杂的影响; 流动应力预测值与试验值具有较高的吻合度, 表明建立的应变补偿型本构方程能够精确预测流动应力.
关键词:高锰TWIP钢热变形流动特性本构方程应变补偿
Hot Deformation Behavior of a High-Mn TWIP Steel and Establishment of Strain-Compensated Constitutive Equation
CHEN Yong1, WEN Guang-qi2,3, ZHANG Xiao-ming1

 , DING Hua2,3
, DING Hua2,3 1. State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang 110819, China;
2. School of Materials Science & Engineering, Northeastern University, Shenyang 110819, China;
3. Key Laboratory of Lightweight Structural Materials, Liaoning Province, Shenyang 110819, China
Corresponding author: ZHANG Xiao-ming, E-mail: zhangxm@ral.neu.edu.cn.
Abstract: Hot deformation behaviors of a high-Mn twinning induced plasticity (TWIP) steel were investigated using isothermal hot compression tests at different temperature ranging from 850 ℃ to 1 100 ℃ and constant strain rates of 0.01, 0.1, 1, 5 and 10 s-1, respectively. The effects of deformation temperature and strain rate on flow behavior were analyzed. A developed constitutive equation considering the strain compensation was established and its accuracy was evaluated based on three standard statistical parameters. The results indicate that the flow stress is strongly sensitive to deformation temperature and strain rate, which decreases with the increase in temperature or the decrease in strain rate. Strain rate has a complex influence on the kinetics of dynamic recrystallization. Since the predicted flow stress is in good agreement with the experimental one, it proves that the strain-compensated constitutive equation can estimate the flow stress accurately.
Key words: high-Mn TWIP steelhot deformationflow behaviorconstitutive equationstrain compensation
高锰TWIP钢同时具备高强度和高韧性, 已成功应用于低温储罐的制造[1-4]. 目前, 高锰储罐钢通常在热轧后直接使用, 且热轧工艺参数, 如轧制温度、压下量分布和冷却速率等在高锰钢钢板的微观组织和力学性能的调控中起着至关重要的作用. 因此, 为使高锰钢满足使用需求, 需制定合理的热轧工艺参数. 热轧工艺参数的制定需充分考虑高锰钢在不同热加工条件下的流动特性. 而本构方程能够将应力和应变与相应的加工条件(比如温度和应变速率)联系起来, 是研究高锰钢高温流动特性的有效工具. 因此, 有必要构建合适的本构方程.
近年来, 国内外****对高锰TWIP钢的本构特性进行了大量的研究[5-9]. 然而, 绝大多数先前的研究仅仅考虑了温度和应变速率的影响, 应变的影响通常被忽视. 已有研究指出, 应变对本构方程中的材料常数和变形激活能具有强烈的影响, 因此, 在建立本构方程时应考虑应变补偿[10-12].
本文以高锰TWIP钢为研究对象, 通过不同温度和应变速率的热压缩试验研究了高锰钢热变形行为, 建立了应变补偿型本构方程, 并评估了应变补偿型本构方程在整个试验范围内的精确度.
1 试验材料和方法本试验使用的高锰钢是化学成分为25.98Mn-0.21C-0.97Al-0.51Si (质量分数)的锻坯. 该锻坯的微观组织和X射线衍射图谱如图 1所示. 从图 1可以看出, 锻坯的微观组织由等轴的奥氏体晶粒组成, 且奥氏体的平均晶粒尺寸为50 μm. 尺寸为?8 mm×h15 mm的圆柱试样直接取自于高锰钢锻坯. 采用MMS-200热模拟试验机, 对圆柱试样进行不同温度(850~1 100 ℃)和应变速率(0.01, 0.1, 1, 5, 10 s-1)的绝热压缩. 在压缩之前, 先将试样加热到1 200 ℃并保温5 min, 然后冷却到变形温度. 所有试样在变形温度保温30 s, 然后进行真应变为0.8的压缩, 压缩完以后, 立即将试样水冷到室温. 本试验将厚度为0.1 mm的钽片置于试样两端, 以减小压缩过程中的摩擦.
图 1(Fig. 1)
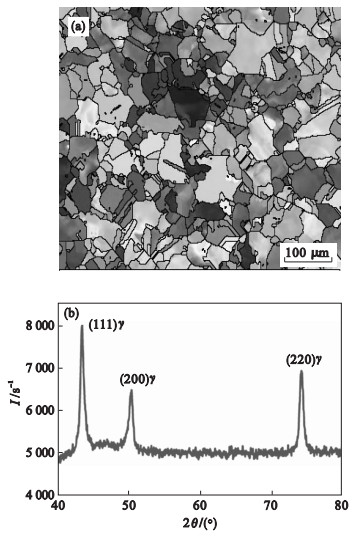 | 图 1 锻坯的反极图和X射线衍射图谱Fig.1 IPF map and X-ray diffraction pattern of the forging stock (a)-反极图;(b)-X射线衍射图. |
2 试验结果与讨论2.1 流变应力行为图 2为不同温度和应变速率下压缩所获得的真应力-真应变曲线. 从图 2可以看出, 在相同应变速率下, 流动应力随着温度的升高而降低, 而在相同温度下, 流动应力随着应变速率的升高而升高. 主要是由于温度升高时, 金属原子的扩散速度加快, 加工硬化增殖的位错更容易发生交滑移或攀移, 从而使动态软化作用增强; 而应变速率升高缩短了累积畸变能和位错湮灭的时间, 不利于软化行为的发生[13]. 从图 2还可以看出, 大多数曲线存在峰值, 表明在压缩变形过程中发生了动态再结晶现象. 动态再结晶一般发生在大角度晶界处, 如变形晶粒的晶界、动态再结晶晶粒的晶界或变形过程中产生的大角度晶界(与变形带或形变孪晶相关的晶界)[14]. 微观组织的观察(图 3)也证实了动态再结晶的存在. 从图 3可以看出, 当变形温度为850 ℃, 应变速率为0.1 s-1时, 微观组织主要由拉长的变形晶粒组成. 变形晶粒的晶界呈锯齿状, 且在晶界处形成了新的动态再结晶晶粒. 保持应变速率不变, 当温度升高到1 050 ℃时, 大量变形晶粒被细等轴晶粒替代, 说明提高变形温度有助于动态再结晶的进行. 在1 050 ℃的变形温度下, 将应变速率降低到0.01 s-1时, 微观组织为等轴的奥氏体晶粒, 将应变速率升高到1 s-1时, 微观组织也由等轴的奥氏体晶粒组成, 但与应变速率为0.01 s-1的试样相比, 该变形条件下的试样晶粒尺寸更加细小. 由此可知, 应变速率对再结晶过程有着很复杂的影响. 在低应变速率下(< 0.1 s-1), 晶界有更多的时间迁移, 动态再结晶以晶粒的长大为主, 因此, 动态再结晶晶粒尺寸较为粗大. 在高应变速率下(≥1 s-1), 高储存能和绝热温升共同作用, 使晶界以更快的速度迁移, 促进了动态再结晶晶粒的形核, 而由于变形时间较短, 动态再结晶晶粒尺寸较为细小. 在中应变速率下变形时(0.1 s-1), 储存能不够高, 晶界迁移的时间也不够长, 动态再结晶过程缓慢, 试样内部仍存在变形组织.
图 2(Fig. 2)
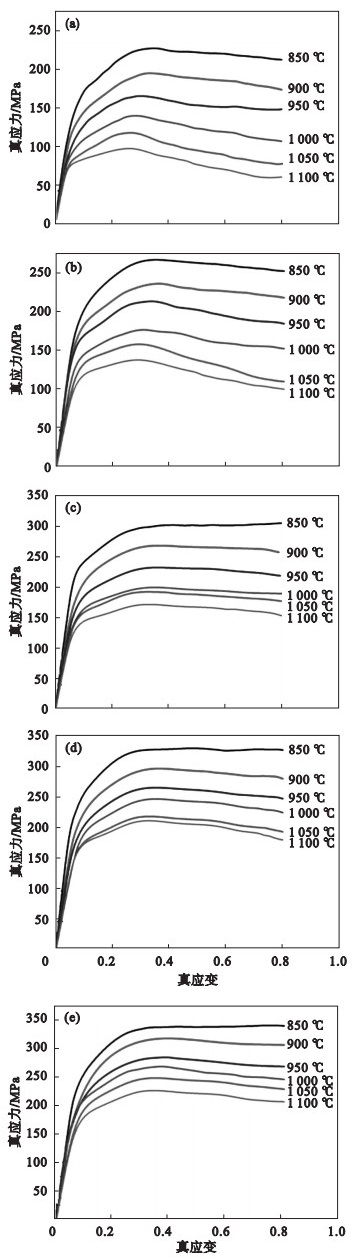 | 图 2 不同温度和应变速率下的真应力-真应变曲线Fig.2 True stress-true strain curves of the tested specimen deformed at different temperatures and strain rates (a)-0.01 s-1; (b)-0.1 s-1; (c)-1 s-1; (d)-5 s-1; (e) -10 s-1. |
图 3(Fig. 3)
 | 图 3 变形试样的反极图Fig.3 IPF maps of the deformed specimens (a)-850 ℃, 0.1 s-1; (b)-1 050 ℃, 0.01 s-1; (c)-1 050 ℃, 0.1 s-1; (d) -1 050 ℃, 1 s-1. |
2.2 本构方程为进一步研究试验钢的热变形行为, 有必要建立合适的本构方程. Zener和Hollomon提出了Zener-Hollomon参数(式(1)) 用来表示温度(T)和应变速率(
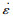
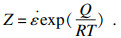 | (1) |
 | (2) |
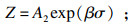 | (3) |
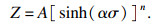 | (4) |
结合式(1)~式(4), 可以获得以下3个本构方程:
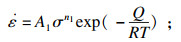 | (5) |
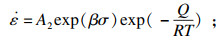 | (6) |
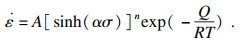 | (7) |
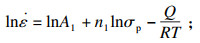 | (8) |
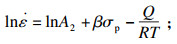 | (9) |
 | (10) |
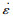
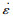
图 4(Fig. 4)
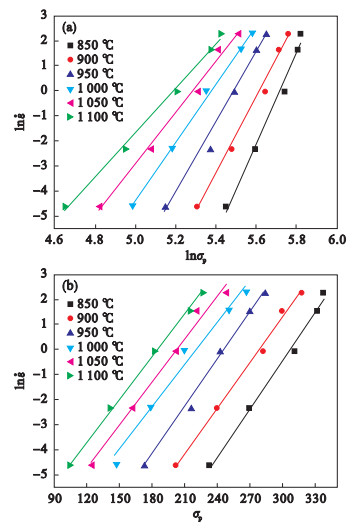 | 图 4 n1和β值的确定Fig.4 Determination of the values of n1 and β (a)-n1; (b)-β. |
另外, 式(10)可以改写为
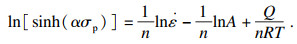 | (11) |
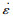
图 5(Fig. 5)
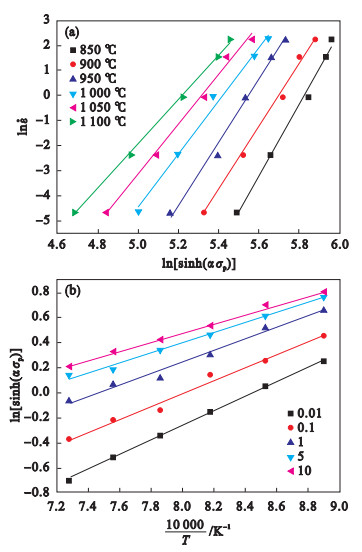 | 图 5 n和Q/(Rn)值的确定Fig.5 Determination of the values of n and Q/(Rn) (a)-n; (b)-Q/(Rn). |
对式(4)两边取自然对数, 并用σp替代σ, 可以得到如下公式:
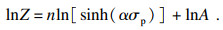 | (12) |
图 6(Fig. 6)
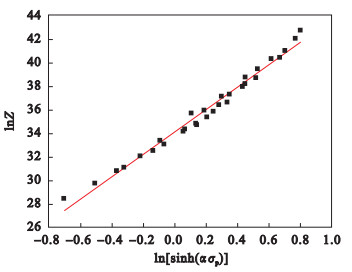 | 图 6 lnA和A值的确定Fig.6 Determination of the values of lnA and A |
通过以上分析, 把A, α, n和Q的值代入式(7), 可以求得用于表示试验钢热加工特性的峰值应力本构方程, 如式(13)所示:
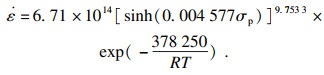 | (13) |
图 7(Fig. 7)
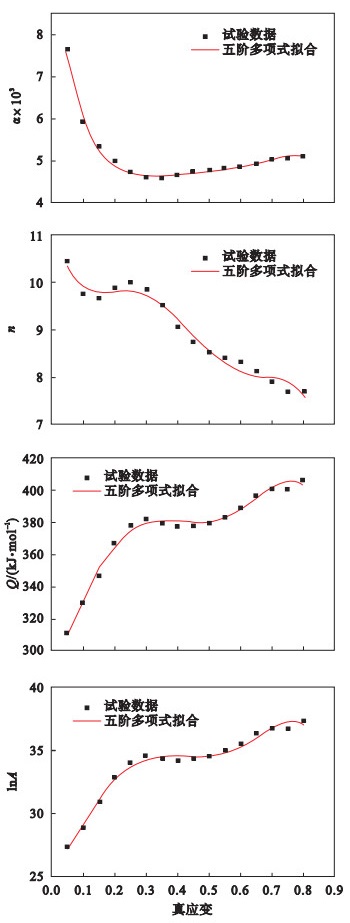 | 图 7 不同应变水平下的材料常数和变形激活能Fig.7 Material constant and deformation activation energy at different strain levels |
表 1(Table 1)
| 表 1 α, n, Q和lnA的多项式拟合结果 Table 1 Polynomial fitting results of α, n, Q and lnA |
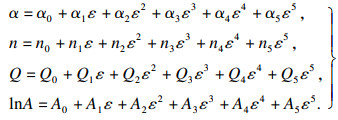 | (14) |
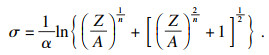 | (15) |
图 8(Fig. 8)
 | 图 8 预测的流动应力(符号)与试验测量的流动应力曲线(实线)对比Fig.8 Comparisons between the predicted flow stress (symbols) and measured one (solid lines) (a)-0.01 s-1; (b)-0.1 s-1; (c)-1 s-1; (d) -5 s-1; (e) -10 s-1. |
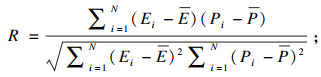 | (16) |
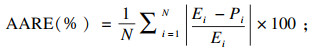 | (17) |
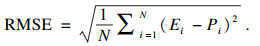 | (18) |
作为常用的统计参数, R能够用来评估试验值和预测值的线性相关程度. 然而, 更高的R值并不总是表示一个模型或公式具有更好的预测能力, 主要是因为该模型或公式可能存在偏向更高值或更低值的趋势. 因此, 为评估应变补偿型本构方程的预测能力, 本文也计算了无偏统计参数AARE和RMSE. 图 9所示为预测的流动应力与试验值的综合对比. 从图中可以看出, 绝大多数数据点靠近最佳线, 且R, AARE和RMSE的值分别为0.994 58, 3.132%和6.972 MPa. 从以上结果可知, 建立的应变补偿型本构方程能够精确预测本试验范围内的流动应力.
图 9(Fig. 9)
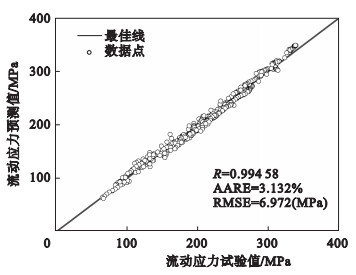 | 图 9 预测的流动应力与试验值在整个应变、应变速率和温度范围内的相关性Fig.9 Correlation between the predicted flow stress experimental one within the entire range of strain, strain rate and temperature |
3 结论1) 流动应力对变形温度和应变速率的敏感程度很高. 随着温度的升高, 流动应力呈下降趋势, 而随着应变速率的升高, 流动应力呈上升的趋势.
2) 应变速率对再结晶过程有着很复杂的影响. 在低应变速率下(< 0.1 s-1), 晶界有更长的时间迁移, 动态再结晶以晶粒的长大为主, 导致动态再结晶晶粒尺寸较为粗大. 在高应变速率下(≥1 s-1), 高储存能、绝热温升和较短的变形时间共同作用, 使动态再结晶以晶粒的形核为主, 动态再结晶晶粒尺寸较为细小. 在中应变速率下变形时(0.1 s-1), 形核与长大均不占主导地位, 动态再结晶过程缓慢.
3) 建立了试验钢在850~1 100 ℃温度范围内的峰值应力本构方程:
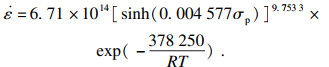 |
参考文献
| [1] | Li Y, Lu Y F, Li W, et al. Hierarchical microstructure design of a bimodal grained twinning-induced plasticity steel with excellent cryogenic mechanical properties[J]. Acta Materialia, 2018, 158: 79-94. DOI:10.1016/j.actamat.2018.06.019 |
| [2] | Wang X J, Sun X J, Song C, et al. Enhancement of yield strength by chromium/nitrogen alloying in high-manganese cryogenic steel[J]. Materials Science & Engineering A, 2017, 698: 110-116. |
| [3] | Chen Y, Zhang X M, Cai Z H, et al. Effects of rolling temperature on the microstructure and mechanical properties of a high-Mn austenitic steel for cryogenic applications[J]. Steel Research International, 2020, 91(7): 1900660. DOI:10.1002/srin.201900660 |
| [4] | Chen J, Ren J K, Liu Z Y, et al. The essential role of niobium in high manganese austenitic steel for application in liquefied natural gas tanks[J]. Materials Science & Engineering A, 2020, 772: 138733. |
| [5] | Hamada A, Juuti T, Khosravifard A, et al. Effect of silicon on the hot deformation behavior of microalloyed TWIP-type stainless steels[J]. Materials & Design, 2018, 154: 117-129. |
| [6] | Li D J, Feng Y R, Yin Z F, et al. Prediction of hot deformation behaviour of Fe-25Mn-3Si-3Al TWIP steel[J]. Materials Science & Engineering A, 2011, 528(28): 8084-8089. |
| [7] | Li D Z, Wei Y H, Liu C Y, et al. Hot deformation behaviors of Fe-30Mn-3Si-3Al TWIP steel during compression at elevated temperature and strain rate[J]. Steel Research International, 2013, 84(8): 740-750. DOI:10.1002/srin.201200254 |
| [8] | Mejía I, Reyes-Calderón F, Cabrera J M. Modeling the hot flow behavior of a Fe-22Mn-0.41C-1.6Al-1.4Si TWIP steel microalloyed with Ti, V and Nb[J]. Materials Science & Engineering A, 2015, 644: 374-385. |
| [9] | Li D J, Bai Q, Feng Y R, et al. Influences of Nb-microalloying on the hot deformation behavior of Fe-25Mn-3Si-3Al TWIP steel[J]. Materials Research Express, 2019, 6(8): 0865g6. DOI:10.1088/2053-1591/ab25b9 |
| [10] | Cai J, Li F G, Liu T Y, et al. Constitutive equations for elevated temperature flow stress of Ti-6Al-4V alloy considering the effect of strain[J]. Materials & Design, 2011, 32(3): 1144-1151. |
| [11] | Ji G L, Li F G, Li Q H, et al. A comparative study on Arrhenius-type constitutive model and artificial neural network model to predict high-temperature deformation behaviour in Aermet100 steel[J]. Materials Science & Engineering A, 2011, 528(13/14): 4774-4782. |
| [12] | Haghdadi N, Zarei-Hanzaki A, Abedi H R. The flow behavior modeling of cast A356 aluminum alloy at elevated temperatures considering the effect of strain[J]. Materials Science & Engineering A, 2012, 535: 252-257. |
| [13] | McQueen H J, Ryan N D. Constitutive analysis in hot working[J]. Materials Science & Engineering A, 2002, 322(1/2): 43-63. |
| [14] | Marandi A, Zarei-Hanzaki A, Haghdadi N, et al. The prediction of hot deformation behavior in Fe-21Mn-2.5Si-1.5Al transformation-twinning induced plasticity steel[J]. Materials Science & Engineering A, 2012, 554: 72-78. |
| [15] | Zener C, Hollomon J H. Effect of strain rate upon plastic flow of steel[J]. Journal of Applied Physics, 1944, 15(1): 22-32. DOI:10.1063/1.1707363 |
| [16] | Medina S F, Hernandez C A. General expression of the Zener-Hollomon parameter as a function of the chemical composition of low alloy and microalloyed steels[J]. Acta Materialia, 1996, 44(1): 137-148. DOI:10.1016/1359-6454(95)00151-0 |
| [17] | Sellars C M, Mctegart W J. On the mechanism of hot deformation[J]. Acta Metallurgica Sinica, 1966, 14(9): 1136-1138. DOI:10.1016/0001-6160(66)90207-0 |
| [18] | Sellars C M, Mctegart W J. La relation entre la résistance et la structure dans la deformation à chaud[J]. Mémoires Scientifiques de la Revue de Metallurgie, 1966, 63: 731-746. DOI:10.1051/metal/196663090731 |
| [19] | Jonas J J, Sellars C M, Mctegart W J. Strength and structure under hot-working conditions[J]. Revue De Metallurgie Cahiers Dinformations Techniques, 1969, 14(1): 1-24. |
| [20] | Sellars C M, Mctegart W J. Hot workability[J]. International Metallurgical Reviews, 1972, 17: 1-24. |
| [21] | Zhang J Q, Di H S, Wang X Y, et al. Constitutive analysis of the hot deformation behavior of Fe-23Mn-2Al-0.2C twinning induced plasticity steel in consideration of strain[J]. Materials & Design, 2013, 44: 354-364. |
| [22] | Hamada A S, Karjalainen L P, Somani M C. The influence of aluminum on hot deformation behavior and tensile properties of high-Mn TWIP steels[J]. Materials Science & Engineering A, 2007, 467(1/2): 114-124. |
| [23] | Cai J, Li F G, Liu T Y, et al. Constitutive equations for elevated temperature flow stress of Ti-6Al-4V alloy considering the effect of strain[J]. Materials & Design, 2011, 32(3): 1144-1151. |
| [24] | Changizian P, Zarei-Hanzaki A, Roostaei A A. The high temperature flow behavior modeling of AZ81 magnesium alloy considering strain effects[J]. Materials & Design, 2012, 39: 384-389. |
