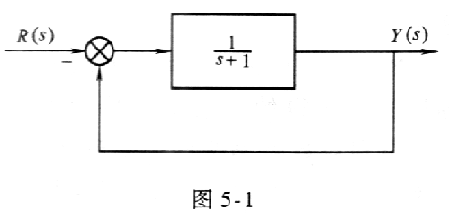
4-1 某系统结构图如图5－1所示。试根据频率特性的概念，求下列输入信号作用下系统的稳态误差。

　　　（1）　r(t)=sin2t

　　　（2）　r(t)=sin(t+30)－2cos(2t-45)

　4-2 若系统单位阶跃响应y(t)=1-1.8e^-4t +0.8e^-9t t>=0，试求系统频率特性。

　4-3 绘出下列系统的极坐标图。

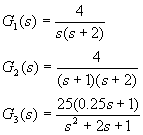
　4-4 绘出下列传递函数的幅相特性。

　4-5 绘出下列传递函数的近似对数频率特性。

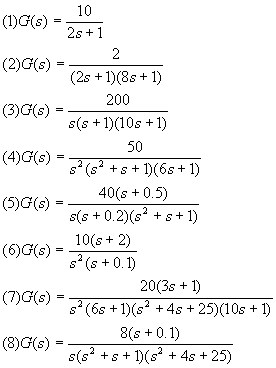
　4-6 设系统的开环对数幅频特性的分段直线近似表示如图5－2所示（设为最小线性相位系统）。试写出系统的开环传递函数。

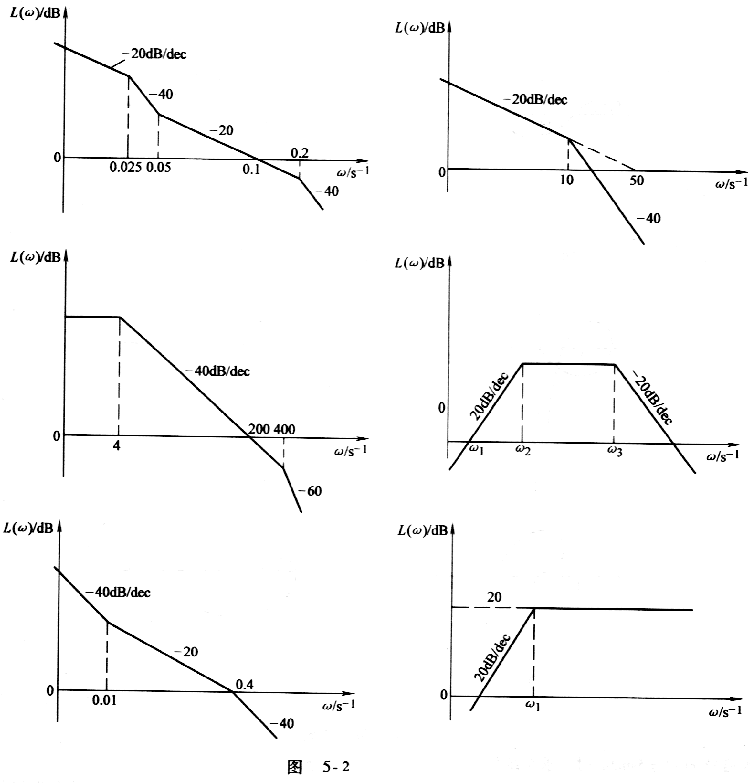
　4－7 设系统的开环幅相频率特性如图5－3所示。试判断闭环系统的稳定性。图中，p表示系统开环极点在右半s平面上的数目。　　　　若闭环不稳定，试计算在右半s平面的闭环极点数。

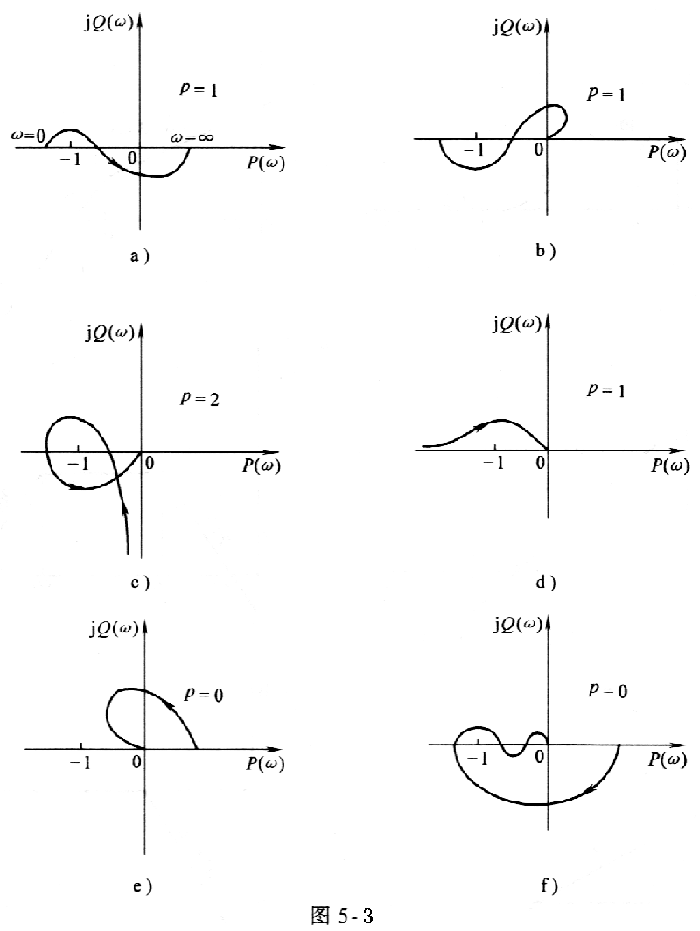
　4－8 画出下列开环传递函数的幅相特性，并判断其闭环系统的稳定性。

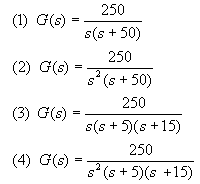
　4-9 已知系统开环传递函数分别为

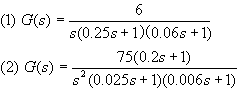
　　　　试绘制波德图，求相位裕量，并判断闭环系统的稳定性。

　4-10 设单位反馈系统的开环传递函数为

　　　　当输入信号r(t)=5sin2ω 时，求系统的稳态误差。

　4-11 已知单位反馈系统的开环传递函数，试绘制系统的闭环频率特性，试计算系统的谐振频率及谐振峰值。

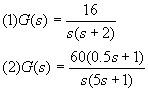
　4-12 单位反馈系统的开环传递函数为

　　　　试用频域和时域关系求系统的超调量δ%及调节时间t_s 。

　4-13 设一单位反馈控制系统的开环传递函数

　　　　（1）确定使系统的谐振峰值M _p＝1.4的K值。

　　　　（2）确定使系统的幅值裕度G₁M₁＝20db的K值。

　　　　（3）确定使系统的相角裕量r（ω_c）＝60⁰ 时的K值。