3-l 一单位反馈系统的开环传递函数为　G_K(s)=1/s(s+1)，求系统的单位阶跃响应及动态性能指标σ%，ts ，tp。

3-2 一单位反馈系统的开环传递函数为 G_K(s)=K/s(τs+1)，其单位阶跃响应曲如图 3－1，图中yp=1.25，tp=1.5s。试确定系统参数k 、τ值。

　3-3 一单位反馈系统的开环传递函数为 G _k(s)=ω²n /s(s+2ξωn)

　已知系统的r(t)=1(1),误差时间函数为　e (t)=1.4e^-1.7t-0.4^-3.74t ，求系统的阻尼比ξ,自然振荡角频率ωn、系统的闭环传递函数及系统的稳态误差。

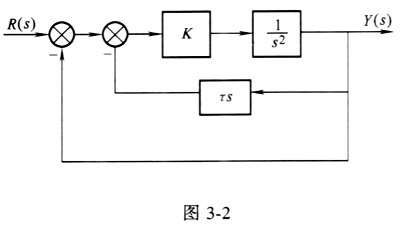
　3-4 一闭环反馈控制系统的结构图如3-2所示、求：①当δ％≤20％，ts (5%)=1.8s时,系统的参数K及τ值．

　②求上述系统的位置误差系数Kp、速度误差系数Kv和加速度误差系数Ka。

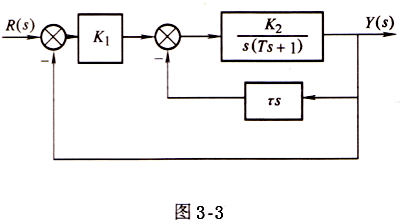
　3-5 某随动系统结构图如图3-3所示。已知K1=40v／rad．K2=0.5rad/(v.s),T=0.2s,τ=2v/rad.

　试求：①加入速度反馈前后闭环系统动态性能指标σ%，ts;

　　　　②为使加入速度反馈后闭环系统出现临界阻尼的非振荡阶跃响应，τ应取何值？计算其调节时间。

　3-6 单位阶跃信号作用下某惯性环节各时刻的输出值如下，试求该环节的传递函数。

　3-7 已知系统如图3-4所示。试分析参数τ应取何值时，系统方能稳定？

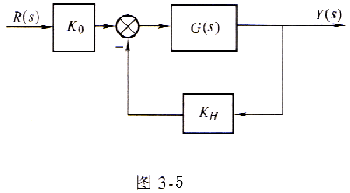
　3-8 已知系统如图3-29所示，图中的G(s)=10/0.2s+1，引入K_H和K_O的目的是，是过渡时间tS减小为原来的1/10，又保证总放大系数不变。试选　择K_H和K_O的值。

　3-9 有闭环系统的特征方程式如下，试用劳斯判据判定系统的稳定性，并说明特征根在复平面上的分布。

　　　　S³+20s²+4s+50=0

　　　　S⁴+2s³+6s²+8s=0

　　　　S⁶+3s⁵+9s⁴+18s³+22s²+12s+12=0

　3-10 单位反馈系统的开环传递函数为Gk(s)=K(0.5s+1)/s(s+1)(0.5s²+s+1), 试确定使系统稳定的K值范围。

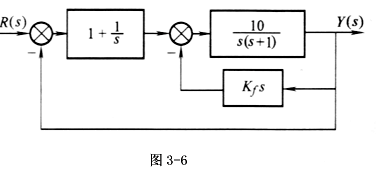
　3-11 已知系统的结构图如图3-6所示。试用劳斯判据确定使系统稳定的 k_f 值范围。

　　　　　　　　　　　　

　3-12 设有单位反馈系统，其开环传递函数分别为

　　　　G_k(s)=10 / s(s+4)(5s+1)

　　　　G_k(s)=10(s+0.1) / s² (s+4) (5s+1)

　　　　求输入量r(t)=t和r(t)=2+4t+5t²时系统的稳态误差。

　3-13 设具有单位反馈的随动系统，开环传递函数分别为

　　　　　G_k(s)=1/(0.2s+1)

　　　　　G_k(s)=150 / s (s+10) (s+5)

　　　　　G_k(s)=(2s+1) / s² (s²+3s+3)

　试求系统的位置，速度和加速度的误差系数。

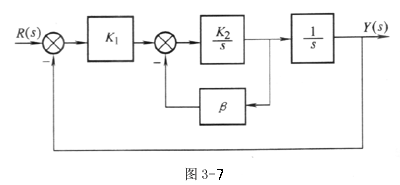
　3-14 某控制系统如图 3-7 所示，其中 K₁, 和 K₂ 为正常数，β＞ 0 ，试分析：

　　①β值的大小对系统稳定性的影响

　　②β值的大小对系统在阶跃信号作用下其动态品质σ % ， ts 的影响。

　　③β值的大小对系统在等速作用下（ r(t)=at ）其稳定误差的影响。

　3-15 设单位反馈系统的开环传递函数为Gk(s)=K/ s(1+0.33s)(1+0.167s)，要求闭环特征根实部均小于-1，求K值的取值范围。

　3-16 设单位反馈系统的开环传递函数分别为

　　　　① Gk(s)=K(s+1) / s(s-1)(s+5)

　　　　② Gk(s)=K / s(s-1)(s+5)

　试确定分别使闭环系统稳定的开环增益的取值范围。

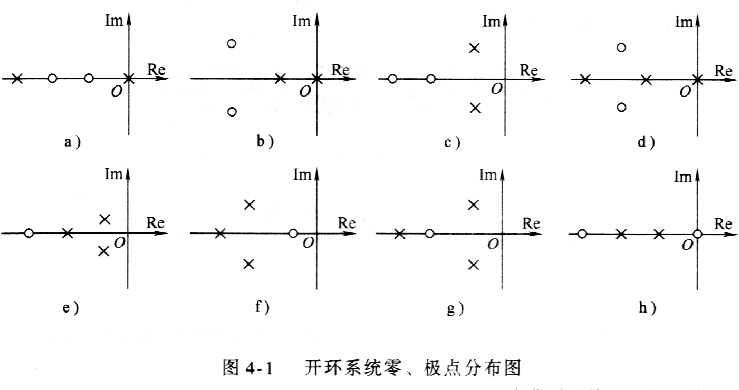
　3-17 设开环系统的零、极点在s平面上的分布图如下图4-1所示，试绘制相应的根轨迹草图。

　3-18 已知单位反馈系统的开环传递函数如下，试绘制系统随 变化时的根轨迹草图。

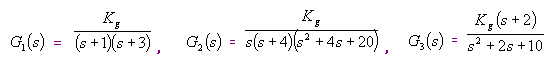
　3-19 设单位反馈系统的开环传递函数

　　　（1） 试绘制系统根轨迹大致图形，并分析系统的稳定性。

　　　（2） 若增加一个零点z=-1,试问根轨迹图有何变化，对系统稳定性有何影响。

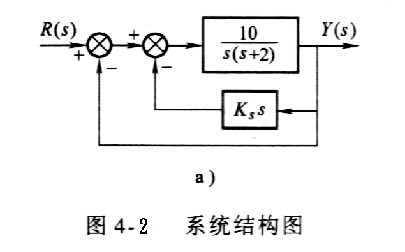
　3-20 设系统结构图如图4-2所示。图a中 为速度反馈系数，试绘制以 为参变量的根轨迹图。

　3-21 已知单位负反馈系统的开环传递函数

　　　　试用根轨迹法来确定使闭环主导极点的阻尼比 ζ=0.5和自然角频率ωn =2时的 取值。

　3-22 设单位反馈系统的开环传递函数

　　　　试绘制系统在单位负反馈情况下的根轨迹。

　3-23 设单位反馈系统的开环传递函数

　　　　若要求系统的增益为 =90，试求a为何值才能满足闭环系统最大超调量 的要求？