

兰州交通大学环境与市政工程学院, 兰州 730070
收稿日期: 2019-04-10; 修回日期: 2019-05-08; 录用日期: 2019-05-08
基金项目: 国家自然科学基金(No.21277065)
作者简介: 常青(1947-), 男, 教授, E-mail:changq47@mail.lzjtu.cn
通讯作者(责任作者): 常青
摘要:疏水絮凝是天然水中经常发生的现象,也是水处理中常被利用的原理.而疏水作用力则是引起疏水絮凝的最主要原因,具有重要的科学意义和应用价值.在过去30多年里,科学家们从实验测定、数值模拟及理论研究3个方面做了大量的研究,使人们对疏水作用力有了一定的认识,但由于问题的复杂性及研究所具有的高难度,目前疏水作用力的理论仍不够完善.为有助于进一步研究,本文综述了疏水作用力的一些特性及影响因素,如疏水作用力的实验规律、疏水作用的距离范围、疏水作用力的粒度界限、表面接触角对疏水作用力的影响、电解质对疏水作用力的影响及温度对疏水作用力的影响等.对大量文献的分析归纳表明,实验规律有单指数函数模型、双指数函数模型及幂函数模型,作用距离范围分为短程作用力及长程作用力,微粒半径大于临界半径时才可产生疏水作用力,疏水作用力随接触角的增大而增大,电解质对疏水作用力基本无影响,关于温度的影响,迄今尚有不同的看法和争论,还需更进一步的研究.
关键词:絮凝疏水作用力疏水絮凝DLVO理论扩展的DLVO
Discussion on the characteristics and influence factors of hydrophobic force
CHANG Qing


School of Environmental and Municipal Engineering, Lanzhou Jiaotong University, Lanzhou 730070
Received 10 April 2019; received in revised from 8 May 2019; accepted 8 May 2019
Abstract: Hydrophobic flocculation is a common process which occurs in natural water and one of the mechanisms which are employed in water treatment. The hydrophobic force is the most important mechanism which induces the hydrophobic flocculation and is of important scientific significance and great application value. Since more than 30 years ago, many scientists have made the great efforts in the research on hydrophobic force by experimental measurements, numerical simulations and theoretical analyses, which have led a better understanding of hydrophobic force, but the theory about hydrophobic force has still not been satisfactory for today because of its complexity and the difficulties in research method. In order to promote this research further, this article reviews some characteristics and influence factors of hydrophobic forces which were reported in the past literatures, for example, the experimental laws of hydrophobic force, the effect distance-range of hydrophobic force, the particle size-limit for hydrophobic force, the effect of contact angle on hydrophobic force, the effect of electrolyte on hydrophobic force and the effect of temperature on hydrophobic force et al. According to the analysis and the summarization of available literatures, the experimental law is of single exponential, double exponential and power functions respectively, the effect distance-ranges are divided into a short range one and a long range one, hydrophobic interaction takes place only when the radii of hydrophobic particles are greater than the critical radius, hydrophobic force increases with the increase in contact angle, electrolyte has nearly no influence on hydrophobic force, in addition, there have been still a lots of different viewpoints on the temperature dependence of hydrophobic force for today, which need further research very much.
Keywords: flocculationhydrophobic flocculationhydrophobic forceDLVO theoryextended DLVO theory
1 引言(Introduction)疏水絮凝是天然水中经常发生的现象, 也是水处理中常被利用的原理(常青, 2018), 而疏水作用力则是引起疏水絮凝最主要的原因, 具有重要的科学意义和应用价值.疏水作用力指在水为介质的分散体系中, 具有疏水表面的微粒之间除DLVO综合作用力之外的额外吸引力.在疏水作用力发现之前, 人们已初步认识到在疏水微粒间存在疏水作用力, 并将其称为接触作用力(contact force)或疏水键(hydrophobic bound), 但尚未涉及到其大小与微粒间距离的依赖关系.Pashley等(1981)和Israelachvili等(1982)首次以表面力测定仪(SFA)对以阳离子表面活性剂十六烷基三甲基溴化胺(CTAB)包覆的微小云母片之间的作用力进行了直接测定, 以其对表面曲率半径标化后的值对表面间隔距离作曲线得图 1.图中实线为经典DLVO理论的预测值(作了同样的标化处理), 用以比较.图 1显示了表面之间的作用力随表面间隔距离变化, 其中曲线a和曲线b分别表示表面具有不同电荷密度的情况.可以看出, 在间隔距离较远处测定值与DLVO理论预测值能很好吻合, 随着距离的减小, 测定值逐渐偏离并超过了DLVO理论预测值, 一般将偏离开始点即图中箭头所指处称为跳入聚结距离或跳入聚结点(jump in distance or snap in distance), 而插图中未包覆表面活性剂的云母片间的作用力与DLVO理论预测值在整个距离范围内都有极好的符合性.Israelachvili和Pashley认为在包覆了CTAB的云母片之间吸引作用力超过wan der Waals吸引力的部分即为疏水作用力.
图 1(Fig. 1)
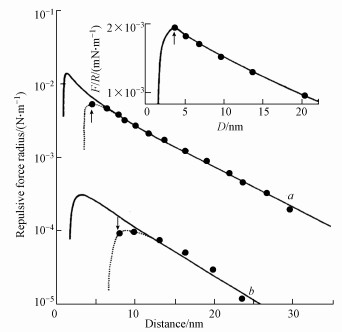 |
| 图 1 疏水作用力的发现 (F是颗粒表面之间的作用力, R是颗粒表面曲率半径) Fig. 1Discovery of hydrophobic force |
经过30多年的研究, 疏水作用力的存在已被众多科学家所认可, 因此经典的DLVO理论应补充疏水作用力, 成为扩展的DLVO理论, 经典的絮凝理论也应包括疏水絮凝的贡献.迄今疏水絮凝在矿物分选领域已取得了巨大成功(宋少先, 1993; Song et al., 2012), 成为20世纪该领域最有价值的技术创新成果, 但在水处理领域尚缺乏认识和研究.本文作者曾经综述了疏水作用力的发现, 探讨了疏水作用力的热力学解释和微观机理(常青, 2018), 提出水处理工作者应大力开展疏水絮凝的研究, 以疏水絮凝的理论进一步推动水处理科学技术的发展, 为此再以本文对疏水作用力特性及影响因素做以下综述性介绍.
2 疏水作用力的实验规律(Experimental law of hydrophobic force)对实验测定值作数学模拟后共提出了3种实验规律.
① 单指数函数模型:在某些情况下, 将实验测得的疏水微粒之间的疏水作用力标化后对其间隔距离作图, 再经拟合得单指数函数模型(Pashley et al., 1981; Israelachvili et al., 1982).单指数函数模型表示疏水作用力随微粒之间的最短距离的增大按指数函数规律衰减:
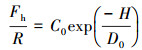 | (1) |
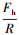
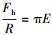
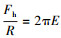
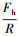
② 双指数函数模型:在某些情况下, 将实验测得的疏水微粒之间的疏水作用力标化后对其间隔距离作图, 再经拟合得双指数函数模型(Claesson et al., 1988;Yoon et al., 1996):
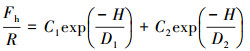 | (2) |
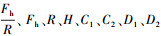
③ 幂函数模型:在某些情况下, 将实验测得的疏水颗粒之间的疏水作用力标化后对其间隔距离作图, 再经拟合得幂函数模型(Rabinovich et al., 1994; Pazhianur et al., 2003):
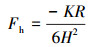 | (3) |
基于疏水作用力的发现, 传统的DLVO理论应修正为扩展的DLVO理论, 其数学表达式为:
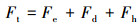 | (4) |
3 疏水作用力的作用范围(Effect range of hydrophobic force)疏水作用力的范围远较van der Waals作用力长, 所以常被称为长程吸附作用力(long-range attraction), 但其本身也分为短程作用力和长程作用力.图 1中的跳入聚结距离显示疏水作用力发生在距表面约10 nm的距离内, 称为短程作用力.以后的研究(Aston et al., 2000)表明, 疏水作用力发生的范围主要依赖于疏水表面的类型及制备方式.改变用来包覆微粒表面的表面活性剂的类型, 可以使作用范围延长至15 nm (Claesson et al., 1988)、30 nm(Claesson et al., 1988)、80 nm(Claesson et al., 1988), 乃至超过100 nm(Parker et al., 1994).
当表面活性剂为二甲基双十八烷溴化铵(DDOA)时, 实验规律如图 2a所示.图中实心圆代表在测试仪器弹簧的刚性较弱的条件下得到的数据, 实心方块代表在测试仪器弹簧刚性较强的条件下得到的数据, 实线则表示疏水作用力完全不存在, 仅有van der Waals作用力的情况.可以看出, 当微粒相互接近时, 在弹簧刚性较弱和较强的两种情况下, 在间隔距离分别达到70 nm和10 nm时出现了加速现象, 意味着疏水作用力分别在间隔距离为70 nm和10 nm处开始发生.图 2b中三角形表示流体动力作用, 空心圆表示实验微粒之间的作用力, 实心圆代表疏水作用力(由图 2a左边的曲线计算得到), 显然疏水作用力发生在颗粒间隔距离约为70 nm之内.图 2a和图 2b说明以DDOA包覆颗粒时疏水作用力发生的范围更长, 强度更大, 属于长程作用力.图 2c表明水中有不同数量的十二烷醇存在时, 盐酸十二烷胺(DAHCl)阳离子表面活性剂吸附在云母片上产生的疏水作用力(Yoon et al., 1996).图中上部实线是在DAHCl浓度为5×10-6 mol·L-1时DLVO(恒电荷模式)的拟合曲线, 其计算式中A=2.2×10-20 J, ψ0=35 mV, κ-1=68 nm, 在跳入聚结点H=14.0 nm处分离出的点线是扩展的DLVO理论(式(4))拟合结果, 其中疏水作用以单指数函数(式(1))表示, 其D0=1.3 nm, 可以看出, 扩展的DLVO理论拟合结果远大于DLVO理论的预见值, 意味着疏水作用力的存在, 且为短程作用力.当水中存在10-7 mol·L-1十二烷醇时, DLVO(恒电荷模式)理论曲线以下方实线表示, 分离出的点线和短划线为扩展的DLVO理论(式(4))拟合结果, 其中点线代表疏水作用以双指数函数拟合的结果, 其C1=-45×103 N·m-1, D1=1.2 nm, C2=-1.2×103 N·m-1, D2=6.8 nm, 短划线代表疏水作用力以幂函数拟合的结果, 其K=1.5×10-19 J, 是Hamaker常数的7倍.可以看出, 在较远的间距处综合作用排斥力几乎减弱为零, 在0~40 nm范围呈现为净吸附作用力, 显著超过了DLVO理论对应的wan der Waals吸引力的强度, 其跳入聚结点出现在更远的18.0 nm处, 意味着作用范围更大, 为长程作用.同样看出, 当十二烷醇浓度增加至5×10-7 mol·L-1时, 以扩展的DLVO拟合, 分离出的点线代表疏水作用力以双指数函数拟合, 其D1=1.2 nm, D2=9.0 nm, 分离短划线代表疏水作用力以幂函数规律表示, K=3.3×10-19 J.可以看出, 相互作用力甚至在远至70 nm处都显示为吸引, 跳入聚结点出现在24 nm处, 为长程作用.
图 2(Fig. 2)
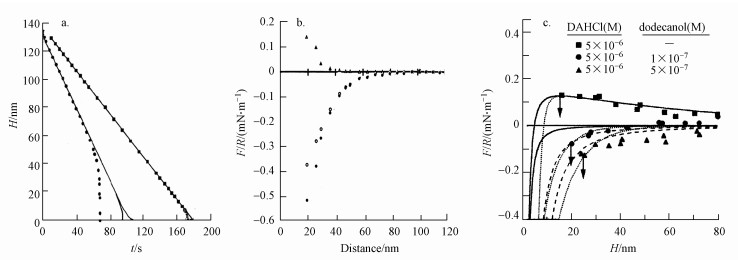 |
| 图 2 疏水作用力的作用范围 (a. DDOA表面疏水作用力引起的加速现象, H是颗粒间隔距离, t是时间, b. DDOA表面疏水作用力发生的范围, F是颗粒之间的作用力, R是颗粒表面的曲率半径, D是颗粒间隔距离, c添加中性表面活性剂时DAHCl表面的疏水作用力) Fig. 2Effect range of hydrophobic force |
综上所述, 疏水作用力在一些条件下表现为短程作用力, 即出现在疏水颗粒的间隔距离较近的范围内, 而在另一些条件下表现为长程作用力, 即出现在疏水颗粒间隔距离较远的范围内.Yoon等(1996)指出, 当颗粒(云母)表面上吸附有水溶性单碳链阳离子型表面活性剂时, 疏水作用力出现在相对短的间隔距离0~15 nm的范围内, 衰减规律可用单指数衰减规律式(1)表示, 其衰减长度值通常在1~2 nm范围内.当不溶性双碳链阳离子型表面活性剂沉淀于颗粒(云母)表面时, 疏水作用力可以在长达100 nm的间隔距离内出现, 其衰减长度D1在1~2 nm范围, D2在10~26 nm范围.
对短程和长程疏水作用力的解释是:阳离子表面活性剂以其阳离子端吸附于颗粒表面, 以碳链垂直伸向水中, 形成表面活性剂分子并排的疏水表面层.吸附在云母片表面的水溶性单碳链表面活性剂分子排列较为稀疏, 疏水性较弱, 疏水作用力范围较短, 而吸附在云母片表面的双碳链表面活性剂分子排列较为紧密, 疏水性较强, 疏水作用力范围较长.当在长碳链阳离子型单链表面活性剂中添加碳链较短的中性表面活性剂时, 也可以显现出长程疏水作用力, 原因是中性表面活性剂可与阳离子表面活性剂分子发生共吸附, 穿插在长链表面活性剂分子之间, 增大了吸附层密度及有序性, 造成了更强的疏水性.
4 疏水作用力的粒度界限(Particle size limit for hydrophobic force)有关疏水微粒的尺度对疏水作用力的影响近期已有研究报道.Sun等(2019)认为, 当疏水微粒被分散于水中时, 水合自由能应包括water-water和solute-water两作用项:
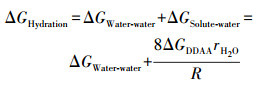 | (5) |
图 3(Fig. 3)
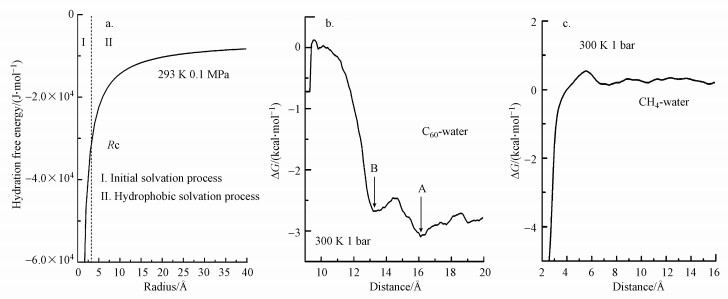 |
| 图 3 粒径对水合自由能的影响 (a.微粒水合自由能与尺度的关系, b.两个富勒烯分子之间的平均力势, c.两个CH4分子之间的平均力势) Fig. 3Particle size dependence of hydration free energy |
ΔGSolute-water>ΔGWater-water, 为使体系自由能更低, 微粒倾向于相互聚结, 导致更多水分子之间的作用, 表现为相互吸引即疏水作用力.
5 接触角的影响(Contact angle dependence)Aston等(2000)认为疏水作用力的强度主要与微粒表面的疏水性强弱相关, 即与接触角大小相关.Pazhianur等(2003)以十八烷基三氯硅烷(OTS)对微小硅片及玻璃小球作了表面硅烷化处理, 使其前进接触角分别为0°、75°、83°和92°, 并以原子力显微镜(AFM)分别测定了它们之间在不同间隔距离处的吸引力, 并以玻璃球半径标化后作图, 如图 4a所示, 由于硅烷化处理不影响表面热力学电位, 上述4种前进接触角情况下的经典DLVO理论的拟合线相同, 均以同一虚线代表, 3条实线则分别代表除0°外的3种情况下的实测曲线.该图表明, 每一种接触角情况下的实测值都与经典DLVO计算值不同, 在前进接触角为0°时表现出额外的近距排斥力, 这是由表面水化层所导致, 而在其它3种情况下, 实测值均比经典DLVO理论值大, 以扩展的DLVO理论式拟合得3条实线, 表明具有疏水作用力, 并随着表面接触角的增大而增大.在研究了前进接触角小于90°的情况后, Pazhianur等(2003)再次使用OTS在更强的条件下对微小玻璃小球和硅片作了表面硅烷化处理, 使其前进接触角大于90°, 分别为109°、105°和100°, 再以原子力显微镜(AFM)测定了它们之间在不同间隔距离处的吸引力得图 4b.可以看出, 实验测得值超过了图 4a接触角小于90°时扩展的DLVO理论式拟合线, 说明疏水作用力随接触角的增大而进一步增强.
图 4(Fig. 4)
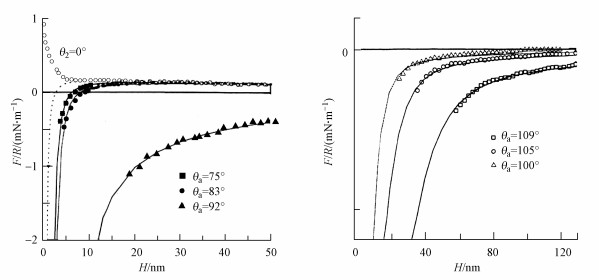 |
| 图 4 硅烷化玻璃球和硅片表面之间相互作用的F/R-H曲线 (a.接触角较小, 实线为扩展的DLVO理论预测值, b.接触角较大, 实线为扩展的DLVO理论预测值) Fig. 4The F/R-H curves for the interaction betweensilanated glass spheres and silica plates |
Soga等(2015)以十八烷基三氯硅烷(OTS)溶液浸泡包覆微小硅片和微小硅颗粒, 通过改变OTS浓度和浸泡时间改变表面疏水性强弱, 得到不同接触角的微小硅颗粒及硅片, 以原子力显微镜(AFM)测定了当它们分散于水中时表面之间的相互作用力与间隔距离的关系, 结果如图 5所示.
图 5(Fig. 5)
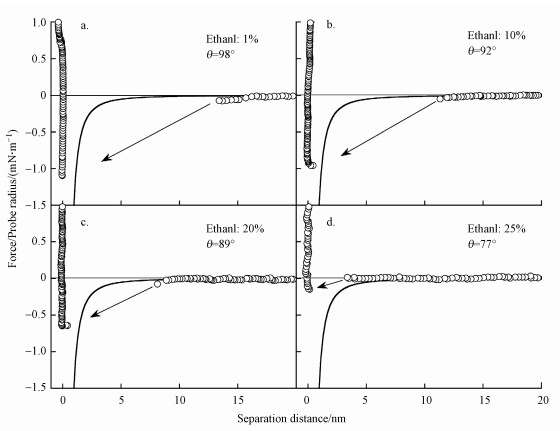 |
| 图 5 具有不同接触角的表面之间的相互作用力及作用范围 (a.前进接触角θ=98°; b.前进接触角θ=92°; c.前进接触角θ=89°; d.前进接触角θ=77°) Fig. 5Interaction and effect range of surfaces with different contact angles |
图中箭头指跳入聚结距离, 实线表示由理论计算得到的wan der Waals吸引力曲线, 以供比较.可以看出, 当接触角θ大于90°时显现出较远的跳入聚结距离, 说明疏水作用力具有较大的作用范围, 随接触角θ的减小, 跳入聚结距离变近, 疏水作用范围变短, 当θ=89°时疏水作用力的存在已不十分清楚, 图 5c显示测定共在硅片表面上3个不同点上进行, 微粒间的作用在测定点1和2处得到的作用范围较wan der Waals吸引力长, 说明尚有疏水作用力存在, 在测定点3上与wan der Waals吸引力相当.当θ=77°时表面作用力可完全拟合为wan der Waals吸引力曲线, 无疏水作用力显现.
综上所述, 微粒表面的疏水作用强度及作用范围随着微粒表面接触角的增大而增大, 当前进接触角大于90°时微粒之间的疏水作用力更为显著.
6 电解质的影响(Electrolyte dependence)Parker等(1994)通过共价反应将十三烷基-氟代四氢辛基-二甲基-一氯硅烷(tridecafluoro-1, 1, 2, 2-tetrahydrooctyldimethylchlorosilane, FSCl1)和十三烷基-氟代四氢辛基-甲基-二氯硅烷(tridecafluoro-1, 1, 2, 2-tetrahydrooctylmethyldichlorosilane, FSCl2)分别包覆在表面积为2 nm×2 nm的玻璃小圆柱表面上, 得到了电中性且表面疏水的微粒, 然后用表面力测定仪(SFA)分别测定了介质为水和不同浓度电解质溶液时这些微粒之间的相互吸引力.图 6a中相互吸引力为负值, 且作用范围远超van der Waals作用力范围, 意味着存在疏水作用力.左上方的两条曲线分别为FSCl2覆盖表面的小柱在纯水和1 mol·L-1的KBr溶液中的相互吸引力, 右下方的一组曲线是FSCl1覆盖表面的小柱在纯水和NaCl溶液中的相互吸引力, 其中NaCl溶液的浓度分别为2×10-3、1×10-1、0.1、1.0、和5.0 mol·L-1, 由此可以看出, 随着电解质浓度的增大小柱间的吸引力略有增强, 也可以说加入电解质仅有很小的影响.
图 6(Fig. 6)
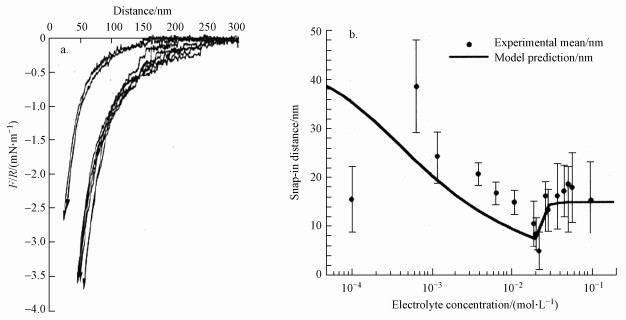 |
| 图 6 电解质浓度对疏水作用力的影响 (a.电解质浓度对疏水作用强度的影响, b.电解质浓度对跳跃聚结距离的影响) Fig. 6Electrolyte concentration dependence of hydrophobic forces |
Aston等(2000)以辛烷基-三乙氧基-硅烷(octyltriethoxysilane, OTES)包覆玻璃微球和微小石英薄片, 以原子力显微镜(AFM)测定了此硅烷化疏水小球和疏水薄片之间在一价电解质中的相互作用力, 以电解质滴定法研究了电解质浓度改变时原子力显微镜悬臂的跳入聚结距离的动力学特征, 如图 6b所示, 图中实线为以扩展的DLVO理论计算得出的跳入聚结距离, 可以看出跳入聚结距离随着电解质浓度的增大而缩短, 当一价电解质的浓度超过2×10-2 mol·L-1时达到极小值7 nm, 如果电解质浓度再略有升高, 疏水作用力则成为占优势的作用力, 跳入聚结距离迅速升高至渐进值15 nm, 形成一个平台, 不再随电解质浓度的增大而变化, 与图中小点所表示的实验值十分吻合.如图所示, 在电解质浓度较低时, 实验得到的跳入聚结距离大得多, DLVO模型不能与之相符合, Aston等(2000)认为这是由于在低电解质浓度时, 微粒间还存在静电相关作用.当电解质浓度升高至一定值时, 静电作用消失, 疏水作用力成为占优势的作用力, 由于疏水作用力不受电解质的影响, 所以跳入聚结距离也不受电解质浓度的影响, 在图中表现为一个平台.
Philipp等(2015)通过烷基硫醇与金的共价结合反应修饰原子力显微镜悬臂的金质尖端和微小金片, 在其表面形成电中性的单分子疏水薄膜, 然后以原子力显微镜(AFM)测定两疏水表面之间的作用力, 研究了电解质对疏水作用力的影响.图 7a~7c显示了两个疏水表面相互接近, 且介质中NaCl的浓度从5 mmol·L-1升高至1000 mmol·L-1时, 疏水表面之间作用力与间隔距离之间的关系, 图中虚线是由范德华力公式得到的曲线, 实线是以范德华力公式和疏水作用力公式的加和式对实测数据拟合得到的曲线, 此图表明用包括了范德华力和疏水作用力的总作用力公式拟合实验数据, 可以很好地描述NaCl浓度从5 mmol·L-1升高至750 mmol·L-1时疏水表面之间的相互作用力(为节省篇幅, 省略了NaCl的浓度为50、250及500 mmol·L-1的图示), 其值随间隔距离增大按指数规律衰减, 并随电解质浓度的增大略有减小, 作用范围略有增加, 但当NaCl的浓度升高至1000 mmol·L-1时, 则出现了显著的偏差, 以跳入聚结距离所表现出的不稳定性移至更远处, 也得不到清晰的疏水作用力拟合曲线.图 7d显示在不同浓度的NaCl介质中将两个疏水表面分开时所测得的表面粘附力和表面相互接近时表现出的平均跳入聚结距离, 可以看出当NaCl的浓度从5 mmol·L-1升高至750 mmol·L-1时, 表面粘附力微弱下降约6.6%, 平均跳跃聚结距离有微弱增大, 但在1000 mmol·L-1的NaCl介质中跳跃聚结距离显著增大, 意味着溶解盐的影响显著增大, 研究者认为这是由离子吸附或离子相互作用引起的.
图 7(Fig. 7)
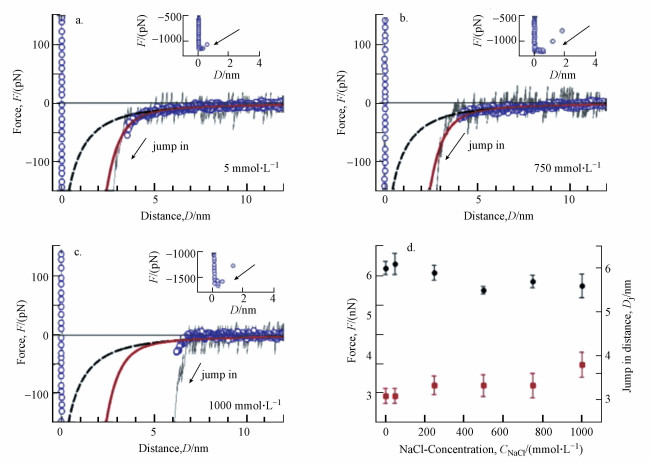 |
| 图 7 电解质浓度对疏水作用力的影响 (a~c.电解质浓度对疏水作用强度的影响, d.电解质浓度对表面粘附力及跳跃聚结距离的影响) (实心小园表示表面粘附力, 实心正方形表示跳跃聚结距离) Fig. 7Effect of electrolyte concentration on hydrophobic force |
综上所述, 可以认为电解质对疏水作用力基本无影响.
7 温度的影响(Temperature dependence)迄今关于温度对疏水作用力的影响尚未得到统一的认识, 不同的研究者采用不同的理论处理和不同的实验得到过不同的结果.一些研究报道, 微粒间的疏水作用强度随温度的升高而增大, 而另一些研究却得出了相反的结果.
Parker等(1994)将十三烷基-氟代四氢辛基甲基-二氯硅烷[(tridecafluoro-1, 1, 2, 2-tetrahydrooctyl) methyldichlorosilane, FSCl2]通过共价反应包覆在玻璃小圆柱(2 nm×2 nm)表面上, 赋予其表面疏水性, 然后测定了22 ℃和41 ℃下这些疏水小柱之间的标化疏水作用力(F/R), 如图 8a所示, 当温度从常温升高至41 ℃时, 小柱之间的相互吸引力强度有显著的增强, 跳入聚结距离有明显增大, 即疏水作用范围增大.但当测试体系被冷却至室温时, 相互吸引力却不能立即恢复至室温时的强度, 如中间曲线所示, 再经24 h室温保存后, 仍然高于升温之前的强度
图 8(Fig. 8)
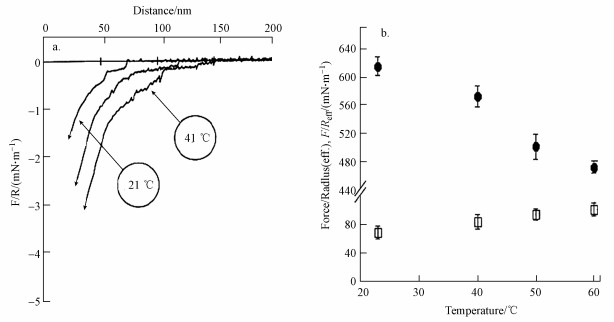 |
| 图 8 温度对疏水作用力的影响 (a. FSCl2表面之间的疏水作用力;b.烷基硫醇表面之间的疏水作用力及作用范围) Fig. 8Effect of temperature on hydrophobic forces |
还有研究(Philipp et al., 2015)表明, 通过烷基硫醇与金的共价结合反应包覆原子力显微镜的金质悬臂尖端和待测试微小金片, 形成电中性单分子层烷基疏水表面, 然后以原子力显微镜(AFM)测定两疏水表面之间的作用力, 研究了介质温度对疏水作用力的影响, 结果如图 8b所示.可以看出, 当温度从23 ℃升高至60 ℃时, 跳入聚结距离约增大10%, 意味着疏水作用力范围随温度的升高略有增大, 但标化粘附力约减小20%, 意味着疏水作用力随温度的升高而减小.
一般实验研究中最大的困难在于将疏水作用力与其他种类的作用力清楚地分离或区别开来, 否则会带来较大的误差, 甚至导致错误结论, 或许理论方法能避免此问题.Zangi等(2008)以分子动力学模拟(molecular dynamics simulations)研究了大尺度疏水表面(>1 nm)的聚结热力学, 如图 9a所示, 当两微小平板从相距1.44 nm相互接近至相距0.36 nm时所发生的体系自由能变化ΔG、熵变ΔS及焓变ΔH, 可以看出, 在所研究的温度范围内, 聚结过程的熵变(正值)及ΔH(负值)均具有较强的温度依赖关系, 随着温度的升高, 呈现迅速降低, 根据热力学公式ΔG=ΔH-TΔS, 二者的作用可相互抵消, 因此自由能ΔG的变化呈现出较弱的温度依赖关系, 即温度对疏水表面之间的作用影响不显著, 但自由能显示出的较大的负值表明表面之间有较强的结合强度.
图 9(Fig. 9)
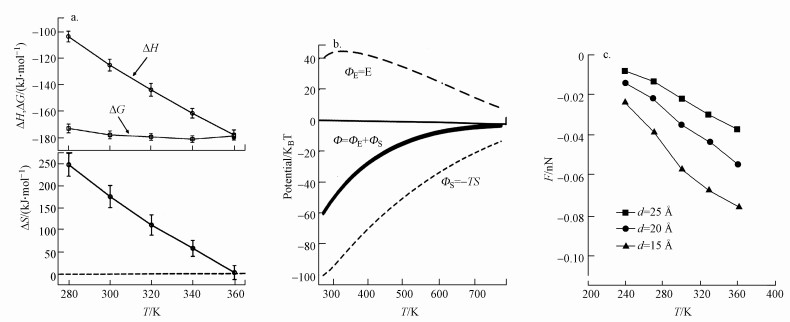 |
| 图 9 温度对疏水聚结自由能和疏水作用力的影响 (a.温度对聚结自由能变的影响;b.温度对聚结过程中平均力势的影响;c.温度对疏水作用力的影响) Fig. 9Effect of temperature on the free energy of hydrophobic coalescence |
Djikaev等(2010)提出了一个概率氢键模型(probabilistic hydrogen bond model), 用来模拟微小疏水平板微粒相互接近时的相互作用, 模型认为当二平板微粒相互接近至一定距离时, 位于表面附近的水分子氢键网状结构相互重叠, 产生了对微粒间平均力势(potential of mean force)的贡献, 由于平均力势从本质上属于自由能, 按照亥姆霍兹自由能的热力学式F=E-TS, 可以将平均力势Ф分为能量分量E和熵分量-TS.该研究考察了温度对此平均力势贡献的影响.图 9b表示当两个疏水平板微粒相互接近至其间距离为水分子氢键长度的2倍时, 温度对平均力势贡献Ф及其能量分量ФE、熵分量ФS的影响, 图中短虚线表示熵分量, 长虚线表示能量分量, 实线表示二者的加和, 即温度对平均力势贡献.可以看出, 疏水表面相互聚结时熵分量为主导变量, 导致平均力势为负值, 有利于微粒的聚结, 但当温度升高时平均力势绝对值减小, 削弱了微粒的聚结.
Tuhin等(2018)也以分子动力学模拟(molecular dynamics simulations)方法研究了温度对石墨烯表面疏水作用力的影响, 如图 9c所示, 疏水表面之间的有效疏水作用力F(即疏水压力乘以表面面积得到的作用力)随温度的降低而减弱, 随温度的升高而增强.其机理可解释为当温度降低时, 表面对水分子的亲和力增强, 导致疏水表面之间的疏水作用力减弱, 反之亦然.
综上所述, 不同研究所得到的结果尚有较大差异, 还需进一步研究.
8 结论(Conclusions)1) 疏水作用力的实验规律有单指数函数模型、双指数函数模型和幂函数模型.
2) 疏水作用力在一些条件下表现为短程作用, 即出现在疏水微粒的间隔距离较近的范围内, 一般不超过10 nm, 而在另一些条件下表现为长程作用力, 即出现在疏水微粒间隔距离较远的范围内, 可达80~100 nm.
3) 当疏水微粒的半径大于临界半径时微粒间产生疏水作用力, 小于临界半径时无疏水作用, 有相互排斥作用.
4) 疏水作用力随接触角的增大而增大, 当前进接触角大于90°时, 微粒之间的疏水作用力更为显著.
5) 电解质对疏水作用力基本无影响.
6) 迄今关于温度对疏水作用力的影响尚未得到统一的认识, 一些研究表明, 微粒间的疏水作用强度随温度的升高而增大, 而另一些研究却得出微粒间的疏水作用强度随温度的升高而减小的结果, 也有研究认为温度对疏水作用力的影响不大.
参考文献
| Aston D E, John C B. 2000. Long-range attraction between silanated silica materials studied by an electrolyte titration with atomic force microscopy[J]. Colloid and surfaces A:Physicochemical and Engineering Aspects, 163: 247-263. |
| 常青. 2018. 论疏水絮凝与疏水作用力[J]. 环境科学学报, 38(10): 3787-3796. |
| Chang Q. 2016. Colloid and chemistry for water quality control[M]. London: Elsevier, 239-240. |
| Claesson P M, Christenson H K. 1988. Very long range attractive forces between uncharged hydrocarbonand fluorocarbon surfaces in water[J]. Journal of Chemical Physics, 92(6): 1650-1655. DOI:10.1021/j100317a052 |
| Djikaev Y S, Ruckenstein E. 2010. Temperature effect on the hydrophobic interaction of parallel plates in framework of the probabilistic approach to hydrogen bonding[J]. Journal of Colloid and interface Science, 343: 510-521. DOI:10.1016/j.jcis.2009.12.011 |
| Isrelachvili J, Pashley R. 1982. The hydrophobic interaction is long range, decaying exponentiallywith distance[J]. Nature, 300(25): 341-342. |
| Israelachvili J N, Pashley R M. 1983. Molecular layering of water at surfaces and origin of repulsive hydration forces[J]. Nature, 306(5940): 249-250. DOI:10.1038/306249a0 |
| Pashlea R M, Israelachvili J N. 1981. A comparison of surface forces and interfacial properties of mica inpurified surfactant solutions[J]. Colloids and Surfaces, 2(2): 169-187. DOI:10.1016/0166-6622(81)80006-6 |
| Parker J L, Claesson P M. 1994. Bubble, cavities, and the long-ranged attraction between hydrophobic surfaces[J]. Journal of Physical Chemistry, 98(34): 8468-8480. DOI:10.1021/j100085a029 |
| Pazhianur R, Yoon R H. 2003. Model for the origin of hydrophobic force[J]. Minerals and Metallurgical Processing, 20(4): 178-184. |
| Philipp S, Thomas U, Markus V. 2015. Direct and quantitative measurements of concentration andtemperature dependence of thehydrophobic force law at nanoscopic contacts[J]. Journal of Colloid andInterface Science, 446: 244-251. DOI:10.1016/j.jcis.2015.01.032 |
| Rabinovich Y I, Yoon R H. 1994. Use of atomic force microscope for the measurement of hydrophobic forces[J]. Colloid and surface A:Physicochemical and Engineering Aspects, 93(5): 263-273. |
| 宋少先. 1993. 疏水絮凝理论与分选工艺[M]. 北京: 煤炭工业出版社, 5-8. |
| Song S, Zhang X, Yang B, et al. 2012. Flotation of molybdenite fines as hydrophobic agglomerats[J]. Separation & Purification Technology, 98(3): 451-455. |
| Sun Q. 2017. The physical origin of hydrophobic effects[J]. Chemical Physics Letters, 672: 21-25. DOI:10.1016/j.cplett.2017.01.057 |
| Sun Q, Su X W, Cheng C B. 2019. The dependence of hydrophobic interactions on solute size[J]. Chemical Physics, 516: 199-205. DOI:10.1016/j.chemphys.2018.09.014 |
| Tuhin S, Biman B. 2018. Temperature effects on the hydrophobic force between two grapheme-like surface in liquid water[J]. Journal of Chemical Science, 130(29): 1-10. |
| Yoon R H, Ravishankar S A. 1996. Long-range hydrophobic forces between mica surface in Dodecylammonium chloride solutions in the presence of dodecanol[J]. Journal of Colloid & Interface Science, 179(2): 391-402. |
| Soga Y, Imanaka H, Imamura K, et al. 2015. Effect of hydrophobicity on short-range hydrophobic attraction between silanated silica surfaces[J]. Advanced Powder Technology, 26: 1729-1733. DOI:10.1016/j.apt.2015.10.017 |
| Zangi R, Berne B J. 2008. Temperature dependence of dimerization and dewetting of large-scale hydrophobes:A molecular dynamics study[J]. Journal of Physical Chemistry B, 112(29): 8634-8644. DOI:10.1021/jp802135c |
