 , 张宏昇1
, 张宏昇1
 , 葛红星2, 蔡旭晖3, 宋宇3, 康凌3
, 葛红星2, 蔡旭晖3, 宋宇3, 康凌31. 北京大学物理学院大气与海洋科学系, 气候与海-气实验室, 北京 100871;
2. 南京电子技术研究所, 南京 210039;
3. 北京大学环境科学与工程学院环境科学系, 环境模拟与污染控制国家重点联合实验室, 北京 100871
收稿日期: 2019-12-22; 修回日期: 2020-03-15; 录用日期: 2020-03-15
基金项目: 国家重点基础研究发展规划项目(No.2017YFC0209600,2016YFC0203300);国家自然科学基金(No.91837209,41544216);新疆维吾尔自治区高层次(柔性)人才引进项目(2018)
作者简介: 卫茁睿(1996-), 女, E-mail:zhrwei@pku.edu.cn
通讯作者(责任作者): 张宏昇, E-mail:hsdq@pku.edu.cn
摘要:利用2018年12月27日-2019年1月8日山东省平原县大气环境实验站观测资料,基于近地面层各物理量湍流输送特征的相似性,以温度(T)作为代理变量,采用松弛涡旋累积法(The Relaxed Eddy Accumulation,REA)计算了重霾天气过程细颗粒物湍流通量,并给出了可信度验证.结果表明:实验观测期间,温度(T)、水汽(H2O)、二氧化碳(CO2)等不同物理量的REA法获取的湍流通量的经验系数b分别为bT=0.56、bH2O=0.56、bCO2=0.56.经验系数b的中位数随归一化采样阈值HREA的增大而逐渐减小;b值的离散性随HREA的变化存在一个极小值;考虑到温度b值的离散性最小,建议选取温度作为代理变量.REA法计算的细颗粒物湍流通量结果与细颗粒物湍流通量测量装置的结果具有较好的一致性,说明采用代理变量的REA法适用于细颗粒物湍流通量的获取.
关键词:松弛涡旋累积法代理变量细颗粒物湍流通量重霾天气
Estimating the turbulent flux of the fine particulate matter by the relaxed eddy accumulation method
WEI Zhuorui1
 , ZHANG Hongsheng1
, ZHANG Hongsheng1
 , GE Hongxing2, CAI Xuhui3, SONG Yu3, KANG Ling3
, GE Hongxing2, CAI Xuhui3, SONG Yu3, KANG Ling31. Laboratory for Climate and Ocean-Atmosphere Studies, Department of Atmospheric and Oceanic Sciences, School of Physics, Peking University, Beijing 100871;
2. Nanjing Research Institute of Electronics Technology, Nanjing 210039;
3. State Key Joint Laboratory of Environmental Simulation and Pollution Control, Department of Environmental Science, College of Environmental Sciences and Engineering, Peking University, Beijing 100871
Received 22 December 2019; received in revised from 15 March 2020; accepted 15 March 2020
Abstract: Based on the relaxed eddy accumulation (REA) method, the turbulent flux of the fine particulate matter was estimated by using the data collected at the atmospheric environmental station in Pingyuan county, Shandong Province during a heavy haze event from December 27, 2018 to January 8, 2019. The results show that the empirical coefficients b of various physical quantities (temperature(T), water vapor(H2O), and carbon dioxide(CO2)) for estimating the turbulent fluxes by the REA method are bT=0.56, bH2O=0.56, and bCO2=0.56, respectively. The median of b gradually decreases with the increase of the normalized sampling threshold HREA. The corresponding parameters were selected when the dispersion of b reaches minimum. The turbulent flux calculated by the REA method is compared well with the observations from the rapid response measuring equipment. The method proposed in this study could be used to estimate the turbulent flux of the fine particulate matter.
Keywords: the Relaxed Eddy Accumulation methodrepresentative quantitythe fine particulate matterturbulent fluxheavy haze pollution
1 引言(Introduction)近年来, 随着经济的快速增长和城市规模的不断扩大, 我国大气环境污染问题日趋加剧, 大中型城市重霾天气频发, 而细颗粒物PM2.5是主要污染物之一(吴兑, 2012;吴兑等, 2014;Ao et al., 2016).目前, 大多数大气污染过程的实验观测和数值模拟研究主要集中在与污染过程有关的天气条件变化(蒋伊蓉等, 2015;Ye et al., 2016;Li et al., 2018;Wang et al., 2018;吴战平等, 2019)、边界层高度变化(王耀庭等, 2012;杜川利等, 2014;Luan et al., 2018;Miao et al., 2018)和气象要素变化(Zhang et al., 2015;吴序鹏等, 2018;Zhong et al., 2018;尹承美等, 2019)等方面, 少有针对重霾天气过程大气细颗粒物的湍流垂直输送和湍流通量的研究.而细颗粒物湍流垂直通量的准确估算是影响空气质量预报准确与否的重要参量之一, 有利于空气质量和气候数值模式中排放参数化方案的发展与改进.
由于目前缺乏较为成熟可靠且使用广泛的颗粒物快速响应测量仪器, 而利用传统的涡动相关法(Eddy Covariance, EC)直接计算颗粒物湍流通量存在一定的难度, 因此, 基于条件采样的松弛涡旋累积法(The Relaxed Eddy Accumulation, REA)逐渐成为一种实用、有效的获取气态物质或颗粒物湍流通量的方法.REA法利用采样时间区间内气态物质或颗粒物的平均浓度计算湍流通量, 其显著优点在于不需要气态物质或颗粒物的快速响应测量仪器, 计算湍流通量时不需要进行复杂的仪器学修正, 后期的数据处理过程较为简单(Ueyama et al., 2013), 可有效解决缺少气态物质或颗粒物快速涨落测量手段的情形或测量精度低、误差大的问题.因此, 在大气气溶胶和大气成分分析领域, REA法比EC法适用范围更为广泛, 目前经常用于CH4(葛红星等, 2016;Ueyama et al., 2012;2013;2018)、NO2(Desjardins et al., 2010)、氨(Nelson et al., 2017;2019)、挥发性有机物(VOC)(Arnts et al., 2013)等气态物质和气溶胶(Held et al., 2008)湍流通量的获取.
由于目前缺少EC法所需的颗粒物快速响应测量仪器, 因而难以获取细颗粒物的湍流通量.因此, 本文采用REA法进行模拟条件采样, 利用山东省平原县大气环境实验站观测资料, 计算2018年12月27日—2019年1月8日持续重霾天气过程的细颗粒物湍流通量, 并与细颗粒物湍流通量测量装置给出的结果进行对比, 以验证REA法计算细颗粒物湍流通量的适用性.
2 数据获取与处理(Data acquisition and processing)平原县大气环境实验站位于山东省德州市平原县气象局(37.154144°N, 116.476774°E, 见图 1), 地处中国华北平原, 德州市南部, 观测场海拔高度为23.8 m, 周围是相对平坦的农田, 无高大建筑.本文选取大气环境加强实验期间, 即2018年12月27日—2019年1月8日13 d重霾天气过程的大气湍流和颗粒物实验观测数据.与本文分析有关的主要观测项目包括:涡动相关系统(IRGASON, Campbell Scientific, Inc., USA)获取风速、温度、湿度和CO2快速涨落信息, 超声风温仪朝向正北方向, 采样频率为10 Hz;颗粒物连续测量仪(E-Sampler, Met One, Inc., USA)获取细颗粒物质量浓度的高频信息, 采样频率为1 Hz.细颗粒物湍流通量测量系统(一种细颗粒物湍流通量测量方法, 专利受理号:201811376291.9)是一种利用大气消光特征获取颗粒物湍流通量的测量装置(Ren et al., 2020).仪器安装高度均为2.8 m.
图 1(Fig. 1)
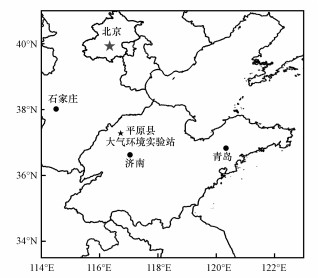 |
| 图 1 山东省平原县大气环境实验站位置 Fig. 1Location of the atmospheric environmental station in Pingyuan County, Shandong Province |
大气湍流观测数据采用EddyPro软件(Advanced 6.2.1, LI-COR Biosciences, Inc., USA)进行数据质量控制和预处理.具体过程包括:野点剔除(Vickers et al., 1997)、二次坐标旋转(Wilczak et al., 2001)、仪器学订正等, 同时剔除了明显不合理的数值, 数据平均时间区间为30 min.后续研究主要使用EddyPro软件Advanced模式中高级设置后输出的经过以上修正的10 Hz高频Level 6数据, 并对垂直风速数据分段每10 s取一个平均得到1 Hz的数据, 用于模拟条件采样计算细颗粒物湍流通量.
细颗粒物质量浓度脉动数据的预处理仅包括野点剔除, 平均时间为30 min, 通过计算其平均值和标准差对野点进行判别, 即:若脉动数据中某一数值相对其平均值的偏差超过4倍的标准差, 即: C-C ≥4σC, 则认为该数据点为一个“野点”, 将“野点”用其前后相邻两数据的线性内插代替.
3 理论和计算方法(Theory and calculation method)松弛涡旋累积法是一种基于条件采样的气态物质或颗粒物湍流通量获取方法(Businger et al., 1990), 是在涡旋累积法(Eddy Accumulation, EA)基础上, 放宽采样条件的简化方法(Desjardins, 1977).REA法不需要EA法中进行条件采样所必需的复杂阀门装置, 仅需用恒定速率抽气即可.一般来说, 湍流通量的计算方法都存在一定的前提假设, EC法的相关假设也适用于EA法和REA法(Bowling et al., 1998).首先, 大气中的标量气体应具有无化学反应的或惰性的属性, 如甲烷、二氧化碳等(Businger et al., 1990);其次, 假设某一实验站垂直输送的全部通量代表实验站所在区域的湍流通量的总体平均值(Businger, 1986);最后, 大气运动比较平稳, 流场水平均匀(忽略平流的影响), 准平稳(定常)湍流, 近地层满足常通量层假设, 影响湍流通量的各种尺度涡旋都能被测量到(徐自为等, 2008).REA法基于垂直风速进行条件采样, 当垂直风速向上(w>0)时, 将气态物质收集至向上的采样罐;当垂直风速向下(w < 0)时, 将气态物质收集至向下的采样罐, 从而获取一定时间区间内垂直风速向上和向下两个采样罐内待测气态物质或颗粒物的平均浓度

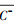
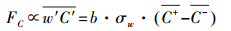 | (1) |
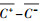
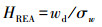 | (2) |
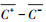
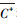
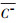
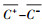
基于近地面层各物理量湍流输送特征的相似性, 利用REA法计算大气气态物质或颗粒物的湍流通量时, 通常以较易获取快速涨落信息的温度(T)、水汽(H2O)和二氧化碳(CO2)等作为代理变量, 确定经验系数b值.前人的许多实验研究发现, 以EC法获取的湍流通量FEC为参考, REA法的经验系数b可通过式(3)计算.即, 对待测气态物质或颗粒物及某种代理变量(温度(T)、水汽(H2O)和二氧化碳(CO2))进行高频采样, 在每个采样平均时间区间内, 将EC法计算的代理变量的湍流通量、垂直风速标准差及模拟条件采样获取的代理变量的平均浓度差(
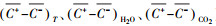

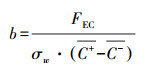 | (3) |
图 2分别给出了温度(T)、水汽(H2O)和二氧化碳(CO2)不同代理变量的b值bT、bH2O、bCO2随归一化采样阈值HREA变化的箱线图.其中, 箱体中间的实线代表HREA对应的b值时间序列的中位数, 箱体的上、下两端分别代表第三四分位点Q3(75%)和第一四分位点Q1(25%), 箱体的高度为Q3与Q1之间的差值, 代表四分位距(Interquartile Range, IQR=Q3-Q1);箱体以外两端虚线上、下延伸至的横实线为数据的上、下限, 分别定义为:上限MAX=Q3+1.5IQR, 下限MIN=Q1-1.5IQR.上、下限以外的数据点称为离群点, 未在图 2中体现.IQR和上、下限范围可在一定程度上体现b值的离散性.
由图 2可以看出, 不同代理变量T、H2O和CO2的b值的中位数均随HREA的增大而减小, 箱线图的箱体高度及箱体上、下限范围均表现出先减小后增大的趋势, 说明b值的离散性均随HREA的增大表现为先减小后增大.HREA的数值范围在0.6~0.9之间对应的代理变量b值的离散性较小.当HREA=0, 即采样阈值为0时, 不同代理变量b值的中位数分别为bT=0.56, bH2O=0.56, bCO2=0.56.
图 2(Fig. 2)
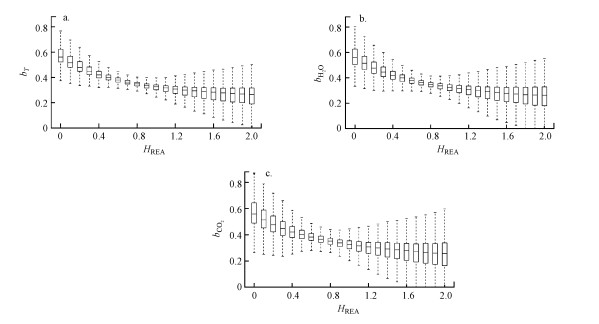 |
| 图 2 各代理变量的经验系数b值随归一化采样阈值HREA的变化(a.bT, b.bH2O, c. bCO2 Fig. 2Relationship between the empirical coefficients b of each representative quantity bT(a), bH2O(b), bCO2(c) and the normalized sampling threshold HREA |
对于REA法来说, 经验系数b的取值对气态物质或颗粒物湍流通量的获取十分重要.前人的理论研究发现, 当垂直风速与待测气体浓度之间的联合概率密度分布(JFD)满足理想的二维正态分布关系时, 经验系数
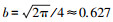
表 1(Table 1)
| 表 1 不同下垫面条件下REA法的经验系数b的取值 Table 1 Empirical coefficients b of the REA method under different underlying surfaces | ||||||||||||||||||||||||||||||||||||||||||||||||||||
表 1 不同下垫面条件下REA法的经验系数b的取值 Table 1 Empirical coefficients b of the REA method under different underlying surfaces
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
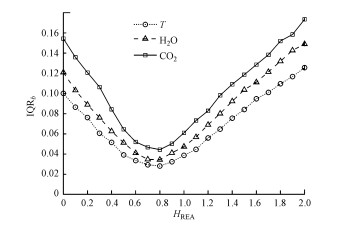
图 3给出了不同代理变量b值的IQR随HREA的变化关系.从图中可以看到, 不同代理变量b值的IQR均随HREA的变化存在一个极小值, HREA=0.8时的代理变量b值的离散性最小, 这与Tsai等(2012)和葛红星(2018)的结果一致.由图 2可见, HREA=0.8时对应的温度(T)、水汽(H2O)和二氧化碳(CO2)的经验系数b值的中位数分别为bT=0.3491、bH2O=0.3481、bCO2=0.3516.另外, 温度(T)的IQR最小, 说明温度对应的b值的离散性最小, 水汽(H2O)次之, 二氧化碳(CO2)的b值的离散性最大.所以, 温度(T)更适合作为代理变量计算细颗粒物的湍流通量.另外, 温度还具备显著优势:三维超声风温仪比气体分析仪更为成熟, 温度快速涨落信息较易获取, 观测精度较高(Bowling et al., 1998).
图 3(Fig. 3)
 |
| 图 3 温度(T)、水汽(H2O)和二氧化碳(CO2)的经验系数bT、bH2O、bCO2的四分位距IQRb随归一化采样阈值HREA的变化 Fig. 3Relationship between the interquartile range IQRb of empirical coefficients bT, bH2O, bCO2 for temperature(T), water vapor(H2O), and carbon dioxide(CO2) and the normalized sampling threshold HREA |
4.2 细颗粒物湍流通量的获取与验证利用公式(2)可计算每个采样时间区间内的采样阈值wd, 本文取其均值0.1 m · s-1作为最终的采样阈值, 通过模拟条件采样获取细颗粒物平均浓度差.计算细颗粒物湍流通量时, 经验系数b的使用通常有3种方法:①“同步b值”(Myles et al., 2007), 即:由于不同时间区间内的b值不同, 利用每个采样平均时间区间内的b值计算该时间区间内的湍流通量.Oncley等(1993)使用“同步b值”计算了棉花田下垫面的二氧化碳通量;Gao(1995)使用“同步b值”计算了森林下垫面的动量通量、感热通量和潜热通量;Myles等(2007)使用“同步b值”计算了草地下垫面氨、二氧化硫等气体的湍流通量.但由于经验系数b值本身随时间变化不大, 用“同步b值”反而会引入b值的离散性带来的误差, 不建议采用.②“固定b值”(Sakabe et al., 2012;Ueyama et al., 2012), 即:对代理变量的b值时间序列取中位数计算所有时间区间内的湍流通量, 剔除b值之间的差异造成的离散性所带来的误差.Baker等(1992)使用“固定b值”计算了大豆田下垫面的感热通量;Sakabe等(2012)和Ueyama等(2012)都使用“固定b值”计算了森林下垫面的甲烷通量.③“修正b值”(Ammann et al., 2002), 即:考虑大气层结状况对经验系数b值的影响, 用稳定度参数z/L对固定b值进行修正.Ammann和Meixner(2002)研究了谷物田下垫面温度、水汽和二氧化碳的经验系数b值与稳定度参数之间的关系, 提出了“修正b值”, 并发现计算通量结果优于“同步b值”.但由于使用经验公式给出的“修正b值”本质上是对“固定b值”进行稳定度补偿, 其离散性明显小于“同步b值”, 因此, 该对比研究并不能确定通量获取结果的改善是加入稳定度修正还是离散性减小的作用, 使用“修正b值”的效果是否优于“固定b值”无法确定.可见利用经验系数b值的何种方式计算湍流通量似乎与下垫面没有太大联系.葛红星(2018)使用“固定b值”和“修正b值”计算了水稻田下垫面的甲烷通量, 发现两种方法的结果差异很小, 且加入采样阈值后不同稳定度条件下b值的差异将缩小, “固定b值”与“修正b值”获取的通量结果差异将更小.因此, 本文也沿用了其结论:“固定b值”的获取过程比较简单, 在大气层结状况变化不大的情况下是更好的选择.
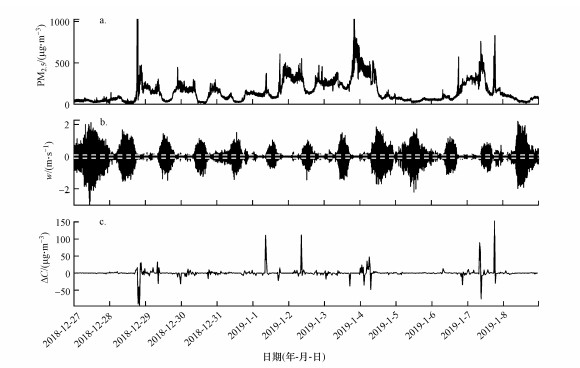
图 4为山东省平原县大气环境实验站2018年12月27日—2019年1月8日重霾天气过程的细颗粒物质量浓度、垂直风速及REA法计算的细颗粒物平均质量浓度差的时间序列.图 4b中两条白色虚线分别表示采样阈值wd=0.1 m · s-1和-wd=-0.1 m · s-1.可以看到, 当细颗粒物质量浓度较大时, 即重污染时期, 垂直风速脉动较弱, 细颗粒物平均质量浓度差越大;反之, 垂直风速脉动较强, 细颗粒物平均质量浓度差越小, 这与颗粒物的干沉降有关, 而造成干沉降的原因之一即是湍流扩散.垂直风速绝对值小于阈值wd的时段, 忽略其对大气细颗粒物湍流通量的贡献, 取其平均浓度差和湍流通量为0.
图 4(Fig. 4)
 |
| 图 4 山东省平原县大气环境实验站2018年12月27日—2019年1月8日各物理量的时间序列(a.细颗粒物质量浓度, b.垂直风速, c.细颗粒物平均质量浓度差) Fig. 4Time series of mass concentration of the fine particulate matter(a), vertical velocity(b), average mass concentration difference of the fine particulate matter(c) from December 27, 2018 to January 8, 2019 at the atmospheric environmental station |
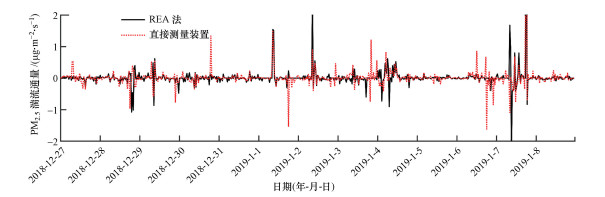
图 5给出了山东省平原县大气环境实验站2018年12月27日—2019年1月8日重霾天气过程中的细颗粒物湍流通量时间序列.其中, 黑色实线为REA法的计算结果, 红色点线为利用大气消光系数特征的细颗粒物湍流通量测量装置的计算结果.由图 5可以看出, 整体上两种方法获取的细颗粒物湍流通量有较好的一致性.由于湿度的影响, REA法计算得到的细颗粒物湍流通量比细颗粒物湍流通量测量装置的结果略有偏大, 且在污染较为严重的1月4日和1月7日时段的偏差略有增加, 说明REA法在获取大气细颗粒物湍流通量上是可行的.
图 5(Fig. 5)
 |
| 图 5 细颗粒物湍流通量的时间序列(黑色实线:REA法;红色点线:细颗粒物湍流通量测量装置) Fig. 5Time series of the turbulent flux of the fine particulate matter obtained by the REA method (black solid line) and the rapid response measuring equipment (red dotted line) |
图 6给出了REA法和细颗粒物湍流通量测量装置获取的细颗粒物湍流通量的对比, 其中, 虚线斜率为1:1, 实线为两种方法计算结果的线性拟合, 拟合系数为0.93, R2=0.7987, 较分散数据组对应了细颗粒物湍流通量较大的重霾天气污染时段.
图 6(Fig. 6)
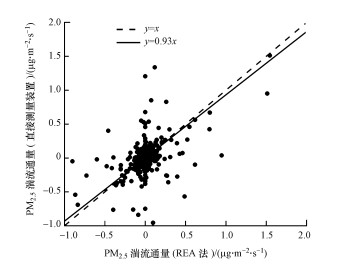 |
| 图 6 REA法计算的细颗粒物湍流通量与细颗粒物湍流通量测量装置结果的对比 Fig. 6Comparison between the turbulent flux of the fine particulate matter obtained by the REA method and the rapid response measuring equipment |
以上对比说明两种方法在计算颗粒物湍流通量上的结果是比较一致的, 但在重污染时段依旧存在微小差别.大气消光法和REA法计算垂直湍流通量各有优势, 也有不足.大气消光系数法的优点在于不需要颗粒物浓度的快速响应测量仪器, 缺点是当相对湿度较高时颗粒物质量浓度并不是影响消光系数的唯一因素, 两者之间的函数关系需要一定修正, 因此, 大气消光法往往用于相对湿度较低(RH < 80%)的情形;另外, 大气消光法对能见度测量的精度要求较高.松弛涡旋累积法的优点同样不需要颗粒物浓度的快速响应测量仪器, 缺点是计算过程中的气态物质平均浓度差为两个较大数值之差, 是颗粒物湍流通量相对误差增加的原因之一.
5 结论(Conclusions)本文利用山东省平原县大气环境实验站加强观测期间的大气湍流和细颗粒物质量浓度脉动观测资料模拟条件采样, 采用REA法计算了2018年12月27日—2019年1月8日重霾天气过程的细颗粒物湍流通量.结果显示, 加强实验观测期间, 温度(T)、水汽(H2O)、二氧化碳(CO2)等不同代理变量的REA法获取的湍流通量的经验系数b分别为bT=0.56、bH2O=0.56、bCO2=0.56;经验系数b值的中位数随归一化采样阈值HREA的增大而减小;考虑四分位距IQR代表b值的离散性, 不同代理变量的IQR数值随HREA的变化均存在一个最小值, 据此确定了b值离散性最小时对应的理想归一化采样阈值HREA=0.8和各自的b值bT=0.3491、bH2O=0.3481、bCO2=0.3516.基于近地面层不同物理量湍流输送特征的相似性, 将较易获取快速涨落信息的温度(T)、水汽(H2O)、二氧化碳(CO2)等作为代理变量确定经验系数b值, 选取b值离散性最小的温度(T)的经验系数b值和平均采样阈值wd=0.1 m · s-1, 采用REA法进行模拟条件采样, 计算了细颗粒物的湍流通量, 并与利用大气消光系数特征的细颗粒物湍流通量测量装置的结果进行对比.结果显示, 尽管在重霾天气时段, REA法计算的细颗粒物湍流通量与细颗粒物湍流通量测量装置结果的差异略有偏大, 但整体表现出了较好的一致性, 说明了利用REA法计算细颗粒物湍流通量方法的可行性.
参考文献
| Ammann C, Meixner F. 2002. Stability dependence of the relaxed eddy accumulation coefficient for various scalar quantities[J]. Journal of Geophysical Research:Atmospheres, 107(D8): 71-79. |
| Andreas E L, Hill R J, Gosz J R, et al. 1998. Stability dependence of the eddy-accumulation coefficients for momentum and scalars[J]. Boundary-Layer Meteorology, 86(3): 409-420. DOI:10.1023/A:1000625502550 |
| Ao X, Grimmond C S B, Chang Y, et al. 2016. Heat, water and carbon exchanges in the tall megacity of Shanghai:challenges and results[J]. International Journal of Climatology, 36(14): 4608-4624. |
| Arnts R R, Mowry F L, Hampton G A. 2013. A high-frequency response relaxed eddy accumulation flux measurement system for sampling short-lived biogenic volatile organic compounds[J]. Journal of Geophysical Research:Atmospheres, 118(10): 4860-4873. DOI:10.1002/jgrd.50215 |
| Baker J M, Norman J M, Bland W L. 1992. Field-scale application of flux measurement by conditional sampling[J]. Agricultural and Forest Meteorology, 62(1/2): 31-52. |
| Bowling D R, Turnipseed A A, Delany A C, et al. 1998. The use of relaxed eddy accumulation to measure biosphere-atmosphere exchange of isoprene and other biological trace gases[J]. Oecologia, 116(3): 306-315. DOI:10.1007/s004420050592 |
| Businger J A. 1986. Evaluation of the accuracy with which dry deposition can be measured with current micrometeorological techniques[J]. Journal of Climate and Applied Meteorology, 25(8): 1100-1124. DOI:10.1175/1520-0450(1986)025<1100:EOTAWW>2.0.CO;2 |
| Businger J A, Oncley S P. 1990. Flux measurement with conditional sampling[J]. Journal of Atmospheric and Oceanic Technology, 7(2): 349-352. |
| Desjardins R L. 1977. Energy budget by an eddy correlation method[J]. Journal of Applied Meteorology, 16(3): 248-250. DOI:10.1175/1520-0450(1977)016<0248:EBBAEC>2.0.CO;2 |
| Desjardins R L, Pattey E, Smith W N, et al. 2010. Multiscale estimates of N2O emissions from agricultural lands[J]. Agricultural and Forest Meteorology, 150(6): 817-824. DOI:10.1016/j.agrformet.2009.09.001 |
| 杜川利, 唐晓, 李星敏, 等. 2014. 城市边界层高度变化特征与颗粒物浓度影响分析[J]. 高原气象, 33(5): 1383-1392. |
| Gao W. 1995. The vertical change of coefficient b, used in the relaxed eddy accumulation method for flux measurement above and within a forest canopy[J]. Atmospheric Environment, 29(17): 2339-2347. DOI:10.1016/1352-2310(95)00147-Q |
| 葛红星.2018.华东地区水稻田下垫面甲烷湍流通量获取及特征的实验研究[D].北京: 北京大学 |
| 葛红星, 张宏升, 罗帆, 等. 2016. 华北地区冬小麦田水热、二氧化碳和甲烷湍流输送特征的实验研究[J]. 地球物理学报, 59(4): 1235-1248. |
| Held A, Patton E, Rizzo L, et al. 2008. Relaxed eddy accumulation simulations of aerosol number fluxes and potential proxy scalars[J]. Boundary-Layer Meteorology, 129(3): 451-468. DOI:10.1007/s10546-008-9327-5 |
| 蒋伊蓉, 朱蓉, 朱克云, 等. 2015. 京津冀地区重污染天气过程的污染气象条件数值模拟研究[J]. 环境科学学报, 35(9): 2681-2692. |
| Katul G G, Albertson J, Chu C R, et al. 1994. Sensible and latent heat flux predictions using conditional sampling methods[J]. Water Resources Research, 30(11): 3053-3059. DOI:10.1029/94WR01673 |
| Katul G G, Finkelstein P L, Clarke J F, et al. 1996. An investigation of the conditional sampling method used to estimate fluxes of active, reactive, and passive scalars[J]. Journal of Applied Meteorology, 35(10): 1835-1845. DOI:10.1175/1520-0450(1996)035<1835:AIOTCS>2.0.CO;2 |
| Li X, Wang Y, Shen L, et al. 2018. Characteristics of boundary layer structure during a persistent haze event in the central liaoning city cluster, northeast China[J]. Journal of Meteorological Research, 32(2): 302-312. |
| Luan T, Guo X, Guo L, et al. 2018. Quantifying the relationship between PM2.5 concentration, visibility and planetary boundary layer height for long-lasting haze and fog-haze mixed events in Beijing[J]. Atmospheric Chemistry and Physics, 18(1): 203-225. DOI:10.5194/acp-18-203-2018 |
| Miao Y, Liu S, Guo J, et al. 2018. Unraveling the relationships between boundary layer height and PM2.5 pollution in China based on four-year radiosonde measurements[J]. Environmental Pollution, 243: 1186-1195. DOI:10.1016/j.envpol.2018.09.070 |
| Myles L T, Meyers T P, Robinson L. 2007. Relaxed eddy accumulation measurements of ammonia, nitric acid, sulfur dioxide and particulate sulfate dry deposition near Tampa, FL, USA[J]. Environmental Research Letters, 2(3): 034004. DOI:10.1088/1748-9326/2/3/034004 |
| Nelson A J, Koloutsou-Vakakis S, Rood M J, et al. 2017. Season-long ammonia flux measurements above fertilized corn in central Illinois, USA, using relaxed eddy accumulation[J]. Agricultural and Forest Meteorology, 239: 202-212. |
| Nelson A J, Lichiheb N, Koloutsou-Vakakis S, et al. 2019. Ammonia flux measurements above a corn canopy using relaxed eddy accumulation and a flux gradient system[J]. Agricultural and Forest Meteorology, 264: 104-113. DOI:10.1016/j.agrformet.2018.10.003 |
| Oncley S P, Delany A C, Horst T W, et al. 1993. Verification of flux measurement using relaxed eddy accumulation[J]. Atmospheric Environment.Part A.General Topics, 27(15): 2417-2426. DOI:10.1016/0960-1686(93)90409-R |
| Pattey E, Desjardins R L, Rochette P. 1993. Accuracy of the relaxed eddy-accumulation technique, evaluated using CO2 flux measurements[J]. Boundary-Layer Meteorology, 66(4): 341-355. DOI:10.1007/BF00712728 |
| Ren Y, Zhang H, Wei W, et al.2020.Determining the fluctuation of PM2.5 mass concentration and its applicability to Monin-Obukhov similarity[J].Science of the Total Environment, 136398 |
| Sakabe A, Hamotani K, Kosugi Y, et al. 2012. Measurement of methane flux over an evergreen coniferous forest canopy using a relaxed eddy accumulation system with tuneable diode laser spectroscopy detection[J]. Theoretical and Applied Climatology, 109(1/2): 39-49. |
| Tsai J L, Tsuang B J, Kuo P H, et al. 2012. Evaluation of the relaxed eddy accumulation coefficient at various wetland ecosystems[J]. Atmospheric Environment, 60: 336-347. DOI:10.1016/j.atmosenv.2012.06.081 |
| Ueyama M, Hamotani K, Nishimura W, et al. 2012. Continuous measurement of methane flux over a larch forest using a relaxed eddy accumulation method[J]. Theoretical and Applied Climatology, 109(3/4): 461-472. |
| Ueyama M, Takai Y, Takahashi Y, et al. 2013. High-precision measurements of the methane flux over a larch forest based on a hyperbolic relaxed eddy accumulation method using a laser spectrometer[J]. Agricultural and Forest Meteorology, 178-179: 183-193. DOI:10.1016/j.agrformet.2013.04.029 |
| Ueyama M, Yoshikawa K, Takagi K. 2018. A cool-temperate young larch plantation as a net methane source-A 4-year continuous hyperbolic relaxed eddy accumulation and chamber measurements[J]. Atmospheric Environment, 184: 110-120. |
| Vickers D, Mahrt L. 1997. Quality control and flux sampling problems for tower and aircraft data[J]. Journal of Atmospheric and Oceanic Technology, 14(3): 512-526. DOI:10.1175/1520-0426(1997)014<0512:QCAFSP>2.0.CO;2 |
| Wang J, Zhang X, Li D, et al. 2018. Interdecadal changes of summer aerosol pollution in the Yangtze River Basin of China, the relative influence of meteorological conditions and the relation to climate change[J]. Science of the Total Environment, 630: 46-52. DOI:10.1016/j.scitotenv.2018.01.236 |
| 王耀庭, 李威, 张小玲, 等. 2012. 北京城区夏季静稳天气下大气边界层与大气污染的关系[J]. 环境科学研究, 25(10): 1092-1098. |
| Wesely M L, Hart R L.1994.On eddy accumulation with limited conditional sampling to measure air-surface exchange[R].United States: Argonne National Lab., IL |
| Wilczak J M, Oncley S P, Stage S A. 2001. Sonic anemometer tilt correction algorithms[J]. Boundary-Layer Meteorology, 99(1): 127-150. DOI:10.1023/A:1018966204465 |
| Wyngaard J C, Moeng C H. 1992. Parameterizing turbulent diffusion through the joint probability density[J]. Boundary-Layer Meteorology, 60(1/2): 1-13. |
| 吴兑. 2012. 近十年中国灰霾天气研究综述[J]. 环境科学学报, 32(2): 257-269. |
| 吴兑, 廖碧婷, 陈慧忠, 等. 2014. 珠江三角洲地区的灰霾天气研究进展[J]. 气候与环境研究, 19(2): 248-264. |
| 吴序鹏, 刘端阳, 谢真珍, 等. 2018. 江苏淮安地区大气污染变化特征及其与气象条件的关系[J]. 气象与环境科学, 41(1): 31-38. |
| 吴战平, 白慧, 陈早阳, 等. 2019. 贵阳市两次空气污染过程的气象条件分析[J]. 干旱气象, 37(5): 827-835. |
| 徐自为, 刘绍民, 宫丽娟, 等. 2008. 涡动相关仪观测数据的处理与质量评价研究[J]. 地球科学进展, (4): 357-370. DOI:10.3321/j.issn:1001-8166.2008.04.005 |
| Ye X, Song Y, Cai X, et al. 2016. Study on the synoptic flow patterns and boundary layer process of the severe haze events over the North China Plain in January 2013[J]. Atmospheric Environment, 124: 129-145. DOI:10.1016/j.atmosenv.2015.06.011 |
| 尹承美, 何建军, 于丽娟, 等. 2019. 多尺度气象条件对济南PM2.5污染的影响[J]. 高原气象, 38(5): 1120-1128. |
| Zhang L, Sun J Y, Shen X J, et al. 2015. Observations of relative humidity effects on aerosol light scattering in the Yangtze River Delta of China[J]. Atmospheric Chemistry and Physics, 15(14): 8439-8454. |
| Zhong J, Zhang X, Dong Y, et al. 2018. Feedback effects of boundary-layer meteorological factors on cumulative explosive growth of PM2.5 during winter heavy pollution episodes in Beijing from 2013 to 2016[J]. Atmospheric Chemistry and Physics, 18(1): 247-258. DOI:10.5194/acp-18-247-2018 |
