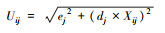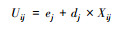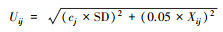, 袁自冰1
, 郑君瑜1, 林小华1, 刘启汉2, 郁建珍2, 余立之31. 华南理工大学环境与能源学院, 广州 510006;
2. 香港科技大学环境学部, 香港 999077;
3. 香港环境保护署, 香港 999077
收稿日期: 2018-01-08; 修回日期: 2018-03-10; 录用日期: 2018-03-10
基金项目: 国家自然科学基金重大研究计划重点支持项目（No.91644221）；香港环境保护署项目（No.CE28/2014（EP），CE15/2016（EP））
作者简介: 张夏夏(1993-), 女, E-mail:13242893162@163.com
通讯作者（责任作者）: 袁自冰, E-mail:zibing@scut.edu.cn
摘要: 目前，正定矩阵因子法（PMF）在大气污染物来源解析中得到了广泛应用，而监测数据不确定度评估是PMF源解析的重要内容之一.当前绝大部分研究采用的数据不确定度仅通过借鉴前人的方法简单计算而得，缺乏对计算方法的合理性和适用性进行评估.本研究通过3种常用的不确定度算法交互应用建立了一套有效评估不确定度的方法体系.通过对香港荃湾站点1998—2008年PM10组分监测数据进行源解析并与平行采样数据源解析结果进行对比，对该方法体系的合理性进行了验证.结果发现，应用该方法体系可以将某些常规方法无法分离的因子进一步分解，得到的源解析结果的残差值甚至小于平行采样方法解析结果的残差值，得到的因子贡献率均处于常规方法得出的因子贡献率之间.这些均表明了该方法体系所得源解析结果的可靠性和全面性.因此，本研究建立的评估不确定度的方法体系具有较强的可行性，对确保源解析结果的准确性有重要意义.
关键词:不确定度评估方法体系源解析正定矩阵因子法
Establishment of an uncertainty assessment framework for atmospheric pollutant monitoring data and its impact on PMF source apportionment
ZHANG Xiaxia1
, YUAN Zibing1 , ZHENG Junyu1, LIN Xiaohua1, Alexis K. H. Lau2, YU Jianzhen2, Alfred L. C. Yu3 1. School of Environment and Energy, South China University of Technology, Guangzhou 510006;
2. Division of Environment, the Hong Kong University of Science and Technology, Hong Kong 999077;
3. Hong Kong Environmental Protection Department, Hong Kong 999077
Received 8 January 2018; received in revised from 10 March 2018; accepted 10 March 2018
Abstract: Positive matrix factorization (PMF) has been applied extensively in source apportionment of atmospheric pollutants. Data uncertainty is one of the most important input information for PMF analysis. Currently, data uncertainty is calculated by some simple formulae referenced from previous studies, lacking evaluation of their reasonableness and applicability. In this study, we develop an uncertainty assessment framework (UAF) by utilizing three common uncertainty calculation algorithms. The effectiveness of this UAF is assessed by comparing with the source apportionment results on parallel measurement of PM10 compositions at Tsuen Wan station in Hong Kong during 1998—2008. It is found that applying UAF could further decompose some factors which couldn't by traditional methods. The derived scaled residuals are even smaller than those from source apportionment on parallel measurement. Source contributions derived by UAF are well in between those from traditional methods. All above indicates the reliability and completeness of source apportionment by UAF. It is thus concluded that this UAF has great applicability and usefulness in ensuring the accuracy of source apportionment results.
Keywords: uncertainty assessment frameworksource apportionmentpositive matrix factorization
1 引言(Introduction)源解析技术是通过环境污染物浓度监测对其来源进行定性或定量研究的主要技术, 在污染物控制管理中发挥了重要的指导作用(Wang et al., 2014; Zhang et al., 2017).受体模型法是目前源解析技术的常用方法之一(环境保护部, 2013), 以污染物质量守恒特性平衡分析为前提, 应用数学统计方法定量解析不同因子(通常识别为污染源)对污染物浓度的贡献.目前常用的受体模型主要包括化学质量平衡(Chemical Mass Balance, CMB)、正定矩阵因子分析(Positive Matrix Factorization, PMF)、主成分分析(Principal Component Analysis, PCA)、多元线性模型(Multi-linear Engine, ME)和Unmix等.
由于具有对源谱信息依赖程度低且能够解析出低贡献源等优势, PMF法得到了越来越广泛的应用(张延君等, 2015).在我国北京(Zhang et al., 2013; Tan et al., 2014; 梁林林等, 2015; 王琴等, 2015; Tian et al., 2016; Tao et al., 2016; Zikova et al., 2016)、上海(Cai et al., 2010; 边璐等, 2013; Wang et al., 2015; Fang et al., 2016)、广州(Gao et al., 2013, 2015; Huang et al., 2014)、香港(Friend et al., 2011; Yuan et al., 2013; Wang et al., 2017)等城市都已广泛开展了利用PMF法对大气污染物进行来源解析的研究.
在利用PMF法进行源解析的过程中, 监测数据的不确定度是其重要的输入文件, 在计算分析过程中起到非常关键的作用.某种化学组分数据的不确定度决定了其在PMF计算中的权重, 不确定度越低则其所占权重就越大.另外, PMF法中不确定度值将直接影响目标函数Q的取值, 而Q的取值将直接影响PMF模型中最理想结果的选择.因此, 不确定度值的准确性将直接影响到源解析结果的准确性, 如何准确地评估PMF输入数据的不确定度是源解析工作中重要内容之一.
数据的不确定度是指对研究变量的真值缺乏认识和了解, 可用置信区间或概率密度函数进行描述.不确定度取决于对研究对象相关信息掌握的情况, 可通过对数据的质量与数量及对数据来源过程和测试方法等的了解进行评价(郑君瑜等, 2013).源解析数据的不确定度主要来自于样品采集和化学成分测量的不确定度(即所用仪器带来的不确定度)及样品本身浓度存在的不确定度(主要是人为误差)等.理论上讲, 数据不确定度应利用平行采样的方法进行衡量, 通过对比多组数据以更为准确地评估测量值的误差分布(Hyslop et al., 2008; Yuan et al., 2013).但由于经济等条件的限制, 很多时候都不能实现平行采样.到目前为止, 对于非平行采样的监测数据不确定度估算尚无成熟的方法体系.在绝大部分源解析研究中, 其输入数据的不确定度主要通过借鉴前人的方法加以计算, 而缺乏对采用该方法的原因进行充分阐述.因此, 建立一套科学严谨的不确定度评估方法体系, 从而更准确地识别数据不确定度, 对于保证大气污染物源解析结果的准确性和科学性至关重要.
本研究采用香港荃湾地区1998—2008年PM10平行采样的数据, 通过3种常用的不确定度评估算法交互应用建立一套有效评估不确定度的方法体系, 并将利用该方法体系得到的源解析结果与利用平行采样的源解析结果进行对比, 评估该方法体系的可行性和优势.
2 材料与方法(Materials and methods)2.1 数据来源本研究采用的大气污染物数据为1998年1月—2008年12月在香港荃湾站点(22.37°N, 114.11°E)采集的PM10组分数据.PM10样品每6 d采集一次, 每次采样24 h, 两台采样器(Andersen Instrument, GA, USA)平行采集, 共收集可用样品662×2个, 检测出As、Be等27种化学组分.在PMF分析中, 将低于检出限的样品数超过总样品数50%的组分删除(Huang et al., 1999), 最终保留As、Cd、Pb、V、Ni、Al、Mn、Fe、Ca、Mg、Na+、Cl-、NH4+、NO3-、SO42-、K+、OC、EC共18种化学组分.其中, OC、EC是由热/光碳分析仪(Sunset Laboratory, OR, USA)测得, Al、Ca、Cd、Fe、Mg、Mn、Ni、Pb、V和Zn由等离子体原子发射光谱仪(ICP-AES)测得, As由流动注射分析-原子吸收仪(FIA-AA)测得, 水溶性离子SO42-、NO3-、Cl-、NH4+、Na+和K+由离子色谱仪(IC)测得.关于PM10组分测量更详细的信息请参考相关文献(Yu et al., 2004; Yuan et al., 2006).本研究利用一台采样器的监测数据建立不确定度评估方法体系, 并综合运用两台采样器的平行监测结果对不确定度评估方法体系的合理性进行评估.
2.2 PMF原理PMF模型是由芬兰赫尔辛基大学的Dr. Paatero开发(Paatero et al., 1994; 1997).随着PMF2、PMF3、ME2、PMF5等版本的发布, 该模型已被广泛用于空气质量源解析的研究中.本次研究采用最新版本EPA PMF5.0模型, 本文只对其进行简单介绍, 详细介绍请参考其使用手册(EPA, 2014).
PMF模型不需要污染源的成分谱信息, 只需输入目标污染物各化学组分浓度及其不确定度即可完成计算.PMF的基本方程为：
 | (1) |
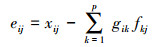 | (2) |
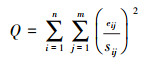 | (3) |
2.3 不确定度评估方法体系建立目前的PMF源解析研究中通常只采用单一的不确定度计算方法.然而, 污染物不同化学组分的物理化学性质不同, 在进行仪器分析前经不同的实验前处理, 不同组分又经不同的仪器基于不同的分析原理进行测定, 这就使得每种组分不确定度的程度及来源存在差别.因此认为, 在不确定度的计算过程中, 应以某一种计算方法为基础, 并结合运用其它计算方法进行尝试, 最终得到最优的源解析结果, 这也是我们建立不确定度计算方法体系的理论基础.通过该方法体系, 可以在使用一种不确定度算法不能得到一个非常理想结果的情况下, 利用更多的不确定度算法对数据的不确定度进行持续优化, 从而提高源解析结果的准确性.
2.3.1 3种不确定度值算法比较不确定度评估方法体系需要选取数种常用的不确定度计算方法作为出发点.本研究选取颗粒物源解析中3种常用的不确定度算法, 它们之间的异同见表 1.
表 1(Table 1)
| 表 1 3种不确定度值算法比较 Table 1 Comparison of three uncertainty algorithms | ||||||||||||||||
表 1 3种不确定度值算法比较 Table 1 Comparison of three uncertainty algorithms
| ||||||||||||||||
 |
上述3种不确定度的计算方法可分为Uij=
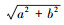
2.3.2 3种不确定度算法参数值确定3种不确定度算法中参数的取值将直接影响到不确定度的大小.受体模型假设因子谱在分析时段保持不变, 因此, 对于实际情况下可能变化的组分, 如具有挥发性或有二次生成或损耗(如Cl-具有较强的挥发性, 则dj和cj赋值相对较大), 应给予相对较大的不确定度取值.另外, PMF计算中对于检出限上下的数据不确定度计算方法不同, 因此, 对于浓度接近检出限的组分也应给予较大的不确定度取值(如本研究中的As、Cd、Pb、V、Ni 5种组分).根据以上原则对分析化学组分分成两类(表 2), 分别将算法1和算法2中对应的dj值赋予0.1和0.25.算法3中数据的标准偏差实际上代表的是仪器误差, 并且当物质的浓度较小时则标准偏差偏离真值所占的比例就越大, 即cj值越大.据此对分析化学组分分成3类(表 2), 分别将对应的cj值赋予0.05、0.1和0.5.
表 2(Table 2)
| 表 2 算法1、算法2的dj值及算法3的cj值 Table 2 Values of dj in algorithm #1 and #2 and cj in algorithm #3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 2 算法1、算法2的dj值及算法3的cj值 Table 2 Values of dj in algorithm #1 and #2 and cj in algorithm #3
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 结果与讨论(Results and discussion)3.1 3种不确定度算法对应的源解析结果比较为了能得到准确且更为全面的污染源个数, 在PMF源解析中依次尝试了设定4~9个因子, 最终发现利用3种不确定度算法的源解析最为合理的结果均为8个因子, 分别代表机动车、重油、新鲜海盐、老化海盐、扬尘源、二次硫酸盐、二次硝酸盐及生物质/煤燃烧污染源, 生物质燃烧和煤燃烧无法分开.利用3种不确定度算法解析的因子谱图见图 1.关于香港地区各污染源示踪物选取在之前的研究文献中已有详细说明(Guo et al., 2009;Cheng et al., 2010 ), 在此不再赘述.
图 1(Fig. 1)
 |
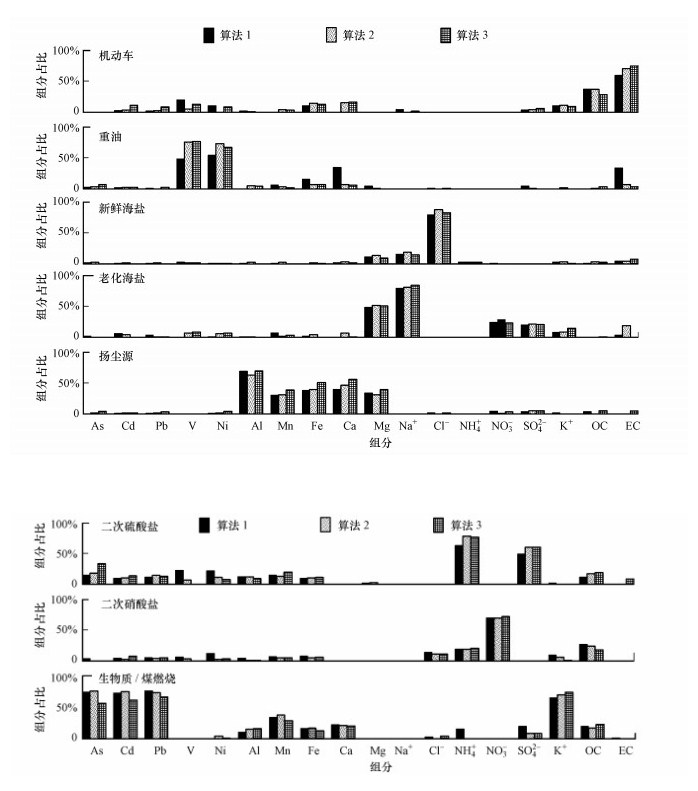| 图 1 利用算法1、2、3得到的8个因子谱图 Fig. 1Eight-factor profiles obtained from the three algorithms for uncertainty calculation |
尽管利用3种不确定算法都能得到8个因子, 但各因子的谱图存在一定差异.理论上讲, 每个因子的示踪物应该尽可能富集在单一因子中.比较而言, 算法2中各因子对应的示踪物的含量相对较多, 例如, 重油的V和Ni及新鲜海盐的Cl-在算法2所得的结果中较高, 因此, 利用算法2计算的不确定度所得的源解析结果相对更为准确.
3.2 不确定度评估方法体系的建立利用3种不确定度算法得出的解析结果中, 生物质燃烧和煤燃烧均属于同一个因子, 这可能是由于两种排放源贡献的时间变化存在较强的共线性.因此, 需要继续对数据进行深入挖掘, 探究是否可以通过改善数据不确定度从而使生物质燃烧与煤燃烧能够分离为两个因子.如前所述, 利用算法2得到的源解析结果相对准确, 更适合作为基准结果对该批数据的不确定度进行评估.为了验证算法1和算法3中是否对某些化学组分的不确定度分析更加准确, 本文以算法2的结果为基准, 以生物质燃烧和煤燃烧的示踪物(K+、As、Cd、Pb)和图 1中利用3种不确定度算法得到的源谱图中组分浓度相对标准偏差超过10%的组分(Mn、Fe、Ca和Al)作为不确定度应改善的对象.将算法1和算法3中这8种组分的不确定度依次带入到算法2中, 如果源解析的结果有改善, 则保留算法1或算法3中该算法的不确定度值, 否则继续使用算法2的不确定度作为最佳结果.
首先利用算法1所计算的As的不确定度替换算法2中As的不确定度, 尽管可以得出9个因子, 但煤燃烧因子中的K+含量依然较高, 说明部分生物质燃烧依然与煤燃烧混合在一起(图 2).由于结果有所改善, 本文将算法2中As的不确定度值替换为算法1中As的不确定度值进行后续分析.然后, 将算法1所计算的Cd的不确定度替换算法2中Cd的不确定度, 结果并没有明显改善, 因此, 依然保留算法2中Cd的不确定度值.依照上面的方法依次将算法1和算法3中Pb、K+、Mn、Fe、Ca和Al的不确定度值替换算法2中对应元素的不确定度值, 最终经过16次的替换实验, 发现当算法2中Pb的不确定度换成算法1计算的不确定度值, 把算法2中K+的不确定度值换成算法3计算的不确定度值时, 结果有很大的改善, 即As、Cd、Pb的含量在煤燃烧因子中是最高的, 而K+在生物质燃烧因子中的含量也是最多的, 生物质燃烧和煤燃烧完全分离为两个因子, 具体如图 3所示.对于Mn、Fe、Ca和Al, 算法2已给出最优解析结果.表 3列出了这8种化学组分对应的最佳不确定度评估算法.
图 2(Fig. 2)
 |
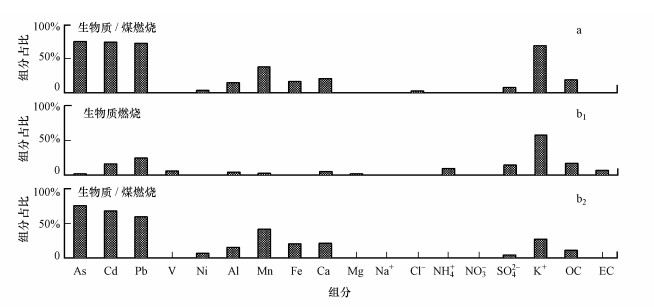| 图 2 利用算法2得到的生物质/煤燃烧因子谱图(a)和将算法1中As的不确定度带入算法2中生物质燃烧和煤燃烧源谱图(b1和b2) Fig. 2Biomass burning/coal combustion factor profile using algorithm #2(a) and biomass burning and coal combustion factor profiles when the uncertainty of As was estimated by algorithm #1(b1 and b2) |
图 3(Fig. 3)
 |
| 图 3 利用不确定度评估方法体系识别的生物质和煤燃烧源谱图 Fig. 3Biomass burning and coal combustion factor profiles determined by uncertainty assessment framework |
表 3(Table 3)
| 表 3 8种化学组分适宜的不确定度算法 Table 3 Best-fit uncertainty algorithm for eight fitting components | ||||||||
表 3 8种化学组分适宜的不确定度算法 Table 3 Best-fit uncertainty algorithm for eight fitting components
| ||||||||
|
图 4描述了利用该方法体系识别最佳源解析结果的分析流程.首先, 选取2、3个或更多的不确定度算法计算输入数据的不确定度.在利用所得的不确定度数据分别进行源解析后, 应考虑将多个不确定度算法综合使用以进一步提高源解析效果.首先通过对比N种不确定度算法对应的N种源解析结果的因子谱图, 选定相对最优源解析结果对应的算法(设为算法X)及需要改善不确定度的化学组分(设为m个), 然后将N-1个(排除最优结果对应的算法)算法中需改善组分的不确定度依次替换算法X中对应组分的不确定度, 并对比因子谱图观察源解析结果是否改善, 如解析结果得到改善, 将算法X中对应组分的不确定度替换, 如源解析结果未改善则继续使用算法X得到的该组分的不确定度, 最终经过(N-1)×m次实验, 得到对每个组分最为适合的不确定度算法及最理想的源解析结果.
图 4(Fig. 4)
 |
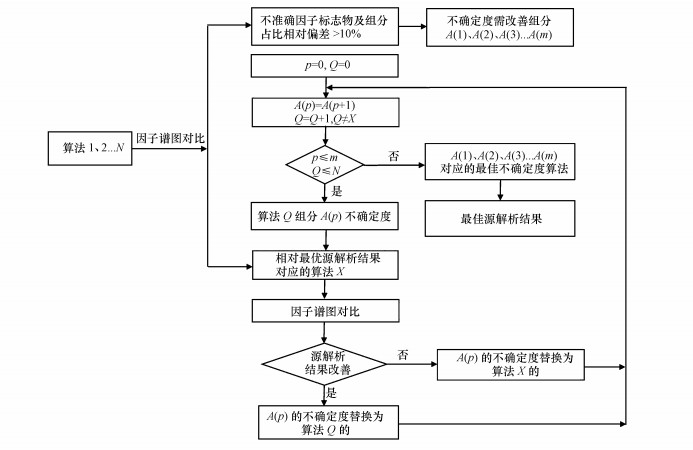| 图 4 不确定度方法体系流程图 Fig. 4Flow chart of uncertainty assessment framework |
3.3 不确定度评估方法体系源解析结果的评价3.3.1 不确定度评估方法体系与平行采样解析因子谱比较在应用不确定度评估方法体系识别最优源解析结果后, 利用平行采样数据所识别的不确定度的源解析结果对其进行评估.理论上讲, 平行采样通过对比多组数据可以更为准确地评估测量值的误差分布.Hyslop等(2008)和Yuan等(2013)对平行采样不确定度的计算方法进行了详细阐述.如图 5所示, 利用平行采样计算的不确定度进行PMF源解析, 同样可以解析出9个因子, 因子谱及因子贡献与方法体系解析结果基本相同.这一方面证实了平行采样是准确衡量不确定度的有效手段, 不必像利用单一采样方式那样通过多次试验找出适合的不确定度算法；另一方面也表明香港荃湾地区PM10确实是存在9个主要的贡献源, 生物质燃烧和煤燃烧污染源可以通过更准确地评估不确定度进行分离, 同时也表明能否对数据不确定度进行准确评估将直接影响到PMF源解析结果.
图 5(Fig. 5)
 |
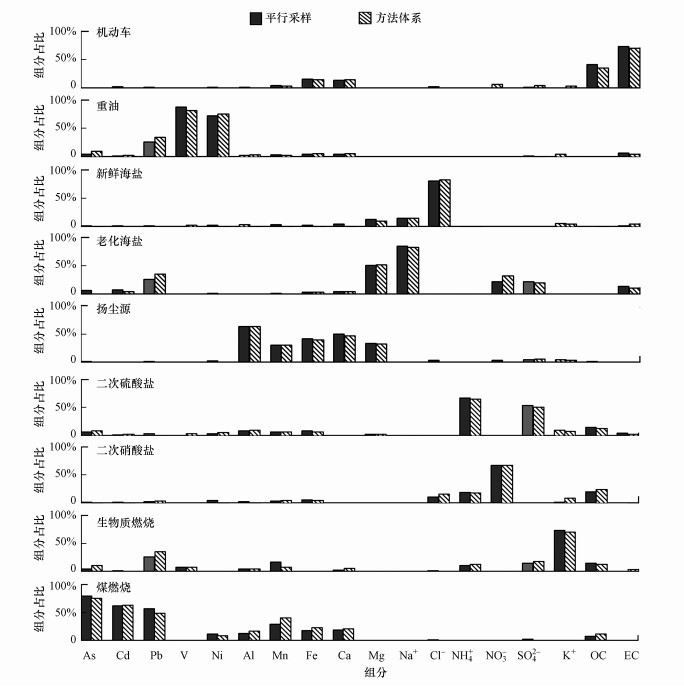| 图 5 利用平行采样与不确定度方法体系解析出的因子谱图比较 Fig. 5Comparison of factor profiles between parallel sampling and uncertainty assessment framework |
3.3.2 不确定度评估方法体系与平行采样解析残差值比较对残差(eij)进行频率分布检验也是评价PMF模型源解析结果的一种常用方法(Polissar et al., 1998).如果某组分的残差属于正态分布且标准偏差较小, 那么就表明PMF对该组分能够较完整的解析.从图 6可以看出, 除Mn以外, 利用方法体系解析的化学组分的残差分布都要比利用平行采样的化学组分的残差分布更加集中, 均值也更接近于0.这表明相比于平行采样, 利用方法体系得到的不确定度更为准确, 源解析结果也更为合理.
图 6(Fig. 6)
 |
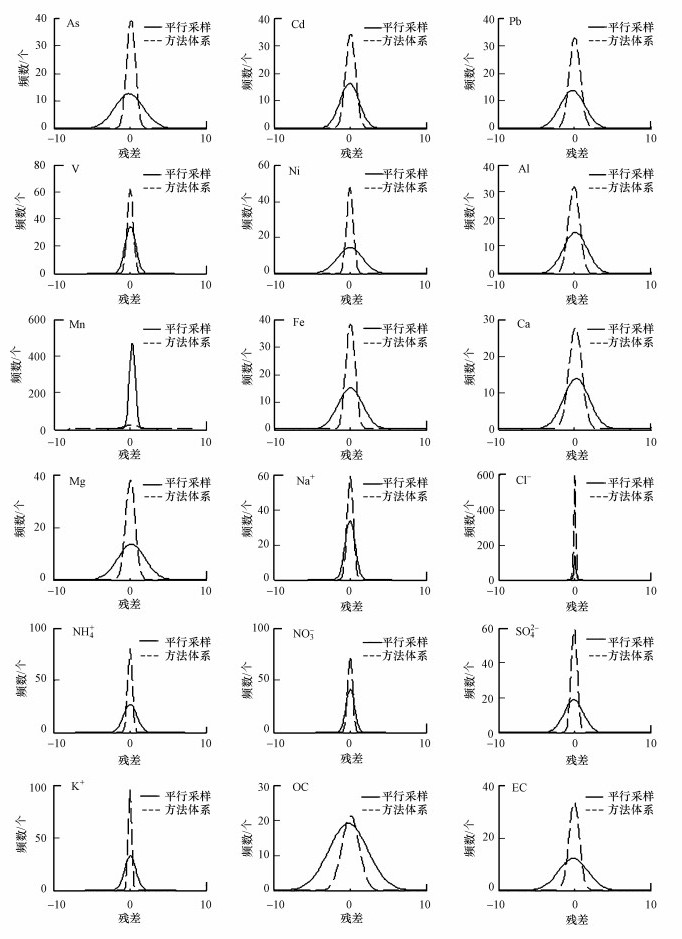| 图 6 利用平行采样与不确定度评估方法体系解析出的化学组分残差图比较 Fig. 6Comparison of frequency distributions of scaled residuals between parallel sampling and uncertainty assessment framework |
3.4 不确定度评估方法体系与单一算法源解析比较对数据不确定度进行调整的最终目的是为了提高源解析结果的准确性.如图 7所示, 利用方法体系得出的各污染源贡献率和残差贡献率都处于利用算法1、算法2、算法3得到的各污染源的贡献率范围之间, 这表明方法体系的源解析结果是比较可靠的, 没有出现异常值.另外, 利用常规方法只能得到生物质和煤燃烧污染源总的贡献占比为9.3%~14.6%, 利用方法体系则可以得到生物质燃烧和煤燃烧两个污染源的贡献率分别为11.4%和4.2%, 与常规方法所得的结果相差不大.另外, 该结果也表明相对于煤燃烧, 生物质燃烧在研究时段占比较高, 应该重点对生物质燃烧污染源进行防控.
图 7(Fig. 7)
 |
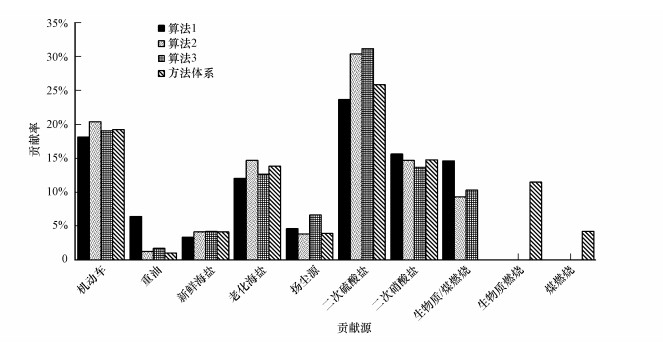| 图 7 利用不确定度评估方法体系与算法1、算法2、算法3得到的污染源贡献对比 Fig. 7Comparison of source contributions between uncertainty assessment framework and algorithm #1, #2 and #3 |
4 结论(Conclusions)1) 鉴于准确评估不确定度在PMF源解析中的重要性及大部分研究中监测数据不确定度信息缺乏的问题, 本研究建立了一套识别污染物组分监测数据不确定度的评估方法体系.通过与平行采样所得不确定度的源解析结果进行对比, 结果表明, 应用该方法体系可以更准确地评估监测数据的不确定度, 更精细地对污染物组分数据进行PMF源解析.
2) 以香港荃湾站点1998—2008年PM10组分监测数据源解析作为示范, 应用该方法体系可以将常规方法无法分离的生物质/煤燃烧因子分解成两个因子, 源解析残差值甚至小于平行采样方法解析结果的残差值, 应用该方法体系得到的因子贡献率均处于常规方法得出的因子贡献率之间.这些均说明应用该方法体系所得源解析结果的可靠性和全面性.
3) 本研究建立的不确定度方法体系流程简明, 可操作性强, 在监测数据缺乏不确定度相关信息时可以更有效地识别输入数据的不确定度, 以确保PMF源解析结果的科学性和准确性.
参考文献
| Anttila P, Paatero P, Tapper U, et al. 1995. Source identification of bulk wet deposition in Finland by positive matrix factorization[J]. Atmospheric Environment, 29(14): 1705–1718. |
| 边璐, 李田, 侯娟. 2013. PMF和PCA/MLR法解析上海市高架道路地表径流中多环芳烃的来源[J]. 环境科学, 2013, 34(10): 3840–3846. |
| Cheng Y, Lee S C, Ho K F, et al. 2010. Chemically-speciated on-road PM2.5 motor vehicle emission factors in Hong Kong[J]. Science of the Total Environment, 408(7): 1621–1627. |
| Cai C, Geng F, Tie X, et al. 2010. Characteristics and source apportionment of VOCs measured in Shanghai, China[J]. Atmospheric Environment, 44(38): 5005–5014. |
| US Environmental Protection Agency. EPA Positive Matrix Factorization 5.0 Fundamentals and User Guide[OL]. 2018-01-06.https: //www.epa.gov/sites/production/files/2015-02/documents/pmf_5.0_user_guide.pdf. |
| Fang Y, Chen Y, Tian C, et al. 2016. Application of PMF receptor model merging with PAHs signatures for source apportionment of black carbon in the continental shelf surface sediments of the Bohai and Yellow Seas, China[J]. Journal of Geophysical Research - Oceans, 121(2): 1346–1359.DOI:10.1002/2015JC011214 |
| Friend A J, Ayoko G A, Guo H. 2011. Multi-criteria ranking and receptor modelling of airborne fine particles at three sites in the Pearl River Delta region of China[J]. Science of the Total Environment, 409(4): 719–737. |
| Gao B, Guo H, Wang X M, et al. 2013. Tracer-based source apportionment of polycyclic aromatic hydrocarbons in PM2.5, in Guangzhou, southern China, using positive matrix factorization (PMF)[J]. Environmental Science - & Pollution Research International, 20(4): 2398–2409. |
| Gao B, Wang X M, Zhao X Y, et al. 2015. Source apportionment of atmospheric PAHs and their toxicity using PMF: Impact of gas/particle partitioning[J]. Atmospheric Environment, 103: 114–120.DOI:10.1016/j.atmosenv.2014.12.006 |
| Guo H, Ding A J, So K L, et al. 2009. Receptor modeling of source apportionment of Hong Kong aerosols and the implication of urban and regional contribution[J]. Atmospheric Environment, 43(6): 1159–1169.DOI:10.1016/j.atmosenv.2008.04.046 |
| 环境保护部.2013.大气颗粒物来源解析技术指南(试行)[OL].2018-01-08.http://www.zhb.gov.cn/gkml/hbb/bwj/201308/W020130820340683623095.pdf |
| Huang R J, Zhang Y, Bozzetti C, et al. 2014. High secondary aerosol contribution to particulate pollution during haze events in China[J]. Nature, 514(7521): 218–222.DOI:10.1038/nature13774 |
| Huang S, Rahn K A, Arimoto R. 2008. Testing and optimizing two factor-analysis techniques on aerosol at Narragansett, Rhode Island[J]. Atmospheric Environment, 33(14): 2169–2185. |
| Hyslop N P, White W H.. An evaluation of interagency monitoring of protected visual environments (IMPROVE) collocated precision and uncertainty estimates[J]. Atmospheric Environment, 42(11): 2691–2705.DOI:10.1016/j.atmosenv.2007.06.053 |
| Ito K, Xue N, Thurston G. 2004. Spatial variation of PM2.5, chemical species and source-apportioned mass concentrations in New York City[J]. Atmospheric Environment, 38(31): 5269–5282.DOI:10.1016/j.atmosenv.2004.02.063 |
| Jiang Y, Liu P. 2014. Feature extraction for identification of drug and explosive concealed by body packing based on positive matrix factorization[J]. Measurement, 47(1): 193–199. |
| 梁林林, Guenter, Engling, 段凤魁, 等. 2015. 北京市大气气溶胶中糖类化合物的组成及来源[J]. 环境科学, 2015, 36(11): 3935–3942. |
| Liu P, Li Z, Li B, et al. 2013. The analysis of time-resolved optical waveguide absorption spectroscopy based on positive matrix factorization[J]. Journal of Colloid & Interface Science, 403: 134. |
| 刘胜林. 2003. 误差分析与测量不确定度评定[M]. 北京: 中国计量出版社. |
| Paatero P, Tapper U. 1994. Positive matrix factorization: A non-negative factor model with optimal utilization of error estimates of data values[J]. Environmetrics, 5(2): 111–126.DOI:10.1002/(ISSN)1099-095X |
| Paatero P. 1997. A weighted non-negative least squares algorithm for three-way 'PARAFAC' factor analysis[J]. Chemometrics & Intelligent Laboratory Systems, 38(2): 223–242. |
| Polissar A V, Hopke P K, Paatero P, et al. 1998. Atmospheric aerosol over Alaska: 2.Elemental composition and sources[J]. Journal of Geophysical Research - Atmospheres, 103(D15): 19045–19057.DOI:10.1029/98JD01212 |
| Prendes P, Andrade J M, López-MahíA P, et al. 1999. Source apportionment of inorganic ions in airborne urban particles from Coru?a city(N.W.of Spain)using positive matrix factorization[J]. Talanta, 49(1): 165–178.DOI:10.1016/S0039-9140(98)00356-7 |
| Tan J H, Duan J C, Chai F H, et al. 2014. Source apportionment of size segregated fine/ultrafine particle by PMF in Beijing[J]. Atmospheric Research, 139(6): 90–100. |
| Tao J, Zhang L, Zhang R, et al. 2016. Uncertainty assessment of source attribution of PM2.5 and its water-soluble organic carbon content using different biomass burning tracers in positive matrix factorization analysis-a case study in Beijing, China[J]. Science of the Total Environment, 543(Pt A): 326–335. |
| Tian S L, Pan Y P, Wang Y S. 2017. Size-resolved source apportionment of particulate matter in urban Beijing during haze and non-haze episodes[J]. Atmospheric Chemistry & Physics Discussions, 16(1): 9405–9443. |
| Wang Q, He X, Huang X H H, et al. Impact of secondary organic aerosol tracers on tracer-based source apportionment of organic carbon and PM2.5: A case study in the Pearl River Delta, China[J]. ACS Earth Space Chemistry: 1562–1571. |
| Wang F, Lin T, Feng J, et al. 2015. Source apportionment of polycyclic aromatic hydrocarbons in PM2.5 using positive matrix factorization modeling in Shanghai, China[J]. Environmental Science Processes & Impacts, 17(1): 197–205. |
| Wang Y, Li L, Chen C, et al. 2014. Source apportionment of fine particulate matter during autumn haze episodes in Shanghai, China[J]. Journal of Geophysical Research Atmospheres, 119(4): 1903–1914.DOI:10.1002/2013JD019630 |
| 王琴, 张大伟, 刘保献, 等. 2015. 基于PMF模型的北京市PM2.5来源的时空分布特征[J]. 中国环境科学, 2015, 35(10): 2917–2924.DOI:10.3969/j.issn.1000-6923.2015.10.005 |
| Xie Y L, Hopke P K, Paatero P, et al. 1999. Identification of source nature and seasonal variations of Arctic aerosol by the multilinear engine[J]. Atmospheric Environment, 33(16): 2549–2562. |
| Yao L, Yang L, Yuan Q, et al. 2016. Sources apportionment of PM2.5, in a background site in the North China Plain[J]. Science of the Total Environment, 541: 590–598. |
| Yu J Z, Lau A K H, Louie K K, et al. 2004. Abundance and seasonal characteristics of elemental and organic carbon in Hong Kong PM10[J]. Atmospheric Environment, 38(10): 1511–1521.DOI:10.1016/j.atmosenv.2003.11.035 |
| Yuan Z, Lau A K H, Zhang H, et al. 2006. Identification and spatiotemporal variations of dominant PM10, sources over Hong Kong[J]. Atmospheric Environment, 40(10): 1803–1815.DOI:10.1016/j.atmosenv.2005.11.030 |
| Yuan Z, Yadav V, Turner J R, et al. 2013. Long-term trends of ambient particulate matter emission source contributions and the accountability of control strategies in Hong Kong over 1998—2008[J]. Atmospheric Environment, 76(3): 21–31. |
| Zhang Y, Jing C, Wang S, et al. 2017. Review of receptor-based source apportionment research of fine particulate matter and its challenges in China[J]. Science of the Total Environment, 586: 917–929. |
| Zhang R, Jing J, Tao J, et al. 2013. Chemical characterization and source apportionment of PM2.5 in Beijing: seasonal perspective[J]. Atmospheric Chemistry & Physics, 13(14): 7053–7074. |
| Zíková N, Wang Y, Yang F, et al. 2016. On the source contribution to Beijing PM2.5 concentrations[J]. Atmospheric Environment, 134: 84–95.DOI:10.1016/j.atmosenv.2016.03.047 |
| 郑君瑜, 王水胜, 黄志炯, 等. 2013. 区域高分辨率大气排放源清单建立的技术方法与应用[M]. 北京: 科学出版社. |
| 张延君, 郑玫, 蔡靖, 等. 2015. PM2.5源解析方法的比较与评述[J]. 科学通报, 2015: 109–121. |
