 , 宋翀芳1
, 宋翀芳1
 , 王世杰1, 赵敬源2
, 王世杰1, 赵敬源21. 太原理工大学环境科学与工程学院, 太原 030024;
2. 长安大学建筑学院, 西安 710061
收稿日期: 2018-01-26; 修回日期: 2018-03-28; 录用日期: 2018-03-28
基金项目: 国家自然科学基金(No.51678058)
作者简介: 秦成君(1992-), 男, E-mail:424384295@qq.com
通讯作者(责任作者): 宋翀芳, E-mail:scfcindy@163.com
摘要: 城市街道中复杂的高架桥结构会影响街谷内污染物的扩散.本文利用CFD软件FLUENT,采用标准k-ε方程和组分输运方程,对含双层高架桥的理想街谷内空气流场和CO浓度场进行了数值模拟.结果表明,高架桥破坏了理想街谷内CO浓度分布的爬墙效应,自地面沿高度方向CO浓度逐渐减小,超过每层高架桥面后激增,而后再次降低.双层高架桥改变了污染面源位置和街谷内流场分布.当双层高架桥都处于街谷内部时,来流风垂直于街谷方向自左向右吹送,街谷内涡旋整体结构保持顺时针方向,高架桥附近出现小涡旋,使得CO在街谷内部循环,引起背风面和街谷内CO平均浓度的升高,高架桥的"盖子效应"显著,与无高架桥街谷相比,CO平均浓度升高39.5%.当双层高架的上层高架与街谷建筑顶部持平,下层高架桥位于街谷中部时,街谷内部产生4个较大涡旋,能够显著地提高街谷内地面和背风面CO扩散速率,高架桥的"盖子效应"被破坏;与无高架桥街谷相比,CO平均浓度仅升高8.7%,与双层高架桥都处于街谷内相比,CO平均浓度降低22.1%,为城市多层高架桥建设提供了参考依据.
关键词:城市街谷双层高架桥数值模拟污染物浓度分布
Numerical study on the air environment of ideal street valley with double viaduct in vertical windward
QIN Chengjun1
 , SONG Chongfang1
, SONG Chongfang1
 , WANG Shijie1, ZHAO Jingyuan2
, WANG Shijie1, ZHAO Jingyuan2 1. College of Environmental Science and Engineerig, Taiyuan University of Technology, Taiyuan 030024;
2. College of Architecture, Chang'an University, Xi'an 710061
Received 26 January 2018; received in revised from 28 March 2018; accepted 28 March 2018
Supported by the National Natural Science Foundation of China(No.51678058)
Biography: QIN Chengjun(1992—), male, E-mail:424384295@qq.com
*Corresponding author: SONG Chongfang, E-mail:scfcindy@163.com
Abstract: The complex viaduct structures in urban streets affect the spread of pollutants in street streets. Used CFD software FLUENT, the standard k-ε equation and component transportation equation were used to simulate the characteristics of air flow field and CO concentration field in the street canyon with double viaduct layout. The results showed that when the viaduct was located in the street canyon, the viaduct destroyed 'climbing wall effect' of the concentration distribution of CO in the ideal street. The concentration of CO decreased along the height from the ground surface and increases sharply after exceeding the viaduct. The existence of double viaducts changed the location of surface pollution sources and the distribution of flow field in the street canyon. When the double viaducts were all inside the street canyon, the overall structure of the vortices in the street canyon keeps a clockwise direction, and small vortices appear near the viaduct, causing CO to circulate inside the street canyon, causing an increase in the mean CO concentration in the leeward side and in the street canyon, the "cover effect" of the viaduct was significant, and the average concentration of CO was 39.5% higher than that of the viaduct without the viaduct. When the height of the double-storey overhead was the same as the height of the top of the street canyon, four large vortices were generated in the street canyon, which can significantly increase the CO diffusion rate in the street canyon, and the CO concentration increased only compared with that of the viaduct street canyon 8.7%. Compared with the double viaducts in the street canyon, CO concentration decreased by 22.1%, which provided a reference for the construction of urban multi-viaduct.
Keywords: city street canyondouble viaductnumerical simulationconcentration distribution of pollutant
1 引言(Introduction)随着中国经济的不断发展和城市化进程的持续向前推进, 城市规模不断增大, 建筑高度、人口密度随之不断提升(王建国, 2009);私家车保有量的持续上升导致汽车尾气污染物的排放量不断增加(曹国良等, 2011), 交通拥堵现象也日益严重, 部分大城市(如北京、上海等)通过大量建设高架桥以缓解交通压力.与此同时, 不同形态的城市街谷相继涌现, 抑制了来流风对街谷内污染物的清除作用, 风速死角处淤积的高浓度污染物严重威胁着居民日常生活健康(Cooke et al., 2007;胡彬等, 2007).这引起了众多****的重视, 现有研究表明, 街谷内流场和污染物的扩散受高宽比(赵宝芹等, 2005)、建筑结构形态(谢晓敏等, 2005)、大气温度(Dallman et al., 2014)、城市绿化(Gromke et al., 2015)、来流风场(王乐等, 2012;朱继宏等, 2015)、交通诱导湍流等多重因素的影响, 高架桥的引入进一步增加了街谷内污染物扩散的复杂程度.李鹏飞等(1999)通过现场观测分析了造成城市高架道路下CO浓度差异的原因, 认为高架桥会犹如盖子一样阻碍街道尾气的扩散.王嘉松(2002)模拟确认了高架道路与峡谷等高会形成“盖子效应”.蒋德海等(2006)、张传福等(2012)和李政桐等(2017)进一步模拟发现, 高宽比越大, 高架桥街谷内污染物浓度越高.Kondo等(2009)则在高架道路两侧的建筑物上设置仪器对NOx进行采样, 发现高架桥街谷污染物浓度值均超过背景值.李志远(2016)实测表明, 高架桥街谷污染物分布不符合爬墙效应, 沿高度方向可吸入颗粒物浓度先逐渐减小, 在超过高架路面高度后突增.
必须指出的是, 目前对街道峡谷内污染物分布和扩散特性的研究大都集中在结构简单的单层高架上, 而对于现已建成并且不断发展的含双层乃至多层高架城市街谷(如上海南北高架)鲜有涉猎, 而随着城市化发展的不断加速, 可以预见多层高架定会成为未来大型都市的常态建设, 大量建成的高架桥在街谷中引入更多的汽车通量, 造成尾气排放量增加的同时, 其复杂的结构会抑制街谷中的空气流通和污染物扩散, 对人体健康造成伤害.基于此, 本研究以双层高架桥理想街谷为研究对象, 考虑高架桥的结构、高度和宽度等重要几何参数, 分析双层高架桥对街谷内空气流场和CO浓度场分布规律的影响.
2 计算模型与方法(Calculation model and method)2.1 计算模型高架桥街谷模型如图 1所示, 两侧建筑物高度为40 m, 建筑物宽度为20 m, 两建筑物之间的街道峡谷宽度为40 m, 构成高宽比1:1的理想街谷.考虑单个车道宽度为3.5 m, 设地面污染源为双向八车道, 每个单向车道宽度D为14 m, 与建筑距离S为3 m, 单向车道之间距离F为6 m;低层高架桥高度为H1, 宽度为G1, 与建筑距离为L1;高层高架桥高度为H2, 宽度为G2, 与建筑距离为L2.表 1中明确显示出各模型物理参数.考虑到CO性质稳定, 选取CO作为尾气的重要指示标准, 假设CO的排放强度Q为0.001 g·s-1·m-1(Chan et al., 1996).环境风速入口为速度入口边界, 来流风自左向右垂直于街道, 出口边界设置为自由出流, 顶部设置为对称边界条件, 地面污染源和高架桥桥面都设为质量入口, 其余面为绝热墙体.
图 1(Fig. 1)
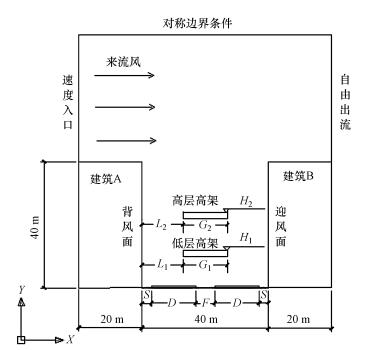 |
| 图 1 街谷模型示意图 Fig. 1Street model schematic |
表 1(Table 1)
| 表 1 模型概况 Table 1 General situation of model | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 1 模型概况 Table 1 General situation of model
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.2 数值方程标准k-ε方程(黄远东等, 2008)在湍流模型中具有计算时间少、准确性好、预测结果好的优点.在街道峡谷内数值计算中, 采用FLUENT-6.3.26为基本程序, 将来流空气按照不可压缩流动处理, 认为流动是稳态绝热的, 控制方程包括质量守恒方程(式(1))、动量守恒方程(式(2))、标准k-ε方程和组分输运方程.采用有限容积法离散控制方程, 控制方程的离散采用二阶迎风格式(Nazridoust et al., 2006), 计算精度为0.00001.
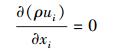 | (1) |
 | (2) |
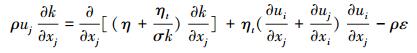 | (3) |
 | (4) |
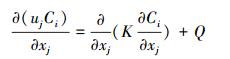 | (5) |
为方便比较, 对污染物浓度进行无量纲化处理(顾兆林等, 2011), 其计算公式如下:
 | (6) |
2.3 模型验证为了对计算模型和计算方法进行可靠性验证, 以Meroney等(1996)的实验数据为基准, 按照本文所采用的离散模式、划分网格方法和控制方程绘制与风洞实验中相对应(60 mm×60 mm)的理想街谷数值模型, 取来流风速1 m·s-1下, 污染物释放量Qe=1.4 h-1、来流空气流量Qa=100 h-1的实验数据, 对无量纲CO浓度进行了对比.图 1反映了背风模拟与背风实测, 以及迎风模拟与迎风实测的无量纲浓度对比情况, C*趋势分布基本吻合, 表明本文所建立的模型及采用的计算方法, 能够很好地分析街谷的大气流场和污染物浓度场.
图 2(Fig. 2)
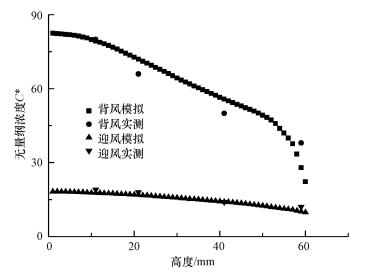 |
| 图 2 数值模型与风洞实验的无量纲浓度对比 Fig. 2Comparison of the nonsense concentration of numerical model and wind tunnel experiment |
3 模拟结果与分析(Results and analysis)3.1 街谷内的涡旋特性和污染物浓度分布采用实验验证后的计算方法对双层高架桥街谷污染物扩散问题进行了数值模拟.以上述6个模型为例, 在来流风速为3 m·s-1且来流风向垂直于街道走向的条件下, 分别模拟其街谷内部的污染物浓度和涡旋特性的分布规律, 计算结果如图 3和图 4所示, 图中X方向为试验桥梁宽度方向, Y方向为高度.
图 3(Fig. 3)
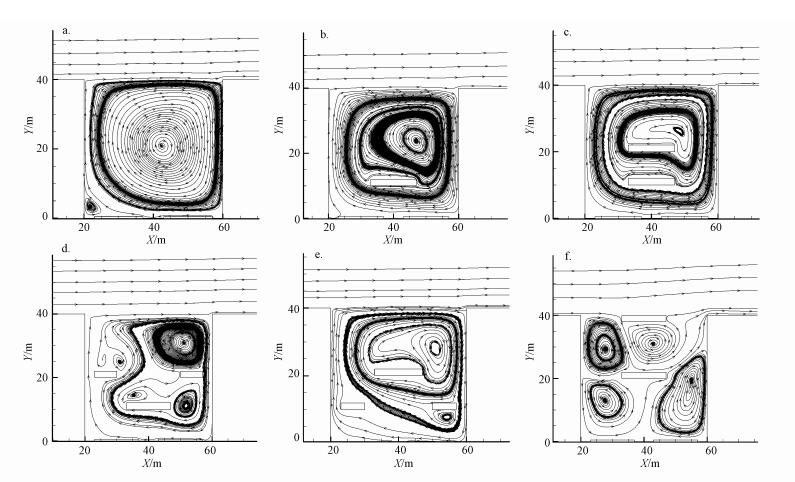 |
| 图 3 不同模型下的流场特性(a.模型1, b.模型2, c.模型3, d.模型4, e.模型5, f.模型6) Fig. 3Flow field characteristics in different modles |
图 4(Fig. 4)
 |
| 图 4 不同模型下的污染物分布规律(a.模型1, b.模型2, c.模型3, d.模型4, e.模型5, f.模型6) Fig. 4The distribution of pollutants in different modles |
图 3a和图 4a显示模型1无高架桥的标准街谷, 其涡旋为一个顺时针大涡旋, 涡旋中心在街谷中心, 污染物在背风面爬墙效应明显.图 3b和图 4b显示模型2单层高架桥的标准街谷, 其涡旋形式基本保持原有形态, 单层高架上方产生绕流, 涡旋中心轻微向右上移, 近地面处污染物分布规律与无高架街谷较为相似, 高架桥上方存在的污染面源导致街谷中部污染物浓度升高.图 3c和图 4c显示模型3双层高架桥的标准街谷, 双层高架桥并没有改变涡旋的主形态, 涡旋中心继续轻微向右上移, 污染物分布规律与单层高架相近似, 双层高架污染面源的存在导致街谷中受污染区域进一步增大.图 3d和图 4d显示模型4双层高架桥的标准街谷, 除右上角的主涡旋外, 街谷内高架桥附近形成4个小涡旋, 高架排放的污染物随涡旋运动在街谷内部扩散, 使街谷内部污染物浓度分布更加均匀.而图 3e和图 4e显示模型5双层高架桥的标准街谷, 其右上角主涡旋与模型4较为近似, 污染物浓度分布规律也较为接近, 但下层高架桥附近的小涡旋只有一个, 污染区域在整个街谷内部占比极大.图 3f和图 4f显示模型6双层高架桥的标准街谷, 当双层高架的上层高架桥桥面与建筑顶部高度持平时, 流场结构与模型3、4、5都大为不同, 出现两个顺时针涡旋和两个逆时针涡旋, 导致污染物浓度分布极为不均匀, 爬墙效应完全被破坏, 污染区域在街谷内部占比较小;上层高架桥上排放的污染物绝大部分被来流风直接带走, 一小部分进入街谷内部;下层高架桥上排放的污染物被上部涡旋带到迎风面, 导致迎风面污染物浓度高于背风面污染物浓度;地面道路受街谷底部两涡旋的影响, 地面中心附近的污染物浓度高于地面道路两侧.
3.2 街谷内无量纲污染物浓度分布规律3.2.1 近地面1.5 m处行人呼吸高度的无量纲CO浓度分布在近地面1.5 m处行人呼吸高度的无量纲CO浓度分布如图 5a所示, 含高架桥的街谷内CO浓度分布规律大致相似, 其中, 模型1~4中近地面处污染物浓度分布极为重合, 皆为机动车道路上方CO浓度最高, 街谷中心和靠近街谷背风面位置为CO高浓度聚积区, 靠近街谷迎风面位置浓度最低且距离道路越远浓度越低.模型5在街谷内部地面宽度0~20 m处的浓度较低, 在20~40 m处的浓度又与上述街谷相重合;模型6与模型1~5相比近地面的无量纲CO浓度最低, 且越靠近街谷背风面位置CO浓度越低, 由图 3f可知, 这是受街谷左下角的逆时针涡旋影响所致.
图 5(Fig. 5)
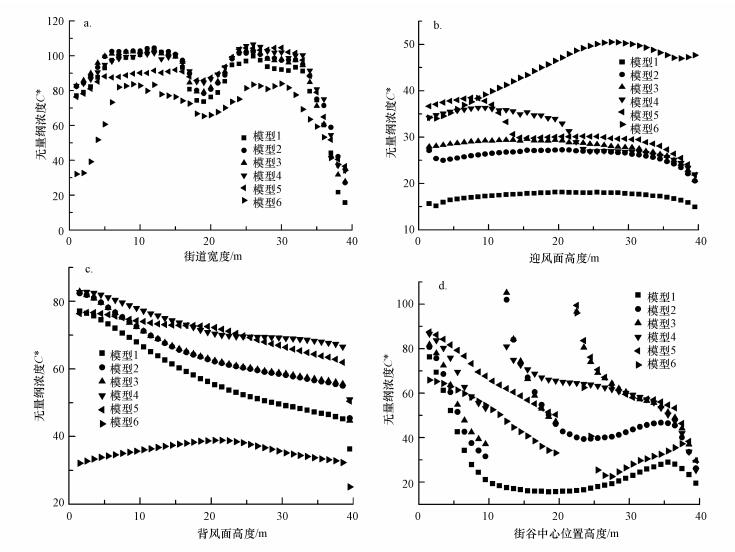 |
| 图 5 距地面1.5 m(a)、迎风面1.5 m (b)、背风面1.5 m(c)及街谷中心(d)无量纲CO浓度分布 Fig. 5Concentration distribution of dimensionless pollutants at pedestrian height(a), windward surface (b), leeside surface(c) at near 1.5 m and in the center of the street canyon |
3.2.2 距迎风面1.5 m处的无量纲CO浓度分布在距迎风面1.5 m处沿地面高度1.5~39.5 m处每间隔1 m取40个点, 得出其无量纲CO浓度分布如图 5b所示.模型1无高架桥街谷CO浓度最低, 且均匀分布, 稳定在15左右;模型2单层高架桥街谷CO浓度为26;模型3的双层高架桥因流场结构与模型2单层高架桥街谷相似, 因而迎风面浓度分布近似重合, 模型3 CO浓度为30, 稍高于单层高架桥街谷的CO;模型4近地面处(1.5~20 m)处浓度最高, 在上层高架桥高度20~25 m处出现明显拐点, CO浓度明显下降, 在25~40 m处与模型3接近重合, 由图 3d可知其拐点的出现主要受右上方涡旋影响, 来流清洁空气将上层高架桥排放的CO带走, 使街谷迎风面上部浓度稀释, 而高架桥下方则因高架桥的阻挡, 导致地面与下层高架排放的污染物在街谷内部循环, CO浓度较高;模型5则是近地面处(1.5~10 m处)CO浓度最高, 在10~15 m低层高架高度出现明显拐点, CO浓度显著下降, 在15~40 m处与模型2、3的浓度分布规律重合, 由图 3e可知其拐点出现的原因与模型4相同, 直接受右上方的涡旋作用影响, 来流清洁空气能够有效带走高架桥排放的CO, 高架桥上部CO浓度显著降低, 因高架桥的遮蔽作用, 使得地面的CO浓度较高.模型6在迎风面处浓度最高, 对照图 3f可知受上层高架桥的影响, 街谷内部涡流将地面和下层高架桥排放的CO带到了迎风面, 受流场结构和涡旋特性的直接影响, 导致其迎风面CO浓度随着高度的升高而升高.
3.2.3 距背风面1.5 m处的无量纲CO浓度分布距背风面1.5 m处沿地面高度1.5~39.5 m处每间隔1 m取40个点, 得到其无量纲CO浓度分布如图 5c所示.模型1~5背风面CO浓度都是随着高度的升高而降低, 其中, 模型1无高架桥街谷的CO浓度自78降至45, 降低幅度最大, 其街谷环流的清洁能力较强;模型2、3的CO浓度分布近乎于完全重合, 表明其流场分布的相似性极高;模型4、5的CO浓度分布近似, 且CO浓度明显大于其它模型, 表明街谷内存在双层高架桥不利于CO的扩散;模型4背风面浓度在距地面高度1.5~20 m处降低速率较快, 在20~40 m处降低速率较慢;模型5的背风面浓度在距地面高度1.5~20 m处降低速率较慢, 在20~40 m处降低速率较快, 与街谷内部涡旋流场分布密切相关;模型6背风面的无量纲CO浓度最低, 其在距地面1.5~20 m高度处浓度升高, 而在距地面20~40 m高度处则逐渐降低, 其拐点出现在20 m处, 即低层高架所在高度, 由图 3f可知, 这是由背风面下部的逆时针涡旋与背风面上部的顺时针涡旋综合作用所致, 从而使该处出现CO浓度的拐点.
3.2.4 街谷中心无量纲CO浓度分布在街谷中心位置沿地面高度1.5~39.5 m处每间隔1 m取40个点, 得到其无量纲CO浓度如图 5d所示.模型1自1.5~10 m的CO浓度降低幅度极大, 在10~30 m处保持稳定, 在30~35 m处略有提升, 在35~40 m处再次降低;模型2、3的CO浓度在1.5~10 m及10~20 m处极为重合, 这是由其街谷底部流场特性的相似性所引起的, 在20~40 m处, 模型2的无量纲CO浓度保持稳定在40左右, 而模型3因其双层高架桥上部排放源的影响, 无量纲CO浓度突增至80, 而后降低至35, 其拐点的位置受高架桥排放源的直接影响;模型4在1.5~10 m处降低幅度相对较低, 其无量纲CO浓度显著大于模型1、2、3, 在低层高架上方10~40 m处持续降低;模型5在1.5~20 m及20~40 m处持续降低, CO浓度分布规律与高架所在位置相符合;模型6在20~30 m处CO浓度降低幅度极大, 表明其污染物扩散和清除效果好.CO浓度分布规律满足自地面至高架下方逐渐降低, 在高架上方瞬时增高, 而从高架上方至街谷上部又再次降低.
3.2.5 街谷内平均无量纲CO浓度对图 5中各模型所取的近地面处、迎风面、背风面和街谷中心位置的无量纲CO浓度共160点进行求和并取平均, 得到图 6中各模型街谷内无量纲CO浓度的平均值.模型1的平均无量纲CO浓度最低, 为46, 表明无高架街谷受CO污染的面积最小;模型2、3平均无量纲CO浓度分别为57.9和60.7, 因其流场特性极为相似, 扩散效果也较为相似;模型4、5平均无量纲CO浓度分别为64.2和63.34, 与无高架桥街谷相比, 模型4街谷内的无量纲CO浓度升高39.5%, 因其上下两层高架桥的遮盖效果和阻挡作用, 使污染物在街谷内产生循环, 不利于污染物的扩散, 应在城市规划中尽量避免;模型6的无量纲CO浓度为50, 与无高架桥街谷相比, 无量纲CO浓度仅升高8.7%, 与模型4中双层高架桥都处于街谷内相比, 无量纲CO浓度降低22.1%.
图 6(Fig. 6)
 |
| 图 6 街谷内平均无量纲CO浓度 Fig. 6The average dimensionless concentration of pollutants in the street canyon |
4 结论(Conclusions)1) 当高架桥位于街谷内部时, 与标准街谷相比, 无论单层高架桥或双层高架桥布局都会对街谷内流场产生绕流阻挡的遮蔽作用, CO分布不符合爬墙效应, 自地面沿高度方向CO浓度逐渐减小, 超过高架桥面后激增.
2) 当双层高架桥都处于街谷内部时, 街谷内涡旋整体结构保持顺时针方向, 在高架桥附近出现小涡旋, 使得CO在街谷内部循环, 引起背风面和街谷内平均无量纲CO浓度的升高.高架桥的“盖子效应”显著, 与无高架桥街谷相比, 无量纲CO浓度升高39.5%.
3) 当双层高架的上层高架与街谷建筑顶部高度持平时, 其内部产生了4个较大涡旋, 流场结构较为理想, 能够显著地提高街谷内CO扩散速率, 与无高架桥街谷相比, 无量纲CO浓度仅升高8.7%, 与双层高架桥都处于街谷内相比, 无量纲CO浓度降低22.1%, 在进行城市多层高架建设前应予以考虑.
参考文献
| 曹国良, 张小曳, 龚山陵, 等. 2011. 中国区域主要颗粒物及污染气体的排放源清单[J]. 科学通报, 2011, 56(3): 261–268. |
| Chan L Y, Zeng L, Qin Y, et al. 1996. CO concentration inside the cross harbor tunnel in Hong Kong[J]. Environment International, 22(4): 405–409. |
| Cooke R M, Wilson A M, Tuomisto J T, et al. 2007. A probabilistic characterization of the relationship between fine particulate matter and mortality:elicitation of European experts[J]. Environmental Science & Technology, 41(18): 6598–6605. |
| Dallman A, Magnusson S, Britter R, et al. 2014. Conditions for thermal circulation in urban street canyons[J]. Building & Environment, 80(10): 184–191. |
| Gromke C, Blocken B. 2015. Influence of avenue-trees on air quality at the urban neighborhood scale.Part Ⅱ:Traffic pollutant concentrations at pedestrian level[J]. Environmental Pollution, 196: 176–184.DOI:10.1016/j.envpol.2014.10.015 |
| 顾兆林, 张云伟, 雷康斌. 2011. 不同大气稳定度下绿化街谷流动的大涡模拟[J]. 中国科学:技术科学, 2011(1): 109–118. |
| 胡彬, 陈瑞, 徐建勋, 等. 2015. 雾霾超细颗粒物的健康效应[J]. 科学通报, 2015, 60(30): 2808–2823. |
| 黄远东, 王守生, 金鑫, 等. 2008. 城市街道峡谷内污染物扩散模拟中不同湍流模型的比较研究[J]. 水动力学研究与进展, 2008, 23(2): 189–195. |
| 蒋德海, 蒋维楣, 苗世光. 2006. 城市街道峡谷气流和污染物分布的数值模拟[J]. 环境科学研究, 2006, 19(3): 7–12.DOI:10.3321/j.issn:1001-6929.2006.03.004 |
| Kondo H. 2009. A numerical experiment of roadside diffusion under traffic-produced flow and turbulence[J]. Atmospheric Environment, 43(27): 4137–4147.DOI:10.1016/j.atmosenv.2009.05.047 |
| 李鹏飞, 周洪昌. 1999. 城市高架道路建设对机动车尾气污染的影响分析[J]. 上海环境科学, 1999(10): 448–450. |
| 李志远. 2016. 高架下街谷内可吸入颗粒物浓度扩散的实验研究[D]. 上海: 东华大学 |
| Meroney R N, Pavageau M, Rafailidis S, et al. 1996. Study of line source characteristics for 2-D physical modelling of pollutant dispersion in street canyons[J]. Journal of Wind Engineering & Industrial Aerodynamics, 62(1): 37–56. |
| Nazridoust K, Ahmadi G. 2006. Airflow and pollutant transport in street canyons[J]. Journal of Wind Engineering & Industrial Aerodynamics, 94(6): 491–522. |
| 王建国. 2009. 基于城市设计的大尺度城市空间形态研究[J]. 中国科学E辑:技术科学, 2009, 39(5): 830–839. |
| 王乐, 张云伟, 顾兆林. 2012. 动态风场及交通流量下街道峡谷内污染物扩散模拟[J]. 中国环境科学, 2012, 32(12): 2161–2167.DOI:10.3969/j.issn.1000-6923.2012.12.008 |
| 王嘉松. 2002. 城市高架道路对局地大气环境影响的数值模拟研究[J]. 上海环境科学, 2002(3): 132–135. |
| 谢晓敏, 黄震, 王嘉松. 2005. 建筑物顶部形状对街道峡谷内污染物扩散影响的研究[J]. 空气动力学学报, 2005, 23(1): 108–113.DOI:10.3969/j.issn.0258-1825.2005.01.021 |
| 杨方. 2015. 街区与建筑室内空气环境耦合特征的研究[D]. 上海: 东华大学http://www.doc88.com/p-0082379243508.html |
| 张传福, 曾建荣, 文谋, 等. 2012. 高架桥对街道峡谷内大气颗粒物输运的影响[J]. 环境科学研究, 2012, 25(2): 159–164. |
| 张云伟, 张海炜, 顾兆林. 2015. 行驶车辆诱导城市街谷内流场的大涡模拟[J]. 环境科学与技术, 2015(9): 64–69. |
| 赵宝芹, 王嘉松, 汪立敏, 等. 2005. 城市对称街道峡谷气流及污染物扩散特征的研究[J]. 水动力学研究与进展, 2005, 20(5): 610–615. |
| 朱继宏, 李德英. 2015. 室外交通污染物对临街建筑室内环境的影响分析[J]. 环境污染与防治, 2015, 37(11): 1–5. |
