杨平, 叶淑君
南京大学水科学系, 南京 210023
收稿日期: 2017-08-12; 修回日期: 2017-12-01; 录用日期: 2017-12-01
基金项目: 国家自然科学基金（No.41472212）
作者简介: 杨平(1994-), 男, E-mail:MG1629074@smail.nju.edu.cn
通讯作者（责任作者）: 叶淑君, E-mail:sjye@nju.edu.cn

摘要: 运用环境同位素氚（³H）建立模型来定量研究地下水运动规律已被广泛应用于水文地质和环境监测领域，大气降水氚浓度是这类模型中必须的输入值.目前已建立的全球大气降水氚浓度模型（MGMTP）为这一领域的研究提供了一种恢复全球范围内年平均氚浓度的新方法，但该氚浓度模型后期恢复数据出现异常负值及面临适用年限等问题.因此，本文选用国际原子能机构和世界气象组织提供的1960—2014年全球氚浓度值实测资料，基于因子分析法拓展了MGMTP模型的适用年份，并对不同的数据预处理及分析方法进行了对比，同时对MGMTP模型提及的"异常负值"问题进行了进一步明确与改进.最后把模型应用于南北半球的典型站点，将恢复得到的数据与实测数据进行对比，发现拓展后的MGMTP模型结果能较好地拟合实测数据.研究表明，该模型具有简单易用、时间序列长、全球性适用等优点，尤其对缺少大气降水氚浓度实测数据的地区具有重要参考价值.
关键词:大气降水氚浓度因子分析法全球模型
Global model of the annual mean concentration of tritium in precipitation, 1960-2014
YANG Ping, YE Shujun
Department of Hydrosciences, Nanjing University, Nanjing 210023
Received 12 August 2017; received in revised from 1 December 2017; accepted 1 December 2017
Supported by the National Natural Science Foundation of China (No.41472212)
Biography: YANG Ping(1994—), male, E-mail:MG1629074@smail.nju.edu.cn
^*Corresponding author: YE Shujun, E-mail:sjye@nju.edu.cn
Abstract: The use of environmental isotope of tritium to establish the quantitative model of groundwater flow has been widely applied in the field of hydrogeology and environmental monitoring. Zhang Yanhong et al. developed 'MGMTP'(modified global model of tritium in precipitation) to provide a new method for the quantitative study of tritium concentration in the global scale, but the tritium model is now facing a problem of limit period and predicts negative values for the year after 1990. In this paper, we used the dataset over the period from 1960 to 2014 provided by the International Atomic Energy Agency and World Meteorological Organization (IAEA&WMO) to extend the time period of MGMTP model based on factor analysis. At the same time, we also compared the difference between data preprocessing and analysis methods. The problem of negative values predicted by MGMTP model mentioned by Zhang et al. was further clarified and fixed. This extended MGMTP model was applied to the typical stations of the northern and southern hemispheres. The results showed that it can well calculate the annual mean tritium concentration in precipitation over the world from 1960 to 2014, which is especially necessary and valuable for the area with few or without the monitoring data.
Key words: precipitationtritium concentrationfactor analysisglobal model
1 引言(Introduction)氚(³H或T)是氢(¹H)元素的一种具有放射性的同位素，半衰期为(12.33±0.03) a(Lucas et al., 2000)，常被作为降水输入的示踪信号对地下水进行研究(程中双, 2015; 许乃政, 2015; 靳书贺等, 2016; Gleeson et al., 2016; Cauquoin et al.2017)，如Gleeson等(2016)利用氚对全球现代地下水含量及分布进行了研究.在地表水和地下水领域，常利用水中氚浓度进行定量研究.如王绍令等(1990)利用各类水(冰)中氚含量研究了青藏高原多年冻土区地下水动态变化、水力联系；崔亚莉等(2015)利用氚浓度数据建立数学物理模型，计算了诺木洪地区冲洪积扇不同位置地下水的更新速率；Birkel等(2016)利用氚作为示踪剂研究了降雨和径流过程等.这些利用水中氚浓度开展的定量研究往往需要降雨中的氚浓度值作为背景值(王瑞久, 1984; 连炎清, 1990; 马致远等, 1997; 陈宗宇等, 2004; 马致远, 2004; 张应华等, 2006).然而，大气降水氚浓度历史观测数据(以下简称实测数据)稀少且空间分布不均，仅有少部分地区能直接使用由国际原子能机构(International Atomic Energy Agency, IAEA)和世界气象组织(World Meteorological Organization, WMO)在全球范围建立的有限站点的观测数据，而大多数地区只能借助于实验手段获取数据，或基于IAEA及WMO公布的站点数据采用数学方法进行恢复(连炎清, 1990).实测数据的缺失成为广大水文工作者利用氚进行研究的极大障碍.
大气降水氚浓度恢复模型研究中，前人提出的数学分析方法主要有吴秉钧法(吴秉钧, 1986)、插值法(王凤生, 1998; 巴琦等, 2010)、双曲线参考法(连炎清, 1990)、不同影响因素的一元线性相关法(马致远等, 1997)、人工神经网络法(龙文华, 2008)、因子分析法(Doney et al., 1992; Zhang et al., 2011; 章艳红等, 2011)等.因子分析法恢复氚浓度相比于上述其他方法而言，在实际应用上较为简单，而且从恢复结果上来看，其具有更长时间和更大空间的适用性.Doney等(1992)于1992年首次将因子分析法应用于大气降水年均氚浓度分析，并由此建立了1960—1986年间的全球大气降水氚浓度模型(GMTP).章艳红等(2011)基于GMTP模型建立了改进的全球大气降水氚浓度模型(MGMTP)，可以恢复全球1960—2005年大气降水年平均氚浓度.对比Doney等及章艳红等的模型发现，其区别主要在于因子获取过程中，Doney等是先对实测数据进行衰变矫正后，再应用协方差矩阵求解因子得分与因子载荷；而章艳红等是直接对实测数据进行标准化相关阵处理.GMTP模型涉及的时间序列较短，通过衰变矫正可以减小数据间的量级差异以便直接采用协方差矩阵进行无损原始变量离散程度差异处理(金在温等, 2015)；而MGMTP模型中数据恢复年份序列较长，实测数据取值范围大，进行衰变矫正有可能导致低氚浓度值数据的数值过小且后续使用数据时面临需对衰变数据进行恢复的麻烦，因此，MGMTP模型直接对实测数据进行了标准化相关阵处理.以上两种模型均根据实测数据情况选择了合适的方法，其中，MGMTP模型更适合较长时间序列数据恢复，但该模型现已面临适用年限有限的问题，即数据只恢复到2005年；另外，该模型对1990年后数据的恢复不理想，负值出现频率较高.
本文基于MGMTP模型的理论和方法，对该模型出现的拟合结果出现异常负值问题及其解决方法进行进一步明确与改进，并将该模型扩展到2014年.同时，考虑到IAEA和WMO提供的站点有一部分建成时间较晚，有一部分仅有些不连续性的实测数据，导致这些站点的实测数据在时间序列上不连续或仅有短期数据，与GMTP模型和MGMTP模型不同，本次研究拟针对这一问题进行数据预处理.
2 模型建立(Model establishment)前人对实测数据的观察和研究表明，全球各测站中大气降水的氚浓度年均变化在各自半球内具有相似的曲线形态(Doney et al., 1992; Koster et al., 1989; Michel, 1992)，这就为本研究利用因子分析法导出参考曲线进而对全球各地区降水年平均氚浓度变化进行归纳、模拟、恢复提供了依据.因子分析法的基本思想是根据相关性把原始变量分组，使同组内变量之间的相关性较高(即它们的共性成分较多)而不同组变量之间的相关性较低(即它们的共性成分较少).由此得到的共性成分称为公共因子，而与公共因子无关的则称为特殊因子(李永江等, 2016).在获得公共因子得分后，进而应用公共因子建模.
MGMTP模型在获取公共因子得分时，对分组内的数据缺乏分析整理，导致特殊因子占比较大，所求公共因子得分不能代表大部分数据特征，导致模型恢复的氚浓度时间序列数据在后期出现负值.了解到负值数据出现的本质原因，本文在数据处理时采取了特定预处理方法，取得了较好效果.
2.1 公共因子得分求解本文全部的数据分析资料均来自IAEA和WMO官网提供的氚浓度值监测数据(IAEA&WMO, 2016)，数据按站点的监测时间序列(1960—2014年)列表给出，共计612个站点.数据处理是基于SPSS(Statistical Product and Service Solutions)，即“统计产品与服务解决方案”这一软件为平台实现的.本文的数据分析方法与MGMTP模型在公共因子获取方法上(章艳红等, 2011; Zhang et al., 2011)稍有不同.
考虑到监测站点分布的空间情况，本文只对站点分布较为集中的南纬50°(记为-50°，本文南纬纬度均用负值表示)至北纬70°之间的区域进行恢复.首先，本文对数据进行特殊预处理：①删除个别极端值，此外，考虑到不足3组监测数据的站点不仅不能反映该地区的氚浓度值变化趋势，还会给分组内的其它数据带来干扰，本文对其进行了删除以减少特殊因子对模型的影响；②由于IAEA和WMO对某些地区的站点进行了年份选择性监测，部分站点在实测数据接近背景值后便停止了数据监测，进而导致这些站点缺乏近年来的监测数据.变量分组时，由于这部分数据无规律地出现或缺失，组内均值出现异常波动.基于上述原因，考虑到现今大气中氚的输入源主要为宇宙输入(章艳红等，2011)，2005年之前的数据稳定、变化小于1TU但之后无监测记录的站点，按照同分组内其他站点监测数据变化规律合理插值至2014年.数据经预处理后，开始数据分析：将站点数据按每10°纬度带进行分组并标准化原始数据，使其每一分带内的数据均值为0、方差为1；建立相关矩阵、求其特征值和标准化单位特征向量.通过对特征值累计贡献率，即累计方差贡献率的计算(图 1)，发现前两个特征值累计贡献率已达94.31%，说明前两个因子包含了全部数据的绝大部分信息，所以本研究用这两个特征值建立初始因子载荷矩阵.考虑到因子载荷阵的不唯一性及为了寻找更简单和更容易解释的因子，本研究又对初始因子载荷阵施行方差最大正交旋转，使得各个因子在各纬度分带上的载荷取值尽可能的两极分化(靠近0或1)，满足一个纬度分带只在一个因子上有较大载荷，以便因子可以由纬度分带进行差异性解释(图 2a)，即因子的大小具有纬度效应(章艳红等, 2011).最后按照因子得分函数估计最终公共因子得分(表 1).
图 1(Fig. 1)

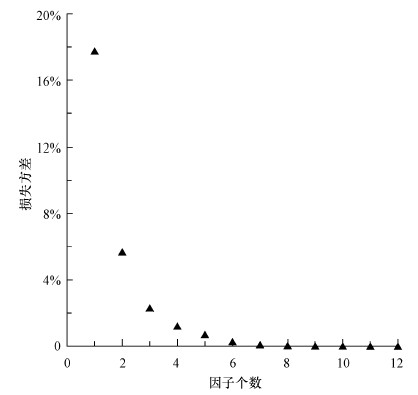图 1 公共因子个数和方差信息损失量关系曲线 Fig. 1Plot of the numbers of factors vs. uncounted variances

图 2(Fig. 2)

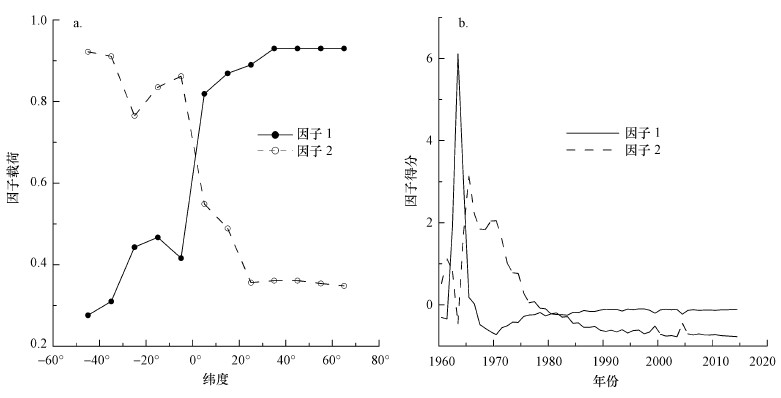图 2 1960—2014年旋转因子载荷(最大方差旋转法)(a.横坐标负值表示南纬，正值表示北纬)及因子得分曲线(b) Fig. 2Factor loadings rotated by maximum variance rotation method (a) and factor scores calculated from the zonally averaged precipitation tritium data(b)

表 1(Table 1)

表 1 预测降水中氚浓度(单位:TU)的标准化公因子得分 Table 1 Normalized factors score for predicting tritium in precipitation

表 1 预测降水中氚浓度(单位:TU)的标准化公因子得分 Table 1 Normalized factors score for predicting tritium in precipitation 日期(年-月) 得分 因子1 因子2 1960-5 -0.30405 0.51835 1961-5 -0.34242 1.12310 1962-5 1.89543 0.81889 1963-5 6.10936 -0.46427 1964-5 3.04969 1.72218 1965-5 0.18224 3.13392 1966-5 0.02491 2.21833 1967-5 -0.47978 1.84484 1968-5 -0.57042 1.83422 1969-5 -0.65676 2.03962 1970-5 -0.72465 2.05089 1971-5 -0.55746 1.60497 1972-5 -0.50991 1.01735 1973-5 -0.41875 0.78235 1974-5 -0.42762 0.76816 1975-5 -0.28035 0.29362 1976-5 -0.24713 0.05155 1977-5 -0.23766 0.07805 1978-5 -0.18607 -0.07993 1979-5 -0.26803 -0.09558 1980-5 -0.21789 -0.21899 1981-5 -0.23298 -0.19349 1982-5 -0.23815 -0.29761 1983-5 -0.25057 -0.28506 1984-5 -0.18343 -0.44753 1985-5 -0.19082 -0.43672 1986-5 -0.13645 -0.54714 1987-5 -0.15782 -0.54580 1988-5 -0.15994 -0.52370 1989-5 -0.12782 -0.61688 1990-5 -0.10721 -0.64721 1991-5 -0.11017 -0.61477 1992-5 -0.11097 -0.66055 1993-5 -0.15025 -0.60182 1994-5 -0.10243 -0.68723 1995-5 -0.11911 -0.62650 1996-5 -0.09793 -0.61276 1997-5 -0.09759 -0.70479 1998-5 -0.13034 -0.66115 1999-5 -0.20163 -0.51372 2000-5 -0.12210 -0.71475 2001-5 -0.10630 -0.75926 2002-5 -0.11890 -0.74607 2003-5 -0.11159 -0.77479 2004-5 -0.22575 -0.45070 2005-5 -0.13381 -0.70579 2006-5 -0.11795 -0.73032 2007-5 -0.13427 -0.70685 2008-5 -0.12655 -0.73048 2009-5 -0.12545 -0.73319 2010-5 -0.13299 -0.72419 2011-5 -0.12199 -0.74755 2012-5 -0.12015 -0.75459 2013-5 -0.11612 -0.76482 2014-5 -0.11316 -0.77385

2.2 全球降水氚模型2.2.1 直接求参法在得到随年份变化的公共因子得分后，再利用最小二乘法对实测数据进行多元线性拟合，由此得到模型参数的过程称为直接求参法，即：

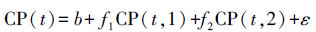(1)

式中，CP(t)为随年份变化的氚浓度，f₁、f₂分别为公因子得分CP(t, 1)、CP(t, 2)的回归系数，b值为回归拟合数据均值，ε为误差项，经过多元线性拟合得到的方程(1)(何晓群, 2010; 汪东华, 2010)就是所说的全球大气降水中年平均氚浓度恢复模型.
运用直接求参法求解的站点需要具有5年以上核爆中期(20世纪60年代)的监测数据.因为通过公因子得分曲线(图 2b)可以看出，这两条曲线在核爆之后虽然有数值上的差异(Weiss et al., 1980)，但形状上却具有相似性，若没有核爆中期的数据对模型进行总体控制，将会导致求解方程(1)出现困难或假解(Doney et al., 1992).
2.2.2 间接求参法通过直接求参法求得的参数只能用于本站点的数据恢复，由于满足直接求参法求解的站点数有限(部分恢复结果见表 2)，对于广大没有该类站点的地区，应用间接求参法求解参数是模型的关键.
表 2(Table 2)

表 2 部分直接求参法恢复的站点模型参数及其代表性检测 Table 2 Part of the station model parameters calculated by thedirect solution method and their representative testing

表 2 部分直接求参法恢复的站点模型参数及其代表性检测 Table 2 Part of the station model parameters calculated by thedirect solution method and their representative testing 站点名 纬度 经度 b f1 f2 SEE N R2 F 显著度 Alexandria, 埃及 31.2° 30.00° 58.341±8.456 120.252±4.569 46.853±6.496 31.664 18 0.977 364.741 0.000 Antananarivo, 马达加斯加 -18.90° 47.50° 9.231±5.137 0.894±1.614 8.575±2.642 5.386 9 0.534 5.584 0.043 Apia, 萨摩亚 -13.80° -171.80° 4.376±2.382 4.818±0.7 2.521±1.383 4.326 13 0.797 24.563 0.000 Bamako, 马里 12.69 -8.00 77.112±12.586 166.195±6.53 73.583±7.509 21.634 12 0.988 428.848 0.000 Bangkok, 泰国 13.73° 100.50° 15.756±2.208 25.284±8.392 14.036±1.726 1.296 39 0.966 536.822 0.000 Barbados (Seawell Airport), 巴巴多斯 13.07° -59.50° 10.318±0.562 19.835±0.689 9.235±0.442 2.289 22 0.987 751.762 0.000 Barranquilla, 哥伦比亚 10.88° -74.78° 16.959±2.313 40.872±9.075 13.457±1.705 0.642 12 0.944 93.648 0.000 Belem, 巴西 -1.43° -48.48° 6.751±0.54 8.97±1.269 5.752±0.267 1.195 17 0.968 240.970 0.000 Bet Dagan, 以色列 32.00° 34.81° 53.547±3.333 111.792±2.639 44.711±3.016 19.251 36 0.983 984.831 0.000 Bogota, 哥伦比亚 4.70° -74.13° 17.35±2.057 33.315±7.518 14.677±1.546 0.811 23 0.959 259.045 0.000 Brasilia (Airport), 巴西 -15.90° -47.90° 14.082±3.445 10.399±5.071 8.591±1.499 4.259 10 0.826 22.348 0.001 Brisbane, 澳大利亚 -27.43° 153.08° 10.221±2.767 6.948±1.693 7.937±2.203 12.212 26 0.500 13.522 0.000 Campbell Is. (Pacific O.), 新西兰 -52.55° 169.15° 9.27±1.988 3.285±0.645 8.205±1.202 4.121 14 0.800 26.979 0.000 Cape Town Airport, 南非 -33.97° 18.60° 7.51±0.455 1.827±0.374 7.154±0.491 2.432 29 0.886 109.822 0.000 Cuiaba, 巴西 -15.60° -56.10° 14.317±3.063 11.525±6.382 12.465±1.508 5.918 15 0.832 35.558 0.000 Entebbe (Airport), 乌干达 0.05° 32.45° 15.459±3.749 19.045±1.011 10.827±2.256 4.668 8 0.985 227.036 0.000 Fortaleza, 巴西 -3.72° -38.55° 6.531±1.423 12.855±2.749 5.71±0.763 1.733 10 0.873 32.011 0.000 Genoa (Sestri), 意大利 44.42° 8.85° 92.066±7.367 222.327±5.5 73.191±6.395 39.793 32 0.983 866.739 0.000 Gibraltar, 直布罗陀 36.15° -5.35° 47.721±2.116 90.525±1.724 39.031±1.919 12.604 38 0.988 1549.072 0.000 Gough Island (Atlantic O.), 南非 -40.35 -9.88° 7.44±0.873 2.409±0.67 7.296±0.728 4.365 28 0.790 52.009 0.000 Grimsel, 瑞士 46.57° 8.33° 206.46±36.827 494.216±140.183 190.11±28.636 22.340 39 0.844 103.614 0.000 Har Kna′an (Tirat Yael), 以色列 33.00° 35.50° 106.383±8.896 311.831±11.709 79.465±8.901 38.610 23 0.976 451.278 0.000 Harare, 津巴布韦 -17.80° 31.0° 8.626±0.633 4.79±0.419 8.212±0.517 2.929 23 0.947 198.501 0.000 Hatteras (North Carolina), 美国 35.27° -75.35° 53.538±1.796 127.305±1.458 43.638±1.621 10.633 37 0.996 4088.284 0.000 Hof-Hohensaas, 德国 50.30° 11.85° 95.757±11.261 148.219±34.445 93.629±10.925 3.683 30 0.782 52.912 0.000 Hof-Saale, 德国 50.30° 11.90° 152.365±6.294 336.398±9.996 131.709±5.424 34.213 34 0.983 934.094 0.000 Hong Kong (King′s Park), 中国 22.32° 144.17° 39.61±2.212 104.367±8.705 32.428±1.46 8.421 43 0.923 252.469 0.000 Howard Afb (Panama Canal Zone), 巴拿马 8.92° -79.60° 10.634±3.066 16.477±11.877 9.563±2.505 1.595 25 0.915 129.305 0.000 Huddinge, 瑞典 59.23° 17.98° 134.49±81.374 313.921±19.51 114.708±42.476 100.969 10 0.974 172.454 0.000 Isla De Pascua (Pacific O.), 智利 -27.17° -109.43° 3.916±0.413 0.014±1.582 2.868±0.266 1.286 24 0.861 72.462 0.000 Izobamba, 厄瓜多尔 -0.37° -78.55° 14.504±3.105 20.277±12.189 11.423±2.605 1.213 11 0.943 82.572 0.000 Jakarta, 印度尼西亚 -6.20° 106.80° 6.873±0.238 6.488±0.281 4.713±0.19 0.933 18 0.988 674.984 0.000 Kaitaia, 新西兰 -35.07° 137.28° 6.466±0.427 2.598±0.319 7.178±0.368 2.245 30 0.933 212.556 0.000 Kaitoke, 新西兰 -41.10° 175.17° 8.106±0.341 2.634±0.332 9.21±0.338 2.434 51 0.942 402.682 0.000 Khartoum, 苏丹 15.60° 32.50° 88.424±23.531 210.764±8.548 80.883±17.74 57.367 17 0.975 313.081 0.000 Manaus, 巴西 -3.12° -60.02° 8.38±4.014 5.438±14.89 6.431±3.039 1.427 11 0.924 61.154 0.000 Marion Island (Indian O.), 南非 -46.88° 37.87° 8.044±0.561 -0.974±1.022 7.791±0.48 2.364 22 0.927 133.863 0.000 Melbourne, 澳大利亚 -37.82° 144.97° 14.171±1.004 6.151±0.65 15.409±0.828 4.556 27 0.939 200.655 0.000 Menlo Park (California), 美国 37.45° -122.13° 56.422±2.839 118.424±1.992 43.003±2.334 13.960 28 0.993 1853.463 0.000 Miami (Inst. Marine Science Florida), 美国 25.75° -80.38° 18.068±0.51 36.908±0.826 16.305±0.442 2.828 35 0.991 1826.051 0.000 Midway Is. (Pacific O.), 美国 28.22° -177.37° 18.268±1.356 41.143±0.81 16.432±1.027 5.623 23 0.992 1334.233 0.000 Mumbai, 印度 18.90° 72.80° 29.465±17.665 50.026±5.604 14.666±10.853 35.574 13 0.873 42.177 0.000 Nicosia, 塞浦路斯 35.20° 33.30° 124.592±43.49 249.845±7.809 80.84±20.829 25.997 7 0.994 512.778 0.000 Ocala (Florida), 美国 29.18° -82.13° 33.691±1.735 79.999±1.421 29.451±1.549 9.969 34 0.991 1725.557 0.000 Ottawa (Ontario), 加拿大 45.32° -75.67° 181.321±6.973 437.445±6.874 154.021±7.21 50.276 52 0.989 2285.661 0.000 Perth, 澳大利亚 -31.95° 115.98° 8.866±1.337 3.479±0.529 8.864±9.856 3.523 16 0.889 60.893 0.000 Ponta Delgada (Azores Is.), 葡萄牙 37.77° -25.65° 29.411±1.214 68.534±0.834 25.909±0.926 5.908 25 0.997 3766.328 0.000 Porto Alegre, 巴西 -30.08° -51.18° 18.162±1.654 17.353±4.713 16.051±0.992 3.070 16 0.952 151.177 0.000 Pretoria, 南非 -25.73° 28.18° 15.673±1.631 6.951±0.784 14.359±1.506 4.689 14 0.902 60.770 0.000 Prodhromos, 塞浦路斯 35.00° 32.80° 79.665±18.274 145.211±29.192 55.683±9.201 18.307 10 0.850 26.569 0.001 Puerto Montt (La Chamiza), 智利 -41.47° -72.93° 8.77±1.401 3.476±1.558 8.871±1.001 5.117 17 0.850 46.285 0.000 Rarotonga-Cook Is. (Pacific O.), 新西兰 -21.20° -159.80° 3.766±0.317 1.751±0.247 3.193±0.276 1.529 24 0.875 81.221 0.000 Salvador (Ondina), 巴西 -13.00° -38.50° 4.588±0.993 6.007±1.429 4.259±0.43 1.249 12 0.926 69.895 0.000 San Juan (Puerto Rico), 波多黎各 18.43° -66.00° 14.955±1.074 34.196±0.595 11.649±0.833 4.119 21 0.994 1672.177 0.000 Santa Maria (California), 美国 34.90° -120.45° 41.551±6.415 107.133±1.966 37.458±4.009 12.362 12 0.997 1575.013 0.000 Sao Gabriel, 巴西 -0.13° -67.08° 11.638±1.519 14.36±5.752 9.741±1.264 0.670 12 0.957 122.406 0.000 Sao Tome (Atlantic O.), 圣多美和普林西比 0.38° 6.72° 19.393±1.996 30.835±1.014 13.222±1.163 3.440 13 0.990 583.386 0.000 Shillong, 印度 25.57° 91.88° 51.123±19.621 96.523±45.641 31.925±9.958 12.410 5 0.912 21.707 0.044 St. Helena (Atlantic O.), 英国 -15.97° -5.70° 3.993±0.97 0.22±0.411 2.359±0.544 1.392 12 0.621 10.029 0.005 Stanley Falkland Is. (Atlantic O.), 马尔维纳斯群岛 -51.70° -57.87° 12.166±2.759 4.277±0.858 14.005±1.702 5.520 15 0.831 35.429 0.000 Stuttgart, 德国 48.83° 9.20° 179.4±14.267 434.41±14.304 144.657±16.453 93.784 45 0.957 496.107 0.000 Tarawa (Pacific O.), 基里巴斯 1.35° 172.92° 2.655±0.84 -0.315±3.225 1.401±0.595 0.516 19 0.865 58.540 0.000 Thonon-Les-Bains, 法国 46.22° 6.28° 172.672±8.732 414.049±16.558 143.024±9.02 56.614 46 0.952 449.110 0.000 Valentia (Observatory), 爱尔兰 51.93° -10.25° 55.208±3.059 145.707±2.878 48.674±2.969 21.103 48 0.984 1404.928 0.000 Veracruz, 墨西哥 19.20° -96.13° 20.229±1.898 46.377±7.23 16.331±1.198 1.009 16 0.981 397.496 0.000 Vernadsky (Argentine Is.), 南极洲 -65.08° -63.98° 25.437±1.763 6.699±3.21 29.13±1.788 10.968 42 0.868 136.085 0.000 Vienna (Hohe Warte), 奥地利 48.25° 16.37° 173.035±6.652 437.944±6.471 151.91±6.565 47.483 51 0.990 2554.015 0.000 Waco (Texas), 美国 31.62° -97.22° 57.176±11.191 129.824±6.136 42.659±8.688 44.026 24 0.951 225.790 0.000 Weathership E (Atlantic O.), 美国 35.00° -48.00° 30.161±8.648 58.233±1.676 23.565±5.115 6.641 7 0.998 1320.720 0.000 Windhoek, 纳米比亚 -22.95° 17.15° 16.663±1.327 9.045±0.707 17.371±1.3 4.052 14 0.949 121.397 0.000 注：纬度数据，正值表示北纬，负值表示南纬；经度数据，正值表示东经，负值表示西经；N值为该拟合站点包含的实测数据量，其余如前述.

间接求参法是将符合直接求参法求解要求的全部站点作为基站点，利用临近站点模型参数进行插值以估算全球范围内任意一点氚浓度的方法.该方法不要求氚浓度恢复地区具有长时间监测序列(精度允许的情况下甚至不要求有监测数据)，但仍可以计算全球任意位置的年均氚浓度.
2.3 模型恢复实例与检测2.3.1 直接求参法为了验证直接求参法模型拟合效果，本文对恢复结果进行了回归模型代表性检测，包括对修正拟合优度系数(R²)、显著度(F)检测、估计标准误差(SEE)3个常用监测指标的计算.任取南、北半球具有代表性的监测站点，线性拟合模型如下.
新西兰凯托克(Kaitoke，41.10°S，175.17°E)，CP(t)=8.106+2.634×CP(t, 1)+9.210×CP(t, 2)，该站点的R²为0.942，SEE为2.434，且通过F检测，显著度明显.
中国香港(HongKong，22.32°N，144.17°E)，CP(t)=39.610+104.367×CP(t, 1)+32.428×CP(t, 2)，该站点的R²为0.923，SEE为8.421，且通过F检测，显著度明显.
加拿大渥太华(Ottawa，45.32°N，75.67°W)，CP(t)=181.321+437.445×CP(t, 1)+154.021×CP(t, 2)，该站点的R²为0.989，SEE为50.276，且通过F检测，显著度明显.
3组数据与实测数据的对比见图 3a~c，其它直接求参法求得的部分站点模型恢复参数及其代表性检测数据见表 2.
图 3(Fig. 3)

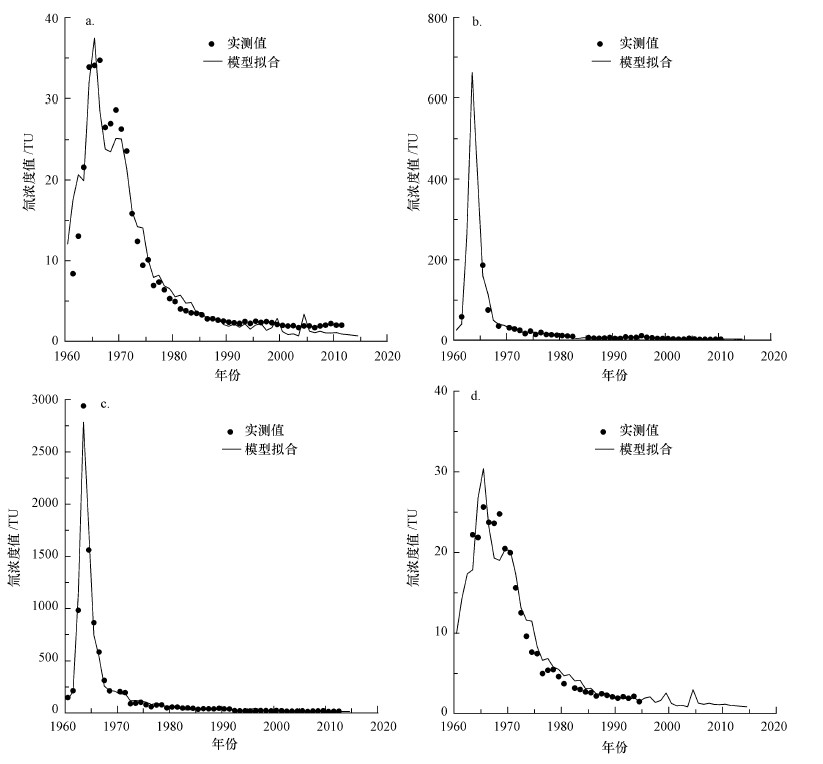图 3 模型恢复氚浓度与实测值对比图(a.凯托克, b.香港, c.渥太华站-直接求参法, d.凯塔亚站-间接求参法) Fig. 3Comparisons of observed and predicted annual mean tritium concentrations in precipitation in Kaitoke(a), HongKong(b), Ottawa stations with the direct calibrated parameters(c) and Kaitaia station with the interpolated parameters(d)

2.3.2 间接求参法同MGMTP模型一致，本文同样对间接求参法的应用进行举例验证.为了更好的体现模型恢复效果，选用实测数据较多的凯塔亚站(Kaitaia，35.07°S，137.28°E)作为待对比的站点.首先，选取与Kaitaia临近的且可通过直接求参法求得模型参数的两个站点，即Kaitoke(41.10°S，175.17°E)及Rarotonga-Cook Island(35.27°N，75.35°W站点恢复模型：CP(t)=3.766+1.751×CP(t, 1)+3.193×CP(t, 2))作为间接求参的参考点.然后，利用纬度关系对Kaitaia站点的待求参数进行线性插值，得到其模型为：CP(t)=6.791+2.366×CP(t, 1)+7.387×CP(t, 2)，该模型计算结果与实测数据的对比见图 3d.
3 模型改进与探索(Model improvement and exploration)本文提出了2个特殊数据预处理方法，一是删除不足3组监测数据的站点，二是对缺少近期监测数据站点的数据进行合理化延长.为了考察这些数据预处理方法对模型恢复结果的影响，本文做了相关模型之间的对比，结果显示，该处理方法在达到应用精度要求的情况下，极大地降低了负值站点出现的频率，使一次性得到模型参数的站点数得到了较大提升(表 2).
在经过如前所述的数据预处理后，部分站点在20世纪90年代后的恢复数据还是会出现负值.除去因子分析法本身带有的系统误差外，出现负值的主要原因是站点后期，尤其是1990年后监测数据不足.在应用最小二乘法多元线性拟合时，模型数据尽可能地拟合现有的监测数据，而对没有监测数据控制的模型后期恢复数据，会偶现不符合实际情况的负值.出现负值的解决方法在MGMTP模型中有介绍(章艳红等, 2011)：包括背景值替代、同纬度分带内插值及分段处理法等.本文就其提出的第3种方法——分段处理法，做进一步说明与改进.
在有1990年后(至少是1980年后)监测数据的情况下，可直接利用MGMTP模型提及的分段处理法来对负值进行消除.以美国Albuquerque站点为例(图 4)，1960—1989年分段及1990—2014年分段的模型参数分别为：

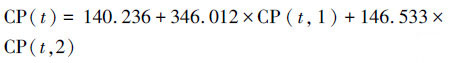(2)

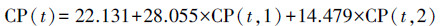(3)

图 4(Fig. 4)

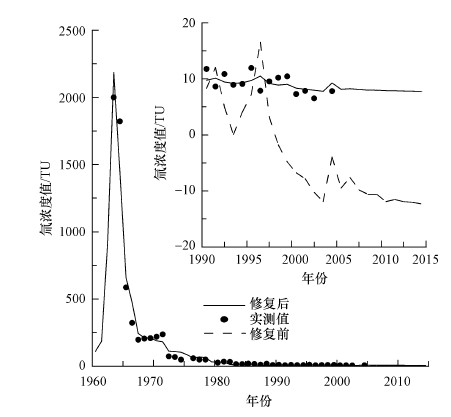图 4 1990年代后有实测数据的负值修复情况 Fig. 4Restoration with monitoring data after the 1990s

而对于那些缺少1990年后数据但之前实测数据量较多的站点，本文建议先利用临近站点对该点进行模型参数线性插值，然后将1990年后的插值数据加入实测数据序列，再利用直接求参法求解.这样做的目的是尽可能的利用实测数据，使叠加误差降到最低(直接求参误差相对较小，间接求参误差相对较大).
为了说明这种改进方法去除负值的效果，本文以美国的St.Louis(38.75°N，90.38°W)站点为例进行说明.
选用与St.Louis站点较近的加拿大的Ottawa(45.32°N，75.67°W)及美国的Hatteras(35.27°N，75.35°W; 站点恢复模型：CP(t)=53.538+127.305×CP(t, 1)+43.638×CP(t, 2))两站点对其进行纬度线性插值，得到初步的间接求参法模型：

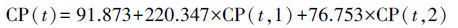(4)

用间接求参法模型计算出的1990年后氚浓度数据补足缺失的实测数据，然后再进行一次直接求参法拟合，拟合模型为：

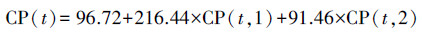(5)

通过图 5可以看出，该修正方法对于1990年代后无实测数据的站点给出了更为可靠的模型，恢复出更合理的氚浓度值.
图 5(Fig. 5)

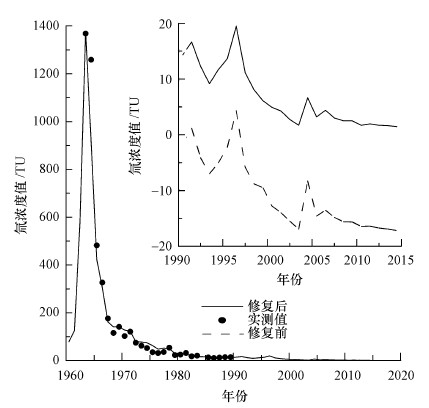图 5 1990年代后无实测数据的负值修复情况 Fig. 5Restoration without monitoring data after the 1990s

对于少量拟合效果不佳的站点，可能与特殊的地形条件、水文条件、气象条件或局部地区人为影响等因素有关.此外，由于IAEA及WMO提供的数据相对全球尺度来说还是较为稀少，本文所做的是将可获取的实测资料最大化与最合理地整合利用到全球范围.站在全球尺度上来说，因子分析法对氚浓度值进行的模拟恢复已达到了应用的效果与精度.
该模型恢复精度受限于数据量，如果后期有其他来源的数据，可以将这些数据拟合到模型中，重新求取参数，并将其作为全球氚浓度的基站点以缩短插值距离，提高插值精度.如果有大量精准数据，就可以将这些数据导入该模型进行因子重算，进而推导出能与实测数据更为匹配的因子得分数据，以提高模型的精度及适应性.
4 结论(Conclusions)基于MGMTP模型的理论和方法，根据因子分析法分析数据的原理及监测数据的实际情况，进行了合理的数据预处理，重建了全球大气降水氚浓度模型.结果表明，本文提出的新模型不仅克服了MGMTP模型的氚浓度“异常负值”问题，而且能恢复全球1960—2014年间大气降水年平均氚浓度.同时，该模型具有简单易用、时间序列长、全球性适用等优点，对缺少大气降水氚浓度实测数据的地区具有重要参考价值.

参考文献

巴琦, 徐永福. 2010. 氚输入函数的构造与北太平洋氚分布的模拟[J]. 中国科学:地球科学, 2010, 40(1): 115–126.

Birkel C, Soulsby C. 2016. Advancing tracer-aided rainfall-runoff modelling:a review of progress, problems and unrealised potential[J]. Hydrological Processes, 29(25): 5227–5240.

Cauquoin A, Jean-Baptiste P, Risi C, et al. 2017. Modeling the global bomb-tritium transient signal with the AGCM LMDZ-iso:a method to evaluate aspects of the hydrological cycle[J]. Journal of Geophysical Research, 121(21): 12612–12629.

陈宗宇, 聂振龙, 张荷生, 等. 2004. 从黑河流域地下水年龄论其资源属性[J]. 地质学报, 2004, 78(4): 560–567.

程中双. 2015. 强烈开采含水层的水化学和同位素响应及其水文地质指示[D]. 北京: 中国地质科学院

崔亚莉, 刘峰, 郝奇琛, 等. 2015. 诺木洪冲洪积扇地下水氢氧同位素特征及更新能力研究[J]. 水文地质工程地质, 2015, 42(6): 1–7.

Doney S C, Glover D M, Jenkins W J. 1992. A model function of the global bomb tritium distribution in precipitation, 1960-1986[J]. Journal of Geophysical Research Oceans, 97(C4): 5481–5492.DOI:10.1029/92JC00015

Gleeson T, Befus K M, Jasechko S, et al. 2016. The global volume and distribution of modern groundwater[J]. Nature Geoscience, 9(2): 161–167.DOI:10.1038/ngeo2590

何晓群. 2010. 应用多元统计分析[M]. 北京: 中国统计出版社: 253–316.

IAEA, WMO. 2016. GNIP Database: Global network of tritium in precipitation[OL]. https://websso.iaea.org.

靳书贺, 姜纪沂, 迟宝明, 等. 2016. 基于环境同位素与水化学的霍城县平原区地下水循环模式[J]. 水文地质工程地质, 2016, 43(4): 43–51.

金在温, 查尔斯·M·米勒. 2015. 因子分析: 统计方法与应用问题[M]. 叶华译. 上海: 格致出版社+上海人民出版社

Koster R D, Broecker W S, Jouzel J, et al. 1989. The global geochemistry of bomb-produced tritium:General circulation model compared to available observations and traditional interpretations[J]. Journal of Geophysical Research, 94(D15): 18305–18326.DOI:10.1029/JD094iD15p18305

李永江, 刘春雨. 2016. 多元分析原理及应用[M]. 北京: 经济科学出版社: 78–107.

连炎清. 1990. 大气降水氚含量恢复的多元统计学方法:以临汾地区降水氚值恢复为例[J]. 中国岩溶, 1990, 9(2): 157–166.

龙文华, 陈鸿汉, 段青梅, 等. 2008. 人工神经网络方法在大气降水氚浓度恢复中的应用[J]. 地质与资源, 2008, 17(3): 208–212.

Lucas L L, Unterweger M P. 2000. Comprehensive review and critical evaluation of the half-life of tritium[J]. Journal of Research of the National Institute of Standards & Technology, 105(4): 541–549.

马致远. 2004. 环境同位素方法在平凉市岩溶地下水研究中的应用[J]. 地质论评, 2004, 50(4): 433–439.

马致远, 高文义. 1997. 用天然氚确定隐伏岩溶水滞留时间及含水层参数[J]. 煤田地质与勘探, 1997, 25(4): 34–38.

Michel R L. 1992. Residence times in river basins as determined by analysis of long-term tritium records[J]. Journal of Hydrology, 130(1/4): 367–378.

汪东华. 2010. 多元统计分析与SPSS应用[M]. 上海: 华东理工大学出版社: 93–226.

王凤生. 1998. 吉林省大气降水氚浓度恢复的区域模型探讨[J]. 吉林地质, 1998, 17(3): 75–81.

王瑞久. 1984. 山西娘子关泉的地下水储量估算[J]. 水文地质工程地质, 1984(6): 38–42.

王绍令, 李作福, 刘景寿, 等. 1990. 青藏高原东部地表水、地下水的氚同位素研究[J]. 环境科学, 1990, 11(1): 24–27, 23.

Weiss W, Roether W. 1980. The rates of tritium input to the world oceans[J]. Earth & Planetary Science Letters, 49(2): 435–446.

吴秉钧. 1986. 我国大气降水中氚的数值推算[J]. 水文地质工程地质, (4):42-45, 1986(4): 42–45, 53.

许乃政, 刘红樱, 魏峰, 等. 2015. 江苏洋口港地区地下水的环境同位素组成及其形成演化研究[J]. 环境科学学报, 2015, 35(12): 3862–3871.

章艳红, 叶淑君, 吴吉春. 2011. 全球大气降水中年平均氚浓度的恢复模型[J]. 地质论评, 2011, 57(3): 409–418.

Zhang Y, Ye S, Wu J. 2011. A modified global model for predicting the tritium distribution in precipitation, 1960-2005[J]. Hydrol Process, 25(15): 2379–2392.DOI:10.1002/hyp.v25.15

张应华, 仵彦卿, 温小虎, 等. 2006. 环境同位素在水循环研究中的应用[J]. 水科学进展, 2006, 17(5): 738–747.