 , 张秋兰1
, 张秋兰1
 , 崔亚莉1, 邵景力1, 韩占涛2
, 崔亚莉1, 邵景力1, 韩占涛21. 中国地质大学(北京)水资源与环境学院, 北京 100083;
2. 中国地质科学院水文地质环境地质研究所, 石家庄 050061
收稿日期: 2017-08-16; 修回日期: 2017-09-19; 录用日期: 2017-09-19
基金项目: 国家自然科学基金青年科学基金(No.41502228)
作者简介: 于映雪(1992-), 女, E-mail:1152589021@qq.com
通讯作者(责任作者): 张秋兰(1981—), 女, 副教授, 研究方向为胶体在多孔介质中的运移机理.以第一作者在Water Resources Research, Vadose Zone Journal等国际SCI期刊发表论文7篇. E-mail:qlzhang919@cugb.edu.cn
摘要: 通过室内砂柱实验,研究了饱和多孔介质中,相同离子强度条件下,混合钠-钙电解质溶液的Ca2+/Na+物质的量比和胶体粒径对胶体运移的影响.实验结果表明,胶体粒径相同时,随着背景电解质溶液物质的量比的增大,胶体的滞留量增多;物质的量比相同时,相同质量浓度条件下,粒径越小的胶体滞留量越大.经模型拟合,考虑Langmuirian动力学阻塞和与深度有关的沉积行为的对流-弥散-吸附-解吸方程能够很好地描述本次实验条件下胶体在饱和多孔介质中的运移行为.
关键词:胶体运移胶体粒径Ca2+/Na+物质的量比模拟饱和多孔介质
Effects of molar ratio in mixed Na-Ca electrolyte solutions and colloid size on the transport of colloids in saturated porous media
YU Yingxue1
 , ZHANG Qiulan1
, ZHANG Qiulan1
 , CUI Yali1, SHAO Jingli1, HAN Zhantao2
, CUI Yali1, SHAO Jingli1, HAN Zhantao2 1. School of Water Resources and Environment, China University of Geosciences(Beijing), Beijing 100083;
2. Institute of Hydrogeology and Environmental Geology, Chinese Academy of Geological Sciences, Shijiazhuang 050061
Received 16 August 2017; received in revised from 19 September 2017; accepted 19 September 2017
Supported by the National Natural Science Foundation of China Youth Fund(No.41502228)
Biography: YU Yingxue(1992—), female, E-mail:1152589021@qq.com
*Corresponding author: ZHANG Qiulan, E-mail:qlzhang919@cugb.edu.cn
Abstract: In this paper, we conducted a series of sand column experiments to investigate the influence of molar ratio scenarios of Ca2+/Na+ in mixed Na-Ca electrolyte systems under the same ionic strength and the influence of colloid size on the transport of colloids in saturated porous media. Results showed that retention of colloids increased with the increasing in molar ratio of electrolyte solution when the sizes of colloid were same; under the same colloid mass concentration, colloid retention increased with the decreasing in colloid size when the molar ratios were same. A numerical advection-dispersion-attachment-detachment equation considering the combined processes of Langmuirian dynamics blocking and depth-dependent deposition behavior successfully described colloid transport in saturated porous media under the conditions mentioned in the paper.
Key words: colloid transportcolloid sizemolar ratio of Ca2+/Na+simulationsaturated porous media
1 引言(Introduction)胶体一般是指粒径在10 nm~10 μm之间的微小颗粒, 其广泛分布于土壤和含水层中, 主要包括粘土颗粒、含铁氧化物、细菌、病毒、天然有机大分子(如腐殖酸)等.胶体具有巨大的表面能与比表面积, 对污染物通常具有很强的吸附能力, 可作为土壤和地下水中污染物的“运输载体”(Grolimund et al., 2005; Metreveli et al., 2007; 陈亚妮等, 2016);同时, 一些胶体本身就是污染物, 如细菌、病毒等.因此, 研究胶体在地下环境中的运移过程和机理对于土壤和地下水安全具有十分重要的意义.
近年来的研究结果表明, 胶体在多孔介质中的迁移行为受胶体本身的性质(粒径(Pelley et al., 2008)、形状(Knappenberger et al., 2015)、类型和表面性质等)、多孔介质的性质(粒径(Mitropoulou et al., 2013)、含水量(Knappenberger et al., 2014)和表面特性(Shen et al., 2011)等)、溶液化学性质(pH(Zhou et al., 2011)、离子强度(Torkzaban et al., 2010; 孙慧敏等, 2012)、离子组成类型(Fan et al., 2015)、溶解性有机质含量和种类(Pelley et al., 2008)等)及水动力条件(流速(Zhang et al., 2015)等)的影响.这些物理化学因素使得胶体与多孔介质发生界面反应, 产生聚沉、堵塞、截留等现象, 导致胶体在多孔介质中的迁移能力发生变化.Torkzaban等(2006)研究表明, 低pH、高离子强度有利于病毒在饱和多孔介质中的滞留;Mitropoulou等(2013)研究发现, 纯水条件下非饱和多孔介质中, 粒径大的胶体相比粒径小的胶体滞留稍多, 且相比于细砂, 胶体在中砂中的滞留量较大;Lanphere等(2013)研究发现, 当离子强度小于0.01 mol·L-1时, 氧化石墨烯的运移能力增强, 约5%的氧化石墨烯吸附在砂柱中, 而当离子强度等于0.1 mol·L-1时, 氧化石墨烯全部滞留在砂柱中;Xia等(2017)的研究结果显示, 碱金属离子对氧化石墨烯和硫化物还原氧化石墨烯运移的抑制效果为Na+<K+<Cs+, 碱土金属离子对氧化石墨烯和硫化物还原氧化石墨烯运移的抑制效果为Mg2+<Ca2+<Ba2+;Fan等(2015)发现, 在Na-Ca混合体系中, Ca2+浓度越高, 氧化石墨烯的运移能力越差, 且氧化石墨烯的运移能力受到离子强度和离子组成的共同影响.
自然条件下, Na+和Ca2+通常共存于地下水中, 且二者的相对含量随水文地球化学过程的改变而改变(Ping et al., 2013; Moussa et al., 2014);胶体的粒径变化会改变胶体在电解质溶液中的Zeta电势, 进而影响胶体与多孔介质间的相互作用能, 造成不同粒径胶体之间沉积行为的差异.以往研究并未探讨饱和多孔介质中Ca2+和Na+以不同物质的量比共存时对不同粒径胶体运移的影响.本文以3种粒径(0.3、0.5、1 μm)的聚苯乙烯微球作为实验胶体, 研究不同粒径胶体在不同Ca2+/Na+物质的量比(0(溶液中只含有NaCl)、0.5、1、∞(溶液中只含有CaCl2))的混合钠-钙体系中的运移规律, 结合DLVO理论和形变阻塞效应分析不同沉积行为的成因, 并采用对流-弥散-吸附模型对胶体的穿透曲线进行模拟.
2 材料与方法(Materials and methods)2.1 胶体悬浮液与背景电解质溶液本次实验选用的胶体为3种粒径(0.3、0.5、1 μm)的球状聚苯乙烯微球(购自上海辉质生物科技有限公司, 质量浓度为500 mg·L-1, 密度为1.05 g·cm-3, 折射率为1.59), 根据厂家提供的数据, 0.3、0.5、1 μm 3种粒径胶体储备悬浮液的初始个数浓度分别为3.37×1015、7.28×1015、9.09×1013个·mL-1.实验中胶体悬浮液的配制方法如下:先将胶体储备悬浮液放在超声波清洗器中超声10 min, 使胶体颗粒均匀分布, 再向胶体储备悬浮液中分别加入不同物质的量比的CaCl2和NaCl混合溶液, 稀释成Ca2+/Na+物质的量比分别为0、0.5、1、∞且离子强度为10 mmol·L-1的20 mg·L-1的胶体悬浮液, 储存在冰箱中(-4 ℃)备用.
用CaCl2和NaCl配制Ca2+/Na+物质的量比分别为0、0.5、1、∞且离子强度为10 mmol·L-1的背景电解质溶液, 溶液的pH约为6.1.采用ZetaPlus粒度电位分析仪(Zeta-PALS, Brookhaven Instruments, Corporation Holtsville, NY)对3种胶体在不同物质的量比电解质溶液中的水动力学粒径和Zeta电势进行测定.
2.2 多孔介质实验中采用粒径0.2~0.425 mm的石英砂作为多孔介质, 平均粒径为0.3 mm.实验开始之前, 先用0.01 mol·L-1的NaOH溶液将石英砂超声清洗30 min, 之后用超纯水将NaOH冲洗掉, 再将石英砂置于0.01 mol·L-1 HCl中超声清洗30 min, 之后再用超纯水清洗.清洗后的石英砂用烘箱以105 ℃烘干, 储存在无菌烧杯中备用.采用ZetaPlus粒度电位分析仪对不同物质的量比条件下石英砂颗粒的Zeta电势进行测定, 测定方法如下:取清洗干净后的石英砂于玛瑙研钵中研磨成小于2 μm的粉末, 用电解质溶液稀释后超声20 min, 然后取上清液测定(Wang et al., 2017).
2.3 砂柱实验实验装置如图 1所示, 主要由储液瓶、蠕动泵、石英砂柱、部分收集器组成.实验所用有机玻璃柱内径2 cm, 长15 cm, 柱子上、下两端分别装有300目的筛网, 以均匀分散水流并防止石英砂外漏.采用湿装法装填石英砂于有机玻璃柱内, 装砂过程中需要不断搅动砂子, 以使装填的石英砂更加均质并去除其中的气泡, 每次实验装砂质量约为66.5 g, 孔隙度为0.47.使用蠕动泵控制实验过程中砂柱内溶液的流动方向为自上而下, 且流量恒定为0.586 mL·min-1, 达西流速为0.186 cm·min-1.下文中所提PV为孔隙体积, 1 PV约为37 min.
图 1(Fig. 1)
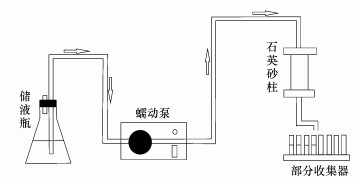 |
| 图 1 实验装置示意图 Fig. 1Experimental setup |
实验步骤如下:实验开始之前, 先向砂柱中通入约14个PV的背景电解质溶液, 以平衡砂柱;然后向砂柱中通入约4.6个PV相应物质的量比及离子强度的胶体悬浮液;最后向砂柱中通入4.6个PV相应物质的量比及离子强度的背景电解质溶液, 以洗脱砂柱.出流液中的胶体浓度采用紫外-可见光分光光度计测定, 测定波长分别为240 nm(0.3 μm胶体)、288 nm(0.5 μm胶体)、440 nm(1 μm胶体).
2.4 示踪实验示踪实验是为了估算水动力弥散系数, 本次实验选用Cl-作为示踪剂.砂柱准备好后, 先向砂柱中通入约4.6个PV的NaCl溶液, 然后通入超纯水直至出流液中检测不到Cl-为止, 使用硫氰酸汞高铁光度法测定样品中的Cl-浓度(GB 13580.9-92).采用对流-弥散方程对示踪曲线进行描述, 方程如下:
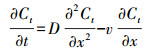 | (1) |
2.5 胶体运移的数学模型采用一维对流-弥散-吸附-解吸方程对本次实验所获得的胶体浓度穿透曲线进行模拟, 液相中胶体质量平衡控制方程如下:
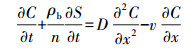 | (2) |
相应的固相中胶体质量平衡方程如下:
 | (3) |
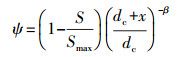 | (4) |
2.6 DLVO理论本文利用Derjaguin-Landau-Verwey-Overbeek (DLVO)理论计算胶体与多孔介质之间的相互作用能, 该理论认为胶体与多孔介质之间的总势能ΦDLVO(h)等于范德华引力势能Φvdw(h)和双电层静电力势能Φdl(h)之和(Loveland et al., 1996):
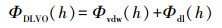 | (5) |
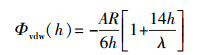 | (6) |
 | (7) |
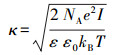 | (8) |
3 结果与讨论(Results and discussion)3.1 胶体和石英砂的特性表 1和表 2列出了3种粒径的胶体及石英砂在4种物质的量比、离子强度为10 mmol·L-1的电解质溶液中的水动力学粒径、Zeta电势及根据DLVO理论计算的胶体与石英砂之间的势垒和次级势阱.
表 1(Table 1)
| 表 1 水动力学粒径 Table 1 Hydrodynamic diameters | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 1 水动力学粒径 Table 1 Hydrodynamic diameters
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 2(Table 2)
| 表 2 Zeta电势及DLVO势能值 Table 2 Zeta potentials and DLVO interaction energy parameters | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 2 Zeta电势及DLVO势能值 Table 2 Zeta potentials and DLVO interaction energy parameters
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 1数据显示, 在4种物质的量比条件下, 0.3、0.5、1 μm 3种粒径胶体的水动力学粒径分别为0.315~0.446、0.519~0.737、1.036~1.250 μm;3种胶体均发生了不同程度的团聚, 粒径增大程度分别为4.9%~48.8%、3.8%~47.4%、3.6%~25.0%.随着溶液物质的量比的增大, 同一粒径的胶体的团聚程度逐渐增大;当物质的量比等于0和0.5时, 3种粒径的胶体的水动力学粒径增大程度接近(小于5%);当物质的量比由0.5增大至1时, 0.3 μm胶体和0.5 μm胶体的粒径增大程度(从约21%增大至约47%)较1 μm胶体的粒径增大程度(从20.1%增大至23.4%)更为明显;当物质的量比由1增大至∞时, 3种胶体的粒径增大程度不明显.这说明胶体的团聚程度受到溶液物质的量比和胶体固有粒径的共同影响, 且3种胶体在物质的量比等于1和∞时的团聚程度类似.
根据表 2中的数据可知, 在4种物质的量比的电解质溶液中, 0.3、0.5、1 μm 3种粒径胶体的势垒变化范围分别为94.7~345.6、225.4~603.0、466.9~1335.7 kT, 次级势阱的变化范围分别为-27.9~-4.6、-10.9~-7.5、-18.5~-14.9 kT.由此可见, 对于同一粒径的胶体而言, 物质的量比越大, 势垒越小, 次级势阱负值越大;在相同物质的量比的电解质溶液中, 粒径越大的胶体, 势垒越高, 次级势阱负值越大.势垒越高越不利于胶体沉积在初级势阱处, 而次级势阱的出现为胶体提供了吸附区.
3.2 Cl-及胶体的穿透曲线测试及模拟Cl-实测和模拟的穿透曲线如图 2所示, 从图中可以看出, 对流-弥散方程能够很好地描述Cl-在饱和多孔介质中的运移情况, 模拟得到的水动力弥散系数D=0.0231 cm2·min-1.
图 2(Fig. 2)
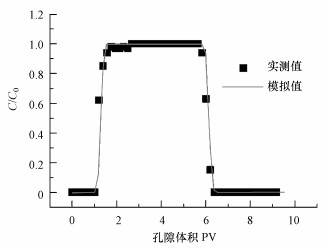 |
| 图 2 Cl-实测和模拟的穿透曲线 Fig. 2Observed and simulated breakthrough curves of Cl- |
图 3是3种粒径的胶体在离子强度为10 mmol·L-1、不同物质的量比的电解质溶液中的实测及模拟穿透曲线, 模拟及计算得到的穿透曲线的参数如表 3所示.从图中可以看出, 3种胶体的穿透曲线峰值均随溶液物质的量比的增大而降低, 且相同物质的量比条件下, 粒径越小的胶体, 峰值越低.从表 3可以看出, 相同粒径的胶体, 背景电解质溶液的物质的量比越大, katt和Smax越大;相同物质的量比的背景电解质溶液条件下, 粒径越小的胶体katt和Smax越大.而所有实验中, kdet的数量级相同, 变化范围不大, 数值较小, 这与穿透曲线的拖尾较小相一致.
图 3(Fig. 3)
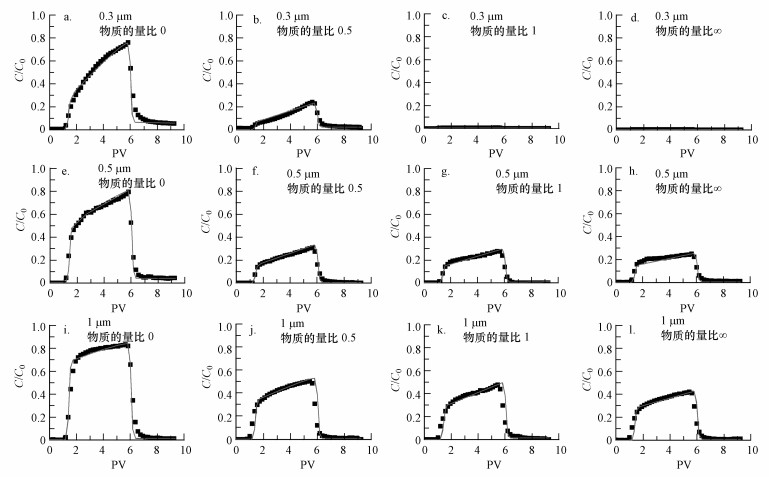 |
| 图 3 胶体实测和模拟的穿透曲线 Fig. 3Observed and simulated breakthrough curves of colloid |
表 3(Table 3)
| 表 3 胶体穿透曲线参数 Table 3 Parameters for breakthrough curves of colloid | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 3 胶体穿透曲线参数 Table 3 Parameters for breakthrough curves of colloid
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
本次实验得到的穿透曲线均是非对称的, 通常认为是阻塞效应(阻塞效应是指由于Langmuirian动力阻塞产生的, 随着时间的延续, 吸附区域逐渐被填充的过程(Xu et al., 2016))导致的, 模拟数据与实验数据拟合程度较好, 验证了阻塞效应对穿透曲线形状的影响.
3.3 物质的量比对胶体运移的影响横向对比图 3a~d(胶体粒径0.3 μm)、图 3e~h(胶体粒径0.5 μm)及图 3i~l(胶体粒径1 μm)可以看出, 随着物质的量比的增大, 3种粒径胶体的滞留量都呈增多的趋势, 这与Fan等(2015)的研究结果一致.根据表 3中的数据可知, 当背景电解质溶液的物质的量比增大时, 胶体滞留量的变化范围分别为38.14%~99.2%(0.3 μm胶体)、30.91%~77.22%(0.5 μm胶体)、19.57%~62.84%(1 μm胶体), 当电解质溶液的物质的量比等于1和∞时, 几乎全部(大于99%)注入的0.3 μm胶体均滞留在砂柱中.
DLVO计算结果(表 2)显示, 随着电解质溶液物质的量比的增大, 3种粒径的胶体与石英砂之间的势垒逐渐降低, 次级势阱负值逐渐增大, 这些都有利于胶体吸附在石英砂表面.此外, 4种物质的量比条件下, 3种胶体均发生了不同程度的团聚作用(表 1), 且物质的量比越高团聚作用越显著;0.5 μm胶体和1 μm胶体的dc/dp均大于0.0017, 会受到形变阻塞(Bradford et al., 2002)的影响, 且dc/dp值随物质的量比增大而增大, 由此推断对于0.5 μm胶体和1 μm胶体而言, 物质的量比的增大使得形变阻塞的效果更为明显.
3.4 胶体粒径对胶体运移的影响纵向对比图 3a、3e、3i(背景电解质溶液IS=10 mmol·L-1, 物质的量比0), 图 3b、3f、3j(IS=10 mmol·L-1, 物质的量比0.5), 图 3c、3g、3k(IS=10 mmol·L-1, 物质的量比1)及图 3d、3h、3l(IS=10 mmol·L-1, 物质的量比∞)可以看出, 在相同物质的量比的背景电解质溶液条件下, 相同质量浓度的3种胶体, 粒径越小的胶体滞留量越大, 其吸附率和质量回收率如表 3所示.
Bradford等(2002)发现, 在相同的多孔介质中, 注入约相同质量的胶体, 粒径越小的胶体滞留量越小, 他们认为, 导致这一现象的主要原因是形变阻塞(胶体直径与多孔介质平均直径比dc/dp大于0.0017时, 会发生形变阻塞, 且比值越大形变阻塞越显著).本文计算了3种粒径胶体的水动力学粒径与石英砂的平均粒径比, 从表 1可以看出, 在4种物质的量比条件下, 0.3、0.5、1 μm 3种胶体的dc/dp分别为0.0011~0.0015、0.0017~0.0025、0.0038~0.0042.说明在4种物质的量比条件下, 0.3 μm胶体的dc/dp都不大于0.0017, 不受形变阻塞的影响, 0.5 μm胶体和1 μm胶体均受到了形变阻塞的影响, 且在相同物质的量比条件下1 μm胶体所受的形变阻塞影响较0.5 μm胶体更为显著, 两种胶体所受的形变阻塞效应影响均随物质的量比的增大而增大.实验结果显示, 粒径越小的胶体的滞留量越大, 这表明虽然形变阻塞对0.5 μm胶体和1 μm胶体产生了影响, 但不是导致其滞留的主要原因.
值得注意的是, Bradford等(2002)的实验是在由NaCl组成的离子强度为1 mmol·L-1的背景电解质溶液中进行的, 在此条件下, 胶体与石英砂之间的势垒较高, 不利于胶体在石英砂表面的吸附, 形变阻塞成为控制胶体沉积的主要原因.而本文计算了离子强度为10 mmol·L-1、4种物质的量比的电解质溶液中3种粒径的胶体与石英砂之间的相互作用能(表 2), 结果显示, 物质的量比相同时, 粒径越小的胶体势垒越低, 这会使得粒径越小的胶体更容易越过势垒沉积在初级势阱处, 而大粒径胶体与石英砂之间的势垒较高, 不易于胶体越过势垒吸附在初级势阱处.计算结果(表 2)显示, 在4种物质的量比的电解质溶液中, 0.3、0.5、1 μm 3种粒径胶体和石英砂之间的次级势阱分别为-27.9~-4.6、-10.9~-7.5、-18.5~-14.9 kT, 可见次级势阱值较小, 对胶体的吸附产生的影响有限, 次级势阱的存在不是造成粒径越小的胶体吸附量越大的主要原因.
4 结论(Conclusions)1) 同一粒径的胶体, 背景电解质溶液的物质的量比越高, 滞留量越大.背景电解质溶液的物质的量比增大使得胶体与石英砂之间的势垒降低, 次级势阱负值增大, 易于胶体吸附;物质的量比的增大造成0.5 μm胶体和1 μm胶体受形变阻塞的影响更加明显, 形变阻塞也是造成0.5 μm胶体和1 μm胶体沉积量随物质的量比增大而增大的重要原因.
2) 相同物质的量比的背景电解质溶液中, 粒径越小的胶体滞留量越大.物质的量比相同时, 粒径越小的胶体, 胶体与多孔介质之间的势垒越低, 越容易越过势垒沉积在初级势阱处, 势垒低是造成粒径小的胶体滞留量高于粒径大的胶体的主要原因.
参考文献
| Adamczyk Z, Siwek B, Zembala M, et al. 1994. Kinetics of localized adsorption of colloid particles[J]. Advances in Colloid & Interface Science, 48(94): 151–280. |
| Bradford S A, Yates S R, Bettahar M, et al. 2002. Physical factors affecting the transport and fate of colloids in saturated porous media[J]. Water Resources Research, 38(12).DOI:10.1029/2002WR001340 |
| Bradford S A, Simunek J, Bettahar M, et al. 2003. Modeling colloid attachment, straining, and exclusion in saturated porous media[J]. Environmental Science & Technology, 37(10): 2242–2250. |
| Bradford S A, Simunek J, Bettahar M, et al. 2006. Significance of straining in colloid deposition:Evidence and implications[J]. Water Resources Research, 42(12): 12–15. |
| Bradford S A, Torkzaban S. 2008. Colloid Transport and retention in unsaturated porous media:A review of interface-, collector-, and pore-scale processes and models[J]. Vadose Zone Journal, 7(2): 667–681.DOI:10.2136/vzj2007.0092 |
| 陈亚妮, 董姝楠, 孙媛媛, 等. 2016. 氧化石墨烯对铅在饱和多孔介质中运移的影响[J]. 农业环境科学学报, 2016, 35(7): 1392–1397.DOI:10.11654/jaes.2016.07.023 |
| Fan W, Jiang X H, Yang W, et al. 2015. Transport of graphene oxide in saturated porous media:Effect of cation composition in mixed Na-Ca electrolyte systems[J]. Science of the Total Environment, 511: 509–515.DOI:10.1016/j.scitotenv.2014.12.099 |
| Gregory J. 1981. Approximate expressions for retarded van der waals interaction[J]. Journal of Colloid & Interface Science, 83(1): 138–145. |
| Grolimund D, Borkovec M. 2005. Colloid-facilitated transport of strongly sorbing contaminants in natural porous media:Mathematical modeling and laboratory column experiments[J]. Environmental Science & Technology, 39(17): 6378–6386. |
| Hogg R, Healy T W, Fuerstenau D W. 1966. Mutual coagulation of colloidal dispersions[J]. Trans Faraday Soc, 62: 1638–1651.DOI:10.1039/tf9666201638 |
| James S C, Chrysikopoulos C V. 2000. Transport of polydisperse colloids in a saturated fracture with spatially variable aperture[J]. Water Resource Research, 36(6): 1457–1465.DOI:10.1029/2000WR900048 |
| Knappenberger T, Flury M, Mattson E D, et al. 2014. Does water content or flow rate control colloid transport in unsaturated porous media[J]. Environmental Science & Technology, 48(7): 3791–3799. |
| Knappenberger T, Aramrak S, Flury M. 2015. Transport of barrel and spherical shaped colloids in unsaturated porous media[J]. Journal of Contaminant Hydrology, 180: 69–79.DOI:10.1016/j.jconhyd.2015.07.007 |
| Loveland J P, Ryan J N, Amy G L, et al. 1996. The reversibility of virus attachment to mineral surfaces[J]. Colloids & Surfaces A Physicochemical & Engineering Aspects, 107(4): 205–221. |
| Lanphere J D, Luth C J, Walker S L. 2013. Effects of solution chemistry on the transport of graphene oxide in saturated porous media.[J]. Environmental Science & Technology, 47(9): 4255–4261. |
| Mccarthy J F, Zachara J M. 1989. Subsurface transport of contaminants[J]. Environmental Science & Technology, 23(5): 496–502. |
| Metreveli G, Frimmel F H. 2007. Influence of Na-bentonite Colloids on the Transport of Heavy Metals in Porous Media[M]. Berlin Heidelberg: Springer: 29–53. |
| Mitropoulou P N, Syngouna V I, Chrysikopoulos C V. 2013. Transport of colloids in unsaturated packed columns:Role of ionic strength and sand grain size[J]. Chemical Engineering Journal, 232: 237–248.DOI:10.1016/j.cej.2013.07.093 |
| Moussa A B, Mzali H, Zouari K, et al. 2014. Hydrochemical and isotopic assessment of groundwater quality in the quaternary shallow aquifer, Tazoghrane region, north-eastern Tunisia[J]. Quaternary International, 338(4): 51–58. |
| Pelley A J, Tufenkji N. 2008. Effect of particle size and natural organic matter on the migration of nano-and microscale latex particles in saturated porous media[J]. Journal of Colloid & Interface Science, 321(1): 74–83. |
| Ping W, Yu J, Zhang Y, et al. 2013. Groundwater recharge and hydrogeochemical evolution in the Ejina Basin, northwest China[J]. Journal of Hydrology, 476: 72–86.DOI:10.1016/j.jhydrol.2012.10.049 |
| Qi Z, Zhang L, Wang F, et al. 2014. Factors controlling transport of graphene oxide nanoparticles in saturated sand columns[J]. Environmental Toxicology & Chemistry, 33(5): 998–1004. |
| Shen C, Li B, Wang C, et al. 2011. Surface roughness effect on deposition of nano-and micro-sized colloids in saturated columns at different solution ionic strengths[J]. Vadose Zone Journal, 10(3): 1071–1081.DOI:10.2136/vzj2011.0011 |
| 孙慧敏, 殷宪强, 曹秀蓉. 2012. 离子强度对蒙脱石胶体在饱和多孔介质中运移与释放的影响[J]. 环境科学学报, 2012, 32(5): 1120–1125. |
| Torkzaban S, Hassanizadeh S M, Schijven J F, et al. 2006. Virus transport in saturated and unsaturated sand columns[J]. Vadose Zone Journal, 5(3): 877–885.DOI:10.2136/vzj2005.0086 |
| Torkzaban S, Bradford S A, van Genuchten M T, et al. 2008. Colloid transport in unsaturated porous media:the role of water content and ionic strength on particle straining[J]. Journal of Contaminant Hydrology, 96(1/4): 113–127. |
| Torkzaban S, Kim H N, Simunek J, et al. 2010. Hysteresis of colloid retention and release in saturated porous media during transients in solution chemistry[J]. Environmental Science & Technology, 44(5): 1662–1669. |
| Wang Y, Li Y, Pennell K D. 2008. Influence of electrolyte species and concentration on the aggregation and transport of fullerene nanoparticles in quartz sands[J]. Environmental Toxicology & Chemistry, 27(9): 1860–1867. |
| Wang D, Shen C, Jin Y, et al. 2017. Role of solution chemistry in the retention and release of graphene oxide nanomaterials in uncoated and iron oxide-coated sand[J]. Science of the Total Environment, 579: 776–785.DOI:10.1016/j.scitotenv.2016.11.029 |
| Xu S, Qi J, Chen X, et al. 2016. Coupled effect of extended DLVO and capillary interactions on the retention and transport of colloids through unsaturated porous media[J]. Science of the Total Environment, 573: 564–572.DOI:10.1016/j.scitotenv.2016.08.112 |
| Xia T, Yu Q, Jing L, et al. 2017. Cation-inhibited transport of graphene oxide nanomaterials in saturated porous media:The hofmeister effects[J]. Environmental Science & Technology, 51(2): 828–837. |
| Zhang Q, Raoof A, Hassanizadeh S M. 2015. Pore-scale study of flow rate on colloid attachment and remobilization in a saturated micromodel[J]. Journal of Environmental Quality, 44(5): 1376–1383.DOI:10.2134/jeq2015.01.0058 |
| Zhou D, Wang D, Long C, et al. 2011. Transport and re-entrainment of soil colloids in saturated packed column:effects of pH and ionic strength[J]. Journal of Soils and Sediments, 11(3): 491–503.DOI:10.1007/s11368-010-0331-2 |
