申丽铭^,1, 郭雨蒙^,2, 王文珂^,1,*1.国防科技大学,气象海洋学院,湖南 长沙 410003
2.军事科学院军队政治工作研究院,北京 100091

Streamline Parallel Distribution Method Based on Vector Complete Information Entropy

SHEN Liming^,1, GUO Yumeng^,2, WANG Wenke^,1,*1. College of Meteorology and Oceanography, National University of Defense Technology, Changsha, Hunan 410003, China
2. Academy of Military Political Work, Academy of Military Sciences, Beijing 100091, China

通讯作者: ^*王文珂（E-mail:wangwenke@nudt.edu.cn）

收稿日期:2021-06-10

基金资助:

国家自然科学基金“非结构网格线性矢量场高效拓扑可视化关键技术研究”(61972411) 国家自然科学基金“高精度海洋声场模型的可扩展并行算法与千亿网格应用”(61972406)

Received:2021-06-10
作者简介 About authors

申丽铭,国防科技大学,硕士研究生,研究方向为科学可视化与信息可视化等,已发表SCI论文2篇。
本文中负责数据处理、模型构建、实验、论文撰写。
SHEN Liming is a master's student of National University of Defense Technology. Her research int-erests include scientific visualization and information visuali-zation. She has published 2 academic papers.
In this paper, she is responsible for data processing, model con-struction, experiments, and paper writing.
E-mail: slmwow@nudt.edu.cn


郭雨蒙,现工作于军事科学院军队政治工作研究院,博士,研究方向为虚拟现实与可视化。
本文主要承担工作为实验与协助模型构建。
GUO Yumeng, Ph.D., currently works at the Academy of Military Political Work of the Academy of Military Sciences. His research interets include virtual reality and visualization.
In this paper, he is responsible for conducting experiments and assisting model construction.
E-mail: guoyumeng@nudt.edu.cn


王文珂,国防科技大学气象海洋学院可视化团队负责人,博士,副研究员,主要研究方向为科学计算可视化,主持和参与了国家重大专项、973、863、自然科学基金等多项课题,获军队科技进步二等奖1项,发表学术论文50余篇,撰写学术专著1部,授权国家发明专利5项。
本文主要承担工作为流线分布算法研究框架设计。
WANG Wenke, Ph.D., associate professor, is currently the Director of Visualization Teaching and Research Section of College of Meteorology and Oceanography, National University of Defense Technology. His main research interests include Scientific Computing Visualization. He has presided over and participated in a number of national major projects, including 973, 863, Natural Science Foundation and other projects. He has won Second Prize of Military Science and Technology Progress, published more than 50 academic papers, written 1 academic monograph, and granted 5 national invention patents.
In this paper, he is responsible for the design of streamline distribution algorithm research framework.
E-mail: wangwenke@nudt.edu.cn



摘要
【目的】流线可视化效果依赖于流线分布方法,其对矢量场数据的理解有着重要作用。现有的流线分布方法只考虑了矢量场的方向分量,忽略了另一重要的矢量长度信息。此外,为了提高计算效率,本文提出了一种基于矢量完全信息熵的并行流线分布方法。【方法】该方法考虑了矢量方向和长度分量,分块并行计算熵场并以此指导流线的放置。在放置过程中,采用了一种改进的精简剪枝方法来提高算法的效率。【结果】本文选取了三组实验数据,产生不同数量的流线与已有方法进行对比实验。实验结果表明,该方法能够高效生成可反映矢量场方向和长度变化信息的流线。【结论】本文提出的并行流线分布方法,能够高效揭示更多的矢量场信息,且不遗漏矢量场的显著特征。
关键词： 流线可视化;流线分布;完全信息熵

Abstract
[Objective] Streamline visualization depends on the streamline distribution method, which plays an important role in understanding flow field data. The existing streamline distribution methods only consider the directional component of the vector field and ignore magnitude information. In addition, considering that the flow field data are steadily on the increase, a parallel streamline distribution method based on complete vector information entropy is proposed in this paper. [Methods] The proposed method considers both direction and magnitude components of the vector and calculates the entropy field in parallel in blocks to guide the placement of streamlines. An improved pruning method is applied to improve the efficiency of the algorithm. [Results] In this paper, different numbers of streamlines are generated to conduct comparative experiments with existing methods on three flow field datasets. The experimental results show that the proposed method can generate streamlines that reflect the information of both direction and magnitude of the flow field efficiently. [Conclusions] The parallel streamline distribution method proposed in this paper can effectively reveal more flow field information without missing the significant characteristics of the flow field.
Keywords：streamline visualization;streamline distribution;complete vector information entropy


PDF (8208KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
申丽铭, 郭雨蒙, 王文珂. 基于矢量完全信息熵的流线并行分布方法[J]. 数据与计算发展前沿, 2021, 3(4): 44-53 doi:10.11871/jfdc.issn.2096-742X.2021.04.004
SHEN Liming, GUO Yumeng, WANG Wenke. Streamline Parallel Distribution Method Based on Vector Complete Information Entropy[J]. Frontiers of Data and Computing, 2021, 3(4): 44-53 doi:10.11871/jfdc.issn.2096-742X.2021.04.004

引言

矢量场可视化是重要的科学可视化方法,可以帮助科研工作人员从大量数据中观测与提取关键特征。流线可以简洁地表示流场中流体的运动趋势,且计算量少、易于观测,是矢量场可视化中最常用的可视化方法之一^[1]。

流线分布方法决定了矢量场可视化表达的效果,主要分为两类：基于均匀分布的流线分布与基于特征的流线分布方法。采用均匀分布的方法在生成流线数目较少时,容易丢失矢量场中的重要特征。而基于特征的流线分布方法,将流线集中分布在矢量场的关键区域附近,有利于科研人员分析矢量场的重要特征。作为一种成功的信息度量理论,信息论为矢量场特征提供了定量描述工具。基于信息论的流线分布方法使得大多数流线被放置在具有复杂信息的区域附近,突出其显著特征。然而,现有的基于信息论的流线分布方法,仅考虑了矢量的方向分量,这将忽略某些矢量幅度变化剧烈的现象,例如CFD流场^[2]中的激波。

本文提出了一种基于矢量完全信息熵的流线分布方法,该方法建立矢量方向和长度的联合直方图计算完全信息熵,引导流线集中放置于矢量方向或矢量大小变化迅速的高熵值区域,从而更完整地揭示矢量场的潜在信息。同时,为了提高效率,算法采用了网格用于流线剪枝,消除距离过近的流线,并对部分步骤进行了并行化。实验表明,与现有的基于信息熵的流线分布方法相比,本文方法得到的流线分布效果既能体现矢量大小变化剧烈的区域,又能保留矢量方向变化的显著特征。

1 国内外研究现状

为了有效展现矢量场信息,往往需要生成多条流线,为此需要考虑流线如何合理布局。流线分布方法可以分为基于均匀分布的流线种子点分布与基于特征的流线种子点分布两类。

Turk和Banks首先提出了一种图像引导（Image guided）的流线种子点选择方法^[3],尝试生成分布均匀的流线,但是只能用于二维矢量场,且效率较低。而后,Mao等人^[4]扩展了这种图像引导的方法,用于在曲线网格中的三维参数曲面上创建均匀分布的流线。为了解决在三维矢量场中生成流线而不考虑其在屏幕空间投影而产生的视觉混乱问题,Li等人^[5]扩展了图像引导方法,流线的密度和渲染样式可以根据各种标准灵活控制,可以更有效地可视化三维矢量场。

然而,均匀分布的方法在流线数目较少时会丢失矢量场中的重要特征。为此,Verma等人^[6]首先提出了基于特征的流线分布策略,可以有效反映临界点等矢量场的重要特征。他们使用类似于拓扑分析的概念定义特征区域,并针对特征区域不同的流动模式使用不同的种子点放置模板。Chen等人^[7]定义了两条流线的相似距离,通过阻止相似距离较小的流线生长,避免生成影响视觉效果的冗余流线。由于特征区域的流线相似距离较大,该算法产生的流线在特征区域周围较为密集,而非特征区域的流线比较稀疏。

为了定量度量矢量场特征,近年来有****利用信息论解决流线的分布问题。Furuya和Itoh^[8]首先将信息理论应用于流线生成,他们根据切线方向分布度量流线的复杂性,获得其信息熵场,用于指导流线生成。Xu等人^[9]利用信息熵与特征区域的关系引导种子点放置,同时利用条件熵度量当前流线与原矢量场的信息差异,以引导信息缺失区域的进一步布种。Lu^[10]提出了一种基于纹理的可视化方法,该方法根据矢量方向熵提取不同的特征结构,以类似纹理的处理方式实现流线的生成。考虑到矢量大小变化剧烈的区域也可视为一类流场特征,Guo等人^[11]在其基于信息熵的流线分布方法上提出了矢量长度熵的计算方法,以揭示矢量场更多的信息。

2 基于完全信息熵的流线分布方法

本节对提出的基于矢量完全信息熵的流线分布方法进行了详细描述。该方法不同于已有的忽略矢量长度信息的信息熵方法,同时考虑了矢量方向与长度信息,以更完整地揭示矢量场的信息。算法利用矢量完全信息熵引导流线集中放置于矢量方向或矢量大小变化迅速的高熵值区域,而后根据现有流线建立中间矢量场并计算其与原始矢量场的矢量完全条件熵。条件熵值可反映两个矢量场之间的信息差异,因此可据此进一步迭代指导放置流线直至达到停止条件。

并且,为了提高效率,算法采用网格以利用已有流线限制新流线生成（见2.3节）,使得在流线生成过程中可以判断流线间距离,提前终止距离过近的流线生成,加速流线剪枝过程。

2.1 算法流程

算法流程如图1所示,包括以下步骤：

图1

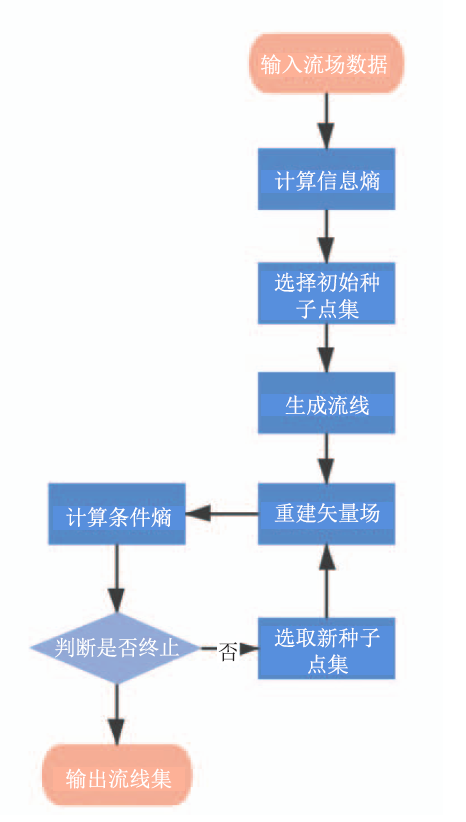新窗口打开|下载原图ZIP|生成PPT
图1基于矢量完全信息熵的流线分布算法流程图

Fig.1Flow chart of streamline distribution algorithm based on vector complete information entropy



(a) 计算信息熵：遍历每个数据网格点,建立矢量信息直方图,计算信息熵场（详见2.2节）;

(b) 选择初始种子点集：计算信息熵场的局部极大值点,以局部极大值点为中心放置种子点（种子点模板参考文献[9]）,作为初始种子点集;

(c) 生成流线：为了有效捕捉矢量场特征,模板布点会布置多个种子点,使得生成的流线中某些流线间距离过小,已有方法生成流线后再判断流线间距进行流线删除。为了加速此过程,本文在流线生成过程中利用D_sep网格修剪流线（详见2.3节）;

(d) 重建矢量场：通过扩散法（Diffusion meth-od）^[13]由生成的流线重建矢量场;

(e) 计算条件熵：建立重建矢量场与原始流场的联合直方图,并计算条件熵场（详见2.2节）;

(f) 判断是否终止：判断原始矢量场和重建矢量场之间的条件熵是否满足终止条件（小于某个预设阈值E_t）。如果满足或已达到算法迭代次数,则算法停止,输出当前流线集;否则,执行步骤(g);

(g) 选取新种子点集：对于条件熵值高于阈值的点,按条件熵值的大小赋予其重要性,采用重要性采样的方法选取候选种子点,返回步骤(c)。

2.2 计算信息熵与条件熵

香农提出的信息熵用于解决信息的量化度量问题,他直观地将信息熵H(X)定义为特定离散信息的出现概率,条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。

假设有离散随机变量X,其具有可能值{X₁, X₂, …, X_n}。令p(X_i)表示X=X_i的概率,可用下式计算变量X的信息熵H(X)：

(2-1) $ H(X)=-\sum_{X_{i} \in X} p\left(X_{i}\right) \log p\left(X_{i}\right) $
对于两个随机变量X、Y,在已知Y的情况下,X的条件熵H(Y|X)由以下公式定义：

(2-2) $ H(X \mid Y)=\sum_{y \in Y} p(y) H(X \mid Y=y) \\ =-\sum_{y \in Y} \sum_{x \in X} p(x, y) \log p(x \mid y) $
式中H(X|Y=y)代表变量Y取特定值y的条件下变量x的熵。p(y)代表边缘概率,p(x,y)为联合概率,p(x|y)为y约束下x的条件概率。

计算矢量方向信息熵E_d时,以矢量方向作为变量X,建立矢量方向的直方图,通常为圆形（三维为球形）。对于图2(a)所示的矢量场区域,将平面上的单位圆划分为有限个扇形区间X_i(i=1, …, n),矢量场中每个矢量根据自身方向划分至某个特定区间中,如图2(b)所示。通过统计直方图中各个区间X_i内的矢量数量C(X_i),可利用下式计算区间X_i内的矢量方向概率p(X_i)：

(2-3) $ p\left(X_{i}\right)=-\frac{C\left(X_{i}\right)}{\sum_{i=1}^{n} C\left(X_{i}\right)} $

图2

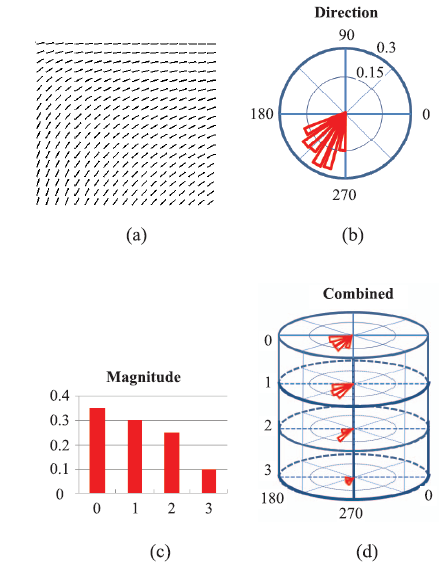新窗口打开|下载原图ZIP|生成PPT
图2计算信息熵所用的直方图。（a）矢量场数据;（b）矢量方向信息熵直方图;(c) 矢量长度信息熵直方图;(d) 矢量完全信息熵直方图

Fig.2Histogram for calculating information entropy. (a) Vec-tor field data; (b) Histogram of vector direction information entropy;(c) Histogram of vector magnitude information entr-opy;(d) Histogram of vector complete information entropy



结合公式(2-1)和(2-3),即可计算得出给定矢量场区域的方向信息熵。

矢量方向条件熵计算与方向信息熵相似,即通过公式（2-3）得到p(x|y)与p(x,y)后,代入公式（2-2）可得矢量方向条件熵。

对于矢量长度信息熵E_m,以矢量长度为变量X,建立矢量长度值的直方图,如图2(c)所示。同时以矢量长度与方向作为参考变量,计算矢量完全信息熵E_c时,需要将上述两个直方图一并考虑：以矢量方向直方图为xy平面,以矢量长度值为z轴,建立的直方图是由离散的圆平面构成的圆柱体,如图2(d)所示;获得直方图后,通过统计每个矢量在各区间内的数量,即可应用公式(2-3)完成完全信息熵与完全条件熵的计算。

另外,由图2可知,完全信息熵直方图区间的数量是分别采用矢量长度与矢量方向直方图的区间数量的乘积。为了体现矢量长度变化对流线分布效果的不同影响,定义α为矢量长度（z轴）和矢量方向（xy平面）的区间数的比值。若α的值较大,说明对矢量长度的分组更精细,矢量大小快速变化区域的熵值增加,流线分布更侧重于体现矢量大小的变化信息。反之,若α的值较小,说明矢量方向的分组更精细,则流线分布主要体现的是矢量方向的变化。特别地,若α=0,本文算法与现有的基于信息熵的流线分布方法相同。在本文实验中,矢量方向直方图的分组数默认设置为,矢量长度分组数则由α控制。参数α对流线分布的影响将在第4节实验部分进一步介绍。

2.3 基于D_sep网格修剪流线

在生成种子点集时,为了有效捕捉矢量场特征,本文使用模板布点：二维时放置4个,位于以信息熵极大值点为中心的菱形顶点上;三维时放置8个,位于以信息熵极大值点为中点的正八面体顶点上。模板布点通常会导致流线在某一区域过于密集,因此修剪冗余流线是十分必要的。现有的流线分布方法在流线生成结束后进行流线剪枝。通过比较任意两条流线的距离（或相似度）,以删除距离相近（或形状相似）的冗余流线,从而避免视觉混乱。此类剪枝过程要计算每两条流线的最短距离,且每当生成新的流线后都需要执行一次剪枝过程,时间开销较大。

考虑到计算采样点到流线距离的过程可能反复出现,本文通过建立一个D_sep网格结构,使得在流线生成过程中可以判断流线间距离,提前终止距离过近的流线生成,加速流线剪枝过程。D_sep网格是一个完全包围原矢量场的标准网格结构,每个网格单元主要存储一个是否可用的标志,有“可用”和“不可用”两种状态。D_sep网格的作用是让已生成流线的网格标记为“不可用”,新流线生成时只能通过“可用”的网格单元,如图3所示。为了让流线分布体现特征,即在特征附近允许容纳更多的流线,一个点对其它流线的限制距离取决于其信息熵值。若某一点熵值很高,说明其重要度高,则该点附近应容纳更多流线以突出显示,因此对其它流线的间隔限制应该很低。反之若熵值很低,则间隔限制应设置较大。

图3

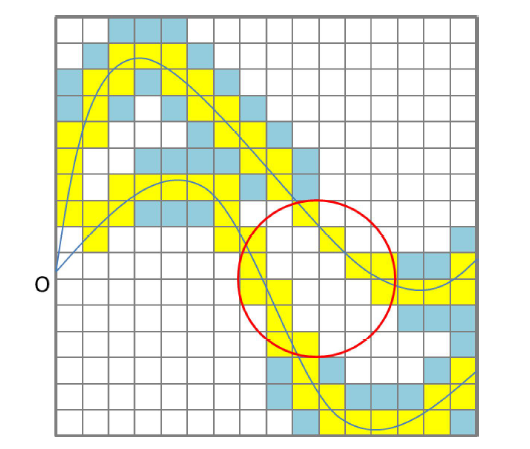新窗口打开|下载原图ZIP|生成PPT
图3网格示意图：黄色网格为流线通过的“不可用”网格,蓝色网格为低熵值的“不可用”网格。

Fig. 3Diagram of D_sep grid: yellow grids are “unavailable” grids with streamlines passing through, and blue grids are “unavailable” grids with low entropy.



图3给出了两个流线的“不可用”网格的示例。一般情况下,若流线通过了网格,且该网格点信息熵值没有高过一个阈值,则此网格的标志直接由“可用”变为“不可用”。如图3中的红色圆圈区域具有低熵值,将流线通过的网格置为“不可用”（图中黄色网格）。但是,若流线通过的某些点的熵值高于阈值,为了让更多流线突出表示特征,这些点所在的网格仍被设置为“可用”,如图3中临界点O所在的网格。另外,对于流线通过的熵值较低（低于某给定阈值）的采样点所在的网格,要求其它流线距其间隔更远,那么除包含它的网格外,其相邻的网格也被设置为“不可用”。为方便区分,这些因低熵值点而标记为“不可用”的相邻网格在图3中用蓝色显示。

本文算法中,由于流线间的距离由网格结构控制,流线生成时只需判断下一个网格是否“可用”,若不可用则提前终止流线生成。虽然D_sep网格结构需要额外开销用于计算每个点的限制间隔等操作,但仍可有效对流线剪枝过程进行加速。在第4节的实验中会对网格限制法与流线生成后剪枝法进行效率对比。

3 流线分布方法的并行实现

如图1所示,本文算法流程中需要大量计算,如计算信息熵场与条件熵场,根据已有流线重建矢量场等;并且相比仅考虑矢量方向的信息熵计算,矢量完全信息熵计算过程增加了维度,引入了额外的计算负担。为提高算法效率,本文采用了并行技术对算法进行加速。

3.1 信息熵与条件熵并行计算

在2.2小节的熵值计算过程中,每个点的邻域都需要进行一次信息熵与条件熵的计算,且任意两个点的熵计算互不影响,彼此独立,为此,采用如下的并行计算过程：

首先,将矢量场数据划分为子块,每个子块关联到一个指定的线程上,然后遍历子块的每个点。处理一个点时,需要先从共享内存里读取原始矢量场或重建矢量场的邻域数据至线程缓存中。特别的是,为了减少读取次数,便于子块边界区域附近点的熵值计算,当读取子块数据时,边界需要向外扩展,即多读取一定范围内相邻子块的数据。

然后,建立矢量长度与方向的信息熵直方图或原矢量场和重建矢量场的联合直方图,并在每个线程独立计算该点的信息熵或条件熵。

3.2 重建矢量场

此步骤通过对所有已生成流线使用扩散法重建矢量场,下面介绍其并行化过程。

在基于信息熵的流线分布算法^[9]中,详细描述了根据已生成流线重建矢量场的过程。该步骤以二维为例,需要最小化一个如下的能量函数ε(Y)：

(3-1) $ \varepsilon(Y)=\int \varepsilon_{1}(Y(x), \widetilde{X}(x))+\mu \varepsilon_{2}(Y(x)) d x $
其中,

$\varepsilon_{1}(Y(x), \widetilde{X}(x))=|\widetilde{X}(x)|^{2}|Y(x)-\widetilde{X}(x)|^{2}$

$\varepsilon_{2}(Y(x)=(u(x), v(x)))=|\nabla u(x)|^{2}+|\nabla v(x)|^{2}$

Y(x)代表重建的矢量场,当点x在流线上时,$\widetilde{X}(x)$与原始场X(x)的矢量值相同,否则为0。

这个能量函数的最小值可以通过使用广义扩散方程来求解。设(i, j)为某一点的索引,且$u_{i,j}^{n}$和$v_{i,j}^{n}$表示第n层迭代中点(i, j)处矢量的两个分量,$\widetilde{X}$和Y的采样步长为(Δx, Δy),每次迭代的时间步长Δt和固定系数μ,即可使用以下递推公式迭代计算$u_{i,j}^{n}$和$v_{i,j}^{n}$：

(3-2) $ u_{i, j}^{n+1}=\left(1-b_{i, j} \Delta t\right) u_{i, j}^{n}+c_{i, j}^{1} \Delta t+r\left(u_{i+1, j}^{n}+u_{i, j+1}^{n}+u_{i-1, j}^{n}+\right.\\ \left.\qquad u_{i, j-1}^{n}-4 u_{i, j}^{n}\right) $
(3-3) $ v_{i, j}^{n+1}=\left(1-b_{i, j} \Delta t\right) v_{i, j}^{n}+c_{i, j}^{2} \Delta t+r\left(v_{i+1, j}^{n}+v_{i, j+1}^{n}+v_{i-1, j}^{n}+\right. \\ \left.v_{i, j-1}^{n}-4 v_{i, j}^{n}\right) $
其中：

(3-4) $ r=\frac{\mu \Delta t}{\Delta x \Delta y}, b_{i, j}=\widetilde{X}_{x}(i, j)^{2}+\widetilde{X}_{y}(i, j)^{2}, \\ c_{i, j}^{1}=b_{i, j} \widetilde{X}_{x}(i, j), c_{i, j}^{2}=b_{i, j} \widetilde{X}_{y}(i, j), \\ \left(u_{i, j}^{0}, v_{i, j}^{0}\right)=\widetilde{X}(i, j) $
每进行一次迭代,每个点的(u_i,j, v_i,j)的值就越接近最终结果。理论上这个迭代过程会在固定次数内收敛,且这个次数小于原始场中网格数的平方。



第n次迭代层中点($u_{i,j}^{n}, v_{i,j}^{n}$)的计算彼此独立,而计算它们需要调用第n-1次迭代层的各个数值,因此每一层迭代结束时必须进行同步。算法伪码3-1显示了这个同步的并行过程。可以看到,该步骤通过栅栏完成数据同步,即进入下一层迭代前当前迭代层的所有线程操作必须已经完成。该步骤是对递推公式(3-2)与(3-3)的混合并行实现,对同一层是并行计算,不同层则是串行,需要等待前一层所有操作完成。栅栏的存在一定程度上影响了并行加速效果,但并行方法总体上仍提高了整个算法的效率。

4 结果与分析

本节中,我们在3个数据集上测试了基于矢量完全信息熵的流线分布方法,并与现有的基于信息熵的分布方法^[9]进行了对比。实验中的算法全部由C++编码实现。实验用的计算机配置6核Intel Xeon X5675 3.06 GHz CPU、32 GB内存、NVIDIA GeForce GTX 550 Ti显卡和64位Windows 7操作系统。

4.1 可视化效果分析

（1）数据集1是简单的人工模拟矢量场,数据规模为50*50,在矢量场中心有一个鞍点。矢量长度颜色映射后分布如图4(a)所示,暖色表示长度大、冷色表示长度小,可见左下角区域矢量长度迅速从红色变为蓝色和绿色,矢量大小变化剧烈。为了验证实验效果,每个对比实验均生成了相同数量的流线。

图4

新窗口打开|下载原图ZIP|生成PPT
图4数据1的可视化实验结果。(a)中热力图为矢量长度场映射结果,(b)-(d)中的热力图为信息熵场映射结果

Fig.4Visualization experiment results of data 1. The heat map in (a) is the mapping result of vector magnitude field, and the heat map in (b)-(d) is the mapping result of information entropy field.



图4(b) ~ (d)中的背景场均为信息熵场的颜色映射,颜色从暖到冷代表熵值从高到低。三张图中均生成了21条流线。

图4为设置不同的长度与方向区间比值α（取值范围为0、0.3、0.6）后所得的可视化效果。α=0为长度不占比重的情况,即等同于已有的基于信息熵的流线分布方法。随着α增大,左下区域流线数目逐步增加。当α=0.6时,具有速度大小剧烈变化的矢量场左下区域聚集了更多的流线,特征更加明显。因此,后续两个实验均取α=0.6以突出体现本文效果。

由当前流线与原流场矢量信息计算得到的条件熵值是一种流线可视化效果的量化评价方式,条件熵值越低则可认为可视化结果越还原原矢量场。当α取值分别为0、0.3、0.6时,整个矢量场的条件熵值分别为0.976765、0.97011、0.932224,也说明了α取0.6时确实具有更好的可视化效果。

（2）数据集2是一个120*120的气象风场,结果如图5所示,每张图中均生成24条流线。各图中位置相同的红色方框标注出了最具有代表性的区域。

图5

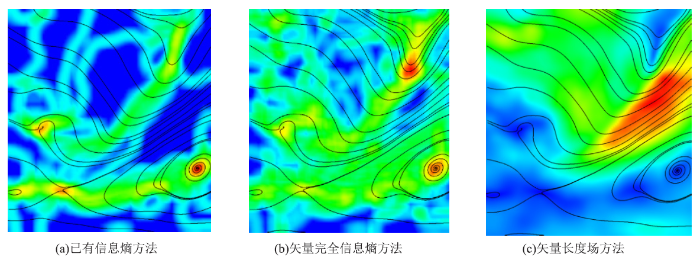新窗口打开|下载原图ZIP|生成PPT
图5数据2的可视化实验结果。红色方框标识出了三种方法效果的对比处,(a)-(c)中热力图分别为矢量方向信息熵场、完全信息熵场与矢量长度场映射结果。

Fig.5Visualization experiment results of data 2. The red box indicates the comparison of the effects of the three methods. The heat maps in (a)-(c) are the mapping results of the vector direction information entropy field, the complete information entropy field and the vector magnitude field, respectively.



由图5(c)可知,红色方框区域内的矢量长度场中冷暖色变化剧烈,说明该区域中的矢量大小变化很快。因此,在以完全信息熵为依据得到的流线图5(b)中,红色方框区域内熵值明显增加,出现流线聚集现象。作为对比,以矢量方向信息熵为依据的图5(a)的红色方框区域内分布了较少的流线,未能体现风速大小变化。

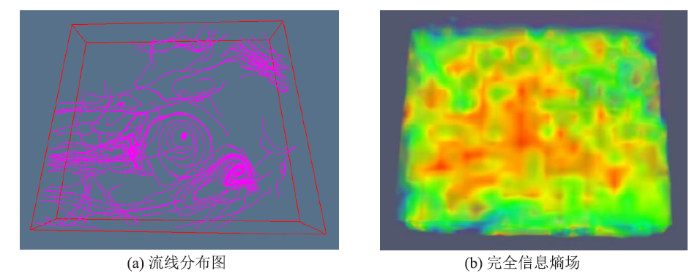
（3）数据集3是尺寸为210*180*27的三维真实气象风场,图6为本文算法的三维可视化效果,共生成45条流线。可以看到,流线大部分聚集在方向变化剧烈的经典特征区域（涡旋、鞍点等）附近。同时,右上和左下的红框区域矢量大小变化显著,流线更加密集。

图6

新窗口打开|下载原图ZIP|生成PPT
图6数据3的三维可视化实验结果

Fig.63D visualization experimental results of data 3. (a) Streamline distribution diagram. (b) Complete information entropy field.

4.2 效率分析

本节对D_sep网格剪枝效率与计算步骤并行效率进行实验对比分析。

为了降低因流线过于密集而产生的视觉混乱,现有基于信息熵的流线分布方法在生成所有流线后对冗余流线进行剪枝,本文提出的D_sep网格剪枝方法则是通过已有流线限制新流线生成。

上述两种方法在数据集1与数据集2的执行时间如表1和表2所示,与生成所有流线后剪枝相比,本文提出的通过已有流线间隔（D_sep网格）限制流线生成过程的剪枝方法运行时间减少约10％,证明了本文提出的D_sep网格剪枝方法效率更高。

Table 1
表1
表1对数据集1采用不同剪枝策略的算法运行时间
Table 1Running time of different pruning strategies

	生成所有流线后剪枝	已有流线限制新流线生成
流线数量	24	24
运行时间	74.562 s	68.145 s

新窗口打开|下载CSV

Table 2
表2
表2对数据集2采用不同剪枝策略的算法运行时间
Table 2Running time of different pruning strategies for dataset 1 for dataset 2

	生成所有流线后剪枝	已有流线限制新流线生成
流线数量	21	21
运行时间	11.091 s	9.945 s

新窗口打开|下载CSV

表3列出了本文方法的串行实现与不同线程数目下本文算法的并行运行时间。由表可知,相比串行实现,使用6线程并行时算法运行时间可降低约40％,有效提高了算法效率。

Table 3
表3
表3不同并行线程数量的本文算法运行时间
Table 3Running time of the algorithm in this paper with different number of parallel threads

	串行	2线程	4线程	6线程
数据集1	9.945 s	7.75 s	6.436 s	5.903 s
数据集2	68.145 s	54.931 s	44.623 s	40.976 s
数据集3	186.935 s	133.084 s	121.296 s	115.564 s

新窗口打开|下载CSV

5 结论与展望

本文从可视效果与效率两个角度对提出的基于矢量完全信息熵的流线分布方法进行了分析。该方法同时考虑了矢量的方向和长度信息,能够有效揭示更多的矢量场信息,且不遗漏原始数据的显著特征。此外,通过在流线生成过程中利用D_sep网格进行流线剪枝,以及对算法过程中的耗时计算进行并行加速,本文也有效提高了算法效率。

由结果与分析可得,本文提出的算法在效率上仍有较大的提升空间,未来将进一步采用GPU和并行加速技术对算法效率进行优化。此外,视点选择在三维矢量场可视化中也是十分重要的。通过信息论对不同视点所揭示的信息进行量化并推荐信息量丰富的视点,可以有效协助专家进行科学数据分析。下一步工作中,我们也将基于完全信息熵对视点选择进行优化。

利益冲突声明

所有作者声明不存在利益冲突关系。

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] 李思昆, 蔡勋, 王文珂, 等. 大规模流场科学计算可视化[M]. 北京: 国防工业出版社, 2013.
[本文引用: 1]

[2] Buning P, Steger J. Graphics and flow visualization in computational fluid dynamics
[C]. 1985 Computational Physics Conference. 1985: 1507.
[本文引用: 1]

[3] Turk G, Banks D. Image-guided streamline placement
[C]//Proceedings of the 23rd annual conference on Com-puter graphics and interactive techniques. ACM, 1996: 453-460.
[本文引用: 1]

[4] Mao X, Hatanaka Y, Higashida H, et al. Image-guided streamline placement on curvilinear grid surfaces
[C]//Proceedings Visualization' 98. IEEE, 1998: 135-142.
[本文引用: 1]

[5] Li L, Shen H W. Image-based streamline generation and rendering
[J]. IEEE Transactions on Visualization and Computer Graphics, 2007,13(3):630-640.
DOI:10.1109/TVCG.2007.1009URL [本文引用: 1]

[6] Verma V, Kao D, Pang A. A flow-guided streamline seed-ing strategy
[C]//Proceedings Visualization 2000. IEEE, 2000: 163-170.
[本文引用: 1]

[7] Chen Y, Cohen J, Krolik J. Similarity-guided streamline placement with error evaluation
[J]. IEEE Transactions on Visualization and Computer Graphics, 2007,13(6):1448-1455.
DOI:10.1109/TVCG.2007.70595URL [本文引用: 1]

[8] Furuya S, Itoh T. A Streamline Selection Technique for Integrated Scalar and Vector Visualization
.[J]. The Journal of the Society for Art and Science, 2009,8(3):1-2.
DOI:10.3756/artsci.8.1URL [本文引用: 1]

[9] Xu L, Lee T Y, Shen H W. An information-theoretic fra-mework for flow visualization
[J]. IEEE Transactions on Visualization and Computer Graphics, 2010,16(6):1216-1224.
DOI:10.1109/TVCG.2010.131URL [本文引用: 4]

[10] Lu D. Information-theoretic exploration for texture-based visualization
[J]. Journal of Visualization, 2017,20(2):393-404.
DOI:10.1007/s12650-016-0376-4URL [本文引用: 1]

[11] Guo Y, Wang W, Li S. Streamline Distribution Method based on Vector-magnitude -aware Entropy
[C]//Proce-edings of the 12th International Symposium on Visual Information Communication and Interaction. ACM, 2019: 22.
[本文引用: 1]

[12] Xu C, Prince J L. Gradient vector flow: A new external force for snakes
[C]//IEEE Conference on Computer Vision and Pattern Recognition. 1997,97:66.