,1,*1. 2.
3.
Modeling the Effects of Individual and Group Heterogeneity on Multi-Aspect Rating Behavior
Liu Kunpeng1, Zhao Xiaosa2, Hu Yirui3, Fu Yanjie,1,*1. 2.
3.
收稿日期:2019-12-10网络出版日期:2020-04-20
Corresponding authors: * Fu Yanjie（E-mail:yanjie.fu@ucf.edu）
Received:2019-12-10Online:2020-04-20
作者简介 About authors
Liu Kunpeng is a Ph.D. student in University of Central Florida. His research interests are data mining and automated data science.
Role in this paper: Responsible for the formula derivation, experiment design and paper writing.
E-mail: kunpengliu@knights.ucf.edu
Zhao Xiaosa is a Ph.D. student in Northeast Normal University. Her research interests are data mining and bioinformatics.
Role in this paper: Responsible for literature review and paper formatting.
E-mail: zhaoxs686@nenu.edu.cn
Hu Yirui got her Ph.D. degree from Department of Statistics, Rutgers, the State University of New Jersey in 2016. She is an Assistant Professor in Geisinger. Her research interests are statistics, biostatistics and predictive modeling.
Role in this paper: Responsible for coordinating the paper writing.
E-mail: yhu1@geisinger.edu
Fu Yanjie got his Ph.D. degree from Department of Management Science and Information Systems, Rutgers, the State University of New Jersey in 2016. He is an Assistant Professor in University of Central Florida. His research interest are data mining, spatial and mobile computing, and automated data science.
Role in this paper: Contact Author. Responsible for framework design and attending technical discussion on technologies. E-mail：yanjie.fu@ucf.edu
摘要
【目的】除了提供总体评分,多方面评分系统还可以提供更详细的方面评分,因此它可以帮助消费者更好地理解商品和服务。通过对多方面评分系统评分模式的建模,我们可以更好地发现潜在的评分组以及定量地理解这些评分组的评分行为。另外,这种建模也可以帮助服务提供者更好地改进他们的服务以吸引更多消费者。但是,由于多方面评分系统的复杂特性,对它的建模存在很多挑战。【方法】为了解决这些问题,本文提出了一种两步框架来从多方面评分系统中学习评分模式。详细地说,我们首先提出一种多分解关系学习方法（MFRL）来得到用户和商品的方面因素矩阵。在MFRL中,我们将矩阵分解,多任务学习和任务关系学习引入到同一个优化框架内。然后,我们将MFRL学习得来的用户和商品向量表征作为输入,通过高斯混合模型来构建组与组之间总体评分预测。【结果】我们在真实数据集上验证了提出的研究框架。大量实验结果表明我们提出的方法的有效性。【结论】用户异质性会潜在地影响用户的评分行为,因此在对个体及团体的评分行为进行建模时,要充分考虑到目标异质性带来的影响。
关键词：
Abstract
[Objective] Multi-aspect rating system could help customers better understand the item or service, because it provides not only the overall rating but also more detailed aspect ratings. By modeling the rating patterns on multi-aspect rating systems, we can better find out latent rating groups and quantitatively understand the rating behaviors lie in these groups. This can also help service providers improve their service and attract more targeted customers. However, due to the complex nature of multi-aspect rating system, it is challenging to model its rating patterns. [Methods] To address this problem, in this paper, we propose a two-step framework to learn the rating patterns from multi-aspect rating systems. Specifically, we first propose a multi-factorization relationship learning (MFRL) method to obtain the user and item aspect factor matrices. In MFRL, we unify matrix factorization, multi-task learning and task relationship learning into one optimization framework. And then, we model the rating patterns by exploiting group-wise overall rating prediction via mixture regression, whose inputs are the factor vectors of users and items learned from MFRL method. [Results] We apply the proposed framework on a real-world dataset (i.e., the crawled hotel rating dataset from TripAdvisor.com) to evaluate the performance of our proposed method. Extensive experimental results demonstrate the effectiveness of the proposed framework. [Conclusions] Individual and Group Heterogeneity could affect the behaviors behind the rating acts, which should be taken into account in modeling the rating patterns.
Keywords：
PDF (16920KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
刘鲲鹏, 赵宵飒, 胡一睿, 傅衍杰. 个体及团体异构多方面评分行为建模. 数据与计算发展前沿[J], 2020, 2(2): 59-77 doi:10.11871/jfdc.issn.2096-742X.2020.02.005
Liu Kunpeng.
1 Introduction
Multi-aspect rating system is a popular rating system in many online rating websites. Unlike the traditional rating system which only contains the overall rating, multi-aspect rating system also comprises several aspect ratings. With the help of aspect ratings, multi-aspect rating system provides more detailed rating information thus can better reflect user’s preferences and item’s (e.g. a hotel) attributes.Modeling the rating patterns on multi-aspect rating system is very important as it takes aspect ratings into account and could produce more accurate recommendations. After analyzing big multi-aspect rating data, we found that user-item pairs can be divided into several groups, where user-item pairs in the same group share the same rating pattern, while user-item pairs from different groups differ in rating patterns. However, most of existing works focus on either the correlations among aspect ratings[1,2,3] or the relationship between aspect ratings and the overall rating[4,5]. Less efforts have been made for capturing the rating heterogeneity in the modeling process. To this end, in this paper, we aim to model the rating patterns on multi-aspect rating system. Along this line, an important objective is to model and predict the overall rating of a given user-item pair.
Intuitively, to predict the overall rating of a given user-item pair, we should firstly obtain representations of the user and the item. To quantify the representations, we intend to simultaneously factorize multiple aspect rating matrices by sharing the latent representation vector of users or items using Collective Matrix Factorization (CoMF)[6,7]. However, while CoMF could partially capture the representations of users and items from multiple rating aspects, it could not capture entire representations from the view of correlations between aspect ratings and the overall rating.
All the above pieces of evidence suggest that modeling the rating patterns on multi-aspect rating system is not an easy task. Two unique challenges arise in achieving this goal:
Representation Learning: how to collectively learn the representations of users and items from multiple aspect ratings and overall ratings.
Rating Pattern Modeling: how to capture different rating patterns in user-item pair groups in the process of modeling overall rating from user and item representations.
First, it is revealed by low-dimensional factor models[8,9] that preferences or attitudes of a user are represented by a small number of unobserved factors. Similarly, characteristics or attributes of an item are represented by some other unobserved factors. In a linear factor model, the rating of a user-item pair is modeled by the product of user and item factor vectors. For example, suppose User i has a D×1 factor vector ui and Item j has a D×1 factor vector vi, then the rating of User i over Item jrij can be modeled by uTi·vj. More generally, for N users and M items, the N×M rating matrix R is modeled by the D×N user factor matrix U and the D×M item factor matrix V, i.e., R=UT·V.
For multi-aspect rating system which has more than one rating, the ratings are modeled in a similar way. The only difference is that the item is not determined by an individual factor vector, rather, each of its aspect has a corresponding factor vector. For example, User i has a D×1 factor vector ui while aspect 1 and aspect 2 of Item j have two corresponding D×1 factor vectors ej and cj, then the rating of User i over aspect 1 of Item jgij can be modeled by uTi·e1 and rating of User i over aspect 2 of Item jgij can be modeled by uTi·c1.
As Collective Matrix Factorization (CoMF) could simultaneously factorize multiple aspect rating matrices by sharing the factor vector of users or items [6, 7, 10], it is widely used in multiaspect rating system. However, it does not take the relationship of different aspect ratings into account. From the view of optimization, we regard the factorization of each aspect rating matrix as one task, and how individual aspect ratings affect overall rating as a task relationship regularization term in multi-task learning optimization. In this paper, we unify matrix factorization, multi-task learning and task relationship learning into one optimization framework. Eventually we develop a multi-factorization relationship learning (MFRL) method.
Second, after obtaining the user and item aspect factor matrices, we intend to explore the rating pattern among user-item pairs. Due to the uniqueness of individuals and commonness of groups, it is naturally promising to assume that user-item pairs in the same group share the same rating pattern, while user-item pairs from different groups differ in rating patterns. To characterize these rating patterns, we exploit group-wise overall rating prediction via mixture regression, whose inputs are the factor vectors of users and items learned from MFRL method. Let the rating pattern of a user-item group denote characterized by a parameter vector, the rating pattern is then modeled using the following idea: user- item pairs from the same group will use the same parameter vector to predict overall ratings; user-item pairs from different groups will use different parameter vectors to predict overall ratings.
To summarize, in this paper, we propose a step by step framework to model rating patterns from the multi-aspect rating data. Specifically, the followings are our three main contributions: (1) We propose a multi-factorization relationship learning (MFRL) method to simultaneously factorize multiple aspect rating matrices and incorporate the relationship between aspect ratings and the overall rating as a regularization term in the multi-task learning framework. (2) Given the user and item aspect factor matrices, we model the rating patterns among user-item pairs. (3) We apply the proposed framework to explore hotel rating system and predict overall ratings, and the extensive experimental results on real-world hotel rating data demonstrate the effectiveness of our approach.
The rest of paper is structured as follows. Section 2 introduces the relevant problem statement. The proposed two-step model framework for multi-aspect rating system is presented in Section 3. The detail experimental results are presented and discussed in Section 4. Section 5 shows the related work. Finally, Section 5 summarizes the work.
2 Problem statement
In this section, we first introduce some important definitions as well as the problem statement, and then provide an overview of our proposed model.Definition 2.1. (Multi-Aspect Rating System) Multi-aspect rating System includes one overall rating and multiple aspect ratings for an item/service. For example, after resting in a hotel, users rate the overall experience together with their ratings on location and cleanliness. The simplest case is one overall rating along with two aspect ratings; the most complex case might be an overall rating along with dozens of aspect ratings. To simplify the modeling of multi-aspect ratings, without loss of generosity, we consider the simplest case in the proposed method, i.e., one overall rating with two aspect ratings (aspect-1 rating and aspect-2 rating).
Definition 2.2. (Rating Pattern Heterogeneity). In the multi-aspect ratings, there exist multiple latent rating behavior groups, in which user-item pairs in the same group share the same rating pattern, while user-item pairs from different groups differ in rating patterns. For example, as shown in Figure 1, User A and B coupling with Hotel 1, 2, 3 form six pairs, which are clustered into three rating groups, revealing three different rating patterns correspondingly.
Fig.1
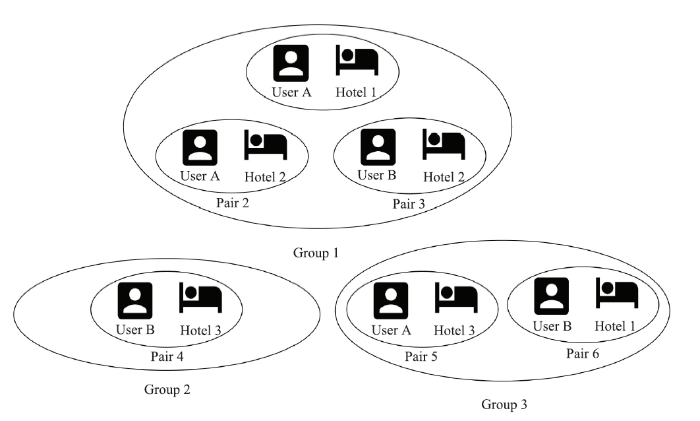新窗口打开|下载原图ZIP|生成PPTFig.1Pair rating groups
Definition 2.3. (Problem Statement). In this paper, we study the problem of modeling user and item representations as well as group heterogeneity in multi-aspect ratings. Let yij, gij and hij be the overall rating, aspect-1 rating, and aspect-2 rating of user i for item j respectively, ui, ej and cj be the latent representations of the i-th user, the aspect-1 latent representations of j-th item and the aspect-2 latent representations of j-th item respectively. Formally, given the historical multi-aspect rating records {< yij, gij, hij > |i ∈ [1, I], j ∈ [1, J]},our objective is to find a mapping function that takes a new user ID i* and a new item ID j* as inputs, and accurately outputs the overall rating y*ij, aspect-1 rating g*ij, aspect-2 rating h*ij, via effectively modeling representations and rating pattern heterogeneity.
Table 1
Table 1Mathematical notations
| Symbol | Size | Description |
|---|---|---|
| Y | I×J | Overall rating matrix |
| G | I×J | Aspect-2 rating matrix |
| H | I×J | Aspect-1 rating matrix |
| yij | 1 | Overall rating of user i for item j |
| gij | 1 | Aspect-1 rating of user i for item j |
| hij | 1 | aspect-2 rating of user i for item j |
| U | K×1 | User latent matrix |
| E | K×J | Item aspect-1 latent matrix |
| C | K×J | Item aspect-2 latent matrix |
| ui | K×1 | Latent features of user i |
| ej | K×1 | Aspect-1 latent features of item j |
| cj | K×1 | Aspect-2 latent features of item j |
| uki | 1 | k-th latent feature of user i |
| ekj | 1 | k-th latent feature of aspect-1 of item j |
| ckj | 1 | k-th latent feature of aspect-2 of item j |
新窗口打开|下载CSV
2.1 Framework Overview
Figure 2 shows the framework overview of our proposed method. This framework consists of two major stages.Fig.2
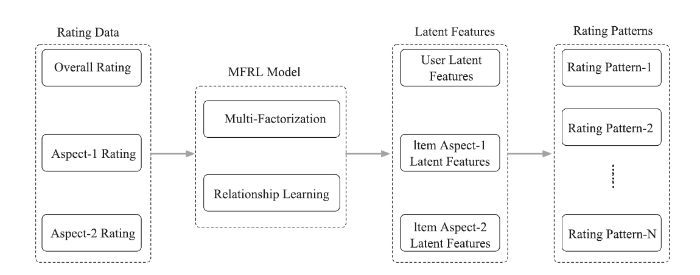新窗口打开|下载原图ZIP|生成PPTFig.2Framework overview
(1) Modeling of the Generative Process. We propose to model the individual heterogeneity in multi-aspect rating behavior by combining multi-factorization learning and factorization relationship learning. The multi-factorization learning is to model the individual differences in preferences for aspect-1 and aspect-2 ratings; the factorization relationship learning is to model the individual differences in preferences for the relationship between the overall ratings and the aspect-1 and aspect-2 ratings. Figure 3 shows the graphical model of generating overall, aspect-1, and aspect-2 ratings. Specifically, we first draw the user latent features ui. The aspect-1 rating gij is generated by the interaction between user latent features ui and aspect-1 latent features ej. Similarly, the aspect 2 rating hij is generated by the interaction between user latent features ui and item aspect-2 latent features cj. The overall rating is generated by the parameterized aspect ratings. Therefore, the aspect-1 rating is gij ∝ uTiej, the aspect-2 rating is hij ∝ uTicj, and the overall rating is
Where p and q are constant weights. Table 2 summarizes the multi-aspect rating behavior of how user i rates item j.
Fig.3
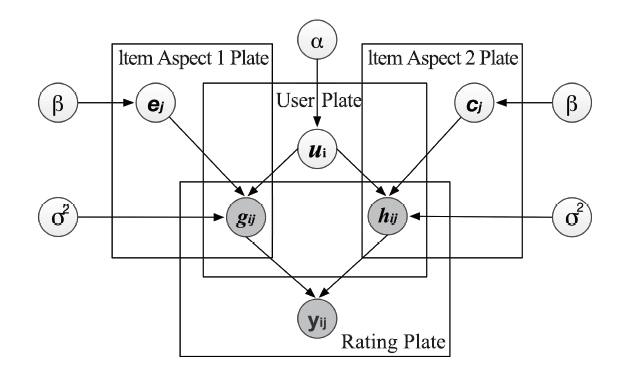新窗口打开|下载原图ZIP|生成PPTFig.3The framework overview and the proposed MFRL Model
(2) Modeling of the Rating Pattern Heterogeneity. After modeling the generative process, we obtain the latent features of users, item aspect-1, and item aspect-2, respectively denoted by {uTi, eTi, cTi,}. In the rating pattern heterogeneity, we assume there are N latent groups in the rating behavior. Each group has a unique rating pattern, which exhibits a unique relationship between overall rating and the latent features of user-item pairs in the same group. Consequently, the overall ratings can be regarded as the mixture overall ratings generated by N groups.
Where y(n)ij is the overall rating of the i-th user and the j-th item in the n-th group, and f(n) is the mapping function from the latent features of the i-th user and the j-th item to the overall rating.
Table 2
Table 2The generative process
| 1. | Draw user latent factor ${{u}_{i}}\tilde{\ }P({{u}_{i}};{{\sigma }_{{{u}_{i}}}})$ |
| 2. | Generate aspect-1 rating a. Draw item aspect-1 latent factor ${{e}_{j}}\tilde{\ }P({{e}_{j}};{{\sigma }_{{{e}_{j}}}})$ b. Draw item aspect-1 rating ${{g}_{ij}}\tilde{\ }P(u_{i}^{T}\cdot {{e}_{j}})$ |
| 3. | Generate aspect-2 rating a. Draw aspect-2 latent factor ${{c}_{j}}\tilde{\ }P({{c}_{j}};{{\sigma }_{{{c}_{j}}}})$ b. Draw aspect-2 rating ${{h}_{ij}}\tilde{\ }P(u_{i}^{T}\cdot {{c}_{j}})$. |
| 4. | Generate overall rating a. Draw aspect weights $p$ and $q$, s.t. $p+q=1$ b. Draw overall rating ${{y}_{ij}}\tilde{\ }P(p\cdot u_{i}^{T}\cdot {{e}_{j}}+q\cdot u_{i}^{T}\cdot {{c}_{j}})$ |
新窗口打开|下载CSV
3 Proposed method
We first introduce how to model the generative process in multi-aspect rating behavior, and then develop a multi-factorization relationship learning method. Later, we extend the multi-factorization relationship learning method by integrating the modeling of rating pattern heterogeneity via group-wise mixture regression.3.1 Model Intuitions
There are individual preferences as well as rating pattern heterogeneities among multi-aspect rating behavior. Therefore, in our approach, we model the generative mechanism of multi-aspect ratings based on the following three intuitions.Intuition 1: We assume aspect ratings are generated by the interaction between user latent features and item aspect features, thus we can infer user latent features and item aspect latent features from the aspect-rating factorizations. For example, cleanliness rating of a hotel can be generated by user latent features and cleanliness latent features, thus we can infer user latent features and cleanliness latent features from cleanliness ratings. Since there are multiple aspect ratings, we combine both multi-task learning and matrix factorization to develop a multi-task factorization method, in order to simultaneously factorize aspect rating matrices to learn user latent vectors and multiple item-aspect latent vectors.
Intuition 2: The overall rating has strong correlations with aspect ratings, which could connect user and aspect latent features with the overall rating. For example, the overall rating of a hotel can be predicted by its cleanliness rating and location rating, while these two aspect ratings can be predicted by their corresponding user and aspect latent features. Consequently, to improve the accuracy of overall rating prediction, we incorporate the relationship between aspect ratings and overall ratings into the multi-task factorization method, so as to simultaneously factorize aspect ratings while learning the overall-aspect rating relationship. We call the method multi-factorization relationship learning (MFRL).
Intuition 3: There are different latent groups of user-item pairs, where each group exhibits a unique rating pattern. We integrate the group-wise mixture regression model that takes the user latent features and item-aspect latent features as inputs. The group-wise mixture regression model can exploit the reinforcement of clustering user-item pairs and predicting user-item overall ratings. That is, suppose the unknown rating pattern is characterized as a b-dimensional coefficient vector α in a linear system. Let X be the a×b feature matrix of the user-item pairs in the group, Y be the a-sized overall ratings of the user-item pairs in the group. We can obtain Y=X·α that shows how the user-item pairs in the same group share the same rating pattern mathematically in regressions.
3.2 Multi-Task Matrix Factorization
Matrix Factorization based methods have been widely used to analyze users’ rating behavior. Probabilistic Matrix Factorization (PMF)[9] is one of the matrix factorization based methods that can be applied for single aspect rating. Considering the simplest triple case: [user, item, aspect-1 rating], where aspect-1 rating of the i-th user for the j-th item is gij, the aspect-1 rating gij can be factorized with ui and ej, which represent the user latent features and item aspect-1 latent features respectively. ui and ej encode the affinity of the i-th user and the aspect-1 of the j-th item in the latent space. In single rating matrix factorization, we place exponential distribution on ukj and ekj as the empirical prior, and an inverse gamma distribution on ${{\sigma }^{2}}$. Then we assume the rating ${{g}_{ij}}$ is drawn from normal distributions with the mean $u_{i}^{T}{{e}_{j}}$ and the variance ${{\sigma }^{2}}$. The generative process of ${{g}_{ij}}$ follows: [1] Draw ${{u}_{ki}}\tilde{\ }Exp(\alpha )$; [2] Draw ${{c}_{kj}}\tilde{\ }Exp(\beta )$; [3] Draw ${{\sigma }^{2}}\tilde{\ }Inv-Gamma(a,b)$; [4] Generate ${{g}_{ij}}\tilde{\ }N(u_{i}^{T}{{e}_{j}},{{\sigma }^{2}})$.Unlike single rating systems, in our multi-aspect rating problem, we have multiple ratings given by individual user for each item. Let us consider the four-tuple rating case: [user, item, aspect-1 rating, aspect-2 rating]. Figure 3 shows that the interaction between user plate and aspect-1 plate generates the aspect-1 rating gij, and similarly the interaction between the user plate and aspect-2 plate generates the aspect-2 rating hij. Table 3 shows that the two aspect ratings share the same user latent features. By regarding the factorization of each aspect rating matrix as one task, we develop a Multi-Task Matrix Factorization (MTMF) to co-factorize the rating triplet via maximizing the likelihood of the observed aspect ratings.
Table 3
Table 3The generative process of MTMF
| 1. | Generate latent factors a. Draw ${{u}_{ki}}\tilde{\ }Exp(\alpha )$ b. Draw ${{e}_{kj}}\tilde{\ }Exp(\beta )$ c. Draw ${{c}_{kj}}\tilde{\ }Exp(\beta )$ |
| 2. | Generate variance a. Draw ${{\sigma }^{2}}\tilde{\ }Inv-Gamma(a,b)$ |
| 3. | Generate ratings a. Generate ${{g}_{ij}}\tilde{\ }N(u_{i}^{T}{{e}_{j}},{{\sigma }^{2}})$ b. Generate ${{h}_{ij}}\tilde{\ }N(u_{i}^{T}{{c}_{j}},{{\sigma }^{2}})$ |
新窗口打开|下载CSV
3.3 Multi-Factorization Relationship Learning
We identify that overall rating has strong correlations with aspect ratings, and thus propose to incorporate the overall-aspect rating relationship learning into the multi-task learning.Let us consider the five-tuple rating case: [user, item, overall rating, aspect-1 rating, aspect-2 rating]. Be sure to notice that the interaction between the aspect-1 rating gij and the aspect-2 rating hij generates the overall rating yij, while the aspect-1 rating gij is drawn from uTiej, and the aspect-2 rating hij is drawn from uTicj. We assume the rating yij is drawn from the normal distributions with the mean $u_{i}^{T}{{e}_{j}}$ and the variance ${{\sigma }^{2}}$. The generative process of ${{g}_{ij}}$ follows: [1] Draw ${{u}_{ki}}\tilde{\ }Exp(\alpha )$; [2] Draw ${{c}_{kj}}\tilde{\ }Exp(\beta )$; [3] Draw ${{\sigma }^{2}}\tilde{\ }Inv-Gamma(a,b)$; [4] Generate ${{g}_{ij}}\tilde{\ }N(u_{i}^{T}{{e}_{j}},{{\sigma }^{2}})$.
As a result, we take into account the relationship between the overall ratings and the aspect ratings. Table 4 shows the Multi-Factorization Relationship Learning (MFRL) is a uniform three layer hierarchical framework. From top to bottom, the first layer specifies how to generate a rating triplet in terms of the overall, aspect-1 and aspect-2 utilities that the i-th user obtains from the j- th item. The second layer describes how to extract the overall, aspect-1 and aspect-2 utilities. Finally, the third layer presents all the latent factors and the variance.
Table 4
Table 4MFRL: a hierarchical view
| Overall Rating | ${{y}_{ij}}\tilde{\ }N(\mu _{ij}^{y},{{\sigma }^{2}})$ |
| Aspect-1 Rating | ${{g}_{ij}}\tilde{\ }N(\mu _{ij}^{g},{{\sigma }^{2}})$ |
| Aspect-2 Rating | ${{h}_{ij}}\tilde{\ }N(\mu _{ij}^{h},{{\sigma }^{2}})$ |
| Overall Utility | $\mu _{ij}^{y}=p\cdot u_{i}^{T}{{e}_{j}}+q\cdot u_{i}^{T}{{c}_{j}}$ |
| Aspect-1 Utility | $\mu _{ij}^{g}=u_{i}^{T}{{e}_{j}}$ |
| Aspect-2 Utility | $\mu _{ij}^{h}=u_{i}^{T}{{c}_{j}}$ |
| User Latent Factors | ${{u}_{ki}}\tilde{\ }Exp(\alpha )$ |
| Aspect-1 Latent Factors | ${{e}_{kj}}\tilde{\ }Exp(\beta )$ |
| Aspect-2 Latent Factors | ${{c}_{kj}}\tilde{\ }Exp(\beta )$ |
| Variance | ${{\sigma }^{2}}\tilde{\ }Inv-Gamma(a,b)$ |
新窗口打开|下载CSV
3.4 Parameter Estimation in MFRL
We denote all the parameters by $\Theta =\{U,E,C,{{\sigma }^{2}}\}$, the observed dataset by $D=\{Y,G,H\}$, and the hyper-parameters by $\Psi =\{\alpha ,\beta ,a,b,p,q\}$. Given $D$ and $\Psi $, our goal is to find the parameters $\Theta $ that maximize the posterior probability $P(\Theta |D,\Psi )$.According to Table 4, G, H, Y are generated by:
Where Δ1 is the posterior of overall rating generated by User i and Item j.
What’s more, we draw the elements in U, E, C from exponential distributions:
In addition, we draw the variance ${{\sigma }^{2}}$ from Inv-Gamma distribution:
Eventually we get the log of posterior for the MFRL model by Eq. 7. For simplicity, let ${{\delta }_{1}}=\sum\nolimits_{k'\ne k}^{K}{{{u}_{ki}}}\cdot {{e}_{kj}}$ and ${{\delta }_{2}}=\sum\nolimits_{k'\ne k}^{K}{{{u}_{ki}}}\cdot {{c}_{kj}}$, We apply Iterated Conditional Modes (ICM)[11] method and obtain the updating rules for the parameters in $\Theta $by Eq. 8
3.5 Incorporating Group Heterogeneity
To incorporate the group heterogeneity in the modeling of multi-aspect rating behavior, we combine group-wise mixture regression into the Multi-Factorization Relationship Learning (MFRL) and develop the framework of Mix-MFRL.Considering a rating triple: [user, item, overall rating]. With the Multi-Factorization Relationship Learning (MFRL), we use the obtained user latent features ui to represent the i-th user. We use the obtained item latent aspect features ej, cj to represent the aspect-1 and aspect-2 of the j-th item. We assume there are N rating groups for the rating pairs (yij, [ui, ej, cj]). For the n-th rating group, we use a regression method to model the correlation between yij and [uTi, eTi, cTi]. Table 5 shows the overall rating predictions that are based on group-wise mixture regressions.
Table 5
Table 5The generative process of Mix-MTMF
| 1. | Generate latent factors Generate ${{u}_{i}}$, ${{e}_{j}}$, ${{c}_{j}}$ from MFRL |
| 2. | Generate distributions for each group a. Draw ${{\lambda }_{n}}$, $\sigma _{n}^{2}$ for each group b. Draw ${{f}_{n}}(x)\tilde{\ }N([u_{i}^{T},e_{j}^{T},c_{j}^{T}]\cdot {{\lambda }_{n}},\sigma _{n}^{2}$ |
| 3. | Generate overall rating b. Generate weight in the mixture model c. Generate ${{y}_{ij}}\tilde{\ }\sum\nolimits_{n=1}^{N}{{{\alpha }_{n}}N([u_{i}^{T},e_{j}^{T},c_{j}^{T}]\cdot {{\lambda }_{n}},\sigma _{n}^{2})}$ |
新窗口打开|下载CSV
3.6 Parameter Estimation of Mix-MFRL
We denote all the parameters by $\Lambda =\{{{\alpha }_{n}},{{\lambda }_{n}},\sigma _{n}^{2},|n\in [1,N]\}$, the concatenation of latent vectors $V=\{{{v}_{ij}}=[{{u}_{i}},{{e}_{j}},{{c}_{j}}]|i\in [1,I],j\in [1,J]$ and the rating pairs $R=\{{{r}_{ij}}=({{y}_{ij}},{{v}_{ij}})|i\in [1,I],j\in [1,J]$. Given $R$, our goal is to find the parameters $\Lambda $ that maximize the likelihood probability $P(R|\Lambda )$. According to Table 5:We apply Expectation Maximization (EM)[12] algorithm to optimize Equation 9. Specifically, we introduce latent variables $Z=\{{{z}_{ij}}=[1,N]|i\in [1,I],j\in [1,J]$, where each zij indicates which group the rating pair rij belongs to. In the (g+1)-th iteration, we first get the expectation of likelihood in E-step based on the parameters derived from g-th iteration and then obtain the (g+1)-th optimized parameters through the maximization of expectation of likelihood in M-step.
In E-step of (g+1)-th iteration, the expectation of likelihood:
where,
We conduct the integration operation and then obtain:
In M-step, we maximize the expectation of likelihood over $\Lambda $ and obtain the (g+1)-th optimized parameters:
Where ${{\mu }_{n}}={{v}_{ij}}{{\lambda }_{n}}$ for every ${{v}_{ij}}$ in group $n$, ${{\lambda }_{[n,s]}}$ denotes the s-th element of ${{\lambda }_{n}}$, and ${{v}_{[ij,s]}}$ denotes the s-th component of ${{v}_{ij}}$.
4 EXPERIMENTAL RESULTS
We evaluate the proposed model with real-world data in terms of various tasks.4.1. Data Description
We crawled the experiment dataset from the website of ‘TripAdvisor.com’ which provides hotel and restaurant reviews and ratings. The dataset comprises 191 192 ratings from 132 215 users for 1 800 hotels. The rating values range from 1 to 5, where 1 indicates that the user does not like the hotel, and 5 denotes a high preference. In this dataset, the number of users who rate more than 1, 2, 3 times are 17 904, 4 911 and 1 787 respectively, which means most users only rate onc and thus the dataset is very sparse. In addition, besides the overall rating, there are six aspect ratings: value, rooms, location, cleanliness, sleep quality and service. We select two of them, i.e., cleanliness rating and location rating by Chi-Square feature selection[13].4.2 Evaluation Metrics
Prediction Accuracy: We will evaluate the model with Mean Absolute Error (MAE) and Root Mean Square Error (RMSE) defined as follows:Where yij denotes the observed overall rating and ${{\hat{y}}_{ij}}$ denotes the predicted overall rating. The smaller the value of MAE and MSE, the more accurate the modeling.
Top-M Recommendation: We also evaluate the algorithms in terms of ranking performance. We provide each user with two groups of M hotels sorted by their predicted overall ratings and observed overall ratings respectively. And then we evaluate the ranking accuracy based on Normalized Discounted Cumulative Gain (NDCG). The Discounted Cumulative Gain (DCG@M) metric assumes that highly rated hotel should appear earlier in the recommendation list of the length M. The DCG@M from predicted ratings can be represented as:
Also, the Ideal Discounted Cumulative Gain (IDCG) from observed ratings can be represented as:
Then, NDCG@M can be formulated as $NDCGM=\frac{DCGM}{IDCGM}$.
4.3 Baseline Algorithms
Since our work is related to Matrix Factorization (MF) and clustering, we compared our method with the following algorithms. (1) Probabilistic Matrix Factorization (PMF)[9]: factorizes overall rating matrix. (2) Bayesian Co-Nonnegative Matrix Factorization (BCoNMF)[14]: co-factorizes overall matrix with the aspect rating matrix. (3) Multi-task Learning (MTL)[15]:factorizes overall rating matrix and the aspect rating matrix independently and optimize them simultaneously. (4) Hierarchical Model (HM)[16]: firstly clusters latent vectors, and then learns the model of each cluster independently, at last combine each cluster model together.4.4 Study of Latent Group Number
At first stage, we try to figure out the most appropriate number of latent group in Mix-MFRL, thus we explore the performance of Mix-MFRL with latent group number N = 1, 2, ..., 10 respectively. Since we also need the hyper-parameter K in the experiment, which denotes the latent dimension in matrix factorization, we compare the performances of Mix-MFRL with different latent dimension K (K = 2, 5, 10, 20 respectively) for each N.As we can see from Figure 4, 5, 6, 7, for all evaluation metrics, with N increasing from 1 to 6, the performances improve monotonously, while with N increasing continuously, the performances drop gradually. We then infer that N = 6 is the best latent group number for our dataset. In the following experiment, we will fix N = 6.
Fig.4
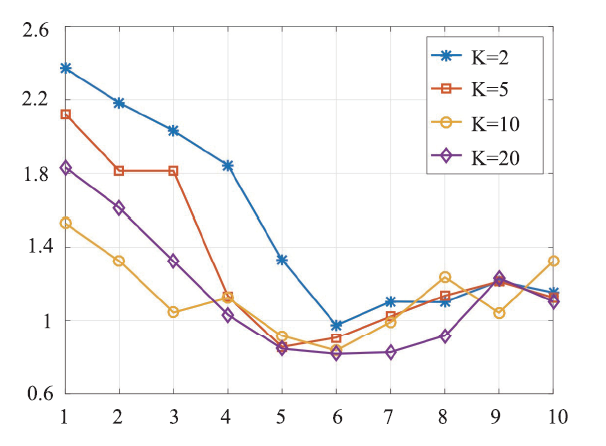新窗口打开|下载原图ZIP|生成PPTFig.4MAE performances of Mix-MFRL at different latent group numbers
Fig.5
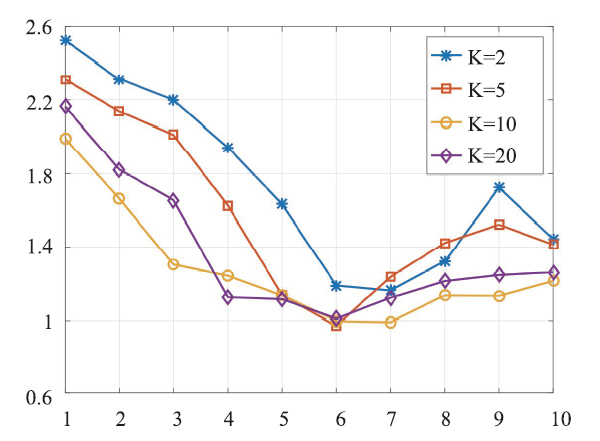新窗口打开|下载原图ZIP|生成PPTFig.5RMSE performances of Mix-MFRL at different latent group numbers
Fig.6
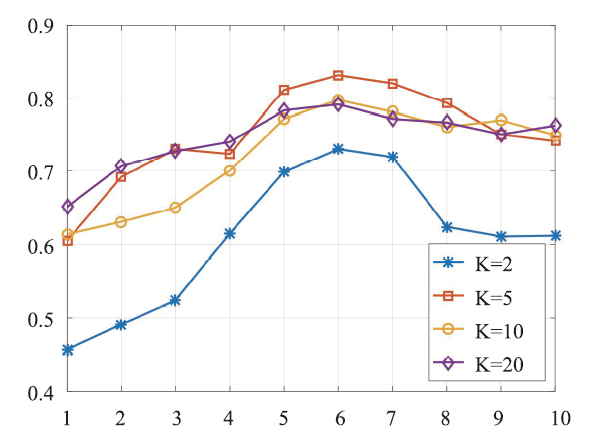新窗口打开|下载原图ZIP|生成PPTFig.6NDCG_3 performances of Mix-MFRL at different latent group numbers
Fig.7
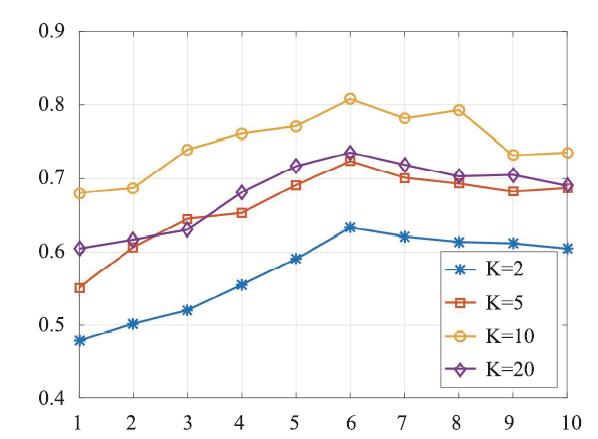新窗口打开|下载原图ZIP|生成PPTFig.7NDCG_5 performances of Mix-MFRL at different latent group numbers
4.5 Overall Performances
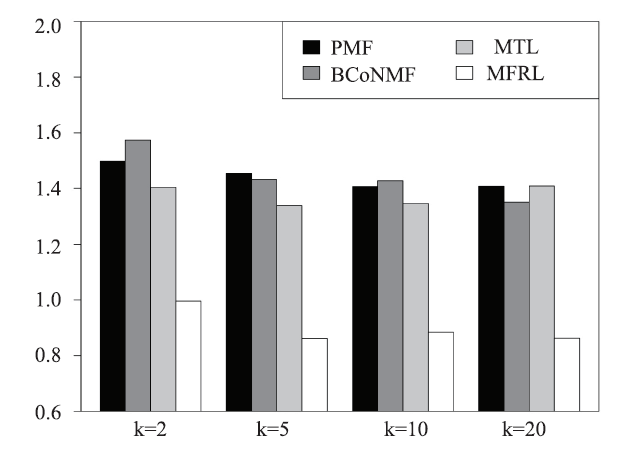
Here, we present the performance comparison on overall rating in terms of accuracy and top-M recommendation.Prediction Accuracy. We compare our method with baseline methods in terms of MAE and RMSE, with latent dimensions K = 2, 5, 10, 20 respectively. The MAE comparisons are shown in Figure 8. Overall, MFRL outperforms baselines with significant margins and Mix-MFRL further improves the performance of MFRL. In addition, in all the baselines, BCoNMF and MTL work slightly better than PMF and HM in all K value settings. Figure 9 shows the RMSE comparisons: MFRL outperforms all the competing models and Mix-MFRL improves MFRL.
Fig.8
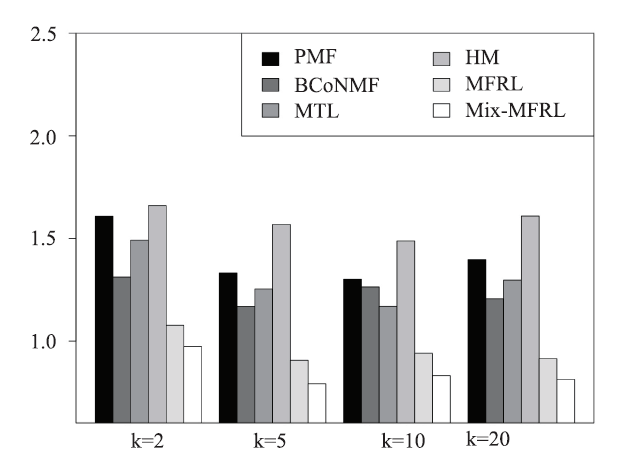新窗口打开|下载原图ZIP|生成PPTFig.8The MAE values at different latent dimensions
Fig.9
新窗口打开|下载原图ZIP|生成PPTFig.9The RMSE values at different latent dimensions
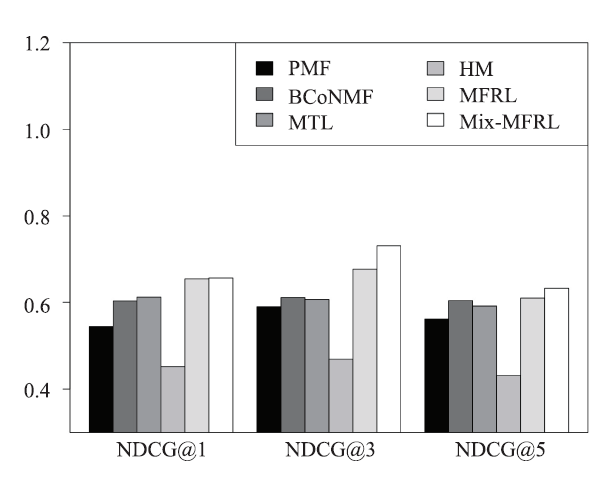
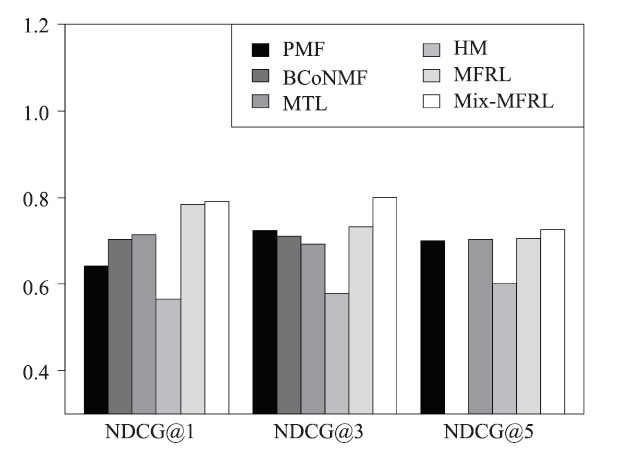
Top-M Recommendation. Figure 10, 11, 12, 13 show the top-M recommendation performances of MFRL and Mix-MFRL with four baselines in terms of NDCG@M (M = 1, 3, 5 respectively). In the experiment, we choose those who rate more than M hotels. Then, we apply all the six methods to recommend an M-length hotel list to those users and calculate the NDCG@M of the Top-M recommendation against its ground truth. We can see from Figure 10-13 that MFRL and Mix-MFRL still achieve the best results with list length M = 1, 3, 5 and latent dimension K = 2, 5, 10, 20.
Fig.10
新窗口打开|下载原图ZIP|生成PPTFig.10NDCG at different latent dimensions 2
Fig.11
新窗口打开|下载原图ZIP|生成PPTFig.11NDCG at different latent dimensions 5
Fig.12
新窗口打开|下载原图ZIP|生成PPTFig.12NDCG at different latent dimensions 10
Fig.13
新窗口打开|下载原图ZIP|生成PPTFig.13NDCG at different latent dimensions 20
4.6 Study of Aspect Rating Prediction
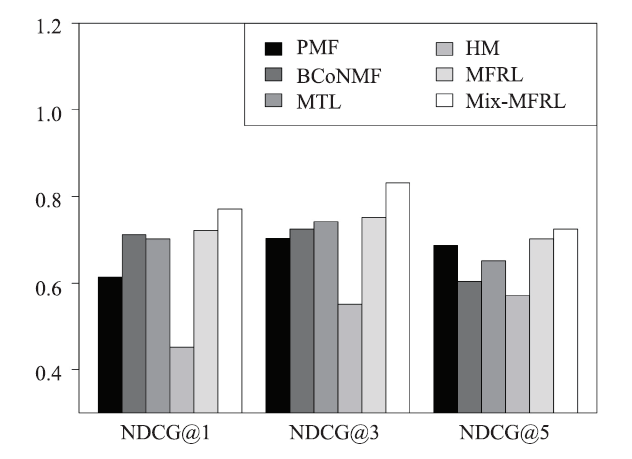
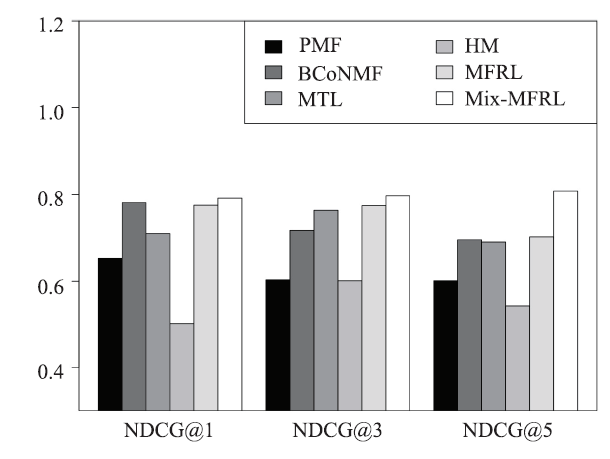
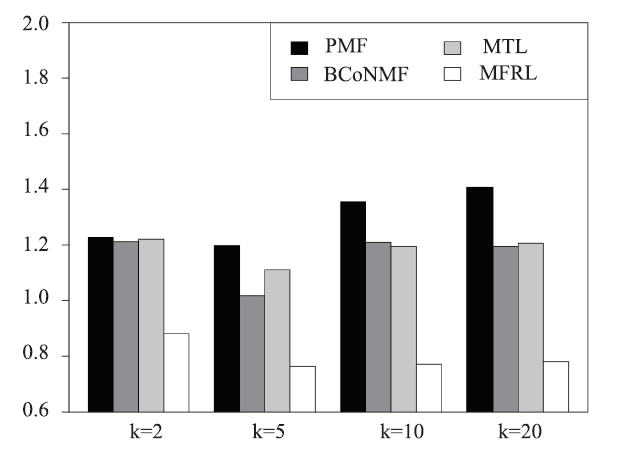
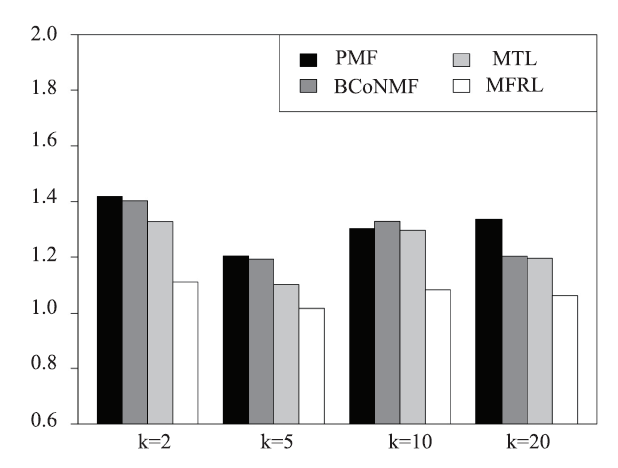
Besides overall ratings, we evaluate the prediction accuracy of location ratings and cleanliness ratings and check if the proposed model can correctly capture the aspect ratings. There are no latent groups in the prediction of aspect ratings, thus there is no need for clustering. Without clustering, Mix-MFRL degenerates to MFRL and HM is no longer qualified as a baseline. We then compare PMF, BCoNMF, MTL and MFRL in the prediction of aspect ratings. Figure 14 and Figure 15 report the MAEs and RMSEs of location rating prediction of MFRL comparing with other three baselines, where we can see significant advantage of MFRL over baselines. Similarly, in the MAEs and RMSEs of cleanliness ratings, RMFL is better than baselines with significant margins as shown in Figure 16 and Figure 17. The consistent high accuracy in both location and cleanliness ratings proves the correctness of jointly factorizing the overall and aspect ratings.Fig.14
新窗口打开|下载原图ZIP|生成PPTFig.14MAE of location rating
Fig.15
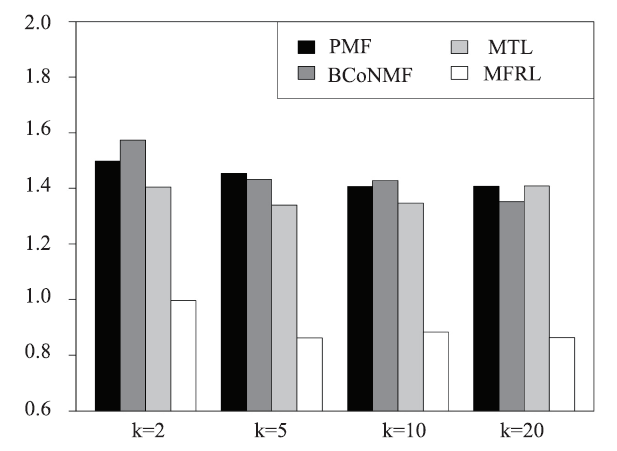新窗口打开|下载原图ZIP|生成PPTFig.15RMSE of location rating
Fig.16
新窗口打开|下载原图ZIP|生成PPTFig.16MAE of cleanliness rating
Fig.17
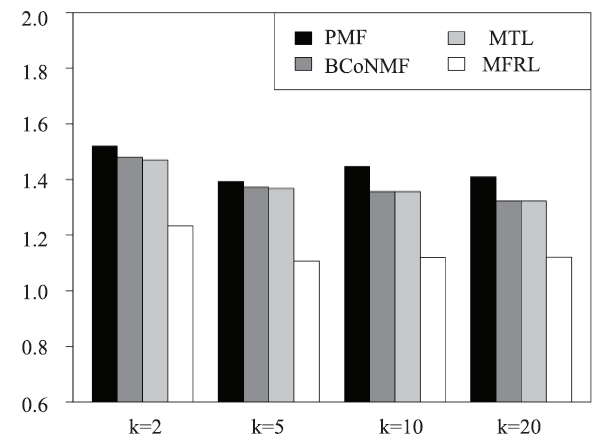新窗口打开|下载原图ZIP|生成PPTFig.17RMSE of cleanliness rating
4.7 Robustness Check
We fix N = 6 to carry out the robustness check of proposed models with K = 5 and K = 20 respectively. We use 5-fold cross validation, where we partition the entire dataset into 5 complementary subsets. The cross validation of dataset consists 5 rounds, each of which involves training the model on 4 subsets and validating the performance on the remaining subset. From Table 6, we can see both MFRL and Mix-MFRL perform steady without significant fluctuations in different rounds. In Table 6, we denote round cross validation as Ri (i=1,2,3,4,5).Table 6
Table 6Performance of MFRL and Mix-MFRL in 5-fold cross validation
| Methods | K=5 | K=20 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | NDCG@1 | NDCG@3 | NDCG@5 | MAE | RMSE | NDCG@1 | NDCG@3 | NDCG@5 | ||
| MFRL(R1) | 0.907 | 1.100 | 0.721 | 0.751 | 0.702 | 0.915 | 1.117 | 0.784 | 0.732 | 0.705 | |
| MFRL(R2) | 0.912 | 1.073 | 0.706 | 0.784 | 0.697 | 0.881 | 1.251 | 0.799 | 0.738 | 0.711 | |
| MFRL(R3) | 0.903 | 1.106 | 0.732 | 0.770 | 0.707 | 0.914 | 1.228 | 0.807 | 0.727 | 0.691 | |
| MFRL(R4) | 0.915 | 1.119 | 0.710 | 0.783 | 0.716 | 0.901 | 1.255 | 0.791 | 0.742 | 0.709 | |
| MFRL(R5) | 0.912 | 1.092 | 0.714 | 0.762 | 0.710 | 0.925 | 1.239 | 0.810 | 0.715 | 0.699 | |
| Mix-MFRL(R1) | 0.792 | 0.970 | 0.771 | 0.831 | 0.724 | 0.813 | 1.009 | 0.791 | 0.801 | 0.726 | |
| Mix-MFRL(R2) | 0.813 | 0.995 | 0.769 | 0.812 | 0.742 | 0.837 | 1.052 | 0.779 | 0.809 | 0.744 | |
| Mix-MFRL(R3) | 0.782 | 0.930 | 0.757 | 0.794 | 0.734 | 0.797 | 0.819 | 0.787 | 0.813 | 0.709 | |
| Mix-MFRL(R4) | 0.801 | 1.014 | 0.780 | 0.805 | 0.781 | 0.781 | 1.280 | 0.799 | 0.786 | 0.727 | |
| Mix-MFRL(R5) | 0.810 | 0.978 | 0.746 | 0.830 | 0.762 | 0.774 | 1.212 | 0.781 | 0.791 | 0.736 | |
新窗口打开|下载CSV
5 RELATED WORK
Related work can be grouped into (i) recommen-dations in multi-aspect rating systems, (ii) multi-task learning and relational regularization, (iii) collective factorization and finite mixture models, and (iv) user heterogeneity in economics.Modeling Multi-Aspect Rating Data. Our work is related to the studies of modeling multi-aspect rating data. For example, Lee et al.[17] reduced the problem to a multiple criteria ranking task and applied an adapted skyline query algorithm. Adomavicius et al.[18] extended the single criteria CF to include multi-criteria ratings in the calculation of the similarity between users or items by applying average similarity or worst-case similarity schema. Also, Adomavicius et al. proposed to use standard CF to predict single criteria rating, then a weighted linear regression function was applied to aggregate multiple criteria ratings to a global rating[19]. Singh et al. proposed to view rating matrix as a pairwise relationship between two participants and simultaneously factorized multiple rating matrices into latent space[10]. Singh et al. formulated the generic problem of collective factorization, but only provided the model inference for co-factorizing two rating matrices U×V→R1,V×I→×R2. Baas et al. proposed a framework to deal with multiple-alternative decision problems under the assumption that all the alternatives in the choice set could be characterized by a number of aspects and that information was available to assign weights to these aspects and to construct a rating scheme for the various aspects of each alternative[4]. Liu et al. proposed a destination prediction framework via multi-view spatiotemporal data [39]. Zhu et al. proposed an aspect-based segmentation algorithm to first segment a user review into multiple single-aspect textual parts, and an aspect-augmentation approach to generate the aspect-specific feature vector of each aspect for aspect-based rating inference[3].
Multi-task learning with task-relation regulari-zation. The framework of this paper is inspired by the idea of multi-task learning. Argyriou et al. presented a method for learning a low-dimensional representation which was shared across a set of multiple related tasks[20]. Jalali et al. considered the multiple linear regression problem in a setting where some of the set of relevant features could be shared across the tasks[21]. Lounici et al. studied the problem of estimating multiple linear regression equations for both prediction and variable selection[22]. Liu et al. proposed two frameworks to capture the relationship between different agents in the learning process [40,41]. Zhou et al. proposed a multi-task learning formulation for predicting the disease progression measured by the cognitive scores and selecting markers predictive of the progression [23]. Kumar et al. proposed a framework for multi-task learning that enabled one to selectively share the information across the tasks[24]. Evgeniou modeled the relation between tasks in terms of a novel kernel function that used a task-coupling parameter[25]. Liu et al. proposed to accelerate the computation by reformulating the optimization problem as two equivalent smooth convex optimization problems which were then solved via the Nesterov’s method[26]. Zhang et al. proposed a regularization formulation for learning the relationships between tasks in multi-task learning[27]. Xue et al. developed computationally efficient algorithms for two different forms of the multi-task learning problem relying on a Dirichlet process based model to learn the extent of similarity between classification tasks[28].
Finite Mixture Models. Moreover, our work also has a connection with finite mixture models. Figueiredo proposed an unsupervised algorithm for learning a finite mixture model from multivariate data which seamlessly integrated estimation and model selection in a single algorithm[29]. Zivkovic et al. proposed a recursive algorithm that estimated the parameters of the mixture and that simultaneously selected the number of components[30]. Chen proposed a modified likelihood ratio test for homogeneity in finite mixture models with a general parametric kernel distribution family[31]. Bapna et al. simultaneously classified firms into homogeneous segments based on firm-specific characteristics and estimated the model’s coefficients relating predictor variables to electronic payments systems adoption decisions for each respective segment[32]. MuthÃľn et al. discussed the analysis of an extended finite mixture model where the latent classes corresponding to the mixture components for one set of observed variables influenced the second set of observed variables[33]. Yu et al. proposed a multi-mode process monitoring approach based on finite Gaussian mixture model and Bayesian inference strategy[34].
User Heterogeneity. User Heterogeneity is a nontrivial factor in the proposed CMRL model, which is also a big topic in economics and market. Teratanavat et al. presented a research technique exploring differences in consumer preferences and valuations for a novel functional food products[35]. Cicia et al. investigated the preferences of an important category of consumers of organic products allowing for preference heterogeneity[36]. Dhar et al. found out that the decision to defer choice was influenced by the absolute difference in attractiveness among the alternatives provided and was not consistent with trade-off difficulty or the theory of search[37]. Kamakura et al. developed a choice model that simultaneously identified consumer segments on the basis of their preferences, response to the marketing mix, and choice processes[38]. Breffle et al. investigated several different parametric methods to incorporate heterogeneity in the context of a repeated discrete-choice model [42]. Cutler et al. presented empirical evidence in five difference insurance markets in the United States that was consistent with this potential role for risk tolerance. Poulsen et al. presented a new model that combined latent class regression analysis with random coefficient regression models together with principal components regression [43].
6 CONCLUSION REMARKS
User heterogeneity is widely observed in users’ rating behavior. In this study, we identified the rating pattern heterogeneity after learning the latent features of users and items. We find that it is essential to jointly model the generative process of rating as well as the rating pattern heterogeneity for understanding users’ multi-aspect rating behavior. Along this line, we first developed a multi-factorization relationship learning method to model the generative process in multi-aspect rating. Later, we developed an extended method by integrating group-wise mixture regression method to model the effects of rating pattern heterogeneity. Finally, we presented extensive experiments on the real-world multi-aspect rating data of TripAdvisor.com to demonstrate the effectiveness of the proposed methods.参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[C].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 2]
[J].
[本文引用: 2]
[C].
[本文引用: 1]
[C].
[本文引用: 2]
[J].
[本文引用: 2]
[C].
[本文引用: 1]
[J].
[本文引用: 3]
[C].
[本文引用: 2]
[C].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[C].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[C].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[C].
[本文引用: 1]
[J].
[本文引用: 1]
[C].
[本文引用: 1]
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[C].
[本文引用: 1]
[C].
[本文引用: 1]
[C].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
