删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

Heat transfer analysis of MHD rotating flow of FeO nanoparticles through a stretchable surface

本站小编 Free考研考试/2022-01-02
Faisal Shahzad1, Wasim Jamshed1, Tanveer Sajid1, Kottakkaran Sooppy Nisar2, Mohamed R Eid,3,4,∗1Department of Mathematics, Capital University of Science and Technology (CUST), Islamabad, 44000, Pakistan
2Department of Mathematics, College of Arts and Sciences, Prince Sattam bin Abdulaziz University, Wadi Aldawaser, Saudi Arabia
3Department of Mathematics, Faculty of Science, New Valley University, Al-Kharga, Al-Wadi Al-Gadid, 72511 Egypt
4Department of Mathematics, Faculty of Science, Northern Border University, Arar, 1321, Saudi Arabia

First author contact: Author to whom any correspondence should be addressed.
Received:2021-02-12Revised:2021-04-12Accepted:2021-04-16Online:2021-06-01


Abstract
The flow of a magnetite-H2O nanofluid has been considered among two rotating surfaces, assuming porosity in the upper plate. Furthermore, the lower surface is considered to move with variable speed to induce the forced convection. Centripetal as well as Coriolis forces impacting on the rotating fluid are likewise taken into account. Adequate conversions are employed for the transformation of the governing partial-differential equations into a group of non-dimensional ordinary-differential formulas. Numerical solution of the converted expressions is gained by means of the shooting technique. It is theoretically found that the nanofluid has less skin friction and advanced heat transport rate when compared with the base fluid. The effect of rotation causes the drag force to elevate and reduces the heat transport rate. Streamlines are portrayed to reveal the impact of injection/suction.
Keywords： rotating frame;magnetite-water;nanofluid flow;magnetic field;stretching sheet


PDF (2783KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Faisal Shahzad, Wasim Jamshed, Tanveer Sajid, Kottakkaran Sooppy Nisar, Mohamed R Eid. Heat transfer analysis of MHD rotating flow of Fe3O4 nanoparticles through a stretchable surface. Communications in Theoretical Physics, 2021, 73(7): 075004- doi:10.1088/1572-9494/abf8a1

Nomenclature

Nomenclature $(x,y,z)$ Cartesian coordinate system
$m$shape factor
${c}_{p}$ specific heat
${\boldsymbol{V}}$flow field
$T$ fluid temperature
Subscripts
${T}_{0}$lower temperature at upper wall
$f$fluid phase
${T}_{h}$higher temperature at lower wall
$s$ solid phase
$u,v,w$ velocity components
$N$ nanofluid
$k$ thermal conductivity
Greek symbols
${U}_{w}$ velocity of stretching sheet
$\rho $density
$N{u}_{x}$local Nusselt number
$\mu $dynamic viscosity
$p$pressure
$\nu $kinematic viscosity
${q}_{w}$wall heat flux
$\alpha $thermal diffusivity
$Pr$Prandtl number
$\sigma $electrical conductivity
${C}_{f}$ skin friction coefficient
${\rm{\Omega }}$ angular velocity
$a$ stretching rate
$\eta $ similarity variable
${B}_{0}$ uniform magnetic field
$\theta $ dimensionless temperature
$f^{\prime} ,g$ dimensionless velocity along $x,y$ direction
$\phi $ nanoparticle volume fraction


1. Introduction

Rotating flow and heat transportation problems have importance in a vast range of geophysical as well as engineering applications. The rotating flow has greater utilization [1] in chemical reactors, rotating machinery, magnetohydrodynamic (MHD) pumps, petroleum refineries, biochemical problems, lubrication and refrigeration systems etc. Wang [2] has analyzed rotating flow over an elongated sheet. Nazar et al [3] studied time-dependent rotating flow via a stretching sheet. Rosali et al [4] interrogated the boundary-layer rotating flow result in a shrinking surface by considering the suction effect. Sulochana et al [5] considered the radiative, viscous dissipative flow and chemical reaction influences on flow past a rotating sheet. Seth et al [6] examinated the boundary-layer flowing of rotating nanofluid with entropy generation results in an expandable plate. Gireesha et al [7] probed the impact of nonlinear thermal radiation on time-dependent rotating fluid flow of nanotubes using the shooting method technique.

In recent times, there have been many publications about nanotechnology in the area of science by a huge number of researchers, attributable to its larger thermal conductance. The outlook of nanofluid has been initially introduced by Choi [8]. Nanofluid is an amalgamation of nanometer-sized (10−9 to 10−11 nm) solid nanoparticles with conventional liquid. The metallic very small particles utilized in nanofluid are prepared from metals (e.g. Ti, Ag, Cu), non-metals (e.g. carbon nanotubes) and oxides (e.g. TiO2,Al2O3). Buongiorno [9] has studied convective heat transport augmentation using nanofluid. Nanoliquids were found to obtain suitable thermophysical characteristics, such as thermal conductivity and thermal diffusivity, together with viscosity [10–13]. The effect of metallic oxide sub-microns on the flux and heat transfer has been studied by Pak and Cho [14]. They found that the heat rate for the dispersed fluids was enhanced with raising the concentration of nanoparticles and Reynolds number. Zaraki et al [15] assessed the influence on convective border layer flow and heat transfer of nanofluid on the size, shape and form of metallic components. The effect of various types on the normal convection of ${{\rm{SiO}}}_{2}$-water nanofluid in the trapezoidal cavity has been studied by Selimefendigil [16]. Nayak et al [17] reviewed the mixed convective flow of a nanoliquid inside a skewed enclosure. They investigated the influences of Brownian diffusivity and thermophoretic diffusion on the mixed convective flow of a nanoliquid. Ashorynejad et al [18] deliberated on the nanofluid flow through a wavy U-turn channel. They concluded that the thermal-hydraulic functionality factor improves by boosting the volume fraction of nanoparticles. Jeong et al [19] experimentally scrutinized the impact of particle shape on the thermal conductance besides the viscosity of the nanofluid flow. They noticed that the rectangular shape nanoparticle viscosity is enhanced as compared to that of the spherical nanoparticles. Timofeeva et al [20] experimentally revealed that the nanoparticle shape played a significant role in the rise in the thermal conductance of the base fluid. They also revealed, in contrast to other types, that the blades have a greater thermal conductivity.

The investigation of nanofluids with the impacts of MHD has substantial applications in areas of metallurgy, as well as engineering development. In recent years, the cooling aspects of the heat transport equipment have been restricted, resulting in the lowered thermal conductance of traditional coolants such as H2O, ethylene glycol and oil. Metals possess greater thermal conductivity than fluids. An electrical conductivity nanofluid with the influence of the magnetic parameter known as the ferrofluid is very helpful in lots of applications. Ferrofluid consists of nanoparticles dependent on iron, such as magnetite, cobalt ferrite, hematite, etc. This kind of iron-based nanoparticle works extremely well in proficient drug transportation, by controlling the particles by means of external magnets [21, 22]. Magnetofluids are of distinctive use in magnetic cell separation, ecological remediation, malignant tumor treatment (chemotherapy and radiotherapy), magnetic resonance imaging, and magnetic particle imaging. Sheikholeslami et al [23] inspected the combined impacts of MHD and ferrohydrodynamics on the heat transport flow of ferrofluid confined in a semi annulus box with a sinusoidal warm surface. They argued that the amount of Nusselt increases both with the Rayleigh count and with a strong volume fraction. Li et al [24] addressed the impact on heat transport and ferronanofluid flow due to a magnetic field of Lorentz force and anisotropical heat conductivity. They found that with the use of MHD, vortices in the wake area are suppressed, so the flow becomes more stable. Jue [25] evaluated the influences of thermal buoyancy and magneto gradient on ferrofluid flowing inside a cavity using a numerical method. Salehpour et al [26] experimentally discussed the impacts of the alternating as well as constant magnetic fields on the MHD ferrofluid flow within a rectangle-shaped permeable channel. In light of the results of the Cattaneo-Christov heat flow model, Ali and Sandeep [27] examinated Magneto Casson heat transport of ferrofluid. Karimipour et al [28] analyzed the heat transfer flowing of MHD nanoliquid with slip velocities and temperature differences in the presence of diverse nanoparticles. The effect of quadrupole electromagnetic effect on heat transport of Mn-Zn ferrite-H2O ferrofluid flow in a circular pipe has been examined by Bahiraei et al [29]. Flow of nanofluid and heat transport with to the magnetic effect can also be initiated in [30–34].

Stretching/extending sheet flow problems are important in a vast variety of production, metallurgical and manufacturing processes. These contain polymer sheets, spinning of fibers, food processing, film coating, glass wasting, drawing of Cu wires, and so on. Sakiadis [35] found the analytical solution for a flow of boundary-layer via a continuous solid sheet. Tsou et al [36] presented the analytical and experimental analysis of heat transportation boundary layer flow past an expanding wall. Dutta [37] examined the impact of injection (suction) on heat transfer due to a movement unremitting flat sheet. The impacts of viscous and ohmic dissipations on MHD viscoelastic fluid flowing and heat transport is discussed by Abel et al [38]. Vajravelu [39] performed a study to explore the influences of thermophysical features on the flowing and heat transportation in a thin film of a Ostwald-de Waele fluid via an extending wall with viscous dissipative flow. In recent times, several articles [40–43] have been produced on the heat transport of boundary-layer nanofluid flow near an elongated surface. Notably, the consideration of nanofluid movement within a channel under the lower surface expanding into flow has not been emphasized so much. The effect of magnetic field on thermal flow in a revolving device has been seen by Borkakoti and Bharali [44]. Freidoonimehr et al [45] investigated the effects of different nanoparticles on fluid flow and heat transport in a rotating frame. Hussain et al [46] worked on the heat transportation and fluid flowing amongst parallel surfaces with carbon nanotubes. They also established that nanoparticles greatly affect skin friction and heat transfer rate. Rasool et al [47] scrutinized the effect of second-grade nanoflow over the Riga plate. They expressed that the opposite flow reduced the wall drag due to Lorentz force, and that a binary chemical reaction enriches the concentration of the nano suspension. Recent additions considering nanofluids with heat and mass transfer in various physical situations are given by [48–59].

The theme of the current article is to explore the impacts of Fe3O4 nanoparticles on the heat transport flow of H2O-based nanoliquid in a rotating frame, considering the influence of the magnetic field by using the Tiwari and Das model [60]. In this model (single-phase model) the fluid, velocity and temperature are taken as the same. The advantage of the single-phase model is that we ignore the slip mechanisms, so the model is a simplified one and is easy to solve numerically. However, the disadvantage of this method is that in some cases the numerical results differ from those obtained by experiments. In this model, the volume concentration of nanoparticles ranges between 3% and 20%. Numerical solutions by shooting procedure are applied to the governing scheme of nonlinear ordinary differential equations. Emphasis is given to the effect of embedded flow factors on the velocities and temperature outlines. The flow, along with thermal fields, are discussed by plotting graphs. Additionally, the graphs of surface drag force coefficient and heat transport rate (local number of Nusselt) are plotted to evaluate the coefficient of skin friction and the rate of heat exchange for the volume fraction of nanoparticles, together with other relevant parameters.

2. Problem formulation

Let us contemplate a steady MHD rotating flow of H2O-based Fe3O4 nanofluids between two plates having angular swiftness ${\boldsymbol{\Omega }}$ $[0,{\rm{\Omega }},0].$ The lower surface is stretched in the x-direction having the velocity ${U}_{w}=ax\left(a\gt 0\right)$ and the higher surface is permeable. The steady flow field is represented by ${\boldsymbol{V}}$ $\left[u,v,w\right],$ wherein $u,v,w$ are the swiftness components alongside the x, y and z orientations accordingly. A unvarying magneto impact of strength ${B}_{0}$ is worked parallel to the y-axis. Using the presumption of tiny magnetic Reynolds, the caused magneto field effect is unchecked. The physical configuration of flowing is specified in figure 1.

Figure 1.

New window|Download| PPT slide
Figure 1.Geometry of the problem.


In case of the rotating flow, the conservative momentum equation is given as [61]$\begin{eqnarray}{\rho }_{N}\left(\displaystyle \frac{{\rm{d}}{\boldsymbol{V}}}{{\rm{d}}t}+2{\boldsymbol{\Omega }}\times {\boldsymbol{V}}+{\boldsymbol{\Omega }}\times \left({\boldsymbol{\Omega }}\times r\right)\right)={\rm{div}}{\boldsymbol{T}}+{\boldsymbol{J}}\times {\boldsymbol{B}}.\end{eqnarray}$The governing PDEs in the component form are as follows:$\begin{eqnarray}\displaystyle \frac{\partial u}{\partial x}+\displaystyle \frac{\partial v}{\partial y}=0,\end{eqnarray}$$\begin{eqnarray}\begin{array}{l}{\rho }_{N}\left(u\displaystyle \frac{\partial u}{\partial x}+v\displaystyle \frac{\partial u}{\partial y}+2{\rm{\Omega }}w\right)=-\displaystyle \frac{\partial p* }{\partial x}\\ \,+\,{\mu }_{N}\left(\displaystyle \frac{{\partial }^{2}u}{\partial {x}^{2}}+\displaystyle \frac{{\partial }^{2}u}{\partial {y}^{2}}\right)-{\sigma }_{N}{B}_{0}^{2}u,\end{array}\end{eqnarray}$$\begin{eqnarray}{\rho }_{N}\left(u\displaystyle \frac{\partial v}{\partial x}+v\displaystyle \frac{\partial v}{\partial y}\right)=-\displaystyle \frac{\partial p* }{\partial y}+{\mu }_{N}\left(\displaystyle \frac{{\partial }^{2}v}{\partial {x}^{2}}+\displaystyle \frac{{\partial }^{2}v}{\partial {y}^{2}}\right),\end{eqnarray}$$\begin{eqnarray}{\rho }_{N}\left(u\displaystyle \frac{\partial w}{\partial x}+v\displaystyle \frac{\partial w}{\partial y}-2{\rm{\Omega }}u\right)={\mu }_{N}\left(\displaystyle \frac{{\partial }^{2}w}{\partial {x}^{2}}+\displaystyle \frac{{\partial }^{2}w}{\partial {y}^{2}}\right)-{\sigma }_{N}{B}_{0}^{2}w,\end{eqnarray}$in which $p* \,=\,p-\tfrac{{{\rm{\Omega }}}^{2}{x}^{2}}{2}$ is the modified pressure. The governing energy equation for this problem is given by$\begin{eqnarray}u\displaystyle \frac{\partial T}{\partial x}+v\displaystyle \frac{\partial T}{\partial y}={\alpha }_{N}\left(\displaystyle \frac{{\partial }^{2}T}{\partial {x}^{2}}+\displaystyle \frac{{\partial }^{2}T}{\partial {y}^{2}}\right),\end{eqnarray}$in which ${\alpha }_{N}=\tfrac{{k}_{N}}{{\left(\rho {c}_{p}\right)}_{N}}$ is the impactive thermal diffusivity of the nanoliquid.

Nanofluid active density [60] is described as$\begin{eqnarray}{\rho }_{N}=\left(1-\phi \right){\rho }_{f}+\phi {\rho }_{s}.\end{eqnarray}$The operative heat capacity ${\left(\rho {c}_{p}\right)}_{N}$ and dynamic viscosity ${\mu }_{N}$ of the nanoliquid [62] are defined as$\begin{eqnarray}{\left(\rho {c}_{p}\right)}_{N}=\left(1-\phi \right){\left(\rho {c}_{p}\right)}_{f}+\phi {\left(\rho {c}_{p}\right)}_{s},{\mu }_{N}=\displaystyle \frac{{\mu }_{f}}{{\left(1-\phi \right)}^{2.5}}.\end{eqnarray}$The impactive thermal conductance ${k}_{N}$ [63] of the nanofluids is expressed as$\begin{eqnarray}\displaystyle \frac{{k}_{N}}{{k}_{f}}=\displaystyle \frac{\left({k}_{s}+\left(m-1\right){k}_{f}\right)-\left(m-1\right)\phi \left({k}_{f}-{k}_{s}\right)}{\left({k}_{s}+\left(m-1\right){k}_{f}\right)+\phi \left({k}_{f}-{k}_{s}\right)}.\end{eqnarray}$Additionally, the electrical conductivity ${\sigma }_{N}$ of nanofluids [64] is prescribed as$\begin{eqnarray}\displaystyle \frac{{\sigma }_{N}}{{\sigma }_{f}}=1+\displaystyle \frac{3\left({\sigma }_{s}-{\sigma }_{f}\right)\phi }{\left({\sigma }_{s}+2{\sigma }_{f}\right)-\left({\sigma }_{s}-{\sigma }_{f}\right)\phi }.\end{eqnarray}$

For uniform injection/suction, the velocity component $v$ is fixed at the top surface due to the porosity. The temperature gradient is created across the fluid such that the upper surface has less temperature ${T}_{0}$ than the lower surface temperature ${T}_{h},$ i.e. ${T}_{0}\lt {T}_{h}.$ Thermophysical features of water and magnetite are prearranged in table 1.


Table 1.
Table 1.Thermophysical features of water and magnetite [23].
Physical propertiesWaterMagnetite
ρ (kg m−3)9975180
${c}_{p}$ (J kg−1 K)4179670
$k$ (W m−1 K)0.6139.7
Σ (ω−1 m−1)0.0525000

New window|CSV

The end point conditions at the upper and lower walls are provided below.$\begin{eqnarray}\left.\begin{array}{l}u={U}_{w}=ax,v=0,w=0,T={T}_{h}\,at\,y=0,\\ u=0,v=-{V}_{0},w=0,T={T}_{0},\,at\,y=h,\end{array}\right\}\end{eqnarray}$in which the velocity ${V}_{0}\gt 0$ agrees to the unvarying suction and ${V}_{0}\lt 0$ the unvarying blowing at the upper surface. Invoking the subsequent similarity transformation [46]:$\begin{eqnarray}\begin{array}{l}u=axf^{\prime} \left(\eta \right),\,v=-ahf\left(\eta \right),w=axg\left(\eta \right),\\ \theta \left(\eta \right)=\displaystyle \frac{T-{T}_{0}}{{T}_{h}-{T}_{0}},\,\eta =\displaystyle \frac{y}{h}.\end{array}\end{eqnarray}$The resultant dimensionless scheme of ordinary-differential formulas is provided by$\begin{eqnarray}f^{\prime\prime \prime\prime} -{A}_{1}{\xi }_{1}\left(f^{\prime} f^{\prime\prime} -ff^{\prime\prime \prime} \right)-2{A}_{2}{\xi }_{1}g^{\prime} -{A}_{1}{A}_{3}{\xi }_{4}f^{\prime\prime} =0,\end{eqnarray}$$\begin{eqnarray}g^{\prime\prime} -{A}_{1}{\xi }_{1}\left(gf^{\prime} -fg^{\prime} \right)+2{A}_{2}{\xi }_{1}f^{\prime} -{A}_{1}{A}_{3}{\xi }_{4}g=0,\end{eqnarray}$$\begin{eqnarray}\theta ^{\prime\prime} +Pr{\xi }_{2}\displaystyle \frac{{A}_{1}}{{\xi }_{3}}f\theta ^{\prime} =0,\end{eqnarray}$having the succeeding dimensionless end point constraints$\begin{eqnarray}\left.\begin{array}{l}f\left(0\right)=0,\,f^{\prime} \left(0\right)=1,\,g\left(0\right)=0,\,\theta \left(0\right)=1,\\ f\left(1\right)=S,\,g\left(1\right)=0,\,f^{\prime} \left(1\right)=0,\,\theta \left(1\right)=0.\end{array}\right\}\end{eqnarray}$in which the prime corresponds to the differentiate with respect to η. The parameters associated with the dimensionless equations are written by$\begin{eqnarray}\begin{array}{l}{A}_{1}=\displaystyle \frac{a{h}^{2}}{{\nu }_{f}}\left({\rm{Reynolds}}\,{\rm{number}}\right),\\ {A}_{2}=\displaystyle \frac{{\rm{\Omega }}{h}^{2}}{{\nu }_{f}}\left(\mathrm{rotation}\,\,{\rm{parameter}}\right),\end{array}\end{eqnarray}$$\begin{eqnarray}\begin{array}{l}{A}_{3}=\displaystyle \frac{{\sigma }_{f}}{{\rho }_{f}a}{B}_{0}^{2}{\left(1-\phi \right)}^{2.5}\left({\rm{magnetic}}\,{\rm{parameter}}\right),\\ Pr=\displaystyle \frac{{\mu }_{f}{c}_{f}}{{k}_{f}}\,\left({\rm{Prandtl}}\,{\rm{number}}\right),\,\end{array}\end{eqnarray}$$\begin{eqnarray}\begin{array}{l}{\xi }_{1}=\left[\left(1-\phi \right)+\phi \displaystyle \frac{{\rho }_{s}}{{\rho }_{f}}\right]{\left(1-\phi \right)}^{2.5},\\ {\xi }_{2}=\left[\left(1-\phi \right)+\phi \displaystyle \frac{{\left(\rho {c}_{p}\right)}_{s}}{{\left(\rho {c}_{p}\right)}_{f}}\right],\end{array}\end{eqnarray}$$\begin{eqnarray}\begin{array}{l}{\xi }_{3}=\displaystyle \frac{\left({k}_{s}+\left(m-1\right){k}_{f}\right)-\left(m-1\right)\phi \left({k}_{f}-{k}_{s}\right)}{\left({k}_{s}+\left(m-1\right){k}_{f}\right)+\phi \left({k}_{f}-{k}_{s}\right)}\\ \,\,\times \,\left({\rm{thermal}}\,{\rm{conductivities}}\,{\rm{ratio}}\right),\end{array}\end{eqnarray}$$\begin{eqnarray}\begin{array}{l}{\xi }_{4}=1+\displaystyle \frac{3\left({\sigma }_{s}-{\sigma }_{f}\right)\phi }{\left({\sigma }_{s}+2{\sigma }_{f}\right)-\left({\sigma }_{s}-{\sigma }_{f}\right)\phi },\\ S=\displaystyle \frac{{V}_{0}}{ah}\left(\mathrm{suction}/\mathrm{injection}\,{\rm{parameter}}\right).\end{array}\end{eqnarray}$Now we express the drag force factor ${C}_{f}$ and the local number of Nusse lt $N{u}_{x}$ depicted below$\begin{eqnarray}{C}_{f}=\displaystyle \frac{2{\tau }_{w}}{{\rho }_{N}{U}_{w}^{2}},\,N{u}_{x}=\displaystyle \frac{x{q}_{w}}{{k}_{N}\left({T}_{w}-{T}_{\infty }\right)},\end{eqnarray}$in which ${\tau }_{w}={\mu }_{N}\left(\tfrac{\partial u}{\partial y}\right)$ signifies the shear stress and ${q}_{w}=-{k}_{N}\left(\tfrac{\partial T}{\partial y}\right)$ symbols the heat fluxing at the wall.

Making use of the similarity transformation earlier mentioned, equation (22) is expressed as:$\begin{eqnarray}\left.\begin{array}{l}{C}_{f}R{e}_{x}^{1/2}=\displaystyle \frac{\left(1-\phi +\phi \tfrac{{\rho }_{s}}{{\rho }_{f}}\right)}{{\left(1-\phi \right)}^{2.5}}f^{\prime\prime} \left(0\right),\,R{e}_{x}^{-1/2}N{u}_{x}=-\theta ^{\prime} \left(0\right),\\ {C}_{f}R{e}_{x}^{1/2}=\displaystyle \frac{\left(1-\phi +\phi \tfrac{{\rho }_{s}}{{\rho }_{f}}\right)}{{\left(1-\phi \right)}^{2.5}}f^{\prime\prime} \left(1\right),\,R{e}_{x}^{-1/2}N{u}_{x}=-\theta ^{\prime} \left(1\right),\end{array}\right\}\end{eqnarray}$in which $R{e}_{x}=\tfrac{{U}_{x}}{{\nu }_{f}}$ characterizes the local number of Reynolds.

3. Methodology of solution

The equations (13)–(15) combined with end point conditions (16) establish a nonlinear boundary-value problem of two-point, which has been carried out numerically by means of the shooting procedure [65] for various amounts of the elaborated factors.

The system of nonlinear ordinary-differential formulas (13)–(15) alongside the boundary constraints (16) has been attempted numerically through the shooting technique for diverse amounts of the concerned factors. We have opted for the following substitutions for transforming the BVP to the IVP:$\begin{eqnarray}\begin{array}{l}{z}_{1}=f,\,{z}_{2}=f^{\prime} ,\,{z}_{3}=f^{\prime\prime} ,\,{z}_{4}=f^{\prime\prime \prime} ,\,{z}_{5}=g,\\ {z}_{6}=g^{\prime} ,\,{z}_{7}=\theta ,\,{z}_{8}=\theta ^{\prime} .\end{array}\end{eqnarray}$

The nonlinear energy and momentum equations are transformed into the next eight first-order schemes of ODEs together with the initial conditions. The flow chart of the shooting method is displayed in figure 2.$\begin{eqnarray}\left.\begin{array}{ll}{z}_{1}^{{\prime} }={z}_{2} & {z}_{1}\left(0\right)=0,\\ {z}_{2}^{{\prime} }={z}_{3} & {z}_{2}\left(0\right)=1,\\ {z}_{3}^{{\prime} }={z}_{4} & {z}_{3}\left(0\right)={m}_{1},\\ {z}_{4}^{{\prime} }={A}_{1}{\xi }_{1}\left({z}_{2}{z}_{3}-{z}_{1}{z}_{4}\right)+2{A}_{2}{\xi }_{1}{z}_{6}+{\xi }_{4}{A}_{1}{A}_{3}{z}_{4} & {z}_{4}\left(0\right)={m}_{2},\\ {z}_{5}^{{\prime} }={z}_{6} & {z}_{5}\left(0\right)=0,\\ {z}_{6}^{{\prime} }={A}_{1}{\xi }_{1}\left({z}_{2}{z}_{5}-{z}_{1}{z}_{6}\right)-2{A}_{2}{\xi }_{1}{z}_{2}+{\xi }_{4}{A}_{1}{A}_{3}{z}_{5} & {z}_{6}\left(0\right)={m}_{3},\\ {z}_{7}^{{\prime} }={z}_{8} & {z}_{7}\left(0\right)=1,\\ {z}_{8}^{{\prime} }=-Pr{\xi }_{2}\displaystyle \frac{{A}_{1}}{{\xi }_{3}}{z}_{1}{z}_{8} & {z}_{8}\left(0\right)={m}_{4}.\end{array}\right\}\end{eqnarray}$We employ the fourth-order Runge-Kutta procedure to tackle the above initial value problem. To improve the values of ${m}_{1},{m}_{2},{m}_{3}$ and ${m}_{4},$ we utilize the Newton's technique until the following condition is achieved:$\begin{eqnarray*}\begin{array}{l}\max \left\{\left|{z}_{1}(1)-S\right|,\left|{z}_{2}\left(1\right)-0\right|,\left|{z}_{5}\left(1\right)-0\right|,\right.\\ \left.\left|{z}_{7}\left(1\right)-0\right|\right\}\lt {\epsilon },\end{array}\end{eqnarray*}$in which ${\epsilon }\gt 0$ is a smaller positive real number. All the numerical data in this article are achieved having ${\epsilon }={10}^{-6}.$ To authenticate the accuracy of the current analysis, an extremely justifiable comparison of the local drag force in addition to the local number of Nusselt with those suggested by Hussain et al [46] is given in table 2 for $\phi =0,{A}_{1}=1,{A}_{2}=1,{A}_{3}=0,Pr=6.2,\,m=3$ and $S=-1,0,1.$

Figure 2.

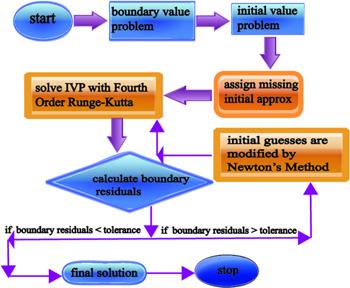New window|Download| PPT slide
Figure 2.Computational flowchart for shooting method.



Table 2.
Table 2.Comparison of ${C}_{f}R{e}_{x}^{1/2}$and $R{e}_{x}^{-1/2}N{u}_{x}$ with results of reference [46] for diverse values of $S$ and $\phi $ at lower/upper surface.
${C}_{f}R{e}_{x}^{1/2}$ at $\eta =0$$R{e}_{x}^{-1/2}N{u}_{x}$ at $\eta =0$${C}_{f}R{e}_{x}^{1/2}$ at $\eta =1$$R{e}_{x}^{-1/2}N{u}_{x}$ at $\eta =1$
$S$$\phi $PresentReference [46]PresentReference [46]PresentReference [46]PresentReference [46]
−10−9.54155−9.541550.390018.857520.390018.857524.822964.82296
00−4.09595−4.095951.336101.336101.952891.952890.802490.80249
102.235652.235652.194982.19498−3.81099−3.810990.057760.05776

New window|CSV

4. Results and discussion

The numerical estimations of $R{e}_{x}^{-1/2}N{u}_{x}\,$ besides ${C}_{f}R{e}_{x}^{1/2}$ for a variety of values of the Reynolds number ${A}_{1},$ rotating parameter ${A}_{2},$ magneto parameter ${A}_{3},$ injection (suction) parameter S and volume fraction of nanoparticle φ are available in tables 3–6. From table 3, it is found that a surge of the concentration of nanoparticles φ is inclined to reduce the local skin friction at lower surface, and a similar trend is noted for the upper surface regarding table 4. Table 5 tells us that an upsurge in the nanoparticles volume concentration φ is inclined to improve the heat rate for $S=-1$ and diminish the heat rate for $S=0,1$ at the lower surface, although an opposite trend is noticed for the upper surface regarding table 6.


Table 3.
Table 3.Values of ${C}_{f}R{e}_{x}^{1/2}$ at $\eta =0$ for diverse amounts of the emergent parameters at lower surface ($Pr=6.2,m=3$).
${A}_{2}=0,{A}_{3}=0$${A}_{2}=0,{A}_{3}=0$${A}_{2}=0,{A}_{3}=1$${A}_{2}=1,{A}_{3}=1$
$S$$\phi \,$${A}_{1}=0.5$${A}_{1}=1$${A}_{1}=0.5$${A}_{1}=1$${A}_{1}=0.5$${A}_{1}=1$${A}_{1}=0.5$${A}_{1}=1$
−10.0−9.73485−9.46810−9.79701−9.54155−9.85479−9.71457−9.91343−9.77916
.05−9.13191−8.86501−9.19873−8.94492−9.26257−9.13383−9.32502−9.20260
0.1−8.90239−8.63544−8.97118−8.71810−9.04916−8.93734−9.11280−9.00691
00.0−4.04282−4.08556−4.05316−4.09595−4.10870−4.21578−4.11862−4.22533
.05−3.80166−3.84440−3.81267−3.85545−3.87325−3.98571−3.88373−3.99574
0.1−3.70986−3.75259−3.72115−3.76393−3.79018−3.91095−3.80085−3.92109
10.02.106942.213272.133982.235652.089222.175912.114872.19632
.051.986352.092602.014782.115841.967022.051811.993792.07274
0.11.940442.046671.969442.070241.918742.000921.945812.02185

New window|CSV


Table 4.
Table 4.Values of ${C}_{f}R{e}_{x}^{1/2}$ at $\eta =1$ for diverse amounts of the emergent parameters at upper surface ($Pr=6.2,m=3$).
${A}_{2}=0,{A}_{3}=0$${A}_{2}=0,{A}_{3}=0$${A}_{2}=0,{A}_{3}=1$${A}_{2}=1,{A}_{3}=1$
S$\phi $${A}_{1}=0.5$${A}_{1}=1$${A}_{1}=0.5$${A}_{1}=1$${A}_{1}=0.5$${A}_{1}=1$${A}_{1}=0.5$${A}_{1}=1$
−10.08.386308.808938.431508.857528.416378.861348.458858.90381
.057.905128.331417.953448.383597.937618.387357.982578.43195
0.17.722008.149827.771638.203517.758408.212257.804088.25710
00.01.976391.953181.975851.952891.960541.923011.959951.92260
.051.855831.832651.855271.832381.838651.800131.838041.79970
0.11.809931.786771.809371.786511.790711.750491.790081.75005
10.0−3.88037−3.77309−3.92117−3.81099−3.94475−3.89718−3.98358−3.93178
.05−3.63962−3.53346−3.68284−3.57339−3.70947−3.66769−3.75030−3.70367
0.1−3.54799−3.44230−3.59221−3.48305−3.62631−3.59253−3.66774−3.62872

New window|CSV


Table 5.
Table 5.Values of $R{e}_{x}^{-1/2}N{u}_{x}\,$at $\eta =0$ for diverse amounts of the emergent parameters at lower surface ($Pr=6.2,m=3$).
${A}_{2}=0,{A}_{3}=0$${A}_{2}=0,{A}_{3}=0$${A}_{2}=0,{A}_{3}=1$${A}_{2}=1,{A}_{3}=1$
$S$$\phi $${A}_{1}=0.5$${A}_{1}=1$${A}_{1}=0.5$${A}_{1}=1$${A}_{1}=0.5$${A}_{1}=1$${A}_{1}=0.5$${A}_{1}=1$
−10.00.679520.390740.679110.390010.678310.387200.677920.38656
0.050.720010.458500.719570.457630.718730.454360.718320.45362
0.10.754380.519500.753960.518590.753040.514880.752650.51412
00.01.161851.336611.161611.336101.160611.331431.160381.33096
0.051.141161.292071.140921.291571.139911.286911.139681.28646
0.11.123721.254871.123501.254411.122471.249741.122261.24933
10.01.628942.195131.628862.194981.627932.191641.627852.19150
0.051.554002.066851.553902.066651.552962.063141.552872.06295
0.11.489161.952371.489071.952151.488101.948481.488011.94828

New window|CSV


Table 6.
Table 6.Values of $R{e}_{x}^{-1/2}N{u}_{x}\,$at $\eta =1$ for diverse amounts of the emergent parameters at upper surface ($Pr=6.2,m=3$).
${A}_{2}=0,{A}_{3}=0$${A}_{2}=0,{A}_{3}=0$${A}_{2}=0,{A}_{3}=1$${A}_{2}=1,{A}_{3}=1$
$S$$\phi $${A}_{1}=0.5$${A}_{1}=1$$A{}_{1}=0.5$${A}_{1}=1$${A}_{1}=0.5$${A}_{1}=1$${A}_{1}=0.5$${A}_{1}=1$
−10.02.430384.822182.430554.822962.431934.830472.432094.83117
.052.200604.141282.200784.142202.202124.149882.202294.15068
0.12.017683.604972.017853.605872.019173.613582.019333.61435
00.00.898720.802170.898890.802490.899640.805600.899810.80590
.050.911010.825790.911180.826110.911950.829300.912120.82960
0.10.921510.846030.921670.846340.922460.849610.922610.84989
10.00.265510.057690.265640.057760.265920.058100.266050.05817
.050.316270.084750.316420.084850.316750.085350.316900.08544
0.10.366290.117060.366460.117190.366850.117870.367000.11799

New window|CSV

Results are described in figures 3–7 for the study of the nanofluid flow and heat transport showing the velocity $f^{\prime} \left(\eta \right),$ $g\left(\eta \right)$ and temperature profile $\theta \left(\eta \right)$ variance within the geometry-defined constrained domain. Figures 3(a)–(c) describe the impact of the diverse amounts of nanoparticle concentration $\phi $ on $f^{\prime} \left(\eta \right),$ $g\left(\eta \right)$ and $\theta \left(\eta \right).$ Figure 3(a) shows that there is a small variation in the velocity $f^{\prime} \left(\eta \right)$ with an increase in $\phi $; however it may be noticed within the insertion of the figure that Fe3O4 has a comparatively higher velocity profile in comparison with the base fluid. For varied $\phi $ values, figure 3(b) exposes the variation in $g\left(\eta \right).$ We can see that the standard liquid has moderately larger velocity outline in comparison with the water -based magnetite. Difference of temperature outlines with $\phi $ is demonstrated in figure 3(c). We can see in figure 3(c) that with an increment in the nanoparticle concentration $\phi ,$ the distribution of temperature is enhanced.

Figure 3.

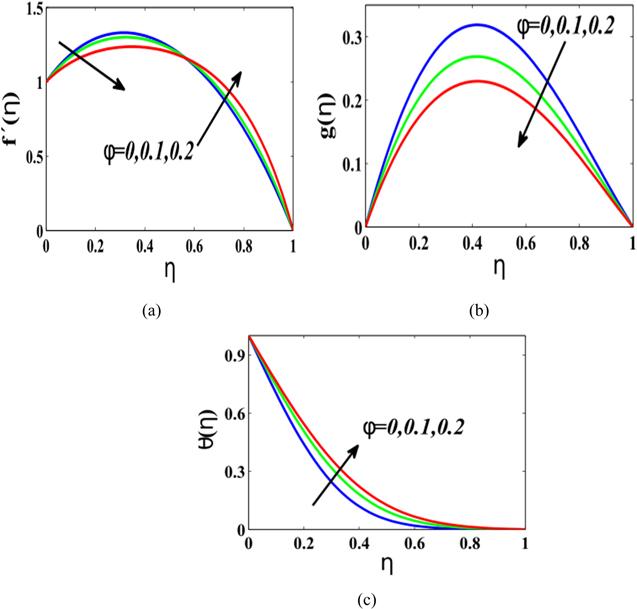New window|Download| PPT slide
Figure 3.(a) $f^{\prime} \left(\eta \right),$ (b) $g\left(\eta \right),$ (c) $\theta \left(\eta \right)\,$ for nanoparticle concentration $\phi $ when ${A}_{1}={A}_{2}={A}_{3}=2,S=1.$


Figure 4.

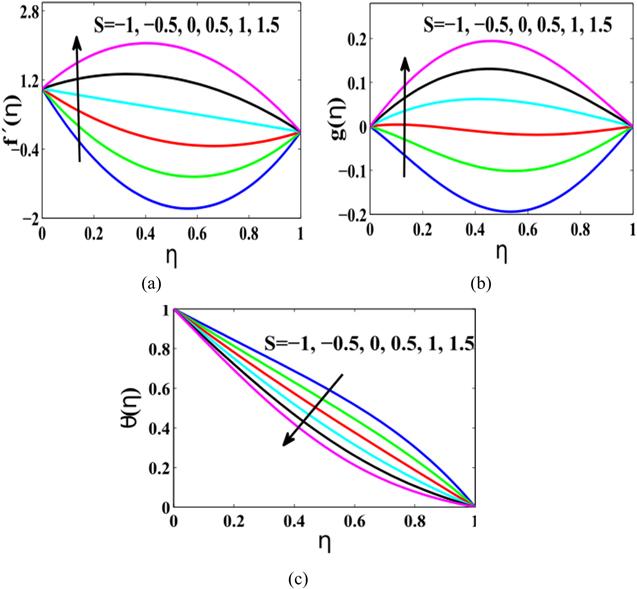New window|Download| PPT slide
Figure 4.(a) $f^{\prime} \left(\eta \right),$ (b) $g\left(\eta \right),$ (c) $\theta \left(\eta \right)\,$ for magnetite-water nanofluid with parameter S when ${A}_{1}={A}_{2}={A}_{3}=0.5,\phi =0.2.$


Figure 5.

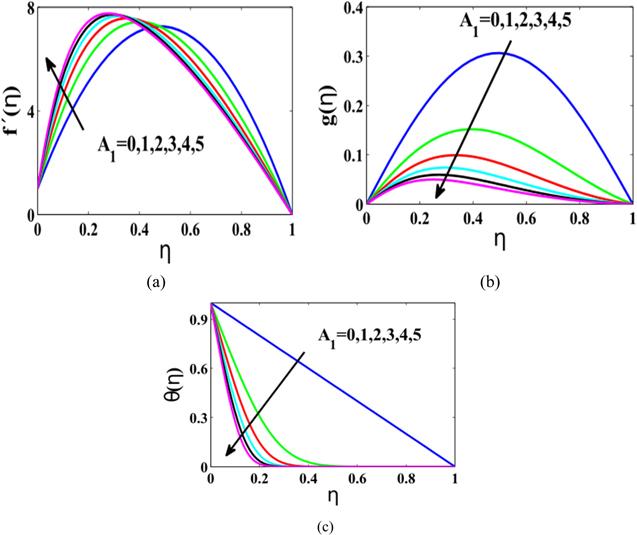New window|Download| PPT slide
Figure 5.(a) $f^{\prime} \left(\eta \right),$ (b) $g\left(\eta \right),$ (c) $\theta \left(\eta \right)\,$ for magnetite-water nanofluid with parameter S when ${A}_{2}=0.2,{A}_{3}=0,\phi =0.2,S=5.$


Figure 6.

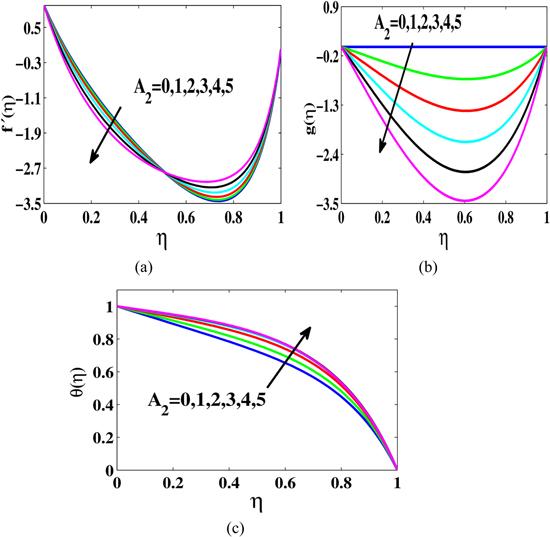New window|Download| PPT slide
Figure 6.(a) $f^{\prime} \left(\eta \right),$ (b) $g\left(\eta \right),$ (c) $\theta \left(\eta \right)\,$ for magnetite-water nanofluid with parameter ${A}_{2}$ when ${A}_{1}=0.2,{A}_{3}=0,\phi =0.2,S=-3.$


Figure 7.

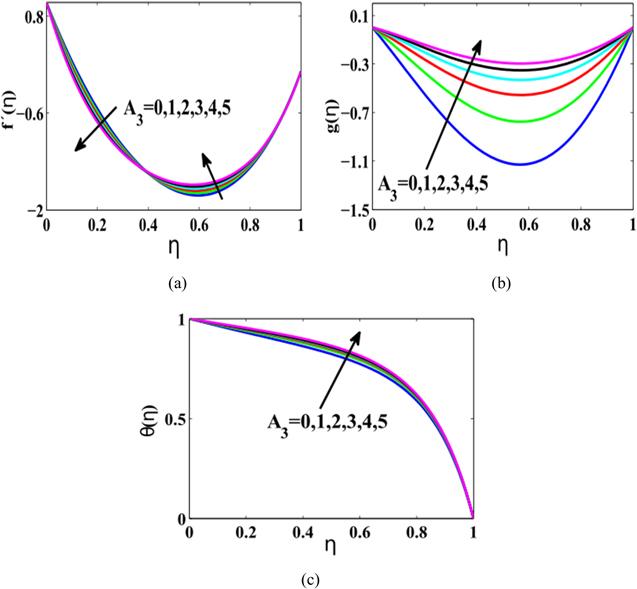New window|Download| PPT slide
Figure 7.(a) $f^{\prime} \left(\eta \right),$ (b) $g\left(\eta \right),$ (c) $\theta \left(\eta \right)\,$ for magnetite-water nanofluid with parameter ${A}_{3}$ when ${A}_{1}=2,{A}_{2}=2,\phi =0.2,S=-1.$


Figures 4(a)–(c) display the impact of injection/suction parameter S on the velocities and temperature. For the injection/suction case, the velocity profile $f^{\prime} \left(\eta \right)$ and $g\left(\eta \right)$ get bigger. Furthermore, it might be noticed that a distinction in the velocities is remarkable at the mean position of the channel. Besides that, the extreme amount of the swiftness moves marginally toward the lower surface for non-negative S, while for negative S it moves marginally toward the higher surface. With diverse amounts of the suction (blowing) parameter $S,$ figure 4(c) provides the temperature distribution profile. It can be identified that escalating the injection/suction parameter $S,$ thwarts the temperature distribution; hence it offers a reduction in the temperature field.

Figures 5(a)–(c) pronounce the influence of the parameter ${A}_{1}$ on swiftness and temperature domain. Figure 5(a) indicates two distinctive characteristics of the velocity field for the parameter ${A}_{1}$ and it is found that velocity field swaps the behaviour from rising to reducing for various values of ${A}_{1}.$ This outcome is mostly a consequence of the expanding of the lesser surface. The velocity distribution $g\left(\eta \right)$ in figure 5(b) exhibits a uniform reducing behaviour for greater values of ${A}_{1}.$ In case the lower plate is fixed, the velocity displays a symmetrical behaviour at the central position. On the other hand, the the highest value of the velocity field moves marginally toward the lower plate when the value of ${A}_{1}$ is enhanced. The thermal field $\theta \left(\eta \right)\,$exhibits a reducing behaviour with a boost in the values of ${A}_{1}$ (figure 5(c)). In case of the lower plate at rest (i.e. ${A}_{1}=0$), the thermal field manifests a linear reducing behaviour, although a nonlinear lessening behaviour is found for the remainder of the values of ${A}_{1}.$

Figures 6(a)–(c) are sketched to observe the influence of ${A}_{2}$ on the dynamics of the velocities $f^{\prime} \left(\eta \right),$ $g\left(\eta \right)$ and thermal field $\theta \left(\eta \right)\,.$ Figure 6(a) elaborates the change in the speed distribution $f^{\prime} \left(\eta \right),$ inside the constrained area exhibiting a double natural behaviour. It is noted that the swiftness distribution $f^{\prime} \left(\eta \right),$ reveals a lessening behaviour inside the domain $0\leqslant \eta \lt 0.5,$; however the outcomes are entirely different inside the domain $0.5\lt \eta \leqslant 1.$ In figure 6(b), it is noted that there is no variation in vertical velocity component when ${A}_{2}=0,$ and consequently the problem reduces to the steady 2D flow without having the rotation parameter. However, it is obvious that an escalation in the values of ${A}_{2}$ reduces the velocity distribution $g\left(\eta \right).$ Furthermore, fluctuation in the velocity is bigger at the central position when compared with the upper as well as lower surfaces. Figure 6(c) implies that the temperature field $\theta \left(\eta \right)\,$is enhanced when the rotation parameter ${A}_{2}$ goes up.

Figures 7(a)–(c) explore the impact of the magneto parameter ${A}_{3}$ on velocities and thermal fields. Figure 7(a) yields dual characteristics of the flow field $f^{\prime} \left(\eta \right),$ within the constrained domain. It can be seen that the velocity profile $f^{\prime} \left(\eta \right),$ demonstrates a lessening behaviour for growing values of the magnetic parameter ${A}_{3}$ within the domain $0\leqslant \,\eta \lt 0.4,$ while the reverse behaviour is found in the domain $0.4\lt \eta \leqslant 1.$ The velocity distribution $g\left(\eta \right)$ offers the escalating behaviour for the rising values of ${A}_{3}$ as shown in figure 7(b). Also, it can be viewed that variation in the velocity is higher at the central position when compared with the upper as well as lower surfaces. Figure 7(c) suggests the influence of the electomagnetic field ${A}_{3}$ on thermal distribution $\theta \left(\eta \right).$ It is observed that heat is enhanced for greater amounts of ${A}_{3}.$

The drag coefficient of the nanofluid is examined at the lesser plate of the channel, and outcomes are designed for various parameters. Figure 8(a) displays the impact of $\phi $ and $S$ on the drag force factor. It is seen that the drag force absolute values escalate as $\phi $ rises for $S\,=\,0,-1,$; however it declines for S=1. Figures 8(b)–(d) portray the difference in the drag force with nanoparticle concentration $\phi .$ Drag force factor reduces with a rise in $\phi .$ The outcomes suggest that it is raised with a boost in ${A}_{1}$ and ${A}_{2}$, but it lessens with an intensification of the electromagnetic field ${A}_{3}.$ Figures 9(a)–(d) depict the impact of physical parameter on the drag force coefficient at the higher surface of the duct. Largely, friction coefficient indicates a reducing behaviour with respect to $\phi $, regardless of the extra related factors. For ${A}_{1},$ the drag force at the higher plate displays a diminishing behaviour.

Figure 8.

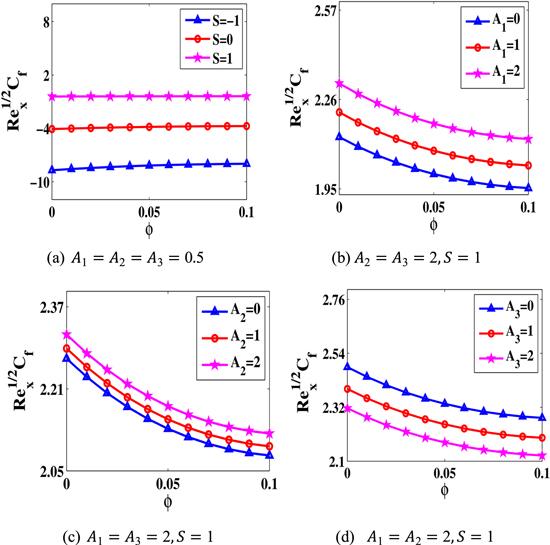New window|Download| PPT slide
Figure 8.Change of $R{e}_{x}^{1/2}{C}_{f}$ at $\eta =0$ for diverse values of (a) S, (b) ${A}_{1},$ (c) ${A}_{2},$ (d) ${A}_{3}.$


Figure 9.

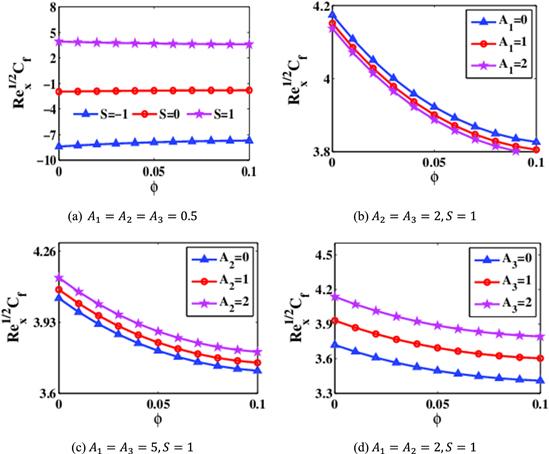New window|Download| PPT slide
Figure 9.Change of $R{e}_{x}^{1/2}{C}_{f}$ at $\eta =1$ for diverse values of (a) S, (b) ${A}_{1},$ (c) ${A}_{2},$ (d) ${A}_{3}.$


Figures 10(a)–(d) demonstrate the variation of rate of heat transport at lower plate versus the nanoparticle concentration. In figure 10(a), it is noted that for S=0 and S=1, there is a declining behaviour in the heat transport rate with $\phi .$ However, the impact of $S\,$= −1 is reverse in nature with respect to $\phi .$ The impact of ${A}_{1},$ ${A}_{2},$ ${A}_{3}$ and $\phi $ on the rate of heat transportation is plotted in figures 10(a)–(d). It is noticed that there is a surge in rate of heat $N{u}_{x}$ with the enhancement in $\phi .$ Furthermore it is observed that Fe3O4 possesses advanced heat transport rate in contrast with the standard liquid. Figures 11(a)–(d) display the dynamics of the heat transfer rate versus Fe3O4 volume fraction at the upper surface. Figures 11(a)–(d) exhibit a rise in $N{u}_{{\rm{x}}}$ producing the enhancing values of $S,$ ${A}_{1},$ ${A}_{2}$ and ${A}_{3}.$ From figure 11(b), we assert that $N{u}_{{\rm{x}}}$ is a reducing function of the concentration $\phi .$ Streamlined variations are plotted in figures 12(a)–(c) for diverse amounts of S. It is seen from figures 12(a)–(c) that the gaps between stream lines decrease with increasing the magnitude of the injection/suction parameter $S.$ The injection/suction parameter S thus significantly alters the fluid dynamics of the stretching sheet region.

Figure 10.

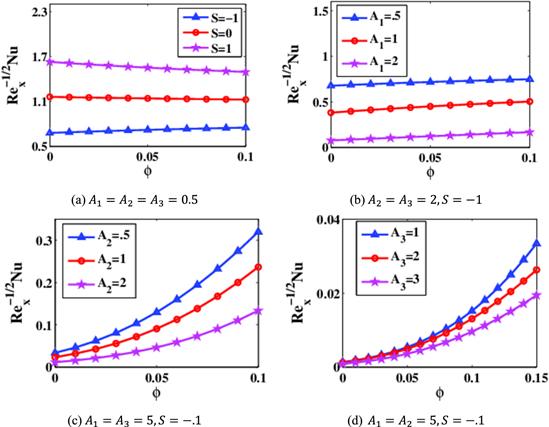New window|Download| PPT slide
Figure 10.Change of $R{e}_{x}^{-1/2}N{u}_{x}$ at $\eta =0$ for various values of (a) S, (b) ${A}_{1},$ (c) ${A}_{2},$ (d) ${A}_{3}.$


Figure 11.

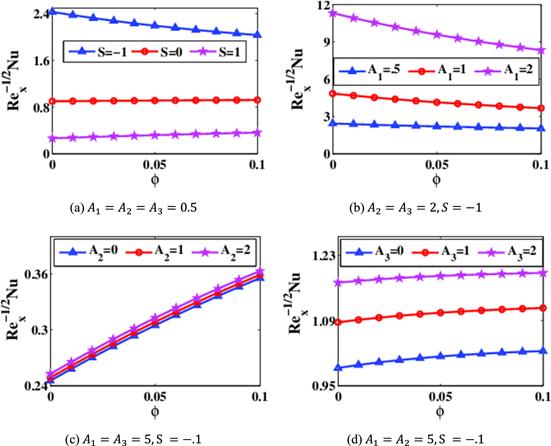New window|Download| PPT slide
Figure 11.Change of $R{e}_{x}^{-1/2}N{u}_{x}$ at $\eta =1$ for diverse values of (a) S, (b) ${A}_{1},$ (c) ${A}_{2},$ (d) ${A}_{3}.$


Figure 12.

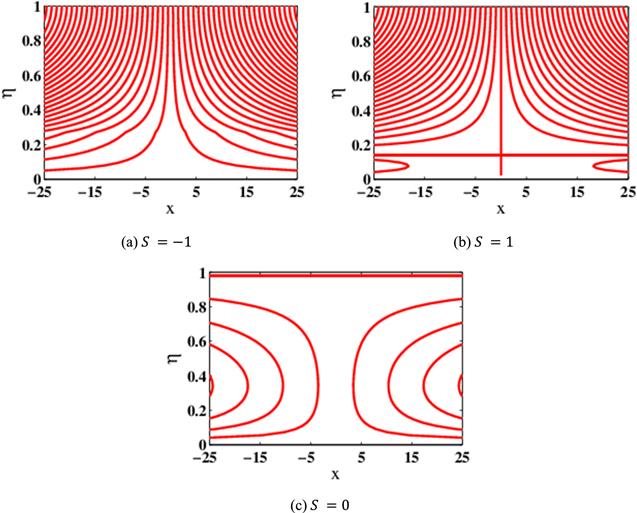New window|Download| PPT slide
Figure 12.Change of streamlines for diverse S values.


5. Conclusions

In the current research, the rotating flow of magnetite-water nanofluid past a stretching surface in the existence of the electromagneto impact is examined. With the aid of graphs, impacts of magnetite nanoparticles on the drag force as well as the Nusselt number are described. The key findings of the analysis are provided below:The concentration of nanoparticles increases the velocity, along with the temperature of the nanofluid.
The flow field is emphatically impacted by the injection/suction parameter.
A surge in the magnetic as well as rotation factor results in a boost in the thermal field.
The rate of heat transfer boosts for the magnetite-water nanofluid when compared to that for the standard fluid against the concentration of nanoparticles.
The magnetic parameter augments the Nusselt number, although it diminishes the coefficient of the drag force.
Drag force coefficient is lower for the magnetite-water nanofluid as compared to that for the standard fluid against the nanoparticle concentration.
The rotation factor tends to increase the drag coefficient, although it slightly diminishes the Nusselt number.



Reference By original order
By published year
By cited within times
By Impact factor

Zuddin M H Nazar R 2014 Numerical solutions of MHD rotating flow and heat transfer over a permeable shrinking sheet
ScienceAsia 40S 58 62
DOI:10.2306/scienceasia1513-1874.2014.40S.058 [Cited within: 1]

Wang C Y 1988 Stretching a surface in a rotating fluid
Zeitschrift für angewandte Mathematik und Physik ZAMP 39 177 185
DOI:10.1007/BF00945764 [Cited within: 1]

Nazar R Amin N Pop I 2004 Unsteady boundary layer flow due to a stretching surface in a rotating fluid
Mech. Res. Commun. 31 121 128
DOI:10.1016/j.mechrescom.2003.09.004 [Cited within: 1]

Rosali H Ishak A Nazar R Pop I 2015 Rotating flow over an exponentially shrinking sheet with suction
J. Mol. Liq. 211 965 969
DOI:10.1016/j.molliq.2015.08.026 [Cited within: 1]

Sulochana C Samrat P Sandeep N 2018 Magnetohydrodynamic radiative nanofluid flow over a rotating surface with Soret effect
Multidiscipline Modeling in Materials and Structures 14 168 188
DOI:10.1108/MMMS-05-2017-0042 [Cited within: 1]

Seth S Kumar R Bhattacharyya A 2018 Entropy generation of dissipative flow of carbon nanotubes in rotating frame with Darcy-Forchheimer porous medium: a numerical study
J. Mol. Liq. 268 637 646
DOI:10.1016/j.molliq.2018.07.071 [Cited within: 1]

Gireesha J Kumar G Krishanamurthy R Rudraswamy G 2018 Enhancement of heat transfer in an unsteady rotating flow for the aqueous suspensions of single wall nanotubes under nonlinear thermal radiation: a numerical study
Colloid. Polym. Sci. 296 1501 1508
DOI:10.1007/s00396-018-4374-z [Cited within: 1]

Choi S U S 1995 Enhancing thermal conductivity of fluids with nanoparticles 1995 Int
Mechanical Engineering Congress and Exhibition San Francisco, CA 12–17 November 1995
[Cited within: 1]

Buongiorno J 2005 Convective transport in nanofluids
J. Heat Transfer 128 240 250
DOI:10.1115/1.2150834 [Cited within: 1]

Choi S U S 2009 Nanofluids from vision to reality through research
J. Heat Transfer 131 1 9
DOI:10.1115/1.3056479 [Cited within: 1]

Yu W France D M Routbort J L Choi S U S 2008 Review and comparison of nanofluid thermal conductivity and heat transfer enhancements
Heat Transfer Eng. 29 432 460
DOI:10.1080/01457630701850851

Das S K Choi S U S Patel H E 2006 Heat transfer in nanofluids
Heat Transfer Eng. 27 3 9
DOI:10.1080/01457630600904593

Eid M R Nafe M A 2020 Thermal conductivity variation and heat generation effects on magneto-hybrid nanofluid flow in a porous medium with slip condition
Waves Random Complex Medium1 25
DOI:10.1080/17455030.2020.1810365 [Cited within: 1]

Pak B C Cho I 1998 Hydromagnetic and heat transfer study of dispersed fluids with submicron metallic oxide particles
Experimental Heat Transfer; an International Journal 11 151 170
DOI:10.1080/08916159808946559 [Cited within: 1]

Zaraki A Ghalambaz M Chamkha J 2015 Theoretical analysis of natural convection boundary layer heat and mass transfer of nanofluids: effects of size, shape and type of nanoparticles, type of base fluid and working temperature
Adv. Powder Technol. 26 935 946
DOI:10.1016/j.apt.2015.03.012 [Cited within: 1]

Selimefendigil F 2018 Natural convection in a trapezoidal cavity with an inner conductive object of different shapes and filled with nanofluids of different nanoparticle shapes
Iranian J. Sci. Technol. Trans. Mech. Eng. 42 169 184
DOI:10.1007/s40997-017-0083-3 [Cited within: 1]

Nayak K Bhattacharyya S Pop I 2018 Effects of nanoparticles dispersion on the mixed convection of a nanofluid in a skewed enclosure
Int. J. Heat Mass Transfer 125 908 919
DOI:10.1016/j.ijheatmasstransfer.2018.04.088 [Cited within: 1]

Ashorynejad R Zarghami A Sadeghi K 2018 Magnetohydrodynamics flow and heat transfer of Cu-water nanofluid through a partially porous wavy channel
Int. J. Heat Mass Transfer 119 247 258
DOI:10.1016/j.ijheatmasstransfer.2017.11.117 [Cited within: 1]

Jeong J Chengguo L Kwon Y Lee J Kim S Yun R 2013 Particle shape effect on the viscosity and thermal conductivity of zinc oxide nanofluids
Int. J. Refrig 36 2233 2241
DOI:10.1016/j.ijrefrig.2013.07.024 [Cited within: 1]

Timofeeva E V Routbort J L Singh D 2009 Particle shape effects on thermophysical properties of alumina nanofluids
J. Appl. Phys. 106 014304
DOI:10.1063/1.3155999 [Cited within: 1]

Rosensweig R E 2002 Heating magnetic fluid with alternating magnetic field
J. Magn. Magn. Mater. 252 370 374
DOI:10.1016/S0304-8853(02)00706-0 [Cited within: 1]

Tangthieng C Finlayson B A Maulbetsch J Cader T 1999 Heat transfer enhancement in ferrofluids subjected to steady magnetic fields
J. Magn. Magn. Mater. 201 252 255
DOI:10.1016/S0304-8853(99)00062-1 [Cited within: 1]

Sheikholeslami M Ganji M Domiri D 2014 Ferrohydrodynamic and magnetohydrodynamic effects on ferrofluid flow and convective heat transfer
Energy 75 400 410
DOI:10.1016/j.energy.2014.07.089 [Cited within: 2]

Li Y Yan H Massoudi M Wu T 2017 Effects of anisotropic thermal conductivity and Lorentz force on the flow and heat transfer of a ferro-nanofluid in a magnetic field
Energies 10 1065
DOI:10.3390/en10071065 [Cited within: 1]

Jue T C 2006 Analysis of combined thermal and magnetic convection ferrofluid flow in a cavity
Int. Commun. Heat Mass Transfer 33 846 852
DOI:10.1016/j.icheatmasstransfer.2006.02.001 [Cited within: 1]

Salehpour A Salehi S Salehpour S Ashjaee M 2018 Thermal and hydrodynamic performances of MHD ferrofluid flow inside a porous channel
Exp. Therm Fluid Sci. 90 1 13
DOI:10.1016/j.expthermflusci.2017.08.032 [Cited within: 1]

Ali M E Sandeep N 2017 Cattaneo-Christov model for radiative heat transfer of magnetohydrodynamic Casson-ferrofluid: a numerical study
Results in Physics 7 21 30
DOI:10.1016/j.rinp.2016.11.055 [Cited within: 1]

Karimipour A Orazio D Shadloo S 2017 The effects of different nano particles of Al2O3 and Ag on the MHD nano fluid flow and heat transfer in a microchannel including slip velocity and temperature jump
Physica E 86 146 153
DOI:10.1016/j.physe.2016.10.015 [Cited within: 1]

Bahiraei M Hosseinalipour S Hangi M 2014 Numerical study and optimization of hydrothermal characteristics of manganese-zinc ferrite nanofluid within annulus in the presence of magnetic field
J. Supercond. Novel Magn. 27 527 534
DOI:10.1007/s10948-013-2299-9 [Cited within: 1]

Pal D Mondal H 2012 MHD non-Darcy mixed convective diffusion of species over a stretching sheet embedded in a porous medium with non-uniform heat source/sink, variable viscosity and soret effect
Commun. Nonlinear Sci. Numer. Simul. 17 672 684
DOI:10.1016/j.cnsns.2011.05.035 [Cited within: 1]

Metri G Metri G Abel S Silvestrov S 2016 Heat transfer in MHD mixed convection viscoelastic fluid flow over a stretching sheet embedded in a porous medium with viscous dissipation and non-uniform heat source/sink
Procedia Eng. 157 309 316
DOI:10.1016/j.proeng.2016.08.371

Eid M R 2020 Thermal characteristics of 3D nanofluid flow over a convectively heated Riga surface in a Darcy–Forchheimer porous material with linear thermal radiation: an optimal analysis
Arab. J. Sci. Eng. 45 9803 9814
DOI:10.1007/s13369-020-04943-3

Alaidrous A A Eid M R 2020 3D electromagnetic radiative non–Newtonian nanofluid flow with Joule heating and higher–order reactions in porous materials
Sci. Rep. 10 14513
DOI:10.1038/s41598-020-71543-4

Eid M R Al-Hossainy A F 2021 Combined experimental thin films, TDDFT-DFT theoretical method, and spin effect on [PEG-H2O/ZrO2+MgO]h hybrid nanofluid flow with higher chemical rate
Surfaces and Interfaces 23 100971
DOI:10.1016/j.surfin.2021.100971 [Cited within: 1]

Sakiadis B C 1961 Boundary layer behavior on continuous solid flat surfaces
American Institute of Chemical Engineers J. 7 221 225
DOI:10.1002/aic.690070211 [Cited within: 1]

Tsou F K Sparrow E M Goldstein R J 1967 Flow and heat transfer in the boundary layer on a continuous moving surface
Int. J. Heat Mass Transfer 10 219 235
DOI:10.1016/0017-9310(67)90100-7 [Cited within: 1]

Dutta B K 1988 Heat transfer from a stretching sheet in viscous flow with suction of blowing
ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik 68 231 236
DOI:10.1002/zamm.19880680617 [Cited within: 1]

Abel S Sanjayanand E Nandeppanavar M 2008 Viscoelastic MHD flow and heat transfer over a stretching sheet with viscous and ohmic dissipations
Commun. Nonlinear Sci. Numer. Simul. 13 1808 1821
DOI:10.1016/j.cnsns.2007.04.007 [Cited within: 1]

Vajravelu K Prasad V Raju T 2013 Effects of variable fluid properties on the thin film flow of Ostwald-de Waele fluid over a stretching surface
J. Hydrodynamics, Ser. B 25 10 19
DOI:10.1016/S1001-6058(13)60333-9 [Cited within: 1]

Jahan S Sakidin H Nazar R Pop I 2017 Boundary layer flow of nanofluid over a moving surface in a flowing fluid using revised model with stability analysis
Int. J. Mech. Sci. 31-32 1073 1081
DOI:10.1016/j.ijmecsci.2017.07.064 [Cited within: 1]

Sheikholeslami M Ganji D D Javed M Y Ellahi R 2015 Effect of thermal radiation on nanofluid flow and heat transfer using two phase model
J. Magn. Magn. Mater. 374 36 43
DOI:10.1016/j.jmmm.2014.08.021

Eid M R 2016 Chemical reaction effect on MHD boundary-layer flow of two-phase nanofluid model over an exponentially stretching sheet with a heat generation
J. Mol. Liq. 220 718 725
DOI:10.1016/j.molliq.2016.05.005

Eid M R 2017 Time-dependent flow of water-NPs over a stretching sheet in a saturated porous medium in the stagnation-point region in the presence of chemical reaction
J. Nanofluids 6 550 557
DOI:10.1166/jon.2017.1347 [Cited within: 1]

Borkakoti A K Bharali A 1982 Hydromagnetic flow and heat transfer between two horizontal plates, the lower plate being a stretching sheet
Q. Appl. Math. 40 461 467
DOI:10.1090/qam/693878 [Cited within: 1]

Freidoonimehr N Rostami B Rashidi M M Momoniat E 2014 Analytical modeling of three-dimensional squeezing nanofluid flow in a rotating channel on a lower stretching porous wall
Mathematical Problems in Engineering 2014 692728
DOI:10.1155/2014/692728 [Cited within: 1]

Hussain S T Haq R U Khan Z H Nadeem S 2016 Water driven flow of carbon nanotubes in a rotating channel
J. Mol. Liq. 214 136 144
DOI:10.1016/j.molliq.2015.11.042 [Cited within: 8]

Rasool G Zhang T Shafiq A 2019 Second grade nanofluidic flow past a convectively heated vertical Riga plate
Phys. Scr. 94 125212
DOI:10.1088/1402-4896/ab3990 [Cited within: 1]

Rasool G Khan W A Bilal S M Khan I 2018 MHD Squeezed Darcy Forchheimer Nanofluid flow between two h-distance apart horizontal plates
Open Physics 18 1 8
DOI:10.1515/phys-2020-0191 [Cited within: 1]

Hayat T Muhammad K Muhammad T Alsaedi A 2018 Melting Heat in Radiative Flow of Carbon Nanotubes with Homogeneous-Heterogeneous Reactions
Commun. Theor. Phys. 69 441
DOI:10.1088/0253-6102/69/4/441

Hayat T Aziz A Muhammad T Alsaedi A 2019 Darcy–Forchheimer Three-Dimensional Flow of Williamson Nanofluid over a Convectively Heated Nonlinear Stretching Surface
Commun. Theor. Phys. 68 387
DOI:10.1088/0253-6102/68/3/387

Khan S U Waqas H Muhammad T Imran M Ullah M Z 2020 Significance of activation energy and Wu's slip features in Cross nanofluid with motile microorganisms
Commun. Theor. Phys. 71 105001
DOI:10.1088/1572-9494/aba250

Rasool G Shafiq A 2020 Numerical Exploration of the features of thermally enhanced chemically reactive radiative powell-eyring nanofluid flow via darcy medium over non-linearly stretching surface affected by a transverse magnetic field and convective boundary conditions
Appl. Nanosci1 18
DOI:10.1007/s13204-020-01625-2

Rasool G Shafiq A Khalique C M 2020 Marangoni forced convective Casson type nanofluid flow in the presence of Lorentz force generated by Riga plate
Discrete and Continuous Dynamical Systems Series S


Rasool G Shafiq A Baleanu D 2020 Consequences of soret-dufour effects, thermal radiation, and binary chemical reaction on darcy forchheimer flow of nanofluids
Symmetry 12 1421
DOI:10.3390/sym12091421

Jamshed W Kumar V Kumar V 2020 Computational examination of Casson nanofluid due to a non‐linear stretching sheet subjected to particle shape factor: tiwari and Das model
Numerical Methods for Partial Differential Equations.
DOI:10.1002/num.22705

Rasool G Wakif A 2021 Numerical spectral examination of EMHD mixed convective flow of second-grade nanofluid towards a vertical Riga plate using an advanced version of the revised Buongiorno's nanofluid model
J. Therm. Anal. Calorim. 143 2379 2393
DOI:10.1007/s10973-020-09865-8

Jamshed W Nisar K S 2021 Computational single phase comparative study of williamson nanofluid in parabolic trough solar collector via keller box method
Int. J. Energy Res.
DOI:10.1002/er.6554

Jamshed W 2021 Numerical investigation of MHD Impact on maxwell Nanofluid
Int. Commun. Heat Mass Transfer 120 104973
DOI:10.1016/j.icheatmasstransfer.2020.104973

Jamshed W Devi S U Nisar K S 2021 Single phase based study of Ag-Cu/EO Williamson hybrid nanofluid flow over a stretching surface with shape factor
Phyisca Scripta. 96 065202
DOI:10.1088/1402-4896/abecc0 [Cited within: 1]

Tiwari R J Das M K 2007 Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids
Int. J. Heat Mass Transfer 50 2002 2008
DOI:10.1016/j.ijheatmasstransfer.2006.09.034 [Cited within: 2]

Rafiq T Mustafa M 2020 Computational analysis of unsteady swirling flow around a decelerating rotating porous disk in nanofluid
Arab. J. Sci. Eng. 45 1143 1154
DOI:10.1007/s13369-019-04257-z [Cited within: 1]

Brinkman H 1952 The viscosity of concentrated suspensions and solutions
J. Chem. Phys. 20 571 581
DOI:10.1063/1.1700493 [Cited within: 1]

Khanafer K Vafai K Lightstone M 2003 Buoyancy driven heat transfer enhancement in a two dimensional enclosure utilizing nanofluids
Int. J. Heat Mass Transfer 46 3639 3653
DOI:10.1016/S0017-9310(03)00156-X [Cited within: 1]

Maxwell J 1873 A Treatise on Electricity and Magnetism. vol 1Oxford Clarendon Press
[Cited within: 1]

Na T Y 1980 Computational Methods in Engineering Boundary Value Problems 145New York Academic
[Cited within: 1]

相关话题/transfer analysis rotating

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.