Xiao Pan(潘霄)¹, You-Tian Zou(邹有 甜)¹, Hong-Ming Liu(刘宏 铭)¹, Biao He(何彪)², Xiao-Hua Li(李小 华)^{,1,3,4,5,∗∗}, Dong Xiang(向东)^{,1,3,4,∗∗1}School of Nuclear Science and Technology, University of South China, Hengyang 421001, China
²College of Physics and Electronics, Central South University, Changsha 410083, China
³National Exemplary Base for International Sci & Tech. Collaboration of Nuclear Energy and Nuclear Safety, University of South China, Hengyang 421001, China
⁴Cooperative Innovation Center for Nuclear Fuel Cycle Technology & Equipment, University of South China, Hengyang 421001, China
⁵Key Laboratory of Low Dimensional Quantum Structures and Quantum Control, Hunan Normal University, Changsha 410081, China

First author contact: ∗Authors to whom any correspondence should be addressed
Received:2020-12-10Revised:2021-04-12Accepted:2021-04-15Online:2021-05-20

Fund supported:

National Natural Science Foundation of China.11205083.11975132 construct program of the key discipline in Hunan province, the Research Foundation of Education Bureau of Hunan Province, China.18A237 Innovation Group of Nuclear and Particle Physics in USC, the Shandong Province Natural Science Foundation, China.ZR2019YQ01 Hunan Provincial Innovation Foundation For Postgraduate.CX20200909

Abstract
In this work, based on the liquid-drop model and considering the shell correction, we propose a simple formula to calculate the released energy of proton radioactivity (Q_p). The parameters of this formula are obtained by fitting the experimental data of 29 nuclei with proton radioactivity from ground state. The standard deviation between the theoretical values and experimental ones is only 0.157 MeV. In addition, we extend this formula to calculate 51 proton radioactivity candidates in region 51 ≤ Z ≤ 83 taken from the latest evaluated atomic mass table AME2016 and compared with the Q_p calculated by WS4 and HFB-29. The calculated results indicate that the evaluation ability of this formula for Q_p is inferior to WS4 while better than HFB-29.
Keywords： the released energy of proton radioactivity;liquid-drop model;shell correction


PDF (381KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Xiao Pan(潘霄), You-Tian Zou(邹有 甜), Hong-Ming Liu(刘宏 铭), Biao He(何彪), Xiao-Hua Li(李小 华), Dong Xiang(向东). Released energy formula for proton radioactivity based on the liquid-drop model^*. Communications in Theoretical Physics, 2021, 73(7): 075302- doi:10.1088/1572-9494/abf822

1. Introduction

With the continuous developments of radioactive beam facilities, the study of exotic nuclei far from the β-stability line has became a hot project in nuclear physics field [1–9]. Exotic nuclei usually exhibit distinctive features that can provide a lot of information about the nuclear structure different from the well-known stable nuclei, such as new shell closures [10], coupling of bound state and unbound state and so on [11]. Proton radioactivity, the spontaneous emission of a proton by the nucleus, is an important decay mode of exotic nuclei. In 1970, this decay mode was firstly observed in an isomeric state of ⁵³Co by Iackson et al [12, 13]. Subsequently, proton emissions from ground state of ¹⁵¹Lu [14] and¹⁴⁷Tm [15] were detected by Hofmann et al and Klepper et al. Up to now, there are 44 proton emitters decaying from their ground states or isomeric states between Z = 51 and Z = 83 [11, 16–22] being identified in experiments.

Proton radioactivity shares the similar theory of barrier penetration with different kinds of charged particles' radioactivity, such as α decay, heavy ion emission, spontaneous fission, etc [23–31]. Theoretically, a great deal of methods have been proposed to deal with proton radioactivity half-life, which can be divided into two categories. One kind is theoretical models that the probability of proton penetration barrier is calculated by the Wentzel–Kramers–Brillouin approximation, such as the unified fission model [32, 33], the single-folding model [17], the modified two-potential approach [20, 34], the Gamow-like model [35], the effective interactions of density-dependent M3Y [36–38], the generalized liquid-drop model [19, 28], the Coulomb and proximity potential model, etc [21, 39, 40]. The other one is empirical formulas, which rely on the accurate released energy Q_p and orbital angular momentum l taken away by emitted proton, such as universal decay law for proton radioactivity [41], the formula of Zhang and Dong [1], the New Geiger–Nuttall law [42], etc. Using these formulas, ones can estimate the half-life of proton radioactivity easily and rapidly. However, without precise Q_p, we can not to predict the half-life of proton radioactivity for the certain nuclei whose proton radioactivity is energetically allowed or observed but not yet quantified. Therefore, obtaining a simple and accurate Q_p formula is very necessary. In 2010, based on the macroscopic-microscopic model, a simple and local formula for calculating α-decay energies of superheavy nuclei was proposed by Dong et al [43]. They used this formula to calculate the α-decay energy, the theoretical calculations can well reproduce the experimental data. Meanwhile, they also predicted the α-decay energy of newly synthesized superheavy nuclei and obtained positive results. Refering to the shell correction form obtained by Dong et al, we propose the Q_p formula including the liquid-drop part and shell correction. The liquid-drop part is the main part of our formula, which is derived from the Bethe–Weizsäcker binding energy formula.

This article is organized as follows. In the next section, the formula of released energy for proton radioactivity is briefly described. The detailed calculations and discussion are presented in section 3. Finally, a summary is given in section 4.

2. The formula of released energy for proton radioactivity

The relationship between the released energy of proton radioactivity and binding energy can be expressed as Q_p = B(A − 1, Z − 1) − B(A, Z). If the change of binding energy with Z and A is relatively smooth, it can be replaced by(1)$\begin{eqnarray}{Q}_{p}={\rm{\Delta }}B\approx \displaystyle \frac{\partial B}{\partial Z}{\rm{\Delta }}Z+\displaystyle \frac{\partial B}{\partial A}{\rm{\Delta }}A,\end{eqnarray}$with ΔA = ΔZ = −1. From the Bethe–Weizsäcker binding energy formula(2)$\begin{eqnarray}\begin{array}{rcl}{\text{}}B(Z,A) & = & {B}_{v}+{B}_{s}+{B}_{c}+{B}_{a}+{B}_{p}\\ & = & {a}_{v}A-{a}_{s}{A}^{2/3}-{a}_{c}{Z}^{2}{A}^{-1/3}\\ & & -\,{a}_{a}{\left(\displaystyle \frac{A}{2}-Z\right)}^{2}{A}^{-1}\,+\,{a}_{p}\delta {A}^{-1/2},\end{array}\end{eqnarray}$we obtain the following formula(3)$\begin{eqnarray}\begin{array}{rcl}{Q}_{p} & = & 2{a}_{c}{{ZA}}^{-1/3}-\displaystyle \frac{1}{3}{a}_{c}{Z}^{2}{A}^{-4/3}-{a}_{v}+\displaystyle \frac{2}{3}{a}_{s}{A}^{-1/3}\\ & & -\,{a}_{a}(\displaystyle \frac{A}{2}-Z)(\displaystyle \frac{3A}{2}-Z){A}^{-2}+{\rm{\Delta }}{B}_{p}.\end{array}\end{eqnarray}$Here ΔB_p is the change of pairing energy terms when the parent nuclei emits a proton. Up to now, the observed nuclei with proton radioactivity are all odd-Z nuclei. Then ΔB_p can be divided into the following categories(4)$\begin{eqnarray}\begin{array}{c}{\rm{\Delta }}{B}_{p}=\left\{\begin{array}{ll}{a}_{p}{\left(A-1\right)}^{-1/2}, & {\rm{o}}{\rm{d}}{\rm{d}}\,Z-{\rm{e}}{\rm{v}}{\rm{e}}{\rm{n}}\,N\\ {a}_{p}{A}^{-1/2}, & {\rm{o}}{\rm{d}}{\rm{d}}\,Z-{\rm{o}}{\rm{d}}{\rm{d}}\,N.\end{array}\right.\end{array}\end{eqnarray}$

So, we can obtained the liquid-drop part of Q_p formula as follows(5)$\begin{eqnarray}\begin{array}{c}{Q}_{p}=\left\{\begin{array}{l}{a}_{1}+{a}_{2}{A}^{-1/3}+{a}_{3}{ZA}^{-1/3}(2-{\textstyle \tfrac{Z}{3A}})\\ +\,{a}_{4}({\textstyle \tfrac{A}{2}}-Z)({\textstyle \tfrac{3A}{2}}-Z){A}^{-2}+{a}_{5}{\left(A-1\right)}^{-1/2},\\ {\rm{o}}{\rm{d}}{\rm{d}}\,Z-{\rm{e}}{\rm{v}}{\rm{e}}{\rm{n}}\,N\\ \,\,{a}_{1}+{a}_{2}{A}^{-1/3}+{a}_{3}{ZA}^{-1/3}(2-{\textstyle \tfrac{Z}{3A}})\\ +\,{a}_{4}({\textstyle \tfrac{A}{2}}-Z)({\textstyle \tfrac{3A}{2}}-Z){A}^{-2}+{a}_{5}{\left(A\right)}^{-1/2}\\ {\rm{o}}{\rm{d}}{\rm{d}}\,Z-{\rm{o}}{\rm{d}}{\rm{d}}\,N.\end{array}\right.\end{array}\end{eqnarray}$

However, simply considering the part of the liquid-drop in this formula, the Q_p can only reflect the average trend of binding energy. While the effect of shell correction on the Q_p is very important to nuclei around shell closures. Refering to the shell correction form for α-decay energies proposed by Dong et al, the final Q_p formula is expressed as(6)$\begin{eqnarray}\begin{array}{c}{Q}_{p}=\left\{\begin{array}{l}{a}_{1}+{a}_{2}{A}^{-1/3}+{a}_{3}{ZA}^{-1/3}\left(2-{\textstyle \tfrac{Z}{3A}}\right)\\ +\,{a}_{4}\left({\textstyle \tfrac{A}{2}}-Z\right)\left({\textstyle \tfrac{3A}{2}}-Z\right){A}^{-2}+{a}_{5}{\left(A-1\right)}^{-1/2}\\ +\,{a}_{6}\left[1-{\left({\textstyle \tfrac{N-{N}_{0}}{{a}_{7}}}\right)}^{2}\right]\exp \left[-\displaystyle \frac{1}{2}{\left(\displaystyle \frac{N-{N}_{0}}{{a}_{7}}\right)}^{2}\right]\\ {\rm{o}}{\rm{d}}{\rm{d}}\,Z-{\rm{e}}{\rm{v}}{\rm{e}}{\rm{n}}\,N,\\ \,\,{a}_{1}+{a}_{2}{A}^{-1/3}+{a}_{3}{ZA}^{-1/3}\left(2-{\textstyle \tfrac{Z}{3A}}\right)\\ +\,{a}_{4}\left({\textstyle \tfrac{A}{2}}-Z\right)\left({\textstyle \tfrac{3A}{2}}-Z\right){A}^{-2}+{a}_{5}{\left(A\right)}^{-1/2}\\ +\,{a}_{6}\left[1-{\left({\textstyle \tfrac{N-{N}_{0}}{{a}_{7}}}\right)}^{2}\right]\exp \left[-{\textstyle \tfrac{1}{2}}{\left({\textstyle \tfrac{N-{N}_{0}}{{a}_{7}}}\right)}^{2}\right]\\ {\rm{o}}{\rm{d}}{\rm{d}}\,Z-{\rm{o}}{\rm{d}}{\rm{d}}\,N,\end{array}\right.\end{array}\end{eqnarray}$where N₀ is the number of neutron for the shell correction, and it will be shown in the results and discussion.

3. Results and discussion

The Σ represents the deviation between the calculated value and experimental ones, in this work, which is defined as follows:(7)$\begin{eqnarray}\sigma ={\left[\displaystyle \sum _{i=1}^{n}[{Q}_{p}^{i}({\rm{expt}}.)-{Q}_{p}^{i}({\rm{cal}}.)]/n\right]}^{1/2},\end{eqnarray}$where ${Q}_{p}^{i}(\mathrm{expt}.)$ and ${Q}_{p}^{i}(\mathrm{cal}.)$ denote the experimental data and calculated ones of the ith proton emitter released energy, respectively.

At first, fitting the experimental data of Q_p for 29 nuclei with proton radioactivity from ground state listed in table 1, we obtain the best parameters for equation (5) as follows:$\begin{eqnarray*}\left\{\begin{array}{l}{a}_{1}=-25.1625\\ {a}_{2}=71.9351\\ {a}_{3}=0.5829\\ {a}_{4}=-31.2540\\ {a}_{5}=-6.9063.\end{array}\right.\end{eqnarray*}$Using equation (5) and the above parameters, we obtain the Σ = 0.179 MeV calculated by equation (7). For a more intuitive displaying the deviation and attempting to find N₀, we plot the difference of Q_p between the calculated value and experimental ones in figure 1(a). From this figure we can clearly see there is a peak around N = 76, meaning that N₀ = 76 required by equation (6).

Figure 1.

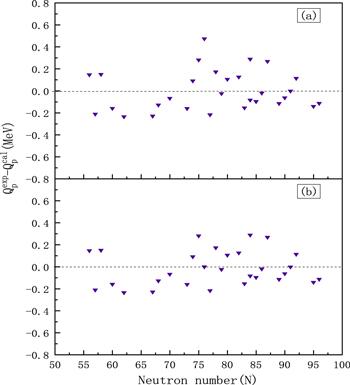New window|Download| PPT slide
Figure 1.The part (a) is the difference of proton radioactivity released energy between the calculated value and experimental one [42] using equation (5) without the shell correction, and the part (b) shows the results obtained using equation (6) with the shell correction term.



Table 1.
Table 1.The experimental data [42] and calculated results for 29 nuclei with proton radioactivity from ground state obtained by equation (6).

Nuclei	${Q}_{p}^{\mathrm{Expt}.}$ (MeV)	${Q}_{p}^{\mathrm{cal}.}$(MeV)	ΔQp(MeV)	Nuclei	${Q}_{p}^{\mathrm{Expt}.}$ (MeV)	${Q}_{p}^{\mathrm{cal}.}$(MeV)	ΔQp(MeV)
109I	0.830	0.683	−0.147	151Lu	1.255	1.149	−0.106
112Cs	0.830	1.040	0.210	155Ta	1.466	1.338	−0.127
113Cs	0.981	0.830	−0.151	156Ta	1.036	1.190	0.154
117La	0.823	0.981	0.158	157Ta	0.956	1.039	0.083
121Pr	0.901	1.135	0.234	159Re	1.816	1.527	−0.289
130Eu	1.043	1.271	0.228	160Re	1.286	1.382	0.096
131Eu	0.963	1.090	0.127	161Re	1.216	1.235	0.019
135Tb	1.193	1.260	0.067	164Ir	1.844	1.575	−0.269
140Ho	1.106	1.266	0.160	166Ir	1.177	1.291	0.114
141Ho	1.190	1.098	−0.092	167Ir	1.087	1.149	0.062
144Tm	1.725	1.443	−0.282	170Au	1.487	1.489	0.001
145Tm	1.754	1.753	−0.001	171Au	1.464	1.350	−0.115
146Tm	0.904	1.121	0.216	176Tl	1.278	1.418	0.140
147Tm	1.133	0.959	−0.174	177Tl	1.172	1.284	0.112
150Lu	1.283	1.306	0.023

New window|CSV

In the following, fixed the parameters a₁ to a₅ as mentioned above and let N₀ in the equation (6) equal to 76, fitting the experimental data of the same 29 nuclei, we obtain the a₆ = 0.4745 and a₇ = −0.0686. Using these parameters and equation (6), we calculate the Q_p for these 29 nuclei. The results are listed in table 1. In this table, the first three columns represent the proton emitter, the experimental Q_p and the calculated result, respecttively. The last column is the difference of Q_p between the calculated value and experimental data. In order to intuitively survey their deviations, we plot the difference of Q_p between the calculated value and experimental ones in figure 1(b). From table 1, it is clearly seen that the deviations of Q_p are almost less than 0.2 MeV except 7 nuclei. The Σ is 0.157 MeV calculated by equation (6). Comparing to equation (5), the result is slightly improved by 12.3% with considering the shell correction. From figure 1(b), we can see that the peak around N = 76 is reduced. It may be the contribution by shell correction.

Finally, as an application, we extend this formula to calculate 51 proton radioactivity candidates in region 51 ≤ Z ≤ 83 taken from the latest evaluated atomic mass table AME2016 [44, 45]. For comparison, the Q_p are also evaluated using Weizsäcker–Skyrme (WS4) formula [46] and Hartree–Fock–Bogoliubov (HFB-29) model [47] In these two models, the Q_p is calculated by [21](8)$\begin{eqnarray}{Q}_{p}={\rm{\Delta }}{M}_{p}-({\rm{\Delta }}{M}_{d}+{\rm{\Delta }}{M}_{{\rm{pr}}})+k({Z}_{p}^{\varepsilon }\,-\,{Z}_{d}^{\varepsilon }),\end{eqnarray}$where ΔM_p, ΔM_d and ΔM_pr are the mass excess of parent nuclei, daughter nuclei and emitted proton, respectively. The last item $k({Z}_{p}^{\varepsilon }-{Z}_{d}^{\varepsilon })$ represents the screening effect of the atmoic electrous [48], where k = 13.6eV, ϵ = 2.408 for Z < 60 and k = 8.7 eV, ϵ = 2.517 for Z ≥ 60 [49].

The detailed results are given in table 2. In this table, the first five columns represent the proton emitter, the experimental data and the calculated Q_p obtained by this work, WS4 and HFB-29, respectively. The last three column are the difference of Q_p between the experimental data and calculated value derived by the three models mentioned above, denoted as Δ₁, Δ₂, Δ₃. From this table, it indicates that all of the Q_p in this work are positive, while in WS4 or HFB-29 the Q_p of some nuclei such as ¹¹⁹La, ¹²⁹Pm , ¹⁴⁵Ho, ^154,155 Lu, ¹⁷¹Ir , ¹⁷⁷Au are negative. To obtain further insight into the well of agreement and the systematics of results, we plot the difference of Q_p between the experimental data and calculated value using these three models in figure 2. From this figure, we can clearly see that the best result is WS4 to reproduce the experimental data but the worst is HFB-29 in these three models. The evaluation abilityour of our work is between them. Furthermore, we calculate the standard deviation between experimental Q_p and calculated ones for this work, WS4 and HFB-29 are 0.347, 0.231 and 0.482 MeV, respectively. The reason may be that this work and WS4 are considered the effect of shell correction, but WS4 considers more comprehensively. Due to the uncertainty of skyme force and the pairing force that its corresponding parameters are obtained by fitting the properties of less nuclei and then extend it to the unknown regions, the results of Q_p calculated by the HFB-29 model are inferior to the first two models.

Figure 2.

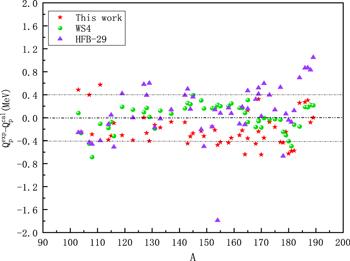New window|Download| PPT slide
Figure 2.The difference of Q_p between the experimental data and calculated value for this work, WS4 and HBF-29.



Table 2.
Table 2.The experimental data and calculated Q_p values of this work, the WS4 model and the HFB-29 model. Δ₁, Δ₂ and Δ₃ are the deviation between experimental data and calculated value for equation (6), the WS4 model and the HFB-29 model.

Nuclei	Qp(MeV)				Δ(MeV)
	Expt.	This work	WS4 [46]	HFB-29 [47]	Δ1	Δ2	Δ3
103 Sb	1.469	0.984	1.389	1.729	0.485	0.080	−0.260
104 Sb	0.519	0.763	0.787	0.779	−0.244	−0.268	−0.260
107 I	1.510	1.113	1.965	1.940	0.397	−0.455	−0.430
108 I	0.610	0.900	1.298	1.070	−0.29	−0.688	−0.460
111 Cs	1.820	1.246	1.927	2.220	0.574	−0.107	−0.400
114 Cs	0.244	0.629	0.423	0.360	−0.385	−0.179	−0.116
115 Cs	0.106	0.423	0.181	0.060	−0.317	−0.075	0.046
116 La	1.091	1.184	1.412	1.601	−0.093	−0.321	−0.510
119 La	0.281	0.588	0.093	−0.139	−0.307	0.188	0.420
123 Pr	0.361	0.754	0.221	0.361	−0.393	0.140	0.000
127 Pm	0.922	0.921	0.828	0.342	0.001	0.094	0.580
128 Pm	0.472	0.741	0.304	0.082	−0.269	0.168	0.390
129 Pm	0.152	0.558	0.140	−0.448	−0.406	0.012	0.600
131 Eu	0.963	1.090	1.155	1.133	−0.127	−0.192	−0.170
133 Eu	0.563	0.737	0.441	0.583	−0.174	0.122	−0.020
137 Tb	0.843	0.917	0.774	0.703	−0.074	0.069	0.140
142Ho	0.854	0.935	0.692	0.464	−0.081	0.162	0.390
143 Ho	0.794	1.244	0.542	0.294	−0.45	0.252	0.500
144 Ho	0.283	0.610	0.048	0.134	−0.327	0.235	0.149
145 Ho	0.174	0.447	−0.218	−0.186	−0.273	0.392	0.360
148 Tm	0.569	0.803	0.268	0.774	−0.234	0.301	−0.205
149 Tm	0.323	0.645	0.163	0.824	−0.322	0.160	−0.501
152 Lu	0.845	0.997	0.679	1.005	−0.152	0.166	−0.160
153 Lu	0.625	0.842	0.460	0.485	−0.217	0.165	0.140
154 Lu	0.215	0.692	−0.007	2.005	−0.477	0.222	−1.790
155 Lu	0.112	0.539	−0.089	0.035	−0.427	0.201	0.077
158 Ta	0.456	0.892	0.254	0.286	−0.436	0.202	0.170
159 Ta	0.389	0.743	0.141	0.316	−0.354	0.248	0.073
165 Ir	1.557	1.430	1.636	1.087	0.127	−0.079	0.470
168 Ir	0.557	1.011	0.721	0.237	−0.454	−0.164	0.320
169 Ir	0.628	0.870	0.673	0.217	−0.242	−0.045	0.411
170 Ir	0.090	0.734	0.260	0.067	−0.644	−0.170	0.023
171 Ir	0.243	0.596	0.249	−0.353	−0.353	−0.006	0.596
169 Au	1.948	1.626	2.011	1.428	0.322	−0.063	0.520
173 Au	1.003	1.078	1.028	0.608	−0.075	−0.025	0.395
175 Au	0.646	0.809	0.673	0.508	−0.163	−0.027	0.138
177 Au	0.117	0.544	0.152	−0.412	−0.427	−0.035	0.529
178 Tl	0.718	1.154	0.963	1.388	−0.436	−0.245	−0.670
179 Tl	0.774	1.021	1.080	0.708	−0.247	−0.306	0.066
180 Tl	0.266	0.892	0.677	0.308	−0.626	−0.411	−0.042
181 Tl	0.179	0.762	0.677	0.258	−0.583	−0.498	−0.079
182 Tl	0.061	0.634	0.182	−0.062	−0.573	−0.121	0.123
184 Bi	1.364	1.106	1.519	0.669	0.258	−0.155	0.695
186 Bi	1.124	0.853	0.938	0.259	0.271	0.186	0.865
187 Bi	1.028	0.726	0.845	0.159	0.302	0.183	0.869
188 Bi	0.521	0.603	0.300	−0.311	−0.082	0.221	0.832
189 Bi	0.479	0.478	0.266	−0.571	0.001	0.213	1.050
162 Re	0.786	1.092	0.616	0.896	−0.306	0.170	−0.110
163 Re	0.723	0.946	0.556	0.536	−0.223	0.167	0.187
164 Re	0.166	0.805	0.083	0.286	−0.639	0.083	−0.120
165 Re	0.302	0.662	−0.005	0.146	−0.36	0.307	0.156

New window|CSV

4. Summary

In summary, based on the liquid-drop model and considered shell correction, we put forward a simple formula for the Q_p. The corresponding parameters are obtained by fitting the experimental data of 29 nuclei with proton radioactivity from ground state. The standard deviation between the theoretical values and experimental ones is 0.157 MeV. In order to further test the reliability of this formula,we calculate the Q_p values of 51 proton radioactivity candidates in region 51 ≤ Z ≤ 83 obtained from the latest evaluated atomic mass table AME2016 and compare with the Q_p values extracted from the WS4 and HFB-29 models. It is found that the accuracy of our formula is higher than that of the HFB-29 model, although its accuracy is lower than that of the WS4 model. This indicates our formula is suitable for the predictions of Q_p to some extent.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Zhang Z X Dong J M 2018 Chin. Phys. C 42 014104
DOI:10.1088/1674-1137/42/1/014104 [Cited within: 2]

[2]Ni D D Ren Z Z 2017 Chin. Phys. C 41 114104
DOI:10.1088/1674-1137/41/11/114104

[3]Cui J P et al. 2020 Phys. Rev. C 101 014301
DOI:10.1103/PhysRevC.101.014301

[4]Giovinazzo J et al. 2002 Phys. Rev. Lett. 89 102501
DOI:10.1103/PhysRevLett.89.102501

[5]Casten R F Sherrill B M 2000 Prog. Part. Nucl. Phys. 45 S171
DOI:10.1016/S0146-6410(00)90013-9

[6]Liu H M et al. 2020 Chin. Phys. C 44 094106
DOI:10.1088/1674-1137/44/9/094106

[7]Alex Brown B 1998 Phys. Rev. C 58 220
DOI:10.1103/PhysRevC.58.220

[8]Wang Y Z et al. 2017 Phys. Rev. C 95 014302
DOI:10.1103/PhysRevC.95.014302

[9]Liu H M et al. 2021 Chin. Phys. C 45 044110
DOI:10.1088/1674-1137/abe10f [Cited within: 1]

[10]Wienholtz F et al. 2013 Nature 498 346
DOI:10.1038/nature12226 [Cited within: 1]

[11]Sonzogni A A 2002 Nucl. Data Sheets 95 1
DOI:10.1006/ndsh.2002.0001 [Cited within: 2]

[12]Jackson K P et al. 1970 Phys. Lett. B 33 281
DOI:10.1016/0370-2693(70)90269-8 [Cited within: 1]

[13]Cerny J Esterl J Gough R Sextro R 1970 Phys. Lett. B 33 284
DOI:10.1016/0370-2693(70)90270-4 [Cited within: 1]

[14]Hofmann S et al. 1982 Z. Phys. A 305 111
DOI:10.1007/BF01415018 [Cited within: 1]

[15]Klepper O Batsch T Hofmann S Kirchner R Kurcewicz W Reisdorf W Roeckl E Schardt D Nyman G 1982 Z. Phys. A 305 125
DOI:10.1007/BF01415019 [Cited within: 1]

[16]Delion D S Liotta R J Wyss R 2006 Phys. Rev. Lett. 96 072501
DOI:10.1103/PhysRevLett.96.072501 [Cited within: 1]

[17]Basu D N Roy Chowdhury P Samanta C 2005 Phys. Rev. C 72 051601R
DOI:10.1103/PhysRevC.72.051601 [Cited within: 1]

[18]Blank B Borge M 2008 Prog. Part Nucl. Phys. 60 403
DOI:10.1016/j.ppnp.2007.12.001

[19]Zhang H F Wang Y J Dong J M Li J Q Scheid W 2010 J. Phys. G: Nucl. Part. Phys. 37 085107
DOI:10.1088/0954-3899/37/8/085107 [Cited within: 1]

[20]Qian Y B Ren Z Z 2016 Eur. Phys. J. A 52 68
DOI:10.1140/epja/i2016-16068-3 [Cited within: 1]

[21]Santhosh K P Sukumaran I 2017 Phys. Rev. C 96 034619
DOI:10.1103/PhysRevC.96.034619 [Cited within: 2]

[22]Budaca R Budaca A I 2017 Eur. Phys. J. A 53 160
DOI:10.1140/epja/i2017-12352-0 [Cited within: 1]

[23]Buck B Merchant A C Perez S M 1991 J. Phys. G: Nucl. Part. Phys. 17 L91
DOI:10.1088/0954-3899/17/6/001 [Cited within: 1]

[24]Delion D S 2009 Phys. Rev. C 80 024310
DOI:10.1103/PhysRevC.80.024310

[25]Poenaru D N Gherghescu R A Greiner W 2011 Phys. Rev. C 83 014601
DOI:10.1103/PhysRevC.83.014601

[26]Santhosh K Sahadevan S Priyanka B Unnikrishnan M 2012 Nucl. Phys. A 882 49
DOI:10.1016/j.nuclphysa.2012.04.001

[27]Bao X J Guo S Q Zhang H F Xing Y Z Dong J M Li J Q 2015 J. Phys. G: Nucl. Part. Phys. 42 085101
DOI:10.1088/0954-3899/42/8/085101

[28]Dong J M Zhang H F Royer G 2009 Phys. Rev. C 79 054330
DOI:10.1103/PhysRevC.79.054330 [Cited within: 1]

[29]Wang Y Z Wang S J Hou Z Y Gu J Z 2015 Phys. Rev. C 92 064301
DOI:10.1103/PhysRevC.92.064301

[30]Lemaire M C et al. 1979 Phys. Lett. B 85 38
DOI:10.1016/0370-2693(79)90772-X

[31]Wang Y Z Xing F Z Xiao Y Gu J Z 2021 Chin. Phys. C 45 044111
DOI:10.1088/1674-1137/abe112 [Cited within: 1]

[32]Balasubramaniam M Arunachalam N 2005 Phys. Rev. C 71 014603
DOI:10.1103/PhysRevC.71.014603 [Cited within: 1]

[33]Dong J M Zhang H F Zuo W Li J Q 2010 Chin. Phys. C 34 182
DOI:10.1088/1674-1137/34/2/005 [Cited within: 1]

[34]Chen J L Cheng J H Deng J G Li X H 2018 Nucl. Phys. Rev. 35 257
DOI:10.11804/NuclPhysRev.35.04.470 [Cited within: 1]

[35]Zdeb A Warda M Petrache C M Pomorski K 2016 Eur. Phys. J. A 52 323
DOI:10.1140/epja/i2016-16323-7 [Cited within: 1]

[36]Qian Y B Ren Z Z Ni D D 2010 Chin. Phys. Lett. 27 072301
DOI:0.1088/0256-307X/27/7/072301 [Cited within: 1]

[37]Bhattacharya M Gangopadhyay G 2007 Phys. Lett. B 651 263
DOI:10.1016/j.physletb.2007.06.012

[38]Basu D N 2004 J. Phys. G: Nucl. Part. Phys. 30 B7
DOI:10.1088/0954-3899/30/6/B01 [Cited within: 1]

[39]Guo C Zhang G Le X 2013 Nucl. Phys. A 897 54
DOI:10.1016/j.nuclphysa.2012.10.003 [Cited within: 1]

[40]Deng J G Li X H Chen J L Cheng J H Wu X J 2019 Eur. Phys. J. A 55 58
DOI:10.1140/epja/i2019-12728-0 [Cited within: 1]

[41]Qi C Delion D S Liotta R J Wyss R 2012 Phys. Rev. C 85 011303R
DOI:10.1103/PhysRevC.85.011303 [Cited within: 1]

[42]Chen J L Xu J Y Deng J G Li X H He B Chu P C 2019 Eur. Phys. J. A 55 214
DOI:10.1140/epja/i2019-12927-7 [Cited within: 3]

[43]Dong T K Ren Z Z 2010 Phys. Rev. C 82 034320
DOI:10.1103/PhysRevC.82.034320 [Cited within: 1]

[44]Huang W Audi G Wang M Kondev F G Naimi S Xu X 2017 Chin. Phys. C 41 030002
DOI:10.1088/1674-1137/41/3/030002 [Cited within: 1]

[45]Wang M Audi G Kondev F G Huang W Naimi S Xu X 2017 Chin. Phys. C 41 030003
DOI:10.1088/1674-1137/41/3/030003 [Cited within: 1]

[46]Wang N Liu M Wu Z Meng J 2014 Phys. Lett. B 734 215
DOI:10.1016/j.physletb.2014.05.049 [Cited within: 2]

[47]Goriely S 2014 Nucl. Phys. A 933 68
DOI:10.1016/j.nuclphysa.2014.09.045 [Cited within: 2]

[48]Denisov V Y Ikezoe H 2005 Phys. Rev. C 72 064613
DOI:10.1103/PhysRevC.72.064613 [Cited within: 1]

[49]Huang K N Aoyagi M Chen M H Crasemann B Mark H 1976 At. Data Nucl. Data Tables 18 243
DOI:10.1016/0092-640X(76)90027-9 [Cited within: 1]