删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

Significance of activation energy and Wu's slip features in Cross nanofluid with motile microorgani

本站小编 Free考研考试/2022-01-02
Sami Ullah Khan1, Hassan Waqas2, Taseer Muhammad,3, Muhammad Imran2, Malik Zaka Ullah41Department of Mathematics, COMSATS University Islamabad, Sahiwal 57000, Pakistan
2Department of Mathematics, Government College University, Faisalabad 38000, Pakistan
3Department of Mathematics, College of Sciences, King Khalid University, Abha 61413, Saudi Arabia
4Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia

Received:2020-01-04Revised:2020-06-01Accepted:2020-06-02Online:2020-09-16


Abstract
The current article investigates the impact of the bioconvection in an unsteady flow of magnetized Cross nanofluid with gyrotactic microorganisms and activation energy over a linearly stretched configuration. The analysis has been performed by utilizing the realistic Wu's slip boundary and zero mass flux conditions. The effects of nonlinear thermal radiation and the activation energy are also addressed. The governing flow equations are deduced to a dimensionless form by considering suitable transformations which are numerically targeted via a shooting algorithm. The physical visualization of each physical parameter governing the flow problem has been displayed graphically for distribution of velocity, temperature, concentration and motile microorganisms. The numerical treatment for the variation of skin friction coefficient, local Nusselt number, local Sherwood number and motile density number is performed in tabular forms.
Keywords： Cross nanofluid;nonlinear thermal radiation;gyrotactic motile microorganism;Wu's slip;shooting technique


PDF (1516KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Sami Ullah Khan, Hassan Waqas, Taseer Muhammad, Muhammad Imran, Malik Zaka Ullah. Significance of activation energy and Wu's slip features in Cross nanofluid with motile microorganisms. Communications in Theoretical Physics, 2020, 72(10): 105001- doi:10.1088/1572-9494/aba250

Nomenclature

${K}_{n}$ Knudsen number

${\alpha }^{* }$ momentum accommodation coefficient

${\beta }^{* }$ molecular mean free path

${K}_{1}$ combine parameter

n power law index parameter

$f$ velocity distribution

$\gamma $ first order slip factor

$\delta $ second order slip factor'

h heat transfer coefficient

$\phi $ nanoparticle concentration

$\beta $ time constant

$\varphi $ porous medium

${\rho }_{p}$ nanoparticle density

${\rho }_{m}$ density of motile microorganism

${\alpha }_{m}$ thermal diffusivity

${\left(\rho c\right)}_{f}$ fluid heat capacity

${D}_{T}$ thermodiffusion constant

$\kappa $ Boltzmann constant

${E}_{a}$ activation energy

${W}_{e}$ speed of cells

$\lambda $ mixed convection parameter

$We$ Weissenberg parameter

$Nr$ buoyancy ratio parameter

$Bi$ Biot parameter

$Le$ Lewis number

$Nb$ Brownian motion parameter

$Rd$ radiation parameter

$Pe$ Peclet number

${q}_{w}$ heat flux

${q}_{j}$ mass flux

$\tilde{N}{u}_{x},$ local Nusselt number

$\sigma * $ electrical conductivity

$k* $ porous medium permeability

$g$ gravity

$\tilde{T}$ nanoparticle temperature

$\tilde{C}$ nanoparticle concentration

${\left(\rho c\right)}_{p}$ nanoparticles' effective heat capacity

${D}_{B}$ diffusion constant

$Kr$ reaction constant

${b}_{1}$ chemotaxis constant

$Ha$ combined parameter

${\rm{\Gamma }}$ unsteady parameter

$Nc$ bioconvection Rayleigh number

$Pr$ Prandtl number

${\theta }_{w}$ temperature ratio parameter

$Nt$ thermophoresis parameter

$E$ activation energy parameter

${{\rm{\Omega }}}_{1}$ bioconvection constant

$Lb$ bioconvection Lewis number

${q}_{m}$ density flux

$S{h}_{x}$ local Sherwood number

$\tilde{N}{h}_{x}$ local density number

1. Introduction

Due to the rapid commercial, engineering and industrial significance of nanofluids, a fundamental interest has been developed by numerous researchers in recent days. The nanoparticles, a complex mixture of nano-sized particles (1-100 nm), attained highly improved thermo-physical features. Due to excellent enhanced resistance and miscellaneous characteristics, nanoparticles are efficiently used in mechanical, industrial, chemical and biological sciences such as cooling of various electronic chips, thermal reactors, chemical processes, fission reactions, sensor technology, catalysis, diagnoses and treatment of cancer tissue, brain tumors, antibacterial applications and many more. The fundamental applications of nanoparticles in thermal extrusion systems also overcome the attention of poor energy reservoirs. From the literature surveyed, it is noted that basic investigation on nanofluids was proposed by Choi [1]. This involuntary idea insisted scientists perform further interesting contributions in the flow of nanofluids in the presence of some unique flow features. For instance, Sheikholeslami et al [2] studied the forced convection flow of nanoparticles subjected to a magnetic field by utilizing the Lattice Boltzmann technique. Khan et al [3] analyzed the wedge flow of a Carreau nanofluid with the existence of heat absorption and generation features by employing the shooting technique. The combined heat and mass transportations based on modified Cattaneo-Christov theories in the flow of viscoelastic nanoparticles over a moving geometry was scrutinized by Hayat et al [4]. Mahanthesh et al [5] analyzed the mixed convective flow over a rotating frame with evaluation of Hall current effects. Siddiqui and Turkyilmazoglu [6] initiated an interesting contribution based on the flow of ferro-nanoparticles in a cavity. Hsiao [7] performed a theoretical model based on the flow of micropolar nanoparticles in the presence of viscous dissipation characteristics over a moving surface. The flow of rate type nanoliquid with a heat source and sink features over a rotating disk has been thrashed out numerically by Ahmed et al [8]. The study of graphene-water nanoparticles over a stretching/shrinking surface subject to suction and injection characteristics was examined by Aly [9]. The stability analysis for each critical value was determined and various results have been reported graphically. Rout and Mishra [10] performed a comparative study regarding magnetized nanoparticles over a moving surface. The interaction of SA-Al2O3 and SA-Cu nanoparticles with chemical reaction effects and slip features was reported by Tlili et al [11]. Hayat et al [12] studied a second grade nanofluid in two parallel disks where magnetic field effects were proposed perpendicularly. Khan and Shehzad [13] captured the Brownian motion and thermophoresis features in a third grade nanofluid over an accelerated surface. The flow of Maxwell viscoelasticity-based nanoparticles in the presence of slip consequences was specified numerically by Waqas et al [14]. Sheikholeslami et al [15] investigated the forced convective flow of a nanofluid in a three-dimensional enclosure in the presence of a hot cubic obstacle. Shehzad et al [16] explored both the magnetic field and porous medium effects on the flow of a micropolar nanofluid configured by a stretched surface. The study of Cross magneto-nanofluid in stagnation point flow of a contracting and expanding cylinder has been recently presented by Ali et al [17]. Li et al [18] evaluated the characteristics of nanoparticles in a storage finned in the presence of melting heat transfer.

It is commonly observed that when microorganisms gathered near the upper surface of a fluid, the phenomenon of unstable density stratification appeared, which causes bioconvection. The variation in microorganisms is self propelled and due to the swimming of such microorganisms, some precise direction in the base fluid results in an enhanced base liquid density. During this process the microorganisms migrated towards the lower region due to density difference. The microorganisms are classified as gyrotaxis, gravitaxis and oxytaxis organisms. An interesting conflict between microorganisms and nanoparticles is justified as microorganisms are being self propelled while nanoparticles' movement is driven due to Brownian and thermophoresis features. The utilization of microorganisms in the nanoparticles can efficiently improve the suspension stability. The first continuation of the involvement of microorganisms in nanoparticles was presented by Kuznetsov [19]. Later on some inspired contributions have been reported by numerous researchers with various flow features. Alsaedi et al [20] inspected the bioconvection phenomenon with the utilization of nanoparticles over a moving configuration. The constituted problem was treated analytically via a homotopic algorithm. Alwatban et al [21] analyzed the features of bioconvection in a flow of Eyring Powell nanoparticles in the presence of an activation energy.

The anisotropic slip flow in the presence of Stefan blowing features and microorganisms over a rotating cone was numerically executed by Zohra et al [22]. Waqas et al [23] examined the phenomenon of motile microorganisms in nanomaterials over a porous surface. The flow of Sisko nanomaterials with second order slip effects and gyrotactic microorganisms was conducted by Farooq et al [24]. For numerical computation a famous finite difference approach was utilized with excellent accuracy. Khan et al [25] performed analysis dealing with the bioconvection flow of nanofluids. The boundary layer flow over a thin needle in a non-Newtonian nanofluid with motile microorganisms subject to the Stefan blowing consequences was determined by Amirsom et al [26]. The role of chemical reactions and energy activations in various fields of science oil emulsions, mechanical engineering, nuclear reactor cooling, chemical processes, and thermal reservoirs is quite necessitated. The activation energy is the amount of energy required to undergo the reaction processes. The basic work on this topic was initiated by Svante Arrhenius, which has been extended by much further research [27-31].

Due to the attractive response of bioconvection flow of nanofluids, the aim here is to examine the rheological consequences of a non-Newtonian nanofluid containing microorganisms in the presence of nonlinear thermal radiation and activation energy. A famous Cross fluid is utilized to examine the viscoelastic behavior [32, 33]. The main motivation of the present analysis is to report the bioconvection phenomenon in a flow of Cross nanofluid, which encountered some diverse and unique rheological characteristics. Moreover, this investigation has been executed by introducing the slip effects of second order. The utilization of a magnetized Cross nanofluid, thermal radiation, activation energy, gyrotactic microorganism and second order slip make this analysis quite versatile and motivating. The consideration of second order slip is more realistic, which involves two slip factors to control the thickness of the associated boundary layer. The formulated flow problem is numerically treated by using the shooting algorithm. A detailed graphically-based investigation for each flow parameter has been reported with relevant physical consequences.

2. Mathematical formulation

The unsteady and two-dimensional flow of a Cross nanoliquid over a stretched configuration has been examined with utilization of nonlinear thermal radiation and motile microorganisms. The considered flow has been assumed in the xy-plane where the velocity component u is taken in the x-direction and v is considered along the y-axis. A time-dependent magnetic force has been employed in the perpendicular direction where the influence of induced magnetic force is ignored with low Reynolds' number approximations. A well-known Buongiorno's nanoliquid model is incorporated to visualize the important consequences of Brownian movement and thermophoresis features. Additionally, the second order slip constraints (Wu's slip) are used near the stretched flow geometry. The transportation of combined heat and mass are controlled via a convective boundary and zero nanoparticles' mass flux constraints. The flow equations modeled on such assumptions may be expressed as [32, 33]:$\begin{eqnarray}\displaystyle \frac{\partial \tilde{u}}{\partial x}+\displaystyle \frac{\partial \tilde{v}}{\partial y}=0,\end{eqnarray}$$\begin{eqnarray}\begin{array}{l}\displaystyle \frac{\partial \tilde{u}}{\partial t}+\tilde{u}\displaystyle \frac{\partial \tilde{u}}{\partial x}+\tilde{v}\displaystyle \frac{\partial \tilde{u}}{\partial y}=\nu \displaystyle \frac{\partial }{\partial y}\left[\displaystyle \frac{\displaystyle \frac{\partial u}{\partial y}}{1+\beta \left(\displaystyle \frac{\partial \tilde{u}}{\partial y}\right)}\right]\\ \,-\left(\displaystyle \frac{\sigma * {B}_{0}^{2}\left(t\right)}{{\rho }_{f}}+\displaystyle \frac{\nu \varphi }{k* }\right)\tilde{u}\\ \,+\displaystyle \frac{1}{{\rho }_{f}}\left[\begin{array}{l}\left(1-{\tilde{C}}_{f}\right){\rho }_{f}\beta * g* \left(\tilde{T}-{\tilde{T}}_{\infty }\right)\\ \,-\left({\rho }_{p}-{\rho }_{f}\right)g* \left(\tilde{C}-{\tilde{C}}_{\infty }\right)\\ \,-\left(\tilde{N}-{\tilde{N}}_{\infty }\right)g\gamma * * \left({\rho }_{m}-{\rho }_{f}\right)\end{array}\right],\end{array}\end{eqnarray}$$\begin{eqnarray}\begin{array}{l}\displaystyle \frac{\partial \tilde{T}}{\partial t}+\tilde{u}\displaystyle \frac{\partial \tilde{T}}{\partial x}+\tilde{v}\displaystyle \frac{\partial \tilde{T}}{\partial y}=\left({\alpha }_{m}+\displaystyle \frac{16\sigma * {T}_{\infty }^{3}}{3k* {\left(\rho c\right)}_{f}}\right)\displaystyle \frac{{\partial }^{2}\tilde{T}}{\partial {y}^{2}}\\ \,+\displaystyle \frac{{\left(\rho c\right)}_{f}}{{\left(\rho c\right)}_{p}}\left({D}_{B}\displaystyle \frac{\partial \tilde{C}}{\partial y}\displaystyle \frac{\partial \tilde{T}}{\partial y}+\displaystyle \frac{{D}_{T}}{{\tilde{T}}_{\infty }}{\left(\displaystyle \frac{\partial \tilde{T}}{\partial y}\right)}^{2}\right),\end{array}\end{eqnarray}$$\begin{eqnarray}\begin{array}{l}\displaystyle \frac{\partial \tilde{C}}{\partial t}+\tilde{u}\displaystyle \frac{\partial \tilde{C}}{\partial x}+\tilde{v}\displaystyle \frac{\partial \tilde{C}}{\partial y}={D}_{B}\displaystyle \frac{{\partial }^{2}\tilde{C}}{\partial {y}^{2}}\,+\displaystyle \frac{{D}_{T}}{{\tilde{T}}_{\infty }}\displaystyle \frac{{\partial }^{2}\tilde{T}}{\partial {y}^{2}}\\ \,-K{r}^{2}\left(\tilde{C}-{\tilde{C}}_{\infty }\right){\left(\displaystyle \frac{\tilde{T}}{{\tilde{T}}_{\infty }}\right)}^{2}\exp \left(\displaystyle \frac{-{E}_{a}}{\kappa \tilde{T}}\right),\end{array}\end{eqnarray}$$\begin{eqnarray}\begin{array}{l}\displaystyle \frac{\partial \tilde{N}}{\partial t}+\tilde{u}\displaystyle \frac{\partial \tilde{N}}{\partial x}+\tilde{v}\displaystyle \frac{\partial \tilde{N}}{\partial y}+\displaystyle \frac{{b}_{m}{W}_{c}}{\left({\tilde{C}}_{w}-{\tilde{C}}_{\infty }\right)}\left[\displaystyle \frac{\partial }{\partial y}\left(\tilde{N}\displaystyle \frac{\partial \tilde{C}}{\partial y}\right)\right]\\ \,={D}_{m}\left(\displaystyle \frac{{\partial }^{2}\tilde{N}}{\partial {y}^{2}}\right).\end{array}\end{eqnarray}$The following boundary conditions are entertained for the continued flow problem:$\begin{eqnarray}\begin{array}{l}\tilde{u}={\tilde{u}}_{w}+{\tilde{U}}_{{\rm{s}}{\rm{l}}{\rm{i}}{\rm{p}}},v=0,-k\displaystyle \frac{\partial \tilde{T}}{\partial y}={h}_{f}\left({\tilde{T}}_{f}-\tilde{T}\right),\\ {D}_{B}\displaystyle \frac{\partial \tilde{C}}{\partial y}+\displaystyle \frac{{D}_{T}}{{\tilde{T}}_{\infty }}\displaystyle \frac{\partial \tilde{T}}{\partial y}=0,\tilde{N}={\tilde{N}}_{w}\,{\rm{at}}\,y=0,\end{array}\end{eqnarray}$$\begin{eqnarray}\begin{array}{l}\tilde{u}\to {\tilde{U}}_{\infty }=0,\,\tilde{T}\to {\tilde{T}}_{\infty },\,\tilde{C}\to {\tilde{C}}_{\infty },\\ \tilde{N}\to {N}_{\infty }\,as\,y\to \infty .\end{array}\end{eqnarray}$

The second order slip boundary constraints (Wu's slip) for the flow problem are [34-37]:$\begin{eqnarray}\begin{array}{l}{\tilde{U}}_{{\rm{s}}{\rm{l}}{\rm{i}}{\rm{p}}}=\displaystyle \frac{2}{3}\left(\displaystyle \frac{3-\alpha * {p}^{2}}{\alpha * }-\displaystyle \frac{3}{2}\displaystyle \frac{\left(1-{p}^{2}\right)}{{k}_{n}}\right)\beta * \displaystyle \frac{\partial \tilde{u}}{\partial y}\\ \,-\displaystyle \frac{1}{4}\left[{p}^{4}+\displaystyle \frac{2}{{k}_{n}^{2}}\left(1-{p}^{2}\right)\right]{\beta }^{* 2}\displaystyle \frac{{\partial }^{2}\tilde{u}}{\partial {y}^{2}},\end{array}\end{eqnarray}$$\begin{eqnarray}{\tilde{U}}_{{\rm{s}}{\rm{l}}{\rm{i}}{\rm{p}}}={A}_{1}\displaystyle \frac{\partial \tilde{u}}{\partial y}+{B}_{1}\displaystyle \frac{{\partial }^{2}\tilde{u}}{\partial {y}^{2}},\end{eqnarray}$where $l=\,\min \left[\tfrac{1}{{k}_{n}},1\right]$ while ${A}_{1},$ ${B}_{1}$ are constants. Selecting [28]:$\begin{eqnarray}\begin{array}{l}\eta =y\sqrt{\displaystyle \frac{{\tilde{U}}_{w}}{\nu x}},\,\psi =\sqrt{\nu x{\tilde{U}}_{w}}f\left(\eta \right),\,\theta \left(\eta \right)=\displaystyle \frac{\tilde{T}-{\tilde{T}}_{\infty }}{{\tilde{T}}_{w}-{\tilde{T}}_{\infty }},\\ \phi \left(\eta \right)=\displaystyle \frac{\tilde{C}-{\tilde{C}}_{\infty }}{{\tilde{C}}_{w}-{\tilde{C}}_{\infty }},\chi \left(\eta \right)=\displaystyle \frac{\tilde{N}-{\tilde{N}}_{\infty }}{{\tilde{N}}_{w}-{\tilde{N}}_{\infty }}.\end{array}\end{eqnarray}$

By interaction of the above variables, we obtained the following set of dimensionless equations:$\begin{eqnarray}\begin{array}{l}\left[1+\left(1-n\right)\left(We{\left(f^{\prime\prime} \right)}^{n}\right)\right]f\prime\prime\prime +\left(ff^{\prime\prime} -{\left(f^{\prime} \right)}^{2}\right.\\ \,-\left.{\rm{\Gamma }}\left(f^{\prime} +0.5\eta f^{\prime\prime} \right)\right){\left(1+{\left(Wef^{\prime\prime} \right)}^{n}\right)}^{2}\\ \,-\left(1+{\left(Wef^{\prime\prime} \right)}^{n}\right)Haf^{\prime} +{{\rm{\Lambda }}}_{1}\left(\theta -Nr\phi -Nc\chi \right)=0,\end{array}\end{eqnarray}$$\begin{eqnarray}\begin{array}{l}\theta ^{\prime\prime} +Pr\left(f^{\prime} \theta -0.5{\rm{\Gamma }}\eta \theta ^{\prime} +Nb\theta ^{\prime} \phi ^{\prime} +Nt{\theta }^{{\prime} 2}\right)\\ \,+\displaystyle \frac{4}{3Rn}\displaystyle \frac{{\rm{d}}}{{\rm{d}}\eta }\left(1+{\left(\left({\theta }_{w}-1\right)\theta \right)}^{3}\theta ^{\prime} \right)=0,\end{array}\end{eqnarray}$$\begin{eqnarray}\begin{array}{l}\phi ^{\prime\prime} +PrLe\left(f^{\prime} \phi -0.5\eta \phi ^{\prime} \right)+\displaystyle \frac{Nt}{Nb}\theta ^{\prime\prime} \\ \,-PrLe\sigma {\left(1+\omega \theta \right)}^{m}\exp \left(\displaystyle \frac{-E}{1+\omega \theta }\right)\phi =0,\end{array}\end{eqnarray}$$\begin{eqnarray}\begin{array}{l}\chi ^{\prime\prime} +Lb\left(\left(f^{\prime} \chi -0.5\eta \chi ^{\prime} \right)\right)\\ \,-Pe\left(\phi ^{\prime\prime} \left(\chi +{{\rm{\Omega }}}_{1}\right)+\chi ^{\prime} \phi ^{\prime} \right)=0.\end{array}\end{eqnarray}$

The transformed boundary assumptions are$\begin{eqnarray}\begin{array}{l}f\left(0\right)=0,f^{\prime} \left(0\right)=1+\gamma f^{\prime\prime} \left(0\right)+\delta f^{\prime\prime \prime} \left(0\right),\\ \theta ^{\prime} \left(0\right)=Bi\left(\theta \left(0\right)-1\right),Nb\theta ^{\prime} \left(0\right)+Nt\phi ^{\prime} \left(0\right)=0,\\ \chi \left(0\right)=1,\end{array}\end{eqnarray}$$\begin{eqnarray}f^{\prime} \left(\infty \right)\to 0,\,\theta \left(\infty \right)\to 0,\,\phi \left(\infty \right)\to 0,\,\chi \left(\infty \right)\to 0,\end{eqnarray}$where the following are defined by$\begin{eqnarray}\begin{array}{l}Ha\left(=\displaystyle \frac{\nu \varphi }{{k}^{\ast }b}+\displaystyle \frac{{\sigma }^{* }{B}_{0}^{2}}{{\rho }_{f}b}\right),\lambda =\displaystyle \frac{{T}_{\infty }{\beta }_{1}{g}_{1}\left(1-{C}_{\infty }\right)}{a{\left(\rho c\right)}_{f}},\\ {\rm{\Gamma }}\left(=\displaystyle \frac{a}{c}\right),We=\left(=\displaystyle \frac{Ba{\mathrm{Re}}^{1/2}}{1-ct}\right){\theta }_{w}\left(=\displaystyle \frac{{\tilde{T}}_{w}}{{\tilde{T}}_{\infty }}\right),\\ Nc\left(=\displaystyle \frac{{\gamma }_{1}\left({\rho }_{m}-{\rho }_{f}\right)\left({N}_{w}-{N}_{\infty }\right)}{{\rho }_{f}\left(1-{C}_{\infty }\right){T}_{\infty }\,{\beta }_{1}}\right),\\ Nr\left(=\displaystyle \frac{\left({\rho }_{p}-{\rho }_{f}\right)\left({\tilde{C}}_{w}-{\tilde{C}}_{\infty }\right)}{{\tilde{T}}_{\infty }{\beta }_{1}{\rho }_{f}\left(1-{\tilde{C}}_{\infty }\right)}\right),Pr\left(=\displaystyle \frac{\nu }{\alpha }\right),\\ Bi\left(=\displaystyle \frac{{h}_{f}}{k}\sqrt{\displaystyle \frac{\nu }{a}}\right),Le\left(=\displaystyle \frac{\alpha }{{D}_{B}}\right),\\ Nt\left(=\displaystyle \frac{\tau \left({\tilde{T}}_{w}-{\tilde{T}}_{\infty }\right)\left({D}_{T}\right)}{\rho {c}_{f}\left(\nu \right)}\right),\\ Nb=\left(\displaystyle \frac{\tau \left({\tilde{C}}_{w}-{\tilde{C}}_{\infty }\right)\left({D}_{B}\right)}{\rho {c}_{f}\left(\nu \right)}\right),E\left(=\displaystyle \frac{{E}_{0}}{\kappa {T}_{\infty }}\right),\\ Rd\left(=\displaystyle \frac{4\sigma {T}_{\infty }^{3}}{{{k}_{1}}^{* }k}\right),{{\rm{\Omega }}}_{1}\left(=\displaystyle \frac{{\tilde{N}}_{\infty }}{{\tilde{N}}_{w}-{\tilde{N}}_{\infty }}\right),\\ Pe\left(=\displaystyle \frac{{b}_{m}{W}_{c}}{{D}_{mn}}\right),Lb=\displaystyle \frac{\nu }{{D}_{nn}},\alpha \left(=A\sqrt{\displaystyle \frac{a}{\nu }}\right),\\ \beta \left(=B\left(\displaystyle \frac{a}{\nu }\right)\right).\end{array}\end{eqnarray}$

The mathematical formulations for the local Nusselt number, local Sherwood number and motile density number are as follows:$\begin{eqnarray}\begin{array}{l}\tilde{N}{u}_{x}=\displaystyle \frac{\tilde{x}{q}_{w}}{k\left({\tilde{T}}_{w}-{\tilde{T}}_{\infty }\right)},S{h}_{x}=\displaystyle \frac{\tilde{x}{q}_{j}}{{D}_{B}{\tilde{C}}_{\infty }},\\ \tilde{N}{h}_{x}=\displaystyle \frac{\tilde{x}{q}_{m}}{{D}_{m}\left({\tilde{N}}_{w}-{\tilde{N}}_{\infty }\right)},\end{array}\end{eqnarray}$where the heat flux, mass flux and the density flux are given as below:$\begin{eqnarray}\begin{array}{l}{q}_{w}={\left.\left(-k\left(\displaystyle \frac{\partial \tilde{T}}{\partial y}\right)+{q}_{r}\right)\right|}_{y=0},\,{q}_{j}={\left.-{D}_{B}\left(\displaystyle \frac{\partial \tilde{C}}{\partial y}\right)\right|}_{y=0},\\ {q}_{m}={\left.-{D}_{m}\left(\displaystyle \frac{\partial \tilde{N}}{\partial y}\right)\right|}_{y=0}.\end{array}\end{eqnarray}$

In dimensionless forms, we have$\begin{eqnarray}\begin{array}{l}N{u}_{x}R{e}_{x}^{1/2}=-\left(1+\displaystyle \frac{4}{3Rd}{\left(1+\left({\theta }_{w}-1\right)\theta \left(0\right)\right)}^{3}\right)\theta ^{\prime} (0),\\ S{h}_{x}R{e}_{x}^{1/2}=-\phi ^{\prime} \left(0\right),N{n}_{x}R{e}_{x}^{1/2}=-\chi ^{\prime} \left(0\right).\end{array}\end{eqnarray}$

3. Numerical approach

In order to determine the numerical computations for current dimensionless flow equations, we used a famous shooting technique to simulate the solution. We comprise the system of dimensionless flow equations from the boundary value problem to initial value problem as follows:$\begin{eqnarray}\left.\begin{array}{l}f={g}_{1},\displaystyle \frac{{\rm{d}}f}{{\rm{d}}\eta }={g}_{2},\displaystyle \frac{{{\rm{d}}}^{2}f}{{\rm{d}}{\eta }^{2}}={g}_{3},\displaystyle \frac{{{\rm{d}}}^{3}f}{{\rm{d}}{\eta }^{3}}={g}_{3}^{{\prime} },\\ \theta ={g}_{4},\displaystyle \frac{{\rm{d}}\theta }{{\rm{d}}\eta }={g}_{5},\displaystyle \frac{{{\rm{d}}}^{2}\theta }{{\rm{d}}{\eta }^{2}}={g}_{5}^{{\prime} },\\ \phi ={g}_{6},\displaystyle \frac{{\rm{d}}\phi }{{\rm{d}}\eta }={g}_{7},\displaystyle \frac{{{\rm{d}}}^{2}\phi }{{\rm{d}}{\eta }^{2}}={g}_{7}^{{\prime} },\chi ={g}_{8},\displaystyle \frac{{\rm{d}}\chi }{{\rm{d}}\eta }={g}_{9},\\ \displaystyle \frac{{{\rm{d}}}^{2}\chi }{{\rm{d}}{\eta }^{2}}={g}_{9}^{{\prime} },\\ {g}_{3}^{{\prime} }=\displaystyle \frac{1}{\left(1+\left(1+n\right){\left(We{g}_{3}\right)}^{n}\right)}\\ \,\times \left(\begin{array}{l}1+{\left(We{g}_{3}\right)}^{n}{K}_{1}{g}_{2}\\ \,-\left(\begin{array}{l}{g}_{1}{g}_{3}-{g}_{2}^{2}\\ -{\rm{\Gamma }}\left({g}_{1}+0.5\eta {g}_{3}\right){\left(1+{\left(We{g}_{3}\right)}^{n}\right)}^{2}\end{array}\right)\\ \,-{\lambda }_{1}({g}_{4}-{Nrg}_{6}-{Rbg}_{8})\end{array}\right),\\ {g}_{5}^{{\prime} }=-Pr\left({g}_{1}{g}_{5}-0.5{\rm{\Gamma }}\eta {z}_{5}+Nb{g}_{5}{g}_{7}+Nt{g}_{5}^{2}\right)\\ \,+\displaystyle \frac{4}{3Rn}\displaystyle \frac{{\rm{d}}}{{\rm{d}}\eta }\left(1+{\left(\left({\theta }_{w}-1\right){g}_{4}\right)}^{3}{g}_{5}\right),\\ {g}_{7}^{{\prime} }=-PrLe\left(\left({g}_{1}{g}_{7}-0.5\eta {g}_{7}\right)\right)-\displaystyle \frac{Nt}{Nb}{g}_{5}^{{\prime} }\\ \,+PrLe\sigma {\left(1+\omega {g}_{4}\right)}^{m}\exp \left(-\displaystyle \frac{E}{1+\omega {g}_{4}}\right){g}_{6},\\ {g}_{9}^{{\prime} }=-Lb\left({g}_{1}{g}_{9}-0.5\eta {g}_{9}\right)\\ \,+Pe\left({g}_{7}{g}_{9}+d{g}_{7}({g}_{8}+{{\rm{\Omega }}}_{1})\right)\end{array}\right\}.\end{eqnarray}$

Similarly the boundary conditions are transformed as$\begin{eqnarray}\left.\begin{array}{l}{g}_{1}\left(0\right)=0,{g}_{2}\left(0\right)-1-\gamma {g}_{3}\left(0\right)-\delta {g}_{3}^{{\prime} }\left(0)=0\right),\\ {g}_{6}\left(0\right)=Bi\left({g}_{5}\left(0\right)-1\right),Nb{g}_{5}\left(0\right)+Nt{g}_{7}\left(0\right)=0,\\ {g}_{8}\left(0\right)=1,{g}_{2}\left(\infty \right)\to 0,{g}_{4}\left(\infty \right)\to 0,{g}_{5}\left(\infty \right)\to 0,\\ {g}_{7}\left(\infty \right)\to 0,{g}_{9}\left(\infty \right)\to 0.\end{array}\right\}\end{eqnarray}$

4. Discussion

This section scrutinizes the graphical impact of various emerging parameters on the distribution of velocity, temperature, concentration and motile microorganisms. Each graph is plotted by assigning some constant values while the remaining physical parameters attained constant values such as ${K}_{1}=0.5,$ $We=1.0,$ $n=0.3,$ ${\rm{\Gamma }}=0.2,$ $Nc=0.2,$ $\gamma =1.0,$ $\delta =-1.0,$ $Pr=0.7,Nt=0.3,$ $Nb=0.2,$ ${\theta }_{w}=1.5,$ $R=0.8,Bi=2.0,Pe\,=0.2,Lb=\mathrm{1.0.}$ The authors remark that these assigned numerical values to the flow parameters are arbitrary and not based on any exponential analysis.

The graphical significance for the combine parameter and power law index parameter on the velocity distribution has been portrayed in figure 1. With an increase of ${K}_{1},$ the velocity of fluid particles declines effectively. The physical consequences for this decreasing behavior may be justified as being a combination of the magnetic constant and porosity parameter. The resistive force appeared, which reduces the fluid particles velocity. The magnetic parameter involves the Lorentz force, which is of a resistive nature while the porosity constant characterizes the permeability of a porous medium due to which the velocity distribution decays. Similarly the velocity distribution is defected with increasing $n$ due to shear thinning effects.

Figure 1.

New window|Download| PPT slide
Figure 1.Impacts of ${K}_{1}$ and $n$ on $f^{\prime} .$


The graphical explanations are disclosed in figure 2 for the variation of $\gamma $ and We on ${f}^{{\prime} }$. The observations captured for the variation of $\gamma $ witness that velocity distribution declines with increasing $We.$ In fact, the involvement of viscosity related to the dimensionless Weissenberg number resists the velocity of accelerated fluid particles. The results for $\gamma $ show that the velocity profile altered due to the presence of slip factor. A decreasing behavior for $f^{\prime} $ is observed as $\gamma $ attained increasing values. The graphical observation based on a variation of $\lambda $ and $\delta $ is disclosed in figure 3. An increment in $\lambda $ shows stronger velocity distribution. Further, with the increase of $\delta ,$ velocity distribution boosts up initially with a minor variation and later on decreases as $\delta $ gets maximum values.

Figure 2.

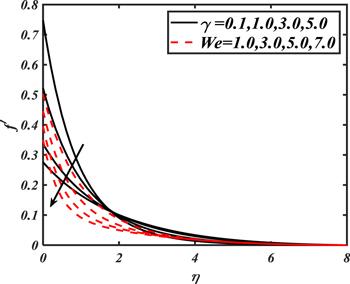New window|Download| PPT slide
Figure 2.Impacts of $\gamma $ and $We$ on $f^{\prime} .$


Figure 3.

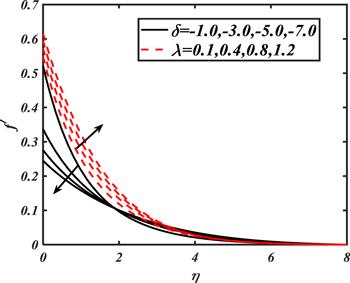New window|Download| PPT slide
Figure 3.Impacts of $\delta $ and $\lambda $ on $f^{\prime} .$


Figure 4 shows the importance of ${\rm{\Gamma }}$ and $Nc$ on $f^{\prime} .$ The velocity distribution decays by varying both flow parameters. The increment in $Nc$ is physical enrolled with the buoyancy forces, which decrease the movement of fluid particles. However, the decreasing trend due to Nc is more dominant than compared to ${\Gamma }$.

Figure 4.

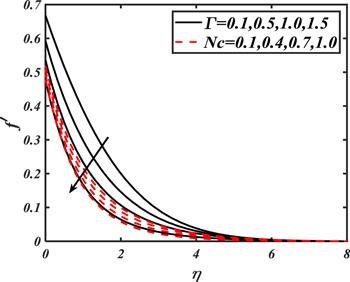New window|Download| PPT slide
Figure 4.Impacts of ${\rm{\Gamma }}$ and $Nc$ on $f^{\prime} .$


Figure 5 is prepared in order to detect the impact of ${K}_{1}$ and $n$ on $\theta .$ It is observed that with a variation of ${K}_{1},$ the temperature distribution is enhanced. Similarly, the increasing variation of $n$ also increases the temperature distribution due to shear thinning features.

Figure 5.

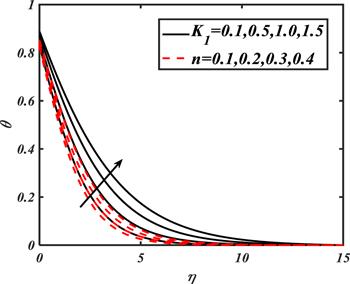New window|Download| PPT slide
Figure 5.Impacts of ${K}_{1}$ and $n$ on $\theta .$


Figure 6 inspects the impact of $Pr$ and $\lambda $ on $\theta .$ The Prandtl number justifies the momentum and thermal diffusivity ratio. Due to the reverse relation with thermal diffusivity, the temperature distribution declines. With variation of $\lambda ,$ the heat transportation between the surfaces to fluid particles becomes slower.

Figure 6.

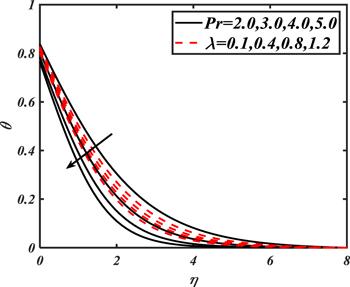New window|Download| PPT slide
Figure 6.Impacts of $Pr$ and $\lambda $ on $\theta .$


Figure 7 is plotted in order to visualize the characteristics of $Bi$ and $We$ on $\theta .$ It is noted that increasing values of $Bi$ maximize the variation in $\theta $ effectively. The enhancement in nanoparticles' temperature due to $Bi$ is physically validated as $Bi$ is directly related to $h.$ While observing the variation of $We$ on $\theta ,$ we noted that the nanoparticles' temperature also increases due to existence of viscosity.

Figure 7.

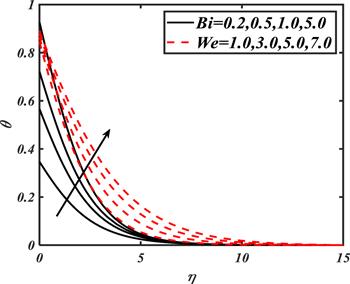New window|Download| PPT slide
Figure 7.Impacts of $Bi$ and $We$ on $\theta .$


The impact of ${\rm{\Gamma }}$ and $Nc$ on $\theta $ are determined in figure 8. Various values have been chosen to investigate the variation of ${\rm{\Gamma }}$ on $\theta .$ The plot shows that $\theta $ increases with arising variation of ${\rm{\Gamma }}.$ For varying numerical values of $Nc,$ an increase in buoyancy ration forces causes an uplift in the nanoparticles' distribution.

Figure 8.

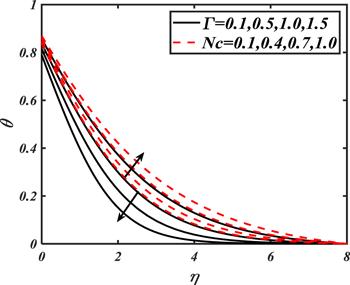New window|Download| PPT slide
Figure 8.Impacts of ${\rm{\Gamma }}$ and $Nc$ on $\theta .$


From figure 9, it is seen that the nanoparticles' temperature enhanced for varying $Nt$ and $Rd.$ The thermophoresis phenomenon occurs due to a temperature gradient between nanoparticles in which tinny fluid particles move from the surface of the cold to hot region. Due to this migration process, the thermal boundary layer increases. The physical consequences for utilization of $Rd$ on $\theta $ show that the nanoparticles' temperature is improved as the radiation source is being considered a more efficient heat transfer mode.

Figure 9.

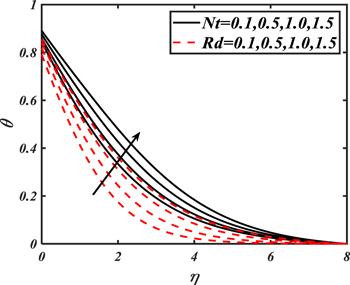New window|Download| PPT slide
Figure 9.Impacts of $Nt$ and $Rd$ on $\theta .$


The variation in concentration distribution for various values of ${K}_{1}$ and $n$ is revealed in figure 10. The nanoparticles' concentration increases for leading values of both ${K}_{1}$ and $n.$

Figure 10.

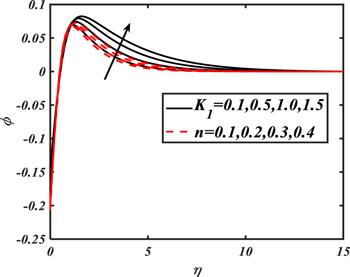New window|Download| PPT slide
Figure 10.Impacts of ${K}_{1}$ and $n$ on $\phi .$


In order to look at the consequences of $Nb$ and $Le$ on $\phi ,$ figure 11 is sketched. Both parameters play a valuable role to control the nanoparticles' concentration in the whole distribution. Since Brownian motion signifies the random movement of nanoparticles over a moving configuration, which reduces as $Nb$ assigned maximum numerical values. On the other hand, Le is inversely related to the mass diffusivity. Therefore, the larger values of $Le$ decreases the mass diffusivity of the nanoparticles, which results in a decay in the nanoparticles' concentration profile. From figure 12, it is examined that the nanoparticles' distribution is resulted with a variation of $Nc$ while a reverse trend is noted for ${\rm{\Gamma }}.$

Figure 11.

New window|Download| PPT slide
Figure 11.Impacts of $Nb$ and $Le$ on $\phi .$


Figure 12.

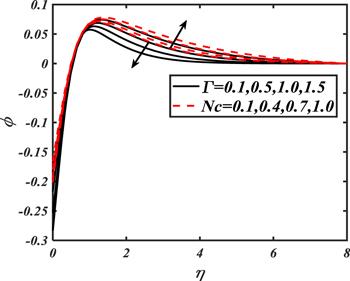New window|Download| PPT slide
Figure 12.Impacts of ${\rm{\Gamma }}$ and $Nc$ on $\phi .$


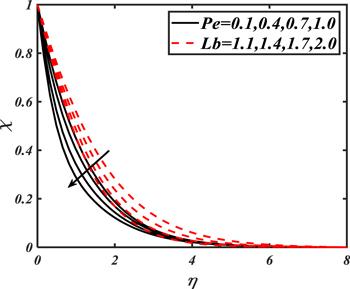
The impacts of various parameters such as ${K}_{1},$ $n,$ ${\rm{\Gamma }},$ $Nc,$ $Pe$ and $Lb$ on motile microorganisms distribution $\chi $ are disclosed in figures 13-15. Figure 13 exhibits the influence of ${K}_{1}$ and $n$ on $\chi .$ The motile microorganisms distribution increases with ${K}_{1}.$ The larger values of $n$ correspond to the shear thinning case which improve the motile microorganisms profile. From figure 14, it has been examined that the unsteady parameter controls the microorganisms' profile while $Nc$ results in an improved microorganisms' profile due to the existence of buoyancy forces. The variation in $\chi $ for different values of $Pe$ and $Lb$ is reported in figure 15. With an increase of $Pe$ motile diffusivity decreases, which increases the motile microorganism profile. Similarly, with the increment in $Lb$ also decay the motile microorganisms profile effectively.

Figure 13.

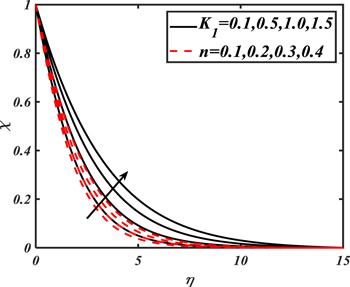New window|Download| PPT slide
Figure 13.Impacts of ${K}_{1}$ and $n$ on $\chi .$


Figure 14.

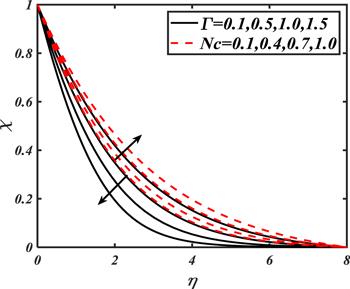New window|Download| PPT slide
Figure 14.Impacts of ${\rm{\Gamma }}$ and $Nc$ on $\chi .$


Figure 15.

New window|Download| PPT slide
Figure 15.Impacts of $Pe$ and $Lb$ on $\chi .$


Table 1 represents the variation of $-f^{\prime\prime} (0)$ for some numerical values of $Ha,$ ${\rm{\Gamma }},$ $Nr,$ $Nc,$ $n,$ $We$ and $\gamma .$ An increasing value of $-{f}^{{\prime} ^{\prime} }(0)$ has been examined for $Ha,$ $Nc,$ $n$ and $We.$ The variation in $-{f}^{{\prime} ^{\prime} }(0)$ is quite minimal by increasing the slip factor $\gamma .$ In order to evaluate the significance of local Nusselt number $-\theta ^{\prime} (0)$ for iterating values of $Ha,$ ${\rm{\Gamma }},$ $Nr,$ $Nc,$ $n,$ $We,$ $Pr,$ $Nt,$ $Nb$ and $\gamma ,$ table 2 is prepared. The heat transfer rate is increased with $Pr,$ ${\rm{\Gamma }}$ while an opposite trend has been captured for all remaining parameters. From table 3, it is noted that the local Sherwood number attained maximum values for ${\rm{\Gamma }},$ $Nc$ and $Le.$ Finally, the numerical computation for the motile density number is inspected in table 4. A maximum variation in motile density number is observed for ${\rm{\Gamma }},$ $Nr$ and $Pe.$


Table 1.
Table 1.Variations of $-f^{\prime\prime} (0)$ for various values of involved parameters.
$Ha$${\rm{\Gamma }}$$Nr$$Nc$$n$$We$$\gamma $$-f^{\prime\prime} (0)$
0.10.20.50.50.30.310.3937
0.60.4740
1.20.5411
0.50.10.5219
0.30.4790
0.50.4423
0.20.10.4618
0.40.4605
0.70.4592
0.50.10.4249
0.40.4523
0.70.4816
0.50.10.4383
0.40.4751
0.70.5288
0.30.10.4577
0.50.4659
1.00.4763
0.12.00.2859
3.00.2078
4.00.1634

New window|CSV


Table 2.
Table 2.Variations of $-\theta ^{\prime} (0)$ for various values of involved parameters.
$Ha$${\rm{\Gamma }}$$Nr$$Nc$$n$$We$$Pr$$Nt$$Nb$$-\theta ^{\prime} (0)$
0.10.20.50.50.30.32.00.30.20.2368
0.60.2055
1.20.1775
0.50.10.1689
0.30.2003
0.50.2203
0.20.10.2112
0.40.2111
0.70.3210
0.50.10.2216
0.40.2140
0.70.2064
0.50.10.2181
0.40.2078
0.70.1972
0.30.10.2127
0.50.2098
1.00.2063
0.11.00.1589
3.00.2486
5.00.3000
2.00.10.2183
0.50.2044
0.80.1948

New window|CSV


Table 3.
Table 3.Variations of $-\phi ^{\prime} (0)$ for various values of involved parameters.
$Ha$${\rm{\Gamma }}$$Nr$$Nc$$n$$We$$Pr$$Le$$-\phi ^{\prime} (0)$
0.10.20.50.50.30.32.00.30.3551
0.60.3082
1.20.2662
0.50.10.2548
0.30.3005
0.50.3304
0.20.10.3169
0.40.3167
0.70.3165
0.50.10.3325
0.40.3210
0.70.3079
0.50.10.3272
0.40.3117
0.70.2960
0.30.10.3190
0.50.3147
1.00.3094
0.11.00.2383
3.00.3729
5.00.4500
2.01.00.3206
2.00.3172
3.00.3163

New window|CSV


Table 4.
Table 4.Variations of $-\chi ^{\prime} (0)$ for various values of involved parameters.
$Ha$${\rm{\Gamma }}$$Nr$$Nc$$n$$We$$Pe$$Lb$$-\chi ^{\prime} (0)$
0.10.20.50.50.30.30.22.00.7875
0.60.6917
1.20.6016
0.50.10.5969
0.30.6796
0.50.7349
0.20.10.7087
0.40.7096
0.70.7099
0.50.10.7467
0.40.7188
0.70.6969
0.50.10.7326
0.40.6959
0.70.6516
0.30.10.7133
0.50.7040
1.00.6925
0.10.20.7383
0.60.8596
1.00.9816
0.20.10.4603
0.50.5950
1.00.6661

New window|CSV

5. Conclusions

In this investigation, the slip flow of a non-Newtonian nanoliquid has been considered in the presence of activation energy and nonlinear thermal radiation. The flow problem is modeled, which is numerically treated by employing the shooting algorithm. The achieved results are summarized as follows: The distribution of velocity is altered slowly with interaction of slip factors, unsteady parameter and Rayleigh number.
The temperature distribution is enhanced in case of shear thinning and thermal Biot number.
The Brownian motion parameter and Lewis number reduce the nanoparticles' concentration distribution.
The local Nusselt number, local Sherwood number and motile density number increase with higher unsteady parameters.
The reported continuations may involve applications of thermal extrusion systems and solar energy processes.
Current analysis has been further extended for three-dimensional flow and by performing stability analysis.


Acknowledgments

The authors extended their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through Research Groups Program under grant number (R.G.P.2/66/40).


Reference By original order
By published year
By cited within times
By Impact factor

Choi S U S 1995 Enhancing thermal conductivity of fluids with nanoparticles
ASME Pub. Fed. 231 99 106
[Cited within: 1]

Sheikholeslami M Hayat T Alsaedi A 2017 Numerical simulation of nanofluid forced convection heat transfer improvement in existence of magnetic field using Lattice Boltzmann method
Int. J. Heat Mass Transfer 108 1870 1883
DOI:10.1016/j.ijheatmasstransfer.2017.01.044 [Cited within: 1]

Khan M Azam M Alshomrani A S 2017 Effects of melting and heat generation/absorption on unsteady Falkner-Skan flow of Carreau nanofluid over a wedge
Int. J. Heat Mass Transfer 110 437 446
DOI:10.1016/j.ijheatmasstransfer.2017.03.037 [Cited within: 1]

Hayat T Aziz A Muhammad T Alsaedi A 2017 Model and comparative study for flow of viscoelastic nanofluids with Cattaneo-Christov double diffusion
PLoS One 12e0168824
DOI:10.1371/journal.pone.0168824 [Cited within: 1]

Mahanthesh B Amala S Gireesha B J Animasaun I L 2019 Effectiveness of exponential heat source, nanoparticle shape factor and Hall current on mixed convective flow of nanoliquids subject to rotating frame
Multidiscipline Model. Mater. Struct. 15 758 778
DOI:10.1108/MMMS-08-2018-0146 [Cited within: 1]

Siddiqui A A Turkyilmazoglu M 2019 A new theoretical approach of wall transpiration in the cavity flow of the ferrofluids
Micromachines 10 373
DOI:10.3390/mi10060373 [Cited within: 1]

Hsiao K L 2017 Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature
Int. J. Heat Mass Transfer 112 983 990
DOI:10.1016/j.ijheatmasstransfer.2017.05.042 [Cited within: 1]

Ahmed J Khan M Ahmad L 2019 Stagnation point flow of Maxwell nanofluid over a permeable rotating disk with heat source/sink
J. Mol. Liq. 287 110853
DOI:10.1016/j.molliq.2019.04.130 [Cited within: 1]

Aly E H 2019 Dual exact solutions of graphene-water nanofluid flow over stretching/shrinking sheet with suction/injection and heat source/sink: critical values and regions with stability
Powder Technol. 342 528 544
DOI:10.1016/j.powtec.2018.09.093 [Cited within: 1]

Rout B C Mishra S R 2018 Thermal energy transport on MHD nanofluid flow over a stretching surface: a comparative study
Eng. Sci. Tech. Int. J. 21 60 69
DOI:10.1016/j.jestch.2018.02.007 [Cited within: 1]

Tlili I Khan W A Khan I 2018 Multiple slips effects on MHD SA-Al2O3 and SA-Cu non-Newtonian nanofluids flow over a stretching cylinder in porous medium with radiation and chemical reaction
Res. Phys. 8 213 222
DOI:10.1016/j.rinp.2017.12.013 [Cited within: 1]

Hayat T Ullah I Muhammad T Alsaedi A 2020 Hydromagnetic squeezed flow of second-grade nanomaterials between two parallel disks
J. Therm. Anal. Calorim. 139 2067 2077
DOI:10.1007/s10973-019-08555-4 [Cited within: 1]

Khan S U Shehzad S A 2019 Brownian movement and thermophoretic aspects in third grade nanofluid over oscillatory moving sheet
Phys. Scr. 94 095202
DOI:10.1088/1402-4896/ab0661 [Cited within: 1]

Waqas H Imran M Khan S U Shehzad S A Meraj M A 2019 Slip flow of Maxwell viscoelasticity-based micropolar nano particles with porous medium: a numerical study
Appl. Math. Mech. (Engl. Ed.) 40 1255 1268
DOI:10.1007/s10483-019-2518-9 [Cited within: 1]

Sheikholeslami M Shehzad S A Abbasi F M Li Z 2018 Nanofluid flow and forced convection heat transfer due to Lorentz forces in a porous lid driven cubic enclosure with hot obstacle
Comput. Meth. Appl. Mech. Eng. 338 491 505
DOI:10.1016/j.cma.2018.04.020 [Cited within: 1]

Shehzad S A Khan S U Abbas Z Rauf A 2020 A revised Cattaneo-Christov micropolar viscoelastic nanofluid model with combined porosity and magnetic effects
Appl. Math. Mech. 41 521 532
DOI:10.1007/s10483-020-2581-5 [Cited within: 1]

Ali M Sultan F Khan W A Shahzad M Arif H 2020 Important features of expanding/contracting cylinder for cross magneto-nanofluid flow
Chaos Solitons Fractals 133 109656
DOI:10.1016/j.chaos.2020.109656 [Cited within: 1]

Li F Sheikholeslami M Dara R N Jafaryar M Shafee A Nguyen-Thoi T Li Z 2020 Numerical study for nanofluid behavior inside a storage finned enclosure involving melting process
J. Mol. Liq. 297 111939
DOI:10.1016/j.molliq.2019.111939 [Cited within: 1]

Kuznetsov A V 2010 The onset of nanofluid bioconvection in a suspension containing both nanoparticles and gyrotactic microorganisms
Int. Commun. Heat Mass Transfer 37 1421 1425
DOI:10.1016/j.icheatmasstransfer.2010.08.015 [Cited within: 1]

Alsaedi A Ijaz Khan M Farooq M Gull N Hayat T 2017 Magnetohydrodynamic (MHD) stratified bioconvective flow of nanofluid due to gyrotactic microorganisms
Adv. Powder Technol. 28 288 298
DOI:10.1016/j.apt.2016.10.002 [Cited within: 1]

Alwatban A M Khan S U Waqas H Tlili I 2019 Interaction of Wu's slip features in bioconvection of Eyring Powell nanoparticles with activation energy
Processes 7 859
DOI:10.3390/pr7110859 [Cited within: 1]

Zohra F T Uddin M J Ismail A I M Anwar Bég O Kadir A 2018 Anisotropic slip magneto-bioconvection flow from a rotating cone to a nanofluid with Stefan blowing effects
Chin. J. Phys. 56 432 448
DOI:10.1016/j.cjph.2017.08.031 [Cited within: 1]

Waqas M Hayat T Shehzad S A Alsaedi A 2018 Transport of magnetohydrodynamic nanomaterial in a stratified medium considering gyrotactic microorganisms
Physica B 529 33 40
DOI:10.1016/j.physb.2017.09.128 [Cited within: 1]

Farooq S Hayat T Alsaedi A Ahmad B 2017 Numerically framing the features of second order velocity slip in mixed convective flow of Sisko nanomaterial considering gyrotactic microorganisms
Int. J. Heat Mass Transfer 112 521 532
DOI:10.1016/j.ijheatmasstransfer.2017.05.005 [Cited within: 1]

Khan W A Rashad A M Abdou M M M Tlili I 2019 Natural bioconvection flow of a nanofluid containing gyrotactic microorganisms about a truncated cone
Eur. J. Mech. B 75 133 142
DOI:10.1016/j.euromechflu.2019.01.002 [Cited within: 1]

Amirsom N A Uddin M J md Ismail A I 2019 MHD boundary layer bionanoconvective non-Newtonian flow past a needle with Stefan blowing
Heat Transfer - Asian Res. 48 727 743
DOI:10.1002/htj.21403 [Cited within: 1]

Haq F Rahman M U Khan M I Hayat T 2019 Transportation of activation energy in development of binary chemical reaction to investigate the behavior of Oldroyd-B fluid with nanomaterial
Phys. Scr. 94 105010
DOI:10.1088/1402-4896/ab194a [Cited within: 1]

Shafique Z Mustafa M Mushtaq A 2016 Boundary layer flow of Maxwell fluid in rotating frame with binary chemical reaction and activation energy
Results Phys. 6 627 633
DOI:10.1016/j.rinp.2016.09.006 [Cited within: 1]

Khan M I Hayat T Khan M I Alsaedi A 2018 Activation energy impact in nonlinear radiative stagnation point flow of Cross nanofluid
Int. Commun. Heat Mass Transfer 91 216 224
DOI:10.1016/j.icheatmasstransfer.2017.11.001

Waqas H Khan S U Shehzad S A Imran M 2019 Radiative flow of Maxwell nanofluids containing gyrotactic microorganism and energy activation with convective Nield conditions
Heat Transfer - Asian Res. 48 1663 1687
DOI:10.1002/htj.21451

Li Z Manh T D Gerdroodbary M B Nam N D Moradi R Babazadeh H 2020 The effect of sinusoidal wall on hydrogen jet mixing rate considering supersonic flow
Energy 193 116801
DOI:10.1016/j.energy.2019.116801 [Cited within: 1]

Cross M M 1965 Rheology of non-Newtonian fluids: a new flow equation for pseudoplastic system
J. Colloid Sci. 20 417 437
DOI:10.1016/0095-8522(65)90022-X [Cited within: 2]

Azam M Shakoor A Rasool H F Khan M 2019 Numerical simulation for solar energy aspects on unsteady convective flow of MHD Cross nanofluid: a revised approach
Int. J. Heat Mass Transfer 131 495 505
DOI:10.1016/j.ijheatmasstransfer.2018.11.022 [Cited within: 2]

Wu L 2008 A slip model for rarefied gas flows at arbitrary Knudsen number
Appl. Phys. Lett. 93 253103
DOI:10.1063/1.3052923 [Cited within: 1]

Abdelmalek Z Khan S U Waqasd H Nabwey H A Tlili I 2020 Utilization of second order slip, activation energy and viscous dissipation consequences in thermally developed flow of third grade nanofluid with gyrotactic microorganisms
Symmetry 12 309
DOI:10.3390/sym12020309

Khan S U Waqas H Bhatti M M Imran M 2020 Bioconvection in the rheology of magnetized couple stress nanofluid featuring activation energy and Wu's slip
J. Non-Equilib. Thermodyn. 45 81 95
DOI:10.1515/jnet-2019-0049

Khan S U Waqas H Shehzad S A Imran M 2019 Theoretical analysis for tangent hyperbolic nanoparticles with combined electrical MHD, activation energy and Wu's slip features: a mathematical model
Phys. Scr. 94 125211
DOI:10.1088/1402-4896/ab399f [Cited within: 1]

相关话题/Significance activation energy

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.