M. Waqas^,1,*, Saira Naz², T. Hayat^2,3, M. Ijaz Khan², A. Alsaedi³1 NUTECH School of Applied Sciences and Humanities, National University of Technology, Islamabad 44000, Pakistan
2 Department of Mathematics, Quaid-I-Azam University 45320, Islamabad 44000, Pakistan
3 Nonlinear Analysis and Applied Mathematics (NAAM) Research Group, Department of Mathematics, Faculty of Science,King Abdulaziz University, Jeddah 21589, Saudi Arabia

Corresponding authors: *E-mail:mwaqas@math.qau.edu.pk

Received:2019-05-28Online:2019-12-1


Abstract
The novel characteristics of magnetic field and entropy generation in mixed convective flow of Carreau fluid towards a stretched surface are investigated. Buongiornio nanoliquid model consists of thermophoresis and Brownian movement aspects is opted for analysis. Energy expression is modeled subject to thermal radiation and viscous dissipation phenomenon. Concentration by zero mass flux condition is implemented. Consideration of chemical reaction and activation energy characterizes the mass transfer mechanism. Total entropy generation rate and Bejan number is formulated. The utilization of transformation variables reduces the PDEs into non-linear ODEs. The obtained nonlinear complex problems are computed numerically through Shooting scheme. The impact of involved variables like local Weissenberg number, magnetic parameter, thermal radiation parameter, Brownian motion parameter, thermophoresis parameter, buoyancy ratio parameter, mixed convection parameter, Prandtl parameter, Eckert number, Schmidt number, non-dimensional activation energy parameter, chemical reaction parameter, Brinkman number, dimensionless concentration ratio variable, diffusive variable and dimensionless temperature ratio variable on velocity, temperature, nanoparticles concentration, entropy generation, Bejan number, surface drag force and heat transfer rate are examined through graphs and tables.
Keywords： carreau nanoliquid;entropy generation;viscous dissipation;activation energy;shooting scheme


PDF (1527KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
M. Waqas, Saira Naz, T. Hayat, M. Ijaz Khan, A. Alsaedi. Hydromagnetic Carreau Nanoliquid in Frames of Dissipation and Activation Energy*. [J], 2019, 71(12): 1416-1424 doi:10.1088/0253-6102/71/12/1416

1 Introduction

Nanoliquids are homogeneous dispersion of a carrier liquid and nanoparticles. The nanoparticles magnitude does not exceed 100 nm and their concentrations are normally small-scale $(＜10$ by volume). The carrier liquids like oils, ethylene glycol and water have poor heat transport competence due to their low thermal conductivity. Choi^[1] was the first who established nanoliquids. Such liquids have the capability to enhance thermal conductivity and thermal performance of carrier liquids. The heat transfer improvement can be modified by type of number of submerged nanoparticles, material and shape of particle. Nanoliquids have large-scale utilization in industrial and technological processes like nuclear reactor cooling, power generator, micro-reactors, melt-spinning, drying and cooling of papers, airplanes and glass fiber technology.Nanoliquids mechanism includes numerous factors such as thermophoretic force, thermal diffusion,micro-convection, particle to particle coupling, Brownian movement and conduction were investigated recently by several scientists. These scientists proved that nanoparticles Brownian movement is the leading factor that improves thermal characteristics and energy productivity of liquids. Some literature regarding nanoliquid flow have been studied (see Refs. ^[2--10]).

Non-Newtonian liquid flows have been widely utilized in the area of petroleum, chemical industries, biorheology and geophysics. Such liquids are highly complicated in nature as well as predicts non-linear relationship between shear stress and shear rate. A quantitative knowledge of flow characteristics of non-Newtonian liquids can not develop single constitutive mathematical relationship. Therefore, several non-Newtonian liquid models have been established to investigate their features. Here we consider the Carreau liquid model which exhibits the Newtonian/power law characteristics at low as well as high shear rates. In fact apparent viscosity increments at high shear rates to show shear thickening or dilatant features e.g.in biological liquids and polymer melts whereas apparent viscosity declines to behave as shear thinning features at high shear rates e.g.in concentrated suspensions of china and titanium dioxide. Boundary layer flow and heat transfer to Carreau liquid model towards a nonlinear stretching sheet is addressed by Khan et al.^[11] Hayat et al.^[12] reported the impacts of MHD and mixed convective flow in peristalsis of non-Newtonian nanomaterial considering zero mass flux condition. Hashim et al.^[13] modeled anti-Fourier theory for Carreau liquid flow subject to slendering sheet. Hayat et al.^[14] established numerical solutions of non-Newtonian liquid flows in the presence of chemical aspects. A numerical investigation for radiative MHD flow of Carreau nanoliquid model is delivered by Waqas et al.^[15] Moreover magnetohydrodynamic flow of nanoliquids greatly attracted the consideration of numerous researchers due to their involvement in heat transfer performance and thermophysical characteristics. The behavior of fluid and heat transport characteristics are controlled by intensity and orientation of magnetic field. Furthermore valuable applications of magneto nanoliquid flow comprise elimination of tumors with hyperthermia, gastric medications, wound treatment, sterilized devices, asthma treatment and cancer therapy. Recent studies associated with magneto nanoliquid flow can be mentioned in the attempts.^[16-21]

To enhance thermal performance and reducing irreversibilities in the system is thought to be an efficient approach.^[22] The measured amount of heat transfer irreversibility and viscous dissipation irreversibility in a process is termed as entropy generation. The investigation on entropy generation has acquired the attention of researchers and investigators due to its extensive utilization in numerous systems such as microchannels, gas turbines, solar thermal, air separators, natural convection, curved pipes, reactors, regular and functionally graded materials, chillers, microchannels and so forth.^[23-28] Entropy analyses enable us to determine how effective thermal process or system operates.^[29-30] To our knowledge mathematical modeling for Carreau nanoliquid with entropy generation minimization is not yet investigated. With this point of view our concern here is to model influence of nanoparticles in stretchable mixed convective flow of magneto Carreau liquid. The effects of viscous dissipation and thermal radiation are reported. Nanofluid modeling comprises the thermophoretic and Brownian movement aspects. Zero mass flux type boundary condition is imposed. Idea of activation energy along with chemical reaction is also introduced. Total entropy generation rate and Bejan number is discussed for various flow variables. By means of Shooting scheme, numeric solutions for nonlinear systems are constructed. Nature of emerging physical variables on velocity, temperature, concentration, surface drag force, local Nusselt number, entropy generation and Bejan number are analyzed through graphs and tables.

2 Formulation

Entropy generation minimization and magnetohydrodynamic (MHD) mixed convective flow of an incompressible carreau nanoliquid bounded by stretchable surface is considered. Coordinate system is taken in such a way that $x$-axis is in the direction of stretchable surface whereas $y$-axis is perpendicular to it (see Fig. 1). Features of Brownian motion and thermophoresis in nanoliquid modeling are examined. Viscous dissipation and thermal radiation aspects in energy expression are acounted. Besides, binary chemical reaction with Arrhenius activation energy are retained. The boundary layer approximation yields the following expressions:%

(1) $$ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0\,, $$
(2) $$ u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\nu \frac{\partial ^{2}u}{\partial y^{2}}\Big[ 1+\Gamma ^{2}\Big( \frac{\% \partial u}{\partial y}\Big) ^{2}\Big] ^{({n-1})/{2}}+\nu (n-1) \Gamma ^{2}\frac{\partial ^{2}u}{\partial y^{2}}\Big( \frac{\%\partial u}{\partial y}\Big) ^{2}\Big[ 1+\Gamma ^{2}\Big( \frac{\partial u}{\partial y}\Big) ^{2}\Big] ^{({n-3})/{2}}\\ \hphantom{u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=}-\frac{\sigma ^{\ast }B_{0}^{2}}{\rho _{f}}u+g\{ \Lambda _{1}(T-T_{\infty }) +\Lambda _{2}( C-C_{\infty }) \}\,, $$
(3) $$ u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \Big( \frac{\partial ^{2}T}{\partial y^{2}}\Big) +\tau \Big(D_{B}\frac{\partial T}{\partial y}\frac{\partial C}{\partial y}+\frac{D_{T}}{T_{\infty }}\Big( \frac{\partial T}{\partial y}\Big) ^{2}\Big) +\frac{\sigma ^{\ast }B_{0}^{2}}{(\rho c)_{f}}u^{2}\\\ \hphantom{u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=} +\frac{16\sigma ^{\ast \ast }T_{\infty }^{3}}{3(\rho c)_{f}m^{\ast }}\Big( \frac{\partial ^{2}T}{\partial y^{2}}\Big) +\frac{\mu }{(\rho c)_{f}}\Big( \frac{\partial u}{\partial y}\Big) ^{2}\Big[ 1+\Gamma ^{2}\Big(\frac{\partial u}{\partial y}\Big) ^{2}\Big] ^{({n-1})/{2}}\,, $$
(4) $$ u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_{B}\frac{\%\partial ^{2}C}{\partial y^{2}}+\frac{D_{T}}{T_{\infty }}\Big( \frac{\%\partial ^{2}T}{\partial y^{2}}\Big) -k_{r}^{2}(C-C_{\infty })\Big( \frac{\%T}{T_{\infty }}\Big) ^{m}\exp \Big( -\frac{E_{a}}{\kappa T}\Big) \,, $$
(5) $$ u=U_{w}(x)=cx\,,\quad v=0\,, \quad T=T_{w}\,,\\\ D_{B}\frac{\partial C}{\partial y}+\frac{D_{T}}{T_{\infty }}\frac{\partial T}{\partial}=0 \ \ \text{at} \ \ y=0\,, \\\ u\rightarrow 0\,, \ \ T\rightarrow T_{\infty }\,, \ C\rightarrow C_{\infty } \ \ {\rm as} \ \ y\rightarrow \infty \,. $$
Here $(u,v)$ represents the velocity components in $(x,y)$ direction, $\rho _{f}$ the density of fluid, $\nu ( ={\mu }/{\rho _{f}}) $ the kinematic viscosity of the fluid, $\mu $ the dynamic viscosity, $\Gamma $ the material constant, $B_{0}$ the uniform magnetic field strength, $\tau ( ={(\rho c)_{p}}/{(\rho c)_{f}}) $ the ratio of heat capacity with $(\rho c)_{f}$ the heat capacity of fluid and $(\rho c)_{p}$ the effective heat capacity of nanoparticles, $\sigma ^{\ast \ast }$ the Stefan-Boltzmann constant, $\alpha ( ={k_{f}}/{(\rho c_{p})_{f}}% ) $ the thermal diffusivity, $k_{f}$ the thermal conductivity of the fluid, $c_{p}$ the specific heat capacity, $m^{\ast }$ the mean absorption coefficient, $\sigma ^{\ast }$ the electrical conductivity, $(D_{B},D_{T})$ the (Brownian, thermophoresis) diffusion coefficients, $( T,C) $ the (temperature, concentration), $( T_{\infty },C_{\infty }) $ the ambient (temperature, concentration), $( T_{w},C_{w}) $ the surface (temperature, concentration), $\kappa =8.61\times 10^{-5}$ eV/K the Boltzmann constant, $k_{r}^{2}$ the reaction rate, $E_{a}$ the activation energy, $m$ the fitted rate constant, $c$ the dimensional constant, $% U_{w}(x) $ the stretching velocity.

New window|Download| PPT slide
Fig. 1(Color online) Physical configuration.



We utilize the transformations^[31-32]

(6) $$ \eta =y\sqrt{\frac{c}{\nu }}\,, \ \ u=cxf^{\prime }(\eta )\,, \ \ v=-\sqrt{c\nu }f(\eta )\,, \\\ \theta (\eta )=\frac{T-T_{\infty }}{T_{w}-T_{\infty }}\,, \ \ \phi (\eta )=\frac{C-C_{\infty }}{C_{w}-C_{\infty }}\,. $$
Here $f^{\prime }(\eta )$, $\theta (\eta )$, and $\phi (\eta )$ depict the non-dimensionalized velocity, temperature and concentration.

Equation (1) is satisfied identically for $u=cxf^{\prime }(\eta )$, $v=-\sqrt{c\nu }f(\eta )$. utilizing expression (6) into the expressions (2)--(5),

we get the differential systems as follows:

(7) $$ (1+nWe^{2}f^{\prime \prime 2})(1+We^{2}f^{\prime \prime 2})^{({n-3})/{2}}f^{\prime \prime \prime }-f^{\prime }{}^{2} \\ \quad +ff^{\prime \prime }-Mf^{\prime}+\lambda (\theta +Nr\phi )=0\,, $$
(8) $$ \Big(1+\frac{4}{3}R\Big)\theta ^{\prime \prime }+Pr f\theta ^{\prime }+Pr Nb\theta^{\prime }\phi ^{\prime }\\\ \quad +Pr Nt\theta ^{\prime 2} +Pr EcMf^{\prime 2} \\\ quad +PrEc(1+We^{2}f^{\prime \prime 2})^{({n-1})/{2}}f^{\prime \prime 2}=0\,, $$
(9)$$ \phi ^{\prime \prime }+Scf\phi ^{\prime }+\frac{N_{t}}{N_{b}}\theta ^{\prime \prime }-Sc\sigma (1+\delta _{1}\theta )^{m}\phi \\\ \quad\times \exp \Big( -\frac{E}{\%1+\delta _{1}\theta }\Big) =0\,, $$
(10) $$ f( 0) =0,\text{ }f^{\prime }( 0) =1\,, \ \ f^{\prime}( \infty ) \rightarrow 0\,, $$
(11) $$ \theta ( 0) =1\, , \ \ \theta ( \infty ) \rightarrow 0\,, $$
(12) $$ Nb\phi ^{\prime }( 0) +Nt\theta ^{\prime }(0)=0\,, \ \ \phi ( \infty ) \rightarrow 0 \,, $$
where prime $( ^{\prime }) $ denotes differentiation with respect to $\eta $, $M( ={\sigma ^{\ast }B_{0}^{2}}/{\rho _{f}c}) $ the magnetic parameter,$ Nr\Big( =\frac{g\Lambda _{2}(C_{w}-C_{\infty })}{g\Lambda _{1}(T_{w}-T_{\infty })}=\frac{Gr_{x}^{\ast }}{Gr_{x}}\Big) $ the buoyancy ratio parameter,$ \lambda \Big( =\frac{g\Lambda_{1}(T_{w}-T_{\infty })}{c^{2}x}=\frac{Gr_{x}}{{ Re}_{x}^{2}}\Big)$ the mixed convection parameter, $Pr ={\nu }/{\alpha }$ the Prandtl number, $R={4\sigma ^{\ast \ast }T_{\infty }^{3}}/{k_{f}m^{\ast }}$ the thermal radiation parameter, $Nb={\tau D_{B}(C_{w}-C_{\infty })}/{\nu }$ the Brownian motion parameter, $Nt={\tau D_{T}(T_{w}-T_{\infty })}/{\nu T_{\infty }}$ the thermophoresis parameter, $Ec={c^{2}x^{2}}/{c_{f}(T_{w}-T_{\infty })}$ the Eckert number, $We^{2}={\Gamma^{2}c^{3}x^{2}}/{\nu }$ the local Weissenberg number, $Sc={\nu }/{D_{B}}$ the Schmidt number, $\sigma ={k{r}^{2}}/{c}$ the dimensionless reaction rate, $E={E_{a}}/{\kappa T_{\infty }}$ the dimensionless activation energy, $\delta _{1}=({T_{w}-T_{\infty }})/{T_{\infty }}$ the temperature difference parameter.

Physial Quantities

We have the following expressions for the drag force $(C_{fx})$ and local Nusselt number $(Nu_{x})$:

(13) $$ C_{fx}=\frac{\tau _{w}}{\rho U_{w}^{2}}\,, $$
(14) $$ Nu_{x}=\frac{xq_{w}}{k(T_{w}-T_{\infty })}\,, $$
where the $( \tau _{w},q_{w}) $ represents the (wall shear stress, wall heat flux) which are given by:

(15) $$ \tau _{w}=\mu \frac{\partial u}{\partial y}\Big[ 1+\Gamma ^{2}\Big( \frac{\%\partial u}{\partial y}\Big) ^{2}\Big] ^{({n-1})/{2}}\,, $$
(16) $$ q_{w}=-k\frac{\partial T}{\partial y}-\frac{16\sigma ^{\ast \ast }T_{\infty }^{3}}{3m^{\ast }}\Big( \frac{\partial T}{\partial y}\Big)\, . $$
Substituting Eqs. (15) and (16) in Eqs. (13)--(14), we have following dimensionless forms of surface drag force and local Nusselt number:

(17) $$ C_{fx}{Re}_{x}^{1/2}=[ 1+We^{2}( f^{\prime \prime }(0)) ^{2}] ^{({n-1})/{2}}f^{\prime \prime }(0)\,, $$
(18) $$ Nu_{x}{ Re}_{x}^{-1/2}=- \Big\{ 1+\frac{4}{3}R \Big\} \theta ^{\prime}(0) \,, $$
where $Re_{x}( ={xU_{w}}/{\nu }) $ signifies local Reynolds number.

3 Analysis of Entropy Generation

The chaos in a particular system is computed through entropy. Entropy generation relies on reversibility of the process. In isolated structures, entropy rises subjected to time for irreversible reactions. Owing to an increase in utilization of nanoliquids in medical and engineering applications, it is essential to examine and comprehend the influence of these nanoliquids versus entropy generation in real mechanisms.^[33]

For carreau liquid flow the volumetric entropy generation equation in dimensional form is defined as:

(19) $$ S_{G} =\;\frac{k_{f}}{T_{\infty }^{2}}\Big[ 1+\frac{16\sigma ^{\ast \ast }T_{\infty }^{3}}{3k_{f}m^{\ast }}\Big] \Big( \frac{\partial T}{\partial y }\Big) ^{2}+\frac{\mu }{T_{\infty }}\Big( \frac{\partial u}{\partial y} \Big) ^{2}\\\ \times \Big[ 1+\Gamma ^{2}\Big( \frac{\partial u}{\partial y}\Big)^{2}\Big] ^{({n-1})/{2}} +\frac{\sigma ^{\ast }B_{0}^{2}}{T_{\infty }} u^{2} \\\ \frac{RD}{C_{\infty }}\Big( \frac{\partial C}{\partial y}\Big) ^{2}+ \frac{RD}{T_{\infty }}\Big( \frac{\partial T}{\partial y}\frac{\partial C}{partial y}\Big)\, . $$
Here the above expression constitutes three factors (i) fluid friction irreversibility, (ii) heat transfer irreversibility,and (iii) diffusive irreversibility. After employing the similarity transformation, Eq. (19) can be reduced into dimensionless form as follows:

(20) $$ N_{G}=\alpha _{1}[ 1+\frac{4}{3}R] \theta ^{\prime 2}+Br(1+We^{2}f^{\prime \prime 2})^{({n-1})/{2}}f^{\prime \prime2}\\\ +MBrf^{\prime 2}+\frac{\alpha _{2}}{\alpha _{1}}L\phi ^{\prime 2}+L\theta^{\prime }\phi ^{\prime }\,, $$
where $N_{G}( ={\nu T_{\infty }S_{G}}/{k_{f}c\Delta T}) $ depicts the entropy generation rate, $Br( ={\mu U_{w}^{2}}/{k_{f}\Delta T}) $ the Brinkman number, $\alpha _{2}( ={\Delta C}/{C_{\infty }}) $ the dimensionless concentration ratio variable, $\alpha _{1}( ={\Delta T}/{T_{\infty }}) $ the dimensionless temperature ratio variable, $L( ={RD(C_{w}-C_{\infty})}/{k_{f}}) $ the diffusive variable.

The Bejan number $(Be) $ is defined as

(21) $$ Be=\frac{\text{Entropy generation subject to heat and mass transfer}}{\text{Total entropy generation}}\,, $$
(22) $$ Be=\frac{\alpha _{1}[ 1+{4R}/{3}] \theta ^{\prime 2}+(\alpha_2/\alpha_1)L\phi^{\prime2}+L\theta'\phi'}{\alpha _{1}[ 1+{4R}/{3}] \theta ^{\prime 2}+Br(1+We^{2}f^{\prime \prime 2})^{({n-1})/{2}}f^{\prime \prime 2}+MBrf^{\prime 2}+({\alpha _{2}}/{\alpha _{1}})L\phi ^{\prime 2}+L\theta^{\prime }\phi ^{\prime }}\,. $$

4 Results and Discussion

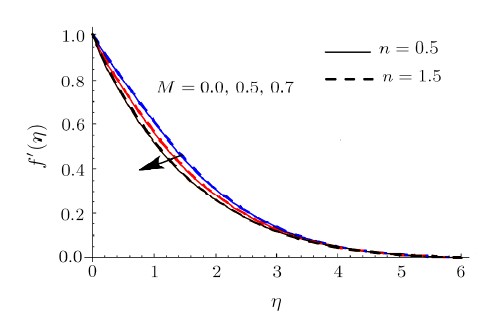
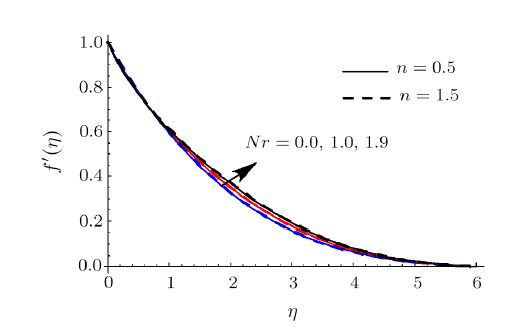
Here Shooting scheme is implemented to compute the nonlinear systems (7)--(9) subject to Eqs. (10)--(12) and (20)--(22). Salient features of emerging variables such as magnetic parameter $( M) $, local Weissenberg number $( We) $, thermal radiation parameter $( R) $, Buoyancy ratio parameter $( Nr) $, Brownian motion parameter $( Nb) $, thermophoresis parameter $( Nt) $, mixed convection parameter $( \lambda ) $, Prandtl parameter $% ( Pr ) $, Eckert number $( Ec) $, non-dimensional activation energy parameter $( E) $, chemical reaction parameter $% ( \sigma ) $, Schmidt number $( Sc) $, entropy generation rate $( N_{G}) $, Brinkman number $( Br) $, dimensionless concentration ratio variable $( \alpha _{2}) $, dimensionless temperature ratio variable $( \alpha _{1}) $ and diffusive variable $( L) $ on velocity $f^{\prime }(\eta )$, temperature $\theta (\eta )$, concentration of nanomaterials $\phi (\eta )$, entropy generation $( N_{G}) $ and Bejan number $( Be) $ are scrutinized through graphs in this section. This objective is achieved through illustration of Figs. 2--27.

These figures are shown for both shear thickening $( n>1) $ and shear thinning $( n＜1) $ cases. The impact of $M$ on $f^{\prime }$ is presented in Fig. 2. Here $% f^{\prime }$ decays via larger $M$. The liquid velocity is much smaller in hydromagnetic case when compared with hydrodynamic case. It is due to the fact that Lorentz force becomes stronger when increments in $M$. Therefore stronger Lorentz force create resistance to transport phenomenon which is accountable for diminishment in the velocity $f^{\prime }$. The curve of $% f^{\prime }$ for values of $\lambda $ is investigated in Fig. 3. We noticed an improvement in $f^{\prime }$ subject to larger $\lambda $. Physically enhancement in buoyancy forces yields higher liquid velocity. Analysis of features of $Nr$ on $f^{\prime }$ is addressed in Fig. 4. Here $f^{\prime }$ is increasing function of larger $Nr$.

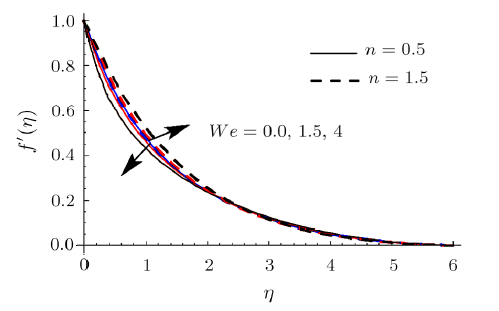
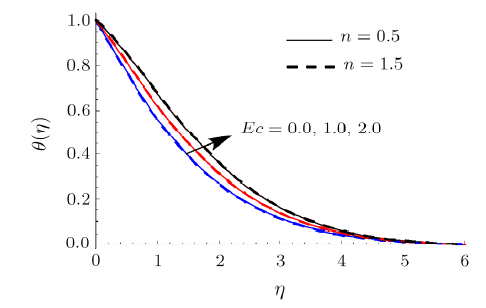
Figure 5 reveals the impact of $We$ on $f^{\prime }$. Here $f^{\prime }$ enhances via larger $We$ for shear thickening liquid whereas decays for shear thinning liquid. Figure 6 interprets $\theta $ variation for $Ec$. Here $\theta $ augments when $% Ec $ is incremented. The relation between the flow of enthalpy difference and kinetic energy is called Eckert number. It elaborates change of kinetic energy into internal energy by work done versus the viscous liquid stresses. The larger Eckert number $Ec$ causes loss of heat from the plate to the liquid i.e. cooling of the plate. In other words larger energy dissipation produces higher liquid temperature.

New window|Download| PPT slide
Fig. 2(Color online) $f^{\prime }$ impact for different $M$.

New window|Download| PPT slide
Fig. 3(Color online) $f^{\prime }$ impact for different $\lambda $.



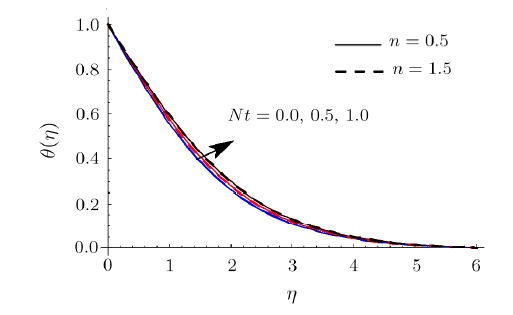
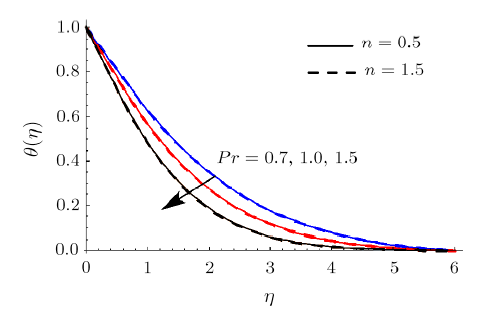
Figure 7 portrays the impact of $Nt$ on $% \theta $. Clearly larger $Nt$ yields higher $\theta $. Physically small number of particles are pulled away from hot region to cold one in thermophoresis phenomenon. Hence large number of nanomaterials are moved away from the heated region which inflates the liquid temperature. Features of $Pr $ on $\theta $ are exhibited in Fig. 8. Here $\theta $ decays when $% Pr $ is incremented. In fact larger $Pr $ reduces the thermal diffusivity which accordingly decay liquid temperature. The role of $R$ on $\theta $ is explored in Fig. 9.

New window|Download| PPT slide
Fig. 4(Color online) $f^{\prime }$ impact for different $Nr$.

New window|Download| PPT slide
Fig. 5(Color online) $f^{\prime }$ impact for different $We$.

New window|Download| PPT slide
Fig. 6(Color online) $\theta $ impact for different $Ec$.

New window|Download| PPT slide
Fig. 7(Color online) $\theta $ impact for different $Nt$.

New window|Download| PPT slide
Fig. 8(Color online) $\theta $ impact for different $Pr $.

New window|Download| PPT slide
Fig. 9(Color online) $\theta $ impact for different $R$.

New window|Download| PPT slide
Fig. 10(Color online) $\theta $ impact for different $We$.

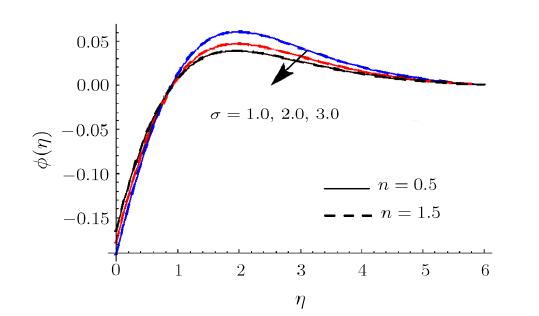
New window|Download| PPT slide
Fig. 11(Color online) $\phi $ impact for different $\sigma $.

New window|Download| PPT slide
Fig. 12(Color online) $\phi $ impact for different $Sc$.

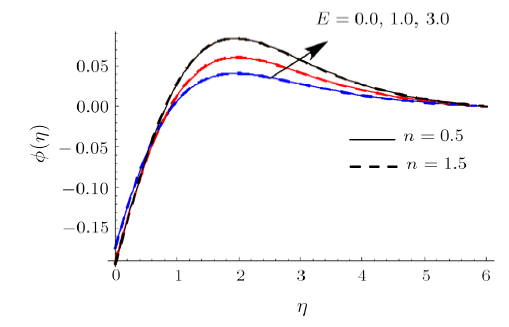
New window|Download| PPT slide
Fig. 13(Color online) $\phi $ impact for different $E$.

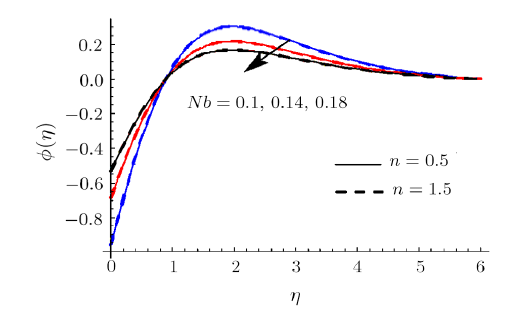
New window|Download| PPT slide
Fig. 14(Color online) $\phi $ impact for different $Nb$.

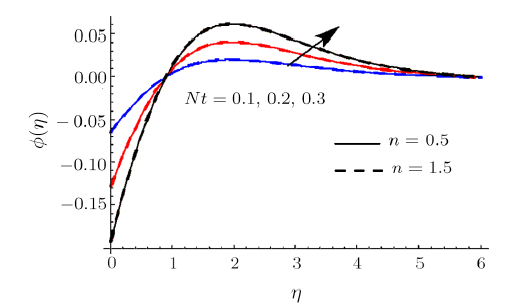
New window|Download| PPT slide
Fig. 15(Color online) $\phi $ impact for different $Nt$.

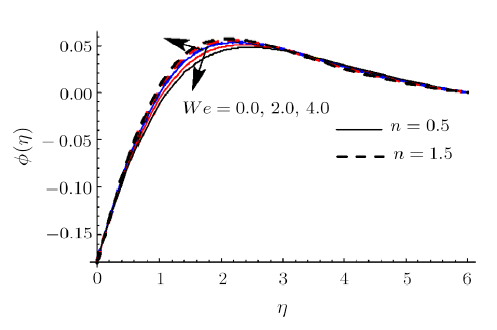
New window|Download| PPT slide
Fig. 16(Color online) $\phi $ impact for different $We$.



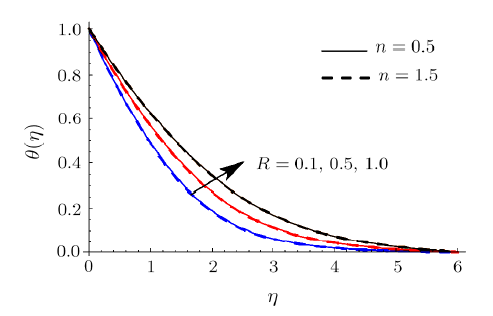
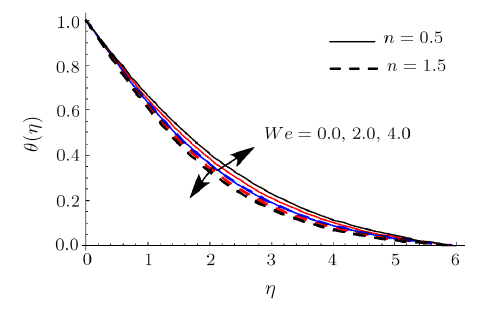
Clearly rise in $R$ augments $\theta .$ Physically radiation process produce more heat in the working liquid therefore $\theta $ and related thermal layer thickness enhances. Influence of $We$ on $\theta $ is reported in Fig. 10. Here $\theta $ increments via larger of $We$ for shear thinning liquid (i.e. $n＜1$) and consequently thermal layer thickness escalates. Moreover $\theta $ has opposite characteristic for higher estimation $We$ for shear thickening liquid (i.e. $n>1$). Figure 11 is plotted to examine the impact of $\sigma $ on $\phi .$ we observed that $% \phi $ enhances for higher estimation of $\sigma $. Actually consumption of reactive species decays rapidly for larger $\sigma $. Therefore $\phi $ reduces. Feature of $Sc$ on $\phi $ are illustrated in Fig. 12. Clearly $% \phi $ is reduced via larger $Sc$. As $Sc$ is the ratio between momentum diffusivity to Brownian diffusion coefficient. Brownian diffusion coefficient decays via larger $Sc$ due to which $\phi $ and its related nanoparticles concentration layer diminishes. Figure 13 depicts the behavior of $E$ on $\phi $. It is examined that the term $\exp ( -{ E_{a}}/{\kappa T}) $ decreases for higher estimation of $E_{a}$. This eventually generates chemical reaction due to which $\phi $ improves. The impacts of $Nt$ and $Nb$ on $\phi $ are interpreted in Figs. $14$ and $15$. For larger $Nt$, $\phi $ and thickness of nanoparticles concentration boundary layer escalates. Actually thermophoretic force increases for higher estimation of $Nt$ due to which nanoparticles moves from higher to lower temperature and $\phi $ boosts up (see Fig. 14). Moreover $\phi $ and its associated concentration layer reduce when $Nb$ is incremented (See Fig. $15$% ). Figure 16 reports $We$ outcome against $\phi $. Here $\phi $ decays via larger $We$ for shear thinning liquid (i.e. $n＜1)$ and nanoparticles concentration boundary layer thickness enhances. Furthermore opposite characteristic is noticed for shear thickening liquid (i.e. $n>1) $.

4.1 Entropy Generation Rate and Bejan Number

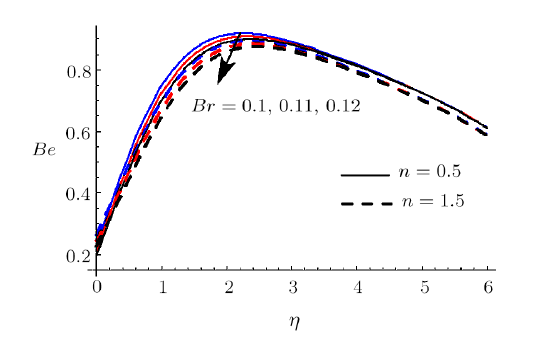
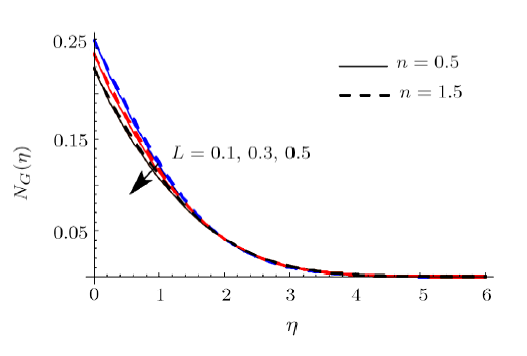
Figures 17 and 18 depict the salient features of $Br$ on $N_{G}$ and $Be$.In fact Brinkman number $Br$ has characteristic to propagate heat by viscousflowing liquid to heat transport through molecular conduction e.g. inpolymer processing. Heat transport via molecular conduction is much greaterthan heat propagation via viscous effects. Consequently movement of liquidparticles generates more heat between the adjacent layers. It enhances theentropy and system disorderness (see Fig. 17). Figure 18 displays that $Be$decays via larger $Br$. It is due to the fact that larger $Br$ correspondsto increase in entropy rate which decays the $Be$. Figure 19 reports theimpact of $L$ on $N_{G}.$ Clearly $N_{G}$ shows decreasing trend for $L$.Figures 20 and 21 disclose the characteristics of $M$ on $N_{G}$ and $Be$.Here it is noticed that $N_{G}$ augments when $M$ is incremented. Physicallyrise in $M$ creates greater Lorentz force due to which resistance in liquidflow increases and $N_{G}$ enhances (see Fig. 20). Larger $M$ correspondsto reduction in $Be.$ It means that liquid friction irreversibility hasdominating impacts over heat and mass transport irreversibility andconsequently $Be$ decays (see Fig. 21).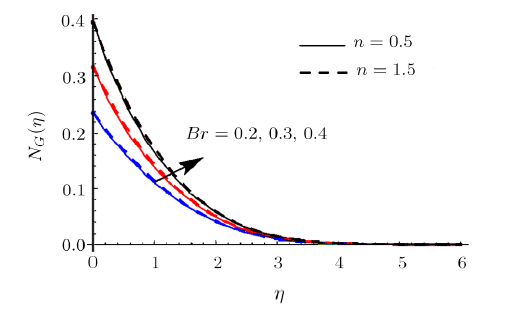

New window|Download| PPT slide
Fig. 17(Color online) $N_{G}$ impact for different $Br$.

New window|Download| PPT slide
Fig. 18(Color online) $Be$ impact for different $Br$.

New window|Download| PPT slide
Fig. 19(Color online) $N_{G}$ impact for different $L$.

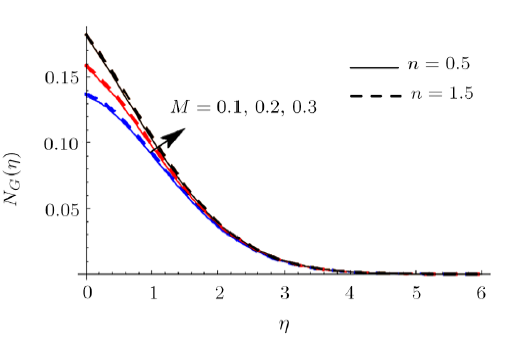
New window|Download| PPT slide
Fig. 20(Color online) $N_{G}$ impact for different $M$.

New window|Download| PPT slide
Fig. 21(Color online) $Be$ impact for different $M$.

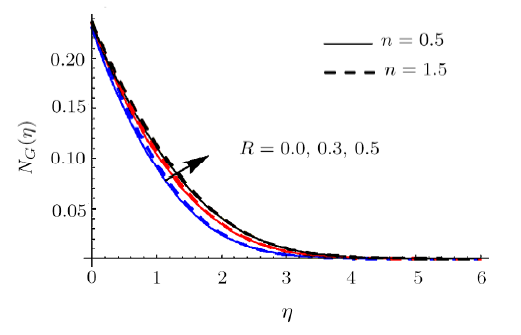
New window|Download| PPT slide
Fig. 22(Color online) $N_{G}$ impact for different $R$.

New window|Download| PPT slide
Fig. 23(Color online) $Be$ impact for different $R$.

New window|Download| PPT slide
Fig. 24(Color online) $N_{G}$ impact for different $We$.

New window|Download| PPT slide
Fig. 25(Color online) $N_{G}$ impact for different $Nb$.

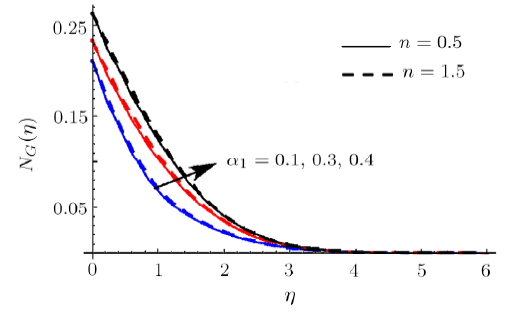
New window|Download| PPT slide
Fig. 26(Color online) $N_{G}$ impact for different $\alpha _{1}$.

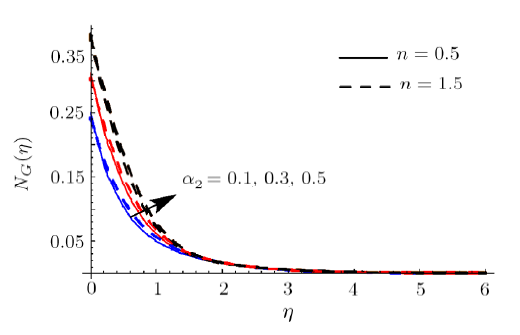
New window|Download| PPT slide
Fig. 27(Color online) $N_{G}$ impact for different $\alpha _{2}$.



Figures 22 and 23 reveal the impact of $R$ on $N_{G}$ and $Be$. Here $N_{G}$ and $Be$ enhance when $R$ is incremented. Physically increase in internal energy is responsible for an enhancement in $N_{G}$. Actually heat and mass transport irreversibility has dominating impacts on liquid friction irreversibility. Salient features of $% We$ for $N_{G}$ are discussed in Fig. 24. Here $N_{G}$ is enhanced for shear thickening case (i.e. $n>1) $ whereas opposite scenario is noted for shear thinning case (i.e. $n＜1) $. Impact of $Nb$ on $N_{G}$ is demonstrated in Fig. 25. Larger $Nb$ corresponds to decreasing trend in entropy generation $N_{G}$. Figure 26 illustrates the characteristics of $\alpha _{1}$ on $N_{G}$. Here $N_{G}$ enhances via larger $\alpha _{1}$. Physically liquid temperature increases for larger $\alpha _{1}$ which accordingly enhances entropy generation rate. The curve of $\alpha _{2}$ on $N_{G}$ is displayed in Fig. 27. It is evaluated that liquid concentration increases when $\alpha _{2}$ is incremented and consequently $N_{G}$ enhances. Moreover surface drag force diminishes for higher estimation $Ha$.

4.2 Characteristics of Surface Drag Force and Heat Transfer Rate

Table 1 portrays the influences of $Ha$ and $We$ on surface drag force for both shear thinning and shear thickening cases. Here surface drag force enhances via larger $We$ for shear thinning liquid while it reduces for shear thickening liquid.


Table 1
Table 1Surface drag force $C_{fx}{ Re}_{x}^{1/2}$ via different estimation of $We$ and $Ha$ when $Ec=Nr=0.1,$ $Nt=0.3$, $Nb=R=0.5$,$Pr=1$, $Sc=1$, $m=0.3$, $\sigma =\lambda =1$, $E=1$, $\delta _{1}=0.2$.

New window|CSV


Table 2
Table 2Heat transfer rate $Nu_{x}{ Re}_{x}^{-1/2}$ via different estimation of $Ec$, $Pr $, $We$, $Nt$, and $R$ when $Nr=0.1$, $Nb=0.5$, $Sc=1$, $m=0.3$, $\sigma =\lambda =1$, $E=1$, $\delta _{1}=0.2$.

New window|CSV

Table 2 points out the features of several embedded physical parameters on heat transfer rate. It is examined that heat transfer rate increases via larger $Pr$ and $R$ whereas it decays for larger $Ec$ and $Nt$.

5 Conclusions

Entropy generation in MHD mixed convective flow of Carreau nanoliquid is investigated numerically in the presence of viscous dissipation and thermal radiation. The key points observed from the flow analysis are as follows:

(i) Liquid velocity retards the flow via larger magnetic parameter for both shear thickening/thinning case.

(ii) Velocity is increasing function of larger local Weissenberg number for shear thickening liquid in comparison to shear thinning liquid.

(iii) Increments in thermal radiation parameter increases the liquid temperature.

(iv) Thermal and nanoparticle concentration boundary layers are boosted via larger thermophoretic parameter. (v) Stronger magnetic variable leads to higher entropy generation rate while decays for Bejan number.

(vi) Opposite scenario is observed for nanoparticles volume fraction through activation energy and chemical reaction rate.

(vii) Larger Brinkman gives rise to entropy generation rate in comparison to Bejan number.

(viii) Surface drag force reduces for larger magnetic parameter.

(ix) Heat transfer rate enhances via larger Prandtl number and radiative parameter when compared with Eckert number and thermophoretic parameter.

(x) Viscous nanoliquid situation can be retrieved by setting $We=n=0$.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1] S. U. S. Choi and J. A. Eastman , ASME Publications-Fed 231 ( 1995) 99.
[Cited within: 1]

[2] M. Sheikholeslami and H.F. Oztop, Chin. J. Phys. 55(2017) 2291.
DOI:10.1016/j.cjph.2017.09.006URL [Cited within: 1]

[3] M. M. Bhatti, A. Zeeshan, R. Ellahi , et al., Microvas. Res. 110(2017) 32.
DOI:10.1016/j.mvr.2016.11.007URLPMID:27908703
In this article, simultaneous effects of coagulation (blood clot) and variable magnetic field on peristaltically induced motion of non-Newtonian Jeffrey nanofluid containing gyrotactic microorganism through an annulus have been studied. The effects of an endoscope also taken into consideration in our study as a special case. The governing flow problem is simplified by taking the approximation of long wavelength and creeping flow regime. The resulting highly coupled differential equations are solved analytically with the help of perturbation method and series solution have been presented up to second order approximation. The impact of all the sundry parameters is discussed for velocity profile, temperature profile, nanoparticle concentration profile, motile microorganism density profile, pressure rise and friction forces. Moreover, numerical integration is also used to evaluate the expressions for pressure rise and friction forces for outer tube and inner tube. It is found that velocity of a fluid diminishes near the walls due to the increment in the height of clot. However, the influence of magnetic field depicts opposite behavior near the walls.

[4] M. Turkyilmazoglu , Eur. J. Mech. B/Fluids 65 ( 2017) 184.


[5] M. Waqas, T. Hayat, S. A. Shehzad , et al., 529(2018) 33.


[6] R. Kandasamy, I. Muhaimin, R. Mohamad , et al., Int. J.Mech. Sci. 70(2013) 146.


[7] A. Behseresht, A. Noghrehabadi, M. Ghalambaz , et al., Chem. Eng. Res. Design 92 ( 2014) 447.


[8] T. Hayat, M. Rashid, M. Imtiaz , et al., Int. J.Heat Mass Transf. 113(2017) 96.


[9] B. Mahanthesh, B. J. Gireesha, R. S.R Gorla . , et al., J.Niger. Math. Soc. 35(2016) 178.


[10] P.S Reddy . and A. J .Chamkha, Adv. Powder Technol. 27(2016) 1207.
DOI:10.1016/j.apt.2016.04.005URL [Cited within: 1]

[11] M. Khan and Hashim, AIP Adv. 5(2015) 107203.
DOI:10.1063/1.4932627URL [Cited within: 1]

[12] T. Hayat, S. Farooq, A. Alsaedi , et al., Results Phys. 7(2017) 451.
DOI:10.1016/j.rinp.2016.12.048URL [Cited within: 1]

[13] Hashim and M. Khan, Results Phys. 7(2017) 310.
DOI:10.1016/j.rinp.2016.12.031URL [Cited within: 1]

[14] T. Hayat, M. I. Khan, M. Waqas , et al., Colloids Surf. A 518 ( 2017) 263.
[Cited within: 1]

[15] M. Waqas, M. I. Khan, T. Hayat , et al., Comput. Meth.Appl. Mech. Eng. 324(2017) 640.
[Cited within: 1]

[16] M. Sheikholeslami and D. D. Ganji , Energy 75 ( 2014) 400.
[Cited within: 1]

[17] R. U. Haq, N. F. M .Noor, Z. H. Khan, et al., Adv. Powder Technol. 27(2016) 1568.
DOI:10.1016/j.apt.2016.05.020URL

[18] A. S. Dogonchi, K. Divsalar, D. D. Ganji , et al., Comput. Methods Appl.Mech. Engrg. 310(2016) 58.


[19] R. Ellahi, M. H. Tariq, M. Hassan , et al., J. Mol.Liq. 229(2016) 339.


[20] M. Turkyilmazoglu , Eur. J. Mech. B Fluids 59 ( 2016) 18.


[21] T. Hayat, M. Waqas, M. I. Khan , et al., Int. J. Heat Mass Transfer 102 ( 2016) 1123.
[Cited within: 1]

[22] G. Ib′a?nez, A. L′opez, J. Pantoja , et al., Energy 50 ( 2013) 143.
[Cited within: 1]

[23] A. Bejan, J. Heat Transf . 101(1979) 718.
[Cited within: 1]

[24] H. Abbasi , Energy 32 ( 2007) 1932.


[25] D. Srinivasacharya and K. H. Bindu , Energy 111 ( 2016) 165.


[26] A. Ebrahimi, F. Rikhtegar, A. Sabaghan , et al., Energy 101 ( 2016) 190.


[27] T. Hayat, S. Qayyum, M. I. Khan , et al., AIP Phys. Fluids 30 ( 2018) 017101.


[28] D. Nouri, M. P. Fard, M. J. Oboodi , et al., Int. J.Heat Mass Transf. 116(2018) 1036.
[Cited within: 1]

[29] Y.A Cengel . and M. A. Boles, Thermodynamics: An En- gineering Approach, pp. 930.
[Cited within: 1]

[30] M. R. Sohel, R. Saidur, N. H. Hassan , et al., Int. Commun.Heat Mass Transf. 46(2013) 85.
[Cited within: 1]

[31] M. I. Khan, M. Waqas, T. Hayat , et al., Int. J.Mech. Sci. 131- 132(2017) 426.
[Cited within: 1]

[32] A. Alsaedi, M. I. Khan, M. Farooq , et al., Adv. Powder Technol. 28 ( 2017) 288.
[Cited within: 1]

[33] H. Sithole, H. Mondal, P. Sibanda, et al., Results Phys. 9(2018) 1077.
DOI:10.1016/j.rinp.2018.04.003URL [Cited within: 1]