Ming Zhang¹, Jing-Fei Zhang¹, Xin Zhang^,1,2,3,∗1Department of Physics, College of Sciences, Northeastern University, Shenyang 110819, China
²Key Laboratory of Data Analytics and Optimization for Smart Industry (Northeastern University), Ministry of Education, Shenyang 110819, China
³Center for Gravitation and Cosmology, Yangzhou University, Yangzhou 225009, China

First author contact: ∗ Author to whom any correspondence should be addressed.
Received:2020-09-4Accepted:2020-09-21Online:2020-12-01


Abstract
Considering the mass splittings of three active neutrinos, we investigate how the properties of dark energy affect the cosmological constraints on the total neutrino mass $\sum {m}_{\nu }$ using the latest cosmological observations. In this paper, several typical dark energy models, including ΛCDM, wCDM, CPL, and HDE models, are discussed. In the analysis, we also consider the effects from the neutrino mass hierarchies, i.e. the degenerate hierarchy (DH), the normal hierarchy (NH), and the inverted hierarchy (IH). We employ the current cosmological observations to do the analysis, including the Planck 2018 temperature and polarization power spectra, the baryon acoustic oscillations (BAO), the type Ia supernovae (SNe), and the Hubble constant H₀ measurement. In the ΛCDM+$\sum {m}_{\nu }$ model, we obtain the upper limits of the neutrino mass $\sum {m}_{\nu }\lt 0.123\,\mathrm{eV}$ (DH), $\sum {m}_{\nu }\lt 0.156\,\mathrm{eV}$ (NH), and $\sum {m}_{\nu }\lt 0.185\,\mathrm{eV}$ (IH) at the 95% C.L., using the Planck+BAO+SNe data combination. For the wCDM+$\sum {m}_{\nu }$ model and the CPL+$\sum {m}_{\nu }$ model, larger upper limits of $\sum {m}_{\nu }$ are obtained compared to those of the ΛCDM+$\sum {m}_{\nu }$ model. The most stringent constraint on the neutrino mass, $\sum {m}_{\nu }\lt 0.080\,\mathrm{eV}$ (DH), is derived in the HDE+$\sum {m}_{\nu }$ model. In addition, we find that the inclusion of the local measurement of the Hubble constant in the data combination leads to tighter constraints on the total neutrino mass in all these dark energy models.
Keywords： neutrino mass;mass hierarchies of neutrinos;dark energy;cosmological constraints;Planck 2018


PDF (524KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Ming Zhang, Jing-Fei Zhang, Xin Zhang. Impacts of dark energy on constraining neutrino mass after Planck 2018. Communications in Theoretical Physics, 2020, 72(12): 125402- doi:10.1088/1572-9494/abbb84

1. Introduction

Neutrino oscillation experiments [1, 2] indicate that the three neutrino flavor eigenstates (ν_e, ν_μ, ν_τ) are actually quantum superpositions of the three mass eigenstates (ν₁, ν₂, ν₃) with masses m₁, m₂, and m₃. However, neutrino oscillation experiments cannot measure the absolute neutrino masses, but can only give the squared mass differences between the different mass eigenstates of neutrino. The solar and reactor experiments gave the result of Δm₂₁² ≃ 7.54×10⁻⁵ eV² and the atmospheric and accelerator beam experiments gave the result of $| {\rm{\Delta }}{m}_{31}^{2}| \simeq 2.46\times {10}^{-3}$ eV² [3, 4], which indicates that there are two possible neutrino mass hierarchies, i.e. the normal hierarchy (NH) with m₁<m₂≪m₃ and the inverted hierarchy (IH) with m₃ ≪ m₁<m₂. The case of neglecting the neutrino mass splitting, namely m₁=m₂=m₃, is called the degenerate hierarchy (DH).

Nevertheless, cosmological observations could provide a useful tool to measure the absolute neutrino total mass. With the decrease of the neutrino temperature, neutrino becomes non-relativistic at T∼0.15 eV in the evolution of the Universe. Then the mass effect of neutrinos begins to appear, which leads to a non-negligible influence on the cosmic microwave background (CMB) and large-scale structure [5-11]. Therefore, we could extract much useful information about neutrino from cosmological observations.

Recently, the observational data of Planck 2018 have been released by the Planck collaboration, and according to the latest data the upper limit of the total neutrino mass is $\sum {m}_{\nu }\,\lt 0.24\,\mathrm{eV}$ (95% C.L., TT,TE,EE+lowE+lensing) [12]. Since the baryon acoustic oscillations (BAO) data at low redshifts can break the geometric degeneracy inherent in CMB, the combination of the acoustic scales measured by the CMB and BAO data can determine the background geometry sufficiently. Combining BAO data with CMB data, the neutrino mass can be constrained to be $\sum {m}_{\nu }\lt 0.12\,\mathrm{eV}$ (95% C.L., TT,TE,EE+lowE+lensing+BAO). Adding the Pantheon type Ia supernovae (SNe) luminosity distance measurements, the constraint only becomes slightly better, with the result still roughly $\sum {m}_{\nu }\lt 0.11\,\mathrm{eV}$ (95% C.L., TT,TE,EE+lowE+lensing+BAO+SNe). It is noted that these results are based on the ΛCDM+$\sum {m}_{\nu }$ model.

Therefore, we wish to investigate the impacts of dark energy on constraining the total neutrino mass. In this work, we consider some typical dark energy models, including the ΛCDM model, the wCDM model, the w₀w_aCDM model (also known as the Chevallier-Polarski-Linder model or the CPL model) [13, 14], and the holographic dark energy (HDE) model [15-22]. In addition, we also consider the effects from the neutrino mass hierarchies (i.e. DH, NH, and IH) in our analysis.

More recently, some related studies of constraints on the total neutrino mass have been made; see, e.g. [23-67]. The cosmological constraints on the total neutrino mass in dynamical dark energy models have been discussed in, e.g. [46, 47], which indicates that the nature of dark energy can have a significant influence on the measurement of the total neutrino mass. As the latest CMB data have been released by the Planck collaboration, the results need to be updated. In this work, we employ the latest cosmological observations, including the CMB, BAO, SNe, and H₀ data to make a new analysis.

In this work, we will use the recent local measurement of the Hubble constant H₀, with the result of H₀=74.03± 1.42 km s⁻¹ Mpc⁻¹ (68% C.L.), by Riess et al [68]. Note that this local measurement result is in more than 4σ tension with the result of the Planck 2018 observation assuming a six-parameter base-Λ CDM model. Thus, we also wish to investigate how the inclusion of the H₀ local measurement would affect the measurement of the total neutrino mass in these dark energy models.

This paper is organized as follows. In section 2, we describe the methodology in our analysis. In section 3, we show the results and make some discussions. Finally, the conclusion is given in section 4.

2. Methodology

We take into account the neutrino mass splittings between the three active neutrinos. We employ the measurement results of neutrino oscillation experiments [3](1)$\begin{eqnarray}{\rm{\Delta }}{m}_{21}^{2}\equiv {m}_{2}^{2}-{m}_{1}^{2}=7.54\times {10}^{-5}\,{\mathrm{eV}}^{2},\end{eqnarray}$(2)$\begin{eqnarray}| {\rm{\Delta }}{m}_{31}^{2}| \equiv | {m}_{3}^{2}-{m}_{1}^{2}| =2.46\times {10}^{-3}\,{\mathrm{eV}}^{2}.\end{eqnarray}$

The total neutrino mass $\sum {m}_{\nu }$ is the sum of three active neutrino mass. For the NH case, $\sum {m}_{\nu }$ is written as(3)$\begin{eqnarray}\sum {m}_{\nu }^{\mathrm{NH}}={m}_{1}+\sqrt{{m}_{1}^{2}+{\rm{\Delta }}{m}_{21}^{2}}+\sqrt{{m}_{1}^{2}+{\rm{\Delta }}{m}_{31}^{2}},\end{eqnarray}$where m₁ is a free parameter. For the IH case, $\sum {m}_{\nu }$ is written as(4)$\begin{eqnarray}\sum {m}_{\nu }^{\mathrm{IH}}=\sqrt{{m}_{3}^{2}+| {\rm{\Delta }}{m}_{31}^{2}| }+\sqrt{{m}_{3}^{2}+| {\rm{\Delta }}{m}_{31}^{2}| +{\rm{\Delta }}{m}_{21}^{2}}+{m}_{3},\end{eqnarray}$where m₃ is a free parameter. For the DH case, ignoring the neutrino mass splittings, $\sum {m}_{\nu }$ can be written as(5)$\begin{eqnarray}\sum {m}_{\nu }^{\mathrm{DH}}={m}_{1}+{m}_{2}+{m}_{3}=3m,\end{eqnarray}$where m is a free parameter. Therefore, the lower bounds of $\sum {m}_{\nu }$ are 0 eV, 0.06 eV and 0.1 eV for DH, NH and IH, respectively. In this way, the total neutrino mass $\sum {m}_{\nu }$ as an additional parameter will be considered in our analysis.

In this paper, we make a global fit analysis on the different dark energy models, i.e. the ΛCDM+$\sum {m}_{\nu }$ model, the wCDM+$\sum {m}_{\nu }$ model, the CPL+$\sum {m}_{\nu }$ model, and the HDE+$\sum {m}_{\nu }$ model. We modify the publicly available Markov chain Monte-Carlo package CosmoMC [69] (that uses the Boltzmann solver CAMB [70]) to do the numerical calculations.

Here, we give a brief introduction to these dark energy models.• The ΛCDM+$\sum {m}_{\nu }$ model: The model containing a cosmological constant Λ and cold dark matter is called the ΛCDM model, which can fit various cosmological observations well. For the ΛCDM+$\sum {m}_{\nu }$ model, the parameter space vector is:(6)$\begin{eqnarray}{P}_{1}\equiv \left({\omega }_{b},{\omega }_{c},{{\rm{\Theta }}}_{{\rm{s}}},\tau ,{n}_{{\rm{s}}},\mathrm{ln}[{10}^{10}{A}_{{\rm{s}}}],\sum {m}_{\nu }\right),\end{eqnarray}$where ${\omega }_{b}\equiv {{\rm{\Omega }}}_{b}{h}^{2}$ and ${\omega }_{c}\equiv {{\rm{\Omega }}}_{c}{h}^{2}$ represent baryon and cold dark matter densities, respectively, Θ_s is the ratio between sound horizon r_s and angular diameter distance D_A at the time of photon decoupling, τ is the optical depth to the reionization of the universe, n_s and A_s are the power-law spectral index and amplitude of the power spectrum of primordial curvature perturbations, respectively, and $\sum {m}_{\nu }$ is the total neutrino mass.
• The wCDM+$\sum {m}_{\nu }$ model: The wCDM model is the simplest dynamical dark energy model, in which the equation-of-state (EoS) parameter w(z) is assumed to be a constant. For the wCDM+$\sum {m}_{\nu }$ model, the parameter space vector is:(7)$\begin{eqnarray}{P}_{2}\equiv \left({\omega }_{b},{\omega }_{c},{{\rm{\Theta }}}_{{\rm{s}}},\tau ,{n}_{{\rm{s}}},\mathrm{ln}[{10}^{10}{A}_{{\rm{s}}}],{\text{}}w,\sum {m}_{\nu }\right).\end{eqnarray}$
• The CPL+$\sum {m}_{\nu }$ model: For probing the evolution of w(z), the most widely used parameterization model is the CPL model [13, 14]. The form of w(z) in this model is given by(8)$\begin{eqnarray}w(z)={w}_{0}+{w}_{a}(1-a)={w}_{0}+{w}_{a}\displaystyle \frac{z}{1+z},\end{eqnarray}$where w₀ and w_a are free parameters. So, for the CPL+$\sum {m}_{\nu }$ model, the parameter space vector is:(9)$\begin{eqnarray}{P}_{3}\equiv \left({\omega }_{b},{\omega }_{c},{{\rm{\Theta }}}_{{\rm{s}}},\tau ,{n}_{{\rm{s}}},\mathrm{ln}[{10}^{10}{A}_{{\rm{s}}}],{\text{}}{w}_{0},{\text{}}{w}_{{\text{}}a},\sum {m}_{\nu }\right).\end{eqnarray}$
• The HDE+$\sum {m}_{\nu }$ model: The HDE model is built based on the the effective quantum field theory together with the holographic principle of quantum gravity. We can put an energy bound on the vacuum energy density, ${\rho }_{\mathrm{de}}{L}^{3}\leqslant {M}_{\mathrm{Pl}}^{2}L$, where M_Pl is the reduced Planck mass, which means that the total energy in a spatial region with size L should not exceed the mass of a black hole with the same size [71]. The largest length size that is compatible with this bound is the infrared cutoff size of this effective quantum field theory. An infrared scale can saturate that bound, and thus the dark energy density can be written as [15](10)$\begin{eqnarray}{\rho }_{\mathrm{de}}=3{c}^{2}{M}_{\mathrm{Pl}}^{2}{L}^{-2},\end{eqnarray}$where c is a dimensionless phenomenological parameter (note that here c is not the speed of light), which plays an important role in determining the properties of the HDE. The value of c determines the evolution of w. In the HDE model, the EoS can be expressed as(11)$\begin{eqnarray}w=-\displaystyle \frac{1}{3}-\displaystyle \frac{2}{3}\displaystyle \frac{\sqrt{{{\rm{\Omega }}}_{\mathrm{de}}}}{c}.\end{eqnarray}$According to this equation, we can find that in the early times $w\to -1/3$ (since ${{\rm{\Omega }}}_{\mathrm{de}}\to 0$) and in the far future $w\to -1/3-2/(3c)$ (since ${{\rm{\Omega }}}_{\mathrm{de}}\to 1$). Thus, when c<1, we can find that the EoS parameter w crosses −1 during the cosmological evolution. For the HDE+$\sum {m}_{\nu }$ model, the parameter space vector is:(12)$\begin{eqnarray}{P}_{4}\equiv \left({\omega }_{b},{\omega }_{c},{{\rm{\Theta }}}_{{\rm{s}}},\tau ,{n}_{{\rm{s}}},\mathrm{ln}[{10}^{10}{A}_{{\rm{s}}}],{\text{}}c,\sum {m}_{\nu }\right).\end{eqnarray}$


The observational data sets used in this work include CMB, BAO, SNe, and H₀. Here we also briefly describe these observational data.• The CMB data: We employ the CMB likelihood including the TT, TE, and EE spectra at ℓ≥30, the low-ℓ temperature Commander likelihood, and the low-ℓ SimAll EE likelihood, from the Planck 2018 release [12].
• The BAO data: We employ the measurements of the BAO signals from different galaxy surveys, including the DR7 Main Galaxy Sample at the effective redshift of z_eff=0.15 [72], the six-degree-field Galaxy Survey (6dFGS) at z_eff= 0.106 [73], and the latest BOSS data release 12 (DR12) in three redshift slices of z_eff=0.38, 0.51, and 0.61 [74].
• The SNe data: We use the latest SNe data given the Pantheon Sample [75], which contains 1048 SNe data in the redshift range of 0.01<z<2.3.
• The Hubble constant: We use the result of the direct measurement of the Hubble constant, with the result of H₀=74.03±1.42 km s⁻¹ Mpc⁻¹, given by Riess et al [68].


In this study, our basic data combination is Planck+BAO+SNe. In addition, in order to investigate the impacts of the H₀ measurement on constraints on the neutrino mass, we also consider the data combination of Planck+BAO+SNe+H₀.

Figure 1.

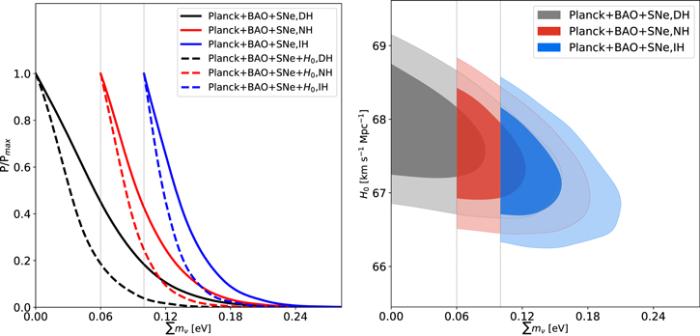
New window|Download| PPT slide
Figure 1.Left: the one-dimensional marginalized posterior distributions for $\sum {m}_{\nu }$ using the Planck+BAO+SNe and Planck+BAO+SNe+H₀ data combinations in the ΛCDM+$\sum {m}_{\nu }$ model. Right: the two-dimensional marginalized contours (1σ and 2σ) in the $\sum {m}_{\nu }$-H₀ plane for three neutrino mass hierarchy cases, i.e. the DH case, the NH case, and the IH case, by using Planck+BAO+SNe data combination in the ΛCDM+$\sum {m}_{\nu }$ model.

3. Results and discussion

In this section, we report the results of constraining the total neutrino mass from the Planck+BAO+SNe and Planck+BAO+SNe+H₀ data combinations. In our analysis, several typical dark energy models, i.e. the ΛCDM+$\sum {m}_{\nu }$ model, the wCDM+$\sum {m}_{\nu }$ model, the CPL+$\sum {m}_{\nu }$ model, and the HDE+$\sum {m}_{\nu }$ model, are investigated. In the meantime, we compare the results of the three neutrino mass hierarchy cases, i.e. the DH case, the NH case, and the IH case. The main results are listed in tables 1-4 and shown in figures 1-4. The best-fit values of χ² in the various cases are also listed. The fit values of parameters are given at 68% C.L. (1σ), and the upper limits of the neutrino mass are given at 95% C.L. (2σ).

Figure 2.

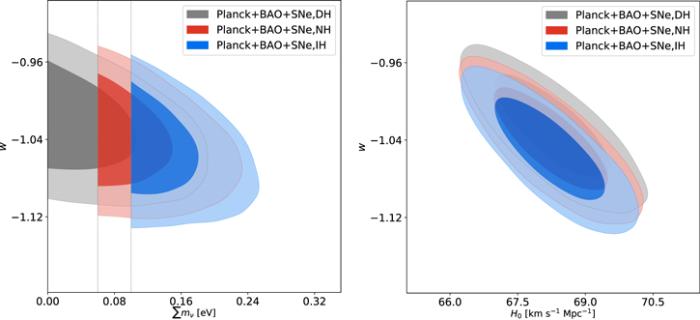
New window|Download| PPT slide
Figure 2.The two-dimensional marginalized contours (1σ and 2σ) in the $\sum {m}_{\nu }$-w and H₀-w planes for three neutrino mass hierarchy cases, i.e. the DH case, the NH case, and the IH case, by using Planck+BAO+SNe data combination in the wCDM+$\sum {m}_{\nu }$ model.



Table 1.
Table 1.Fitting results of the cosmological parameters in the ΛCDM+$\sum {m}_{\nu }$ model for three neutrino mass hierarchy cases, i.e. the DH case, the NH case, and the IH case, using the Planck+BAO+SNe and Planck+BAO+SNe+H₀ data combinations.

Data	Planck+BAO+SNe			Planck+BAO+SNe+H0
Mass ordering	DH	NH	IH	DH	NH	IH
H0 (km s−1 Mpc−1)	67.75±0.49	67.48±0.47	67.26±0.45	68.40±0.44	68.11±0.43	67.88±0.43
Ωm	0.3097±0.0063	0.3126±0.0063	0.3150±0.0060	0.3015±0.0056	0.3044±0.0056	0.3069±0.0056
σ8	${0.812}_{-0.008}^{+0.013}$	${0.801}_{-0.008}^{+0.011}$	${0.793}_{-0.008}^{+0.010}$	${0.813}_{-0.008}^{+0.010}$	${0.801}_{-0.008}^{+0.009}$	${0.792}_{-0.008}^{+0.009}$
$\sum {m}_{\nu }$ (eV)	$\lt 0.123$	<0.156	<0.185	<0.082	<0.125	<0.160
χ2	3805.133	3807.205	3809.012	3821.466	3825.557	3828.810

New window|CSV

3.1. Cases in different dark energy models

Firstly, we compare the constraint results in the different dark energy models from the Planck+BAO+SNe data combination. In table 1, we can obtain $\sum {m}_{\nu }\lt 0.123\,\mathrm{eV}$ for the DH case, $\sum {m}_{\nu }\lt 0.156\,\mathrm{eV}$ for the NH case, $\sum {m}_{\nu }\lt 0.185\,\mathrm{eV}$ for the IH case in the ΛCDM+$\sum {m}_{\nu }$ model (see figure 1). For the wCDM+$\sum {m}_{\nu }$ model, we have $\sum {m}_{\nu }\lt 0.155\,\mathrm{eV}$ (DH), $\sum {m}_{\nu }\,\lt 0.195\,\mathrm{eV}$ (NH), and $\sum {m}_{\nu }\lt 0.220\,\mathrm{eV}$ (IH) corresponding to w=−1.029±0.035 (DH), w=−1.042± 0.035 (NH), and w=−1.051±0.035 (IH), respectively (see table 2 and figure 2), and we find that the upper limits of $\sum {m}_{\nu }$ become larger, compared to the ΛCDM+$\sum {m}_{\nu }$ model. In the CPL+$\sum {m}_{\nu }$ model, the neutrino mass bounds are greatly relaxed (see table 3 and figure 3), and they are $\sum {m}_{\nu }\lt 0.247\,\mathrm{eV}$ (DH), $\sum {m}_{\nu }\lt 0.290\,\mathrm{eV}$ (NH), and $\sum {m}_{\nu }\lt 0.305\,\mathrm{eV}$ (IH). As is showed in figure 3, we find that a phantom dark energy (i.e. w<−1) or an early phantom dark energy (i.e. the quintom evolving from w<−1 to w>−1) is slightly more favored by current cosmological observations, which leads to the fact that a larger upper limit of $\sum {m}_{\nu }$ is obtained in the wCDM+$\sum {m}_{\nu }$ and CPL+$\sum {m}_{\nu }$ models. For the HDE+$\sum {m}_{\nu }$ model, an early quintessence dark energy with c<1 (i.e. the quintom eVolving from w<−1 to w>−1) is favored, and we could obtain the most stringent upper limits of the neutrino mass with $\sum {m}_{\nu }\,\lt 0.080\,\mathrm{eV}$ (DH), $\sum {m}_{\nu }\lt 0.129\,\mathrm{eV}$ (NH), $\sum {m}_{\nu }\lt 0.163\,\mathrm{eV}$ (IH), as also shown in table 4 and figure 4.

Figure 3.

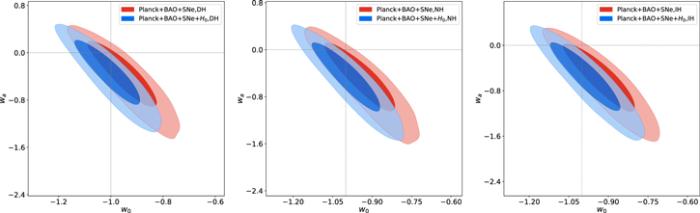
New window|Download| PPT slide
Figure 3.The two-dimensional marginalized contours (1σ and 2σ) in the w₀-w_a plane for three neutrino mass hierarchy cases, i.e. the DH case, the NH case, and the IH case, by using Planck+BAO+SNe and Planck+BAO+SNe+H₀ data combinations in the CPL+$\sum {m}_{\nu }$ model.



Table 2.
Table 2.Fitting results of the cosmological parameters in the wCDM+$\sum {m}_{\nu }$ model for three neutrino mass hierarchy cases, i.e. the DH case, the NH case, and the IH case, using the Planck+BAO+SNe and Planck+BAO+SNe+H₀ data combinations.

Data	Planck+BAO+SNe			Planck+BAO+SNe+H0
Mass ordering	DH	NH	IH	DH	NH	IH
w	−1.029±0.035	−1.042±0.035	−1.051±0.035	−1.078±0.033	−1.090±0.033	$-{1.100}_{-0.031}^{+0.034}$
H0 (km s−1 Mpc−1)	68.27±0.83	68.23±0.83	68.21±0.81	69.79±0.73	69.74±0.73	69.70±0.74
Ωm	0.3064±0.0078	0.3076±0.0078	0.3084±0.0076	0.2932±0.0066	0.2945±0.0066	0.2954±0.0067
σ8	0.819±0.015	${0.811}_{-0.014}^{+0.015}$	0.805±0.014	${0.834}_{-0.013}^{+0.015}$	${0.826}_{-0.013}^{+0.014}$	0.820±0.014
$\sum {m}_{\nu }$ (eV)	<0.155	<0.195	<0.220	<0.145	<0.183	<0.210
χ2	3805.053	3806.381	3807.724	3817.072	3818.757	3819.912

New window|CSV


Table 3.
Table 3.Fitting results of the cosmological parameters in the CPL+$\sum {m}_{\nu }$ model for three neutrino mass hierarchy cases, i.e. the DH case, the NH case, and the IH case, using the Planck+BAO+SNe and Planck+BAO+SNe+H₀ data combinations.

Data	Planck+BAO+SNe			Planck+BAO+SNe+H0
Mass ordering	DH	NH	IH	DH	NH	IH
w0	−0.945±0.087	−0.933±0.089	−0.923±0.089	−1.003±0.082	−0.988±0.086	−0.978±0.088
wa	$-{0.41}_{-0.30}^{+0.44}$	$-{0.52}_{-0.32}^{+0.46}$	$-{0.61}_{-0.33}^{+0.46}$	$-{0.38}_{-0.31}^{+0.41}$	$-{0.50}_{-0.33}^{+0.44}$	$-{0.60}_{-0.34}^{+0.45}$
H0 (km s−1 Mpc−1)	68.22±0.83	68.19±0.83	68.14±0.84	69.78±0.73	69.71±0.74	69.69±0.73
Ωm	0.3087±0.0082	0.3102±0.0083	0.3113±0.0083	0.2948±0.0068	0.2965±0.0070	0.2976±0.0069
σ8	${0.819}_{-0.015}^{+0.018}$	${0.813}_{-0.015}^{+0.018}$	${0.808}_{-0.015}^{+0.018}$	${0.835}_{-0.015}^{+0.017}$	${0.828}_{-0.014}^{+0.017}$	${0.823}_{-0.014}^{+0.017}$
$\sum {m}_{\nu }$ (eV)	<0.247	<0.290	<0.305	<0.216	<0.255	<0.281
χ2	3804.644	3805.938	3806.531	3816.716	3817.806	3818.809

New window|CSV


Table 4.
Table 4.Fitting results of the cosmological parameters in the HDE+$\sum {m}_{\nu }$ model for three neutrino mass hierarchy cases, i.e. the DH case, the NH case, and the IH case, using the Planck+BAO+SNe and Planck+BAO+SNe+H₀ data combinations.

Data	Planck+BAO+SNe			Planck+BAO+SNe+H0
Mass ordering	DH	NH	IH	DH	NH	IH
c	${0.645}_{-0.031}^{+0.027}$	${0.632}_{-0.030}^{+0.026}$	${0.623}_{-0.029}^{+0.025}$	${0.608}_{-0.025}^{+0.023}$	0.595±0.024	${0.587}_{-0.024}^{+0.022}$
H0 (km s−1 Mpc−1)	67.85±0.81	67.79±0.79	67.74±0.80	69.38±0.72	69.33±0.71	69.27±0.71
Ωm	0.3061±0.0077	0.3077±0.0076	0.3087±0.0076	0.2927±0.0065	0.2939±0.0065	0.2951±0.0065
σ8	0.797±0.013	0.789±0.013	0.783±0.013	0.811±0.013	0.803±0.012	0.796±0.12
$\sum {m}_{\nu }$ (eV)	<0.080	<0.129	<0.163	<0.075	<0.123	<0.159
χ2	3822.977	3828.219	3830.980	3838.467	3845.127	3845.289

New window|CSV

In addition, we can compare the best-fit χ² values of these models, which are listed in tables 1-4. For the wCDM+$\sum {m}_{\nu }$ model, the χ² values in the same neutrino mass hierarchy are slightly smaller than those of the ΛCDM+$\sum {m}_{\nu }$ model, at the price of adding one more parameter. We obtain the smallest χ² values in the CPL+$\sum {m}_{\nu }$ model, since this model has the most free parameters. For the HDE+$\sum {m}_{\nu }$ model, the most stringent upper limits of $\sum {m}_{\nu }$ can be obtained, but the χ² values are much larger than those of the ΛCDM+$\sum {m}_{\nu }$ model.

Figure 4.

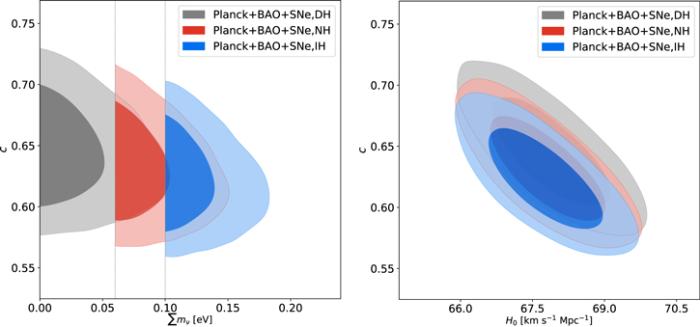
New window|Download| PPT slide
Figure 4.The two-dimensional marginalized contours (1σ and 2σ) in the H₀-c and $\sum {m}_{\nu }$-c planes for three neutrino mass hierarchy cases, i.e. the DH case, the NH case, and the IH case, by using Planck+BAO+SNe data combination in the HDE+$\sum {m}_{\nu }$ model.


For all these models, we discuss the fitting results in the different neutrino mass hierarchies. The prior of the lower bounds of $\sum {m}_{\nu }$ are 0 eV, 0.06 eV and 0.1 eV for DH, NH and IH, respectively, which can affect the constraint results of $\sum {m}_{\nu }$ significantly. In tables 1-4, the upper limits of $\sum {m}_{\nu }$ for the NH case are smaller than those for the IH case in these dark energy models. What's more, we find that the χ² values in the NH case is slightly smaller than those in the IH case for all these models, which indicates that the NH case fits the current observations better than the IH case. This conclusion is still consistent with the previous studies [23, 44, 46, 49, 53, 54, 60, 61].

3.2. Adding the H₀ measurement in data combination

In this subsection, we report the constraint results from the Planck+BAO+SNe+H₀ data combination and investigate the impact of the H₀ measurement on the fit results of $\sum {m}_{\nu }$. As is shown in table 1, we have $\sum {m}_{\nu }\lt 0.082\,\mathrm{eV}$ for the DH case, $\sum {m}_{\nu }\lt 0.125\,\mathrm{eV}$ for the NH case, $\sum {m}_{\nu }\lt 0.160\,\mathrm{eV}$ for the IH case in the ΛCDM+$\sum {m}_{\nu }$ model. Adding the H₀ data leads to a higher H₀ value in the cosmological fit. From the right panel of figure 1, we can see that $\sum {m}_{\nu }$ is anti-correlated with H₀ in the ΛCDM+$\sum {m}_{\nu }$ model. Therefore, we obtain a smaller upper limit of $\sum {m}_{\nu }$ with the Planck+BAO+SNe+H₀ data combination than that with the Planck+BAO+SNe data combination, which can be clearly seen in the left panel of figure 1.

With the Planck+BAO+SNe+H₀ data combination, we have $\sum {m}_{\nu }\lt 0.145\,\mathrm{eV}$ (DH), $\sum {m}_{\nu }\lt 0.183\,\mathrm{eV}$ (NH), $\sum {m}_{\nu }\lt 0.210\,\mathrm{eV}$ (IH) in the wCDM+$\sum {m}_{\nu }$ model (see table 2); we have $\sum {m}_{\nu }\lt 0.216\,\mathrm{eV}$ (DH), $\sum {m}_{\nu }\lt 0.255\,\mathrm{eV}$ (NH), $\sum {m}_{\nu }\lt 0.281\,\mathrm{eV}$ (IH) in the CPL+$\sum {m}_{\nu }$ model (see table 3); we have $\sum {m}_{\nu }\lt 0.075\,\mathrm{eV}$ (DH), $\sum {m}_{\nu }\lt 0.123\,\mathrm{eV}$ (NH), $\sum {m}_{\nu }\lt 0.159\,\mathrm{eV}$ (IH) in the HDE+$\sum {m}_{\nu }$ model (see table 4). In all these models, we find that the inclusion of the H₀ data gives a tighter constraint on $\sum {m}_{\nu }$.

4. Conclusion

In this paper, using the latest cosmological observations (including the Planck 2018 CMB data), we have obtained $\sum {m}_{\nu }\lt 0.123\,\mathrm{eV}$ (DH), $\sum {m}_{\nu }\lt 0.156\,\mathrm{eV}$ (NH), and $\sum {m}_{\nu }\,\lt 0.185\,\mathrm{eV}$ (IH) in the ΛCDM+$\sum {m}_{\nu }$ model with the Planck+BAO+SNe data combination. In addition, we also consider the influence of dynamical dark energy on the constraint results of $\sum {m}_{\nu }$. We investigate the cases of the wCDM+$\sum {m}_{\nu }$ model, the CPL+$\sum {m}_{\nu }$ model, and the HDE+$\sum {m}_{\nu }$ model, and we find that the nature of dark energy could significantly affect the constraints on the total neutrino mass. Compared to the ΛCDM+$\sum {m}_{\nu }$ model, the upper limits of the total neutrino mass become larger in the wCDM+$\sum {m}_{\nu }$ and CPL+$\sum {m}_{\nu }$ models. Using the Planck+BAO+SNe data combination, the most stringent upper limits of the neutrino mass, i.e. $\sum {m}_{\nu }\lt 0.080\,\mathrm{eV}$ (DH), $\sum {m}_{\nu }\lt 0.129\,\mathrm{eV}$ (NH), and $\sum {m}_{\nu }\lt 0.163\,\mathrm{eV}$ (IH), are obtained in the HDE+$\sum {m}_{\nu }$ model.

Comparing the values of χ² between the NH and IH cases, it is found that the NH case fits the current cosmological observations better than the IH case, indicating that the neutrino mass hierarchy is more likely to be the NH case according to the current cosmological data. In addition, it is also found that the inclusion of the local measurement of the Hubble constant in the data combination will lead to a tighter constraint on the total neutrino mass for all the dark energy models considered in this work.

Acknowledgments

We thank Hai-Li Li, Jing-Zhao Qi, and Yun-He Li for helpful discussions. This work was supported by the National Natural Science Foundation of China (Grant Nos. 11975072, 11875102, 11835009, and 11690021), the Liaoning Revitalization Talents Program (Grant No. XLYC1905011), the Fundamental Research Funds for the Central Universities (Grant No. N2005030), and the Top- Notch Young Talents Program of China (Grant No. W02070050).

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Fukuda Y et al. (Super-Kamiokande Collaboration) 1998 Phys. Rev. Lett. 81 1562
DOI:10.1103/PhysRevLett.81.1562 [Cited within: 1]

[2]Ahmad Q R et al. (SNO Collaboration) 2002 Phys. Rev. Lett. 89 011301
DOI:10.1103/PhysRevLett.89.011301 [Cited within: 1]

[3]Olive K A et al. (Particle Data Group) 2014 Chin. Phys. C 38 090001
DOI:10.1088/1674-1137/38/9/090001 [Cited within: 2]

[4]Xing Z Z 2020 Phys. Rep. 854 1 147
DOI:10.1016/j.physrep.2020.02.001 [Cited within: 1]

[5]Abazajian K N et al. (Topical Conveners: K.N. Abazajian, J.E. Carlstrom, A.T. Lee Collaboration) 2015 Astropart. Phys. 63 66
DOI:10.1016/j.astropartphys.2014.05.014 [Cited within: 1]

[6]Lesgourgues J Pastor S 2006 Phys. Rep. 429 307
DOI:10.1016/j.physrep.2006.04.001

[7]Wong Y Y Y 2011 Ann. Rev. Nucl. Part. Sci. 61 69
DOI:10.1146/annurev-nucl-102010-130252

[8]Lesgourgues J Pastor S 2012 Adv. High Energy Phys. 2012 608515
DOI:10.1155/2012/608515

[9]Lesgourgues J Pastor S 2014 New J. Phys. 16 065002
DOI:10.1088/1367-2630/16/6/065002

[10]Archidiacono M Brinckmann T Lesgourgues J Poulin V 2017 J. Cosmol. Astropart. Phys. JCAP02(2017)052
DOI:10.1088/1475-7516/2017/02/052

[11]Lattanzi M Gerbino M 2018 Front. Phys. 5 70
DOI:10.3389/fphy.2017.00070 [Cited within: 1]

[12]Aghanim N (Planck) et al. 2020 Astron. Astrophys. 641A6
[Cited within: 2]

[13]Chevallier M Polarski D 2001 Int. J. Mod. Phys. D 10 213
DOI:10.1142/S0218271801000822 [Cited within: 2]

[14]Linder E V 2003 Phys. Rev. Lett. 90 091301
DOI:10.1103/PhysRevLett.90.091301 [Cited within: 2]

[15]Li M 2004 Phys. Lett. B 603 1
DOI:10.1016/j.physletb.2004.10.014 [Cited within: 2]

[16]Huang Q G Li M 2004 J. Cosmol. Astropart. Phys. JCAP08(2004)013
DOI:10.1088/1475-7516/2004/08/013

[17]Zhang J F Zhao M M Cui J L Zhang X 2014 Eur. Phys. J. C 74 3178
DOI:10.1140/epjc/s10052-014-3178-7

[18]Wang S Wang Y Li M 2017 Phys. Rep. 696 1
DOI:10.1016/j.physrep.2017.06.003

[19]Wang S Geng J J Hu Y L Zhang X 2015 Sci. China Phys. Mech. Astron. 58 019801


[20]Cui J Xu Y Zhang J Zhang X 2015 Sci. China Phys. Mech. Astron. 58 110402
DOI:10.1007/s11433-015-5734-z

[21]He D Z Zhang J F Zhang X 2017 Sci. China Phys. Mech. Astron. 60 039511
DOI:10.1007/s11433-016-0472-1

[22]Xu Y Y Zhang X 2016 Eur. Phys. J. C 76 588
DOI:10.1140/epjc/s10052-016-4446-5 [Cited within: 1]

[23]Roy Choudhury S Hannestad S 2019 JCAP JCAP07(2020)03
[Cited within: 2]

[24]Reid B A Verde L Jimenez R Mena O 2010 J. Cosmol. Astropart. Phys. JCAP01(2010)003
DOI:10.1088/1475-7516/2010/01/003

[25]Thomas S A Abdalla F B Lahav O 2010 Phys. Rev. Lett. 105 031301
DOI:10.1103/PhysRevLett.105.031301

[26]Carbone C Verde L Wang Y Cimatti A 2011 J. Cosmol. Astropart. Phys. JCAP03(2011)030
DOI:10.1088/1475-7516/2011/03/030

[27]Li H Zhang X 2012 Phys. Lett. B 713 160
DOI:10.1016/j.physletb.2012.06.030

[28]Li Y H Wang S Li X D Zhang X 2013 J. Cosmol. Astropart. Phys. JCAP02(2013)033
DOI:10.1088/1475-7516/2013/02/033

[29]Audren B Lesgourgues J Bird S Haehnelt M G Viel M 2013 J. Cosmol. Astropart. Phys. JCAP01(2013)026
DOI:10.1088/1475-7516/2013/01/026

[30]Riemer-Sørensen S Parkinson D Davis T M 2014 Phys. Rev. D 89 103505
DOI:10.1103/PhysRevD.89.103505

[31]Zhang J F Li Y H Zhang X 2015 Phys. Lett. B 740 359
DOI:10.1016/j.physletb.2014.12.012

[32]Zhang J F Li Y H Zhang X 2014 Eur. Phys. J. C 74 2954
DOI:10.1140/epjc/s10052-014-2954-8

[33]Zhang J F Geng J J Zhang X 2014 J. Cosmol. Astropart. Phys. JCAP10(2014)044


[34]Palanque-Delabrouille N et al. 2015 J. Cosmol. Astropart. Phys. JCAP02(2015)045
DOI:10.1088/1475-7516/2015/02/045

[35]Li Y H Zhang J F Zhang X 2015 Phys. Lett. B 744 213
DOI:10.1016/j.physletb.2015.03.063

[36]Zhang J F Zhao M M Li Y H Zhang X 2015 J. Cosmol. Astropart. Phys. JCAP04(2015)038
DOI:10.1088/1475-7516/2015/04/038

[37]Geng C Q Lee C C Myrzakulov R Sami M Saridakis E N 2016 J. Cosmol. Astropart. Phys. JCAP01(2016)049
DOI:10.1088/1475-7516/2016/01/049

[38]Chen Y Xu L 2016 Phys. Lett. B 752 66
DOI:10.1016/j.physletb.2015.11.022

[39]Allison R Caucal P Calabrese E Dunkley J Louis T 2015 Phys. Rev. D 92 123535
DOI:10.1103/PhysRevD.92.123535

[40]Cuesta A J Niro V Verde L 2016 Phys. Dark Univ. 13 77
DOI:10.1016/j.dark.2016.04.005

[41]Chen Y Ratra B Biesiada M Li S Zhu Z H 2016 Astrophys. J. 829 61
DOI:10.3847/0004-637X/829/2/61

[42]Lu J Liu M Wu Y Wang Y Yang W 2016 Eur. Phys. J. C 76 679
DOI:10.1140/epjc/s10052-016-4525-7

[43]Kumar S Nunes R C 2016 Phys. Rev. D 94 123511
DOI:10.1103/PhysRevD.94.123511

[44]Xu L Huang Q G 2018 Sci. China Phys. Mech. Astron. 61 039521
DOI:10.1007/s11433-017-9125-0 [Cited within: 1]

[45]Vagnozzi S Giusarma E Mena O Freese K Gerbino M Ho S Lattanzi M 2017 Phys. Rev. D 96 123503
DOI:10.1103/PhysRevD.96.123503

[46]Zhang X 2017 Sci. China Phys. Mech. Astron. 60 060431
DOI:10.1007/s11433-017-9025-7 [Cited within: 2]

[47]Zhang X 2016 Phys. Rev. D 93 083011
DOI:10.1103/PhysRevD.93.083011 [Cited within: 1]

[48]Lorenz C S Calabrese E Alonso D 2017 Phys. Rev. D 96 043510
DOI:10.1103/PhysRevD.96.043510

[49]Zhao M M Zhang J F Zhang X 2018 Phys. Lett. B 779 473
DOI:10.1016/j.physletb.2018.02.042 [Cited within: 1]

[50]Vagnozzi S Dhawan S Gerbino M Freese K Goobar A Mena O 2018 Phys. Rev. D 98 083501
DOI:10.1103/PhysRevD.98.083501

[51]Wang L F Zhang X N Zhang J F Zhang X 2018 Phys. Lett. B 782 87
DOI:10.1016/j.physletb.2018.05.027

[52]Zhang J F Wang B Zhang X 2020 Sci. China Phys. Mech. Astron. 63 280411
DOI:10.1007/s11433-019-1516-y

[53]Guo R Y Zhang J F Zhang X 2018 Chin. Phys. C 42 095103
DOI:10.1088/1674-1137/42/9/095103 [Cited within: 1]

[54]Zhao M Guo R He D Zhang J Zhang X 2020 Sci. China Phys. Mech. Astron. 63 230412
DOI:10.1007/s11433-019-1474-8 [Cited within: 1]

[55]Loureiro A et al. 2019 Phys. Rev. Lett. 123 081301
DOI:10.1103/PhysRevLett.123.081301

[56]Huang Q G Wang K Wang S 2016 Eur. Phys. J. C 76 489
DOI:10.1140/epjc/s10052-016-4334-z

[57]Bellomo N Bellini E Hu B Jimenez R Pena-Garay C Verde L 2017 J. Cosmol. Astropart. Phys. JCAP02(2017)043
DOI:10.1088/1475-7516/2017/02/043

[58]Hu B Torrado J 2015 Phys. Rev. D 91 064039
DOI:10.1103/PhysRevD.91.064039

[59]Xu L 2016 J. Cosmol. Astropart. Phys. JCAP08(2016)059
DOI:10.1088/1475-7516/2016/08/059

[60]Wang S Wang Y F Xia D M Zhang X 2016 Phys. Rev. D 94 083519
DOI:10.1103/PhysRevD.94.083519 [Cited within: 1]

[61]Feng L Li H L Zhang J F Zhang X 2020 Sci. China Phys. Mech. Astron. 63 220401
DOI:10.1007/s11433-019-9431-9 [Cited within: 1]

[62]Diaz Rivero A Miranda V Dvorkin C 2019 Phys. Rev. D 100 063504
DOI:10.1103/PhysRevD.100.063504

[63]Miranda V Dvorkin C 2018 Phys. Rev. D 98 043537
DOI:10.1103/PhysRevD.98.043537

[64]Ballardini M Braglia M Finelli F Paoletti D Starobinsky A A Umiltš C 2020 arXiv:2004.14349 [astro-ph.CO]


[65]Hagstotz S de Salas P F Gariazzo S Gerbino M Lattanzi M Vagnozzi S Freese K Pastor S 2020 arXiv:2003.02289 [astro-ph.CO]


[66]Vagnozzi S 2019 arXiv:1907.08010 [astro-ph.CO]


[67]Giusarma E Vagnozzi S Ho S Ferraro S Freese K Kamen-Rubio R Luk K B 2018 Phys. Rev. D 98 123526
DOI:10.1103/PhysRevD.98.123526 [Cited within: 1]

[68]Riess A G Casertano S Yuan W Macri L M Scolnic D 2019 Astrophys. J. 876 85
DOI:10.3847/1538-4357/ab1422 [Cited within: 2]

[69]Lewis A Bridle S 2002 Phys. Rev. D 66 103511
DOI:10.1103/PhysRevD.66.103511 [Cited within: 1]

[70]Lewis A Challinor A Lasenby A 2000 Astrophys. J. 538 473
DOI:10.1086/309179 [Cited within: 1]

[71]Cohen A G Kaplan D B Nelson A E 1999 Phys. Rev. Lett. 82 4971
DOI:10.1103/PhysRevLett.82.4971 [Cited within: 1]

[72]Ross A J Samushia L Howlett C Percival W J Burden A Manera M 2015 Mon. Not. R. Astron. Soc. 449 835
DOI:10.1093/mnras/stv154 [Cited within: 1]

[73]Beutler F et al. 2011 Mon. Not. R. Astron. Soc. 416 3017
DOI:10.1111/j.1365-2966.2011.19250.x [Cited within: 1]

[74]Alam S et al. (BOSS Collaboration) 2017 Mon. Not. R. Astron. Soc. 470 2617
DOI:10.1093/mnras/stx721 [Cited within: 1]

[75]Scolnic D M et al. 2018 Astrophys. J. 859 101
DOI:10.3847/1538-4357/aab9bb [Cited within: 1]