Payam Mehdipour Kaldiani^,Department of Physics, Naragh Branch, Islamic Azad University, Naragh, Iran

Received:2020-11-16Revised:2021-04-18Accepted:2021-04-29Online:2021-06-01


Abstract
The fission fragment mass-yields are evaluated for pre-actinide and actinide isotopes using a systematic statistical scission point model. The total potential energy of the fissioning systems at the scission point is presented in approximate relations as functions of mass numbers, deformation parameters and the temperature of complementary fission fragments. The collective temperature, T_coll, and the temperature of fission fragments, T_i, are separated and the effect of collective temperature on mass yields results is investigated. The fragment temperature has been calculated with the generalized superfluid model. The sum of deformation parameters of complementary fission fragments has been obtained by fitting the calculated results with the experimental data. To investigate the transitions between symmetric and asymmetric modes mass yields for pre-actinide and heavy actinides are calculated with this model. The transition from asymmetric to symmetric fission is well reproduced using this systematic statistical scission point model. The calculated results are in good agreement with the experimental data with T_coll = 2 MeV at intermediate excitation energy and with T_coll = 1 MeV for spontaneous fission. Despite the Langevin model, in the scission point model, a constraint on the deformation parameters of fission fragments has little effect on the results of the mass yield.
Keywords： mass yields; deformation parameters; statistical scission point model; symmetric and asymmetric modes; fission fragments


PDF (852KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Payam Mehdipour Kaldiani. Deformation parameter changes in fission mass yields within the systematic statistical scission-point model. Communications in Theoretical Physics, 2021, 73(7): 075303- doi:10.1088/1572-9494/abfcb0

1. Introduction

Since the fission discovery, the experimental and theoretical fission mass yields have been continuously extended and updated [1–24]. At first, Fong [1] had presented the statistical model to obtain the fission fragment mass yields and then Wilkins [2] presented the scission point model as the most widely used theoretical model. With this model, Wilkins was able to explain the transitions between symmetric to asymmetric fission modes. These models have been developed in many branches, such as the Gaussian model [3–5] and the modified scission point models [7–12]. Recently, the time-dependent model has been significantly developed by Randrup [14–16] and some researchers [17–21] to evaluate the mass yields of pre-actinides and actinides. However, recent models have sophisticated computations, which indicate the need for a systematic method to more easily evaluate the mass yields of fission fragments.

The mass yields of fissioning systems with mass numbers between 226 and 258 are asymmetric. With increasing the mass numbers of fissioning systems, the symmetric fission is favored (A > 258). The transition of mass yields from symmetric (asymmetric) to asymmetric (symmetric) occurs by increasing the mass number of thorium (fermium) isotopes. Although the statistical scission point model can predict transition from asymmetric to symmetric fission for heavy actinides [9], the calculated results are not accurate compared with experimental data. This problem is found where the calculated results were refined, as far as they smeared each calculated yield by the Gaussian with the width 1.5 amu to obtain a smoother curve.

The excitation energy (E) of the fissioning nucleus is often manipulated. Some researchers [7–10] have added the difference between the potential energy of fissioning nucleus and the potential energy of one of the complementary fragments at the scission point. Some others [11, 12] have added the energy of the excited compound nucleus (i.e. E^* = Q + E where Q is the Q-values). Here, the height of the fission barrier is added to the excitation energy.

In this study, it is assumed that the collective temperature is independent from the fragment temperature calculated by the generalized superfluid model. The remaining two parameters, namely collective temperature and deformation parameters of fission fragments, are investigated by comparing calculated results and experimental data. At first, the deformation parameters of fission fragments are obtained for a collective temperature equal to 1 MeV. Then the collective temperature is changed (T_coll = 2 MeV) to investigate the effect of this parameter on mass yields.

In the next section, the framework for calculation the mass yields is presented in a systematic method, which has least parameters and refinements. In section 3, the mass yields of asymmetric fission are investigated and the sum of the deformation parameters of complementary fragments is obtained. The effect of collective temperature is also investigated by choosing two values of 1 and 2 MeV for it. In section 4, the results of the transition region from asymmetric to symmetric fission are evaluated and compared with experimental data.

2. Theoretical framework

The relative yield is usually calculated as the ratio between the probabilities of a given fragmentation over the sum of probabilities of all possible fragmentations as follows(1)$\begin{eqnarray}Y({A}_{i},{Z}_{i})=\displaystyle \frac{P({A}_{i},{Z}_{i})}{\sum P({A}_{i},{Z}_{i})},\end{eqnarray}$where P(A_i, Z_i) is the relative probability of each fragment. In the statistical method, the relative probability of each pair fission fragment is given by [2](2)$\begin{eqnarray}P={\int }_{0}^{{\beta }_{\max }}{\int }_{0}^{{\beta }_{\max }}{{\rm{e}}}^{-\tfrac{V(N,Z,s,{\beta }_{1},{\beta }_{2})}{{T}_{\mathrm{coll}}}}{\rm{d}}{\beta }_{1}\,{\rm{d}}{\beta }_{2},\end{eqnarray}$where V(N, Z, s, β₁, β₂) is the total potential energy of the fissioning system at the scission point. T_coll is the collective temperature of the fissioning system. s is the spherical coaxial surface distance and β_i s (i = 1, 2) are the deformation parameters for the light and heavy fragments.

The total potential energies at the scission point is defined as(3)$\begin{eqnarray}V(N,Z,s,{\beta }_{1},{\beta }_{2})={V}_{\mathrm{Interac}}+\sum _{{A}_{L},{A}_{H}}{V}_{{\rm{indiv}},i}.\end{eqnarray}$

The first term is the interaction energy between complementary fragments, V_Interac = V_Coul + V_prox. The individual energy includes macroscopic energy (V_Mac) plus shell correction energy and pairing energy as the microscopic energies (V_Mic), i.e. ${V}_{\mathrm{indiv}}={V}_{\mathrm{Mac},{i}}+{E}_{\mathrm{shell},{i}}+{E}_{\mathrm{pair},{i}}$. In the following sections, these energies are presented separately.

2.1. The interaction energy

The nuclear proximity potential (V_prox) is caculated by [25, 26](4)$\begin{eqnarray}{V}_{\mathrm{prox}}(s)=4\pi \gamma b\left[\displaystyle \frac{{C}_{1}{C}_{2}}{{C}_{1}+{C}_{2}}\right]{\rm{\Phi }}\left(\displaystyle \frac{s}{b}\right),\end{eqnarray}$where the width (diffuseness) of the nuclear surface is b ≈0.88 fm. C₁ and C₂ are the Süsmann central radii of fragments that is related to the sharp radius R_i as(5)$\begin{eqnarray}{C}_{i}={R}_{0,i}-\left[\displaystyle \frac{{b}^{2}}{{R}_{0,i}}\right],\end{eqnarray}$R_0,i is the net radius of each fission fragment obtained through a semi-empirical equation that is a function of the mass number of fission fragments [26] as(6)$\begin{eqnarray}{R}_{0,i}(\mathrm{fm})=1.28{{A}}_{i}^{1/3}-0.76+0.8{{A}}_{i}^{-1/3}.\end{eqnarray}$

In equation (4), γ is the surface tension coefficient of the nucleus and obtained from the Lysekil mass formula by [27](7)$\begin{eqnarray}\gamma =0.9517\sqrt{(1-2.61{I}_{1}^{2})(1-2.61{I}_{2}^{2})}\,{{\rm{MeV}}{\rm{fm}}}^{-2};\,{I}_{i}=\displaystyle \frac{{\left({N}_{i}-{Z}_{i}\right)}^{2}}{{A}_{i}^{2}},\end{eqnarray}$where N_i, Z_i and A_i are the neutron, atomic, and mass number of each fission fragment, respectively. In equation (4), Φ is the universal proximity relation which is a function of distance between two interaction fragments and is defined as [25](8)$\begin{eqnarray}{\rm{\Phi }}\left(\displaystyle \frac{s}{b}\right)=\left\{\begin{array}{l}-1.7817+0.9270+0.0169{\left(\displaystyle \frac{s}{b}\right)}^{2}-0.0514{\left(\displaystyle \frac{s}{b}\right)}^{3}\\ \qquad {\rm{for}}\quad 0\leqslant \displaystyle \frac{s}{b}\leqslant 1.9475\\ -4.41\exp (-\displaystyle \frac{s}{0.7176b})\\ \quad {\rm{for}}\quad \displaystyle \frac{s}{b}\geqslant 1.9475,\end{array}\right.\end{eqnarray}$

The Coulomb energy is written as [4, 13](9)$\begin{eqnarray}\begin{array}{rcl}{E}_{\mathrm{Coul}} & = & \displaystyle \frac{{Z}_{1}{Z}_{2}{e}^{2}}{r}(1+{n}_{1}({{R}_{\mathrm{0,1}}}^{2}{\beta }_{1}+{{R}_{\mathrm{0,2}}}^{2}{\beta }_{2})\\ & & +{n}_{2}({{R}_{\mathrm{0,1}}}^{2}{{\beta }_{1}}^{2}+{{R}_{\mathrm{0,2}}}^{2}{{\beta }_{2}}^{2})\\ & & +{n}_{3}({{R}_{\mathrm{0,1}}}^{4}{{\beta }_{1}}^{2}+{{R}_{\mathrm{0,2}}}^{4}{{\beta }_{2}}^{2})+{n}_{4}{\beta }_{1}{\beta }_{2}),\end{array}\end{eqnarray}$where r = s + R₁ + R₂, ${n}_{1}=\tfrac{3}{2\sqrt{5\pi }{r}^{2}}$, ${n}_{2}=\tfrac{3}{7\pi {r}^{2}}$,${n}_{3}=\tfrac{9}{14\pi {r}^{4}}$, ${n}_{4}=\tfrac{27{{R}_{1}}^{2}{{R}_{2}}^{2}}{10\pi {r}^{4}}$. R_i is the radii of deformed nuclei that can be evaluated using the deformation dependent expansion of nuclear radii as(10)$\begin{eqnarray}{R}_{i}(\theta )={R}_{0,i}\sum (1+{\beta }_{i}{Y}_{j0}(\theta )),\end{eqnarray}$where θ is the angle made by the axis of symmetry with the fission axis, β_i is the quadrupole deformation parameter of each fragment and Y_j0 is the spherical harmonic functions.

2.2. The individual energies

The individual energies include macroscopic energy plus shell correction energy and pairing energy. The macroscopic energy is calculated in the framework of the FRLDM model from [28], and the spheroidally deformed is applied as [23](11)$\begin{eqnarray}\begin{array}{l}{V}_{\mathrm{surf},{i}}=21.18466\,{\text{}}B1\left(1-2.345\,\displaystyle \frac{{\left({\text{}}{N}_{{i}}-{\text{}}{Z}_{{i}}\right)}^{2}}{{\text{}}{A}_{{i}}^{2}}\right)\\ \sqrt[3]{{\text{}}{A}_{{i}}^{2}}\left(1-0.009266\,{\text{}}{T}_{{i}}^{2}\right),\end{array}\end{eqnarray}$(12)$\begin{eqnarray}\begin{array}{l}{V}_{\mathrm{coul},{i}}=\left(0.7448\,\displaystyle \frac{{\text{}}B3{\text{}}{Z}_{{i}}^{2}}{\sqrt[3]{{\text{}}{A}_{{i}}}}-0.5689\,\displaystyle \frac{{\text{}}{Z}_{{i}}^{4/3}}{\sqrt[3]{{\text{}}{A}_{{i}}}}+\displaystyle \frac{{\text{}}f\,{\text{}}{Z}_{{i}}^{2}}{{\text{}}{A}_{{i}}}\right)\\ \,\times \,\left(1-\displaystyle \frac{0.0032}{3}\,{\text{}}{T}_{{i}}^{2}\right),\end{array}\end{eqnarray}$where the quantity B1 is the relation generalized surface or nuclear energy in a model that accounts for the effect of infinite range of nuclear force. The quantity f is the proton form-factor correction to the Coulomb energy. The relative Coulomb energy B3 is used in the first approximation. All parameters are chosen from [28].

The pairing correction energy (E_pair in MeV) is calculated as(13)$\begin{eqnarray}{E}_{\mathrm{pair}}=\left\{\begin{array}{l}0\,\,\,{\rm{for}}\,\,{{Z}}_{i}\,{\rm{and}}\,{{N}}_{i}\,{\rm{even}}\\ 12/\sqrt{{{Z}}_{i}}\,\,{\rm{for}}\,\,{{Z}}_{i}\,{\rm{even}}\,{\rm{and}}\,{{N}}_{i}\,{\rm{odd}}\\ 12/\sqrt{{{N}}_{i}}\,\,\,{\rm{for}}\,\,{{N}}_{i}\,{\rm{even}}\,{\rm{and}}\,{{Z}}_{i}\,{\rm{odd}}\\ 24/\sqrt{{A}_{i}}\,\,{\rm{for}}\,\,{{Z}}_{i}\,{\rm{and}}\,{{N}}_{i}\,{\rm{odd}}.\end{array}\right.\end{eqnarray}$

The shell correction energy is calculated according to [29]. Our systematic method requires the shell correction energy values of fission fragments, which the recent reference has presented good approximate relations. Of course, the results of this method are agreed with the results of the Strutinsky model [30].

2.3. The temperature of fragments

The temperature-dependent relation for pairing energy is given by [31](14)$\begin{eqnarray}{E}_{\mathrm{pair}}(T)=\displaystyle \frac{{E}_{\mathrm{pair}}(0)}{1+{e}^{\left(\tfrac{T}{0.03}-\tfrac{7.37}{0.03\sqrt{A}}\right)}}.\end{eqnarray}$

The temperature dependence of shell energy is applied as [31](15)$\begin{eqnarray}\begin{array}{rcl}{E}_{\mathrm{shell}}(T) & = & {E}_{\mathrm{shell}}(0)\left(\displaystyle \frac{({e}^{-{E}_{1}/{E}_{0}}-1)}{\left({e}^{(E-{E}_{1})/{E}_{0}}-1\right)}\right.\\ & & +\left.\displaystyle \frac{{{TS}}_{0}\left(\tau \cosh (\tau )-1\right)}{\sinh (\tau )}\right),\end{array}\end{eqnarray}$where E_shell(T) is shell correction energy for the excitation energy E (corresponding to the fragment temperature T) and E_shell(0) is the shell correction energy at the zero excitation energy. Also, S₀ = 2.5 MeV⁻¹, τ = 2π²A^1/3T/41, E₁ = − 18.54 MeV, E₀ = 42.28 MeV and E is the excitation energy of fissioning system.

The temperature (T) is calculated using the generalized superfluid model as(16)$\begin{eqnarray}T=\sqrt{(E+{E}_{\mathrm{pair}}-{E}_{\mathrm{con}})/a},\end{eqnarray}$where E is excitation energy and E_con is the condensation energy for the even–even nucleus. We have(17)$\begin{eqnarray}{E}_{\mathrm{con}}=\displaystyle \frac{3a}{2{\pi }^{2}}{{E}_{{\rm{pair}},0}}^{2},\end{eqnarray}$where ${E}_{{\rm{pair}},0}=12/\sqrt{A}$ and the level density parameters, a, is given by(18)$\begin{eqnarray}a=\tilde{a}\left(1+{E}_{\mathrm{shell}}\left(1-{{\rm{e}}}^{-0.05E}\right)/E\right),\end{eqnarray}$where(19)$\begin{eqnarray}\tilde{a}=0.0984\,{\text{}}A-0.253\,{\text{}}{A}^{2/3}+2.07\,\sqrt[3]{{\text{}}A}-4.04.\end{eqnarray}$

2.4. Discussion on method

Similar to [32, 33], the atomic numbers of the fission fragments are obtained by the unchanged charge-density distribution [34](20)$\begin{eqnarray}{Z}_{\mathrm{UCD}}=\displaystyle \frac{{\text{}}{Z}_{{\rm{cn}}}\,{\text{}}(A+\nu )}{{\text{}}{A}_{{\rm{cn}}}},\end{eqnarray}$where ν is the post-scission neutrons obtained from [6, 35].

The extremum values of energy at the scission point is usually used to find the atomic numbers of the fission fragments [36–39]. The exponential function is upward-sloping, so the minimum total energy at the scission point has the greatest effect in equation (2). On the other hand, the collective temperature values of 1 (such as [2, 8]) and 2 MeV have been selected to study its effect on the results of mass yields. Therefore, the collective temperature is separated from the fragment temperature calculated by equation (16). Also, it is clear that the temperature of fragments depends on the excitation energy and it can not be changed arbitrarily (equation (16)). Thus, the minimum value of total energy at the scission point corresponds to the extremum values of deformation parameters. Therefore, the integral equation (2) could be rewritten as(21)$\begin{eqnarray}{P}_{i}\approx {{\rm{e}}}^{-\tfrac{{V}_{\mathrm{Intrac}}({N}_{i},{Z}_{i},s,{\beta }_{m,1},{\beta }_{m,2})+{V}_{\mathrm{Mac}}({N}_{i},{Z}_{i},T,{\beta }_{m,1},{\beta }_{m,2})+{V}_{{\rm{Mic}}}({N}_{i},{Z}_{i},T,{\beta }_{m,1},{\beta }_{m,2})}{{T}_{\mathrm{coll}}}}.\end{eqnarray}$

Here, β_m,i are the value of the deformation parameter of each fragment associated with the minimum total energy at the scission point.

Also, according to [2], the distance of two fragments, s, is 1.44 fm. Using the pairing correction energy, the calculated results fluctuate sharply. Therefore, the pairing correction energy is not included in the calculations.

3. The mass yields of asymmetric fission

Pasha [10] added the fission barrier to the total potential energy of the fissioning system at the scission point. Also, he added the difference between the potential energy of the fissioning nucleus and the potential energy of one of the complementary fragments at the scission point to the excitation energy. Here, the excitation energy E is the energy of gamma ray or initial neutron energy plus the hight of the fission barrier. Therefore, the fission barrier (i.e. 6 MeV ) is added to the initial excitation energy for spontaneous fission of ²³⁸U (in equations (15), and (16)). Also, the excitation energy, E, is shared between the fission fragments according to their masses.

3.1. ²³⁸U exploration

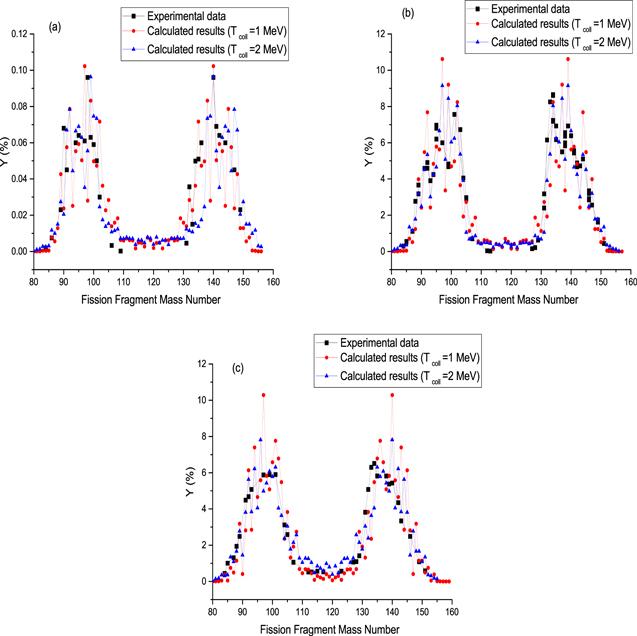
The mass yield for spontaneous fission of ²³⁸U is presented in figure 1(a). The squares and triangulares indicate the calculated results obtained for T_coll = 1 MeV and T_coll = 2 MeV, respectively. The deformation parameters are obtained by fitting the calculated results to the experimental values for T_coll = 1 MeV and T_coll = 2 MeV and presented in table 1 and 2, respectively. Figure 1(a) shows that the calculated results for mass yield are in good agreement to the experimental data for two collective temperatures. However, unlike the β_m,L values in table 1, β_m,L values in table 2 decrease in the symmetric region. This indicates that choosing T_coll = 1 MeV is better than choosing T_coll = 2 MeV for the spontaneous fission of ²³⁸U.

Figure 1.

New window|Download| PPT slide
Figure 1.Calculated mass yield for (a) spontaneous fission, photofission of ²³⁸U at (b) 8 MeV and (c) 68.3 MeV bremsstrahlung endpoint energy along with the experimental data [54–56], respectively. The squares and triangulares indicate the calculated results obtained with T_coll = 1 MeV and T_coll = 2 MeV, respectively.



Table 1.
Table 1.The β_m,L values for spontaneous fission (SP) and photofission of some fissioning systems with T_coll = 1 MeV. (β_m,H = 0.5).

AL	SP 238U	238U	240Pu	239Pu	237Np	237Np
	and 8 MeV	67.8 MeV	10 MeV	28 MeV	9.5 MeV	28 MeV
80–87	0.40	0.33	0.37	0.25	0.3	0.3
87–90	0.40	0.33	0.41	0.32	0.39	0.39
91–93	0.42	0.37	0.41	0.32	0.39	0.39
94	0.42	0.37	0.41	0.36	0.39	0.39
95	0.42	0.4	0.41	0.32	0.39	0.39
96–98	0.47	0.45	0.45	0.36	0.45	0.45
99	0.53	0.53	0.5	0.47	0.45	0.45
100–101	0.53	0.5	0.55	0.45	0.45	0.45
102	0.53	0.52	0.53	0.42	0.45	0.45
103	0.53	0.5	0.5	0.43	0.45	0.45
104	0.53	0.5	0.53	0.46	0.45	0.45
105–109	0.53	0.5	0.5	0.4	0.45	0.45
107	0.53	0.5	0.52	0.4	0.45	0.45
110-	0.53	0.5	0.5	0.4	0.45	0.45

New window|CSV


Table 2.
Table 2.The β_m,L values for spontaneous fission (SP) and photofission of some fissioning systems with T_coll = 2 MeV. (β_m,H = 0.5).

AL	SP 238U	238U	238U	240Pu	239Pu	237Np	237Np
	—	8 MeV	67.8 MeV	10 MeV	28 MeV	28 MeV	9.5 MeV
80–87	0.40	0.4	0.33	0.37	0.25	0.3	0.38
87–90	0.40	0.4	0.33	0.38	0.3	0.39	0.39
91–93	0.38	0.41	0.35	0.38	0.3	0.39	0.39
94	0.38	0.41	0.35	0.38	0.36	0.39	0.39
95	0.38	0.41	0.39	0.38	0.3	0.39	0.39
96	0.43	0.44	0.41	0.38	0.32	0.39	0.39
97	0.55	0.44	0.45	0.38	0.32	0.42	0.39
98–99	0.55	0.5	0.5	0.47	0.42	0.45	0.45
100–101	0.55	0.5	0.48	0.48	0.42	0.42	0.45
102	0.55	0.5	0.52	0.48	0.38	0.49	0.45
103–104	0.43	0.58	0.5	0.48	0.4	0.49	0.45
104–109	0.43	0.58	0.5	0.5	0.38	0.49	0.45
107	0.43	0.58	0.5	0.52	0.38	0.49	0.45
109-	0.43	0.58	0.5	0.5	0.4	0.49	0.45

New window|CSV

Also, the obtained β_m,L values, especially for fragment with mass number 98, are similar to the results of [29], in which the temperature of fission fragments is used instead of the collection temperature to calculate the mass yield for the spontaneous fission of ²³⁸U. For this reason, the changes in β_i values of [29] are less than the changes in our β_m,L values.

The photofission mass yield of ²³⁸U at 8 MeV bremsstrahlung endpoint energy is presented in figure 1(b). The squares and triangulares indicate the calculated results obtained with T_coll = 1 MeV and T_coll = 2 MeV, respectively. This figure shows that the mass yield values with selecting T_coll = 2 MeV are closer to the experimental data than the mass yield values with selecting T_coll = 1 MeV.

The fragment deformation parameters for T_coll = 1 MeV are the same as the deformation parameters for the spontaneous fission of ²³⁸U. This shows that with increasing excitation energy up to 8 MeV, the behavior of photofission and spontaneous fission is the same.

For T_coll = 2 MeV, the values of the deformation parameter for light fragments are presented in table 2. Unlike β_m,L values for spontaneous fission in this table, β_m,L values for photofission at 8 MeV endpoint energy increase in the symmetric region (because this is an asymmetric fission). This increase in β_m,L values for the symmetric fragments and the results presented in figure 1(b) indicates that it is better to choose T_coll = 2 MeV instead of T_coll = 1 MeV for photofission of ²³⁸U at 8 MeV endpoint energy.

In figure 1(c), the photofission mass yield of ²³⁸U at 68.3 MeV bremsstrahlung endpoint energy is presented. This indicates that the calculated values of mass yield with T_coll = 2 MeV are closer to the experimental data than the calculated values with T_coll = 1 MeV. The deformation parameters are obtained by fitting the calculated results to the experimental values for T_coll = 1 MeV and presented in table 1. It can be seen again that β_m,L values increase with increasing mass numbers of fission fragments. However, the increase in β_m,L values is significant only for fragments with mass numbers greater than 98. For T_coll = 2 MeV (table 2), the fission fragments with mass numbers between A_L = 96 to 102 have the semi-magic proton number or magic neutron number (Z_L = 50 and N_H = 82), which makes the large β_m,L values in this region.

As the excitation energy increases from 8 to 68 MeV, the number of cases where the value of the deformation parameter must be expressed separately increases (tables 1 and 2). This indicates the increase in excitation energy causes chaos. On the other hand, β_m,L values decrease with increasing the excitation energy. This indicates that there is no need to deform the fragments much for fission with increasing the excitation energy. Also, by comparing the difference in beta values for symmetric and asymmetric fission fragments, it can be seen that this difference decreases with increasing the excitation energy. For example in table 2, the difference in beta values for fission fragments with mass numbers 100 and 109 in spontaneous fission is 0.12, while the differences in photofission at 8 and 67.8 MeV endpoint energies are 0.08 and 0.02, respectively. This indicates that the probability of the formation of symmetric fragments is reduced, which dues to the increase of weight of symmetric fission mode at high excitation energy.

Why does the fission fragment with mass number A_L = 102, corresponding to the heavy fission fragment ${}_{53}^{135}{\rm{I}}$ with magic number 82, have a large β_m,L value at 68 MeV excitation energy but this fragment does not have this large value at 8 MeV excitation energy? This may be because the magic fragment with mass number A_H = 132 is much heavier than the magic fragment with mass number A_L = 96, so stimulating a heavy nucleus needs more excitation energy.

In tables 1 and 2, comparing β_m,L values in photofission of ²³⁸U at 8 MeV endpoint energy and photofission of ²⁴⁰Pu in 10 MeV endpoint energy, and also in photofission of ²³⁷Np and ²³⁹Pu at 28 MeV endpoint energy, it can be seen that these values decrease with increasing the mass numbers of fission fragments. Therefore, β_m,L values for all fissioning systems decrease with increasing the mass numbers of fission fragments. This indicates that there is no need to deform the fragments much so fission occurs more easily with increasing the mass numbers of fissioning systems.

The sum of β_i values can be calculated by fitting the experimental and theoretical data in the statistical scission model (such as [2]), so the β values of fragments can be considered equal such as [40]. Although the total kinetic energy has been studied in this reference, the β values of fragments can be compared with our β_m values. So that the sum of β_i values for the complementary fission fragments with mass numbers 158 in [40] and 80 in our study are equal to 0.9 and 0.88, respectively. Also, total β values for complementary fission fragments with mass numbers 141 in [40] and 98 in our study are 0.9 and 0.94, respectively. However, with the proximity to the symmetric region, the results are very different. So that the difference between the total β_i values in the results of these studies for complementary fission fragments 129/109 reaches 1.2. This difference can be due to changes in the values of total kinetic energy measured in this region.

3.2. ²⁴⁰Pu and ²³⁹Pu exploration

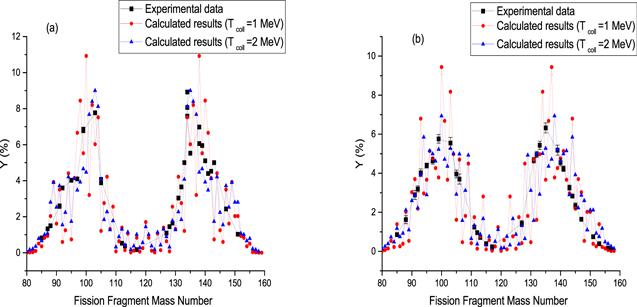
The photofission mass yield of ²⁴⁰Pu at 10 MeV bremsstrahlung endpoint energy is presented in figure 2(a). The deformation parameters of fission fragments are obtained by fitting the calculated results with the experimental values for T_coll = 1 MeV and presented in table 1. The total β values of complementary fission fragments with mass numbers around 110 are so close to the results of [40] in which the total kinetic energy of actinide was studied within the statistical scission point model.

Figure 2.

New window|Download| PPT slide
Figure 2.Calculated mass yield for photofission of ²⁴⁰Pu at 10 MeV bremsstrahlung endpoint energy, accompanied with the experimental data [41] and (b) photofission of ²³⁹Pu at 28 MeV at 28 MeV bremsstrahlung endpoint energy, accompanied with the experimental data [57]. The squares and triangulares calculated results obtained with T_coll = 1 MeV and T_coll = 2 MeV, respectively.


For T_coll = 2 MeV, the deformation parameters of light fragments are presented in table 2. It is seen that the heavy fission fragments with mass numbers around 102 have a magic neutron number (N_H = 82), which makes the large change in β_m,L values. Also, the heavy fission fragments with mass numbers around 106 have magic neutron number (${}_{52}^{134}{\rm{Te}}$), which makes the large change in β_m,L values.

The photofission mass yield of ²³⁹Pu at 28 MeV bremsstrahlung endpoint energy is presented in figure 2(b). The deformation parameters of fission fragments are obtained by fitting the calculated results with the experimental values for T_coll = 1 MeV and presented in table 1. β_m,L values do not increase with increasing mass numbers of fission fragments, so T_coll = 1 MeV may not be suitable for this excitation energy.

For T_coll = 2 MeV, the deformation parameters of light fragments are presented in table 2. The β_m,L values in plutonium-239 fission is lower than the β_m,L values in plutonium-240 fission. This decrease can be due to both an increase in excitation energy and the odd effect of the plutonium-239 nucleus. To examine the odd–even effect on β_m,L values, neptunium nucleus is investigated in the next section.

3.3. ²³⁷Np exploration

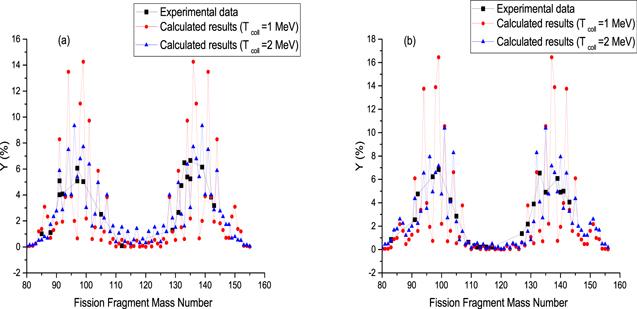
The photofission mass yield of ²³⁷Np at 9.5 MeV bremsstrahlung endpoint energy is presented in figure 3(a). The deformation parameters of fission fragments are presented in table 1, which are obtained by fitting the calculated results to the experimental values for T_coll = 1 MeV. For T_coll = 2 MeV, the deformation parameters are presented in table 2.

Figure 3.

New window|Download| PPT slide
Figure 3.Calculated mass yield (a) for photofission of ²³⁷Np at 9.5 MeV bremsstrahlung endpoint energy, accompanied with the experimental data [58] and (b) for photofission of ²³⁷Np at 28MeV bremsstrahlung endpoint energy, accompanied with the experimental data [59]. The squares and triangulares indicate the calculated results obtained with T_coll = 1 MeV and T_coll = 2 MeV, respectively.


The photofission mass yield of ²³⁷Np is presented in figure 3(b) at 28 MeV bremsstrahlung endpoint energy. The deformation parameters of fission fragments are presented in table 1, which are obtained by fitting the calculated results with the experimental values for T_coll = 1 MeV. Comparing the last two columns of table 1, it can be seen that there is no change in the β_m,L values for fission of ²³⁷Np at two energies (9.5 and 28 MeV). This indicates that calculated results with selecting T_coll = 1 MeV are not very reliable.

For T_coll = 2 MeV, the deformation parameters are presented in table 2. This table indicates that the β_m,L values decrease with increasing mass number of the fissioning systems. Also, unlike fission of ²³⁸U, the β_m,L values increase with increasing the excitation energy. On the other hand, the β_m,L values for photofission of ²³⁸U at 8 MeV endpoint energy are higher than the β_m,L values for photofission of ²³⁷Np at 9.5 MeV endpoint energy, while the mass numbers of fissioning systems has decreased. At first glance, it seems that the odd mass numbers of the fissioning systems reduce the deformation parameters. However, only for the symmetric fragments, the β_m,L values in photofission of ²⁴⁰Pu at 10 MeV endpoint energy increase sharply (such as ²³⁸U) and their values do not differ much difference for the asymmetric fragments. Also, β_m,L values for photofission of ²³⁷Np are higher than those for the photofission of ²³⁹Pu at the same energy. Therefore, the increase in β_m,L values is related to the mass number of fissioning systems, not their odd or even. These changes must be related to the properties of the fission fragments, not to the fissioning systems.

Despite ²⁴⁰Pu fission, β_m,L values of ²³⁷Np fission do not change much with increasing excitation energy. Also, the deformation parameter values for ²³⁷Np fission have the least variations. In addition, with increasing excitation energy, the amount of change in β_m,L values is less than other fission.

Naik and Pomme [41–43] showed that the yields of fission fragments around mass numbers 94–95, 99–100, 104–105 are higher than the yields of other fission fragments for photofission of ²³⁸U and ²⁴⁰Pu in the low energy region. These changes can be also seen in the calculated results of our systematic model. Therefore, our results confirm the changes in the mass yields of these experimental data in some fragments.

As shown in figures 2 and 3, the calculated results of mass yield for odd–even nucleus are in good agreement with the experimental values. This indicates that our model is proper for all fissioning systems. On the other hand, the deformation parameters reduce oscillations when T_coll = 2 MeV, so the mass yields are better to evaluate with selecting T_coll = 2 MeV for photofission in the intermediate excitation energy and T_coll = 1 MeV for spontaneous fission.

As mentioned earlier, the sum of beta values is obtained in the statistical model, therefore, in the next section the β_i values of the complementary fission fragment are considered equal to investigate the difference of these methods.

4. The transition between asymmetric and symmetric fission

In this section, the transition between asymmetric and symmetric fission is investigated by calculating the mass yields of pre-actinides and actinide within the scission point model. As discussed in the previous section, the temperature value is 1 MeV for spontaneous fission and 2 MeV for thermal neutron fission. Also, the β_i values of the complementary fission fragments are equal, such as [40]. By fitting the calculated results to the experimental data, the deformation parameters of fission fragments are presented in table 3.


Table 3.
Table 3.The β_m,L( = β_m,H) values for each fission.

AL	194Po	200Ra	222Th	229Th	248Fm	258Fm
80–87	0.47	0.45	0.525	0.49	0.44	0.4
87–90	0.47	0.55	0.525	0.55	0.44	0.4
90–94	0.48	0.55	0.525	0.55	0.44	0.4
94–99	0.47	0.55	0.525	0.55	0.44	0.4
100	—	0.51	0.48	0.55	0.44	0.4
101	—	—	0.48	0.55	0.44	0.4
102	—	—	0.48	0.51	0.44	0.4
103–104	—	—	0.48	0.51	0.49	0.4
104–109	—	—	0.444	0.51	0.49	0.4
109–115	—	—	0.444	0.51	0.49	0.51
115–125	—	—	—	—	0.55	0.51
125-	—	—	—	—	—	0.49

New window|CSV

The calculated mass yields for the ¹⁹⁴Po and ²⁰⁰Ra fission are presented along with the experimental data in figure 4. The values of mass yields for ²⁰⁰Ra fission are taken from Pomorski [44]. However, the mass yield for fission of ¹⁹⁴Po is measured by Ghys [45]. As can be seen from this figure, the calculated mass yields for pre-actinide nuclei with symmetric fission are also in good agreement with the experimental results.

Figure 4.

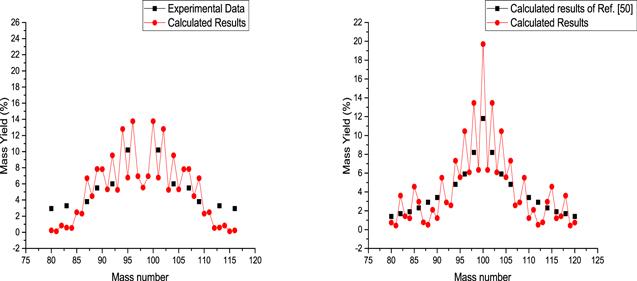New window|Download| PPT slide
Figure 4.The mass yield calculated for fission of ¹⁹⁴Po (left part) and ²⁰⁰Ra (right part), accompanied with the experimental data [45] and the calculated results [44].


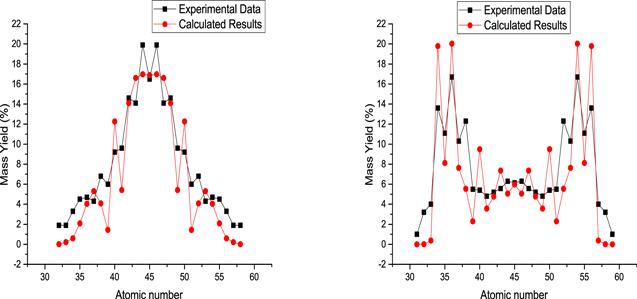
Atomic yields of most thorium isotopes have been measured by Schmitt [46]. In addition, the atomic yields of ^222,229Th have been investigated by Ruan [47] within the improved scission point model and by Randrup [15] within the Brownian shape motion model. Therefore, we study the atomic yields (instead of mass yields) of the ^222,229Th fission. Because the experimental and theoretical atomic distributions for ²²²Th fission as the symmetric fission and for ²²⁹Th fission as the asymmetric fission are known, the atomic yields of these thorium isotopes have been investigated.

In figure 5, atomic yields for fission of ²²²Th (left part) and ²²⁹Th (right part) are presented along with experimental data [46]. As it is seen the transition from symmetric to asymmetric fission is well reproduced for thorium isotopes with increasing mass number. Comparing figure 5 with figure 5 of [47] indicates that our results are closer to the experimental data than the calculated results of other models.

Figure 5.

New window|Download| PPT slide
Figure 5.Calculated atomic yield for fission of ²²²Th (left part) and ²²⁹Th (right part), accompanied with the experimental data [46].


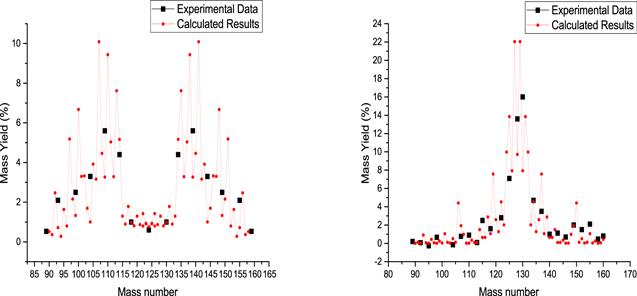
In figure 6, the calculated mass yield for fission of ²⁴⁸Fm and ²⁵⁸Fm is represented along with experimental data [48, 49]. For spontaneous fission of ²⁴⁸Fm the collective temperature is selected 1MeV and for thermal neutron fission of ²⁵⁷Fm T_coll = 2 MeV. The transition from asymmetric to symmetric fission mode is well reproduced in this figure with slight changes in β_m,i values (table 3).

Figure 6.

New window|Download| PPT slide
Figure 6.Calculated mass yield for the spontaneous fission of ²⁴⁸Fm (left part) and fission of ²⁵⁸Fm (right part), accompanied with the experimental data [48, 49].


In table 3, the deformation parameters values of complementary fission fragments are presented for discussed fissioning systems. Despite the increase in β_m,i values for symmetric fission fragments in tables 1 and 2, the β_m,i values of table 3 in the symmetric region decrease, except for ²⁴⁸Fm fission as an asymmetric fission. Therefore, the change in the β_m,i values corresponds to the fission modes. In this way, for the ¹⁹⁴Po, ²⁰⁰Ra, ²²²Th and ²⁵⁸Fm fission whose fission mode are symmetric, the β_m,i values in the symmetric fragments are decreased and these values for the symmetric fragments are increased in ²⁴⁸Fm fission as an asymmetric fission. While ²²⁹Th fission is an asymmetric fission, the β_m,i values do not increase for the symmetric fission fragments. This is because that ²²⁹Th fission is not a completely asymmetric fission. As shown in figure 5, the atomic yield of thorium-229 fission, such as the fission mass yield of thorium-232, has a peak in the symmetric region (i.e. their atomic yields have three peaks).

On the other hand, it is obvious that the shape of the mass (atomic) yields is related to the formation of magic fission fragments. It can be seen that the beta values are maximized for fission fragments with mass numbers around 89 to 98 because according to [50], the fission fragments are produced as follows in ²²⁹Th fission: ^140,139Cs with N_H = 84, ⁸⁹Rb with N_L = 50, ¹³⁰Sn with Z_H = 50, and ⁹⁸⁻¹⁰⁰Zr with Z_L = 40. Of course, this increase in beta due to very unstable complementary fission fragments, otherwise magic fragments have the least deformation. Therefore, the total deformation parameter of these two complementary fragments is maximal.

In the statistical scission point model, the total deformation parameters are usually investigated. The deformation parameters of light and heavy fragments can be assumed equal (i.e. β_L = β_H, which is done in this section) or it can be assumed that one of them is fixed and the other changes (as in the previous section). If one of them remains constant, according to the figures 3 of [29], the change in mass yield is more. However, tables 1–3 indicate that keeping one beta value constant or the equality of both beta values makes little difference in the results. So both cases are not different to investigate the mass yield within the statistical model.

On the other hand, in [40], beta values are obtained by fitting the theoretical and experimental results of the total kinetic energy using the same model. Although in this reference the beta values in the symmetric region are very large, this abnormal increase in the beta value is not related to the model. This is because the amounts of total kinetic energy change (increase) abruptly in the symmetric region, which is probably related to the target thickness [51].

Also, Liu [52] showed that the heavy fragment mass distribution shifts to the right side about several mass units while the light fragment mass distribution shifts to the left side a little bit by introducing the constraint on the heavy fragment deformation. However, as shown in tables 1–3, this shift in mass yields does not occur in the calculated results of the statistical scission point model.

Wei [53] has recently calculated mass distribution using a simplified scission-point model. In these calculations, the deformation values of the fission fragments are equal to the ground state deformation values (such as [47]). For this reason, for low excitation energies (e.g. 1 MeV), the calculation results are in good agreement with the experimental values.

5. Summary

The mass yields for fission of pre-actinides and actinides are calculated within a systematic scission point model. The calculated results are compared with the available experimental data which indicates that the calculated results are in good agreement with the experimental data, specially with selecting the collective temperature equal 2 MeV for intermediate excitation energy and with selecting T_coll = 1 MeV for spontaneous fission. The barrier potential energy is added to the excitation energy (E) to evaluate mass yields. The distance of two fragments surface is 1.44 fm.

The deformation parameters of fission fragments are presented by fitting the calculated results to the experimental data. The deformation values for asymmetric (symmetric) fissions increase (decrease) with increasing the mass numbers of fission fragments (i.e. for the symmetric region). The (shape of) the mass yields can be predicted for the rest of fission systems.

Also, the deformation parameter values decrease with increasing the excitation energy. This indicates that there is no need to deform the fragments much for fission with increasing excitation energy. Of course, this increase causes chaos in deformation parameter values. Also, deformation parameter values decrease with increasing the mass numbers of fissioning systems.

The small increase in the experimental photofission mass yield [41–43] for some fragments with mass numbers around 104–105, 99–100 is related to the total potential energy of the fissioning system at the fission point. These higher values may also exist in mass yields of the other actinides fission, but their small amount causes them to be excluded from the results as measurement errors.

The mass yields in the transitions region between asymmetric and symmetric fission are calculated within the systematic scission point model. The calculated results are compared with the available experimental data. This indicates that there is a good agreement between the calculated results and the experimental data in this region. Therefore, the mass yields in the transitions between asymmetric and symmetric fission modes are well reproduced for thorium and fermium isotopes within our systematic scission point model.

Keeping one beta value constant or the equality of both beta values makes little difference in results. Therefore, the both cases are not different to investigate the mass yield within the statistical scission point model. However, it is recommended to keep one of them (β_L or β_H) constant due to increasing the range of changes.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Fong P 1956 Phys. Rev. 102 434
DOI:10.1103/PhysRev.102.434 [Cited within: 2]

[2]Wilkins B D Steinberg E P Chasman R R 1976 Phys. Rev. C 14 1832
DOI:10.1103/PhysRevC.14.1832 [Cited within: 5]

[3]Brosa U Grossmann S Müller A 1990 Phys. Rep. 197 167
DOI:10.1016/0370-1573(90)90114-H [Cited within: 1]

[4]Denisov V Y Margitych T O Sedykh I Y 2017 Nucl. Phys. A 958 101
DOI:10.1016/j.nuclphysa.2016.11.007 [Cited within: 1]

[5]Mehdipour P 2019 Phys. At. Nucl. 82 450
DOI:10.1134/S1063778819050089 [Cited within: 1]

[6]Pahlavani M R Mehdipour P 2018 Nucl. Sci. Tech. 29 146
DOI:10.1007/s41365-018-0482-1 [Cited within: 1]

[7]Andreev A V Adamian G G Antonenko N V 2012 Phys. Rev. C 86 044315
DOI:10.1103/PhysRevC.86.044315 [Cited within: 2]

[8]Pasca H Andreev A V Adamian G G Antonenko N V 2016 Eur. Phys. J. A 52 369
DOI:10.1140/epja/i2016-16369-5 [Cited within: 1]

[9]Pascaa H Andreeva A V Adamiana G G Antonenko N V 2017 Acta Phys. Pol. Ser. B 48 431
DOI:10.5506/APhysPolB.48.431 [Cited within: 1]

[10]Pasca H Andreev A V Adamian G G Antonenko N V 2018 Nucl. Phys. A 969 226 236
DOI:10.1016/j.nuclphysa.2017.10.001 [Cited within: 2]

[11]Lemaître J-F Dubray N Hilaire S Panebianco S Sida J-L 2013 EPJ Web Conf. 62 04002
DOI:10.1051/epjconf/20136204002 [Cited within: 1]

[12]Lemaître J F Goriely S Hilaire S Sida J-L 2019 Phys. Rev. C 99 034612
DOI:10.1103/PhysRevC.99.034612 [Cited within: 2]

[13]Karthika C Balasubramaniam M 2019 Eur. Phys. J. A 55 59
DOI:10.1140/epja/i2019-12729-y [Cited within: 1]

[14]Randrup J Möller P 2011 Phys. Rev. Lett. 106 132503
DOI:10.1103/PhysRevLett.106.132503 [Cited within: 1]

[15]Randrup J Möller P 2013 Phys. Rev. C 88 064606
DOI:10.1103/PhysRevC.88.064606 [Cited within: 1]

[16]Möller P Randrup J 2015 Phys. Rev. C 91 044316
DOI:10.1103/PhysRevC.91.044316 [Cited within: 1]

[17]Nadtochy P N Karpov A V Vanin D V Adeev G D 2001 Phys. At. Nucl. 64 861
DOI:10.1134/1.1378876 [Cited within: 1]

[18]Ivanyuk F Chiba S Aritomo Y 2014 Phys. Rev. C 90 054607
DOI:10.1103/PhysRevC.90.054607

[19]Ivanyuk F Kawano T Chiba S Paris M W Talou P 2016 EPJ Web Conf. 122 01002
DOI:10.1051/epjconf/201612201002

[20]Mirea M Delion D S Sandulescu A 2010 Phys. Rev. C 81 044317
DOI:10.1103/PhysRevC.81.044317

[21]Pomorski K Nerlo-Pomorska B Bartel J Schmitt C 2018 EPJ Web Conf. 169 00016
DOI:10.1051/epjconf/201816900016 [Cited within: 1]

[22]Sandulescu Zhang A et al. 1996 J. Phys. Rev. C 54 258
DOI:10.1103/PhysRevC.54.258

[23]Duijvestijn M C Koning A J Hambsch F-J 2001 Phys. Rev. C 64 014607
DOI:10.1103/PhysRevC.64.014607 [Cited within: 1]

[24]Goutte H Casoli P Berger J-F 2004 Nucl. Phys. A 734 217
DOI:10.1016/j.nuclphysa.2004.01.038 [Cited within: 1]

[25]Blocki J Swiatecki W J 1981 Ann. Phys. NY 132 53
DOI:10.1016/0003-4916(81)90268-2 [Cited within: 2]

[26]Blocki J Randrup J Swiatecki W J Tsang C F 1977 Ann. Phys. NY 105 427
DOI:10.1016/0003-4916(77)90249-4 [Cited within: 2]

[27]Bao X Zhang H Royer G Li J 2013 Nucl. Phys. A 906 1
DOI:10.1016/j.nuclphysa.2013.03.002 [Cited within: 1]

[28]Moller P Nix J R Myers W D Swiateck W J 1995 At. Data Nucl. Data Tables 59 185
DOI:10.1006/adnd.1995.1002 [Cited within: 2]

[29]Kaldiani P M 2020 Phys. Scr. 95 075306
DOI:10.1088/1402-4896/ab93a9 [Cited within: 4]

[30]Strutinsky V M 1967 Nucl. Phys. A 95 420
DOI:10.1016/0375-9474(67)90510-6 [Cited within: 1]

[31]Ivanyuk F A Ishizuka C Usang M D Chiba S 2018 Phys. Rev. C 97 054331
DOI:10.1103/PhysRevC.97.054331 [Cited within: 2]

[32]Manailescu C Tudora A Hambsch F-J Morariu C Oberstedt S 2011 Nucl. Phys. A 867 12
DOI:10.1016/j.nuclphysa.2011.08.001 [Cited within: 1]

[33]Morariu C Tudora A Hambsch F J Oberstedt S Manailescu C 2012 J. Phys. G: Nucl. Part. Phys. 39 055103
DOI:10.1088/0954-3899/39/5/055103 [Cited within: 1]

[34]Sugarman N Turkevich A 1951 Radiochemical Studies: The Fission Product vol 3Coryell C D Sugarman N New York McGraw-Hill 1396
[Cited within: 1]

[35]Umezawa H Baba S Baba H 1971 Nucl. Phys. A 160 65
DOI:10.1016/0375-9474(70)90174-0 [Cited within: 1]

[36]Andreev A V et al. 2004 Eur. Phys. J. A 22 60
DOI:10.1140/epja/i2004-10017-9 [Cited within: 1]

[37]Santhosh K P Cyriac A Krishnan S 2016 Nucl. Phys. A 949 8
DOI:10.1016/j.nuclphysa.2016.02.036

[38]Pahlavani M R Joharifard M 2019 Phys. Rev. C 99 044601
DOI:10.1103/PhysRevC.99.044601

[39]Zadehrafi M Pahlavani M R Ioan M R 2019 Chin. Phys. C 43 094101
DOI:10.1088/1674-1137/43/9/094101 [Cited within: 1]

[40]Mehdipour P K 2020 Kinetic energy distribution for photofission of light actinides
Phy. Rev. C 102 044612
DOI:10.1103/PhysRevC.102.044612 [Cited within: 6]

[41]Naik H et al. 2011 Nucl. Phys. A 853 1
DOI:10.1016/j.nuclphysa.2011.01.009 [Cited within: 3]

[42]Naik H et al. 2013 Eur. Phys. J. A 49 94
DOI:10.1140/epja/i2013-13094-7

[43]Pomme S Jacobs E Piessens M De Frenne D Persyn K Govaert K Yoneama M-L 1994 Nucl. Phys. A 572 237
DOI:10.1016/0375-9474(94)90174-0 [Cited within: 2]

[44]Pomorski K Dobrowolski A Han R Nerlo-Pomorska B Warda M Xiao Z Chen Y Liu L Tian J-L 2020 Phys. Rev. C 101 064602
DOI:10.1103/PhysRevC.101.064602 [Cited within: 2]

[45]Ghys C et al. 2014 Phys. Rev. C 90 041301R
DOI:10.1103/PhysRevC.90.041301 [Cited within: 2]

[46]Schmitt C Schmidt K H Jurado B 2018 The GEF model: assessment of fission-fragment properties over an extended region
EPJ Web Conf. 169 00022
DOI:10.1051/epjconf/201816900022 [Cited within: 3]

[47]Ruan X H et al. 2019 J. Phys. G: Nucl. Part. Phys. 46 125108
DOI:10.1088/1361-6471/ab4820 [Cited within: 3]

[48]Hoffman D Lee D Ghiorso A Nurmia M Aleldett K 1980 Phys. Rev. C 22 1581
DOI:10.1103/PhysRevC.22.1581 [Cited within: 2]

[49]Hoffman D C 1979 Fission properties of very heavy actinides
IAEA Symp. on Physics and Chemistry of FissionJulich, F.R. GermanyLA-UR-79-1082
[Cited within: 2]

[50]Naik H Singh R J Dange S P 2020 Post-neutron mass chain yield distribution in the thermal neutron induced fission of 229Th
Eur. Phys. J. A 56 82
DOI:10.1140/epja/s10050-020-00080-5 [Cited within: 1]

[51]Göök A Eckardt C Enders J Freudenberger M Oberstedt A Oberstedt S 2017 Phys. Rev. C 96 044301
DOI:10.1103/PhysRevC.96.044301 [Cited within: 1]

[52]Liu L-L Wu X-Z Chen Y-J Shen C-W Li Z-X Ge Z-G 2019 Study of fission dynamics with a three-dimensional Langevin approach
Phys. Rev. C 99 044614
DOI:10.1103/PhysRevC.99.044614 [Cited within: 1]

[53]Wei K Zhang H-F He Z-X Wang X-Y Guo S-Q Hu B-T 2021 Multi-parameter global calculations of fission fragments using a simplified two-dimensional scission-point model
Chin. Phys. C 45 024109
DOI:10.1088/1674-1137/abd083 [Cited within: 1]

[54]Swindle D L Write R J Kurode P K 1971 J. Inorg. Nucl. Chem. 33 876
DOI:10.1016/0022-1902(71)80491-8 [Cited within: 1]

[55]Naik H Shivashankar B S Raj Prakash H G Raj D Sanjeev G Karunakara N Somashekarappa H M Ganesan S Kim G N Goswami A 2014 J. Radioanal. Nucl. Chem. 299 127
DOI:10.1007/s10967-013-2719-0

[56]Belyshev S S Ishkhanov B S Kuznetsov A A Stopani K A 2015 Phys. Rev. C 91 034603
DOI:10.1103/PhysRevC.91.034603 [Cited within: 1]

[57]Kondratko M Y Mosesov A V Petrzhak K A 1981 Product yields of photofission of Pu-239
Sov. At. Energy 50 41
DOI:10.1007/BF01141251 [Cited within: 1]

[58]Parlag O O 2006 (EXFOR Experimental Nuclear Reaction Data Base; targets: Np-237, Reactions: (g,f), quantity: FY.)
Int. Conf. Cur. Prob. in Nucl. Phys. Atom. Energ. Kyiv 369 (https://ctp.itp.ac.cn/article/2021/0253-6102/www-nds.iaea.org/exfor/servlet/X4sShowPubl?File=C,2006KYIV,369,2006)
[Cited within: 1]

[59]Kondratko M Y Korinets V N Petrzhak K A Teodorovich O A 1973 1973KO40
At. Energy 35 211
DOI:10.1016/0039-6028(73)90215-X [Cited within: 1]