Habibur Rahman^,1,2,3,∗, Mansoor Khan¹, Shabir Ahmad¹, Muhammad Tayyab¹, Haseena Bibi², Hazrat Ali⁴¹ Department of Physics, Govt Post Graduate College Dargai Malakand, Pakistan
² Department of Physics, University of Malakand Chakdara, Dir(L), Pakistan
³ Department of Physics, Gomal University Dera Ismail Khan, Pakistan
⁴ Department of Physics, Abbottabad University of Science and Technology, Havellain, Pakistan

First author contact: ^∗ Author to whom any correspondence should be addressed.
Received:2020-05-16Revised:2020-09-3Accepted:2020-09-9Online:2020-10-27


Abstract
In this article we propose a four-level rubidium (Rb⁸⁷ ) atomic system for observing interesting features of polarization state rotation in a fast light medium. We investigate spontaneously generated coherence (SGC) for a spinning medium. We show how SGC can affect different spectral profiles of the polarization state and images in this suggested model. We observe a 0.5 radian rotation and 2.5 microsecond time advancement in our proposed system. Our precise results will provide a new platform for researchers in quantum optics due to its applications in image coding, telecommunications and cloaking technology.
Keywords： spinning medium;SGC effect;image coding


PDF (449KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Habibur Rahman, Mansoor Khan, Shabir Ahmad, Muhammad Tayyab, Haseena Bibi, Hazrat Ali. Polarization state and image rotation via spontaneously generated coherence in a spinning fast light medium. Communications in Theoretical Physics[J], 2020, 72(11): 115502- doi:10.1088/1572-9494/abb7dc

1. Introduction

The propagation of light pulse in a spinning window encounters a pull known as ether drag. The phenomenon of ether drag was first discussed by Fresnel [1]. Jones et al made the experimental confirmation [2 –4]. When a pulse of light gets in a rotating window it becomes pulled in a transverse or linear direction depending upon the situation [5]. Fizeau et al verified the longitudinal dragging of light [6]. The state of electric field vector orientation is called polarization. The process of confinement of light pulse into a single plane is also called polarization. In the presence of polarization state rotation, the transmitting image also rotates. This is because of orbital and spin gyration. It is well known that optical spin and orbital angular momenta both cause rotation of polarization state and images [7, 8]. Optical polarization state rotation occurs due to movement of light through the spinning axes in a rotating window [9]. Light propagating through a spinning medium results in the polarization state rotation and its images. Second harmonic generation and enhancement in photon dragging in a doped graphene was discussed in detail [10]. Photon drag and surface plasmon polariton under Kerr Effect were theoretically investigated [11]. The enhanced dragging effect through a spinning window with electromagnetically induced transparency (EIT) condition for a slow light were studied by Iqbal et al [12]. In recent years enhanced optical rotation has been an active field of research because of its fundamental and practical interest. Superluminal propagation of light in a system occurs due to anomalous dispersion. The time coordinate is negative for a fast light propagation. Enhanced dragging effect has useful applications in the detection of slow/fast motion, position control, image coding and cloaking technology [13]. Light pulse dragging can also be used in four wave mixing [14] and matching the phase condition for Brillouin scattering [15].

Quantum interference and quantum coherence has been an active field for researchers in the last two decades. Quantum interference and coherence in an atomic medium results in different phenomena, like coherent population trapping (CPT) [16], slow/fast light, lasing without inversion (LWI) and electromagnetically induced transparency (EIT) [17 –19]. The optical and spectral profiles of quantum systems can be described using quantum interference. It has been found that LWI can be realized without a decaying beam [20]. Quantum interference has potential application in linear/non-linear optics [21]. The spontaneously generated coherence (SGC) achieved in the decaying laser beams from the upper two excited states into a single ground state is a useful quantum interference. SGC mainly depends on the degeneracy of quantum state and non-orthogonality of the dipole moment. The effect of SGC has been investigated for several different purposes, such as switching on a micro wave field utilizing the anisotropy of vacuum etc [22]. A number of attempts have been successful in manipulating SGC experimentally [23]. SGC can be physically realized in Rb⁸⁷ atoms using the optical trap technique.

In this paper we have explored the effect of SGC to manipulate polarization state rotations and their transmitted images. We show that a fast light rotating medium rotates the polarization states and their images in opposite directions. The results for optical rotation under SGC in fast light medium are several times more enhanced than the results obtained under Kerr Effect [24].

2. Model and equations

The proposed model is a four-level atomic system containing two ground states and two excited degenerate states. The state $\left|2\right\rangle $ and $\left|1\right\rangle $ are coupled by a strong control field of Rabi frequency Ω_c ; similarly $\left|3\right\rangle $ and $\left|4\right\rangle $ are coupled through another coherent strong field of Rabi frequency Ω_k . A weak field having Rabi frequency Ω_p is allowed to perturb the state $\left|3\right\rangle $ and $\left|2\right\rangle $ as shown in figure 1 . The probe field is propagating longitudinally to the axis of the spinning medium. The proposed system is experimental, and can be physically realized in Rb⁸⁷ . This system was considered for different purposes in [24 –26]. We follow the same approach for calculation of electric susceptibility as used in [24]. The Hamiltonian in interaction form is:(1)$ \begin{eqnarray}\begin{array}{rcl}{H}_{I} & = & -\displaystyle \frac{{\hslash }}{2}{{\rm{\Omega }}}_{c}{{\rm{e}}}^{-{\rm{i}}({{\rm{\Delta }}}_{c}+{\kappa }_{1}{{\rm{\Phi }}}_{1})t}\left|1\right\rangle \left\langle 2\right|\\ & & -\displaystyle \frac{{\hslash }}{2}{{\rm{\Omega }}}_{k}{{\rm{e}}}^{-{\rm{i}}({{\rm{\Delta }}}_{k}+{\kappa }_{2}{{\rm{\Phi }}}_{2})t}\left|3\right\rangle \left\langle 4\right|\\ & & -\displaystyle \frac{{\hslash }}{2}{{\rm{\Omega }}}_{p}{{\rm{e}}}^{-{\rm{i}}({{\rm{\Delta }}}_{p}+{\kappa }_{3})t}\left|3\right\rangle \left\langle 2\right|+{\rm{H.}}\,{\rm{c.}},\end{array}\end{eqnarray}$ Δ_c =ω₁₂ −ω_c, Δ_p =ω₃₂ −ω_p and Δ_k =ω₃₄ −ω_b, whereas ${{\rm{\Phi }}}_{\mathrm{1,2}}$ indicates the direction of control fields ${{\rm{\Omega }}}_{c,k}$ with weak field. Similarly ${\kappa }_{\mathrm{1,2,3}}$ represents the wave numbers for the strong and weak applied fields. To study the dynamics we expressed the master equation as:(2)$ \begin{eqnarray}\dot{\rho }=-\displaystyle \frac{{\rm{i}}}{{\hslash }}[\rho ,{H}_{I}]-\displaystyle \frac{1}{2}{\gamma }_{{ij}}\sum ({\tau }^{\dagger }\tau \rho +\rho {\tau }^{\dagger }\tau -2\tau \rho {\tau }^{\dagger }).\end{eqnarray}$ Here τ^† and τ are ladder operators. We use equation (2) to get the coupling rate equations:(3)$ \begin{eqnarray}\begin{array}{rcl}{\dot{\rho }}_{23}^{(1)} & = & [{\rm{i}}({{\rm{\Delta }}}_{p}+{\kappa }_{3})-\displaystyle \frac{1}{2}({\gamma }_{3}+{\gamma }_{2})]{\rho }_{23}^{(1)}+\displaystyle \frac{{\rm{i}}}{2}{{\rm{\Omega }}}_{c}{\rho }_{13}^{(1)}\\ & & -\displaystyle \frac{{\rm{i}}}{2}{{\rm{\Omega }}}_{p}({\rho }_{33}^{(0)}-{\rho }_{22}^{(0)})+\displaystyle \frac{{\rm{i}}}{2}{{\rm{\Omega }}}_{k}{\rho }_{24}^{(1)},\end{array}\end{eqnarray}$(4)$ \begin{eqnarray}\begin{array}{rcl}{\dot{\rho }}_{13}^{(1)} & = & [-{\rm{i}}({{\rm{\Delta }}}_{c}-{{\rm{\Delta }}}_{p}-{\kappa }_{3}+{\kappa }_{1}{{\rm{\Phi }}}_{1}){\rho }_{13}^{(1)}\\ & & +\displaystyle \frac{{\rm{i}}}{2}{{\rm{\Omega }}}_{c}{\rho }_{23}^{(1)}-\displaystyle \frac{{\rm{i}}}{2}{{\rm{\Omega }}}_{p}{\rho }_{12}^{(1)}-\displaystyle \frac{{\rm{i}}}{2}{{\rm{\Omega }}}_{k}{\rho }_{14}^{(1)},\end{array}\end{eqnarray}$(5)$ \begin{eqnarray}\begin{array}{rcl}{\dot{\rho }}_{24}^{(1)} & = & [-{\rm{i}}({{\rm{\Delta }}}_{p}-{{\rm{\Delta }}}_{k}+{\kappa }_{2}{{\rm{\Phi }}}_{2}-{\kappa }_{3}){\rho }_{24}^{(1)}\\ & & +\displaystyle \frac{{\rm{i}}}{2}{{\rm{\Omega }}}_{c}{\rho }_{14}^{(1)}+\displaystyle \frac{{\rm{i}}}{2}{{\rm{\Omega }}}_{p}{\rho }_{34}^{(1)}-\displaystyle \frac{{\rm{i}}}{2}{{\rm{\Omega }}}_{k}{\rho }_{23}^{(1)},\end{array}\end{eqnarray}$(6)$ \begin{eqnarray}\begin{array}{rcl}{\dot{\rho }}_{14}^{(1)} & = & -{\rm{i}}({{\rm{\Delta }}}_{c}-{{\rm{\Delta }}}_{p}-{\kappa }_{1}{{\rm{\Phi }}}_{1}+{\kappa }_{3}+{\gamma }_{3}){\rho }_{14}^{(1)}\\ & & +\displaystyle \frac{{\rm{i}}}{2}{{\rm{\Omega }}}_{c}{\rho }_{24}^{(1)}-\displaystyle \frac{{\rm{i}}}{2}{{\rm{\Omega }}}_{k}{\rho }_{13}^{(1)}.\end{array}\end{eqnarray}$ The initial population condition to be satisfied: ${\rho }_{33}^{(0)}=1$, and ${\rho }_{11}^{(0)}={\rho }_{22}^{(0)}={\rho }_{44}^{(0)}=0$ .

Figure 1.

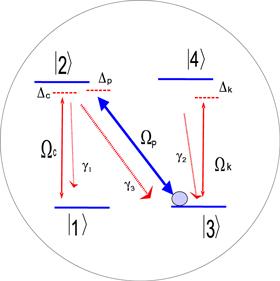New window|Download| PPT slide
Figure 1.Schematic of the proposed four-level N-type Rb⁸⁷ atom.


To derive ${\widetilde{\rho }}_{23}^{(1)}$ we use the relation:(7)$ \begin{eqnarray}Q(t)={\int }_{-\infty }^{t}{{\rm{e}}}^{-Y}Z{\rm{d}}t=-{Y}^{-1}Z.\end{eqnarray}$ Here Q (t), Z and Y represent different matrices. Y is a square matrix while the other two are column matrices. The complex susceptibility can be written as:(8)$ \begin{eqnarray}{\chi }_{e}=\eta \displaystyle \frac{8{\rm{i}}(\tfrac{1}{4}({\rm{i}}{{\rm{\Delta }}}_{c}+{\kappa }_{1}{{\rm{\Phi }}}_{1}+{\rm{i}}{{\rm{\Delta }}}_{p}+{\kappa }_{3}){{\rm{\Omega }}}_{c}^{2}+{A}_{11}{A}_{22}+\tfrac{{{\rm{\Omega }}}_{k}^{2}}{4}}{{A}_{33}},\end{eqnarray}$ where(9)$ \begin{eqnarray}\eta =-\displaystyle \frac{2N{\mu }_{23}^{2}}{{\hslash }{\epsilon }_{0}},\end{eqnarray}$(10)$ \begin{eqnarray}{A}_{11}={\rm{i}}({{\rm{\Delta }}}_{p}+{\kappa }_{3})-\displaystyle \frac{1}{2}({\gamma }_{1}-{\gamma }_{2}),\end{eqnarray}$(11)$ \begin{eqnarray}\begin{array}{rcl}{A}_{22} & = & {\rm{i}}({{\rm{\Delta }}}_{p}+{\kappa }_{3}-{{\rm{\Delta }}}_{c}-{\kappa }_{1}{{\rm{\Phi }}}_{1})\\ & & -\displaystyle \frac{1}{2}({\gamma }_{1}+{\gamma }_{2}+{\gamma }_{3}),\end{array}\end{eqnarray}$(12)$ \begin{eqnarray}\begin{array}{rcl}{A}_{33} & = & {{\rm{\Omega }}}_{k}^{2}4({\gamma }_{1}+{\gamma }_{2}-{\rm{i}}{{\rm{\Delta }}}_{P}+{\kappa }_{3})\\ & & \times ({\gamma }_{1}+{\gamma }_{2}+{\gamma }_{3}-{\rm{i}}{{\rm{\Delta }}}_{P}+{\kappa }_{3})+{{\rm{\Omega }}}_{k}^{2}-{{\rm{\Omega }}}_{c}^{2}\\ & & +16({\gamma }_{3}+{\rm{i}}{{\rm{\Delta }}}_{c}-{\rm{i}}{{\rm{\Delta }}}_{P}+{\kappa }_{3}-{\kappa }_{1}{{\rm{\Phi }}}_{1}),\end{array}\end{eqnarray}$ where N denotes atom density and μ₂₃ represents dipole moments. When ${{\rm{\Phi }}}_{\mathrm{1,2}}=1$, it indicates the same direction of strong and weak fields, and when ${{\rm{\Phi }}}_{\mathrm{1,2}}=-1$, then it shows counter propagating directions. For simplicity, we put ${\kappa }_{1}={\kappa }_{2}={\kappa }_{3}=\kappa $ . To get SGC effect we put ${{\rm{\Omega }}}_{k}\,={{\rm{\Omega }}}_{g}\sqrt{1-{p}^{2}}$ .

The group index can be expressed as:(13)$ \begin{eqnarray}{{\rm{N}}}_{{\rm{g}}}=\mathrm{Re}\left[1+2\pi {\chi }_{e}+2\pi \omega \displaystyle \frac{\partial {\chi }_{e}}{\partial {{\rm{\Delta }}}_{p}}\right].\end{eqnarray}$ The expression for time can be expressed as: ${t}_{a}\,=d({N}_{g}-1)/c$ . Group velocity depends on group index and is expressed as: ${v}_{g}=c/{N}_{g}$ . The phase velocity can be written as: ${u}_{r}={vf}+c/{n}_{r}$, where n_r is the refractive index and f is the Fresnel Drag Coefficient. The rotational angle θ_r ca be written as:(14)$ \begin{eqnarray}{\theta }_{r}=\left[{N}_{g}-\displaystyle \frac{1}{{n}_{r}}\right]\displaystyle \frac{{\omega }_{s}d}{c},\end{eqnarray}$ where ω_s is the spinning velocity, and d is the width of the spinning window.

3. Results and discussion

There is no effect on the polarization state rotation and images when the spinning velocity of medium is zero. A spinning medium having spinning velocity (${\omega }_{s}=1000\,{\rm{rps}}$ ) significantly affects the polarization state and images. SGC effect can make enhancements in the degree of rotation. The decay rate γ is considered to be 1 MHz. For simplicity the parameters (ε₀, ℏ, μ₂₃ =1) are taken in atomic units.

In figure 2 the plot is traced for the absorption of light pulse propagating in a spinning medium. When the SGC factor p is zero the absorption is very small, as shown by the pink solid line. When the SGC factor is increased from p =0 to p =0.5, 0.7 and to 0.9 the absorption increases as shown by the blue, black and green solid lines. Moreover, the absorption peak reaches the saturated region near the resonance point both in the positive as well as in the negative domain. The absorption is positive for negative probe field detuning, while it is negative when the probe detuning is nearly 1γ . When the detuning further increased the absorption again became positively saturated. From figure 2 it is clear that the absorption spectrum enhances with the effect of SGC. However the absorption spectrum vanishes for large probe field detuning on both sides.

Figure 2.

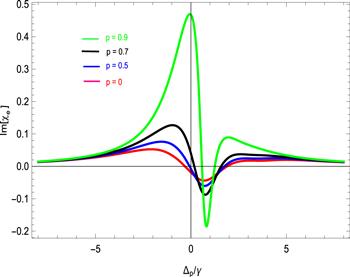New window|Download| PPT slide
Figure 2.Absorption spectral profile of spinning medium with the presence and absence of SGC effect versus Δ_p /γ such that γ =1 MHz, γ₁ =γ₂ =γ₃ =1γ, Δ_c =Δ_k =0γ, $N={10}^{12}\,{\rm{atoms}}\,{{\rm{cm}}}^{-3}$, Φ₁ =Φ₂ =1 Ω_g =4.5γ and Ω_c =1.5γ .


In figure 3 the plot is traced for the dispersion spectrum versus probe field detuning, while other spectroscopic parameters remain the same as in figure 2 . The corresponding group index is negative and enhances in the negative domain. When the SGC factor is zero the dispersion is minimum. The slope of the dispersion spectrum is anomalous near the resonance point as shown by the pink solid line. When we increased the SGC factor from zero to 0.5, 0.7 and then to 0.9 dispersion slope became steeper, revealing an enhancement in superluminal propagation of light due to the SGC effect. The suggested atomic model demonstrates the enhancement in fast light propagation under SGC.

Figure 3.

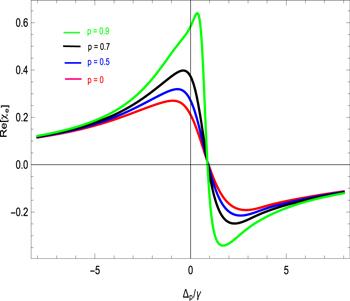New window|Download| PPT slide
Figure 3.Dispersion spectrum of spinning medium with the presence and absence of SGC effect versus Δ_p /γ such that γ =1 MHz, γ₁ =γ₂ =γ₃ =1γ, Δ_c =Δ_k =0γ, $N={10}^{12}\,{\rm{atoms}}\,{{\rm{cm}}}^{-3}$, Ω_g =4.5γ Φ₁ =Φ₂ =1 and Ω_c =1.5γ .


In figure 4 the plot is traced for the group index versus probe field detuning. When ω_s =0 rps then there is no rotation; when ω_s stays on 1000 rps then considerable rotation in polarization state rotation and images were noted. When the SGC factor is zero the group index is minimum, indicating a very small change in the propagating light pulse in this suggested model. When we increase the SGC factor, group index enhances in the negative domain. When the SGC factor is increased from zero to 0.5, 0.7 and then to 0.9, the corresponding group index is negative and enhances in the negative domain as shown by the solid pink, blue, black and green line in figure 4 .

Figure 4.

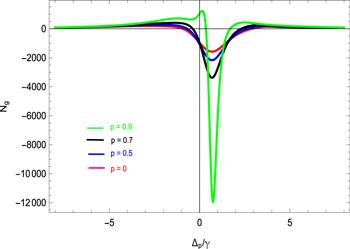New window|Download| PPT slide
Figure 4.Group refractive index in spinning medium with the presence and absence of SGC effect versus Δ_p /γ such that γ =1 MHz, γ₁ =γ₂ =γ₃ =1γ, Δ_c =Δ_k =0γ, $N={10}^{12}\,{\rm{atoms}}\,{{\rm{cm}}}^{-3}$, Ω_g =4.5γ Φ₁ =Φ₂ =1 and Ω_c =1.5γ .


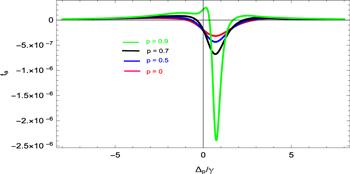
Figure 5 shows the time advancement versus probe field detuning in the proposed atomic medium. The group velocity, group index and time are related as ${v}_{g}=c/{N}_{g}$ and ${t}_{a}=d({N}_{g}-1)/c$ . For the fast light propagation the observed time is negative, as shown in figure 5 . When the SGC factor is zero the observed change in the time is almost negligible. However, as the SGC factor is increased from zero to 0.5, 0.7 and then to 0.9 the observed time is negative and enhances in the negative domain as shown by the solid pink, blue, black and green lines in figure 5 . We noted 0.5 to 2.5 microsecond advancement in the observed time due to SGC effect in the proposed atomic system, which is a remarkable achievement.

Figure 5.

New window|Download| PPT slide
Figure 5.Time advancement in the spinning medium with the presence and absence of SGC effect versus Δ_p /γ such that γ =1 MHz, γ₁ =γ₂ =γ₃ =1γ, Δ_c =Δ_k =0γ, $N={10}^{12}\,{\rm{atoms}}\,{{\rm{cm}}}^{-3}$, Ω_g =4.5γ, Φ₁ =Φ₂ =1, Ω_c =1.5γ and d=6 mm.


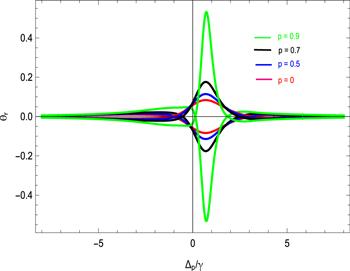
Figure 6 shows the degree of polarization state rotation and images versus probe detuning. We observe 0.5 radian angle of rotation in this suggested atomic model. When the spinning medium is rotating clockwise the polarization state and images will rotate counterclockwise [24]. However, for slow light the rotation will occur in the same direction. The SGC effect significantly enhances the degree of rotation. We report 2.5 times enhancement in the rotational angle measured under SGC.

Figure 6.

New window|Download| PPT slide
Figure 6.Rotations of polarization state of light and their transmitted image in the spinning medium with the presence and absence of SGC effect versus Δ_p /γ such that γ =1 MHz, γ₁ =γ₂ =γ₃ =1γ, Δ_c =Δ_k =0γ, Φ₁ =Φ₂ =1 Ω_g =4.5γ, Ω_c =0.6γ and d=6 mm.


In figure 7 we demonstrate that the polarization states and their transmitted images rotate counterclockwise for a clockwise spinning medium. The SGC factor affecting the rotation of polarization state and images are as shown in figure 7 . The proposed medium is a spinning fast light medium. Figure 7 fulfills the basic theme of a spinning fast light medium. The rotation is zero when ω_s stays on zero. When ${\omega }_{s}$ is gradually increased to 1000 rps considerable rotation in the polarization state and images were noted. Our results can find significant applications in telecommunications, image coding and cloaking technology.

Figure 7.

New window|Download| PPT slide
Figure 7.Rotations of polarization states of light and their transmitted images in the spinning medium with the presence and absence of SGC effect versus ω_s such that γ =1 MHz, γ₁ =γ₂ =γ₃ =1γ, Δ_c =Δ_k =0γ, Φ₁ =Φ₂ =1, Ω_g =4.5γ, Ω_c =1.5γ and d =6 mm.

4. Conclusion

In summary the propagations of fast light pulses in a four-level atomic configuration were studied. The proposed atomic model can be realized in rubidium Rb⁸⁷ atom. We investigate SGC effect on rotary photon. In the fast light spinning medium the rotation of medium and polarization state rotates in the opposite direction. In this suggested model the calculated group index is −12000. The observed rotational angle of polarization states and images due to SGC effect is 0.5 radian. The measured value of the rotational angle under the effect of SGC is several times more enhanced than the results obtained under Kerr Effect. The time for the propagating fast light pulse is negative. We show that the time advances from 0.5 to 2.5 microsecond in our proposed system. These results may find applications in telecommunication systems, image coding and cloaking technology.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Fresnel A 1818 Ann. Chim., Phys. 9 57 66 57–66
[Cited within: 1]

[2]Jones R V 1972 Proc. R. Soc. A 328 337
DOI:10.1098/rspa.1972.008 [Cited within: 1]

[3]Jones R V 1975 Proc. R. Soc. A 345 351 364 351–64
DOI:10.1098/rspa.1975.0141

[4]Jones R V 1976 Proc. R. Soc. A 349 423
DOI:10.1098/rspa.1976.0082 [Cited within: 1]

[5]Arnold S F Gibson G Boyd R W Padgett M J 2011 Science 333 65
DOI:10.1126/science.1203984 [Cited within: 1]

[6]Fizeau H 1859 Ann. Chim., Phys. 57 385 404 385–404
[Cited within: 1]

[7]Allen L Beijersbergen M W Spreeuw R J Woerdman J P 1992 Phys. Rev. A 45 8185
DOI:10.1103/PhysRevA.45.8185 [Cited within: 1]

[8]Leach J Wright A J Gotte J B Girkin J M Allen L Arnold S F Barnett S M Padgatt J M 2008 Phys. Rev. Lett. 100 153902
DOI:10.1103/PhysRevLett.100.153902 [Cited within: 1]

[9]Chichak K S Cantrill S J Pease A R Chiu S H Cave G W V Atwood J L Stoddart J F 2004 Science 304 1308
DOI:10.1126/science.1096914 [Cited within: 1]

[10]Ochiai T Barada D Fukuda T Hayasaki Y Kuuoda K Yatagai T 2013 Opt. Lett. 38 748
DOI:10.1364/OL.38.000748 [Cited within: 1]

[11]Khan N Bacha B A Iqbal A Rahman A U Afaq A 2017 Phys. Rev. A 96 013848
DOI:10.1103/PhysRevA.96.013848 [Cited within: 1]

[12]Iqbal A Khan N Bacha B A Rahman A U Ahmad A 2017 Phys. Lett. A 381 3134
DOI:10.1016/j.physleta.2017.07.037 [Cited within: 1]

[13]Sankar D Rostovtsev Y V 2012 Phys. Rev. A 86 013806
DOI:10.1103/PhysRevA.86.013806 [Cited within: 1]

[14]Rostovtsev Y V Sariyanni Z E Scully M O 2006 Phys. Rev. Lett. 97 113001
DOI:10.1103/PhysRevLett.97.113001 [Cited within: 1]

[15]Matsko A B Rostovtsev Y V Fleischhauer M Scully M O 2001 Phys. Rev. Lett. 86 2006
DOI:10.1103/PhysRevLett.86.2006 [Cited within: 1]

[16]Cardimona D A Raymer M G Stroud C R 1982 J. Phys. B: At. Mol. Phys. 15 55
DOI:10.1088/0022-3700/15/1/012 [Cited within: 1]

[17]Harris S E 1994 Opt. Lett. 19 23
DOI:10.1364/OL.19.002018 [Cited within: 1]

[18]Harris S E Stephen E 1997 Phys. Today 50 36
DOI:10.1063/1.881806

[19]Scully M O Zhu S Y Fearn H 1992 Z Phys. D 22 471
DOI:10.1007/BF01426089 [Cited within: 1]

[20]Bai Y F Guo H Sun H Han D A Liu C Chen X Z 2004 Phys. Rev. A 69 043814
DOI:10.1103/PhysRevA.69.043814 [Cited within: 1]

[21]Yan X Wang L Yin B Jiang W Song J 2009 J. Opt. Soc. Am. B 26 1862
DOI:10.1364/JOSAB.26.001862 [Cited within: 1]

[22]Agarwal G S G S 2000 Phys. Rev. Lett. 84 5500
DOI:10.1103/PhysRevLett.84.5500 [Cited within: 1]

[23]Wang C L Kang Z H Tian S C Jiang Y Gao J Y 2009 Phys. Rev. A 79 043810
DOI:10.1103/PhysRevA.79.043810 [Cited within: 1]

[24]Rahman H Ullah H Jabar M S A Khan A A Ahmad I Bacha B A 2014 Laser Phys. 24 115404
DOI:10.1088/1054-660X/24/11/115404 [Cited within: 4]

[25]Harris S E Field J E Imamoglu A 1990 Phys. Rev. Lett. 64 1107
DOI:10.1103/PhysRevLett.64.1107

[26]Agarwal G S Dasgupta S 2004 Phys. Rev. A 70 023802
DOI:10.1103/PhysRevA.70.023802 [Cited within: 1]