Xiao-Zhen Li(李小珍)¹, Meng-Jiang Xing(邢孟江)^,21 Department of Information and Technology, Kunming University, Kunming, 650214, China
² State Key Laboratory of Electronic Thin Films and Integrated Devices, University of Electronic Science and Technology of China, Chengdu, 610054, China

Received:2020-02-25Revised:2020-06-21Accepted:2020-06-24Online:2020-10-15

Fund supported:

National Natural Science Foundation of China.61864004 National Natural Science Foundation of China.61564005

Abstract
The mechanical anisotropy, structural properties, electronic band structures and thermal properties of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are detailed and investigated in this work. The novel silicon nitride phase Si₂ N₂ (SiH₂ ) and germanium nitride phase Ge₂ N₂ (GeH₂ ) in the Cmc 2₁ structure are proposed in this work. The novel proposed Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are both mechanically and dynamically stable. The electronic band calculation of the HSE06 hybrid functional shows that C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are all wide band gap semiconductor materials, and C₂ N₂ (CH₂ ) and Si₂ N₂ (SiH₂ ) are direct band gap semiconductor materials, while Ge₂ N₂ (GeH₂ ) is a quasi-direct band gap semiconductor material, the band gap of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are 5.634 eV, 3.013 eV, and 2.377 eV, respectively. The three-dimensional and plane distributions of Young’s modulus, shear modulus and Poisson’s ratio of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) show that these materials have different degrees of mechanical anisotropy. The order of Young’s modulus of Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) in different directions is different from that of C₂ N₂ (CH₂ ). When the tensile axis is in a particular direction, the order of the Young’s modulus of Si₂ N₂ (SiH₂ ): E_[110] <E_[120] <E_[111] <E_[101] <E_[010] =E_[100] <E_[011] <E_[001], and the order of the Young’s modulus of Ge₂ N₂ (GeH₂ ): E_[110] <E_[111] <E_[101] <E_[120] <E_[100] <E_[010] <E_[011] <E_[001] .
Keywords： X₂N₂ (XH₂ );mechanical anisotropy;wide band gap semiconductor;Young’s modulus


PDF (1538KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Xiao-Zhen Li(李小珍), Meng-Jiang Xing(邢孟江). Mechanical anisotropy and electronic properties of X₂N₂ (XH₂ ): first-principles calculations^*. Communications in Theoretical Physics[J], 2020, 72(11): 115701- doi:10.1088/1572-9494/aba25c

1. Introduction

Group 14 elements have a variety of allotropes [1 –10] and their own alloy materials [11 –16]. At the same time, the group 14 elements (C, Si, Ge) can form a variety of compounds [17 –26]. The new carbon-nitride-related material C₂ N₂ (CH₂ ) has been investigated in recently year, and C₂ N₂ (CH₂ ) in Cmc 2₁ space group has been synthesized by Sougawa et al [17]. The C₂ N₃ H in Cmc 2₁ phase proposed by Salamat et al [18] has a bulk modulus equivalent to that of high hardness silicon nitride ceramics. Later, Sougawa et al [19] studied the change of structure and bulk modulus of this structure under high pressure. They found that the strength of carbon–nitrogen single bond is the same as that of carbon–carbon single bond in diamond. Then, Takarabe et al [20] investigated the electronic band structures of IV₂ V₂ VI class semiconductors, C₂ N₂ O, C₂ N₂ NH, C₂ N₂ CH₂ used the screened-exchange local density approximation (sX-LDA) [27] by first-principles calculations, the valence of X atom is actually two, so the substitution of X (X quarter O, NH, CH₂ ) is isoelectronic. They found that the upper VB (valence band) is dominated by N 2p and X 2p orbits, and the calculated absorption edge moves to the low energy direction as the substituent shifts from O atom to CH₂ group. The structural properties, mechanical properties, electronic properties and thermodynamic properties of C₂ N₂ (CH₂ ) are study used first-principles calculations by Wei et al [21], C₂ N₂ (CH₂ ) has a large bulk modulus and shear modulus, and it is a kind of potential incompressible hard material. In addition, the maximum value of Young’s modulus of C₂ N₂ (CH₂ ) is along the [001] direction. In the pressure range of 0–100 GPa and 0–2000 K, the thermodynamic properties, such as heat capacity, thermal expansion, and Grüneisen parameters of C₂ N₂ (CH₂ ) were investigated by the quasi harmonic Debye model. Very Recently, Arrerut et al [22] investigated the physical properties under high pressure, in the pressure range of 50 GPa, the band gap within GGA level decreases at the rate of 7.5 meV GPa⁻¹ .

The two novel silicon-nitride-related material Si₂ N₂ (SiH₂ ), and germanium-nitride-related material Ge₂ N₂ (GeH₂ ) are proposed by the first principle method, and their stability is proved. In the present work, using first-principles calculations, the electronic band structures, structural properties, mechanical anisotropy, and thermal properties of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are detailed investigated in this work.

2. Computational detail

This work utilized the Cambridge Serial Total Energy Package plane-wave code [28] based on density functional theory [29, 30]. The structural optimization utilized the Broyden–Fletcher–Goldfarb–Shanno [31] minimization. The interactions between the ionic core and valence electrons were described by the ultrasoft pseudopotential [32] for calculating the elastic properties and structural optimizations in this work. The exchange correlation potential was performed with the LDA [33, 34] and generalized gradient approximation in the form of the Perdew–Burke–Ernzerhof function [35]. For calculating the elastic properties and structural optimizations, a plane wave cut-off energy of 500 eV was adopted. The high Monkhorst–Pack [36] points less than or about 2π ×0.025 Å⁻¹ for the conventional cells of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ), and Ge₂ N₂ (GeH₂ ), in other words, 5×9×10 in the Brillouin zone for C₂ N₂ (CH₂ ); 3×7×8 for Si₂ N₂ (SiH₂ ), 3×7×8 for Ge₂ N₂ (GeH₂ ), respectively. For the electronic band structures, the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional [37] are adopted for sufficiently accurate calculations of the electronic band structures of X₂ N₂ (XH₂ ) (X=C, Si, Ge). In addition, the phonon spectra of X₂ N₂ (XH₂ ) are determined using the linear response approach, called the density functional perturbation theory [38].

3. Results and discussion

3.1. Structural properties

The crystal structures of X₂ N₂ (XH₂ ) (X=C, Si, Ge) are shown in figure 1, here, the dark pink, green and purple spheres represent the X atoms (X=C, Si, Ge), N atoms and H atoms, respectively. The optimized lattice constants of X₂ N₂ (XH₂ ) (X=C, Si, Ge) are listed in table 1 . The C₂ N₂ (CH₂ ) has been synthesized experimentally by Sougawa et al [17], Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are first proposed in this work. The lattice parameters of X₂ N₂ (XH₂ ) increase with the X atoms form carbon, silicon to germanium atom, the fastest growing direction is direction a . Because there are more silicon–silicon bonds in this direction, and the silicon–silicon bond length (Si–Si: bond length: 2.367 35 Å) increases more than the carbon–carbon bond (C–C bond length: 1.553 38 Å), and the silicon–nitrogen bond length (Si–N bond length: 1.761 53 Å) increases less than the carbon–nitrogen bond (C–N bond length: 1.506 54 Å). When X atom changes from carbon atom to silicon atom and then to germanium atom, the lattice parameter a increases the most, 49.46% more than C₂ N₂ (CH₂ ), and the lattice parameter c increases the least, 26.58% more than C₂ N₂ (CH₂ ).

Figure 1.

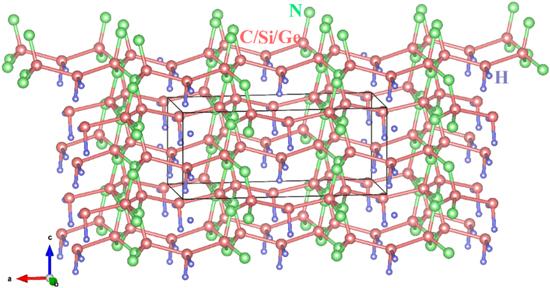New window|Download| PPT slide
Figure 1.The crystal structures of X₂ N₂ (XH₂ ) (X=C, Si, Ge).



Table 1.
Table 1.The calculated lattice parameters (Å) of X₂ N₂ (XH₂ ) (X=C, Si, Ge) with different functionals.

		a	b	c	V
C2 N2 (CH2 )	GGA	8.1403	4.6462	4.1162	155.680
	LDA	8.0061	4.5658	4.0656
	sX-LDAa	8.1222	4.4630	4.1177
	Experimentala	7.6250	4.4900	4.0470
Si2 N2 (SiH2 )	GGA	11.6131	5.5769	4.9216	318.748
	LDA	11.3936	5.4473	4.8228	299.326
Ge2 N2 (GeH2 )	GGA	12.1665	5.9103	5.2103	374.663
	LDA	11.7703	5.6907	5.0368	337.376

^aReference [17].

New window|CSV

3.2. Stability

Although C₂ N₂ (CH₂ ) has been synthesized, the phonon spectrum of C₂ N₂ (CH₂ ) is given in previous work [21]. The phonon spectra of Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are shown in figures 3 (a) and (b), respectively. There is no curve below zero in the phonon spectrum, which proves that the material is dynamically stable. In other words, all the C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are dynamically stable. The elastic constants and elastic moduli of X₂ N₂ (XH₂ ) are listed in table 2 . The all space group of X₂ N₂ (XH₂ ) is Cmc 2₁, it belongs the orthorhombic symmetry. For orthogonal systems, the necessary and sufficient born criteria: C₁₁ >0, C₄₄ >0, C₅₅ >0, C₆₆ >0, C₁₁C₂₂ >${C}_{12}^{2},$C₁₁C₂₂C₃₃ +2C₁₂C₁₃C₂₃ −C₁₁${C}_{23}^{2}$ −C₂₂${C}_{13}^{2}$ − C₃₃${C}_{12}^{2}$ >0, and the elastic constants listed in table 2 meet the mechanical stability conditions of orthorhombic symmetry. The change trend of elastic modulus of X₂ N₂ (XH₂ ) is opposite to that of lattice constant, as shown in figure 2 (b). With the replacement of carbon atom by silicon atom and germanium atom, the change of bulk modulus, shear modulus and Young’s modulus is very large. The shear modulus decreases the most, the shear modulus of Ge₂ N₂ (GeH₂ ) is 75.48% less than that of C₂ N₂ (CH₂ ), the bulk modulus of Ge₂ N₂ (GeH₂ ) is 67.93% less than that of C₂ N₂ (CH₂ ), and the Young’s modulus of Ge₂ N₂ (GeH₂ ) is 74.12% less than that of C₂ N₂ (CH₂ ), respectively. In order to explain the decrease of bulk, shear and Young’s modulus, we try to explain it with electron localization function (ELF), and the ELF distribution of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) with an isovalue of 0.75 are shown in figure 4 . From figure 4, we can see that the distribution range of electrons among atoms is becoming larger and larger; that is to say, the electrons appear in the area farther away from the atoms, the effect of atoms on electrons is becoming smaller and smaller, and the bond energy is also decreasing. Therefore, in terms of its mechanical properties, its elastic modulus is decreasing.


Table 2.
Table 2.The elastic constants (GPa) and elastic modulus (GPa) of X₂ N₂ (XH₂ ) (X=C, Si, Ge).

		C11	C22	C33	C44	C55	C66	C12	C13	C23	B	G	E
C2 N2 (CH2 )	GGA	471	464	712	275	186	150	53	116	104	237	208	483
	GGAa	505	489	728	283	186	143	85	122	99	256	210	494
	LDA	554	547	794	308	212	170	104	137	120	286	234	552
	LDAa	529	510	799	309	201	145	77	142	119	272	222	524
Si2 N2 (SiH2 )	GGA	199	200	240	104	50	43	58	45	48	104	68	167
	LDA	218	176	257	114	51	42	51	63	59	109	69	171
Ge2 N2 (GeH2 )	GGA	137	146	182	74	37	36	44	34	33	76	51	125
	LDA	198	114	152	88	34	57	39	25	13	67	58	135

^a Reference [21].

New window|CSV

Figure 2.

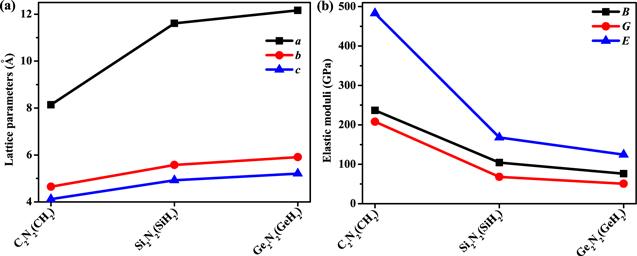New window|Download| PPT slide
Figure 2.The lattice parameters (a) and elastic modulus (b) of X₂ N₂ (XH₂ ) (X=C, Si, Ge), respectively.

Figure 3.

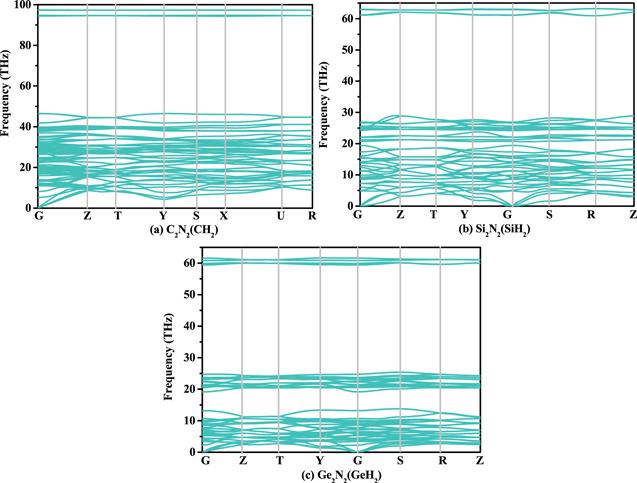New window|Download| PPT slide
Figure 3.The phonon spectra of C₂ N₂ (CH₂ ) (a), Si₂ N₂ (SiH₂ ) (b) and Ge₂ N₂ (GeH₂ ) (c), respectively.

Figure 4.

New window|Download| PPT slide
Figure 4.The electron localization function (ELF) distribution of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) with an isovalue of 0.75.

3.3. Electronic properties

The electronic band structures of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) with HSE06 hybrid functional are shown in figures 5 (a)–(c), respectively. From the figure 5, it is clear that the Ge₂ N₂ (GeH₂ ) is quasi-direct band gap semiconductor materials, while the C₂ N₂ (CH₂ ) and Si₂ N₂ (SiH₂ ) both are direct band gap semiconductor material. The difference of direct band gap and indirect band gap of Ge₂ N₂ (GeH₂ ) is only 0.027 eV. For C₂ N₂ (CH₂ ) and Si₂ N₂ (SiH₂ ), the valence band maximum (VBM) and conduction band minimum (CBM) both located at the G point (also called Γ point), the VBM of Ge₂ N₂ (GeH₂ ) also located at the G point, while the CBM of Ge₂ N₂ (GeH₂ ) located between the G point and S (0.0 0.5 0.0). The Fermi level of X₂ N₂ (XH₂ ) are also investigated in this work, the Fermi level of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) is 8.231 eV, 0.225 eV and −1.449 eV. As X atoms changes from carbon atoms to silicon atoms and then to germanium atoms, the Fermi energy level of X₂ N₂ (XH₂ ) decreases straight forward. The wide band gap and direct band gap imply that of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) can be good semiconductor material and optical material. If group 14 of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are doped (such as C_2−x Si_x N₂ (CH₂ ), C₂ N₂ (C_1−x Si_x H₂ ), or Si_2−x Ge_x N₂ (SiH₂ ), and soon on), their band gap may be adjusted between 2.377 and 5.634 eV.

Figure 5.

New window|Download| PPT slide
Figure 5.The electronic band structures of C₂ N₂ (CH₂ ) (a), Si₂ N₂ (SiH₂ ) (b), and Ge₂ N₂ (GeH₂ ) (c), respectively.

3.4. Debye temperature

The Debye temperature is another important physical quantity reflecting the bonding force between atoms. The Debye temperature of different materials is different, and the melting point is high; that is to say, the stronger the bonding force of atoms is, the higher the Debye temperature is. The Debye temperature, the compressional sound velocity v_p and shear sound velocity v_s, the average sound velocity v_m of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are shown in table 3 . The detailed calculation formula appears in [39]. From table 3, the compressional sound velocity v_p and shear sound velocity v_s, the average sound velocity v_m of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) decreases with the X atoms from C to Si, to Ge atoms. The decrease of average sound velocity v_m is the fastest, the effective rate of compressional sound velocity v_p is only next to v_m, which is 57.62%, it is slightly less than 60.06% of average sound velocity v_m, and the decrease of the shear sound velocity v_s is the slowest, which is 37.79%. The Debye temperature of C₂ N₂ (CH₂ ) is 1589 K, which is the greatest in X₂ N₂ (XH₂ ), and slightly smaller than that of o P8-B₂ CO (1687 K), t I16-B₂ CO (1718 K) and t P4-B₂ CO (1645 K). In addition, the Debye temperature of X₂ N₂ (XH₂ ) reduced by 70.17%.


Table 3.
Table 3.The calculated density (g cm⁻³ ), the longitudinal, transverse and mean wave velocity (v_s, v_p, v_m in m s⁻¹ ), and the Debye temperature (K) for X₂ N₂ (XH₂ ) (X=C, Si, Ge).

	ρ	vp	vs	vm	ΘD
C2 N2 (CH2 )	2.8186	13 508	8590	9445	1589
Si2 N2 (SiH2 )	2.3815	9041	5344	5920	849
Ge2 N2 (GeH2 )	4.3931	5725	3407	3772	474

New window|CSV

3.5. Mechanical anisotropy properties

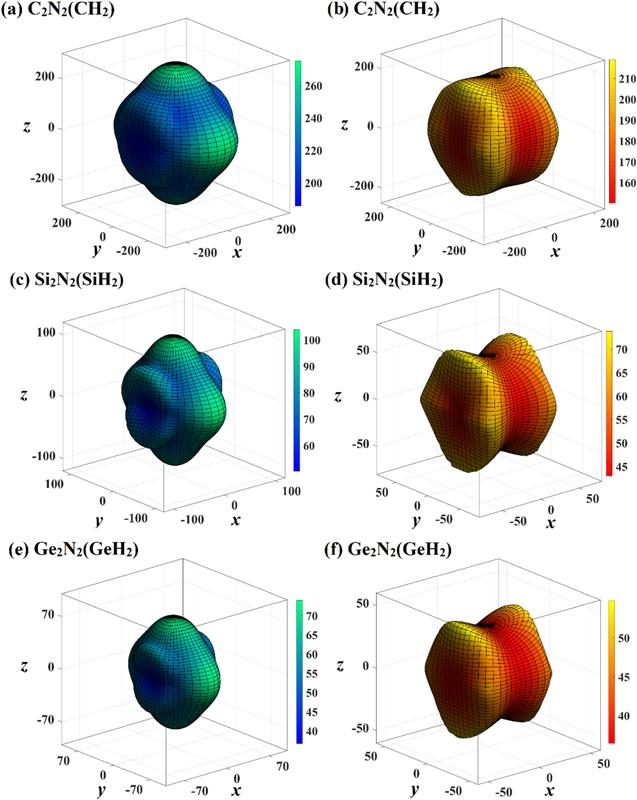
The mechanical anisotropy of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) in Young’s modulus, shear modulus and Poisson’s ratio are systematic investigated in this work. First, we focus on Young’s modulus. The three-dimensional surface constructions of Young’s modulus for X₂ N₂ (XH₂ ) are estimated by elastic anisotropy measures code [40], the related results are shown in figure 6 . As we all know, the three-dimensional surface constructions of Young’s modulus of isotropic materials is a hollow sphere, and any three-dimensional surface constructions of Young’s modulus without hollow sphere can be considered as anisotropic [28]. Some researches have also successfully used this method to predict its mechanical anisotropy [16, 41 –47]. From figure 6, the shape of the three-dimensional surface constructions of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) exhibits the mechanical anisotropy. The values of Young’s moduli of C₂ N₂ (CH₂ ) and Si₂ N₂ (SiH₂ ) are the same in x -axis and y -axis, while the values of Young’s modulus of Ge₂ N₂ (GeH₂ ) in x -axis (120 GPa) is less than that of y -axis (129 GPa). From the shape of the three-dimensional surface constructions of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ), the Young’s modulus in x -axis of Si₂ N₂ (SiH₂ ) deviates a lot from that in z -axis, the E_z /E_x =229/118=1.94, it is much greater than that of C₂ N₂ (CH₂ ) (E_z /E_x =665/449=1.48) and Ge₂ N₂ (GeH₂ ) (E_z /E_x =170/120=1.42, E_z /E_y =170/129=1.32). It also shows that Young’s modulus is mechanical anisotropic on C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ).

Figure 6.

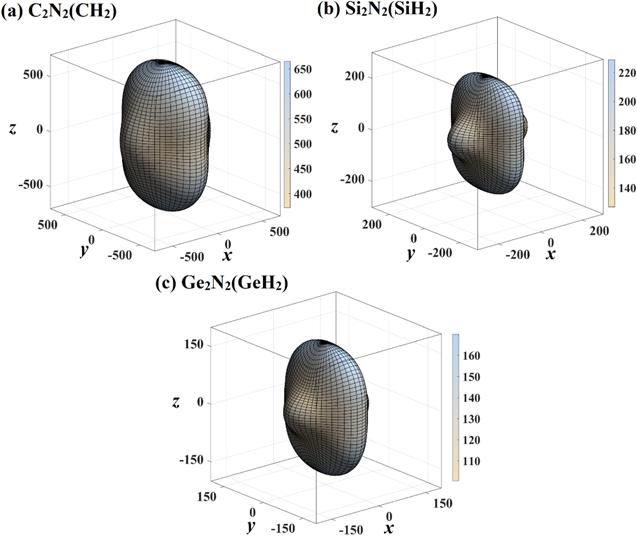New window|Download| PPT slide
Figure 6.The directional dependence of Young’s modulus of C₂ N₂ (CH₂ ) (a), Si₂ N₂ (SiH₂ ) (b), and Ge₂ N₂ (GeH₂ ) (c), respectively.


In order to study the anisotropy of Young’s modulus more systematically, the distribution of Young’s modulus in three main planes was also studied in this work. The maximum values, the minimum values and E_max /E_min ratio of Young’s modulus of X₂ N₂ (XH₂ ) are listed in table 4, and the maximum values, the minimum values, and E_max /E_min ratio of Young’s modulus of in (001) plane, (010) plane and (100) plane are listed in table 5 . The maximum values of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are 665 GPa, 229 GPa, and 170 GPa, respectively, and the minimum values of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are 372 GPa, 127 GPa, and 101 GPa, respectively. From tables 4 and 5, one can see that only the maximum values of Young’s modulus of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ), and Ge₂ N₂ (GeH₂ ) appear in (100) plane, and only the maximum values and the minimum values of Ge₂ N₂ (GeH₂ ) both appear in (010) plane. Therefore, the anisotropy of Young’s modulus in the three main planes is not as good as that of the whole material, except for (010) plane of Ge₂ N₂ (GeH₂ ). For these three main planes, Young’s modulus shows the largest mechanical anisotropy in (010) plane.


Table 4.
Table 4.The calculated the maximum values, the minimum values, and ratio of Young’s modulus, shear modulus and Poisson’s ratio of X₂ N₂ (XH₂ ) (X=C, Si, Ge).

	E			G			v
	Emax	Emin	Ratio	Gmax	Gmin	Ratio	vmax	vmin	Ratio
C2 N2 (CH2 )	665	372	1.79	275	150	1.83	0.29	0.07	4.14
Si2 N2 (SiH2 )	229	127	1.80	104	43	2.42	0.48	0.07	6.86
Ge2 N2 (GeH2 )	170	101	1.68	74	36	2.05	0.42	0.07	6.00

New window|CSV


Table 5.
Table 5.The calculated the maximum values, the minimum values, and ratio of Young’s modulus, shear modulus and Poisson’s ratio of X₂ N₂ (XH₂ ) (X=C, Si, Ge) in (100) plane, (010) plane, and (001) plane.

	(100) plane			(010) plane			(001) plane
	Emax	Emin	Ratio	Emax	Emin	Ratio	Emax	Emin	Ratio
C2 N2 (CH2 )	665	446	1.49	665	446	1.49	449	372	1.21
Si2 N2 (SiH2 )	229	178	1.29	223	140	1.59	178	127	1.40
Ge2 N2 (GeH2 )	170	129	1.32	170	101	1.68	129	102	1.27
	(100) plane			(010) plane			(001) plane
	Gmax	Gmin	Ratio	Gmax	Gmin	Ratio	Gmax	Gmin	Ratio
C2 N2 (CH2 )	275	150	1.83	275	150	1.83	275	150	1.83
Si2 N2 (SiH2 )	104	43	2.42	104	43	2.42	104	43	2.42
Ge2 N2 (GeH2 )	74	36	2.06	74	36	2.06	74	36	2.06
	(100) plane			(010) plane			(001) plane
	vmax	vmin	Ratio	vmax	vmin	Ratio	vmax	vmin	Ratio
C2 N2 (CH2 )	0.22	0.07	3.14	0.28	0.08	3.50	0.24	0.08	3.00
Si2 N2 (SiH2 )	0.26	0.07	3.71	0.40	0.19	2.11	0.47	0.10	4.70
Ge2 N2 (GeH2 )	0.29	0.07	4.14	0.39	0.14	2.76	0.41	0.11	3.73

New window|CSV

Furthermore, we study the magnitude of Young’s modulus of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) in different directions on the main plane. When the Young’s modulus of the tensile axis is in the (001) plane, let α be the angle of between [hk 0] and [100], the orientation dependence of Young’s modulus of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) can be expressed as follows [21]: E⁻¹ =s₁₁ cos⁴α +s₂₂ sin⁴α + 2s₁₂ sin²α cos²α +s₆₆ sin²α cos²α . For (100) plane, let β be the angle of between [001] and [0kl ], the orientation dependence of X₂ N₂ (XH₂ ) can be expressed as follows: E⁻¹ =s₂₂ sin⁴β + s₃₃ cos⁴β +(s₂₃ sin² 2β)/2+(s₄₄ sin² 2β)/4. For (010) plane, let γ be the angle of between [001] and [h 0l ], the orientation dependence of X₂ N₂ (XH₂ ) can be expressed as follows: E⁻¹ = s₁₁ sin⁴γ +s₃₃ cos⁴γ +(s₁₃ sin² 2γ)/2+(s₅₅ sin² 2β)/4. For (1-10) plane, let δ be the angle of between [001] and [hkl ], the orientation dependence of X₂ N₂ (XH₂ ) can be expressed as follows: E⁻¹ =[sin⁴δ /(a² +b² )² ][a⁴s₁₁ +b⁴s₁₂ +a²b² (2s₁₂ +s₆₆ )] + s₃₃ cos⁴δ +[sin²δ cos²δ /(a² +b² )][a² (2s₁₃ +s₅₅ )+b² (2s₂₃ + s₄₄ )]. The related results of orientation dependence of X₂ N₂ (XH₂ ) are illustrated in figure 7 . The greatest value and the smallest value of Young’s modulus of C₂ N₂ (CH₂ ) is 665 GPa and 372 GPa when the tensile axis is along [001] direction and along [120] direction, respectively, it is much closed the previous report (686 and 376 GPa) [5]. When the tensile axis is in a particular direction, the order of the Young’s modulus of Si₂ N₂ (SiH₂ ): E_[110] <E_[120] <E_[111] <E_[101] <E_[010] = E_[100] <E_[011] <E_[001], and the order of the Young’s modulus of Ge₂ N₂ (GeH₂ ): E_[110] <E_[111] <E_[101] <E_[120] <E_[100] < E_[010] <E_[011] <E_[001] . The order of Young’s modulus of Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) in different directions is different from that of C₂ N₂ (CH₂ ).

Figure 7.

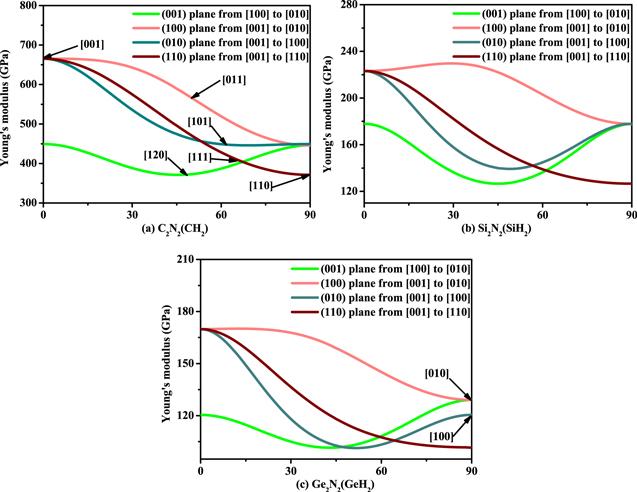New window|Download| PPT slide
Figure 7.Orientation dependence of Young’s modulus of C₂ N₂ (CH₂ ) (a), Si₂ N₂ (SiH₂ ) (b), and Ge₂ N₂ (GeH₂ ) (c), respectively.


The three-dimensional surface constructions of the maximum values and the minimum values of shear modulus and Poisson’s ratio in different directions of X₂ N₂ (XH₂ ) are displayed in figure 8 and 9, respectively. For shear modulus, the blue green surface constructions represents the maximum values surface construction, and red yellow surface constructions represents the minimum values surface construction. For Poisson’s ratio, the light blue pink surface constructions and light blue purple surface constructions represents the maximum values surface construction and the minimum values surface construction, respectively. From the shapes of three-dimensional surface constructions of shear modulus and Poisson’s ratio of X₂ N₂ (XH₂ ), one can see that the C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) also exhibits mechanical anisotropy in shear modulus and Poisson’s ratio. The maximum values, the minimum values and G_max /G_min ratio of shear modulus of X₂ N₂ (XH₂ ) are also listed in table 5, and the maximum values, the minimum values, and v_max /v_min ratio of Poisson’s ratio of in (001) plane, (010) plane and (100) plane are also listed in table 5 . Unlike Poisson’s ratio and Young’s modulus, only the maximum and minimum of shear modulus of X₂ N₂ (XH₂ ) appear in three main planes, (001) plane, (010) plane and (100) plane. In addition, the mechanical anisotropy in shear modulus of Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are both slightly greater than that of C₂ N₂ (CH₂ ), and the mechanical anisotropy in shear modulus of Si₂ N₂ (SiH₂ ) is the greatest. For Poisson’s ratio, similar to Young’s modulus, only the minimum values of Poisson’s ratio of X₂ N₂ (XH₂ ) appears in three main planes. The mechanical anisotropy in Poisson’s ratio of Si₂ N₂ (SiH₂ ) is the greatest. For three main planes, the mechanical anisotropy in Poisson’s ratio in (001) plane of Si₂ N₂ (SiH₂ ) is the greatest, while mechanical anisotropy in Poisson’s ratio in (010) plane of Si₂ N₂ (SiH₂ ) is the smallest. The (010) plane and (001) plane of C₂ N₂ (CH₂ ) exhibits the greatest and smallest mechanical anisotropy in Poisson’s ratio, respectively. While (100) plane and (010) plane of Ge₂ N₂ (GeH₂ ) exhibits the greatest mechanical anisotropy in Poisson’s ratio, respectively.

Figure 8.

New window|Download| PPT slide
Figure 8.The directional dependence of shear modulus of C₂ N₂ (CH₂ ) (a), (b), Si₂ N₂ (SiH₂ ) (c), (d), and Ge₂ N₂ (GeH₂ ) (e), (f), respectively. The blue green three-dimensional surface constructions represent the maximum values of shear modulus, and the red yellow surface constructions represent the minimum values of shear modulus, respectively.

Figure 9.

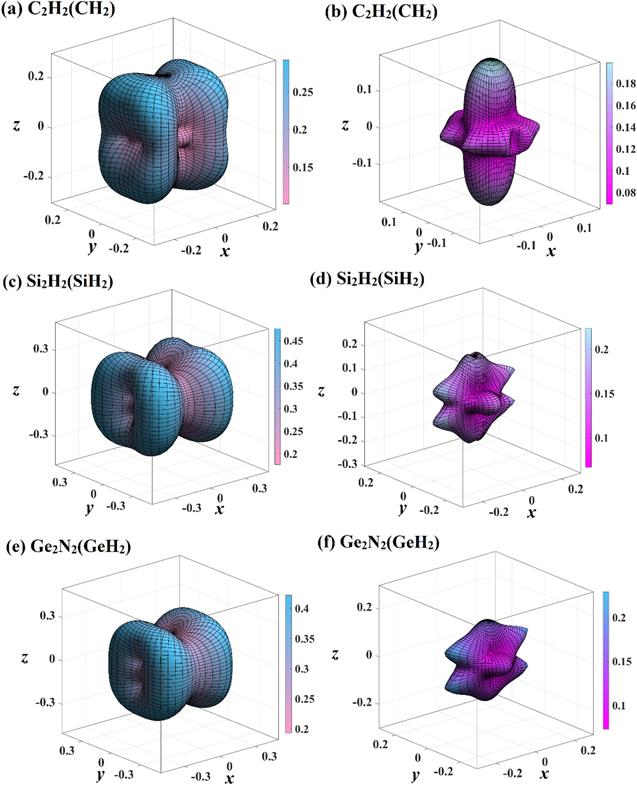New window|Download| PPT slide
Figure 9.The directional dependence of Poisson’s ratio of C₂ N₂ (CH₂ ) (a), (b), Si₂ N₂ (SiH₂ ) (c), (d), and Ge₂ N₂ (GeH₂ ) (e), (f), respectively. The light blue pink three-dimensional surface constructions represent the maximum values of Poisson’s ratio, and the light blue purple surface constructions represent the minimum values of Poisson’s ratio, respectively.

4. Conclusion

The novel silicon nitride phase Si₂ N₂ (SiH₂ ) and novel germanium nitride phase Ge₂ N₂ (GeH₂ ) in Cmc 2₁ structure are proposed in this work. Then, the structural, mechanical anisotropy, electronic band structures and thermal properties of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are detailed investigated in this work. First, their stability has been confirmed by phonon spectrum and elastic constants. Secondly, the electronic band calculation of hybrid functional shows that C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are all wide band gap semiconductor materials, and C₂ N₂ (CH₂ ) and Si₂ N₂ (SiH₂ ) are direct band gap semiconductor materials, while silicon is a quasi-direct band gap semiconductor material. The wide band gap and direct band gap imply that of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) can be good semiconductor material and optical material. The Debye temperature of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) is 1589 K, 849 K and 474 K, respectively. Then, the three-dimensional surface constructions of Young’s modulus, shear modulus and Poisson’s ratio of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) all shows the different levels mechanical anisotropy. For these (100), (010), (001) planes, Young’s modulus shows the largest mechanical anisotropy in (010) plane. For Poisson’s ratio, the (010) plane of C₂ N₂ (CH₂ ) shows the largest mechanical anisotropy, the (001) plane of Si₂ N₂ (SiH₂ ) illustrates the largest mechanical anisotropy, the (100) plane of Ge₂ N₂ (GeH₂ ) illustrates the largest mechanical anisotropy. While the shear modulus of C₂ N₂ (CH₂ ), Si₂ N₂ (SiH₂ ) and Ge₂ N₂ (GeH₂ ) are all mechanical isotropy in (100), (010), (001) planes.

Acknowledgments

This work was funded by the National Natural Science Foundation of China (grant numbers 61864004 and 61564005).

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Fan Q Zhao Y Yu X Song Y Zhang W Yun S 2020 Diam. Relat. Mater. 106 107831
DOI:10.1016/j.diamond.2020.107831 [Cited within: 1]

[2]Li X Z Xing M J 2020 Mater. Chem. Phys. 242 122480
DOI:10.1016/j.matchemphys.2019.122480

[3]Fan Q Wang H Song Y Zhang W Yun S 2020 Comput. Mater. Sci. 178 109634
DOI:10.1016/j.commatsci.2020.109634

[4]Zhang W Chai C Fan Q Song Y Yang Y 2020 Materials 13 1926
DOI:10.3390/ma13081926

[5]Yang X Yao M Wu X Liu S Chen S Yang K Liu R Cui T Sundqvist B Liu B 2017 Phys. Rev. Lett. 118 245701
DOI:10.1103/PhysRevLett.118.245701 [Cited within: 1]

[6]Fan Q Y Chai C C Wei Q Yang Y T 2016 Phys. Chem. Chem. Phys. 18 12905
DOI:10.1039/C6CP00195E

[7]Fan Q Y Niu R Zhang W Z Zhang W Ding Y C Yun S N 2019 ChemPhysChem 20 128
DOI:10.1002/cphc.201800903

[8]He C Y Shi X Z Clark S J Li J Pickard C J Ouyang T Zhang C X Tang C Zhong J X 2018 Phys. Rev. Lett. 121 175701
DOI:10.1103/PhysRevLett.121.175701

[9]Cheng J Zhang Q D 2020 Materials 13 2079
DOI:10.3390/ma13092079

[10]Zhao Y B Zhang W Fan Q Y 2019 Commun. Theor. Phys. 71 1036
DOI:10.1088/0253-6102/71/8/1036 [Cited within: 1]

[11]Zhang W Chai C C Fan Q Y Weng K Q Yang Y T 2018 J. Mater. Sci. 53 9611
DOI:10.1007/s10853-018-2249-9 [Cited within: 1]

[12]Fan Q Y Xu J Zhang W Z Song Y X Yun S N 2019 J. Appl. Phys. 126 045709
DOI:10.1063/1.5095203

[13]Song Y X Chai C C Fan Q Y Zhang W Yang Y T 2019 J. Phys.: Condens. Matter 31 255703
DOI:10.1088/1361-648X/ab11a2

[14]Wang Q K Chai C C Fan Q Y Yang Y T 2017 Commun. Theor. Phys. 68 259
DOI:10.1088/0253-6102/68/2/259

[15]Fan Q Y Chai C C Wei Q Wong K Q Liu Y Q Yang Y T 2018 J. Mater. Sci. 53 2785
DOI:10.1007/s10853-017-1681-6

[16]Fan Q Y Wang H Q Zhang W Z Wei M F Song Y X Zhang W Yun S N 2019 Curr. Appl. Phys. 19 1325
DOI:10.1016/j.cap.2019.08.019 [Cited within: 2]

[17]Sougawa M et al. 2011 Japan. J. Appl. Phys. 50 095503
DOI:10.1143/JJAP.50.095503 [Cited within: 4]

[18]Salamat A Woodhead K McMillan P F Cabrera R Q Rahman A Adriaens D Corà F 2009 Phys. Rev. B 80 104106
DOI:10.1103/PhysRevB.80.104106 [Cited within: 1]

[19]Sougawa M Takarabe K Mori Y Okada T Yagi T Kariyazaki H Sueoka K 2013 J. Appl. Phys. 113 053510
DOI:10.1063/1.4789020 [Cited within: 1]

[20]Takarabe K Sougawa M Kariyazaki H Sueoka K 2012 J. Appl. Phys. 112 013537
DOI:10.1063/1.4731749 [Cited within: 1]

[21]Wei Q Zhang M Guo L Yan H Zhu X Lin Z Guo P 2013 Chem. Phys. 415 36
DOI:10.1016/j.chemphys.2013.02.015 [Cited within: 4]

[22]Arrerut S Takarabe K Pinsook U 2017 J. Phys. Chem. C 121 16959
DOI:10.1021/acs.jpcc.7b06594 [Cited within: 1]

[23]Yan H Y Wei Q Zheng B Guo P 2011 J. Solid State Chem. 184 572
DOI:10.1016/j.jssc.2011.01.004

[24]Yan H Y Zhang M Wei Q Guo P 2013 Phys. Status Solidi b 250 1293
DOI:10.1002/pssb.201248225

[25]Fan Q Y Chai C C Wei Q Yang Y T 2016 Materials 9 333
DOI:10.3390/ma9050333

[26]Fan Q Y Duan Z X Song Y X Zhang W Zhang Q D Yun S N 2019 Materials 12 3589
DOI:10.3390/ma12213589 [Cited within: 1]

[27]Seidl A Gorling A Vogl P Majewski J A Levy M 1996 Phys. Rev. B 53 3764
DOI:10.1103/PhysRevB.53.3764 [Cited within: 1]

[28]Hu W C Liu Y Li D J Zeng X Q Xu C S 2014 Comput. Mater. Sci. 83 27
DOI:10.1016/j.commatsci.2013.10.029 [Cited within: 2]

[29]Hohenberg P Kohn W 1964 Phys. Rev. B 136 864
DOI:10.1103/PhysRev.136.B864 [Cited within: 1]

[30]Kohn W Sham L J 1965 Phys. Rev. 140 A1133
DOI:10.1103/PhysRev.140.A1133 [Cited within: 1]

[31]Pfrommer B G Côté M Louie S G Cohen M L 1997 J. Comput. Phys. 131 233
DOI:10.1006/jcph.1996.5612 [Cited within: 1]

[32]Vanderbilt D 1990 Phys. Rev. B 41 7892
DOI:10.1103/PhysRevB.41.7892 [Cited within: 1]

[33]Ceperley D M Alder B J 1980 Phys. Rev. Lett. 45 566
DOI:10.1103/PhysRevLett.45.566 [Cited within: 1]

[34]Perdew J P Zunger A 1981 Phys. Rev. B 23 5048
DOI:10.1103/PhysRevB.23.5048 [Cited within: 1]

[35]Perdew J P Burke K Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
DOI:10.1103/PhysRevLett.77.3865 [Cited within: 1]

[36]Monkhorst H J Pack J D 1976 Phys. Rev. B 13 5188
DOI:10.1103/PhysRevB.13.5188 [Cited within: 1]

[37]Heyd J Scuseria G E Ernzerhof M 2003 J. Chem. Phys. 118 8207
DOI:10.1063/1.1564060 [Cited within: 1]

[38]Baroni S de Gironcoli S dal Corso A Giannozzi P 2001 Rev. Mod. Phys. 73 515
DOI:10.1103/RevModPhys.73.515 [Cited within: 1]

[39]Qiao L P Jin Z Yan G Y Li P Hang L M Li L 2019 J. Solid State Chem. 270 642
DOI:10.1016/j.jssc.2018.12.012 [Cited within: 1]

[40]Marmier A Lethbridge Z A D Walton R I Smith C W Parker S C Evans K E 2010 Comput. Phys. Commun. 181 2102
DOI:10.1016/j.cpc.2010.08.033 [Cited within: 1]

[41]Ma Z Y Wang P Yan F Shi C L Tian Y 2019 Chin. Phys. B 28 036101
DOI:10.1088/1674-1056/28/3/036101 [Cited within: 1]

[42]Zhang Q Zou Y Fan Q Yang Y 2020 Materials 13 1280
DOI:10.3390/ma13061280

[43]Qiao L P Jin Z 2017 Materials 10 1413
DOI:10.3390/ma10121413

[44]Li X Z Xing M J 2019 Comput. Mater. Sci. 158 170
DOI:10.1016/j.commatsci.2018.11.004

[45]Fan Q Y Wei Q Chai C C Yan H Y Zhang M G Lin Z Z Zhang Z X Zhang J Q Zhang D Y 2015 J. Phys. Chem. Solids 79 89
DOI:10.1016/j.jpcs.2014.12.008

[46]Zhang W Chai C Fan Q Song Y Yang Y 2020 J. Phys.: Condens. Matter 32 355701
DOI:10.1088/1361-648X/ab8982

[47]Fan Q Zhang W Song Y Zhang W Yun S 2020 Semicond. Sci. Technol. 35 055012
DOI:10.1088/1361-6641/ab76ae [Cited within: 1]