,1,?, Jia-Hui Yu2, Xin Tang3 Corresponding authors: ? E-mail:zhoudawei@nynu.edu.cn
Received:2019-03-22Online:2019-11-1
| Fund supported: |
Abstract
Keywords：
PDF (11319KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Chun-Ying Pu, Lin-Xia Lv, Da-Wei Zhou, Jia-Hui Yu, Xin Tang. Structure, Electronic, and Mechanical Properties of Three Fully Hydrogenation h-BN: Theoretical Investigations *. [J], 2019, 71(11): 1363-1369 doi:10.1088/0253-6102/71/11/1363
1 Introduction
Two-dimensional hexagonal boron nitride (2D h-BN) has an sp$^2$-hybridized honeycomb structure similar with graphene. However, it is optical transparent and thus called as white graphene. 2D h-BN has aroused extensive research interest due to its many intriguing properties such as high chemical stabilities, high thermal conductivity, and excellent mechanical properties.[1-2] Different from graphene with zero-gap,[3] 2D h-BN opens a large gap due to the strongn ionicity of B-N bonds. To overcome limitation of the wide band gap and further modify the electronic properties of h-BN layers, a lot of works have been carried out. For example, the variation in band gaps of h-BN nanoribbons with their widths,[4] Stark effect and Hydrogen Passivations[5] have been reported. The functionalization of 2D h-BN using different materials including H,[6] C,[7] metals,[8-9] functional groups[10-12] and organic molecules[13-17] also have been investigated theoretically. Among those methods, hydrogenation is a simple and important approach to modify the physical and chemical properties of 2D materials. For example, hydrogenation leads to widening of the band gap of graphene,[18] while results in a reduction in the band gap of 2D BN sheet.[19] Furthermore, Hydrogenation can lead to hydrogen-induced ferromagnetism and even a phase transition of 2D materials. Hydrogenation also affects the mechanical properties of 2D materials, For example, the Young's modulus of graphene is found to reduce from 354 N$\cdot$m$^{-1}$ in graphene to 248 N$\cdot$m$^{-1}$ in fully hydrogenated graphene.[20] In fact, the mechanical properties of a material is an important parameter for the application of the material, which also is an important way to tune the physical and chemistry properties of materials.[21-28]In this paper, we focus on the strain-dependent mechanical properties of fully hydrogenation h-BN (fh-BN). As we know, h-BN has excellent mechanical properties, which are stable under high temperature up to 1000 K. Full hydrogenation also may affect greatly the mechanical properties of 2D h-BN. Up to now, the fh-BN has been reported to have three possible conformers, which are chair, boat, and stirrup. The effect of full hydrogenation on the mechanical properties of h-BN remains unclear. In this paper, we calculate elastic constant, Young's modulus, Poisson ratio, stress-strain curves, and the band gaps under biaxial tensile strain of three fh-BN, and further compared those properties with h-BN.
2 Computational Methods
Our first-principle calculations were carried out using Density Functional Theory (DFT) with a plane wave basis set as implemented in the CASTEP code.[29] The core electrons are treated with Vanderbilt ultrasoft pseudopotentials.[30] Exchange and correlation are treated within the generalized gradient approximation of Perdew, Burke, and Ernzerhof.[31] All calculations are done with a cutoff energy of 520 eV and the first Brillouin zone sampling grid with a resolution of 2$\pi\times$0.03 is adopted. The optimization of atomic positionsand unit cell are stopped when the change in energy is less than 1$\times10^{-5}$ eV/atom, the force on each atom is less than 0.01 eV/?, the displacements are less than $1\times10^{-3}$ ?, and the tress on the cell is less than 0.02 GPa. To reduce the inter-layer interaction to model the single layer system, there was a 30 ? thick vacuum region.3 Results and Discussion
Figure 1 presents the top and perspective views of three configurations of fully hydrogenation h-BN. For chair structure, it has the hexagonal lattice with space group $P3m1$(156) and optimized lattice parameters being $a=b=2.5910$ ?. Four inequivalent atomic positions are (2/3, 1/3, 0.53392), (1/3, 2/3, 0.44207), (1/3, 2/3, 0.48201) and (2/3, 1/3, 0.49916) for H1, H2, B, and N, respectively. The boat and stirrup structures possess to the same orthorhombic lattice with space group of $Pmn2_1$(31), which have the optimized lattice constants of $a =2.5769$ ?, $c=4.3424$ ? for boat and the lattice constants of $a =2.5932$ ?, $c=3.8328$ ? for stirrup. Both structures also contain four inequivalent atomic positions that are H1 (0.500 00, 0.457 69, 0.243 28), H2 (0.500 00, 0.447 62,0.765 57), B (0.5000, 0.486 77, 0.690 71), N (0.500 00,0.490 12, 0.324 51) in boat conformer and H1 (0.500 00, 0.556 84, 0.142 85), H2 (1.000 00, 0.547 42, 0.679 96), B (0.500 00, 0.521 24, 0.297 92), N (1.000 00, 0.518 50, 0.532 19) in stirrup conformer, respectively. Three structure conformers of fh-BN have two different types of H bonds: the connecting boron bonded to hydrogen atoms (B-H) and the connecting nitrogen atoms bonded to hydrogen atoms (N-H). The bond lengths of N-H are 1.043 ?, 1.035 ?, and 1.036 ? and that of B-H are 1.200 ?, 1.220 ?, and 1.224 ? for chair, boat, and stirrup, respectively, which are close to the previous work of hydrogenated h-BN sheet (B-H bond 1.20 ? and N-H bond length 1.03 ?).[19] The B-N (1.568 ?) bond length in the stirrup conformer is the shortest corresponding the B-N bond lengths in chair (1.582 ?) and boat (1.575 ?), respectively. The hydrogenated h-BN leads to strentching of the B-N bond compared with the bond of h-BN (1.44 ?).[19]Fig. 1
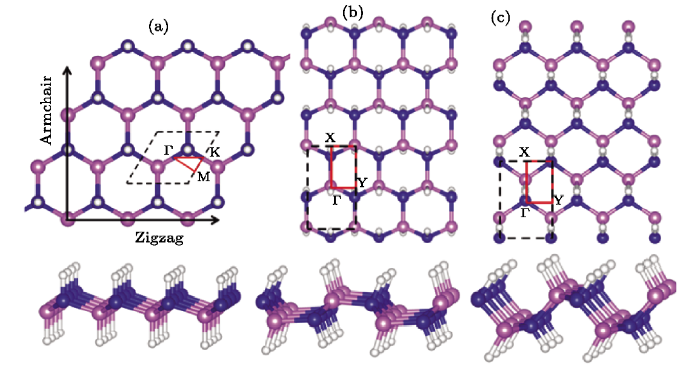New window|Download| PPT slideFig. 1(Color online) Schematic illustration of the top and perspective (bottom panels) views of two-dimensional fh-BN for (a) chair, (b) boat, and (c) stirrup. B, N, and H atoms are represented by pink, blue, and white spheres, respectively. Black dashed line indicates the unit cell of fh-BN and the red solid line represents its first brilloun zone.
To evaluate the thermal stability of three conformers of fh-BN, we calculate their cohesive energy, which is defined as $E_{\rm coh}=(xE_{\rm B}+xE_{\rm N}+2xE_{\rm H}-xE_{\rm BNHH})/4x$, where $E_{\rm B}$, $E_{\rm N}$, and $E_{\rm H}$ are the total energies of a single B atom, a single N atom, a single H atom, and one unit cell of the fh-BN, respectively. In our calculations, the cohesive energy values of chair, boat, and stirrup are estimated to be about 5.79 eV/atom,5.81 eV/atom, and 5.83 eV/atom, respectively. The high cohesive energies in three conformers of fh-BN implied strongly bonded network with high stability. By comparison, the stirrup conformer is found to have the highest stability as seen in Fig. 1(c).
The band structure and projected density of states of h-BN and fh-BN are shown in Figs. 2 and 3. Our calculations on h-BN sheet show that it has an indirect band gap of 4.67 eV, which is in agreement with the LDA (4.5 eV)[32] and GGA (4.6 eV)[19, 33] results reported. It is intersting to note that the boat and stirrup conformers have direct band gaps with the same values of 4.95 eV, larger than the value of h-BN. The character of band gap widen is in consistent with graphane.[18] However, chair fh-BN is estimated to have direct band gap of 3.12 eV, which is in consistent with the previous result (3.1 eV) calculated by Bhattacharya \emph{et al.}[19] Due to the density functional theory calculation always underestimates the energy gap,
Fig. 2
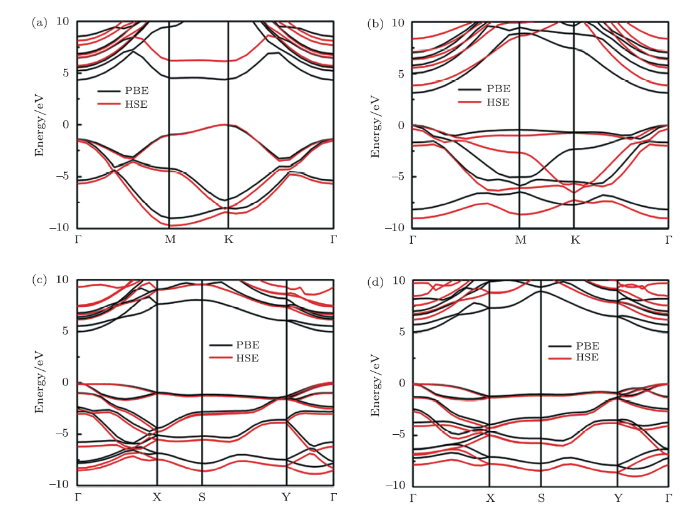New window|Download| PPT slideFig. 2The energy band structures for the conformers of (a) h-BN, (b) chair, (c) boat, (d) stirrup fh-BN.
Fig. 3
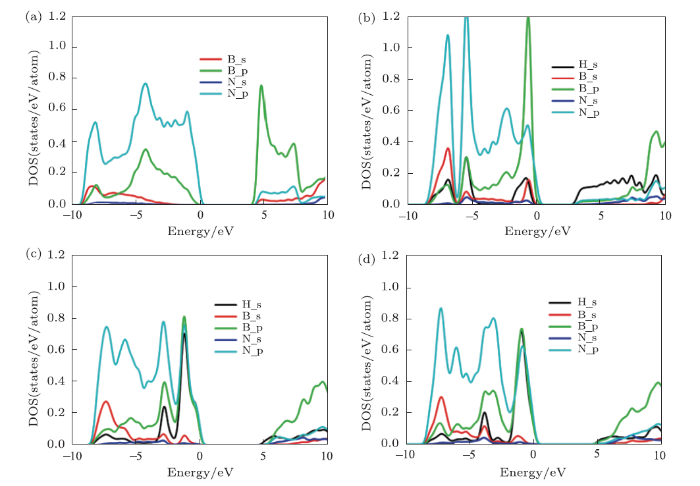New window|Download| PPT slideFig. 3The projected density of states (DOS) for (a) h-BN, (b) chair, (c) boat, (d) stirrup.
we employed a hybrid functional of Heyd-Scuseria-Ernzerhof (HSE06) calculations[34] to calculate the structural electronic structure more accurately. The calculated band gaps of h-BN and fh-BN are 5.69 (h-BN), 3.84 (chair), 6.12 (boat), and 6.18 eV (stirrup), respectively. From the projected density of states, we can see that the mixed existence of the states of N_p, B_p, and H_s around the valence band maximum (VBM) in boat and stirrup conformers but only small contributions of H_s on VBM in chair structure. The formants of partial density of states in three atoms near the Fermi-level implies strong interactions between B-H, N-H, and B-N bond for boat and stirrup conformers of fh-BN, which lead to the results of the band gap widen.
The mechanical properties are investigated by calculating its linear elastic constants. The calculated elastic constants of chair, boat, stirrup fh-BN together with h-BN are listed in Table 1. Due to the symmetry, the hexagonal structures have $C_{11}=C_{22}$ and have the additional relation that $C_{66}=(1/2)(C_{11}-C_{12})$. The four independent elastic constants ($C_{11}, C_{22}, C_{12}, C_{66}$) of h-BN monolayer are calculated to be $C_{11}=C_{22}$=289.4 Nm$^{-1}$, $C_{12}$=65.2 Nm$^{-1}$, and $C_{66}$=112.1 Nm$^{-1}$, respectively, in consistent with previous calculated results.[35-36] The elastic constants in hexagonal chair fh-BN are $C_{11}=C_{22}$=185.7 Nm$^{-1}$, $C_{12}$=25.1 Nm$^{-1}$, and $C_{66}$=80.2 Nm$^{-1}$, respectively. For orthogonal phase, there are also four independent elastic constants $C_{11}$, $C_{22}$, $C_{12}$, and $C_{44}$. The elastic constants in stirrup fh-BN are calculated to be $C_{11}$= 217.2 Nm$^{-1}$, $C_{22}$=91.2 Nm$^{-1}$, $C_{12}$=15.3 Nm$^{-1}$, and $C_{44}$=58.3 Nm$^{-1}$, respectively. For boat fh-BN, the elastic constants are $C_{11}$=198.3 Nm$^{-1}$, $C_{22}$=169.2 Nm$^{-1}$, $C_{12}$=7.8 Nm$^{-1}$, and $C_{44}$=66.5 Nm$^{-1}$, respectively. All the calculated elastic constants meet the necessary mechanical equilibrium conditions[37] for mechanical stability: $C_{11}C_{22}-C^2{12}>0$ and $C_{11}$, $C_{22}$, $C_{44}(C_{66})>0$.
Table 1
Table 1Calculated elastic constants $C_{ij}$(Nm$^{-1}$) of 2D h-BN and fh-BN (chair, boat, and stirrup).
 |
New window|CSV
The in-plane Young's modulus and Poisson ratio along an arbitrary direction $\theta$ ($\theta$ is the angle relative to the positive $x$ direction in the sheet) can be expressed as[38]
where $c$ = cos$\theta$ and $s$ = sin$\theta$. $C_{44}$ is changed to be $C_{66}$ for hexagonal structure above equations. The calculated $E(\theta)$ and $v(\theta)$ of fh-BN are depicted in the polar diagrams in Fig. 4, and that of h-BN is also calculated to be compared. The digrams show that h-BN and chair fh-BN display isotropic mechanical properties, since the shape of orientation-dependent of Young's modulus and Possion's ratio in-plane are all a standard circle. As for boat and stirrup fh-BN, Young's modulus and Poisson ratio exhibit anisotropic due to the $C_{11}$ is not equal to $C_{22}$, which affects its mechanical properties and electronic properties. The anisotropic characteristic originated from the arrangement of the boron, nitrogen, and hydrogen atoms. In addition, we noticed that the values of Young's modulus and Poisson ratio along arbitrary direction are smaller than those for h-BN. The minimum Young's modulus is 90.1 Nm$^{-1}$ for stirrup, which is larger than the value of silicene (62 Nm$^{-1}$).[39] For boat fh-BN, the minumum Young's modulus is 156.6 Nm$^{-1}$, which can comparable with the value of MoS$_2$(129 Nm$^{-1}$).[40]
Fig. 4
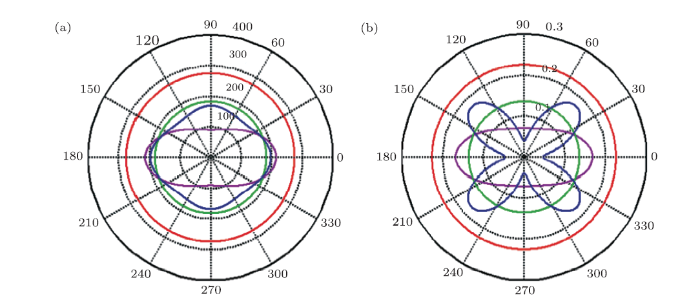New window|Download| PPT slideFig. 4(Color online) Polar diagram for (a) Young's modulus $E$ (N/m) and (b) Poisson's ratio $v$ of h-BN (red solid line), chair fh-BN (green solid line), boat fh-BN (bluesolid line), and stirrup fh-BN (pink solid line).
To estimate the elastic limit of h-BN and fh-BN, we calculated the surface tension (force perunit length)[41] of h-BN and fh-BN using the method described in the references.[42-43] This method of calculating stress-strain relation was originally introduced for three-dimensional crystals. In a 2D layer compounds, the stress calculated from the Hellmann-Feynman theorem was modified to be the surface tension.[41]
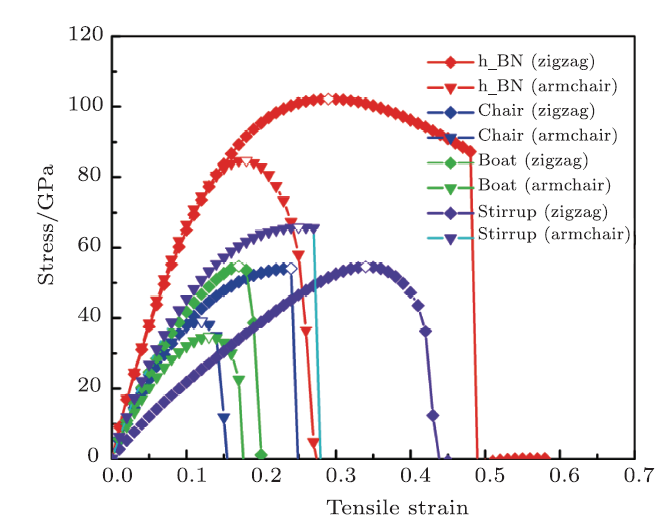
Firstly, the tensile strain is loaded in either the zigzag or armchair direction for $h$-BN and three conformers of fh-BN. As shown in Fig. 5, the maximum stress for uniaxial tension in armchair direction is 84.7 GPa at $\varepsilon=0.18$. h-BN is stronger in zigzag direction with maximum stress of 102.2 GPa at $\varepsilon=0.29$. The calculated peak strength is consistent with the earlier DFT estimation,[35] validating our calculation reliable. For the tension-strain relations of three fh-BN conformers, it shows that fh-BN can sustain a surface tension up to (39.1, 34.6, and 65.8 GPa) for chair, boat, and stirrup conformers in the armchair directions, respectively. The corresponding tensile strain limits are 0.12, 0.13, and 0.25 along the armchair directions, respectively. The maximum stress in zigzag directions are (54.0, 54.7, and 54.5 GPa) for chair, boat, and stirrup, respectively, corresponding the tensile strain at 0.24, 0.17, and 0.34. The predicted elastic strain limit suggests that the chair and boat fh-BN are highly flexible while the stirrup fh-BN can surstain tensile strain stronger than h-BN. One also notices that strain is more easily applied along the armchair direction than the zigzag direction for h-BN and fh-BN.
Fig. 5
New window|Download| PPT slideFig. 5(Color online) Induced tensile stress as a function of applied strain deformation along the zigzag (diamond shape) and armchair (triangle shape) directions for h-BN and fh-BN.
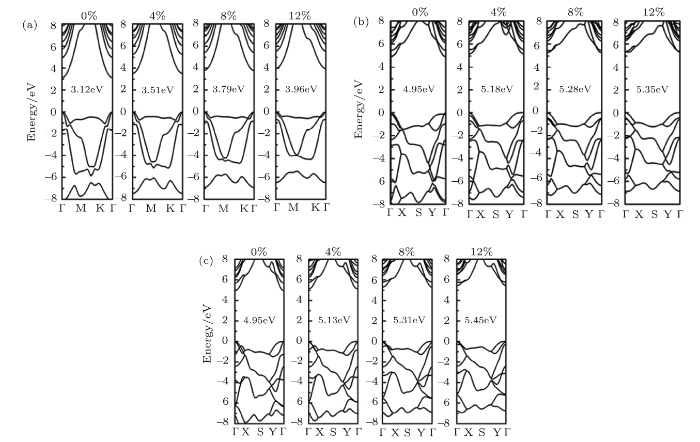
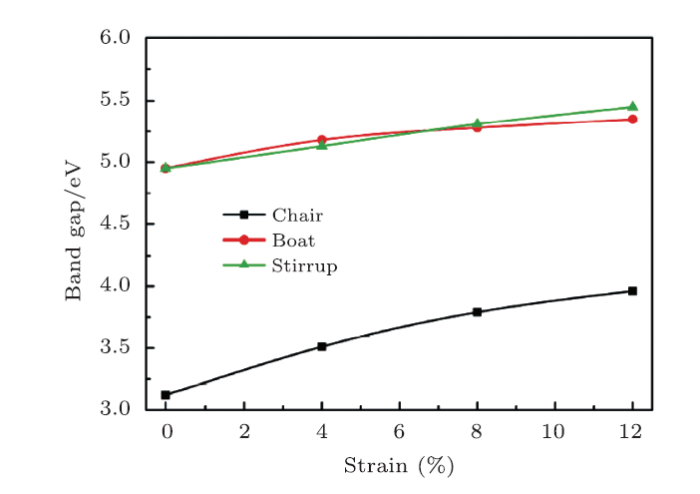
Strain modulation has been commonly used in low-dimensional systems to tune the electronic structures.Then we analyze the biaxial strain effects on the electronic band structures of fh-BN. As shown in Fig. 6, the direct band gap of three conformers was maintained. As seen in Fig. 7, the band gap energies $E_{\rm g}$ in chair and boat conformers increase in the form of parobolic but increase linearly in stirrup by increasing the biaxial tensile strain from 0% to 12%. By fitting to the band gap energies using quadratic and linear functions, we obtained $y=0.111x^2-0.003x+3.120$, $y=0.063x^2-0.003x+4.955$, and $y=0.043x+4.951$ for chair, boat, and stirrup conformers, respectively.
Fig. 6
New window|Download| PPT slideFig. 6(Color online) Band structures of fh-BN with biaxial strains for (a) chair, (b) boat, and (c) stirrup.
Fig. 7
New window|Download| PPT slideFig. 7(Color online) Band gap energies as a function of biaxial-tensile strain of three conformers of fh-BN.
4 Conclusion
In summary, based on first-principles calculations, we investigated the electronic, mechanical properties,stress-strain relations, and biaxial strain effects on the energy band structures for three fully hydrogenated h-BN. The boat and stirrup conformers of fh-BN are electronically different from h-BN sheet, not only showing the band gap is widen to be about 4.95 eV, but also showing an anisotropic elastic mechanical behavior by the Polar diagram of Young's modulus and Poisson's ratio thus exhibiting great potential application in direction-dependent devices. Importantly, the predicted elastic strain limit suggests that the stirrup fh-BN can surstain tensile strain stronger than h-BN and the band gaps in three conformers can be modulated in the condition of biaxial tensile strain. Furthermore, the band gap energies $E_g$ in chair and boat conformers increase in the form of parobolic but increase linearly in stirrup conformer.Reference By original order
By published year
By cited within times
By Impact factor
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 2]
[Cited within: 5]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
