 ,1,?, He-Lin Lu2, Xue-Dong Tian
,1,?, He-Lin Lu2, Xue-Dong Tian ,3,?‡
,3,?‡ Corresponding authors: ?E-mail:lxl7158@163.com‡?E-mail:snowtxd@gxnu.edu.cn
Received:2019-03-4Online:2019-08-1
| Fund supported: |

Abstract
Keywords:
PDF (409KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Li-Hua Zhao, Xian-Li Li, He-Lin Lu, Xue-Dong Tian. Perfect Optical Nonreciprocity with Mechanical Driving in a Three-Mode Optomechanical System *. [J], 2019, 71(8): 1011-1016 doi:10.1088/0253-6102/71/8/1011
1 Introduction
Nonreciprocal optical devices, in which time-reversal symmetry is broken for light propagation, provide several critical applications in quantum signal processing and communication, as they can suppress spurious modes and unwanted signals.[1] For example, they can protect devices from noise emanating from readout electronics in quantum superconducting circuits. The most commonly encountered nonreciprocal devices are isolator sand circulators which allow transmission of signals to exhibit different characteristics if source and observer are interchanged (see Fig. 1(a)). To violate reciprocity and obtain asymmetric transmission, breaking time-reversal symmetry is required in any such device. Traditionally, nonreciprocal transmission has relied on applied magnetic bias fields to break time-reversal symmetry and Lorentz reciprocity.[2-3] But these conventional devices are typically bulky and incompatible with ultra-low loss superconducting circuits.Fig. 1
 New window|Download| PPT slide
New window|Download| PPT slideFig. 1(Color online) (a) Schematic of the nonreciprocal system. (b) Athree-mode optomechanical system with a mechanical mode interactedwith two optical modes. Two strong coupling fields (probe fields) with amplitudes $\varepsilon_{c}$ and$\varepsilon_{d}$ ($\varepsilon_{L}$ and $\varepsilon_{R}$) are used to drivethe cavity modes $c_{1}$ and $c_{2}$ respectively. Meanwhile, the mechanical mode is driven by a weak field with amplitude $\varepsilon_{B}$.
In recent years, the rapidly growing field of cavity optomechanics,[4] where optical fields and mechanical resonators are coupledthrough radiation pressure, has shownpromising potential for applications in quantum informationprocessing and communication.So far, many interesting quantum phenomena have been studied in this field, such as mechanical ground-state cooling,[5-10]optomechanically induced transparency,[11-14] quantum entanglement,[15-22] optomechanical dark state,[23]non-equilibrium dynamics,[24] nonlinear effects,[25-26] and coherent perfect absorption.[27-28] Very recently, it has been realized that optomechanical coupling can lead to nonreciprocal transmission andoptical isolation. In Refs. [29-33], nonreciprocal optical responses are theoretically predicted through optomechanical interactions, and nonreciprocal transmission spectra were recently observed inRefs. [34-40]. In Refs. [41-43], itwas recognized that the mechanically-mediated quantum-state transferbetween two cavity modes can be made nonreciprocal withsuitable optical driving.In Refs. [44-46], nonreciprocal quantum amplificationhas been proposed in an optomechanical system. These schemes are particularly promising becausethey can be integrated on-chip with existing superconductingtechnology.In these references, the well-known nonzero nonreciprocal phase difference is the critical factor to realize nonreciprocal transmission. For example,it needs eight tones to lead to a nonzero nonreciprocal phase difference in Ref. [46]. One question naturally arises: is the well-known nonzero nonreciprocal phase difference a necessary condition to realize nonreciprocal transmission?In addition, in most of these references, perfect optical nonreciprocity can be achieved under the conditions of equal damping rate (mechanical damping rate $\gamma$ is equal to cavity damping rate $\kappa$).
Here, we show a new mechanism to achieve perfect optical nonreciprocity in a three-mode optomechanical system (see Fig. 1(b)), i.e., using the quantum interference of signal transmission between optomechanical interaction and mechanical driving. This setup has been realized in severalrecent experiments,[47-49] and coherent perfect absorption,[27] quantum entanglement[50] and Landau-Zener-Stueckelberg dynamics[51-52] have been theoretically studied in this model. It is worth pointing out that the mechanical drive can be easily realized in experiments through an external electric drive,[53-55] and the system we considered in this paper is similar to the one in Ref. [44], in which the authors detailedly studied how to realize optical amplification through the constructive or destructive interference between different transmission paths. We find that perfect optical nonreciprocity can still be achieved even when the well-known nonreciprocal phase difference is zero if we drive the system by a mechanical driving with a nonzero phase. From the expressions of output fields, we derive essential conditionsto achieve perfect optical nonreciprocity, and find some interesting results. One is that there may exist two sets of couplings which all can make perfect optical nonreciprocity occur. Another interesting result is that the perfect optical nonreciprocity can still occur in the realistic parameter regime ($\gamma\ll\kappa$) in cavity optomechanics. We believe the results of this paper can be used to control optical transmission in modern communicationtechnology.
2 System Model and Equations
The system we consider here is depicted in Fig. 1(b), where a mechanical membrane is placed in the middle of an optical cavity. The operators $c_{1}$ and $c_{2}$ denote geometrically distinct optical modes with same frequency $\omega_{0}$ and decay rates $\kappa_{1}$ and $\kappa_{2}$ respectively. The mechanicalresonator with frequency $\omega_{m}$ and decay rate$\gamma$ is described by operator $b$. Two strong coupling fields (probe fields) with same frequency$\omega_{c}$ ($\omega_{p}$) and amplitudes $\varepsilon_{c}$ and $\varepsilon_{d}$ ($\varepsilon_{L}$ and $\varepsilon_{R}$) are used to drivethe two-cavity system from the left and right fixed mirror respectively.Then the total Hamiltonian in therotating-wave frame of coupling frequency $\omega_{c}$ can be written as($\hbar=1$)Here, $\Delta_{c}=\omega_{0}-\omega_{c}$ ($\delta=\omega_{p}-\omega_{c}$) is the detuning between cavity modes (probe fields)and coupling fields, and $g_{1,2}$ is the single photon couplingconstant between mechanical resonator and optical modes.
The dynamics of the system is described by the quantum Langevin equations for the relevant operators of the mechanical and optical modes
In this paper, we examine the expectation values of the operators arising from weak probe fields, hence we have ignored quantum noise terms $b^{\rm in}$, $c_{1}^{\rm in}$, and $c_{2}^{\rm in}$ in Eq. (2) because the mean values of these noise terms are vanishing. In the absence of probe fields $\varepsilon_{L}$, $\varepsilon_{R}$, $\varepsilon_{B}$ and withthe factorization assumption $\langle bc_{i}\rangle=\langle b\rangle\langle c_{i}\rangle$, we can obtain the steady-state mean values
with
denoting theeffective detunings between cavity modes and coupling fields. The phase difference $\theta$ ($\theta=\theta_{2}-\theta_{1}$) is the well-known nonreciprocal phase difference in cavity-optomechanics. In this paper, we mainly study the optical nonreciprocity when this phase difference $\theta=0$, and withoutloss of generality we set $\theta_{2}=\theta_{1}=0$. In the presenceof the probe fields, we can write each operator as the sum of itsmean value and its small fluctuation, i.e., $b=b_{s}+\delta b$, $c_{1}%=c_{1s}+\delta c_{1}$, $c_{2}=c_{2s}+\delta c_{2}$ to solve Eq. (2) when bothcoupling fields are sufficiently strong. Then keeping only the linear terms offluctuation operators and moving into an interaction picture by introducing $\delta b\rightarrow\delta be^{-i \omega_{m}t}$, $\delta c_{1}\rightarrow \delta c_{1}e^{-i \Delta_{1}t}$,
$\delta c_{2}\rightarrow \delta c_{2}e^{-i \Delta_{2}t}$, and writing $\delta s$ as $s$ ($s=b,c_{1},c_{2}$) for simplicity, we obtain the linearized quantum Langevin equations
with $G_{1}=g_{1}| c_{1s}|$, $G_{2}=g_{2}| c_{2s}|$, and $x=\omega_{b}-\omega_{m}$.Withoutloss of generality we take $G_{i}$ as positive number, and for simplicity we set $\kappa_{1}=\kappa_{2}=\kappa$ in the following.
In this paper, we assume that each strong coupling field drives the cavity mode at the mechanical red sideband ($\Delta_{c}=\omega_{m}$) and $\omega_{m}\gg\{G_{i},\kappa,\gamma\}$. It can be seen from Eq. (3) that the additional detuning $g_{1,2}(b_{s}+b_{s}^{\ast})$ in Eq. (4) will be much less than $\Delta_{c}$ ($\omega_{m}$) as $\omega_{m}\gg G_{i}$. Then, we have the effective detunings $\Delta_{1,2}\approx\Delta_{c}=\omega_{m}$ under which Eq. (5) can be solved by applying rotating wave approximation (neglecting all non-resonant contributions).We set the detuning $\delta$ to match $\delta=\omega_{b}$ (now $x=\delta-\omega_{m}$).Then, Eq. (4) can be simplified to
By assuming $s=s_{+}e^{-i xt}+s_{-}e^{i xt}$ ($s=b,c_{1},c_{2}$), we can solve Eq. (6) as
where $\gamma_{x}=\gamma-2 i x$, $\kappa_{x}=\kappa-2 i x$, and $\delta s_{-}=0$.
To study opticalnonreciprocity, we must study the output optical fields $\varepsilon^{\rm out}%_{L}$ and $\varepsilon^{\rm out}_{R}$, which can be obtained according to theinput-output relation[28,56]
with $\varepsilon_{L/R}^{in}=\varepsilon_{L/R}/\sqrt{\kappa}$. Still following the aforementioned assumption $s=s_{+}e^{-i xt}+s_{-}e^{i xt}$, the output fields can be obtained as
3 Perfect Optical Nonreciprocity
Perfect optical nonreciprocity can be achieved if transmission amplitudes $T_{i\rightarrow j}$ ($i,j=L,R$) satisfyor
It means that the input signal from one side can be completely transmitted tothe other side, but not vice versa. Equations (10) and (11) represent the two different directions of isolation. In this section, we just discuss the case of Eq. (10), as the discussion about Eq. (11) is similar. The subscript $\varepsilon_{R/L}^{in}=0$ indicates that there is not signal injected into the system from right/left side. We omit the subscripts because, in general, nonreciprocity is only related to one-way input, and write transmission amplitudes $T_{i\rightarrow j}$ as $T_{ij}$ for simplicity in the following.
For simplicity, in this paper we set the mechanical driving strength $\varepsilon_{B}=\varepsilon_{L}$ ($\varepsilon_{B}=\varepsilon_{R}$) when the signal is injected into the system from left (right) side. Then, according to Eqs. (7) and (9), the two optical output fields can beobtained as
It can be seen from Eq. (7) that the two output fields in Eq. (12) are equal if the mechanical driving $\varepsilon_{B}=0$ (then without the factor $i\kappa_{x}e^{i \phi}$ in the numerators in Eq. (12)), which indicates the photon transmission is reciprocal.
But if the mechanical driving $\varepsilon_{B}\neq0$, the system will exhibit a nonreciprocal optical response (due to the different numerators in Eq. (12)). It can be clearly seen from the numerators in Eq. (12) that the optical nonreciprocity comes from the different interferences (constructive or destructive interference) between the mechanical driving $\varepsilon_{B}e^{i\phi}$ and the optomechanical interaction $G_{i}$. In other words, in some conditions, the interference between the mechanical driving and the optomechanical interaction $G_{1}$ is constructive, while the interference between the mechanical driving and the optomechanical interaction $G_{2}$ can be destructive. These conditions are what we will study in the following.
We first discuss the case of $\phi={\pi}/{2}$. From Eq. (12), we obtain the conditions to achieve perfect optical nonreciprocity for Eq. (10) as
It can be seen from Eq. (13) that the system can not exhibit perfect optical nonreciprocity when $\gamma>2\kappa$, but there may exist two sets of couplings ($G_{\pm}$, $G_{2}$), which can make the perfect optical nonreciprocity occur when $\kappa<\gamma\leq2\kappa$, and there is only one coupling ($G_{+}$) to make the perfect optical nonreciprocity occur when $\gamma\leq\kappa$.It is surprising that there is not low bound on mechanical decay rate $\gamma$ in $G_{+}$ in Eq. (13). In other words, perfect optical nonreciprocity can still occur even in the case of $\gamma/\kappa\rightarrow0$ as long as the conditions in Eq. (13) are satisfied. This is important because, in general, mechanical decay rate $\gamma$ is much less than cavity decay rate $\kappa$ in cavity optomechanics.
In Figs. 2(a)-2(d), we plot transmission amplitudes $T_{LR}$ (red line) and $T_{RL}$ (black line) vs. normalized detuning $x/\kappa$ with coupling strengths $G_{1}=G_{+}$ and $G_{2}={\kappa}/{2}$ according to Eq. (13) for different mechanical decay rate $\gamma/\kappa=2$, $1$, $1/2$, $1/100$ respectively. It can be clearly seen from Figs. 2(a)-2(d) that perfect optical nonreciprocity occurs at the resonant frequency $(x=0)$ and the transmission spectra $T_{LR}$ (red line) and $T_{RL}$ (black line) take a symmetric form with respect to detuning $x$. When the mechanical decay rate becomes smaller, the transmission amplitudes $T_{RL}$ will be larger than $T_{LR}$ outside the vicinity of resonance frequency ($x=0$)(see Figs. 2(a)-2(d)). Even though the mechanical decay rate is small, perfect optical nonreciprocity can still occur, such as $\gamma/\kappa=1/100$ (see Fig. 2(d)). In addition, due to the mechanical driving besides the signal injected to system from cavity mode, the transmission spectra $T_{LR}$ and $T_{RL}$ will become gain (larger than 1) with smaller mechanical decay rate, such as $\gamma/\kappa=1/2$, $1/100$ (see Figs. 2(c)-2(d)).
Fig. 2
 New window|Download| PPT slide
New window|Download| PPT slideFig. 2(Color online) Transmission amplitudes $T_{LR}$ (red line) and $T_{RL}$ (black line) are plotted vs. normalized detuning $x/\kappa$ for different mechanical decay rate. (a) $\gamma/\kappa=2$, (b) $\gamma/\kappa=1$, (c) $\gamma/\kappa=1/2$, and (d) $\gamma/\kappa=1/100$. The coupling strengths $G_{1}=G_{+}$ and $G_{2}={\kappa}/{2}$ according to Eq. (13).
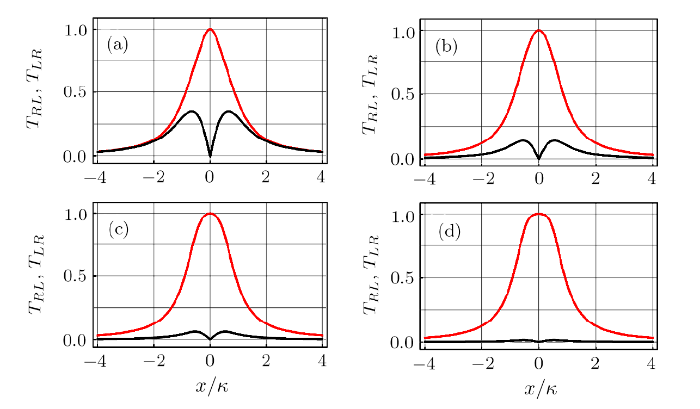
As mentioned above, there are two sets of coupling strengths $G_{1}=G_{\pm}$ which can make perfect optical nonreciprocity occur when $\kappa<\gamma\leq2\kappa$. In Figs. 3(a)-3(d), we plot transmission amplitudes $T_{LR}$ (red line) and $T_{RL}$ (black line) vs. normalized detuning $x/\kappa$ with coupling strengths $G_{1}=G_{-}$ and $G_{2}={\kappa}/{2}$ according to Eq. (13) for different mechanical decay rate $\gamma/\kappa=2$, $1.5$, $1.2$, $1.05$ respectively. Here, the transmission spectra $T_{LR}$ (red line) and $T_{RL}$ (black line) remain the same symmetric form as the case in Fig. 2. It can also be seen from Figs. 3(a)-3(d) that there are no transmission gain in spectra $T_{LR}$ (red line) and $T_{RL}$ (black line) with coupling $G_{1}=G_{-}$ when $\kappa<\gamma\leq2\kappa$. In this case, the amplitude $T_{LR}$ (red line) is always larger than $T_{RL}$ (black line) (see Figs. 3(a)-3(d)). The transmission amplitude $T_{RL}$ will tend to zero as $\gamma/\kappa\rightarrow1$, such as $\gamma/\kappa=1.05$(see black line in Fig. 3(d)). Meanwhile, the bandwidth of $T_{LR}$ (red line) almost remain unchanged with the change of $\gamma$ ($\kappa<\gamma\leq2\kappa$) (see red line in Figs. 3(a)-3(d)).
Fig. 3
 New window|Download| PPT slide
New window|Download| PPT slideFig. 3(Color online) Transmission amplitudes $T_{LR}$ (red line) and $T_{RL}$ (black line) are plotted vs.\ normalized detuning $x/\kappa$ for different mechanical decay rate. (a) $\gamma/\kappa=2$, (b) $\gamma/\kappa=1.5$, (c) $\gamma/\kappa=1.2$, and (d) $\gamma/\kappa=1.05$. The coupling strengths $G_{1}=G_{-}$ and $G_{2}={\kappa}/{2}$ according to Eq. (13).
Now we discuss the general case of mechanical driving phase ($\phi\neq{\pi}/{2}$). For simplicity, we choose equal decay rate ($\kappa=\gamma$) in the following. From Eq. (12), we can obtain the conditions to achieve the perfect optical nonreciprocity for the directions of isolation Eq. (10) and Eq. (11) respectively as
where $\phi\in(0,\pi)$ meets isolation Eq. (10), and $\phi\in(\pi,2\pi)$ meets isolation Eq. (11).It can be seen from Eqs. (14) and (15) that we can easily change the direction of isolation by exchanging the coupling strengths $G_{1}$ and $G_{2}$ and meanwhile adjusting the mechanical driving phase from $\phi$ to $-\phi$.
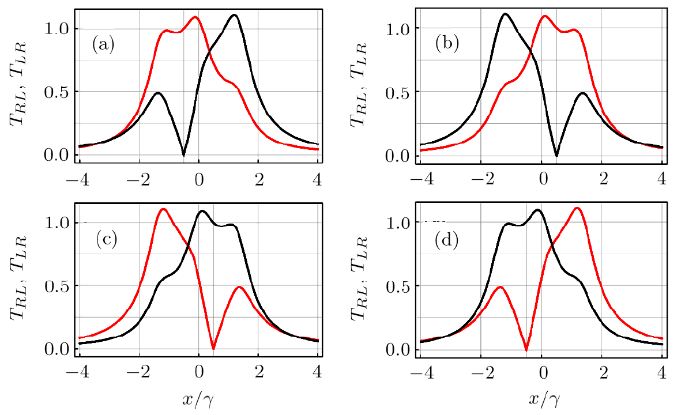
In Figs. 4(a)-4(d), we plot the transmission amplitudes $T_{LR}$ (red line) and $T_{RL}$ (black line) vs. normalized detuning $x/\gamma$ with coupling strength $G_{i}$ according to Eq. (14)(in Figs. 4(a) and 4(b)) and Eq. (15) (in Figs. 4(c) and 4(d)) for differentmechanical driving phase $\phi={\pi}/{4}$, ${3\pi}/{4}$, $-{\pi}/{4}$,$-{3\pi}/{4}$, respectively.It can be seen from Fig. 4 that perfect optical nonreciprocity can indeed occur with the conditions according to Eqs. (14) and (15). Now the transmission spectrums $T_{LR}$ (red line) and $T_{RL}$ (black line) will not take the symmetric form anymore because now perfect optical nonreciprocity occurs at the detuning $(x=\pm{\gamma}/{2})$ according to Eqs. (14) and (15). In addition, the transmission spectrum $T_{LR}$ ($T_{RL}$) for mechanical driving phase $\phi=\phi'$ is symmetric with that for $\phi={\pi}/{2}+\phi'$ with respect to detuning $x=0$, such as $\phi'={\pi}/{4}$(see Figs. 4(a) and 4(b)).
Fig. 4
 New window|Download| PPT slide
New window|Download| PPT slideFig. 4(Color online) Transmission amplitudes $T_{LR}$ (red line) and $T_{RL}$ (black line) are plotted vs.\ normalized detuning $x/\gamma$ for differentmechanical driving phase and couplings $G_{i}$: (a) $\phi={\pi}/{4}$, $G_{1}=\gamma\sqrt[3]{\csc\phi}$, and $G_{2}={\gamma\csc\phi}/{2}$ according to Eq. (14), (b) $\phi={3\pi}/{4}$,$G_{1}=\gamma\sqrt[3]{\csc\phi}$, and $G_{2}={\gamma\csc\phi}/{2}$ according to Eq. (14), (c) $\phi=-{\pi}/{4}$, $G_{1}=-{\gamma\csc\phi}/{2}$, and $G_{2}=-\gamma\sqrt[3]{\csc\phi}$ according to Eq. (15), (d) $\phi=-{3\pi}/{4}$, $G_{1}=-{\gamma\csc\phi}/{2}$, and $G_{2}=-\gamma\sqrt[3]{\csc\phi}$ according to Eq. (15). The other parameter: $\kappa=\gamma$.
4 Conclusion
In summary, we have theoretically studied how to achieve perfect optical nonreciprocity based on mechanical driving in a three-modeoptomechanical system. We obtain the important conditions where the system can exhibit perfect optical nonreciprocity. From the expressions of conditions, we can draw three important conclusions: (i) Perfect optical nonreciprocity can still occur even when nonreciprocal phase difference $\theta=0$ as only as the mechanical driving phase $\phi\neq0$. (ii) There may exist two sets of couplings ($G_{1}, G_{2}$), which all can make perfect optical nonreciprocity occur, and the system can still exhibit perfect optical nonreciprocity even though $\gamma\ll\kappa$. (iii) The direction of isolation can be easily changed by exchanging the coupling strengths $G_{1}$ and $G_{2}$ according to Eqs. (14) and (15), and meanwhile adjusting the mechanical driving phase from $\phi$ to $-\phi$. Our results can also be applied to other parametrically coupled three-mode bosonic systems, besides optomechanical systems.Reference By original order
By published year
By cited within times
By Impact factor
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 2]
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 2]
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
