摘要:基于WBM相场模型对热力学条件和辐照条件下Fe-Cr合金晶界处Cr元素偏析行为进行了模拟. 模拟结果表明温度对Fe-Cr合金晶界处Cr元素的偏析有很大影响: 当温度低于500 ℃时, 晶界处的偏析量很小; 而当温度高于500 ℃时晶界处的偏析量增加明显. 基体中Cr元素含量对晶界Cr元素的相对偏析量也有显著影响: 随着基体中Cr元素含量的增加, 相同模拟条件下晶界处Cr元素的相对浓度增量降低. 辐照条件下, 晶界处Cr元素的相对偏析量比热力学条件下的相对偏析量有明显增加; 随着辐照剂量率的提高, 晶界中心处Cr元素浓度增量变大; 相同辐照条件下, 随着Cr元素含量的增加, 晶界处Cr元素的相对浓度增量也降低.
关键词: 相场模拟/
Fe-Cr合金/
晶界偏析/
辐照加速扩散

English Abstract

全文HTML

--> --> -->

铁素体/马氏体(F/M)钢由于具有优于奥氏体钢的抗辐照肿胀和抗蠕变断裂等综合性能, 是一种非常有应用前景的先进核能系统候选材料^[1-3], 例如钠冷快堆的燃料包壳材料、四代堆的压力容器材料和聚变堆的结构材料等^[4]. F/M钢主要是Fe-Cr系的合金, 其中Cr的原子百分比大约为7%—15%. 研究表明, 晶界是析出相形核长大的有利位置^[5], 而F/M钢在晶界处常常会发现Cr元素的辐照诱导偏析(RIS): 晶界处Cr的富集会增加沉淀, 从而导致材料的脆化; 而晶界处Cr的耗尽可能会极大地弱化晶界的耐腐蚀性^[6]. 实际上, 在热力学条件下, Fe-Cr合金中也会发生晶界处Cr元素的偏析, 然而辐照会极大地加速这一过程. Warry和Was^[7]的实验结果表明: Cr的辐照诱导偏析具有温度依赖性, 在300—600 ℃之间观察到了Cr的富集, 而在400—500 ℃的辐射温度下观察到Cr元素的最大偏析量. 因此, 开展热力学条件和辐照条件下, Fe-Cr合金晶界处Cr元素偏析行为的研究对揭示F/M钢的服役组织演化和性能退化的机理具有十分重要的科学意义.
数值模拟为研究材料的晶界偏析行为提供了一个重要的工具^[8-12]. 辐照诱导偏析的早期数值模型建立在基于耦合速率方程的基础上, 该方程依赖于过多的简化假设, 尤其是在合金化效应处理方面, 忽略了溶剂与局部成分的依赖性^[8]. Terentyev等^[9]利用蒙特卡罗模拟探究了Fe-Cr合金在倾斜晶界处Cr元素的偏析. 虽然该模型可以解决上述简化假设, 但是蒙特卡罗模拟以概率统计理论为基础, 需要进行大量重复的实验, 计算量巨大^[10], 而且还要考虑缺陷类型并精确追踪晶界位置, 从而降低了计算效率. 最近, Was等^[11]提出原子尺度模型对辐照条件下Cr的偏析行为随温度的变化进行研究, 得到了与上述实验结果相同的温度依赖性. Xia等^[12]利用速率理论对Fe-Cr合金中Cr的辐照诱导偏析进行了模拟, 考虑了缺陷和空洞之间的相互作用并引入了晶界结构的影响, 模拟得到了F/M钢中RIS的温度依赖性, 但该方法缺少热力学基础. 相场模拟方法可以同时考虑动力学与热力学两方面因素, 将对元素扩散和再分配的准确描述与较低的计算资源结合起来.
国内外****利用介观尺度的相场方法对晶界析出^[5,13]和界面偏析行为^[14-18]开展了一些研究工作. 相场法是基于20世纪50年代的Ginzburg-Landau理论发展而来的, 其思想是在非均匀性体系中引入扩散界面和相场变量, 通过相场变量的变化来表征体系中组织的演化. 晶界处合金元素偏析的相场模型主要包括Wheeler等^[14]提出的WBM模型和Kim等^[15]提出的KKS模型. 在WBM模型中, 假设两相在界面处具有相等的浓度, 在给定点处基体相和晶界相的溶质浓度是相同的; 而在KKS模型中, 假设两相具有不同的浓度, 这些浓度受到相等的扩散势的约束, 晶界处的溶质浓度由相浓度之间的混合规则给出. 但自由能密度在两种方法中均由局部相自由能密度之间的混合规则给出^[16]. 最近, Badillo等^[17]提出了一维的描述辐照诱导偏析的相场模型. 然而该模型不涉及具体的材料热力学参数, 并且缺少实验结果的验证. Piochaud等^[18]利用蒙特卡罗模拟计算出相场模型所需参数, 使相场模型参数精确化, 并将结果与动力学蒙特卡罗模拟结果进行对比, 在Cr富集对应的温度范围内得到了较好的一致性, 但缺少实验结果的验证. 因此, 关于Fe-Cr合金中Cr元素辐照诱导偏析行为的研究与预测的相场模型目前并不成熟.
本文基于相场模型(WBM模型), 分析了热力学条件下不同组成的Fe-Cr合金晶界Cr元素偏析的影响因素. 然后, 通过引入辐照加速扩散模型对热力学条件下的晶界偏析相场模型进行了修正, 进一步研究了Cr元素含量、辐照剂量率和温度对晶界处Cr元素偏析程度的影响.

2

-->

2.1.相场变量

图1所示为相场变量及其取值的示意图, 引入了两个相场变量?和x来建立相场模型. 取向场变量?用来区分Fe-Cr合金中不同取向的晶粒, 而浓度场变量x表示Cr元素在整个模拟系统中的分布. 其中, ?为非保守型相场变量, x为保守型相场变量. ?在晶粒α内的取值为0, 在晶粒β内的取值为1, 而在晶界处, ?的取值从0连续变为1. x的取值由Cr的含量决定, 初始设置为在整个模拟系统中均匀分布.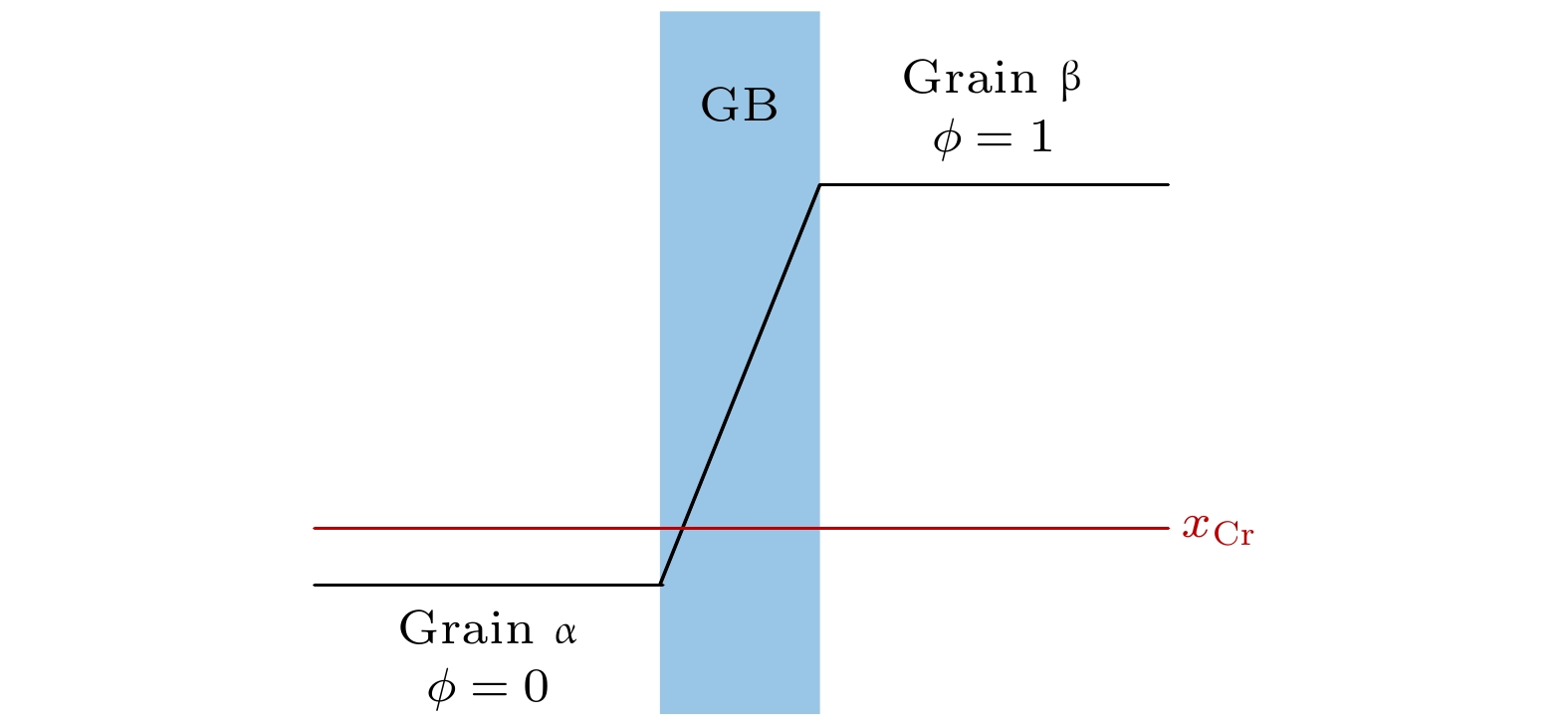
图 1 相场变量?和x的初始分布
Figure1. Initial distribution of phase field variable ? and x.

2 -->

2.2.自由能密度函数的构造

Fe-Cr合金体系的总自由能表达式为^[19]

$ G=\int_{\varOmega} \left[ {\frac{1}{{{V_{\rm{m}}}}}{G_{\rm{m}}}(\phi ,x) + \frac{1}{2}{\varepsilon ^2}{{\left| {\nabla \phi } \right|}^2}} \right] \cdot {\rm{d}}V,$

式中, $ {G}_{{\rm{m}}} $是摩尔吉布斯自由能, x是溶质Cr原子的摩尔分数, $ {V}_{{\rm{m}}} $是系统的摩尔体积, $ {\varepsilon }^{2} $是能量梯度系数, ?是相场变量.
采用的摩尔吉布斯自由能的表达式为^[19]

${G}_{{\rm{m}}}(\phi,x)={G}_{{\rm{m}}}+W\left(x\right)\cdot g\left(\phi \right),$

式中, $ g\left(\phi \right)={\phi }^{2}{(1-\phi )}^{2} $为在晶界区域引入的双阱势函数, W(x)为该双阱势函数的高度. 根据Gr?nhagen和?gren^[19]对晶界偏析的假设, 在W(x)中引入了线性浓度依赖性, 表达式为$W\left(x\right)= $$ w(1-mx)$^[20], 其中w和m均为正数, 系数m描述了溶质与界面之间的相互作用, 可以通过溶质与界面之间的相互作用得出^[20].
每个晶粒的摩尔吉布斯自由能表达式利用正则溶体模型表示为^[20]

$\begin{split} {G}_{{\rm{m}}}=\;&{x}_{\rm{Fe}}{G}_{\rm{Fe}}^{0}+{x}_{\rm{Cr}}{G}_{\rm{Cr}}^{0} +RT[{x}_{\rm{Fe}}{\rm{l}}{\rm{n}}{x}_{\rm{Fe}}\\ &+{x}_{\rm{Cr}}{\rm{l}}{\rm{n}}{x}_{\rm{Cr}}]+\varOmega {x}_{\rm{Fe}}{x}_{\rm{Cr}} , \end{split}$

式中, $ {G}_{\rm{Fe}}^{0} $和$ {G}_{\rm{Cr}}^{0} $为标准状态下纯铁与纯铬的摩尔吉布斯自由能, $ {x}_{\rm{Fe}} $与$ {x}_{\rm{Cr}} $为系统中铁与铬的摩尔分数, R为通用气体常数, T为系统的温度, $ \varOmega {x}_{\rm{Fe}}{x}_{\rm{Cr}} $代表的是混合吉布斯自由能.
2 -->

2.3.热力学条件下相场方程的演化

非保守型相场变量?演化动力学方程为Allen-Cahn方程^[21]:

$\frac{{\partial \phi }}{{\partial t}} = - {M_{\phi} }\frac{{\delta G}}{{\delta \phi }} = {M_{\phi} }\left( {{\varepsilon ^2}{\nabla ^2}\phi - \frac{1}{{{V_{\rm{m}}}}}\frac{{\partial {G_{\rm{m}}}}}{{\partial \phi }}} \right),$

式中, $ {M}_{\phi } $是与界面迁移率$ {M}_{\rm{int}} $相关的参数, 表达式为

${M}_{\phi }=\frac{\sigma }{{\varepsilon }^{2}}{M}_{\rm{int}},$

σ为界面能, ${M}_{\rm{int}}=2.7\times {10}^{-6} {\rm{exp}}\left(\dfrac{-145000}{RT}\right)$^[20].
保守型变量x的演化动力学方程为Cahn-Hilliard方程^[22]:

$\frac{{\partial x}}{{\partial t}} = \nabla \cdot \left( {{M_x}\nabla \frac{{\delta G}}{{\delta x}}} \right) = \nabla \cdot \left( {\frac{{{M_x}}}{{{V_m}}}\nabla \frac{{\partial {G_{\rm{m}}}}}{{\partial x}}} \right),$

式中, $ {M}_{x} $是与扩散系数相关的参数, ${M}_{x}=x(1- $$ x){V}_{{\rm{m}}}M$, 扩散系数与M之间的关系为$ D=MRT $.
基于快速傅里叶谱方法(FFT), 通过编写Matlab程序, 对方程(4)和方程(6)进行联立求解, 得到了相场变量随时间的演化过程, 研究热力学条件下Fe-Cr合金晶界Cr元素偏析行为. 模型中采用了周期性边界条件.
2 -->

2.4.辐照条件下的模型参数

辐照会在材料中产生大量的空位, 而空位会极大地加速扩散过程, 提高扩散系数. 本工作中, 辐照条件下Fe-Cr合金中空位的浓度以及扩散系数的计算参考了Odette等^[23]开发的辐照加速扩散模型. 辐照条件下的原子扩散系数表达式修正为^[24]

${D}^{*}={D}_{\rm{v}}{X}_{{\rm{V}}}^{\rm{r}}\frac{{D}_{\rm{Cr}}}{{D}_{\rm{Fe}}}+{D}_{\rm{Cr}},$

式中, $ {D}_{\rm{Cr}} $为溶质原子Cr的自扩散系数, $ {D}_{\rm{Fe}} $为溶剂原子Fe的自扩散系数, $ {D}_{\rm{Cr}} $和$ {D}_{\rm{Fe}} $都可以从DICTRA数据库中获得^[25]. ${X}_{\rm V}^{\rm{r}}$为在辐照条件下系统的非平衡空位浓度.
辐照条件下非平衡空位浓度${X}_{\rm V}^{\rm{r}}$的表达式为^[26]

${X}_{\rm V}^{\rm{r}}=\frac{{g}_{\rm{s}}{\phi }_{{\rm{d}}{\rm{p}}{\rm{a}}}}{{D}_{\rm{v}}{S}_{t}} ,$

式中, $ {\phi }_{{\rm{d}}{\rm{p}}{\rm{a}}} $代表的是辐照剂量率, $ {D}_{\rm{v}} $代表的是空位扩散系数, 可近似表示为$ {D}_{\rm{v}}={10}^{-4}{\rm{exp}}[-{E}_{{\rm{m}}}/(kT\left)\right] $, $ {E}_{{\rm{m}}} $代表空位的迁移能量^[24], $ {S}_{\rm{t}} $代表总的沉淀强度, 包括位错($ {S}_{{\rm{d}}} $)和空位簇($ {S}_{\rm{c}} $)的贡献. $ {S}_{{\rm{d}}} $通过位错密度进行表征, $ {S}_{\rm{c}} $的表达式为$ {S}_{\rm{c}}=4{\text{π}}{r}_{\rm{c}}{\phi }_{{\rm{d}}{\rm{p}}{\rm{a}}}{\tau }_{\rm{c}}/{V}_{{\rm{a}}} $^[23], 式中, $ {r}_{\rm{c}} $为空位簇的重组半径, $ {\tau }_{\rm{c}} $为空位簇产生的退火时间, $ {V}_{{\rm{a}}} $为原子体积. 空位簇的空间饱和度可能在高辐照剂量率下发生^[27], 因此高辐照条件下, $ {S}_{\rm{c}} $可用空位簇的饱和吸收强度($ {S}_{{\rm{s}}{\rm{a}}{\rm{t}}} $)为3 × 10¹⁵. $ {g}_{\rm{s}} $为空缺产生率, 可由RED模型中的两个速率方程在稳态条件下求解得到, 表达式为^[23]

$1-\frac{{R}_{\rm{r}}\zeta {\phi }_{{\rm{d}}{\rm{p}}{\rm{a}}}{{g}_{\rm{s}}}^{2}}{{D}_{\rm{i}}{D}_{\rm{v}}{{S}_{\rm{t}}}^{2}}-{g}_{\rm{s}}-\frac{\xi {\phi }_{{\rm{d}}{\rm{p}}{\rm{a}}}{{R}_{\rm{t}}}^{2}{X}_{\rm{t}}{\tau }_{\rm{t}}{{g}_{\rm{s}}}^{2}}{{{S}_{\rm{t}}}^{2}(1+{g}_{\rm{s}}\xi {\phi }_{{\rm{d}}{\rm{p}}{\rm{a}}}{R}_{\rm{t}}{\tau }_{\rm{t}}/{S}_{\rm{t}})}=0 ,$

式中, $ {D}_{\rm{i}} $代表间隙原子的扩散系数, $ {X}_{\rm{t}} $代表系统中Cr的原子浓度, $ {R}_{\rm{r}} $代表基体的复合半径, $ {R}_{\rm{t}} $代表的是陷阱的复合半径, ξ为级联效率. $ {\tau }_{\rm{t}} $为捕获空位的退火时间, 表达式为$ {\tau }_{\rm{t}}={d}^{2}/{D}_{\rm{v}}{\rm{e}}^{[-{H}_{\rm{b}}/(kT\left)\right]} $, $ {H}_{\rm{b}} $为捕获空位的结合能, d为体心立方结构(BCC)的Fe-Cr晶格中的最近邻距离, k为玻尔兹曼常数.
将(9)式中得到的空缺产生率$ {g}_{\rm{s}} $以及不同的辐照剂量率代入(8)式求得辐照条件下的非平衡空位浓度$ {X}_{V}^{\rm{r}} $, 再代入(7)式中得到辐照条件下的原子扩散系数替代热力学条件下相场模型中Cr原子的自扩散系数. 将方程(4)和方程(6)进行联立求解, 得到辐照条件下相场变量随时间的演化, 获得辐照条件下Fe-Cr合金中晶界处Cr元素的偏析行为.
2 -->

2.5.模拟参数的确定

本文利用相场模型对热力学条件下和辐照条件下的Fe-Cr合金的晶界偏析情况进行数值模拟, 模拟当中用到的Fe-Cr合金的物理参数如表1所列. Fe-Cr合金相场模型中的吉布斯能量表达式中的溶质元素Cr和溶剂元素Fe在标态下的摩尔吉布斯自由能、混合摩尔吉布斯自由能系数以及溶质元素Cr的自扩散系数可从Thermo-Calc数据库中获得.

物理参数	数值	参考文献
$ {\varepsilon }^{2} $/(J·m–1)	$ 4\times {10}^{-10} $	[20]
$ {V}_{{\rm{m}}} $/(m3·mol–1)	$ 7.0\times {10}^{-6} $	[20]
w/(J·m-1)	$ 3\times {10}^{4} $	[20]
m	4.5	[28, 29]
σ/(J·m–2)	0.3	[30]
R/(J·mol-1·k–1)	8.314

表1Fe-Cr合金的物理参数
Table1.Physical parameters of Fe-Cr alloys.

为了进一步研究辐照条件下Fe-Cr合金的晶界偏析规律, 应用Odette等^[23]开发的辐射增强扩散模型对辐照条件下的原子扩散系数进行修正. 需要的参数如表2所列.

物理参数	数值	参考文献
d/m	$ 2.49\times {10}^{-10} $
k/(J·K–1)	$ 1.38\times {10}^{-23} $
$ {r}_{\rm{c}}/{\rm{m}} $	$ 3\times {10}^{-10} $	[26]
ξ	0.33	[31]
$ {V}_{{\rm{a}}} $/m3	$ 1.18\times {10}^{-29} $
$ {E}_{{\rm{m}}} $/eV	1.1	[32]
$ {S}_{{\rm{d}}} $/m–2	$ 1.0\times {10}^{-13} $
$ {R}_{\rm{r}} $/m	$ 5.7\times {10}^{-10} $	[23]
$ {R}_{\rm{t}} $/m	$ 5.7\times {10}^{-10} $	[23]
$ {H}_{\rm{b}} $/eV	0.094	[33]
$ {S}_{{\rm{s}}{\rm{a}}{\rm{t}}} $/m–2	$ 3.0\times {10}^{-15} $

表2Fe-Cr合金辐照加速扩散模型的参数
Table2.Parameters of radiation enhanced diffusion model of Fe-Cr alloys.

为了便于计算机进行数值模拟, 需要对相场方程中的变量和常数进行无量纲化处理. 长度单位的无量纲处理为$\tilde {z}=z/h$; 本文选取的标准长度为$ h=2\times {10}^{-10}\;{\rm{m}} $. 模拟中选取实际时间间隔为$ \Delta t= $$ 0.0001\;{\rm{s}} $, 模拟时间的无量纲处理为$ \widetilde {\Delta t}=\Delta t\cdot D/{h}^{2} $, 其中$ D=MRT $被选作参考扩散率. 同时, 控制方程中的参数也以无量纲的形式得出${\widetilde {G}}_{{\rm{m}}}= $$ {G}_{{\rm{m}}}/\left(RT\right)$, $ {\widetilde {M}}_{\phi }={M}_{\phi }RT{h}^{2}/\left({V}_{{\rm{m}}}D\right) $, ${\tilde {\varepsilon }}^{2}={\varepsilon }^{2}{V}_{{\rm{m}}}/\left(RT{h}^{2}\right)$, $\widetilde {M}= $$ MRT/D$.
Fe-Cr合金晶界偏析的实验结果^[7]表明, 晶界Cr元素的偏析通常发生于原奥氏体晶界处, 而且原奥氏体晶界宽度为20 nm左右. 由于相场方程中的梯度项系数的取值与晶界宽度密切相关^[34], 本文通过选取合适的梯度项系数, 将界面宽度也设置为20 nm (对应100个空间离散格点); 整个模拟区域为420 nm (对应2100个空间离散格点).

2

-->

3.1.热力学条件下的晶界偏析

利用相场模型, 对Fe-Cr合金的热力学条件下的偏析进行了一维模拟, 分别研究了不同组成的Fe-Cr合金的浓度分布曲线以及温度对Fe-Cr合金热力学条件下的偏析的影响.
3 -->

3.1.1.不同Fe-Cr合金中晶界Cr元素的偏析

图2分别为Fe-9Cr (含Cr 9%), Fe-10Cr (含Cr 10%), Fe-12Cr (含Cr 12%), Fe-15Cr (含Cr 15%)四种合金在500 ℃温度下晶界附近的浓度分布图(浓度用质量分数表示). 本文中所有浓度场分布图的横坐标代表距离晶界中心的距离, 横坐标为0时代表晶界的中心; 纵坐标代表Fe-Cr合金中溶质元素Cr的浓度. 图2中五种颜色的曲线分别代表时间为20—100 s的浓度分布曲线. 可以看出, 浓度分布图以晶界中心呈现两边对称. 在演变过程中, 晶界的位置不随时间的进行而发生变化, 这是由于本文选用的是平直界面, 没有晶界移动的驱动力^[35]. 在晶粒α和晶粒β中, Fe-Cr合金中Cr元素的浓度保持在初始状态不变; 而在晶界处, Cr随着时间的增加向晶界处发生富集, 在晶界中心处达到最大偏析量. 随着时间的进行, 溶质元素Cr的最大偏析量也随之增加.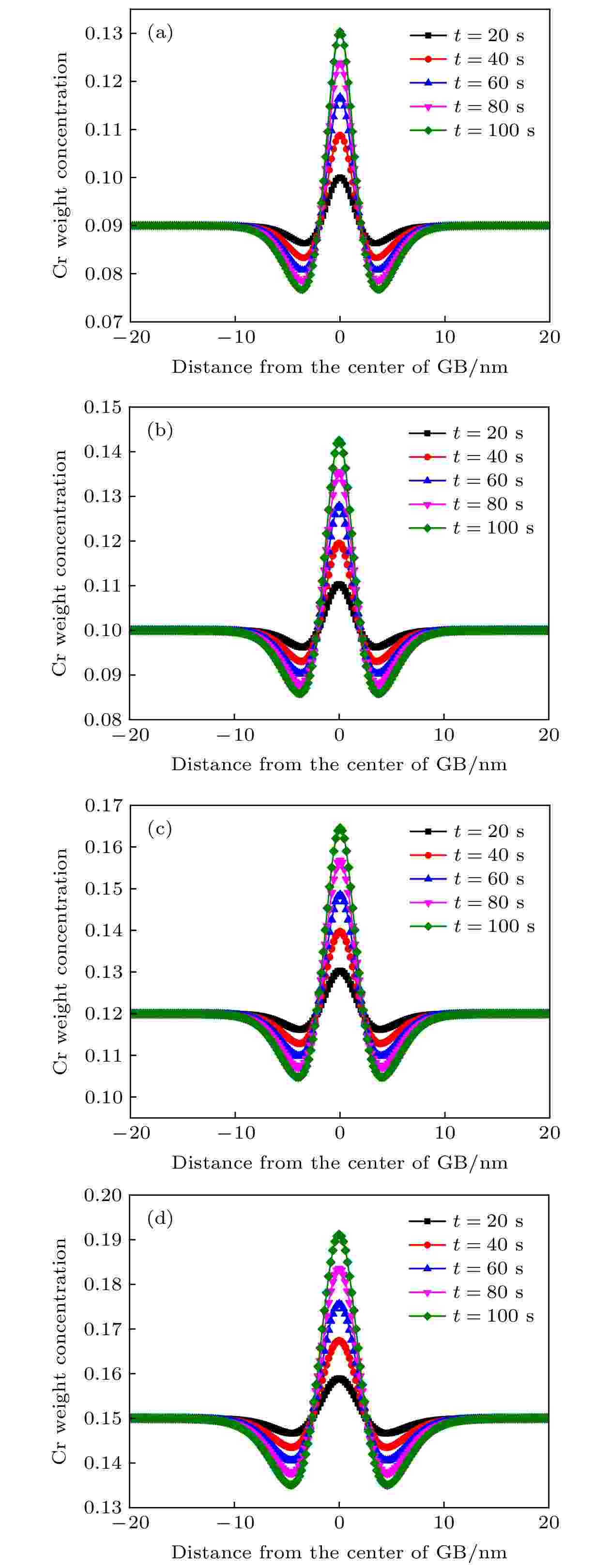
图 2 Fe-Cr合金中晶界处Cr元素浓度的变化曲线　(a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15Cr
Figure2. Evolution of Cr concentration at grain boundary in Fe-Cr alloys: (a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15Cr.

图3(a)为500 ℃时不同组成的Fe-Cr合金在相同时间之后晶界附近的浓度分布图. 可以看出, 随着Cr含量的增加, 浓度演变曲线的峰值也随之增加, 即晶界中心处的最大偏析量随之增大, 这与贾丽霞等^[36]得到的模拟结果一致. 图3(b)为500 ℃时不同组成的Fe-Cr合金在相同时间之后变量?的演变曲线, ?的值从0变化到1的区间即为晶界区域. 可以看出, 随着Cr含量的增多晶界的位置没有发生变化, 但晶界的宽度随着Cr浓度的增加而增加, 合金Fe-15Cr的晶界宽度最大, 说明溶质元素的浓度是影响晶界宽度的因素.
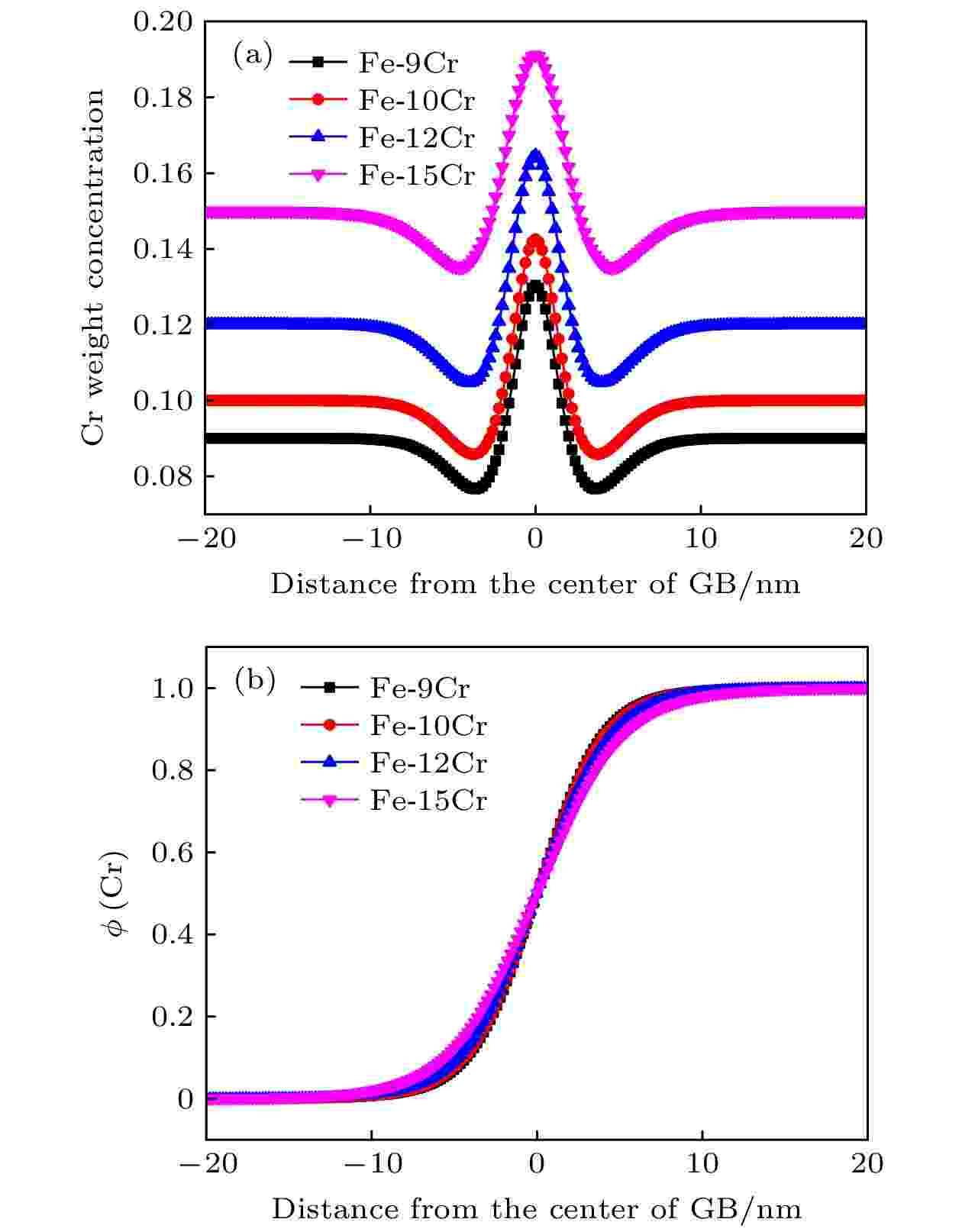图 3 500 ℃模拟100 s后不同成分的Fe-Cr合金的相场变量　(a) x; (b) ?
Figure3. The curves of the phase field variables of Fe-Cr alloys with different compositions after 100 s at 500 ℃: (a) x; (b) ?.

图4为500 ℃时不同组成的Fe-Cr合金在100 s之后晶界中心处的相对Cr浓度增量和初始Cr浓度的关系曲线. 相对Cr浓度增量的计算由公式$\Delta {C_{{\rm{relative}}}} = ({{c - {c_0}}})/{{{c_0}}}$得到, 其中$ {c}_{0} $代表初始Cr浓度, c代表100 s时晶界中心处的最大偏析量. 可以看出, 随着Cr含量的增加, 晶界中心处相对Cr浓度增量在降低, 并且呈现线性降低的关系.
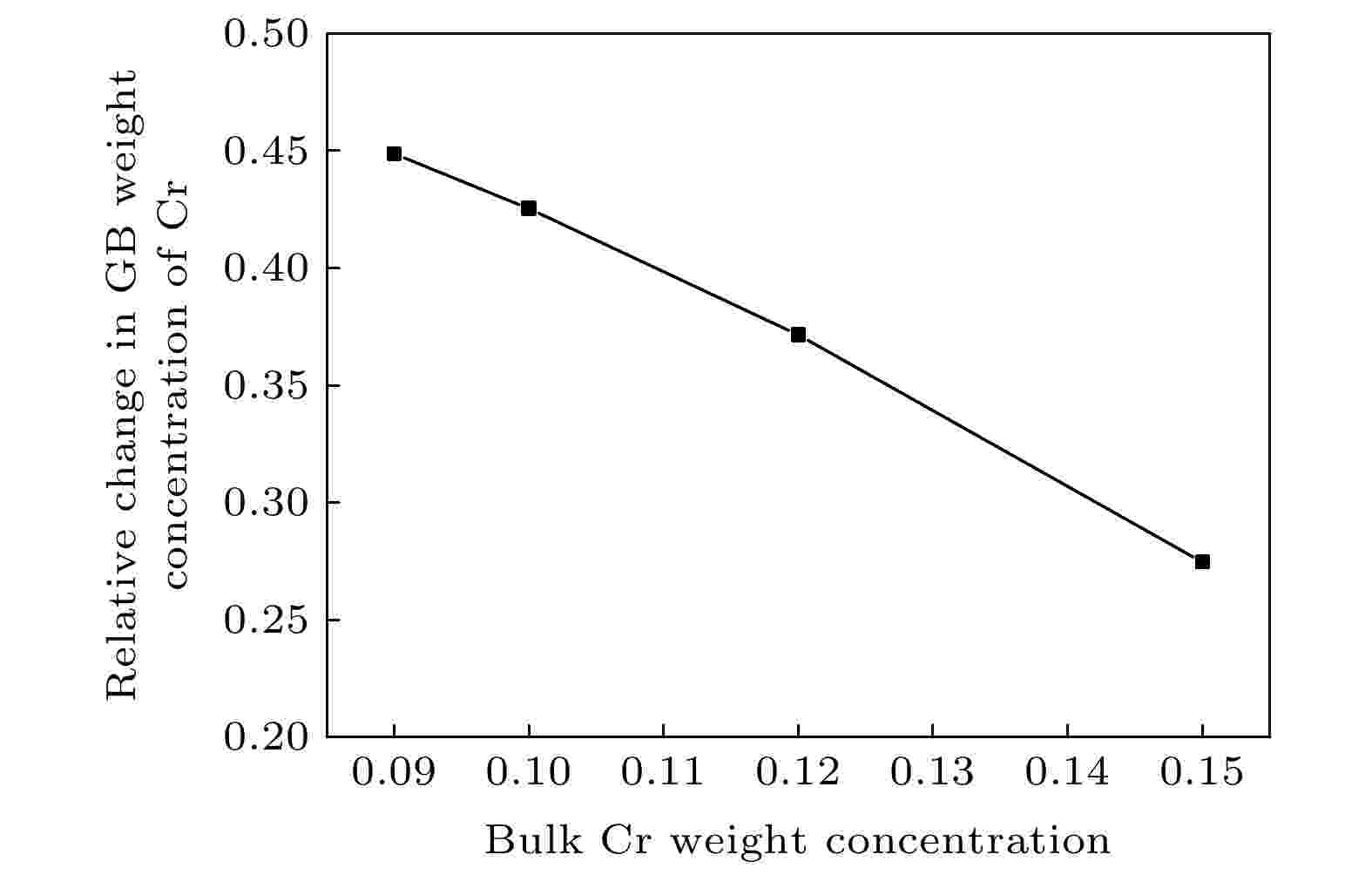图 4 500 ℃下100 s后晶界处的相对Cr浓度增量和基体中Cr浓度的关系曲线
Figure4. The relationship between the relative change of Cr concentration at grain boundary and the bulk Cr concentration after 100 s at 500 ℃.

3 -->

3.1.2.温度对晶界Cr元素偏析的影响

图5中的4个图分别为Fe-9Cr, Fe-10Cr, Fe-12Cr, Fe-15Cr等4种合金在400, 450, 500, 550, 600 ℃下100 s时晶界附近的浓度分布图. 图中5种颜色的曲线代表相同时刻不同温度下的浓度分布曲线. 可以看出, Fe-Cr合金在不同温度下浓度演变曲线的趋势相同, 在晶粒α和晶粒β中, Fe-Cr合金中Cr元素的浓度保持在初始状态不变; 在晶界处, Cr向晶界处发生富集, 在晶界中心处达到最大偏析量. 在相同的时间条件下, 最大偏析量随着温度的升高而升高. 当温度低于500 ℃时, 晶界处的偏析量很小, 晶界偏析不明显; 当温度高于500 ℃时晶界处的偏析量突然增多. McLean理论^[37]指出, 当系统保温很长一段时间之后系统所达到热力学平衡状态下的偏析量会随着温度的升高而降低, 与本文得到的模拟结果相反. 这可能是由于本工作中时间较短且未达到平衡所需要的时间, 所以晶界处的最大偏析量随扩散系数的变化而变化, 温度升高, 扩散系数增大, 晶界处的最大偏析量也相应升高. 这与Sean^[38]利用McLean理论^[37]分析得出的短时间内的晶界偏析动力学基本一致.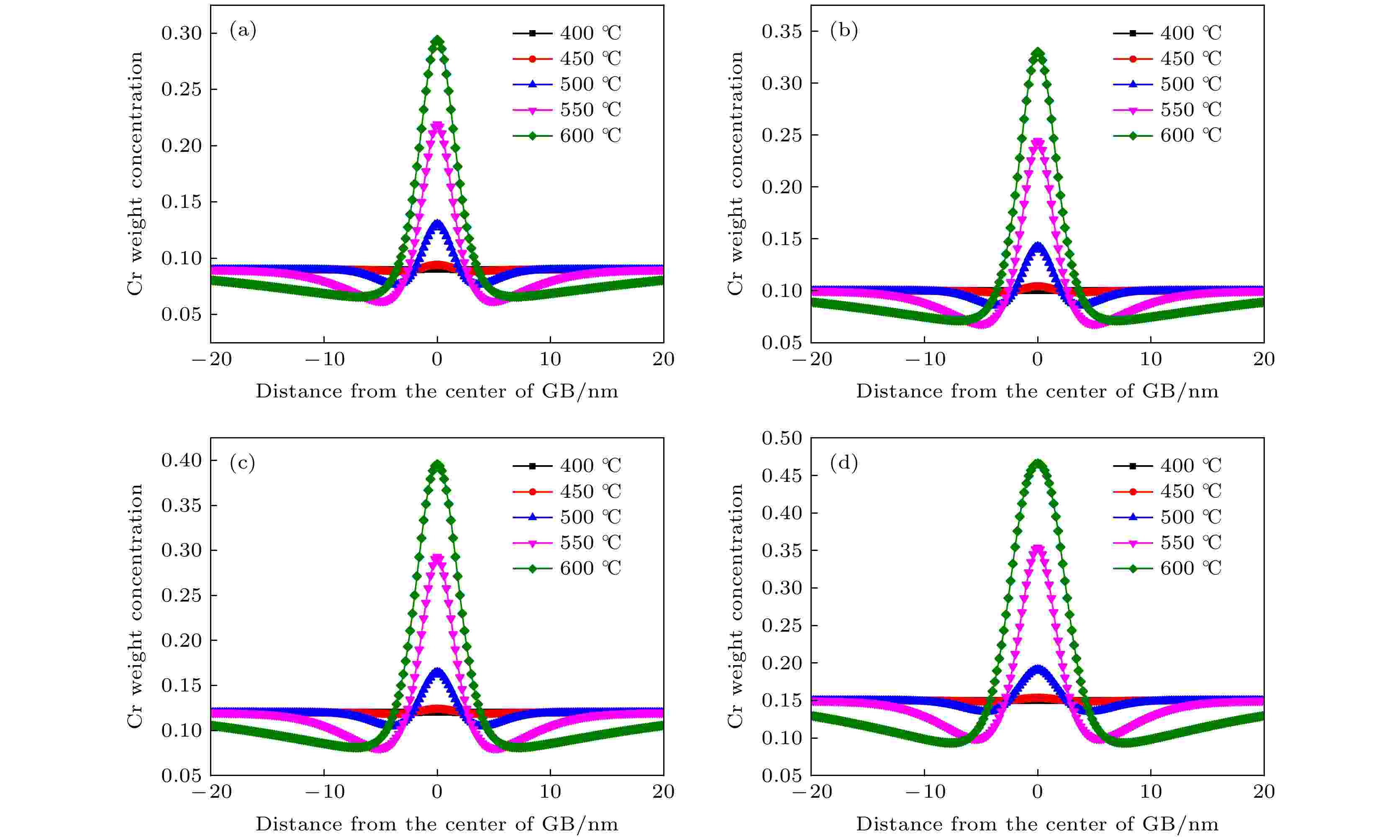
图 5 不同温度下晶界处Cr元素的浓度分布　(a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15Cr
Figure5. Distribution of Cr concentration at grain boundary with different temperatures: (a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15Cr.

2 -->

3.2.辐照条件下的晶界偏析行为

3 -->

3.2.1.不同Fe-Cr合金中晶界Cr元素的偏析

将辐照加速扩散模型引入相场模型, 即对扩散系数进行修正. 对加入辐照之后的Fe-Cr合金的晶界偏析进行了一维模拟. 图6为在450 ℃下辐照剂量率为10^–4 dpa/s时Fe-9Cr, Fe-10Cr, Fe-12Cr, Fe-15Cr等4种合金晶界附近的浓度分布图. 图中5种不同颜色的曲线代表时间为20—100 s的浓度演变曲线. 可以发现, 随着时间的进行, Cr向晶界处发生富集, 在晶界中心处达到最大偏析量.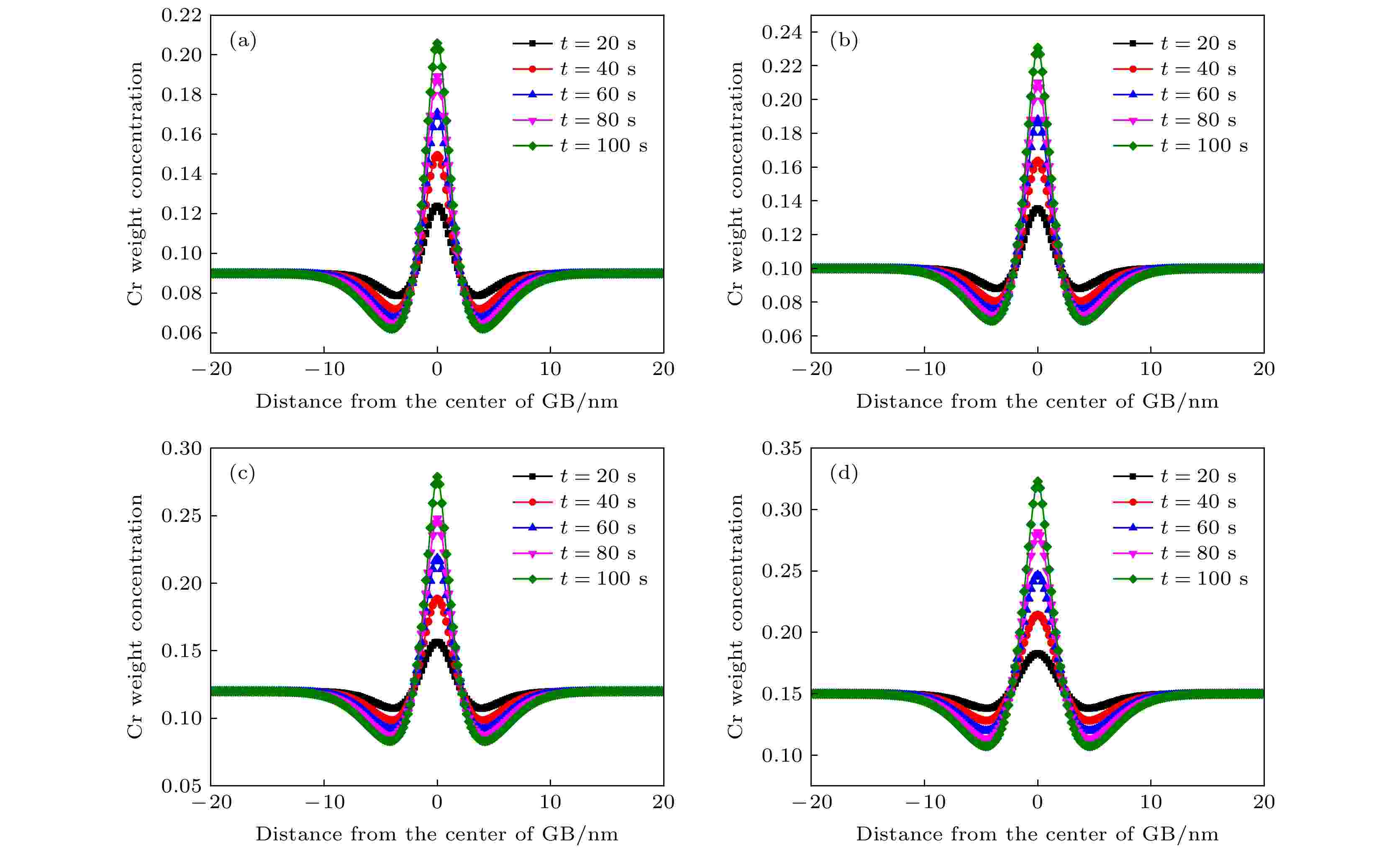
图 6 450 ℃辐照剂量率为10^–4 dpa/s下晶界处Cr元素的浓度分布　(a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15Cr
Figure6. Concentration distribution of Cr element at GB at a dose rate of 10^–4 dpa/s at 450 ℃: (a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15Cr.

图7为450 ℃温度下辐照剂量率为10^–5 dpa/s时Fe-9Cr, Fe-10Cr, Fe-12Cr, Fe-15Cr四种合金的晶界附近的浓度分布图. 图中5种不同颜色的曲线代表20—100 s之后的浓度分布图, 随着时间的进行, Cr元素在晶界处发生富集, 在晶界中心处达到偏析最大量.
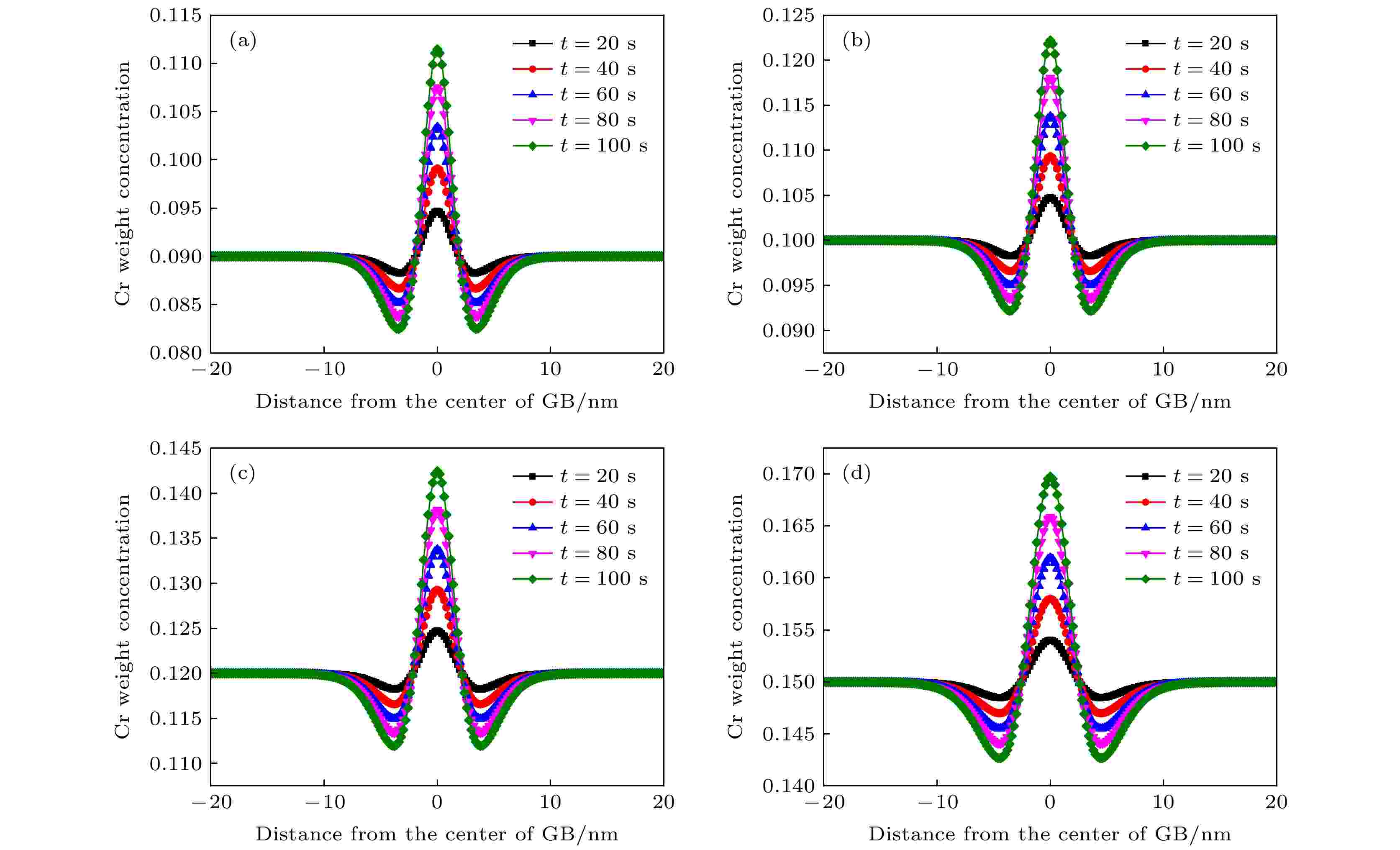图 7 450 ℃辐照剂量率为10^–5 dpa/s下晶界处Cr元素浓度的变化曲线　(a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15Cr
Figure7. Evolution of Cr concentration at grain boundary with a dose rate of 10^–5 dpa/s at 450 ℃: (a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15Cr.

3 -->

3.2.2.辐照剂量率对晶界Cr元素偏析的影响

图8为Fe-9Cr, Fe-10Cr, Fe-12Cr, Fe-15Cr等4种合金在450 ℃下无辐照以及辐照剂量率为${10}^{-4},\; 4\times {10}^{-5}$和$ {10}^{-5}\;{\rm{d}}{\rm{p}}{\rm{a}}/{\rm{s}} $时演变100 s之后晶界附近Cr浓度分布对比图. 可以看出, 同一种合金在相同的温度和时间下随着辐照强度的增加, Cr原子在晶界处的偏析越来越明显, 对应的浓度峰值也越来越大, 实现了辐照对晶界处原子扩散的增强. 该结果与Warry和Was^[7]研究的模型合金在晶界附近Cr浓度分布随辐照强度的变化趋势基本一致.
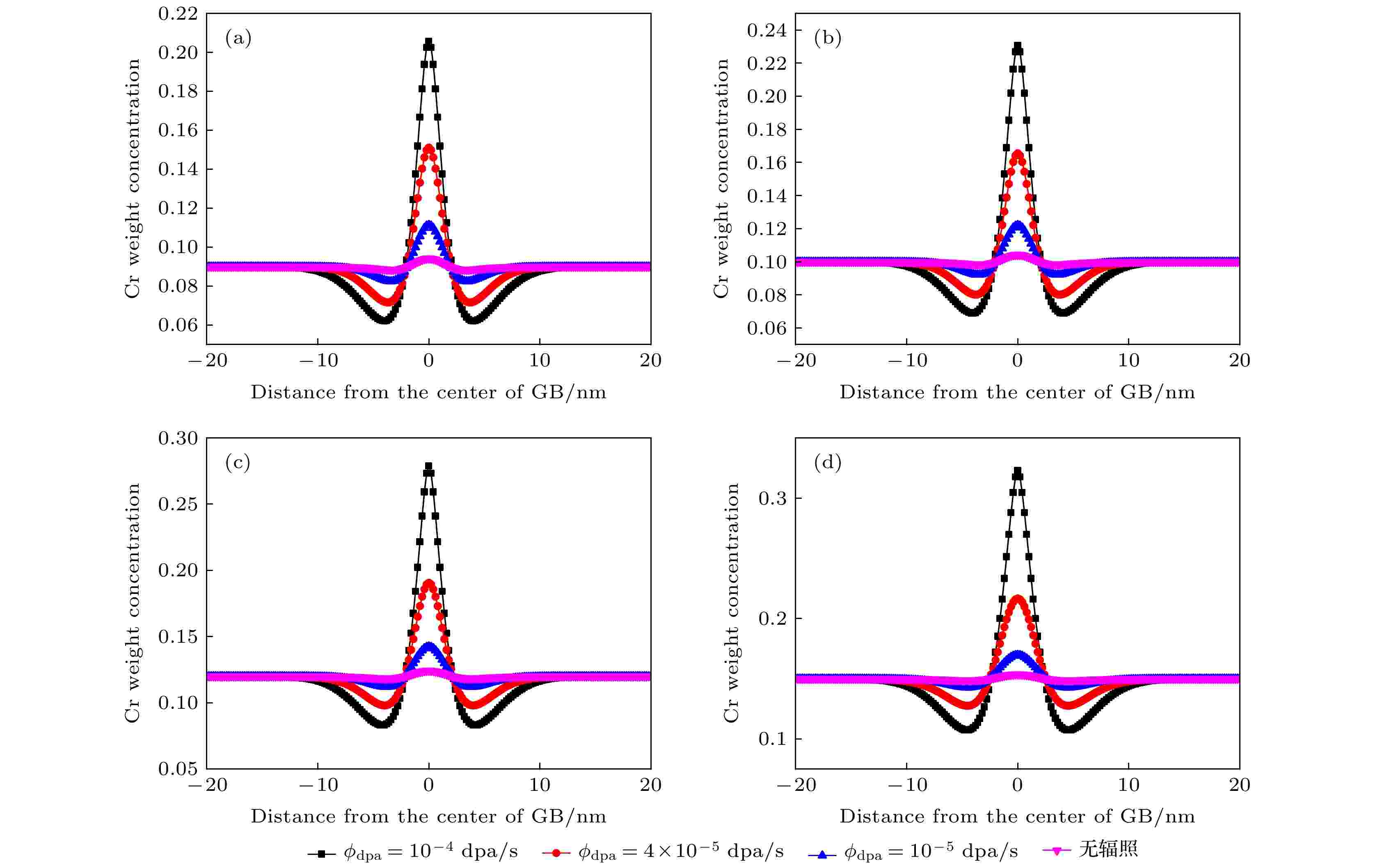图 8 不同辐照剂量率下晶界处Cr元素浓度的分布　(a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15Cr
Figure8. Distribution of Cr concentration with different dose rates: (a) Fe-9Cr; (b) Fe-10Cr; (c) Fe-12Cr; (d) Fe-15Cr.

图9为Fe-9Cr合金在450 ℃不同剂量率条件下晶界处的相对Cr浓度增量和初始Cr浓度的关系曲线. 可以看出, 随着剂量率的升高, 晶界中心处相对Cr浓度增量升高. 辐照剂量率为$4\times $$ {10}^{-5},\; {10}^{-5}\;{\rm{d}}{\rm{p}}{\rm{a}}/{\rm{s}}$时, 同无辐照时随浓度变化趋势相同, 随着浓度的升高相对浓度增量降低, 合金Fe-9Cr的Cr浓度相对增量最多. 但在辐照剂量率为$ {10}^{-4}\;{\rm{d}}{\rm{p}}{\rm{a}}/{\rm{s}} $时, 晶界处相对Cr浓度增量随浓度的升高先升高再降低, Fe-12Cr合金的Cr浓度增量是最多的. Warry和Was^[7]的实验中也得到了随着Cr浓度的升高, 晶界中心处的相对Cr浓度增量降低. 这是由于间隙迁移能对Cr的浓度具有依赖性, 随着Cr浓度的增加单个自间隙原子的迁移能会降低, 从而影响Cr元素的扩散系数^[7]. 因此, 随着基体相中Cr浓度的增加, 较低的间隙迁移能会导致更多的Fe间隙原子向晶界扩散, 从而限制Cr在晶界的富集量.
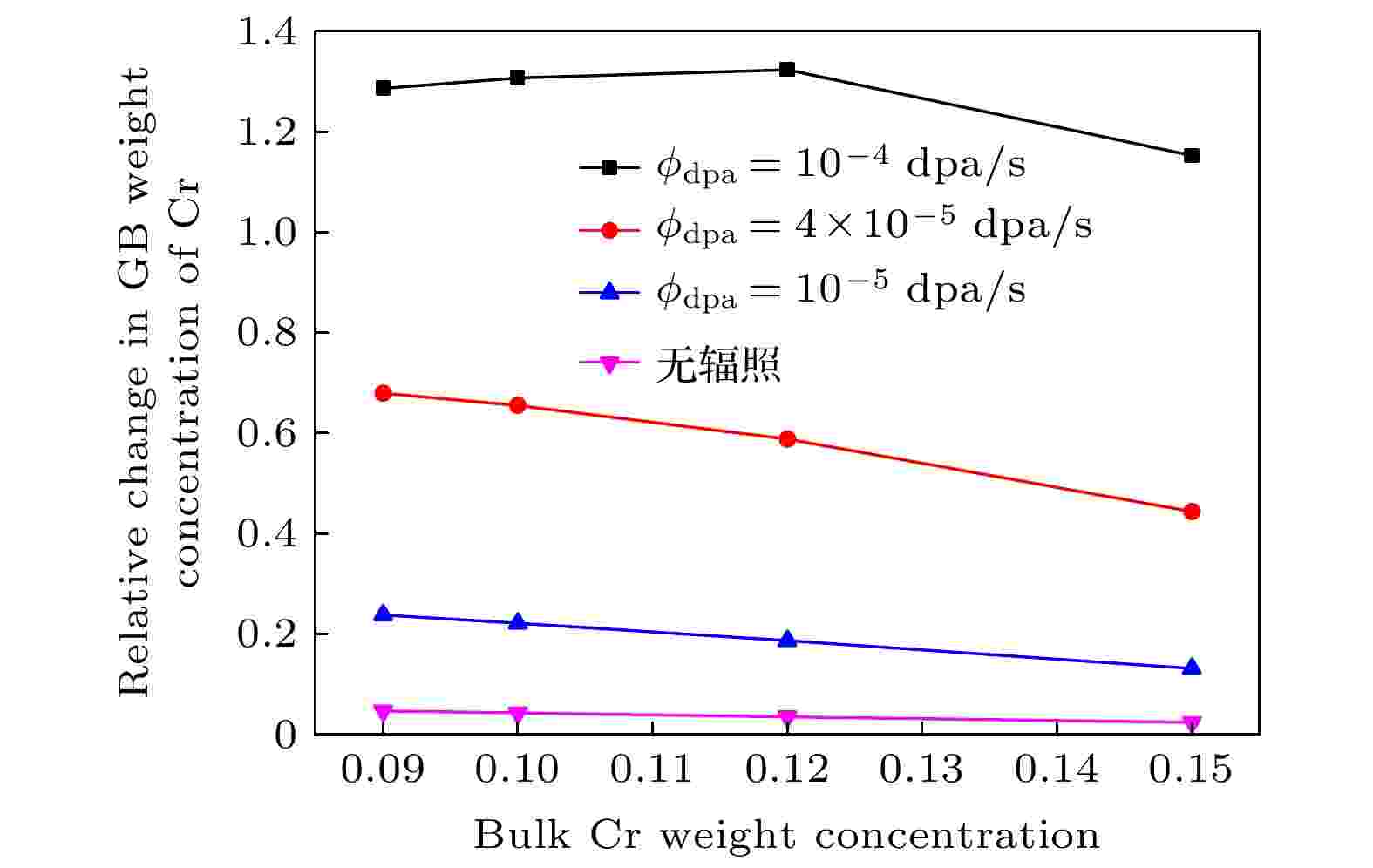图 9 450 ℃时不同剂量率下晶界处的相对Cr浓度增量和初始Cr浓度的关系曲线
Figure9. The relationship between the relative change of Cr concentration at grain boundary and the bulk Cr concentration at different dose rates at 450 ℃

图10为Fe-8.5 Cr模型合金和实验下测得的T91钢在辐照剂量率为1.2 × 10^–5 dpa/s, 温度为400 ℃和450 ℃条件下的浓度分布曲线的对比图. 离散的点代表Warry和Was^[7]关于T91在辐照条件下晶界偏析的实验研究结果, 平滑的曲线代表的是本文利用相场方法模拟的Fe-8.5Cr合金的浓度分布曲线; 黑色曲线代表的是400 ℃时的模拟与实验结果, 红色曲线代表的是450 ℃时的模拟与实验结果. 本工作相场模拟得到的晶界处的最大偏析量与实验结果基本一致; 两个温度对比可知, 在400—450 ℃时对应的最大偏析量随温度的增加而增加, 与实验所测得的趋势一致.
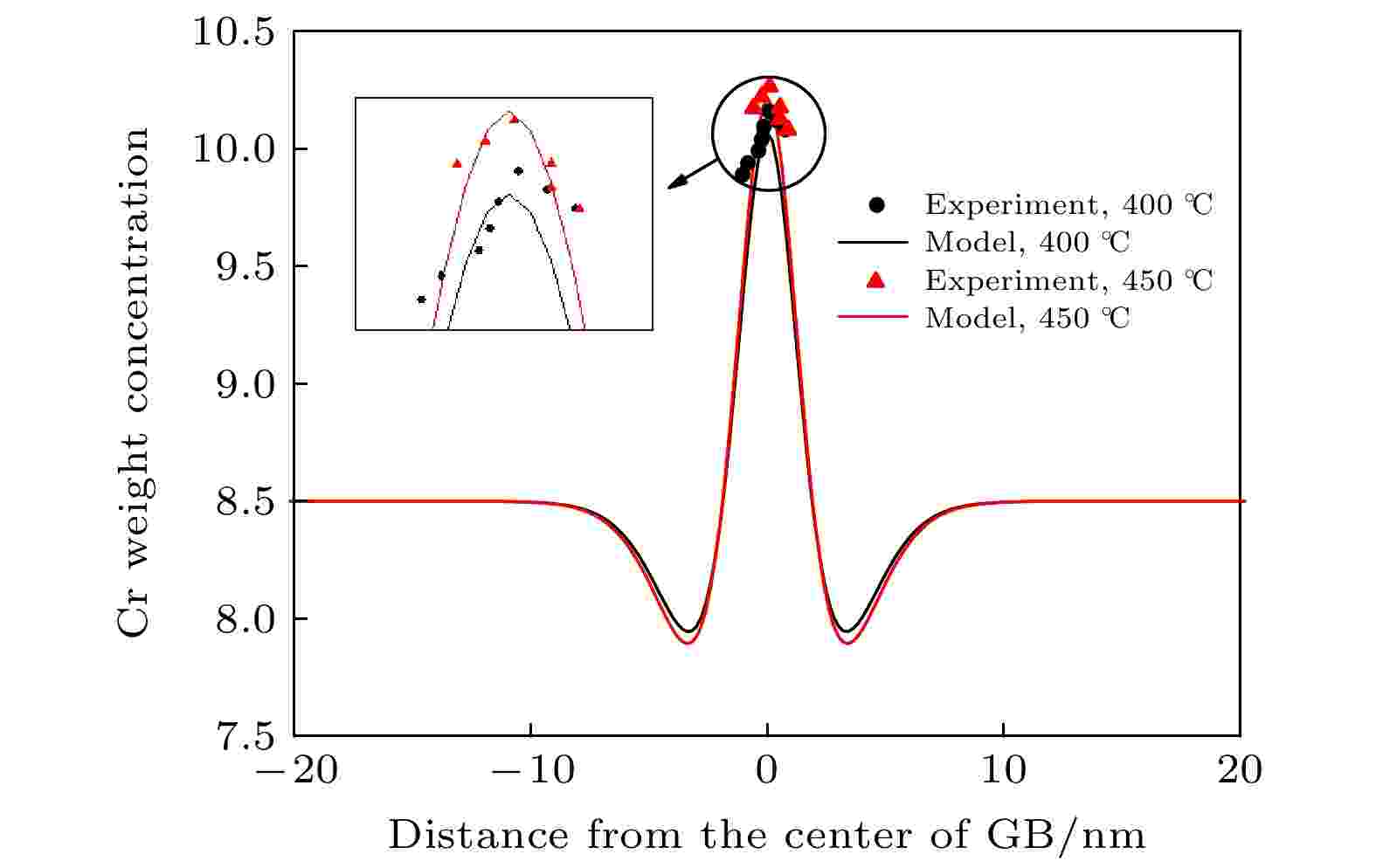图 10 辐照剂量率为1.2 × 10^–5 dpa/s时模拟结果与实验结果对比
Figure10. Comparison of simulation results and experimental results when the dose rate is 1.2 × 10^–5 dpa/s.

温度对Fe-Cr合金晶界处Cr元素的偏析程度有明显的影响. 这是由于随着温度的升高, Cr原子的扩散也快速增加, 导致晶界处Cr元素的偏析程度显著提高. 模拟发现: 当温度低于500 ℃时, 晶界处的偏析量很小, 晶界偏析不明显; 当温度高于500 ℃时晶界处的偏析量增加明显.
基体中Cr元素含量对晶界Cr元素的相对偏析量也有很大的影响. 相同热力学条件下, 随着基体中Cr元素含量的增加, 晶界处Cr元素的相对浓度增量降低.
引入辐照条件后, 晶界处Cr元素的相对偏析量比热力学条件下的偏析量有明显增加. 这是由于辐照产生的大量的点缺陷极大地提高了Cr元素的扩散系数. 随着辐照剂量率的提高, 晶界中心处相对Cr元素浓度增量变大. 相同辐照条件下, 随着Cr元素含量的增加, 晶界处Cr元素的相对浓度增量也降低.