摘要: 本文研究量子输运中马约拉纳费米子与杂质自旋的相互作用, 发现系统能够产生温差驱动的自旋相关电流, 得到了马约拉纳费米子导致的热自旋流. 在大温差下, 马约拉纳费米子与量子点强耦合时, 电流与门电压趋于线性关系, 体现了马约拉纳费米子的鲁棒性, 且马约拉纳费米子导致的自旋流具有振荡特性, 其零点个数与杂质自旋角量子数相关.
关键词: 自旋电子学 /
热致电流 /
马约拉纳费米子 /
杂质自旋 English Abstract Interplay between Majorana fermion and impurity in thermal-driven transport model Niu Peng-Bin 1 ,Luo Hong-Gang 2 1.Department of Physics, Shanxi Datong University, Datong 037009, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11834005, 11674139)Received Date: 31 December 2020Accepted Date: 26 January 2021Available Online: 31 May 2021Published Online: 05 June 2021Abstract: In quantum transport, especially in spintronics, its central theme is to manipulate spin degrees of freedom in solid-state systems, to understand the interaction between the particle spin and its solid-state environments and to make useful devices. Recently, Majorana fermion has been introduced into quantum transport and received much attention. In this paper, we study a thermal-driven transport model which consists of a quantum dot coupled with two normal metal leads, a impurity spin (whose angular quantum number is more than or equal to one-half) and a Majorana fermion. We focus on the interplay between Majorana fermion and the impurity in this exactly solvable model. It is found that the system can generate thermal-induced spin current, and the currents are affected by Majorana fermion and impurity. With large temperature difference, the currents are sensitive to gate voltage, and the quantitative relation between spin-up current and gate voltage tends to be linear when the coupling between Majorana and quantum dot is strong, showing Majorana fermion's robustness. In addition, the spin current induced by Majorana fermion exhibits an oscillating antisymmetric structure around zero-bias point. This spin current’s zero point is related to the angular quantum number of impurity spin. These results are expected to be useful in thermal-electric conversion devices, and may be observed in future experiments.Keywords: spintronics /thermal-induced spin current /Majorana fermion /impurity spin 全文HTML --> --> --> 1.引 言 马约拉纳费米子是意大利物理学家马约拉纳在狄拉克方程的基础上提出的一种粒子, 在高能物理中人们寻找其身影已很多年[1 -3 ] . 马约拉纳费米子具有拓扑性, 凝聚态物理中实现拓扑性质的材料有很多, 例如拓扑绝缘体[4 ,5 ] 、玻色-爱因斯坦凝聚体[6 -8 ] 、Kagome格子[9 ,10 ] 和硅烯[11 ] 等. 近年来, 人们提出在凝聚态物理中寻找准粒子形态的马约拉纳费米子[12 -14 ] , 并且由于其具有非阿贝尔统计特性[15 ,16 ] 以及在量子计算中的潜在应用[2 ] , 引起了人们广泛关注. 凝聚态物理中马约拉纳费米子在拓扑超导线的两端成对出现[17 ,18 ] , 是电子和空穴的零能叠加态, 称为马约拉纳零模.[19 -23 ] . 当马约拉纳费米子被引入量子点输运结构中, 其最明显的特点是1/2电导[19 ] , 即量子点的电导降为了原来的一半. 且新近研究指出, 当杂质自旋也出现在量子点中, 会和马约拉纳费米子联合导致与自旋角量子数相关的分数电导[24 ] .[25 -29 ] , 其研究重点是自旋相关的热输运. 上述提到在量子点输运结构中引入马约拉纳费米子, 人们在实验和理论中发现1/2电导在一定条件下具有鲁棒性[30 ,31 ] , 即不受杂质自旋的影响. 那么一些问题就自然提出: 马约拉纳费米子与杂质自旋相互作用的热输运特性是什么? 马约拉纳费米子能否在热致电流中有所体现? 马约拉纳费米子的鲁棒性又能否在热致电流中有所体现?$4 S + 1$ .2.模型和理论方法 考虑如图1 的模型, 量子点在侧面耦合一个杂质大自旋($S \geqslant {1 / 2}$ )和拓扑超导线, 拓扑超导线的两端支撑两个马约拉纳费米子. 除此外, 量子点外接两个金属电极. 系统的哈密顿量[19 ,20 ,32 ,33 ] 给出为$H = {H_{{\rm{Leads}}}} + {H_{\rm{T}}} + {H_{{\rm{sys}}}}$ . 其中第一项${H_{{\rm{Leads}}}} = $ $ \displaystyle\sum\nolimits_{k\alpha \sigma }\!\! {{\varepsilon _{k\alpha }}c_{k\alpha \sigma }^ + c_{k\alpha \sigma } }$ 描述金属电极中的电子, $c_{k\alpha \sigma }^ + (c_{k\alpha \sigma } )$ 为电子的产生(湮灭)算符. 第二项描述电极与量子点之间的隧穿耦合: ${H_{\rm{T}}} = \displaystyle\sum\nolimits_{k\alpha \sigma } {({t_{k\alpha }}c_{k\alpha \sigma }^ + c_\sigma } + $ $ {\rm{H}}.{\rm{C}}{{.}})$ , $c_\sigma $ 为量子点上的电子湮灭算符, H.C. 为厄米共轭项. 第三项描述系统哈密顿量,图 1 模型示意图. 系统由量子点(QD)、杂质大自旋(S)和拓扑超导线组成, 拓扑超导线的两端有两个马约拉纳费米子. 系统两端连接两个金属电极, 电极两端施加温度差Figure1. Model Diagram. The system consists of a quantum dot, a local large spin and a topological superconductor which supports Majorana fermions. There is a temperature gradient applied to the system.${\varepsilon _0}$ 描述量子点能级, ${s_{z, \pm }}$ 为量子点上电子的自旋算符, ${S_{z, \pm }}$ 为杂质的自旋算符, 二者之间的交换耦合是各项异性的, 用β 描述. 为了简化问题, 本文讨论一种特殊情形, $\beta = 0$ , 即强各向异性耦合情形, 这样(1 )式简化为2 )式中最后一项描述了拓扑超导线左端的马约拉纳零模(${\gamma _1}$ )与量子点电子的隧穿耦合, λ 为二者之间的耦合强度. 马约拉纳零模满足的对易关系为$ \left\{{\gamma }_{i}, {\gamma }_{j}\right\}{=2}{\delta }_{ij}$ , 其可用等价的费米子算符表示: ${\gamma _1} = {f^ + } + f, {\gamma _2} = {\rm{i}}\left( {{f^ + } - f} \right)$ , 这样(2 )式表示为3 )式中大自旋算符写成Hubbard算符形式[34 ,35 ] , 在此表象下, ${S_z} = \displaystyle \sum\nolimits_m {m{Y^{mm}}}$ , 其中${Y^{mm}} = \left| {Sm} \right\rangle \left\langle {Sm} \right|$ . 相应的(3 )式写成:[36 ] :[37 ] 和电荷流为: ${I_{\rm{s}}} = {I_ {\uparrow} } - {I_ \downarrow },\; {I_{\rm{c}}} = $ $ {I_ {\uparrow} } + {I_ \downarrow }$ . (5 )式中${f_{\alpha = {\rm{L}}, {\rm{R}}}}(\omega ) = 1/[1 + \exp (\omega /{k_{\rm{B}}}{T_\alpha })]$ 是费米分布函数, 左右电极的温差表示为${T_{\rm{L}}} = \theta + $ $ {T_{\rm{R}}}$ , ${T_{\rm{R}}}$ 为参考温度, θ 为温差. ${A_\sigma }(\omega ) = - \varGamma {\rm{Im}} G_\sigma ^{\rm{r}}(\omega )$ 是谱函数, Γ 是宽带近似下电极电子态密度常 数. ${\rm{G}}_\sigma ^r(\omega ) = \left. {\langle\langle {c_\sigma }} \right|c_\sigma ^ + \rangle\rangle ^{\rm{r}}$ 是推迟格林函数${\rm{G}}_\sigma ^{\rm{r}}(t) = $ $ - {\rm{i}}\theta \left( t \right)\left\langle\langle {\left\{ {{c_\sigma }(t), c_\sigma ^ + (0)} \right\}} \rangle\right\rangle$ 的傅里叶变换对应. 接下来采用运动方程方法[38 ,39 ] 求解格林函数. 标准的格林函数运动方程在能量空间为$\omega \left. { \langle\langle A} \right|B \rangle\rangle ^{\rm{r}} = $ $ \left\langle\langle {\left\{ {A, B} \right\}} \rangle\right\rangle + \langle\langle [A, H] |B \rangle\rangle ^{\rm{r}}$ . 首先计算自旋向上格林函数$G_ {\uparrow} ^{\rm{r}}(\omega ) = \! {\langle\langle {c_ {\uparrow} }} t|c_ {\uparrow} ^ + \rangle\rangle^r=\!\!\displaystyle \sum\nolimits_m \!{\langle\langle {{c_ {\uparrow} }{Y^{mm}}} |c_ {\uparrow} ^ +\rangle\rangle ^{\rm{r}}}$ , 这里用到了完备关系$\displaystyle\sum\nolimits_m {{Y^{mm}}} {{ = }}1$ . $\langle\langle\left. {{c_ {\uparrow} }{Y^{mm}}} \right|c_ {\uparrow} ^ + \rangle\rangle^{\rm{r}}$ 的运动方程计算结果,$\langle\langle {{Y^{mm}}} \rangle\rangle \!=\! 1/(2S\!+\! 1)$ , 因为每个$\left| m \right\rangle $ 态的占据几率是相同的. (5 )式中最后一项描述电极与系统的耦合, 其运动方程计算结果归结为自能项 $\displaystyle \sum\nolimits_{k\alpha } {t_{k\alpha }^*} \langle\langle c_{k\alpha \uparrow } {Y^{mm}}|c_ {\uparrow} ^ + \rangle \rangle ^{\rm{r}} \!=\! {\varSigma _0} \langle c_ {\uparrow} {Y^{mm}} c_ {\uparrow} ^ + \rangle^{\rm{r}}$ , 其中自能在宽带近似下表示为 ${\varSigma _0} \!=\! $ $ \displaystyle \sum\nolimits_{k\alpha } \dfrac{t_{k\alpha }^2}{\omega - {\varepsilon _{k\alpha }} \!+\! {\rm{i}}{0^ + }} \! $ $ =\! - {\rm{i}}\varGamma$ . 因此(5 )式写为$\left. { \langle\langle f{Y^{mm}}} \right| $ $ c_ {\uparrow} ^ + \rangle\rangle ^{\rm{r}}$ 和$\left. { \langle\langle{f^ + }{Y^{mm}}} \right|c_ {\uparrow} ^ + \rangle\rangle ^{\rm{r}}$ , 其运动方程为$\left. { \langle\langle c_ {\uparrow} ^ + {Y^{mm}}} \right|c_ {\uparrow} ^ + \rangle \rangle ^{\rm{r}}$ 的计算过程与(5 )式类似, 其结果为6 )式—(9 )式求解得到$K( \omega ){{ = 1/}}\omega$ , ${A_m} = \omega - {\varepsilon _0} \!-\! Jm/2\!-\! {\Sigma _0}$ , ${B_m} = $ $ \omega + {\varepsilon _0} \!+\! Jm/2 \!-\! {\Sigma _0}$ , $\tilde K( \omega ) \!=\! K( \omega )/[{B_m} \!-\! 2{\lambda ^2}K( \omega )].$ ${\rm{G}}_ \downarrow ^{\rm{r}}(\omega ) = \left. { \langle\langle {c_ \downarrow }} \right|c_ \downarrow ^ + \rangle\rangle ^{\rm{r}}= $ $ \displaystyle\sum\nolimits_m { \langle\langle \left. {{c_ \downarrow }{Y^{mm}}} \right|c_ \downarrow ^ + \rangle\rangle ^{\rm{r}}}$ , 容易得到10 )式和(11 )式是下文数值讨论的主要出发点.3.结果与讨论 接下来我们数值讨论热偏压驱动下马约拉纳费米子与杂质相互作用下的自旋相关电流.图2 中取右电极参考温度为${T_{\rm{R}}} = 0.01\;{\rm{K}}$ , 左电极${T_{\rm{L}}} = \theta + {T_{\rm{R}}}$ , 杂质自旋先取最小量子数$S = 1/2$ 进行讨论, 其他参数为$J = 4$ , $\varGamma {{ = }}0.02$ , λ 取值则如图中所示, 能量单位为meV. 我们先讨论自旋可分辨电流, 即图2(a) 和图2(b) . 图2(b) 是(11 )式格林函数结果代入(5 )式中后数值所得, 由(11 )式知自旋向下输运电子谱函数的峰值位置(即输运通道)为$\omega = {\varepsilon _0} - {{Jm} / 2}$ . 当${\varepsilon _0}{{ = }}0$ 时, 两条通道(${\varepsilon _0} + $ $ {J / 4}$ 和${\varepsilon _0} - {J / 4}$ )对称分布于费米面两侧, 此时热激发的电子流和空穴流正好抵消, 因而电流为零, 见图2(b) 中${\varepsilon _0} = 0$ 直线. 当${\varepsilon _0} = {{ - }}1$ , 通道分布于费米面处以及下方, 随着左电极温度升高, 左电极部分电子被激发到费米面之上, 留下空穴, 右电极电子通过输运通道流动到左电极, 产生一个费米面下方的反向电流(方向从右到左), 见图2(b) 中${\varepsilon _0} = {{ - }}1$ 曲线. 同理, 当${\varepsilon _0} = 1$ 时, 会产生一个方向从左到右的电子流(正的). 在图2(a) 中可以看到, 当$\lambda {{ = }}0$ , 热致自旋向上电流和图2(b) 中电流是相等的, 此时的电流是自旋不可分辨的. 随着马约拉纳费米子的出现并增强, 可以看到图2(a) 中自旋向上电流是减小的, 这是因为自旋向上电子的谱函数中恒有一个马约拉纳费米子导致的通道位于费米面处(自旋向上电子谱函数的峰值位置[24 ] 为$\omega = 0, \pm {\delta ^m}$ , 其中${\delta ^m}{{ = }}\sqrt {{{({\varepsilon _0} + Jm/2)}^2} + 4{\lambda ^2}} $ ), 会对电流产生中和效应. 这种中和效应会体现在可观测的自旋流中, 见图2(c) , 图中展现了马约拉纳费米子导致的热致自旋流. 图2(d) 给出了电荷流, 可以看到其幅度约为自旋可分辨电流的2倍.图 2 S = 1/2时自旋向上电流(a)、自旋向下电流(b)、自旋流(c)和电荷流(d)随温差的变化图Figure2. Spin-resolved currents (a), (b), spin current (c) and charge current (d) as a function of temperature difference for S = 1/2.图2(c) 中虽然看到了马约拉纳费米子导致的热自旋流, 但其幅度非常小, 实验上不容易观测. 从图2 中可观察到热偏压驱动电流的另外一个特点: 当温差较大时, 电流的变化趋于稳定, 即热偏压将不再影响电流的变化, 而此时电流将会对门电压的变化较敏感, 因而图3 中给出了大温差下电流随门电压的变化规律.图 3 S = 1/2时自旋向上电流 (a)、自旋向下电流(b)、自旋流(c)和电荷流(d)随门电压的变化图Figure3. Spin-resolved currents (a), (b), spin current (c) and charge current (d) as a function of gate voltage for S = 1/2.图3 参数为$S = {1 / 2}$ , $J = 4$ , $\varGamma {{ = }}0.02$ , $\theta = 30$ , λ 取值同样如图中所示. 图3(b) 给出了大温差下自旋向下的热致电流随门电压的变化, 可以观察到明显的台阶现象, 且台阶变化位置对应两个通道${\varepsilon _0} + {J / 4}$ 和${\varepsilon _0} - {J / 4}$ . 这里要提到一点, 通常在电偏压驱动的量子输运系统中, 比如量子点, 电流台阶现象的出现是由固定门电压、调节电偏压得到的, 而热偏压驱动的电流台阶的出现是反过来的. 从图3(a) 可以看出, 当$\lambda = 0$ 时, ${I_ {\uparrow} } = {I_ \downarrow }$ , 可以从图3(a) 和图3(b) 的对比中得到验证. 随着λ 的增大, 台阶现象消失, 逐渐趋于线性关系, 这正是马约拉纳费米子鲁棒性的体现: 在马约拉纳费米子与量子点强耦合时, 其对杂质自旋免疫. 观察图3(c) , 自旋流出现了一个关于原点对称的奇函数振荡结构, 且其零点个数为3个. 在图3(d) 中, 当$\lambda = 0$ 时, 电荷流是自旋可分辨电流(${I_ {\uparrow} }$ 或${I_ \downarrow }$ )的2倍, 而随着λ 增大, 台阶现象也部分被抹平.图3(c) 中马约拉纳费米子导致的零点个数我们猜测其应该是与杂质自旋的角量子数相关的, 为此进一步研究$S = 1$ 时的电流, 见图4 . 因为$S = 1$ 时自旋相关电流随温差的变化图与图2 类似, 这里就不再给出. 而图4 则着重给出$S = 1$ 时自旋相关电流随门电压的变化图.图 4 S = 1时自旋向上电流(a)、自旋向下电流(b)、自旋流(c)和电荷流(d)随门电压的变化图Figure4. Spin-resolved currents (a), (b), spin current (c) and charge current (d) as a function of gate voltage for S = 1.图4 采用的参数为$S = 1$ , $J = 2$ , $\varGamma {{ = }}0.02$ , $\theta = 30$ , λ 取值同样如图中所示. 从图4(b) 中可以看到, 自旋向下电流(或图4(a) 中$\lambda = 0$ 时的自旋向上电流)的台阶数为3个, 这是因为$S = 1$ 时, 没有马约拉纳费米子时系统的通道为${\varepsilon _0} + {J / 2}$ , ${\varepsilon _0}$ , ${\varepsilon _0} - {J / 2}$ . 当调节门电压, 三条通道依次通过费米面会引起电子流的变化. 例如, 当${\varepsilon _0} < - 1$ 时, 三条通道都在费米面下方, 电流为从右到左的电子流(负的). 当$ - 1 < {\varepsilon _0} < 0$ 时, 最上面一条通道${\varepsilon _0} + $ $ {J / 2}$ 位于费米面上方, 贡献从左到右的电子流, 抵消部分负的电子流, 形成图4(b) 中$ - 1 < {\varepsilon _0} < 0$ 区间的第一个台阶. 依次类推, 直到三条通道都位于费米面上方时, 电流变为正的最大值. 图4(a) 得到的结论与图3(a) 一致: 马约拉纳费米子与输运系统强耦合时, 电流与门电压成线性关系, 其对杂质自旋免疫. 从图4(c) 可以观察到自旋流零点个数为5个, 与$S = {1 / 2}$ 对比概括知马约拉纳费米子导致的自旋流的零点个数确实是角量子数相关的, 其个数为$4 S + 1$ .4.结 论 本文讨论了一个热偏压驱动的精确可解量子输运模型, 着重讨论马约拉纳费米子与杂质自旋的相互作用. 研究发现, 系统能够产生温差驱动的自旋相关电流, 并能在可观测物理量(如自旋流)中体现马约拉纳费米子的特性. 我们得到了马约拉纳费米子导致的热自旋流; 在大温差下, 马约拉纳费米子与输运系统强耦合时, 电流与门电压趋于线性关系, 其对杂质自旋免疫, 体现了马约拉纳费米子的鲁棒性, 并且马约拉纳费米子导致的自旋流的零点个数是角量子数相关的. 期望这些研究结果对热-电转换器件的研究有所补充, 并期望其中一些结果能够在实验中观测到. 








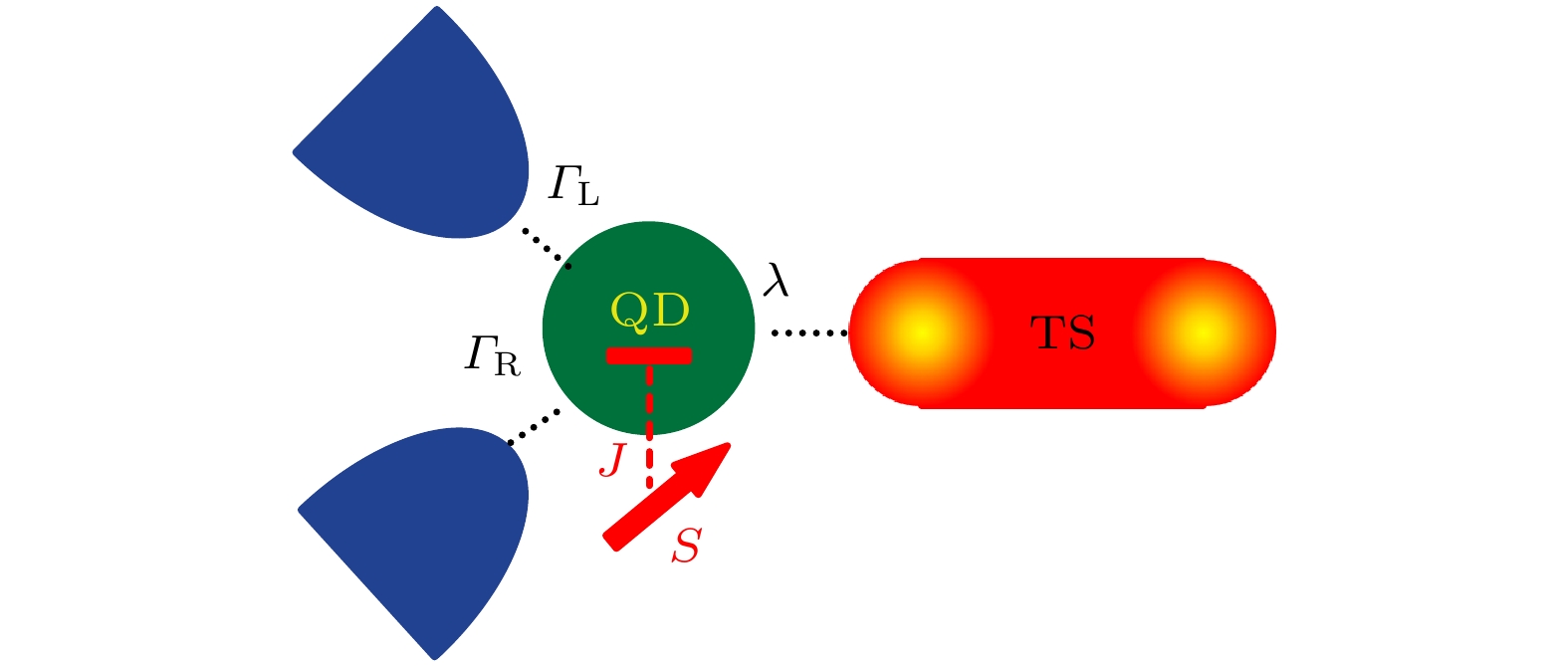 图 1 模型示意图. 系统由量子点(QD)、杂质大自旋(S)和拓扑超导线组成, 拓扑超导线的两端有两个马约拉纳费米子. 系统两端连接两个金属电极, 电极两端施加温度差
图 1 模型示意图. 系统由量子点(QD)、杂质大自旋(S)和拓扑超导线组成, 拓扑超导线的两端有两个马约拉纳费米子. 系统两端连接两个金属电极, 电极两端施加温度差



























































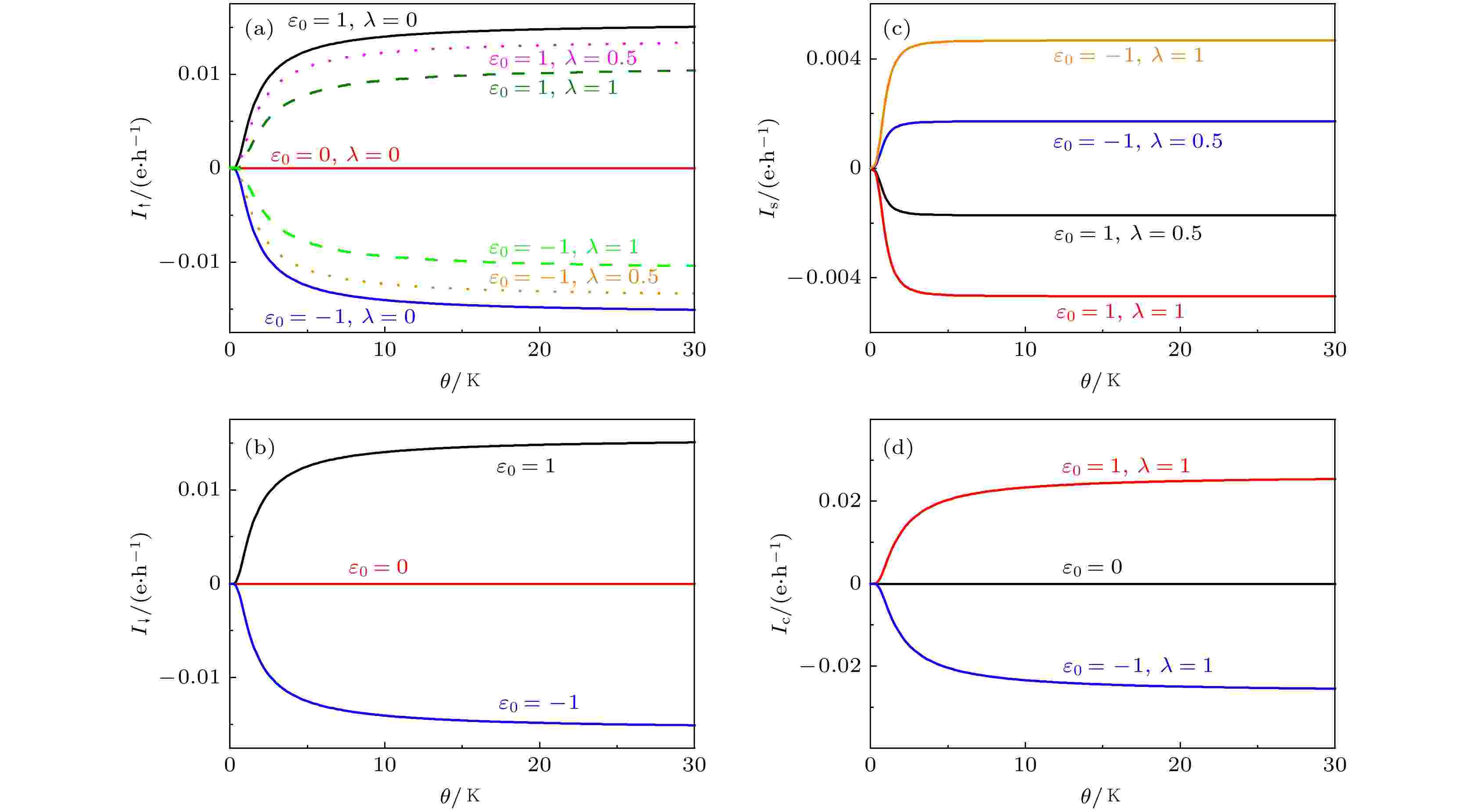 图 2 S = 1/2时自旋向上电流(a)、自旋向下电流(b)、自旋流(c)和电荷流(d)随温差的变化图
图 2 S = 1/2时自旋向上电流(a)、自旋向下电流(b)、自旋流(c)和电荷流(d)随温差的变化图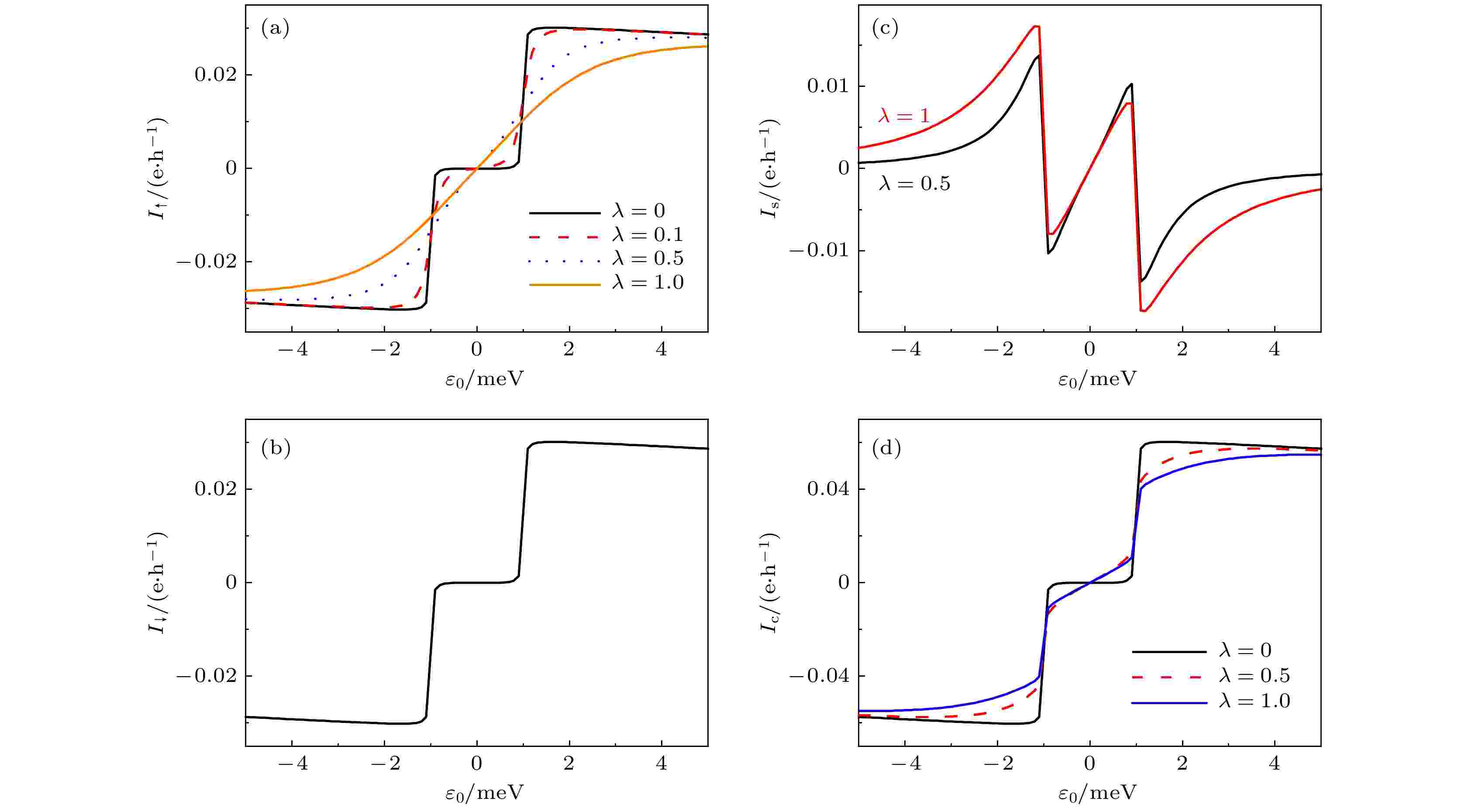 图 3 S = 1/2时自旋向上电流 (a)、自旋向下电流(b)、自旋流(c)和电荷流(d)随门电压的变化图
图 3 S = 1/2时自旋向上电流 (a)、自旋向下电流(b)、自旋流(c)和电荷流(d)随门电压的变化图





















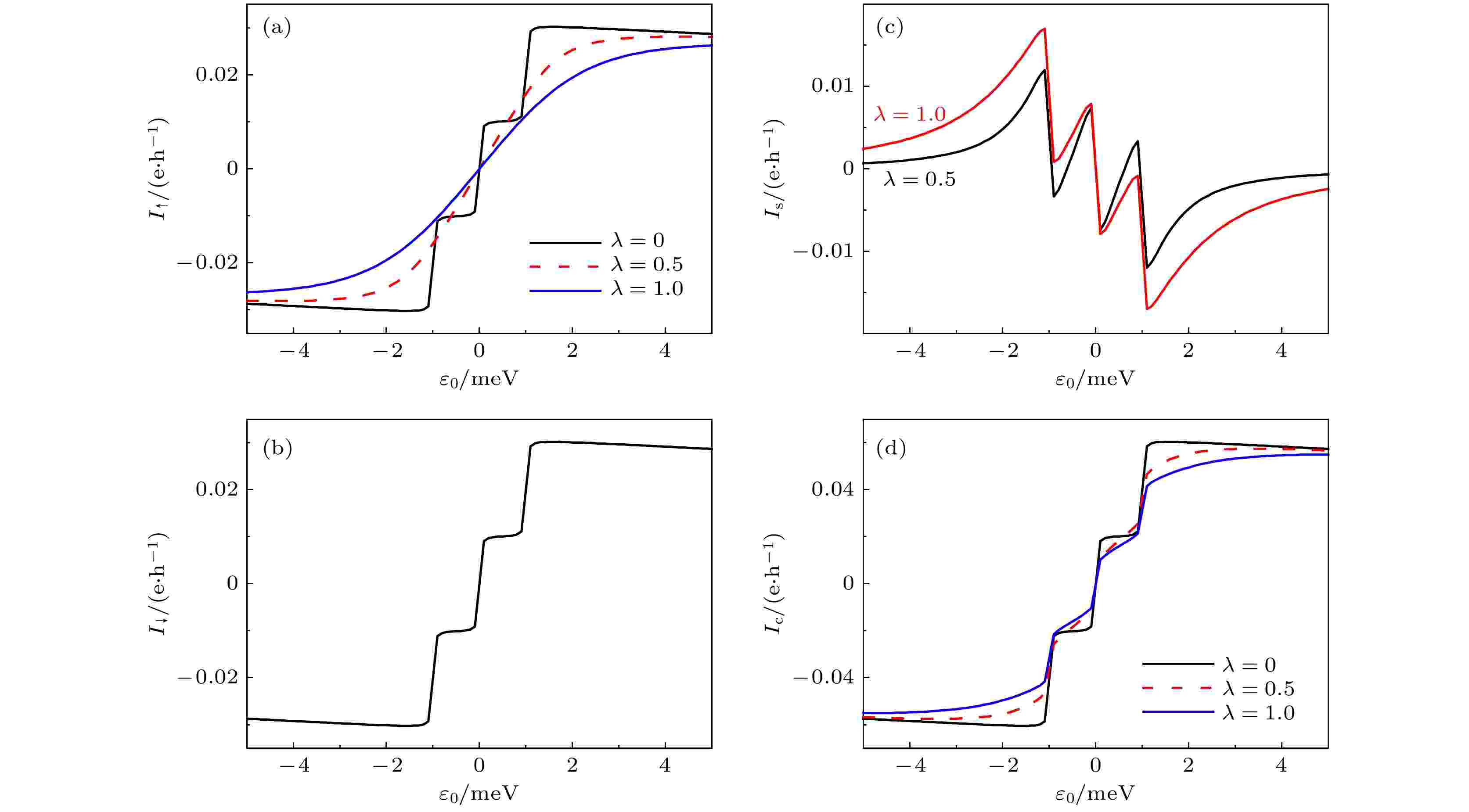 图 4 S = 1时自旋向上电流(a)、自旋向下电流(b)、自旋流(c)和电荷流(d)随门电压的变化图
图 4 S = 1时自旋向上电流(a)、自旋向下电流(b)、自旋流(c)和电荷流(d)随门电压的变化图



















