摘要:流固耦合管路系统广泛应用于各种装备中, 通常用来传递物质和能量或者动量. 由于流固耦合效应, 管壁在流体作用下易产生强烈的振动与噪声, 对装备安全性、隐蔽性产生严重影响, 甚至造成严重破坏. 流固耦合管路振动抑制需求迫切, 意义重大. 声子晶体可以利用其带隙特性抑制特定频率范围内弹性波的传播, 在减振降噪领域具有广泛的应用前景. 本文基于声子晶体理论, 研究了流固耦合条件下的布拉格声子晶体管路冲击振动传递特性. 将传递矩阵法和有限元法相结合, 计算了能带结构与带隙特性, 重点考虑了流固耦合效应下, 不同冲击激励条件下声子晶体管路振动特性, 分析了流固耦合对声子晶体管路振动传递特性的影响. 研究结果为流固耦合条件下管路系统的振动控制提供了技术参考.
关键词: 流固耦合/
声子晶体/
振动带隙/
冲击振动

English Abstract

全文HTML

--> --> -->

输流管路系统通常用来传递物质和能量或者动量, 因而广泛应用于各种装备中. 流体的压力波脉动和管壁结构容易产生耦合作用, 进而诱发强烈的振动与噪声, 对装备的性能与使用产生严重影响. 因此, 研究降低输流管路振动和保证管道输送安全, 在理论和实践上有着重大研究意义^[1].
流固耦合动力学是一门研究固液相互作用的学科, 其主要研究内容是变形固体在流体流场作用下的力学行为与变形固体形态对流场的影响之间的相互作用^[2,3]. 随着计算固体力学和计算流体力学的快速发展以及各种商用有限元软件的开发使用, 流固耦合分析和研究得到快速发展, 研究结果对工程应用和装备设计起到越来越重要的参考价值^[4-6].
近年来, 凝聚态物理领域中声子晶体(phononic crystals)带隙(band gap)理论的不断发展和完善为振动传播控制提供了新的技术支持^[7-11]. 声子晶体是某种或多种材料组成的周期性结构或复合材料. 弹性波在声子晶体内传播时, 受内部介质周期性的作用可以产生弹性波带隙, 因而可以利用声子晶体的带隙特性有效抑制带隙频率范围内的振动与噪声传播. Chen等^[12-14]研究了嵌入式内部谐振器的夹层梁结构, 该结构可改善冲击载荷下弯曲振动性能, 并完成实验验证. Pai等^[15]通过将阻尼元件结合到多谐振器超材料梁中, 实现两个带隙频率区域有效地合并以形成单个宽带能量吸收区域. Chen等^[16]提出了一种由多层黏弹性连续介质构成的耗散超材料的微观结构设计, 可有效地衰减瞬态冲击波. Alamri等^[17]介绍了具有多个Maxwell型谐振器的耗散弹性超材料的发展, 可应用于减轻动态载荷和爆炸波衰减. Li等^[18]提出了一种新颖的超晶格桁架芯夹层结构, 可用于实现脉冲波衰减和动态载荷衰减, 具有缓和冲击能力和动能吸收能力. 李奇奇等^[19,20]提出了一种三谐振器超材料, 以增强冲击应力波的衰减效果, 并对该超材料的多目标优化进行了分析. 而后提出了一种用于衰减冲击应力波的新型多谐振器超材料. 以上对声子晶体冲击波衰减的研究有很多的进展, 并且由理论研究逐渐进展到实际应用中, 但研究对象均为固体结构, 而流固耦合声子晶体冲击振动特性研究较少.
应用声子晶体带隙特性进行流固耦合管路系统设计, 可将管路系统设计成周期性复合结构或在管路上周期性地附加局域共振结构, 进而实现抑制管路系统振动传播, 为管路的减振降噪设计提供了新的技术途径和理论基础, 目前已经得到广泛研究和关注^[21-23]. Koo等^[24]首先确定了带有周期性弹性支撑的输液管路的带隙分布, 并通过实验很好地证明了其理论预测. Sorokin等^[25]则研究了平面弹性波在充液周期壳体中的传播特性, 并分析了充液与否对带隙特性的影响, 随后在研究中发现在流固耦合情况下充液管路系统在某些频段同样存在一些“波阻带”现象^[26], 还进一步研究了周期附加惯性质量系统管路的纵向振动与弯曲振动的耦合振动带隙特性^[27]. 郁殿龙等^[28]通过应用布拉格散射机理和局部共振机理, 实现了周期性复合管路输液的弯曲振动带隙, 并进一步应用传递矩阵法和有限元法研究了各种条件下输液管路的波传播和衰减特性^[29-33], 并且进行了振动试验验证了周期性管路结构的波衰减能力^[34]. 魏振东等^[35]将周期管路应用到液压系统中, 提出了一种考虑流固耦合作用的频响计算方法, 并对其在高压条件下的带隙特性进行了理论和实验研究. 刘东彦等^[36]首次研究了液压油流体特性对周期管路带隙特性的影响. 沈惠杰等^[37,38]重点研究了周期性输液管路的壳体的稳定性并进一步提出了一种由功能梯度材料(FGM)制成的周期壳体模型^[39-41], 以消除或减轻由材料参数的几何不连续性引起的应力集中. Liang等^[42]基于声子晶体管路模型, 考虑管道长度变化, 研究了部署长管输送流体的波传播和带隙特性. 以上研究为声子晶体管路输送流体的振动分析奠定了基础. 但是这些研究中对流固耦合效应考虑得较少, 特别是冲击激励的振动分析不够深入.
本文以流固耦合声子晶体管路为对象, 考虑不同冲击激励条件对振动传递特性的影响. 首先采用传递矩阵法对未充液和充液周期管路的振动传递特性进行数值分析, 分析其带隙特性. 并利用有限元法, 研究不同冲击激励条件下(包括管壁冲击激励、流体冲击激励等)的流固耦合声子晶体管路振动传播特性及其影响规律.

2

-->

2.1.充液声子晶体管路传递矩阵法

充液管路振动模式有弯曲振动、轴向振动、扭转振动, 以及它们之间的复杂耦合振动, 其中弯曲振动指是图1中y方向的振动, 即垂直于管路轴线方向上的振动; 轴向振动指图1中x方向的振动, 即沿管路轴线方向的振动; 扭转振动则是指管路在绕轴线进行的扭转振动, 其一般由旋转机械的主动力矩与负荷反力矩之间失去平衡引起的. 当内部流体以较高或较慢的速度流动时, 管路可能会弯曲或强烈振动, 而且在外部激励下, 管路主要会产生弯曲振动, 轴向振动和扭转振动较小, 可以忽略不计, 故管路弯曲振动是主要的振动模式^[43-45]. 因此, 研究弯曲振动对管路振动控制具有重要的理论意义. 目前研究管路弯曲振动的理论研究大多数基于梁模型.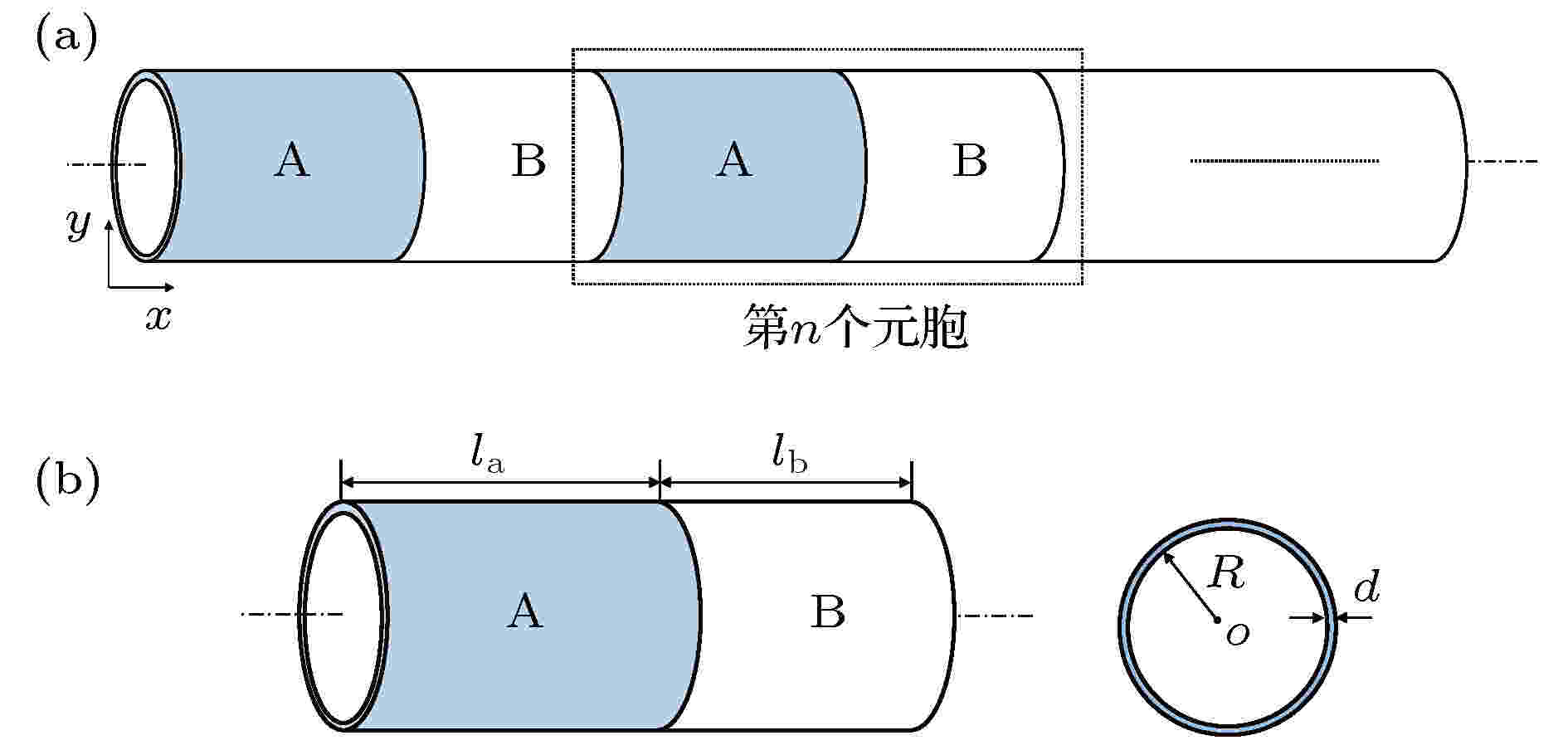
图 1 布拉格声子晶体管路结构示意图　(a)无限周期单元; (b)基本周期单元
Figure1. Schematic diagram of Bragg phononic crystal pipeline structure: (a) Infinite periodic cell; (b) Basic periodic cell.

一般情况下, 当管路长度与管径长之比大于10时, 可以将管路考虑为欧拉梁模型. 为了计算能带结构, 这里我们对流固耦合管路进行简化, 假设管内的液体为理想液体(各向同性、均匀、不可压缩、线性), 液体流速以恒定的速度流动, 液体中未发生空泡现象, 忽略重力的影响, 充液管路弯曲振动Euler梁方程为^[46,47]:

$\begin{split}&EI\dfrac{{{\partial ^4}w}}{{\partial {x^4}}} + \left( {pA + {m_{\rm{f}}}{u^2}} \right)\dfrac{{{\partial ^2}w}}{{\partial {x^2}}} \\+& 2{m_{\rm{f}}}u\dfrac{{{\partial ^2}w}}{{\partial x\partial t}} + ({m_{\rm{f}}} + {m_{\rm{p}}})\frac{{{\partial ^2}w}}{{\partial {t^2}}} = 0, \end{split}$

式中, E为管路材料杨氏模量, I为管路横截面转动惯量, w为弯曲振动位移, p为流体压力, A为管路内横截面积, ${m_{\rm{f}}}$为液体的单位长度质量, ${m_{\rm{p}}}$为管路的单位长度质量, u和t为液体流速和时间.
考虑管路未充液时, 振动方程(1)式可以简化为

$EI\frac{{{\partial ^4}w}}{{\partial {x^4}}} + {m_{\rm{p}}}\frac{{{\partial ^2}w}}{{\partial {t^2}}} = 0. $

对于一简谐波^[48], (1)式的解可以写成$w(x, t) = W{{\rm{e}}^{kx}}{{\rm{e}}^{{\rm{i}}\omega t}}$的形式, 则管路的弯曲振动方程可以表达为

$EI{k^4} + \left( {pA + {m_{\rm{f}}}{u^2}} \right){k^2} + {\rm{i}}2{m_{\rm{f}}}u\omega k - ({m_{\rm{f}}} + {m_{\rm{p}}}){\omega ^2} = 0. $

对于给定的值$\omega $, (3)式中的波数k有两个不同的虚数根和两个互为共轭的复数根, 分别记为${k_1}, {k_2}, {k_3}, {k_4}$, 则(1)式的解可以表示为

$\omega \left( {x,t} \right)\! =\! {{\rm{e}}^{{\rm{i}}\omega t}}\left( {{W_1}{{\rm{e}}^{{k_1}x}} \!+\! {W_2}{{\rm{e}}^{{k_2}x}} \!+\! {W_3}{{\rm{e}}^{{k_3}x}}\! +\! {W_4}{{\rm{e}}^{{k_4}x}}} \right). $

构建的布拉格声子晶体管路见图1所示, 其中a为晶格常数, l_a为管路A的长度, 则在单元n–1和单元n之间的界面处的位移、转角、弯矩和剪切力都是连续的, 即在$x = na$处有^[49]:

${{{K}}_{\rm{1}}}{{{W}}_{n,{\rm{A}}}}={{{H}}_{\rm{1}}}{{{W}}_{n - 1,{\rm{B}}}}, $

式中${{W}} = {[{W_1}, {W_2}, {W_3}, {W_4}]^{\rm{T}}}$.
同理, 在单元n中的管道A和管道B之间的交界面处的位移、转角、弯矩和剪切力都是连续的, 即在$x = na + {l_a}$处有:

${{{K}}_{\rm{2}}}{{{W}}_{n,{\rm{A}}}}={{{H}}_{\rm{2}}}{{{W}}_{n{\rm{,B}}}}. $

根据(5)式和(6)式, 可以求得单元n与单元n–1之间的关系为

${{{W}}_{n,{\rm{B}}}}{{ = T}}{{{W}}_{n - 1,{\rm{B}}}}, $

式中${{T = }}{{{H}}_2}^{-1}{{{K}}_2}{{{K}}_1}^{-1}{{{H}}_1}$.
由于声子晶体管路在x方向的周期性, 根据Bloch定理可以得到:

${{{W}}_n} = {{\rm{e}}^{{\rm{i}}{{q}}a}}{{{W}}_{n - 1}}, $

式中${{q}}$是轴向一维Bloch波矢.
因此, 无限周期管结构特征值是行列式的根:

$\left| {{{T}} - {{\rm{e}}^{{\rm{i}}{{q}}a}}{{I}}} \right| = 0, $

式中${{I}}$为$4 \times 4$单位矩阵. 对于给定的$\omega $值, (9)式给出${{q}}$的对应值, 根据${{q}}$是实部还是虚部, 相应的波分别通过管道传播或被衰减. 同理, 可以从传递矩阵${{T}}$获得振动传递的频率响应曲线(frequency response function, FRF)^[50].
2 -->

2.2.流固耦合管路振动基本原理

通过流体力学N-S方程理论和固体力学小变形弹性理论联合推导出的求解流固耦合的基本方程是如今使用较为普遍的模型, 主要包括4-方程、8-方程、12-方程和14-方程模型等, 目前4-方程模型和8-方程模型在实际应用中得到较为广泛的使用. 通常以Budenkov^[51]在讨论Pochhammer方程时采用的方法为参照, 对流固耦合问题构建合适的数学模型. 将流固耦合运动分解为轴向和横向运动等, 而后分别对其讨论, 最后将两类方程进行合成求解流固管路耦合振动问题.
流体流动过程中遵循质量、能量、动量三大基本物理守恒定律, 当流体中混合有其他成分时, 还要遵循组分守恒定律^[4]; 固体结构部分的控制方程主要遵循牛顿第二定律^[52]. 流固耦合方程遵循基本的物理守恒定律, 在流固耦合交界面上满足流体域与固体域两相之间应力、温度、位移、热流量等变量的守恒或相等^[53].
目前, 直接耦合式解法和分离式解法是用来解决流固耦合问题最主要的两种方法. 直接耦合算法可以同时对流固耦合控制方程进行求解, 不存在时间滞后, 理论上较为理想; 分离解法则不必对流固耦合控制方程进行求解, 只需在不同求解器或者同一求解器中按照预先设置的求解顺序分别对流体和固体控制方程进行求解, 得到固体域和流体域的计算结果, 而后通过设置好的流固耦合面进行两相数据的交互传输, 当此刻收敛达到要求时进行下一时刻的计算求解, 依次计算求解最终结果.
分离解法与直接耦合求解相比, 缺点主要是具有在流固耦合面上能量不完全守恒和时间滞后问题; 其优点是可以较好地结合流体力学和固体力学的方法和程序, 对内存要求较低, 计算速度较快, 目前被应用于大多数商用CAE软件中^[4]. 第4节中基于ANSYS Workbench平台建立的双向流固耦合分析模型就是采用分离解法对流固耦合方程进行求解的.

基于声子晶体理论, 构建布拉格声子晶体管路, 其结构示意如图1所示, 图1 (a)是无限周期单元, 图1 (b)是基本周期单元. 布拉格声子晶体管路是两种不同管壁材料A和B沿x轴交替周期排布形成的周期管路, 其中单个周期单元中管段A的长度为${l_{\rm{a}}}$, 管段B的长度为${l_{\rm{b}}}$, 则周期管路的晶格常数$a = {l_{\rm{a}}} + {l_{\rm{b}}}$, 管路的半径为R, 管壁厚度为d.
本文研究对象为海水管路系统, 其脉动源假设为一台六叶片的离心泵, 转速为2500 r/min, 则推导出的其叶频和次倍频分别为250 Hz和500 Hz, 由于管路内径R和管壁厚度d尺寸为项目应用要求, 因此通过改变晶格常数a和管段A长度l_a和管段B长度l_b来改变管路带隙, 为了使计算得到的管路带隙满足叶频和次频的振动控制要求, 计算中, 管段A和B分别采用结构钢和环氧树脂, 其材料参数如表1所示, 取管段A的长度${l_{\rm{a}}}$ = 0.25 m, 管段B的长度为${l_{\rm{b}}}$ = 0.25 m, 管路的内径R = 0.01 m, 管壁厚度d = 0.001 m, 管内介质为水, 密度为1000 kg/m³, 介质内的声速为1400 m/s. 运用2.1节中由(7)式—(9)式求解传递矩阵T, 并计算上述参数下无限周期单元的能带结构图和频率响应.

材料名称	杨氏模量/GPa	密度/kg·m–3	泊松比
结构钢	200	7850	0.3
环氧树脂	4.35	1180	0.3672

表1管路材料参数
Table1.Pipeline material parameters.

图2是利用传递矩阵法计算的未充液布拉格声子晶体管路弯曲振动的能带结构和频率响应曲线, 其中图2 (a)是波矢实部与频率的关系曲线, 可以表现带隙的频率范围, 图2 (b)表示具有5个周期的声子晶体管路的频率响应曲线. 由图可知, 在0—800 Hz的频率范围内存在两个衰减带隙70—90 Hz和280—690 Hz, 其中观察振动频率响应曲线可知, 有限周期声子晶体管路的振动传递损失曲线较好地对应着无限周期声子晶体管路的带隙频率范围; 第二带隙的衰减强度远大于第一带隙, 且衰减最大可以低至–60 dB.
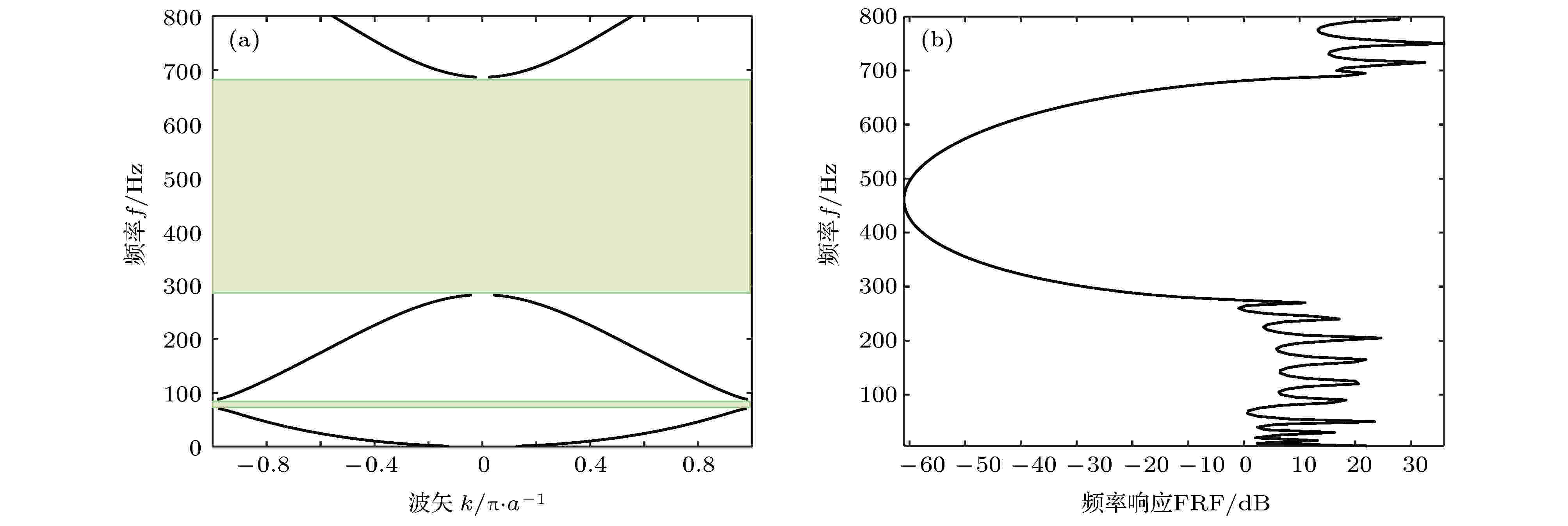图 2 未充液布拉格声子晶体管路的带隙特性　(a)能带结构; (b)振动频率响应曲线
Figure2. Band gap characteristics of the liquid-unfilled Bragg phononic crystal pipeline: (a) Band structure; (b) Flexural vibration FRF.

图3是充液布拉格周期管路弯曲振动的能带结构和振动频率响应曲线, 可以发现充液管路在0—800 Hz内出现3个衰减带隙, 分别是40—65 Hz、180—340 Hz和485—735 Hz, 表明当管路充液时, 布拉格周期管路的弯曲振动带隙会向低频移动. 同时可以看出, 充液管路的第二带隙和第三带隙分别包含叶频与次倍频, 可以对离心泵引起的管路振动起到较好地抑制作用.
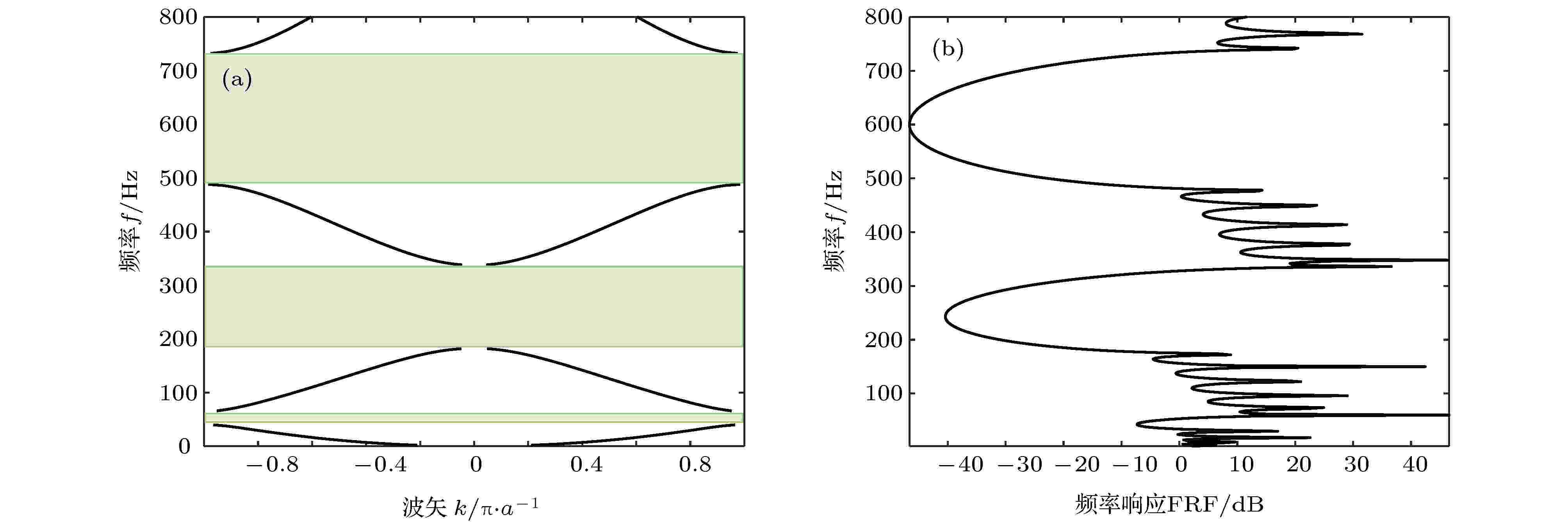图 3 充液布拉格声子晶体管路的带隙特性　(a)能带结构; (b)振动频率响应曲线
Figure3. Band gap characteristics of the liquid-filled Bragg phononic crystal pipeline: (a) Band structure; (b) Flexural vibration FRF.

2

-->

4.1.有限元模型及算法验证

未考虑流固耦合效应时, 基于ANSYS Workbench平台, 利用谐响应模块, 在激励端施加幅值为1的速度信号, 记为${v_{{\rm{in}}}}$, 在响应端拾取速度信号, 记为${v_{{\rm{out}}}}$, 则由公式${\rm{FRF}} = 20 \times \log \left( { {{{v_{{\rm{out}}}}}}/{{{v_{{\rm{in}}}}}}} \right)$计算频率响应, 得到5个周期的声子晶体管路振动频率响应曲线, 与传递矩阵法计算的振动传递响应相对比, 得到图4. 图4是5个周期未充液和充液布拉格管路的弯曲振动传递损失曲线, 其中蓝色虚线和黑色实线分别是有限元法和传递矩阵法的计算结果. 由图可知, 传递矩阵法和有限元法的计算结果比较吻合, 这有力地证明了传递矩阵法的准确性和有效性.
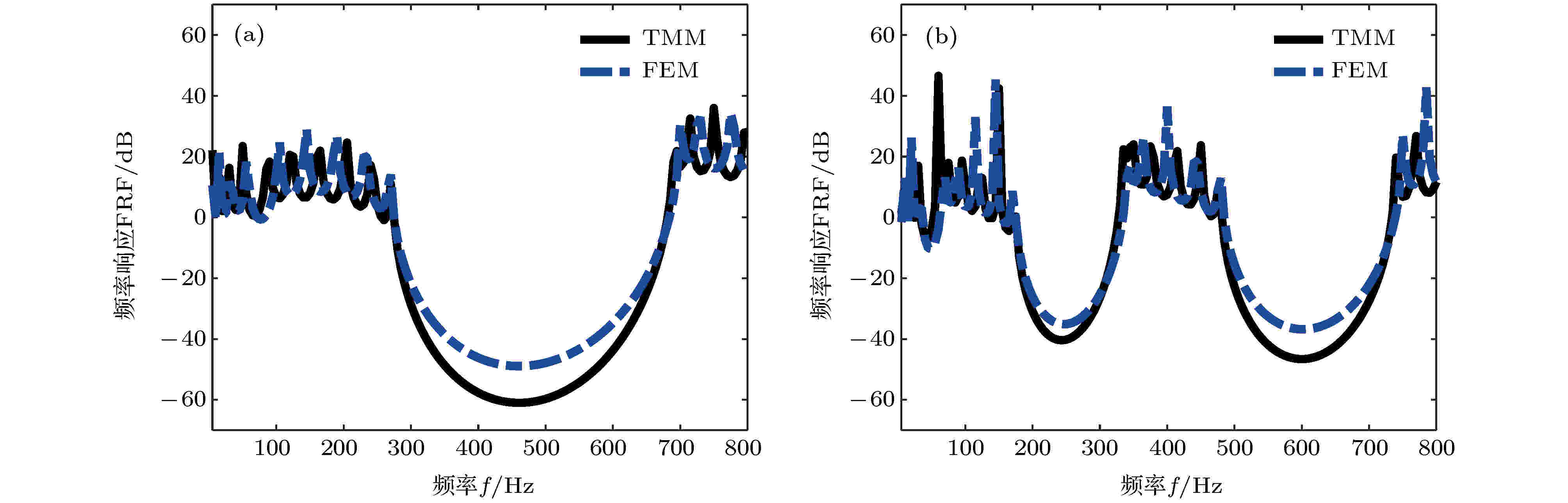图 4 未充液和充液布拉格声子晶体管路弯曲振动频率响应　(a)未充液管路; (b) 充液管路
Figure4. Frequency response of flexural vibration of liquid-unfilled and liquid-filled Bragg phononic crystal pipeline: (a) liquid-unfilled pipe; (b) liquid-filled pipe.

图5是不同频率处未充液和充液布拉格声子晶体管路的速度幅值图, 其中图5(a)表示未充液声子晶体管路在f为250, 500, 750, 1000 Hz处的位移幅值. 可以发现, f = 500 Hz和f = 1000 Hz处管路的弯曲振动在前两个周期已经得到很大的衰减, 后半段的管路几乎没有发生振动, 表明布拉格声子晶体管路对带隙内的振动可以较好地抑制, 且振动衰减效果明显. f = 250 Hz和f = 750 Hz都是带隙外的频率点, 两个频率处的位移幅值远大于带隙内的位移幅值, 且整个管路都处于振动状态, 此时, 弯曲振动可有效传递到管末端. 图5(b)表示充液声子晶体管路在f为125, 250, 400, 600 Hz处的位移幅值. 可以发现, f = 250 Hz和f = 600 Hz处管路的弯曲振动在前两个周期已经得到很大的衰减, 后半段的管路几乎没有发生振动, 表明充液布拉格声子晶体管路对带隙内的振动可以较好地抑制, 且振动衰减效果明显. f = 125 Hz和f = 400 Hz都是带隙外的频率点, 两个频率处的位移幅值远大于带隙内的位移幅值, 且整个管路都处于振动状态, 此时, 弯曲振动可有效传递到管末端. 与图4中声子晶体管路振动频率响应曲线中的带隙相对应.
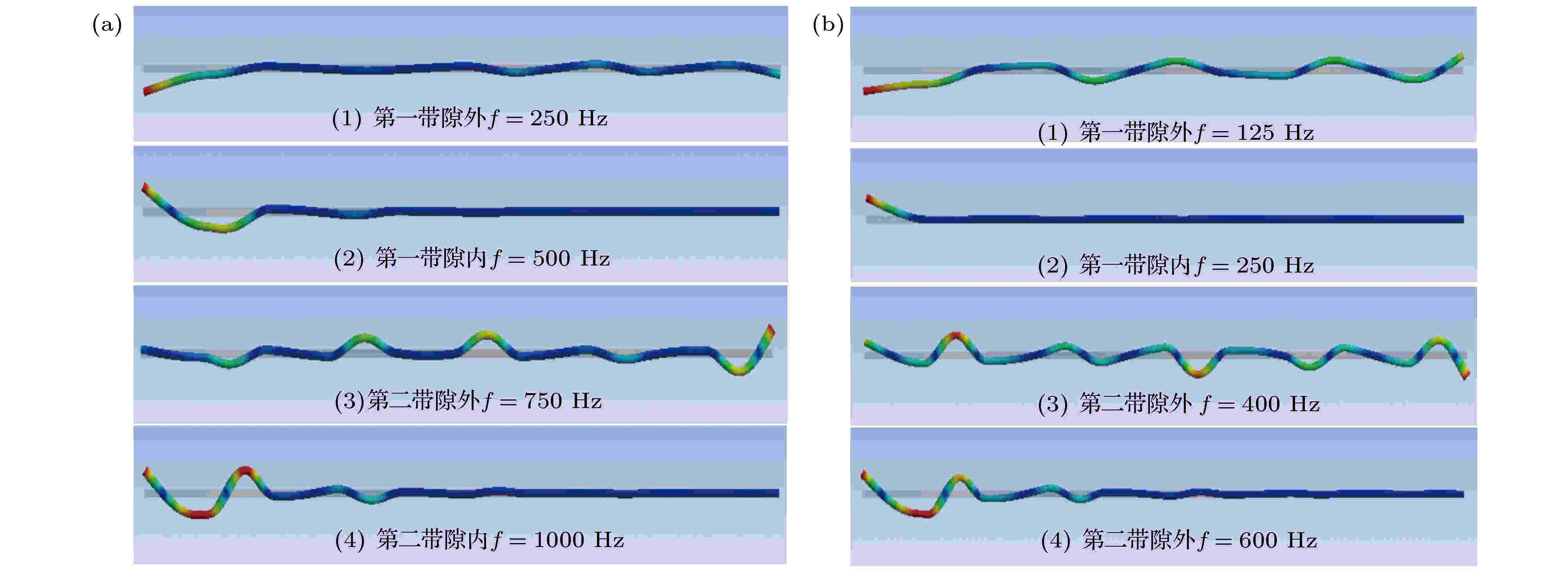图 5 未充液和充液声子晶体管路不同频率处的速度幅值　(a)未充液管路; (b) 充液管路
Figure5. Displacement amplitude of liquid-unfilled and liquid-filled phononic crystal pipeline at different frequencies: (a) liquid-unfilled pipe; (b) liquid-filled pipe.

进一步考虑流固耦合条件下声子晶体管路振动传递特性. 基于ANSYS Workbench平台对不同冲击激励下流固管路进行流固耦合分析, 建立了双向流固耦合分析基本流程如图6所示, 参照图1声子晶体管路参数建立5个周期的声子晶体管路模型如图7所示. 模型选为瞬态结构和流体力学模块. 管路长为2.5 m, 管路内径为0.02 m, 管壁厚度为0.001 m, 弹性管壁, 忽略管道阻尼影响. 流体部分选择水, 不可压缩流体, 其密度为1000 kg/m³, 温度设置为25 ℃, 动力黏性系数选择默认值0.001003 ${\rm{kg}}/({\rm{m}} \cdot {\rm{s}})$. 由于ANSYS Workbench计算双向流固耦合时, 流体通过流固耦合面对管路结构传递的只是湍流运动产生的流体雷诺应力、黏性应力和脉动切应力的流体作用力, 不包括流体质量, 故在仿真计算轻质流体时结果较为准确, 但当管内流体为重质流体时, 仿真结果会产生较大的误差, 故需要在管路上引入附加质量?m = ρπr_p². 本文的流体为水, 属于重质流体, 因此在管路建模时需要设置管路材料的当量密度${\rho _{\rm{e}}}$, 即
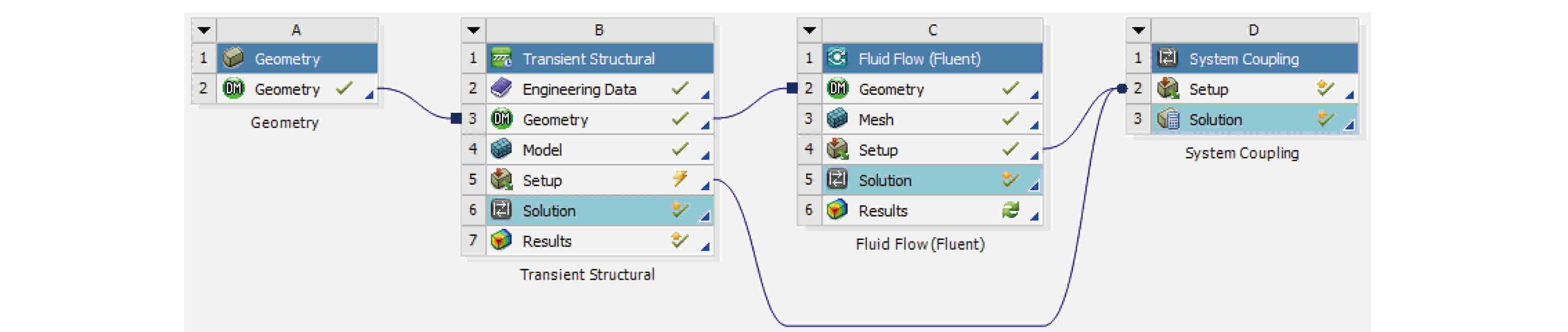图 6 ANSYS Workbench系统耦合配置方式
Figure6. Coupling configuration of ANSYS Workbench system.

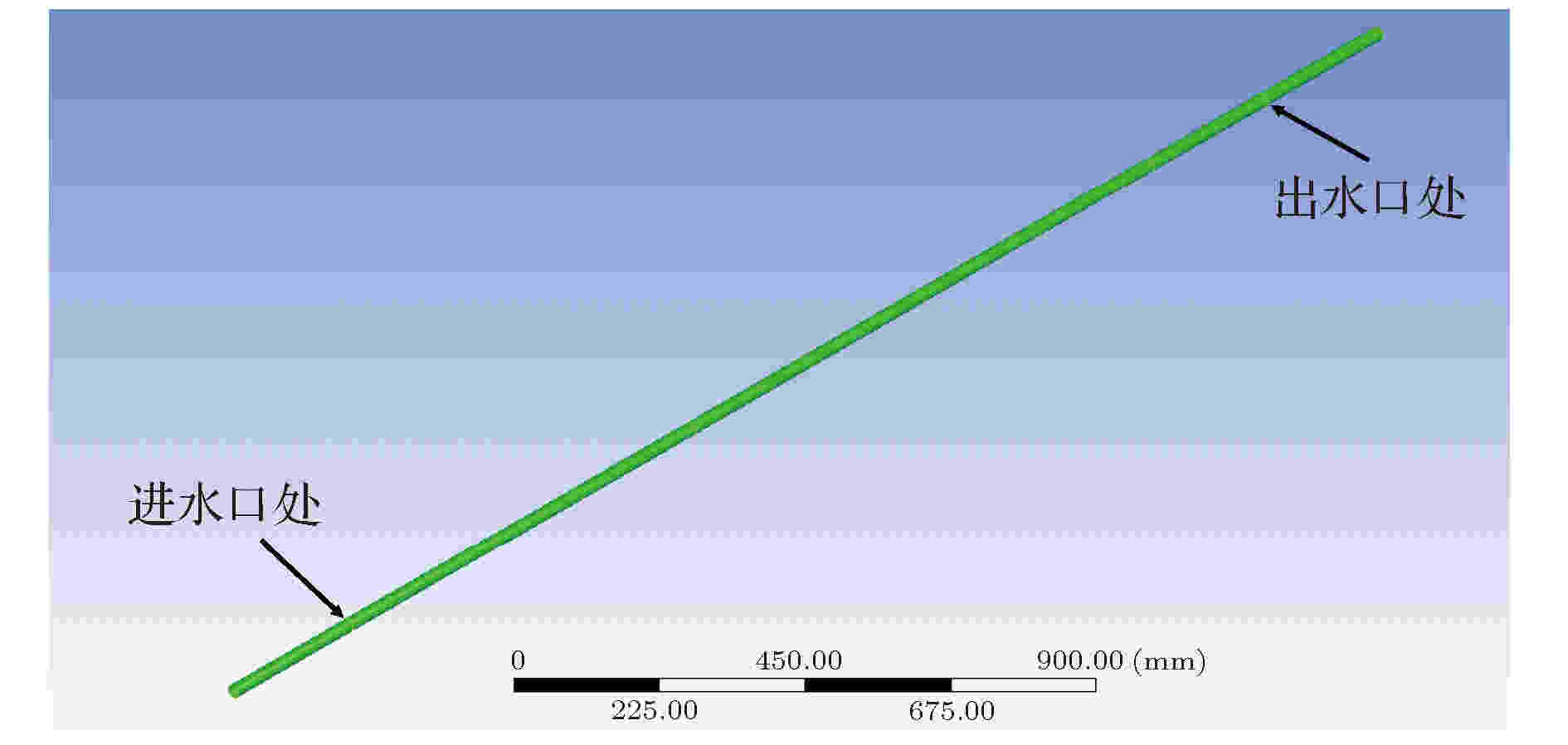图 7 ANSYS中建立流固耦合管路模型
Figure7. Establishment of fluid-structure interaction pipeline model in ANSYS.

${\rho _{\rm{e}}} = {\rho _0} + {\rho _{\rm{f}}}\dfrac{{r_{{\rm{in}}}^2}}{{r_{{\rm{out}}}^2 - r_{{\rm{in}}}^2}}, $

式中, ${\rho _0}$为管路材料密度, ${\rho _{\rm{f}}}$为流体密度, ${r_{{\rm{in}}}}$为管路内径, ${r_{{\rm{out}}}}$为管路外径. 管路材料选择表1中的结构钢和环氧树脂, 则仿真分析中设置的管路材料结构钢和环氧树脂的当量密度分别为12612 kg/m³和5941.9 kg/m³.
本例中主要设置流体和液体接触的管道内壁面为流固耦合面, 设置限制两端面X, Y和Z方向位移为支撑边界条件, 即为固定约束(固支结构). Fluent界面里设置不同的入口速度, 单位为${\rm{m}}/{\rm{s}}$, 出口压力设置为零; 系统耦合分析界面设置耦合时间为0.0512 s和耦合时间步0.0001 s, 选择双向耦合; 初始条件, 视为光滑管壁.
2 -->

4.2.管壁冲击激励条件下流固耦合声子晶体管路振动特性分析

假设距离管路左端进水口处受到冲击载荷, 冲击波的形式满足以下方程:

$\left\{ \begin{aligned}& F = {F_{\max }}{{\rm{e}}^{ \tfrac{{t - {t_0}}}{{{t_{\rm{d}}}}}}},\;\;\;\;t \geqslant {t_0},\\& F = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \leqslant {t_0},\end{aligned} \right.$

式中${F_{\max }}$ = 200 N, ${t_0}$ = 0.0005 s, ${t_{\rm{d}}}$ = 0.0001 s. 冲击时间为0.0005 s, 在管路进出水口处拾取响应信号. 分别仿真计算未充液和充液管路的弯曲振动响应, 充液管路仿真分析时采用流固耦合仿真分析, 设置流速为0.
管壁冲击激励的脉冲响应如图8(a), 利用快速傅里叶变换得到其频域分布如图8(b), 可以看出, 由于管壁冲击激励的作用, 模型中产生的应力波具有0—5000 Hz的宽频带.
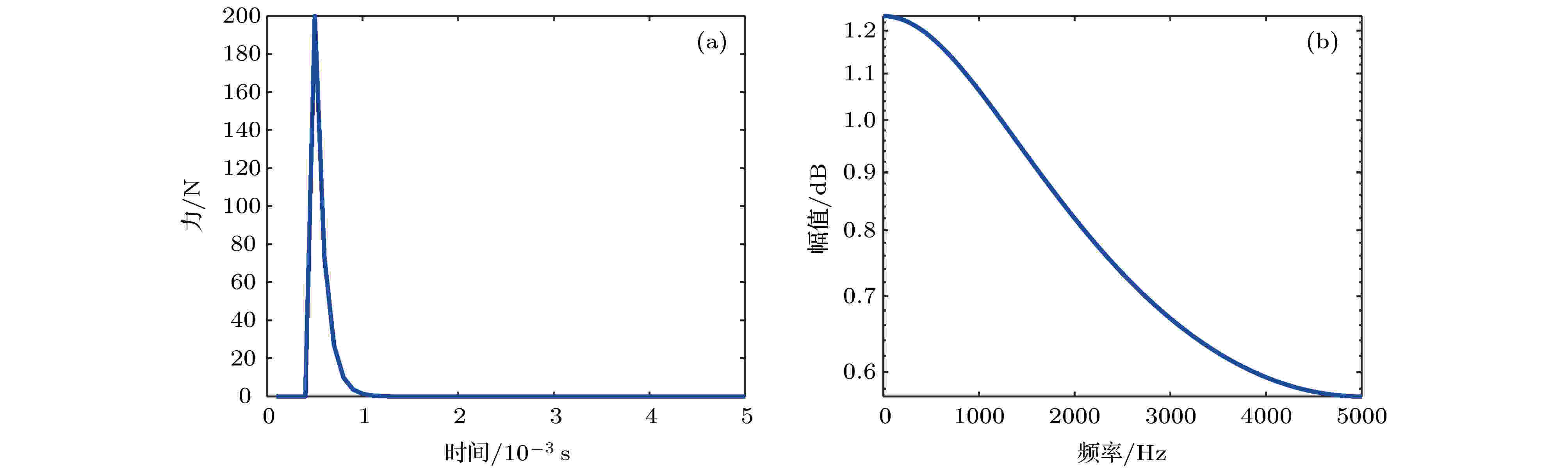图 8 管壁冲击脉冲响应及通过快速傅里叶变换得到的冲击模拟频域　(a) 管壁冲击时域; (b) 管壁冲击频域
Figure8. Pipe wall shock impulse response and shock simulation frequency domain obtained by fast Fourier transform: (a) Time domain of wall impact; (b) Frequency domain of wall impact.

图9是5个周期声子晶体管路未充液和充液时的冲击振动特性. 其中蓝色实线和青色虚线分别表示进水口处速度信号时域以及通过快速傅里叶变换得到的频域分布和出水口处速度信号时域及快速傅里叶变换得到的频域分布. 频域图中阴影部分表示出口处的速度峰值较入口处的速度峰值小, 表明在该频率范围内声子晶体管路具有较好的衰减效果. 对比图9(a)和图9 (b), 可以发现当管路充液时, 管路振动幅值无论在时域还是频域上都有所衰减, 表明当管路充液时, 由于流体质量的影响, 外部冲击引起的管路振动减弱. 综合分析, 未充液声子晶体管路在270—625 Hz内具有较好的衰减作用, 充液声子晶体管路在175—332 Hz和488—725 Hz内具有较好的衰减作用, 与第3节传递矩阵计算的未充液管路带隙280—690 Hz以及充液管路带隙180—340 Hz和485—735 Hz相吻合, 表明未充液和充液布拉格声子晶体管路对管路外部冲击具有较好的抑制作用.
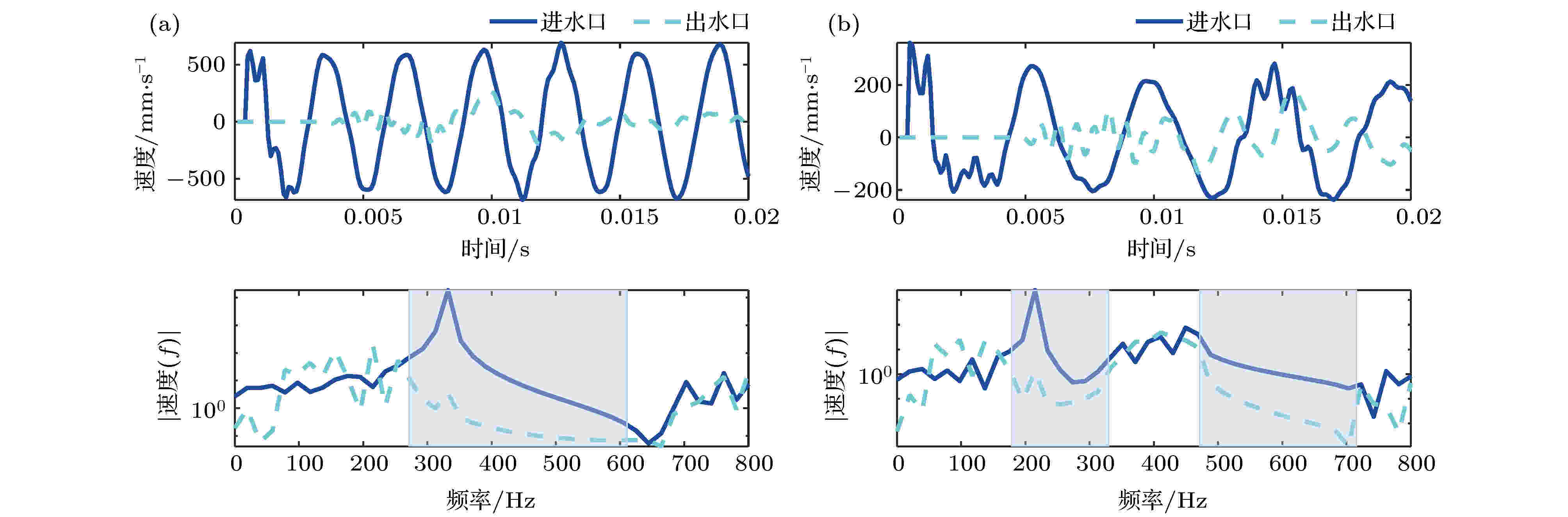图 9 未充液与充液声子晶体管路冲击振动响应　(a)未充液管路; (b) 充液管路
Figure9. Shock vibration response of liquid-unfilled and liquid-filled phononic crystal pipeline: (a) liquid-unfilled pipe; (b) liquid-filled pipe.

图10表示未充液和充液声子晶体管路不同时刻的速度幅值图, 图10(a)表示未充液声子晶体管路在t为0.001, 0.0025, 0.005, 0.01 s处的速度幅值, 图10(b)表示充液声子晶体管路在t为0.001, 0.0025, 0.005, 0.01 s处的速度幅值. 可以发现, 无论声子晶体管路是否充液, 其出口处的振动较入口处滞后, 且振动幅度较小, 这是由于管路入口处的冲击响应沿着管壁传播需要一定时间. 约在0.01 s, 出口处振动幅度达到最大, 与图9中时域图中出口处的振动响应曲线相一致.
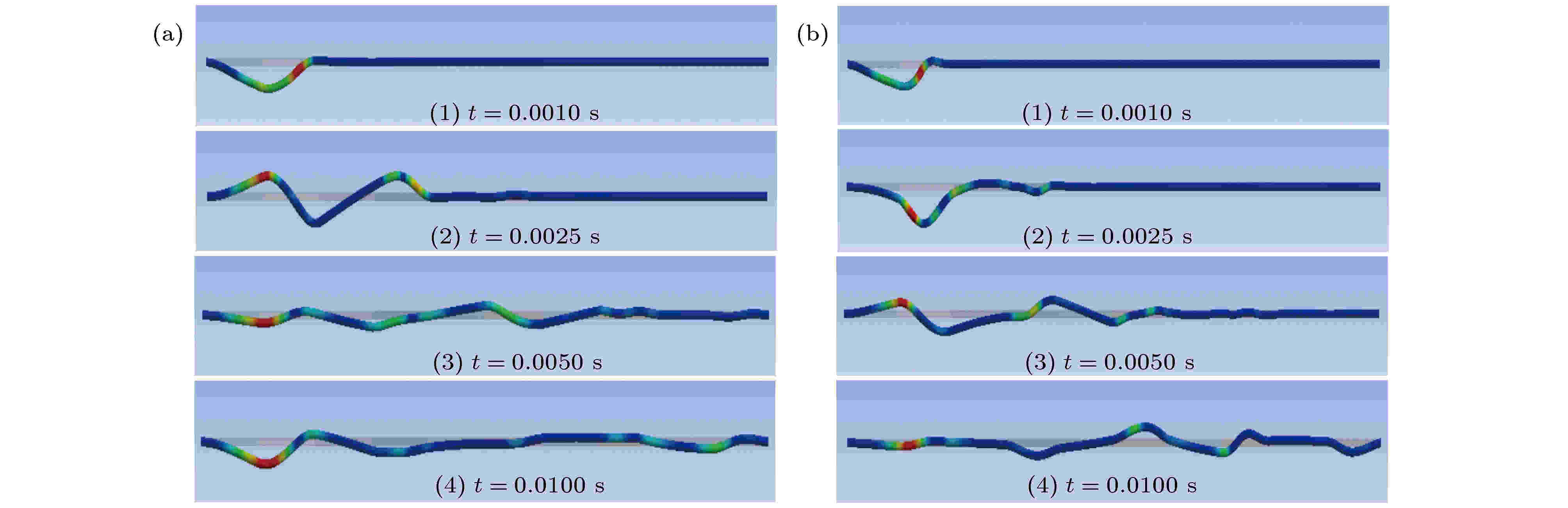图 10 未充液和充液声子晶体管路不同时刻的速度幅值　(a)未充液管路; (b) 充液管路
Figure10. Velocity amplitude of liquid-unfilled and liquid-filled phononic crystal pipeline at different moments: (a) liquid-unfilled pipe; (b) liquid-filled pipe.

接下来考虑流速对管壁冲击响应的影响, 设置流速分别为0, 10 m/s. 仿真分析得到流固耦合声子晶体管路在不同流速下的冲击振动响应.
图11表示流固耦合声子晶体管路在流速为0和10 m/s下的冲击振动响应, 图12表示流固耦合声子晶体管路在流速为0和10 m/s下的出口处的振动响应, 由图可知, 当流速较小时, 流速改变, 布拉格周期管路的衰减频率范围基本不变. 虽然随着流速的增大, 管路的衰减效果减弱, 但影响不大, 这是由于管路在外部冲击作用下, 管路的振动主要由外部冲击引起, 管路内流对管路振动作用较小, 但由于流固耦合效应, 流体运动产生的管壁作用力分布在管路内部流固耦合面上且前端由流体引起的管壁振动会向管路末端传递, 导致管路出口段的振动响应增大, 从而衰减强度降低.
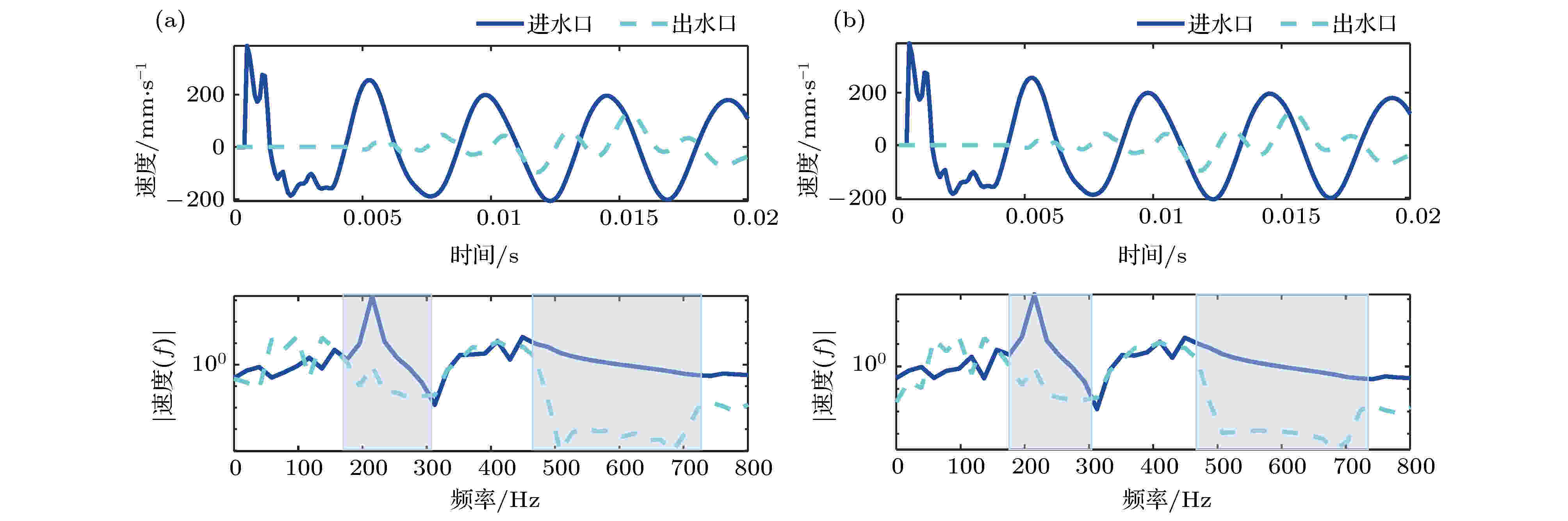图 11 流固耦合声子晶体管路在不同流速下的冲击振动响应　(a)流速为0 m/s; (b) 流速为10 m/s
Figure11. Shock vibration response of fluid-structure interaction phononic crystal pipeline at different velocities of fluid: (a) Flow velocity is 0 m/s; (b) Flow velocity is 10 m/s.

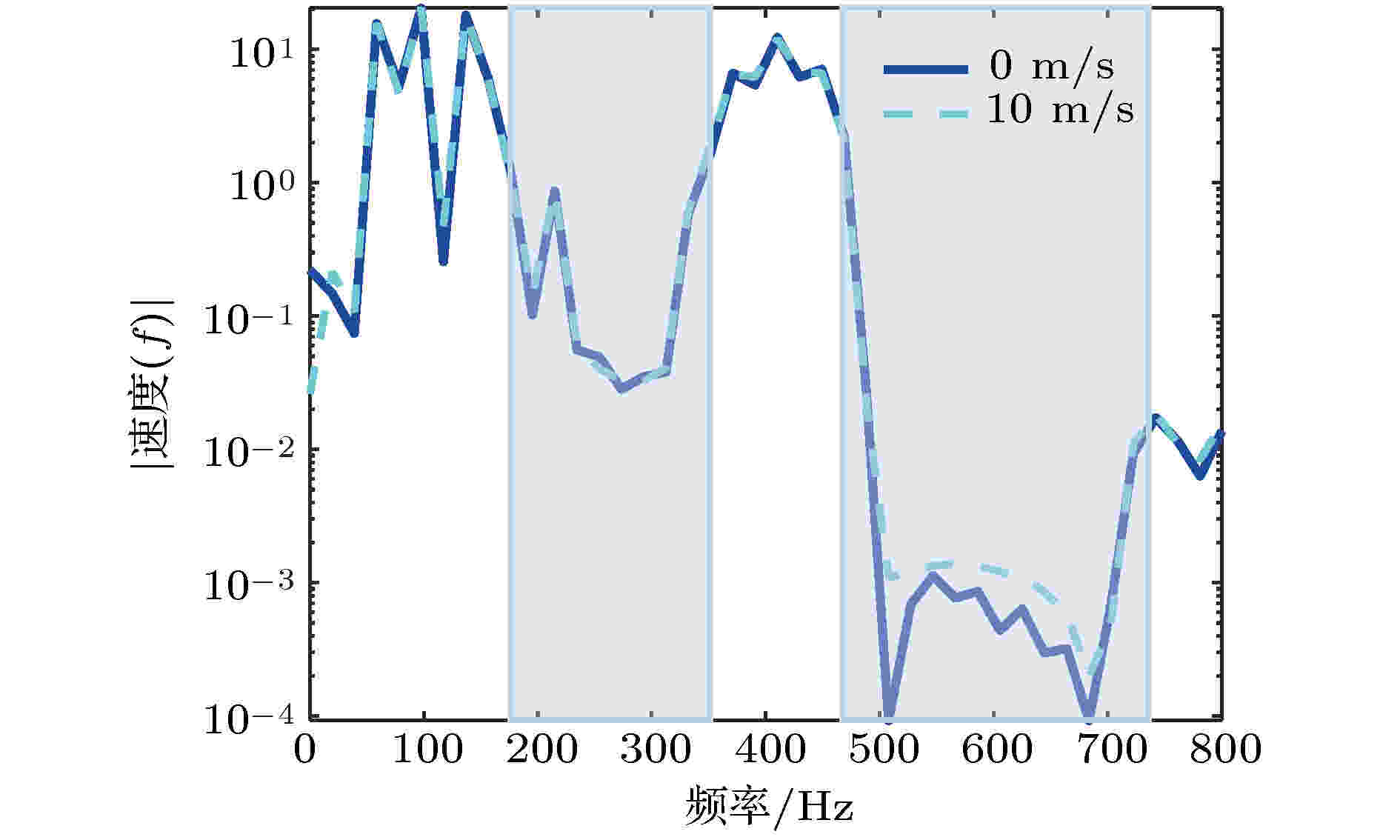图 12 流固耦合声子晶体管路出口处不同流速冲击振动响应
Figure12. Shock vibration response of the outlet of fluid-structure interaction phononic crystal pipeline at different velocities of fluid.

2 -->

4.3.流体冲击激励条件下流固耦合声子晶体管路振动特性分析

假设输流管路内流体流速初始状态为零, 当开泵或者开阀速度较快时, 流体流量发生急剧变化, 从而使流体流速发生剧烈变化, 假设流体流速发生变化时满足以下方程:

$\left\{ \begin{aligned}& V = {V_{\max }}{{\rm{e}}^{ - \tfrac{{t - {t_0}}}{{{t_{\rm{d}}}}}}},\;\;\;t \geqslant {t_0}\\&V = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; t \leqslant {t_0},\end{aligned} \right.$

式中, ${V_{\max }}$ = 50 m/s, ${t_0}$ = 0.0005 s, ${t_{\rm{d}}}$ = 0.0001 s. 冲击时间为0.0005 s, 在管路进出水口处拾取响应信号.
分别考虑单一材料管路(结构钢管)和布拉格周期管路, 以管路出口处和入口处某一截面的弯曲振动为研究对象, 仿真分析得到管路入口和出口处的速度时间曲线和速度频率曲线.
图13是冲击流体激励下结构钢管和声子晶体管弯曲振动响应, 可以发现, 无论是单一材料管路还是声子晶体管路, 在时域上, 其振动响应发生突变出现在流体流速急剧变化时, 随着流速的衰减, 管壁振动响应减小, 出口处管壁振动有所延迟, 且声子晶体管路的振动传递到出口处的时间较单一材料管路长, 表明声子晶体管对振动具有一定的抑制作用. 进水口处的振动响应较入水口处的响应略大, 这是由于冲击流体激励到达出口附近需要一定的时间, 流体流动过程中与管壁发生耦合作用, 能量有所耗散, 到达出口处流速略有降低, 因此振动响应略小. 在频域上, 单一材料管路的进水口和出水口处管壁的响应基本吻合, 但在170—210 Hz范围内存在一定衰减, 而声子晶体管路在415—510 Hz和575—625 Hz范围内都存在衰减, 其衰减频段与第3节中带隙相接近但不完全重合, 表明冲击流体激励时, 由于管路流固耦合效应的存在, 流体通过流固耦合面对管壁的作用力分布在整个管路内部, 因此在出水口处不仅存在流体在出水口处引起的管路振动, 还存在前端由流体引起的管路振动向管路末端传递. 进一步对比图14中冲击流体激励下结构钢管与声子晶体管在进水口和出水口处振动响应, 可以发现, 进水口处, 单一材料管路在时域和频域上的振动较声子晶体管路略大, 在声子晶体管路进水口处, 由于管路材料环氧树脂材料较软, 流体冲击引起的管路振动较单一结构钢管路略大; 出水口处, 在时域上, 声子晶体管路出现峰值时间较单一材料管路滞后, 且峰值略小, 表明声子晶体管路可以有效抑制流体冲击引起的管路振动. 在频域上, 声子晶体管路与单一材料管路振动幅值相当, 在415—505 Hz和585—625 Hz范围内, 声子晶体管路振动幅值较小, 表明衰减程度明显. 进一步对比进水口处单一材料管路与声子晶体管路的振动响应, 可以发现声子晶体管路对流体冲击引起的管路振动具有一定的抑制作用. 综上所述, 声子晶体管路可以在一定程度上抑制流体冲击激励引起的管路振动, 特别在带隙附近的振动衰减效果更好.
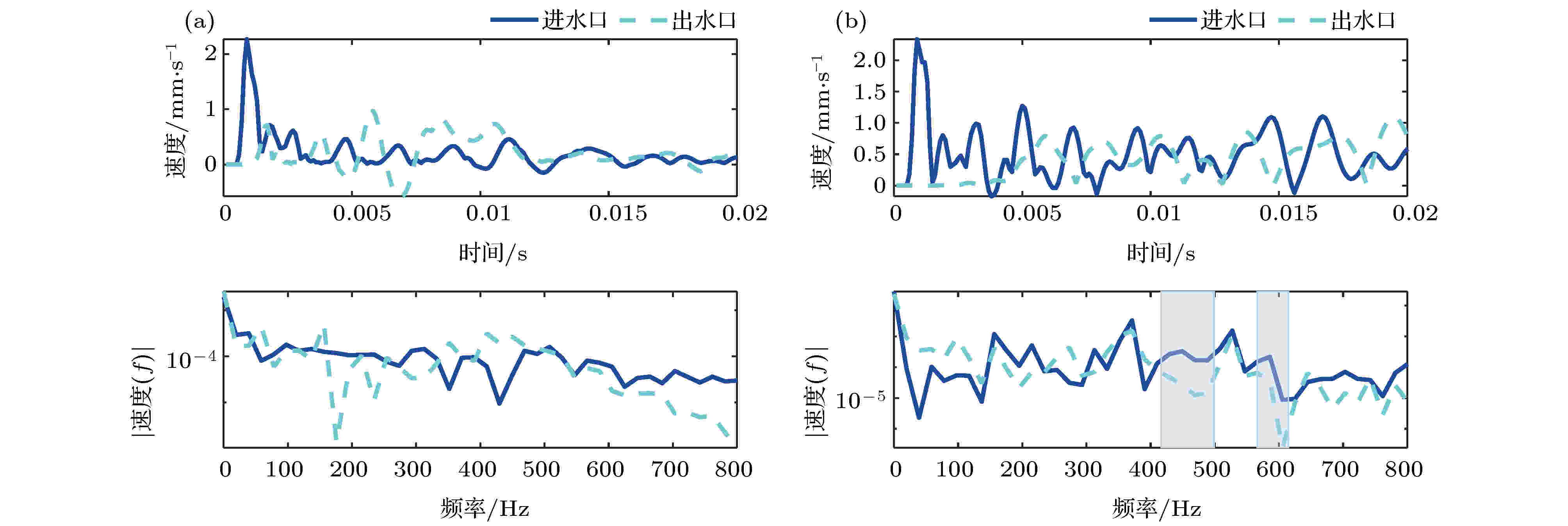图 13 冲击流体激励下　(a)结构钢管和(b)声子晶体管弯曲振动响应
Figure13. Flexural vibration response of (a) structural steel pipe and (b) phononic crystal pipe under shock fluid excitation.

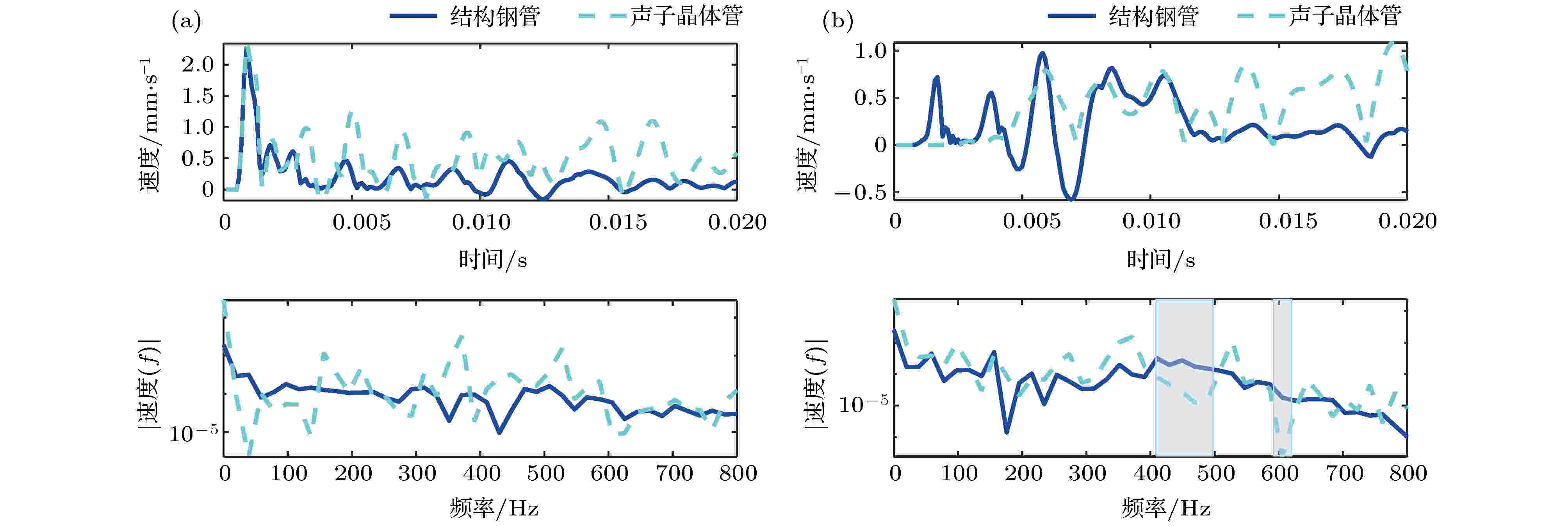图 14 冲击流体激励下结构钢管与声子晶体管　(a) 进水口和 (b) 出水口处振动响应
Figure14. Vibration response at (a) inlet and (b) outlet of structural steel pipe and phononic crystal pipe under shock fluid excitation.

本文对冲击条件下的流固耦合声子晶体管路振动特性进行了分析. 通过本文的研究, 得出以下几点结论:
1)基于传递矩阵法和有限元法, 建立了流固耦合声子晶体管路系统带隙特性数学模型, 为流固耦合声子晶体管路冲击响应分析提供了有效工具.
2)当流固耦合管路系统中流速较小时, 声子晶体带隙频率范围内的管壁冲击激励响应具有显著的抑制作用, 但当流速增大时, 流固耦合效应增大, 振动抑制作用会减弱.
3)流体冲击激励下, 声子晶体管路对流体冲击引起的振动同样具有较好的抑制作用, 表明考虑流固耦合效应时, 声子晶体管路在带隙频率范围内对管路振动具有较好的抑制作用.